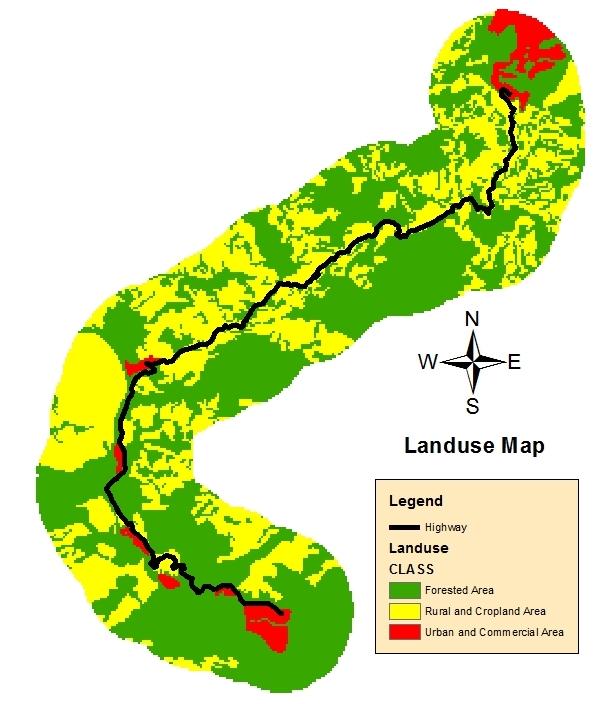
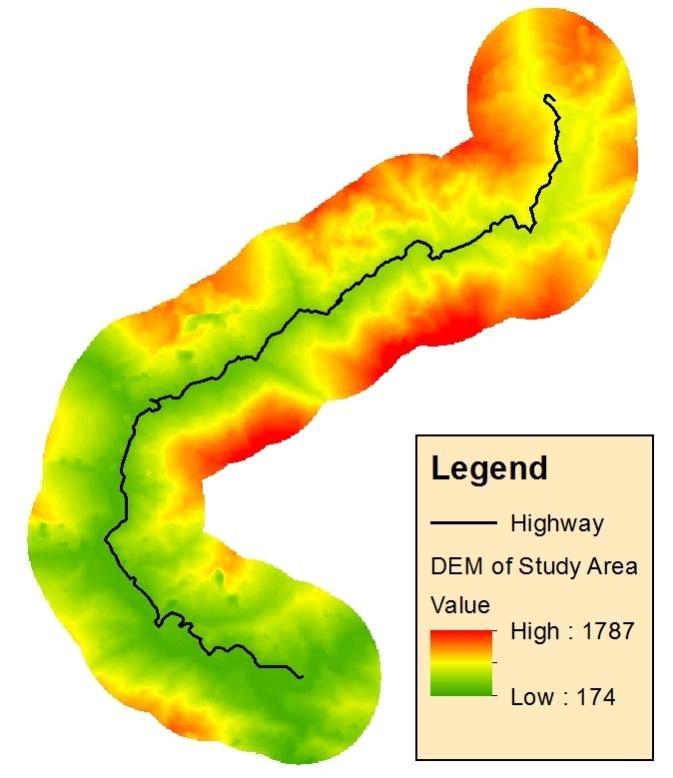
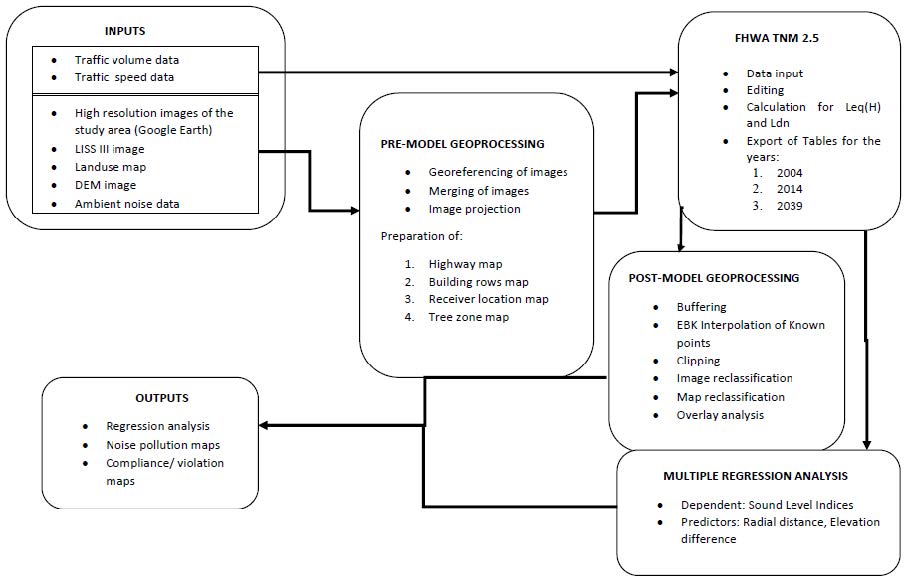
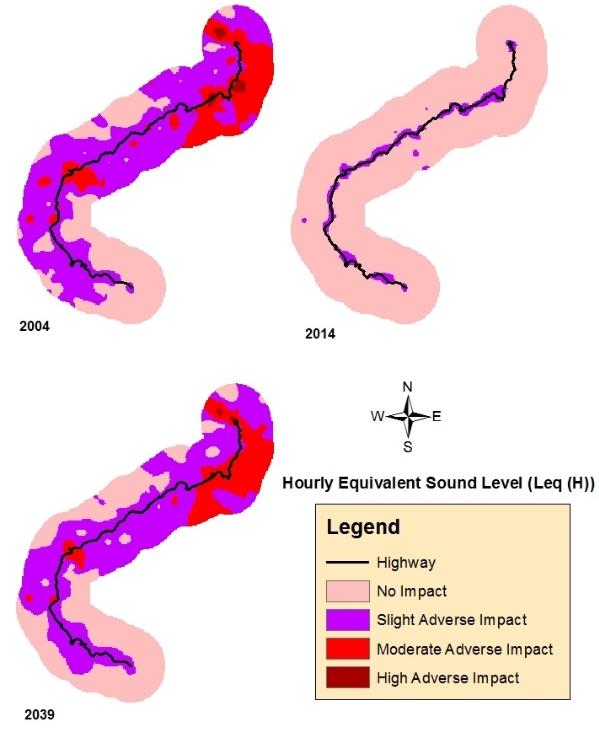
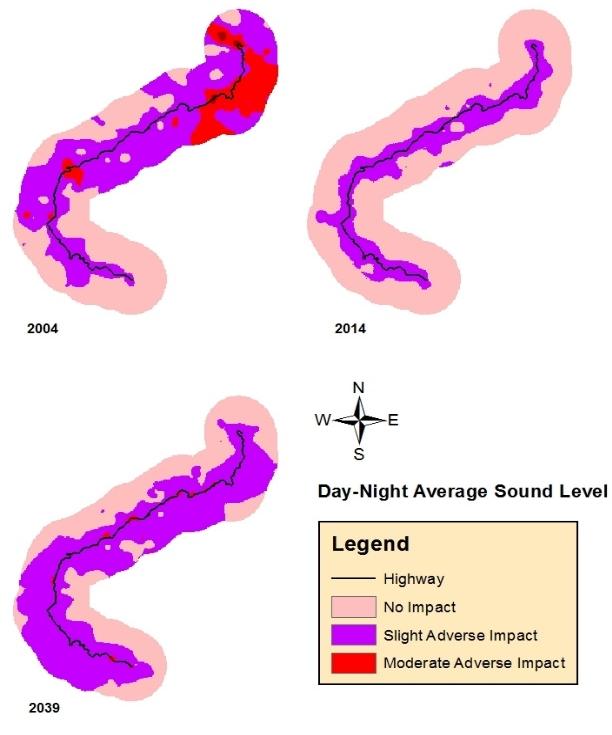
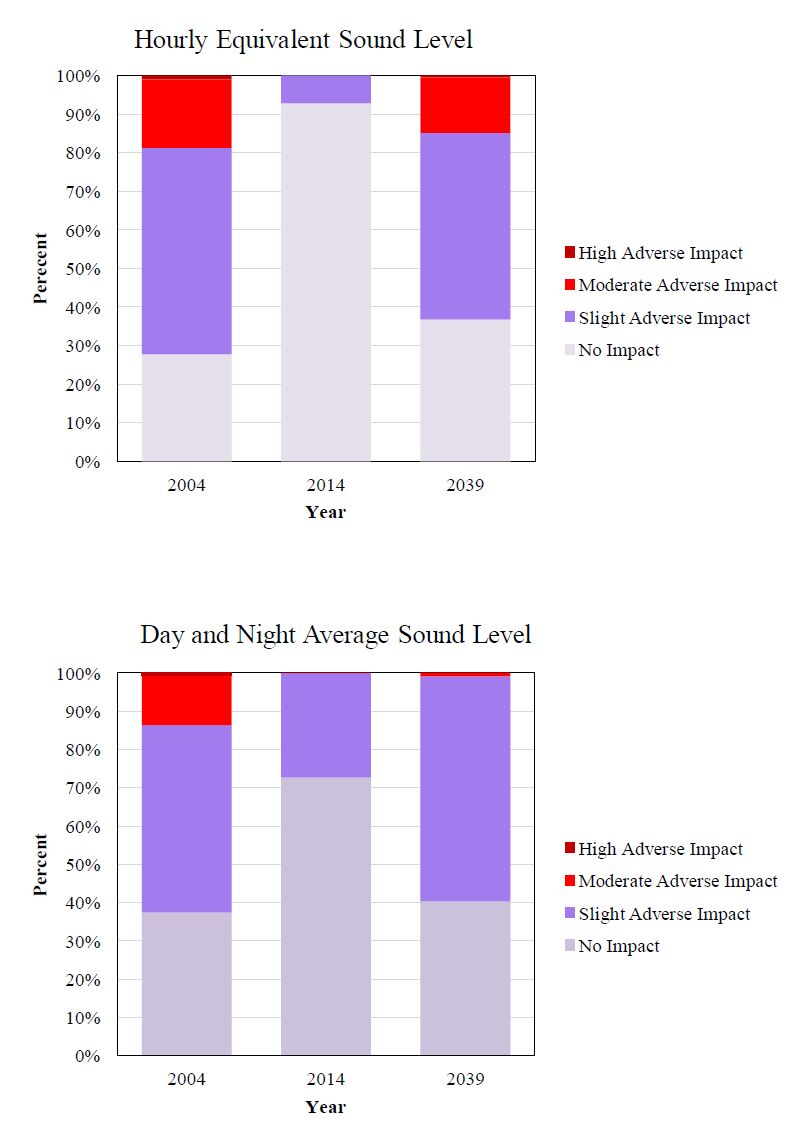
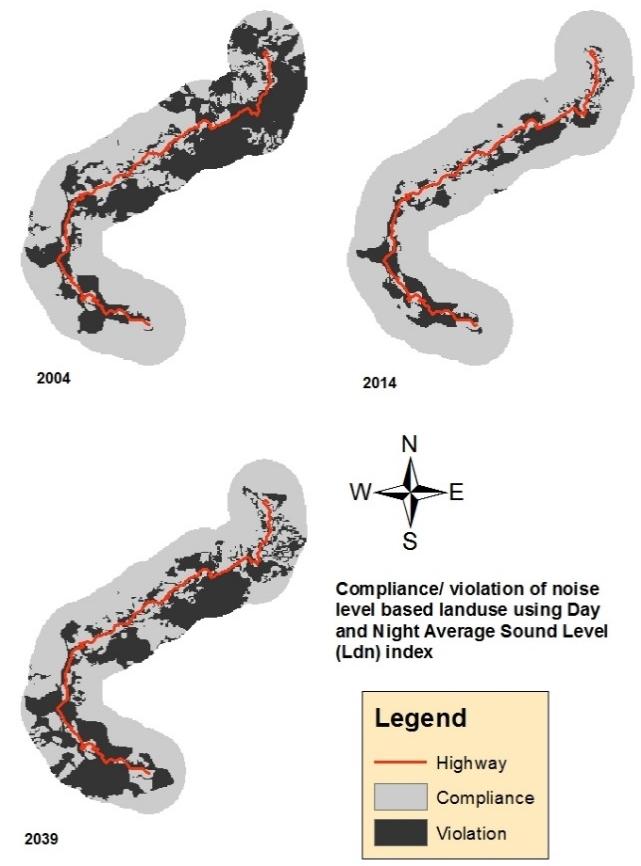
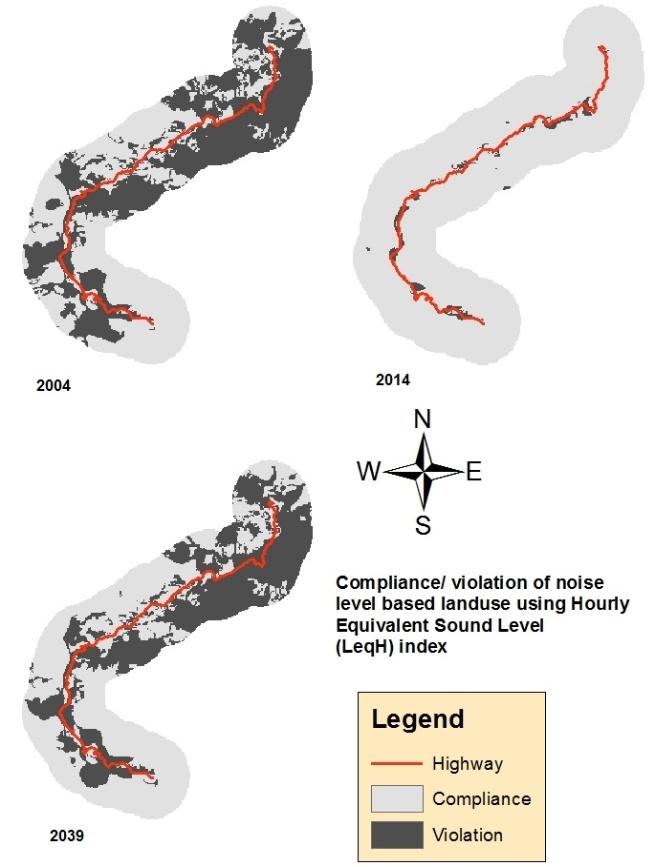
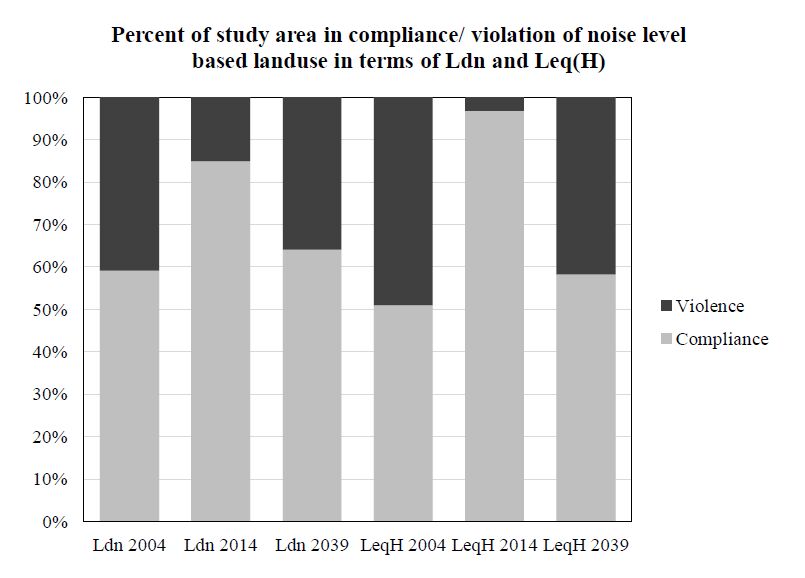
Mountainous areas create a complex and challenging environment to conduct noise impact analysis of development projects. This paper presents a noise impact analysis methodology using Geographic Information Systems (GIS) and Traffic Noise Model (FHWA TNM 2.5) to portray spatial distribution of noise due to the broadening of the national highway in the mountainous terrain of East Sikkim. Two noise level indices viz., Hourly Equivalent Sound Level (Leq(H)) and Day and Night Average Sound Level (Ldn) were calculated for the year 2004 as pre-project scenario, 2014 as project implementation scenario and 2039 as post-project scenario. The overall trend shows that the proportion of area under adverse noise level decreases from pre-project scenario to project implementation scenario. Over the time the adverse noise impact in the post-project scenario reaches very close to pre-project scenario in case of both the noise indices. Overlay analysis of noise based landuse maps over actual landuse map show that non-compliance of noise based landuse will show similar trend. This trend is mainly attributed to traffic composition and highway broadening induced-traffic volume. The study shows that TNM and spatial interpolation of noise data using Empirical Bayesian Kriging (EBK) are reliable tools to perform noise impact analysis in mountainous areas. Multiple regression analysis show that, radial distance and elevation difference of noise receivers from the nearest point in the highway are significant predictors of Leq(H) and Ldn at lower percentage of heavy trucks in traffic composition.
1.
Introduction
The synchronization of complex networks has been one of the most critical issues in recent years [1]. Complex networks, composed of interacting dynamical systems, can be used to represent and analyze real networks [2,3]. The synchronization phenomenon is termed when two or more dynamical systems evolve in common behavior [4]. Numerous natural events can be related to synchronization [1]. Therefore, many studies have focused on the synchronization of coupled oscillators in different fields [5,6]. The synchronizability of a network is strongly associated with the network topology and the coupling between the nodes [4,7]. There are some studies that have considered the synchronization in time-varying networks [8,9]. Belykh et al. [10] showed that adding a few random connections to a network with blinking links enhances synchrony by reducing the required couplings strength for synchronization. Frasca et al. [11] investigated the synchronization of Rossler systems with switching coupling and found that switching between two coupling strengths that cannot separately synchronize the system can lead to synchronization.
In the nervous system, the communications and interactions among neurons create complex networks [12,13]. Therefore, many of their activities lead to the formation and representation of collective behaviors such as synchronization [14]. Previous studies have revealed the significance of the synchronous behavior of neurons in information processing and cognitive tasks [15]. Subsequently, the study of synchronization in neuronal networks has attracted the attention of many scientists [16,17,18]. Belykh et al. [19] investigated the bursting neurons coupled nonlinearly through chemical synapses and found that synchronization depends on the receiving signals by each neuron. In contrast, synchronization of the electrically coupled neurons relies on the network's topology [20]. Previous studies have considered different network topologies such as small-world, scale-free, modular, hierarchical, etc. [21,22,23]. Furthermore, with the development of the multilayer networks that provide multiple interactions, the synchronization of the neurons was also investigated in this type of topology [8,9]. Some of the studies have considered the factors that can enhance the synchronization in neuronal networks. It has been proved that the time delay [24], the activity-dependent coupling [25], considering the neuron–astrocyte interaction [26], proper adjustment of autapse [27], etc., can help enhance the synchronous behavior among neurons.
The neuronal functions rely on the communications between them [28,29]. These communications which occur in the cellular regions are called synapses. It is known that the transmissions among neurons can be through electrical or chemical synapses. The electrical synapses occur through channels (gap junctions) when the cytoplasms of two neurons are connected [30]. While in the chemical synapses, the neurotransmitters are released from one cell and received by another [31]. These two types of transmissions exist in different brain regions and are essential for their normal function. Furthermore, Pereda [28] highlighted that the interaction between these two synapses in the healthy brain is also crucial. There is evidence that the electrical synapse transits to chemical synapses in particular brain regions [32,33,34]. In other words, the formation and elimination of electrical and chemical synapses are sequential [35,36]. Szabo et al. [37] represented this serial synaptic evolution in motoneurons from the snail Helisoma. Furthermore, there is a hypothesis that the former electrical synapses are necessary for developing the chemical synapses. Todd et al. [38] represented this fact in the leech neurons.
Motivated by the above description about the transition of synapses, this paper studies the network of coupled Hindmarsh-Rose neurons coupled with transient synapses. It is assumed that the electrical synapses are initially present, and they are replaced with chemical synapses over time. This sequence of transformations happens with a specific period. The synchronization of the neurons is studied under different conditions by varying the coupling strengths, the period of transitions, and the duration time of the presence of the synapses. The time series of the neurons is also under consideration. Therefore, in the next section, the model, the network, and the coupling are described. The results are presented in the third section, and the conclusions are given in the last section.
2.
Model
A network of Hindmarsh-Rose neurons with electrical and chemical synapses in a small-world structure is constructed as follows:
where x,y,z represent the action potential, the fast and slow recovery variables of the neuron. The parameters of the chemical coupling are vs=2, ϵs=−0.25,λ=10. gij refers to the network structure such that gij=1 shows the presence of a link between nodes i and j. The coupling strength of the electrical and chemical synapses are ge and gc, respectively. N=100 nodes are connected in a small-world configuration with 20 nearest-neighbor couplings and the probability of 0.1. The parameters of the Hindmarsh-Rose model are set at r=0.006, s=4, Iext=2.8, such that the single neuron exhibits periodic bursting. The coupling between neutrons is through periodic time-varying coupling with electrical and chemical synapses. As discussed before, the synapses are transient and change in the time interval τ. In a part of this time interval (0<t<θτ), the electrical synapses are on, and in the next part (θτ<t<τ), the electrical synapses disappear, and the chemical synapses appear. Therefore, we have:
3.
Results
The equations of the network are solved numerically by using the fourth-order Runge-Kutta method with a total run time 3000 and time step 0.01. The network is investigated by considering different periods (τ) for the coupling function. The time of presence of the electrical synapses to chemical ones (θ) is also varied. To quantify the synchronization of the neurons, the average synchronization error is computed as follow:
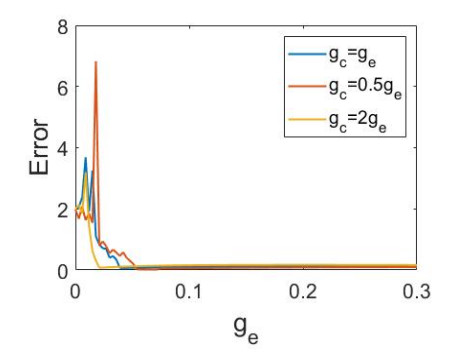
At first, we consider that both synapses exist among neurons constantly. The electrical coupling strength is varied, and the synchronization error is computed. Three cases are assumed for the chemical coupling strength as: 1) gc=0.5ge, 2) gc=ge, 3) gc=2ge. The synchronization errors for three cases are illustrated in Figure 1. When the chemical coupling is smaller than the electrical, gc=0.5ge, the neurons become completely synchronous in the region 0.054<ge<0.072. The time series of the synchronous neurons is shown in Figure 2a. As the electrical coupling grows from 0.072, the complete synchronization disappears, and the neurons become burst synchronous. The time series of neurons, in this case, are shown in Figure 2b and represent that although the neurons burst synchronously, there is a small error due to the difference between neurons when they are repolarized. By strengthening the chemical coupling, the synchronization error decays to zero for smaller electrical coupling strength. But the neurons do not oscillate synchronously and reach the resting state. The time series of the neurons in ge=0.2, and for gc=ge, gc=2ge are illustrated in Figure2c and 2d, respectively.
When the neurons are completely synchronous, all of the variables of the neurons are the same, i.e., x1=x2=⋯=xN, y1=y2=⋯=yN, z1=z2=⋯=zN Therefore, the equation of the synchronous manifold can be derived as
When the chemical coupling strength increases, the coupling term gc(vs−xi)1+expexp(−λ(xi−ϵs))∑Nj=1gij intensifies and overcomes the dynamics of the neurons and leads the neurons to be quiescent.
Next, we investigate the case of transient synapses. A specific period (τ) is considered, and in a part of the period, the electrical synapses are on (gc=0), and in the next part, the synapses are replaced with the chemical ones (ge=0). Firstly, it is assumed that the duration of both synapses is the same, i.e., θ=0.5, and the effect of the transition period is studied. As mentioned in the previous section, with the parameters selected for the Hindmarsh-Rose model, the single neuron bursts periodically, and the period of bursts is T=132. Thus, the synaptic transition period is considered to be the coefficients of the bursts periods as τ=33,66,132,264,396, and 528. The synchronization errors for different periods are presented in Figure 3. Similar to the previous case, as the chemical coupling strength increases, the error reaches its minimum in more miniature electrical couplings. This can be inferred from comparing the error curves in parts a to c. Furthermore, in all cases, the errors do not reach zero, and there is a minimum error which shows that the neurons are burst synchronized. This minimum error becomes larger by increasing the period of synaptic transitions. Moreover, it leads to a change in the waveform of the oscillations and the frequency of the bursts.
The time series of all neurons for different periods are shown in Figure 4. Although the parameters of the neurons were set in such a way to show square-wave bursting, adding the time-varying coupling term alters the neurons' firing pattern. It can be observed that for lower period values, i.e., for τ=33 (Figure 4a) and τ=66 (Figure 4b), the pattern consists of a single spike followed by a relaxation oscillation with short duration, which can be called pseudo-plateau burst. By increasing the period, the pattern changes to relaxation oscillation (for τ=132,264 in Figure 4c, 4d). Raising the period to τ=396 leads to the pattern to be constructed by multiple rapid spikes and a depolarized silence that is known as circle/fold cycle bursters or depolarization block bursting (Figure 4e) [39]. For τ=528, it seems that each burst is composed of both plateau burst type and pseudo-plateau burst type (Figure4f). As mentioned, the neurons are not fully synchronized, and there is a small error that refers to the depolarized silence duration. Figure 4g shows the enlargement of one burst of neurons relating to part e. The difference between neurons in the depolarized silence duration is obvious in this figure.
With the increase in the period of synaptic transitions, the bursts become longer, and the frequency of the bursts decreases. Comparing the period of bursts with the transition period shows that for longer periods, i.e., τ=264,396,528, the period of the bursts is equal to the transition period (τ). For shorter periods as τ=66,132, the period of the bursts is twice the transition period (2τ). For shorter periods, there is no relation between these periods. Furthermore, the spikes refer to the presence of the electrical synapses, while the silence mode refers to the time of the chemical synapses. Figure 5 represents this issue for τ=66,396. In these figures, the parts of the time series related to the presence of the electrical and chemical synapses are shown by red and blue colors, respectively.
Finally, the influence of the time of existence of the electrical and chemical synapses is studied. To this aim, the parameter θ is varied. For example, considering θ=0.1 means that in 0.1τ, the electrical synapses are on, and in the rest of 0.9τ, the chemical synapses are present. Figure 6 represents the synchronization error for τ=132 and θ=0.1,0.3,0.5,0.7, and 0.9 for three cases of chemical coupling strength. It can be observed that similar to the previous cases, the increase of the chemical coupling leads to decay of error in lower electrical strengths. However, the critical electrical coupling for synchronization doesn't depend on the value of chemical strength for θ=0.9, in which the chemical synapses exist in a short interval (0.1τ). Furthermore, as the time of electrical synapses to chemical synapses increases, the final synchronization error decreases. For θ<0.9, by increasing ge, there is a minimum error, and the neurons become burst synchronous. While for θ=0.9, the zero error is obtained, and complete synchronization can be attained. The time series of the neurons for different θ are shown in Figure 7. It can be observed that the time of the presence of synapses also impacts the waveform of the action potential.
Figure 8 presents a complete view of the synchrony error of neurons in the parameter planes by varying the transition period and the timing of synapses for gc=ge. The effects of changing the transitions period (τ) are demonstrated in part (a) for θ=0.5. It is observed that increasing τ leads to burst synchronization occurring in a slightly lower coupling strength ge. However, for higher τ, the final synchronization error by increasing ge is more significant. Part (b) of this figure illustrates the impact of varying the presence time of electrical and chemical synapses (θ) for a fixed transition period τ=132. It is attained that in very low values of θ (θ<0.1), i.e. when the present time of electrical synapses is short, the synchrony error does not decay to zero by increasing ge. For 0.1<θ<0.5, the error becomes zero for intermediate values of coupling strength, and there exists a small error when the coupling becomes stronger. As the present time of electrical synapses increases (θ>0.5), this small error does not appear for strong couplings.
4.
Conclusion
This paper investigated the effects of the transient electrical synapses on the synchronization of the coupled neurons. Previous studies on the brain have revealed that the electrical synapses transit to the chemical synapses in special brain regions. Motivated by this, it was assumed that the electrical synapses exist among neurons for a defined time interval and then change to chemical synapses in the next time interval, and this sequence repeats periodically. The synchronization error of the neurons was computed by considering different periods for synaptic transitions and different time durations for synapses.
At first, the network with constant electrical and chemical synapses was investigated. It was observed that when the chemical coupling was weak, the neurons were completely synchronous in a specific range of electrical coupling strength, further which the burst synchronization emerged. As the chemical coupling became more robust, the oscillations were suppressed, and the neurons stayed in a resting state. When the synapses were transient, the neurons were oscillating in all cases, and the steady resting state was not observed. The results showed that complete synchronization was only obtained when the time duration of electrical synapses was high. In other cases, the burst synchronization was observed. Increasing the period of the synaptic transitions led to the increase of the absolute synchronization error. In all cases, increasing the chemical coupling caused the decay of the synchronization error in lower electrical strengths. Moreover, both the period and the time duration of the electrical and chemical synapses influenced the shape of the time series of the action potentials.
Acknowledgments
This work is supported by the Natural Science Basic Research Program of Shaanxi (2021JM-533, 2021JQ-880, 2020JM-646), the Innovation Capability Support Program of Shaanxi (2018GHJD-21), the Science and Technology Program of Xi'an (2019218414GXRC020CG021-GXYD20.3), the Support Plan for Sanqin Scholars Innovation Team in Shaanxi Province of China, the Scientific Research Program Funded by Shaanxi Provincial Education Department (21JK0960), the Youth Innovation Team of Shaanxi Universities, the Scientific Research Foundation of Xijing University (XJ21B01), and the Scientific Research Foundation of Xijing University (XJ200202). This work is partially funded by Centre for Nonlinear Systems, Chennai Institute of Technology, India vide funding number CIT/CNS/2021/RD/064.
Conflict of interest
The authors declare that they have no conflict of interest.









 DownLoad:
DownLoad: