1. Introduction
Many studies have been devoted in the last years to the probabilistic characterization of Wind Speed (WS), and especially Extreme Wind Speed (EWS) values, in the framework of the significantly increase of wind power production in recent years due to its environmental, technological, and economic benefits [1,2]. In general terms, the probabilistic characterization of WS and EWS is a challenging task in wind power production assessment, mechanical safety, and reliability, as well as for wind gust prediction, so that a large number of different approaches have been proposed to model such phenomenon [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22].
In the last years the power system literature has raised the concern about the high penetration of unpredictable, intermittent renewable power sources in electrical networks in reference to the optimal management of power networks. Indeed, such penetration involves many technical problems such as power quality assessment, network frequency regulation, and transient stability [23], since a variation (i.e. diminution) of system inertia is brought by the increasing share of renewable energy upon the total generation power; the inertia in the rotating masses of synchronous generators and turbines determines the immediate frequency response to the overall power balance, so this variation may be very critical for maintaining power system stability. Probabilistic approaches are mandatory in order to cope with the intrinsic uncertainty of the phenomena; however, they usually require a statistical characterization of the random variables.
When dealing with the more restricted field of EWS, the complexity of the phenomenon is further increased by the scarcity of available data, as EWS events are less frequent. However, they negatively affect wind turbines in many ways [21], and at least three undesirable effects may be individuated:
(1) EWS harm the turbine structural safety.
(2) EWS lead to a shorter wind turbine life, mainly due to the increased rotor blade fatigue.
(3) EWS reduce the overall wind energy output.
Regarding the first and second aspect, the randomness of EWS has a great impact on the mechanical reliability of wind power systems, since EWS may damage sensible components of the structures, such as towers and wind blades [8,9,10,11,12], leading to loss of life or to mechanical breakdowns. Wind turbine design has recently exploited developments from aerospace engineering, material engineering, and nuclear industry, in order to increase safety and reliability levels [14,21]; the wind turbine design is typically developed on a several-years return value of EWS data, to consider the most severe storm events [21]. Several EWS distributions have been applied in literature; e.g., the Wakeby distribution has been used in [21] to tackle this problem. However, due to the scarcity of EWS events, the lack of fitting of a distribution in its upper quantiles could severely invalidate the entire wind turbine design. Thus, new contributions in this field of research are strongly encouraged.
Regarding the third aspect, values of WS that are greater than the "cut-off" value of the wind generator are generally undesirable, since the electric generator has to be disconnected from the wind turbine not to compromise the electrical section of the wind power system [12]; consequently, the "cut-off" value of the generator must be chosen according to the characterization of EWS in the particular location, since it has a great impact on aggregate power production [9,10,11,12,13,14].
Then, considering these disadvantages, the statistical characterization and prediction of such EWS is mandatory in the decision-making process when evaluating yearly output production for the wind power system design [13], and also in real-time operating conditions in order to implement some measures to reduce the corresponding drawbacks.
Contrarily to the literature on WS characterization, which is quite abundant, literature on EWS characterization is more scarce.
For example, when, it is common practice to model short-term WS with the Weibull distribution. However, the choice of an incorrect model may lead to significant errors, especially in the estimation of upper and lower WS quantiles, and thus EWS quantiles. Indeed, several papers have shown that the widely-accepted Weibull distribution provides a poor fit to the distribution of EWS when compared with other models, such as the bimodal Weibull, or the Kappa, Wakeby, Inverse Burr distribution, and more [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22]. Such models, however, share the disadvantage to be rather complex, since they are characterized by three or more parameters (e.g. three for the Inverse Burr distribution, five for the Wakeby distribution).
With the aim of proposing a simpler, yet efficient, model for the above EWS characterization, the paper proposes a new EWS characterization based on a suitable Inverse Log-logistic (ILL) distribution. This distribution has never been used before for EWS, except that in a rare appearance as a particular case of the Inverse Burr distribution proposed in [12].
The rest of the paper is organized as follows. First, in Section 2 the ILL model is described with all its statistical parameters. The Cumulative Distribution Function (CDF), Probability Density Function (PDF), and moments of the ILL model, together with its "classical" estimation methods—i.e. the Maximum Likelihood Estimation (MLE), Moment Estimation (ME) and the so-called Quantile Estimation (QE) methods [12], are then briefly reviewed in Section 3. Moreover, Section 3 provides also some useful aids for the identification of the ILL distribution, and the successful applicability of the ILL model to actual EWS data is illustrated. For such purpose, the ILL distribution is compared to a different distributions that has been widely acknowledged as suitable EWS distribution, i.e., the Inverse Weibull distribution.
A "practical" Bayesian statistical inference approach for estimating the ILL parameters from available data is proposed in Section 4, by using the model CDF as the proper input for the prior assessment of the model.
The applicability and efficiency of the proposed Bayesian approach is verified in Section 5 by means of a broad amount of Monte Carlo simulations, performed starting from typical values of EWS data. The results prove the satisfactory behavior of the Bayesian methodology, especially for quite small samples, which is a desirable property, since small samples are very common in any practical EWS scenarios.
Eventually, the Appendix A reports the characterization of the Inverse Burr distribution, of which the ILL model is a special case, whereas the Appendix B reports deduction of the ILL model from a mixture of Inverse Weibull distribution. Appendix C shows the actual EWS data used in the numerical applications, Appendix D reports the characterization of the Lognormal distribution and Appendix E reports the characterization of the Gamma distributions. A list of symbols and acronyms is in Appendix F.
In summary, the paper aims at developing useful methodological and numerical contributions to EWS modeling, exploiting adequate tools taken from the extreme value theory [24,25] and Bayesian statistical inference [26,27,28,29,30], and also paying attention to the non-trivial issue of model identification, especially in view of estimation of extreme quantiles under model uncertainty [31].
2. The Inverse Log-logistic distribution for wind speed stochastic modeling, and its deduction from a mixture of Inverse Weibull distributions
The ILL distribution is proposed for EWS in this paper, and it is illustrated with hints at its deduction (which is a novelty, as far as the authors know) from a proper mixture of Inverse Weibull probability distributions [25]. Note that the Inverse Weibull distribution is a widely-adopted and well-established distribution for EWS [11]; for example, in [32], the Inverse Weibull distribution was the most suitable model for the EWS characterization in 139 out of 143 tested cases.
The ILL distribution model can be considered as a particular case of the Inverse Burr model—also known in literature as "Dagum distribution"—which has recently been proposed for the first time in EWS studies [12]; the reader is referred to the Appendix A for its characterization.
The analytic expressions of the ILL CDF and PDF are shown as follows, for x>0, being x a generic EWS value:
|
f(x|τ,β)=βτβ[1+(τx)β]2xβ+1
|
(2)
|
where τ is a scale parameter and β is a shape parameter, both defined as positive numbers.
For understanding the derivation of the ILL denomination, and for a better insight into its properties, it is recalled here that a the Random Variable (RV) Y has a "Log-logistic" distribution, if the RV Z = log(Y) has a Logistic distribution [25], i.e., the CDF of the RV Z has the following expression:
|
F(z|m,s)=1/{1+exp[−(z−m)/s]}
|
(3)
|
Then, the RV X defined as the reciprocal (or "Inverse") of the above Logistic RV Y (i.e., X=1Y=1exp(Z)), is characterized by an ILL model with CDF in Eq 1. It is recalled that the Logistic distribution in Eq 3 has a mean value E[Z] = m, and a Standard Deviation (SD) proportional to the parameter s; also, its PDF is similar to the PDF of a Normal distribution with mean value m. This implies that one could expect a significant similarity between the Log-logistic model and the Lognormal one, as it indeed occurs [25]. Consequently, it can be expected also a close remembrance between the ILL and a suitable Lognormal model, given that, if V is a Lognormal RV, then its reciprocal: U = 1/V is still a Lognormal RV.
The median value of the ILL distribution in Eq 1, i.e., the solution m of F(m) = 0.5, is τ. It is indeed trivial to notice that F(τ|τ, β) = 0.5, whatever the value of β. The generic q-quantile xq, i.e. the solution of the equation: F(xq) = q, 0 < q < 1 of the ILL distribution can be expressed as:
where:
Quantile expression Eq 4 is very simple to handle; hence, random numbers from ILL distribution can be easily generated through the inversion method [26]. Of course, xq = τ when q = 0.5. It is useful to express also the mean value μ, the variance σ2, and the generic q-quantile xq of the ILL distribution. It is remarked that mean (or expected) value μ exists only if β > 1, and the variance exists only if β > 2; they are expressed as functions of the ILL parameters as it follows:
|
σ2=τ2[Γ(1+2β)Γ(1−2β)−Γ2(1+1β)Γ2(1−1β)]
|
(7)
|
Being Γ(∙) the Gamma function defined, for an input t > 0, as:
And being B(∙, ∙) the Beta function, defined in terms of the above Gamma function Γ(∙), for inputs r > 0 and s > 0, as:
|
B(r,s)=Γ(r)Γ(s)Γ(r+s)
|
(9)
|
Also, the expression of the generic kth order moment, defined only if β > k, is:
|
E[Xk]=τkB(1+kβ,1−kβ)
|
(10)
|
Now, let us turn our attention to the Inverse Weibull distribution, which is often adopted for EWS modeling [11,24,25,32]. The aim is both to recall the Inverse Weibull model (which is used afterwards as a reference distribution), and to give a brief hint at the deduction of the ILL distribution as a proper mixture of Inverse Weibull distributions (see Appendix B for more details). The Inverse Weibull distribution is widely used in reliability analysis, and it has been proved to be particularly suitable also for EWS characterization [11,12,32]. Various analytic expressions of Inverse Weibull PDF and CDF are reported in literature [25]. Here, the following form of the Inverse Weibull CDF are adopted:
|
F(x|τ,β)=e−(τx)β,x>0
|
(11)
|
As the Burr distribution results from a mixture of Weibull distributions [22], the ILL distribution results from a mixture of Inverse Weibull distributions through a parameterization in θ=1τβ. Since the intrinsic properties of the WS are fixed for a given location, as discussed for the Weibull distribution [4–12], also the shape parameter β of the Inverse Weibull model can be considered as a deterministic value, whereas the scale parameter θ is rather to be considered as a RV [12]. Then, the ILL PDF is obtained by selecting an appropriate Gamma distribution [25] to model the randomness of the inverse scale parameter 1/θ, and following the same approach shown in [22] to obtain the Burr distribution. Further details are in Appendix B.
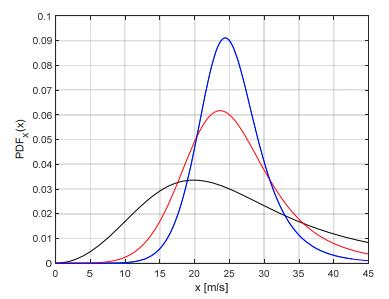
Three different curves of ILL PDFs with the same median τ (25 m/sec)—which is a typical value for EWS PDFs—and different values of β, i.e. β = 3, β = 6, and β = 9 are shown in Figure 1.
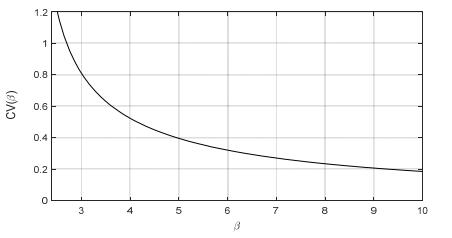
It is clear that the PDF curve becomes narrower as the shape parameter β increases and keeping the scale parameter τ at a fixed value. This is a general property, related to the fact that the Coefficient of Variation (CV)—i.e., the ratio of the SD to the mean value—of the ILL model, which obviously does not depend on the scale parameter, decreases as β increases. This is confirmed by inspecting Figure 2, in which the curve of the CV of the ILL distribution as a function of β is reported in the range 2.5 < β < 10 (we recall that the CV exists only if β > 2). The values of the CV are numerically evaluated from Eq 6 and Eq 7, which clearly show that the ratio of the SD σ to the mean value μ does not depend on τ. Since the CV is evidently a monotone function of β, its value computed from a given sample of ILL observed data can be used to produce an estimate of β.
Finally, some significant statistical parameters of the three curves of Figure 1 are reported in Table 1, and in particular: The mean, median, SD, CV, skewness, kurtosis, 5th percentile, and 95th percentile. The median is of course always equal to 25 m/s, by construction. All of the PDFs show a positive skewness (i.e. they are "right-skewed"), as confirmed by the property that the mean is always greater than the median. However, the skewness (as consistent with theoretical properties, not reported here for brevity) decreases towards zero as β increases. Indeed, when β = 9, the mean (25.51 m/s) is only slightly greater than the median (25.00 m/s) as reported in the 3rd row, corresponding to an almost-symmetrical PDF.
Table 1. Statistical parameters of the three curves of Figure 1: Mean, median, standard deviation, coefficient of variation, skewness, kurtosis, 5th percentile, and 95th percentile.
| Β[–] |
Mean [m/s] |
Median [m/s] |
SD [m/s] |
CV [-] |
Skewness [m/s] |
Kurtosis [m/s] |
5th percentile [m/s] |
95th percentile [m/s] |
| 3 |
30.2300 |
25.0000 |
24.4468 |
0.8087 |
- |
- |
9.3689 |
66.7100 |
| 6 |
26.1799 |
25.0000 |
8.3881 |
0.3204 |
0.2363 |
0.0122 |
15.3043 |
40.8381 |
| 9 |
25.5150 |
25.0000 |
5.2723 |
0.2066 |
0.2137 |
0.0459 |
18.0242 |
34.6756 |
The diminution of the CV as β increases (from 0.8087 for β = 3 to 0.2066 for β = 9) corresponds to a shrinkage of the PDF curves, which appears also from the values of the percentiles. For example, the 5th and 95th percentiles respectively are 9.37 and 66.71 m/s for β = 3, whereas for β = 9 they are 18.02 and 34.68 m/s, corresponding to a much tighter interval. Eventually, note that both skewness and kurtosis are not defined for β < = 3.
3. Hints to the ILL distribution estimation and identification, with numerical applications
Since the topic is already discussed (or deducible from similar models) in literature [12,25,26], only hints to the classical estimation methods of the ILL distribution are reported here, with some highlights on the model identification. The ILL Log-likelihood function L(x|τ, β) of a dataset x = {x1, x2, …, xN} is:
|
L(x|τ,β)=Nlogβ+Nβlogτ−2∑Ni=1log[1+(τxi)β]−(β+1)∑Ni=1logxi
|
(12)
|
The MLE of the parameters τ, β of ILL distribution is therefore achieved by solving the following equation system:
|
{Nβτ−2∑Ni=1βτβ−1[1+(τxi)β]xβi=0Nβ+Nlogτ−2∑Ni=1τβ(logτ−logxi)[1+(τxi)β]xβi−∑Ni=1logxi=0
|
(13)
|
The MLE procedure yields sometimes convergence problems [12]. In such cases, simpler ways to attain parameter estimates are the ME [26] and the QE [12,33] methods, even if sometimes they prove to be less efficient [33]. The ME procedure, consisting in solving a system of two equations for two different values of the first and second sample moments is rather cumbersome due to the special functions involved, and can be found only numerically [12]. Moreover, the above equations lose, of course, their meaning when the shape parameter β is not greater than 2 (recalling that the first two moments, as the mean and variance, exist only if β > 2).
The QE procedure consists in solving a system of two equations for two different values xq* of sample q*-quantiles [26], which of course always exist. Sample quantiles xq1*, xq2* are calculated from dataset x, and the equation system to be solved therefore is:
|
{x∗q1−τ[(1q∗1)−1]−1β=0x∗q2−τ[(1q∗2)−1]−1β=0
|
(14)
|
A comparison between Eq 13 and Eq 14 suggests that QE can be a simpler and more efficient alternative, since the QE procedure can be expressed in closed analytic form, which yields to a significant simplification. In particular, it is of course convenient that one of the above quantiles be the median value, which is equal to the scale parameter τ. Having also discussed the limits of ME procedure, in this paper the parameter estimation is performed through the QE procedure.
As stated in the introduction to this section, it seems opportune to illustrate some hints at the model identification, which is very simple; nonetheless, it is deemed that the following hints may be useful since the ILL model has been, until now, rarely applied. Moreover, the following remarks help to find another simple model for parameter estimation, i.e. the "Least Squares" method applied to an opportune transformation of the CDF, i.e. to the Odds Ratio (OR) defined hereafter. Let F(x) be the CDF (1) of the ILL model, being x a generic EWS value (in our application). Then, let us introduce the OR Q(x), defined as:
In the statistical literature, the OR is the ratio of the probability that the event of interest, here the event X < x (given by F) occurs, to the probability that it does not occur (given by 1-F). It is immediate to verify that the OR Q is proportional to the β-power of the observation x:
Eq 16 implies a log-linear relationship between x and Q1:
1 log(x) always denotes the natural logarithm of x.
|
log(Q)=βlog(x)−βlog(τ)
|
(17)
|
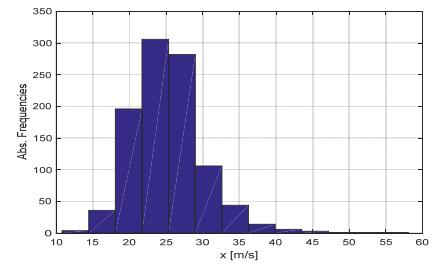
Which suggests a simple way for the model identification and also parameter estimation, through a "Least Squares" method, in particular a linear regression, method applied the above "log-OR" transformation, which is a linear function of β and log(τ). As per the model identification, in the following it is shown how it can be applied, by starting from a simulated random sample from a given ILL model. Random numbers from the ILL distribution are generated through the inversion method applied to the quantile expression Eq 4, in which the values of probabilities q are drawn from an Uniform distribution in (0, 1)2. Figure 3 shows a histogram of 1000 samples obtained from an ILL distribution with median τ = 25 m/s, and β = 9. The theoretical PDF which generates such sample is one of the three curves of Figure 1, the statistical parameters of which are reported in the third row of Table 1. They are reported again in the first row of Table 2, whereas the sample estimates of the same parameters are reported in the second row of Table 2, to show the good fitting of the simulation procedure.
2 The function "unifrnd" of Matlab ® is used for this purpose.
Table 2. Theoretical and simulation sample estimated (briefly "simulated") statistical parameters of the ILL distribution with τ = 25 m/sec, and β = 9.
|
Mean [m/s] |
Median [m/s] |
SD [m/s] |
CV [-] |
5th percentile [m/s] |
95th percentile [m/s] |
| Theoretical |
25.5150 |
25.0000 |
5.2723 |
0.2066 |
18.0242 |
34.6756 |
| Simulated |
25.3002 |
24.8826 |
4.9863 |
0.1973 |
18.4110 |
33.9061 |
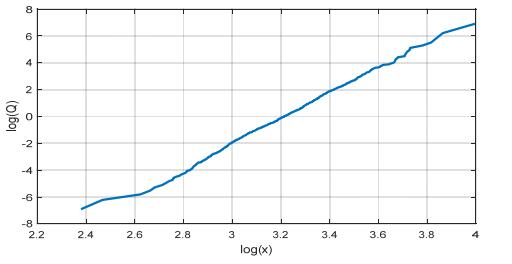
In order to show the application of Eq 17 in the model identification, Figure 4 shows the graph of the log-OR vs. the logarithms of the observations x for the simulated samples in Figure 3. The pseudo-linearity of the curve proves the good fitting of the ILL model.
As a practical example of the QE estimating method, the estimated values of the parameters β and τ are obtained as follows:
1) The median τ is estimated from the sample median, i.e., τ* = 24.8826 (true value: 25);
2) The estimated value of β is estimated from another quantile, e.g. the 55th percentile ("central" quantiles are estimated more efficiently than extreme ones). Such sample quantile is equal to 25.4320; given that kq=1q−1=10.55−1=0.8182, the QE procedure returns, using Eq 4: xq* = τ∗kδq=, for q=0.55→kδq=24.882625.4320=0.9784→δ∗=1β∗=log(0.9784)/log(kq. Eventually, β* = / log(0.9784) = 9.1886 (true value: 9).
This fitting is purely illustrative, since the above samples are simulated data characterized by a large number of elements: In practice, when estimating parameters from a small dataset, a great care must be paid, especially in the extreme tails. For instance, it could be easy to find a good fitting of samples generated from an ILL distribution using an Inverse Weibull distribution [12]. A simple mathematical motivation is the following: Given an ILL distribution (CDF in Eq 1) and an Inverse Weibull distribution with CDF G(x) having the same shape parameter β and a scale parameter τ as in Eq 11:
It is simple to note that when x diverges, i.e., or in practice when x≫τ, the first-order Mac Laurin series expansions of Eq 1 and Eq 18 show that F(x)≅G(x), since:
|
F(x|τ,β)=11+(τx)β≅1−(τx)β
|
(19)
|
And:
|
G(x|τ,β)=e−(τx)β≅1−(τx)β
|
(20)
|
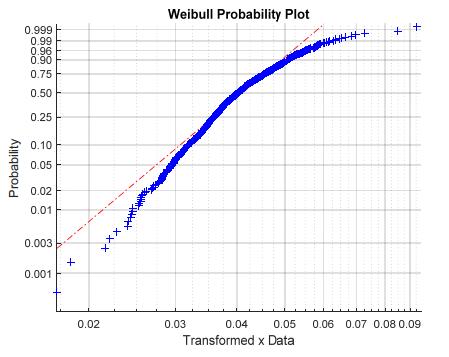
When, however, enough data are available, one could expect that the Inverse Weibull and the ILL distributions behave in similar way in central values, whereas some differences arise for the lower and upper quantiles, i.e. in the "extreme tails" of the distribution. This is exemplified by means of the previously-analyzed sample data, the "Weibull probability plot" of which is shown in Figure 5. The Weibull probability plot [25] is a probability graph that, applied to a sample generated from a RV Y, appears as a linear function if Y comes from Weibull model. Here, it is applied to the RV Y = 1/X (i.e., to transformed X data which correspond to the inverse of the EWS sample data under study); indeed, under the hypothesis that X has an Inverse Weibull distribution, Y has a Weibull distribution.
The graph in Figure 5 shows clearly that the "extreme tails"—or, equivalently, the lower and upper quantiles—of the sample distribution are not well fitted by the Inverse Weibull distribution. However, caution should be taken when few data are observed. Indeed, similarly to what can occur when discriminating between Weibull and Log-logistic distributions for "standard" (not extreme) WS values characterization, the distributions are very similar in correspondence of central values of EWS, whereas a substantial difference can be evidenced in correspondence of the upper tails of distributions; then, even if both distributions could estimate analogous central values (median and mean values), a severe underestimation or overestimation of upper quantiles could occur and therefore EWS could not be well estimated [3,11,12]. Therefore, appropriate models that are suitable for extreme values characterization should be introduced in order to avoid such kind of issues. In practice, in such situations the data could be fitted equally well through two or more different models, so extra information is needed for selecting the "right" model, such as the "physical" motivation which leads to the ILL model.
Eventually, we close this Section by illustrating the usefulness the proposed ILL distribution for EWS characterization by fitting it to four datasets of actual data, which are deeply discussed in Appendix C. The datasets are labeled D1, D2, D3 and D4, and refer to three different sites and to different types of period maxima. Some statistical parameters of the four datasets are reported in Table 3. The results are compared to those obtained through the Inverse Weibull fitting, since it is the most common distribution in EWS scenarios [32].
Table 3. Some statistical parameters of the four datasets reported in Appendix C.
| Dataset |
Mean [m/s] |
Median [m/s] |
SD [m/s] |
CV [-] |
5th percentile [m/s] |
95th percentile [m/s] |
Maximum value [m/s] |
| D1 |
20.5731 |
19.0750 |
6.8118 |
0.3311 |
11.2600 |
32.3300 |
38.8000 |
| D2 |
25.9546 |
24.5025 |
7.2493 |
0.2793 |
14.8589 |
41.0092 |
44.3330 |
| D3 |
16.6355 |
16.9250 |
3.5030 |
0.2106 |
10.4000 |
22.0390 |
29.0500 |
| D4 |
25.5463 |
24.8810 |
5.3920 |
0.2111 |
18.7198 |
34.4272 |
41.9580 |
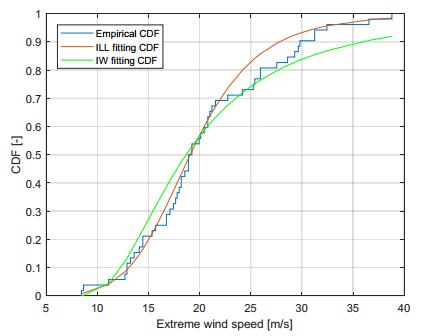
The ILL parameter estimates of D1, obtained through QE estimating method, are τ* = 19.0750 m/s and β* = 5.8300 (dimensionless3). The theoretical ILL CDF with these parameters is shown together with the empirical sample CDF and the fitting Inverse Weibull distribution, used for comparison, in Figure 6. The ILL distribution appears better to fit the EWS data, especially in the upper tail, whereas the Inverse Weibull distribution tends to adapt more its parameters to the central EWS values, thus resulting in underestimating the upper quantiles.
3 The same estimated value of β is obtained also by inverting the CV curve of Figure 2.
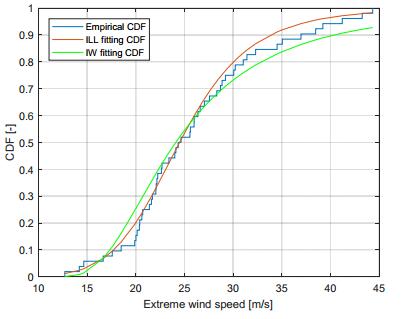
A similar fitting was applied to the other datasets. The ILL parameter estimates of D2, obtained through QE estimating method, are τ* = 24.5025 m/s and β* = 6.7900 (dimensionless). The theoretical ILL CDF with these parameters is shown together with the empirical sample CDF and the fitting Inverse Weibull distribution, used for comparison, in Figure 7. Also in this case, the ILL distribution appears better to fit the EWS data, whereas the Inverse Weibull suffers the same problems evidenced beforehand, although in this case differences are smaller.
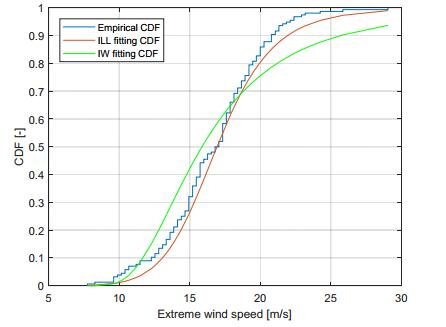
The ILL parameter estimates of D3, obtained through QE estimating method, are τ* = 16.9250 m/s and β* = 8.4740 (dimensionless). The theoretical ILL CDF with these parameters is shown together with the empirical sample CDF and the fitting Inverse Weibull distribution, used for comparison, in Figure 8.
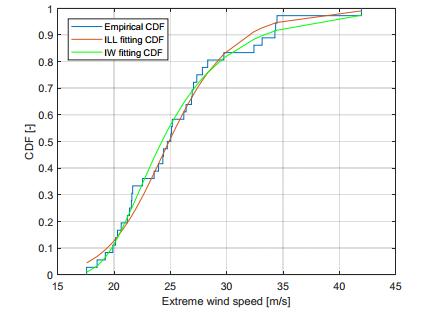
The ILL parameter estimates of D4, obtained through QE estimating method, are τ* = 24.8810 m/s and β* = 8.823 (dimensionless). The theoretical ILL CDF with these parameters is shown together with the empirical sample CDF and the fitting Inverse Weibull distribution, used for comparison, in Figure 9.
Eventually, the estimated mean, median, SD, CV, 5th percentile, and 95th percentile for the ILL fitting distributions of the four datasets are reported in Table 4, for a comparison with the corresponding sample parameters in Table 3.
Table 4. Theoretical parameters of the four ILL distributions fitting the EWS datasets reported in Appendix C.
| Dataset |
Mean [m/s] |
Median [m/s] |
SD [m/s] |
CV [-] |
5th percentile [m/s] |
95th percentile [m/s] |
| D1 |
20.0304 |
19.0750 |
6.6292 |
0.3310 |
11.5113 |
31.6086 |
| D2 |
25.3991 |
24.5025 |
7.0957 |
0.2794 |
15.8811 |
37.8041 |
| D3 |
17.3190 |
16.9250 |
3.8134 |
0.2202 |
11.9571 |
23.9570 |
| D4 |
25.4146 |
24.8810 |
5.3625 |
0.2110 |
17.8211 |
34.7373 |
4. Illustration of the proposed Bayesian estimation procedure
As discussed above, the parameter β of the ILL distribution may be considered known in wind studies. Adopting a Bayesian approach [26–30], the unknown parameter τ is considered as a RV. Consequently, also the CDF and other parameters (e.g. EWS percentiles) are defined as RVs, and thus they are described by appropriate distributions. The Bayes methodology starts by assigning a prior PDF p(η) to the generic parameter η of the model (in the following, η is to be meant as any of the above unknown RVs, i.e. the CDF, or the OR Q(x). Then, given a dataset D made of n EWS observations:
The posterior PDF p(η|D) of η is estimated by means of the Bayes formula, i.e.:
where L(D|η) is the likelihood function of the data (i.e., in this case, the product of the n ILL PDFs of the observations x1, …, xn, conditional to η) and C is a normalizing constant (with respect to η, but function of the given sample D) which has the following expression:
Then, once the posterior PDF p(η|D) of η is obtained, all the information required for the Bayes estimation is provided. This can be used for obtaining the point estimate, the choice of which depends on the chosen criterion, i.e. the "loss function", to minimize [26–30]. A typical choice—if the minimum mean square error criterion is chosen—is the posterior mean of η:, i.e. its expected value computed with respect to the posterior PDF p(η|D) of η. Another possible choice, that is performed in this paper, is the so called Maximum a Posteriori Probability (MAP) estimation, in which the point estimate of η is the value which maximizes the posterior PDF p(η|D). Both the minimum mean square error and the MAP estimator require numerical methods to be computed, but the MAP is somewhat simpler to be estimated, being nonetheless very close to the posterior mean of the generic parameter η, whatever is the choice of such parameter (that is left unspecified, until now). So let us discuss the choice of the parameter. It could be naturally chosen as the unknown quantity τ. However, the uncertainty about the random parameter τ may be in some applications difficult to assess, whereas the CDF has a more direct interpretation, with the advantage of being naturally confined in the (0, 1) interval, and being dimensionless. So, a prior knowledge on the CDF F(x), for a given value x, should be easily available to the engineer on the basis of past wind data, experience on similar wind farm sites, specific databases, or experts' opinions. So, following an approach that is similar to the one proposed in [25] with reference to components lifetime, it is preferable to express a prior knowledge on the CDF F(x0) = P(X≤ x0) at a certain WS value x0. It is remarkable that such value is closely related to the OR4, defined in Eq 15 and reported again here (omitting the assumed argument x0):
4 The quantity Q should be more precisely denoted as Q(x0), but the term is often omitted when it clearly appears from the context.
As reported before, the OR is proportional to the β-power of the observation x0, and an inverse power function of τ; moreover, by introducing the related parameters (that are treated as RV):
The following relations hold between the RV Q and the RVs τ, θ, Z for any argument x0:
So, a prior PDF on F implies a prior PDF on Q, and thus on τ, θ, Z. Each one of these parameters (as well as a given quantile, also simply related to the above parameters as shown in Section 2) can play the role of the generic parameter η of the above equations, leading to the PDF p(η|D). For analytical simplicity, having assumed τ as a basic parameter, the Bayes prior assessment is expressed in terms of τ, also illustrating the implied on Q which may be, as above discussed, the primary prior input for the estimation process.
As per the prior PDF of τ, which is a positive RV, due to the lack of a "conjugate" model5, every model which has desirable features of being flexible and simple enough to carry on the relevant mathematics, can be used. Among the most common models which appear to be very flexible for dealing with positive RV on the open interval (0, ∞), the Lognormal or the Gamma distributions ([25]; see also Appendixes D and E) come easily into mind, the latter model being better substituted by a "Generalized Gamma" model for reasons to be appear clear in short.
5 A model with prior PDF p(ζ) for a given parameter ζ is called a "conjugate" model if the posterior PDF p(ζ|D) of ζ belongs to the same parametric model [26].
In practice, apart from studying the implied priors on Q, what done here resembles studies on the Log-logistic distribution as those performed in [29], in which different prior (such as Maxwell and Chi-Square, which is indeed a particular Gamma distribution) have been used, and where also a "non-informative" prior such as the Uniform distribution has been used. So, also for easier comparison with previous studies6, and for more detailed analysis, in the present study also the Uniform distribution will be used for the median, even if it is expected that more information is available in the prior assessment.
6 As far as the authors know, this paper is the first study of such kind for the ILL model under a Bayes approach. Previous studies on the Log-logistic distribution of a given RV Y(e.g., [29]) could however be used also for the ILL model, if the ILL RV defined by X = 1/Y is introduced.
In summary, the following three choices for the prior PDF will be considered, with more emphasis on the first one which appears the most "practical" and simple analytically:
1) A Lognormal distribution on τ (implying a Lognormal distribution on Q);
2) A Generalized Gamma distribution on τ (implying an Inverted Gamma distribution on Q, see [25] and Appendix E);
3) A Uniform distribution on τ (which does not imply any "practical" distribution on Q: In such case, τ must be considered the prior input for the estimation process, while in the two above alternatives, both τ and Q may be considered as the input RV).
The above choices are better understood recalling that [25]:
a) If V is a Lognormal RV, then its reciprocal U = 1/V, is still a Lognormal RV, and also its c-power W = Vc, and of course also Z = 1/Vc is still a Lognormal RV, for any real number c;
b) If V is a Gamma RV, then its reciprocal U = 1/V is an Inverted Gamma RV, whereas its c-power W = Vc is a Generalized Gamma RV, for any real number c. The RV Z = 1/Vc is instead an Inverted Generalized Gamma RV (see [25] and Appendix E).
Moreover, in the case when Q is the primary prior input for the estimation process (i.e. the prior PDF is assigned on Q), the following relation which expresses τ in terms of Q, inverting Eq 26 is useful for obtaining the prior PDF of τ:
Details on the three assumed prior PDF of τ are given in the following sub-Sections.
4.1. Choice of a Lognormal distribution on
A Lognormal distribution on τ implies (or, is implied by) a Lognormal distribution on Q, on the basis of the aforementioned properties of the Lognormal model. In particular, if Q is a Lognormal RV with parameters α, δ, i.e. Y = log(Q) is a normal RV with mean α and SD δ (see [25] and Appendix D), then, the expression W = log(τ) = log(x0)-χ log(Q) results from Eq 27, implying that τ has a Lognormal distribution with parameters α' = -logx0-αχ, δ' = δχ. Its PDF is:
|
g(τ|α′,δ′)=1δ′τ√2πexp{−[log(τ)−α′]22δ′2},τ>0
|
(28)
|
4.2. Choice of a Generalized Gamma distribution on τ
Let an Inverted Gamma distribution be assumed as a prior PDF on Q, i.e. (see [25] and Appendix E):
|
g(q|ν,δ)=1q(ν+1)δνΓ(ν)exp{−1δq},q>0
|
(29)
|
As discussed in [30] with reference to a different model, the Log-logistic one, this assumption can be useful if the procedure is based upon prior information on the CDF F. For such purpose, a Beta PDF may be successfully adopted, as generally done for RV in (0, 1) [28]. Then, numerical experiments in [30] show that the implied prior information on Q is, with excellent approximation, well represented by an Inverted Gamma distribution on Q (rules for converting the prior PDF on F into a prior PDF on Q, or the converse, are very simple due to the relation Eq 25. They are reported in [30]).
Then, following the properties recalled in Appendix E, it is readily shown, on the basis of Eq 27, that in such case prior PDF on τ is a Generalized Gamma distribution (details are left to the reader, being the parameters of such Generalized Gamma distribution easily deduced by means of what illustrated in Appendix E).
4.3. Choice of a Uniform distribution on τ
As above discussed, an Uniform distribution on τ does not imply any "practical" distribution on Q: This choice nay be useful if τ is considered the prior input for the estimation process, with a "non-informative" prior on such parameter. In the case of the applications here considered, such choice appears to be of little interest, since a certain degree of prior information on the median of the EWS always exists. Nonetheless, such prior information assessment is of interest for evaluating the Bayes procedure as a "cautious" alternative to the two informative priors illustrated above. The experiments of the following section show indeed that, even with less efficiency than the above ones, also this prior assessment behaves very well.
Finally, alternative prior information can be assessed on terms of EWS percentiles: As can be readily seen by the expressions of the ILL percentiles above reported, this is very simple, being them proportional to the median in the framework of the present model.
5. Numerical application for assessing the estimation efficiency of the Bayes approach
The Bayesian methodology was evaluated numerically by means of a large set of simulated experiments aiming at assessing the estimation efficiency of the Bayes approach. This is performed both in "absolute" terms and in terms of "relative efficiency" [7–9] vs. the classical estimator, here assumed as the QE (very similar to the MLE one). Emphasis is given here to the adoption of a Lognormal prior PDF on Q (and so on τ). In any case, a prior mean value of τ is assumed as equal to 26 m/s, which means that prior mean of Q is equal to 1, whereas different values of β (3, 6, 9) and of CV (0.20, 0.10, 0.05) of Q are assumed.
In detail, 9 sets of simulation cases, among the many more performed, are shown in Tables 5-13, with reference to the examples of Section 4.
Table 5. Numerical results of estimation efficiency-case A1.
| n |
RMSEB |
MAREB |
MXREB |
REFF |
| 5 |
0.0058 |
0.0001 |
0.0862 |
3.4780 |
| 10 |
0.0004 |
2.49e-05 |
0.0249 |
2.9914 |
| 25 |
0.0012 |
4.83e-05 |
0.0483 |
5.6636 |
| 50 |
0.0010 |
3.86e-05 |
0.0386 |
2.0992 |
Table 6. Numerical results of estimation efficiency-case A2.
| n |
RMSEB |
MAREB |
MXREB |
REFF |
| 5 |
0.0009 |
3.76e-05 |
0.0376 |
1.4704 |
| 10 |
0.0012 |
4.3309e-05 |
0.0433 |
8.5318 |
| 25 |
0.0002 |
1.8238e-05 |
0.0182 |
13.071 |
| 50 |
1.08e-05 |
3.97e-06 |
0.0040 |
8.8812 |
Table 7. Numerical results of estimation efficiency-case A3.
| n |
RMSEB |
MAREB |
MXREB |
REFF |
| 5 |
0.0004 |
2.42e-05 |
0.0242 |
4.4910 |
| 10 |
1.93e-05 |
5.30e-06 |
0.0053 |
28.274 |
| 25 |
0.0002 |
1.87e-05 |
0.0187 |
7.9368 |
| 50 |
3.17e-05 |
6.86e-06 |
0.0069 |
14.802 |
Table 8. Numerical results of estimation efficiency-case B1.
| n |
RMSEB |
MAREB |
MXREB |
REFF |
| 5 |
6.87e-06 |
1.21e-06 |
0.0097 |
20.472 |
| 10 |
0.0007 |
3.27e-05 |
0.0327 |
2.9593 |
| 25 |
5.92e-08 |
2.96e-07 |
0.0003 |
78.520 |
| 50 |
1.56e-06 |
1.54e-06 |
0.0015 |
16.631 |
Table 9. Numerical results of estimation efficiency-case B2.
| n |
RMSEB |
MAREB |
MXREB |
REFF |
| 5 |
1.02e-05 |
3.89e-06 |
0.0039 |
16.165 |
| 10 |
0.0003 |
2.16e-05 |
0.0216 |
5.0782 |
| 25 |
9.17e-07 |
1.16e-06 |
0.0012 |
3.1079 |
| 50 |
4.72e-05 |
8.54e-06 |
0.0085 |
7.3758 |
Table 10. Numerical results of estimation efficiency-case B3.
| n |
RMSEB |
MAREB |
MXREB |
REFF |
| 5 |
1.35e-05 |
4.49e-06 |
0.0045 |
9.2887 |
| 10 |
9.85e-07 |
1.21e-06 |
0.0012 |
87.145 |
| 25 |
2.38e-07 |
5.94e-07 |
0.0006 |
15.479 |
| 50 |
9.24e-06 |
3.68e-06 |
0.0037 |
14.902 |
Table 11. Numerical results of estimation efficiency-case C1.
| n |
RMSEB |
MAREB |
MXREB |
REFF |
| 5 |
0.0002 |
1.72e-05 |
0.0172 |
7.0199 |
| 10 |
4.12e-05 |
7.66e-06 |
0.0077 |
5.5100 |
| 25 |
9.43e-06 |
3.69e-06 |
0.0037 |
4.6718 |
| 50 |
0.0001 |
1.47e-05 |
0.0147 |
2.6849 |
Table 12. Numerical results of estimation efficiency-case C2.
| n |
RMSEB |
MAREB |
MXREB |
REFF |
| 5 |
0.0003 |
2.25e-05 |
0.0225 |
5.8267 |
| 10 |
1.85e-05 |
5.24e-06 |
0.0052 |
17.260 |
| 25 |
1.75e-05 |
5.11e-06 |
0.0051 |
4.3407 |
| 50 |
1.83e-07 |
5.22e-07 |
0.0005 |
83.400 |
Table 13. Numerical results of estimation efficiency-case C3.
| n |
RMSEB |
MAREB |
MXREB |
REFF |
| 5 |
1.46e-05 |
4.63e-06 |
0.0037 |
17.412 |
| 10 |
5.25e-06 |
1.10e-06 |
0.0085 |
8.0328 |
| 25 |
6.95e-07 |
4.52e-07 |
0.0024 |
21.875 |
| 50 |
2.25e-06 |
7.62e-07 |
0.0052 |
11.908 |
Indeed, many more different models have been adopted in various Monte Carlo simulations, with about the same excellent results shown here.
The first three (shown in Tables 5–7), denoted as "Case A" as a whole, assume a Lognormal prior PDF of Q, with prior mean E[Q] = 1 at x = 26, β = 3, and three different values of prior coefficient of variation (the ratio CV between standard deviation and mean value of Q), giving rise to three different sub-cases (A1, A2, A3) as follows:
- Case A1: β = 3, CV = 0.20;
- Case A2: β = 3, CV = 0.10;
- Case A3: β = 3, CV = 0.05.
The three different cases are chosen in order to show different degrees of prior uncertainty (a larger prior CV value implies a higher degrees of prior uncertainty, so the results are expected to be less efficient, as will be to a certain degree verified by the following results).
The following three more cases (shown in Tables 8–10), denoted as "Case B" as a whole, are similar, with β = 6:
- Case B1: β = 6, CV = 0.20;
- Case B2: β = 6, CV = 0.10;
- Case B3: β = 6, CV = 0.05.
Then, three more cases (shown in Tables 11–13), denoted as "Case C" as a whole, are similar, with β = 9:
- Case C1: β = 9, CV = 0.20;
- Case C2: β = 9, CV = 0.10;
- Case C3: β = 9, CV = 0.05.
In any case, the efficiency of the Bayes estimates has been evaluated by means of Monte Carlo simulations resorting to the following basic statistics [26–28]:
- RMSEB: Root Mean Square Error of the Bayes estimator;
- RMSEL: Root Mean Square Error of the MLE;
- REFF = RMSEL/RMSEB: Relative efficiency of the Bayes estimator compared to the MLE. The REFF index is the most widely adopted measure of the "relative efficiency" [26–28] of the Bayes estimator with respect to the MLE: The more it exceeds unity, the more efficient is the Bayes estimate with respect to the MLE;
- MAREB: Mean Relative Error of the Bayes estimator;
- MXREB: Maximum Relative Error of the Bayes estimator.
With reference to the estimation of Q, the results of the estimates are reported for different values of sample size n, as may typically occur in practice: Small (n = 5, 10) and moderately large (n = 25, 50).
Then, to give an idea of what may happen with the other prior choices, the cases of prior 3 Gamma and prior Uniform distribution are shown in Tables 14 and 15, only (for sake of brevity) in the most "unfavorable" case, which is A1 (which shows the larger prior CV and the smallest value of b, implying a larger CV of the model, see Figure 2).
Table 14. Numerical results of estimation efficiency-case D1 (as case A1, but with prior Gen. Gamma distribution).
| n |
RMSEB |
MAREB |
MXREB |
REFF |
| 5 |
0.0022 |
0.0001 |
0.0580 |
4.8143 |
| 10 |
0.0224 |
0.0002 |
0.1646 |
1.7669 |
| 25 |
0.0032 |
0.0001 |
0.0690 |
1.1676 |
| 50 |
0.0004 |
0.0001 |
0.0523 |
1.7159 |
Table 15. Numerical results of estimation efficiency-case D2 (as case A1, but with prior Uniform distribution).
| n |
RMSEB |
MAREB |
MXREB |
REFF |
| 5 |
0.0006 |
8.14e-06 |
0.0033 |
5.8978 |
| 10 |
0.0164 |
0.0002 |
0.1946 |
1.2126 |
| 25 |
0.0036 |
0.0001 |
0.0862 |
1.8704 |
| 50 |
0.0008 |
7.62e-07 |
0.0388 |
1.5554 |
Finally, a simple "robustness" analysis is presented in Tables 16 and 17, by assuming that the above Lognormal model of case A1 with mean value of 26 is assumed for τ, whereas in fact it is generated by a Lognormal model with mean 24.5 (Table 15), or mean 27.5 (Table 16).
Table 16. Numerical results of estimation efficiency-case E1 (true prior mean of τ = 24.5 m/s, while a prior mean 26 is assumed).
| n |
RMSEB |
MAREB |
MXREB |
REFF |
| 5 |
0.0023 |
0.0001 |
0.0622 |
5.3754 |
| 10 |
0.0072 |
0.0001 |
0.0969 |
3.6507 |
| 25 |
0.0038 |
0.0001 |
0.0785 |
3.9164 |
| 50 |
0.0010 |
0.0001 |
0.0389 |
2.6943 |
Table 17. Numerical results of estimation efficiency-case E2 (true prior mean of τ = 27.5 m/s, while a prior mean 26 is assumed).
| n |
RMSEB |
MAREB |
MXREB |
REFF |
| 5 |
0.0009 |
0.0009 |
0.0341 |
15.869 |
| 10 |
0.0001 |
1.19e-05 |
0.0119 |
14.110 |
| 25 |
0.0012 |
4.25e-05 |
0.0425 |
2.7567 |
| 50 |
0.0005 |
2.75e-05 |
0.0275 |
1.3019 |
6. Conclusions
The ILL distribution is proposed in this paper as a rational and efficient alternative to more popular models for EWS, such as the Gumbel and the Inverse Weibull distributions. The problem of the estimation of the parameters of the proposed ILL model is discussed, also with reference to several real EWS data and applying different procedures, such as classical MLE and QE. The results of a large set of numerical simulations are discussed to illustrate the simplicity and efficiency of the proposed model. After, a practical Bayesian approach, based upon the Lognormal and the Gamma distributions, is developed and the results of a large series of numerical simulations show the efficiency of the method. They also show that the obtained Bayes estimator appears to be robust with respect to "wrong" prior assumptions.
Conflict of interest
The authors declare that no conflict of interest exists in any aspect of the whole activity that they have performed to accomplish the results of the present work.









 DownLoad:
DownLoad: