Skin cancer is a pandemic disease now worldwide, and it is responsible for numerous deaths. Early phase detection is pre-eminent for controlling the spread of tumours throughout the body. However, existing algorithms for skin cancer severity detections still have some drawbacks, such as the analysis of skin lesions is not insignificant, slightly worse than that of dermatologists, and costly and time-consuming. Various machine learning algorithms have been used to detect the severity of the disease diagnosis. But it is more complex when detecting the disease. To overcome these issues, a modified Probabilistic Neural Network (MPNN) classifier has been proposed to determine the severity of skin cancer. The proposed method contains two phases such as training and testing the data. The collected features from the data of infected people are used as input to the modified PNN classifier in the current model. The neural network is also trained using Spider Monkey Optimization (SMO) approach. For analyzing the severity level, the classifier predicts four classes. The degree of skin cancer is determined depending on classifications. According to findings, the system achieved a 0.10% False Positive Rate (FPR), 0.03% error and 0.98% accuracy, while previous methods like KNN, NB, RF and SVM have accuracies of 0.90%, 0.70%, 0.803% and 0.86% correspondingly, which is lesser than the proposed approach.
Citation: J. Rajeshwari, M. Sughasiny. Modified PNN classifier for diagnosing skin cancer severity condition using SMO optimization technique[J]. AIMS Electronics and Electrical Engineering, 2023, 7(1): 75-99. doi: 10.3934/electreng.2023005
| [1] | J. Rajeshwari, M. Sughasiny . Dermatology disease prediction based on firefly optimization of ANFIS classifier. AIMS Electronics and Electrical Engineering, 2022, 6(1): 61-80. doi: 10.3934/electreng.2022005 |
| [2] | Mehdi Tabasi, Pouyan Asgharian . Optimal operation of energy storage units in distributed system using social spider optimization algorithm. AIMS Electronics and Electrical Engineering, 2019, 3(4): 309-327. doi: 10.3934/ElectrEng.2019.4.309 |
| [3] | Jeevani W. Jayasinghe . Application of Genetic Algorithm for Binary Optimization of Microstrip Antennas: A Review. AIMS Electronics and Electrical Engineering, 2021, 5(4): 315-333. doi: 10.3934/electreng.2021016 |
| [4] | Abdullah Yahya Abdullah Amer, Tamanna Siddiqu . A novel algorithm for sarcasm detection using supervised machine learning approach. AIMS Electronics and Electrical Engineering, 2022, 6(4): 345-369. doi: 10.3934/electreng.2022021 |
| [5] | Amleset Kelati, Hossam Gaber, Juha Plosila, Hannu Tenhunen . Implementation of non-intrusive appliances load monitoring (NIALM) on k-nearest neighbors (k-NN) classifier. AIMS Electronics and Electrical Engineering, 2020, 4(3): 326-344. doi: 10.3934/ElectrEng.2020.3.326 |
| [6] | Abdul Yussif Seidu, Elvis Twumasi, Emmanuel Assuming Frimpong . Hybrid optimized artificial neural network using Latin hypercube sampling and Bayesian optimization for detection, classification and location of faults in transmission lines. AIMS Electronics and Electrical Engineering, 2024, 8(4): 508-541. doi: 10.3934/electreng.2024024 |
| [7] | Loris Nanni, Michelangelo Paci, Gianluca Maguolo, Stefano Ghidoni . Deep learning for actinic keratosis classification. AIMS Electronics and Electrical Engineering, 2020, 4(1): 47-56. doi: 10.3934/ElectrEng.2020.1.47 |
| [8] | Shaswat Chirantan, Bibhuti Bhusan Pati . Integration of predictive and computational intelligent techniques: A hybrid optimization mechanism for PMSM dynamics reinforcement. AIMS Electronics and Electrical Engineering, 2024, 8(2): 265-291. doi: 10.3934/electreng.2024012 |
| [9] | B Naresh Kumar, Jai Sukh Paul Singh . Intelligence-based optimized cognitive radio routing for medical data transmission using IoT. AIMS Electronics and Electrical Engineering, 2022, 6(3): 223-246. doi: 10.3934/electreng.2022014 |
| [10] | Farhan Khan, Sing Kiong Nguang . Dual sensing scheduling algorithm for WSN based road network surveillance. AIMS Electronics and Electrical Engineering, 2021, 5(1): 38-54. doi: 10.3934/electreng.2021003 |
Skin cancer is a pandemic disease now worldwide, and it is responsible for numerous deaths. Early phase detection is pre-eminent for controlling the spread of tumours throughout the body. However, existing algorithms for skin cancer severity detections still have some drawbacks, such as the analysis of skin lesions is not insignificant, slightly worse than that of dermatologists, and costly and time-consuming. Various machine learning algorithms have been used to detect the severity of the disease diagnosis. But it is more complex when detecting the disease. To overcome these issues, a modified Probabilistic Neural Network (MPNN) classifier has been proposed to determine the severity of skin cancer. The proposed method contains two phases such as training and testing the data. The collected features from the data of infected people are used as input to the modified PNN classifier in the current model. The neural network is also trained using Spider Monkey Optimization (SMO) approach. For analyzing the severity level, the classifier predicts four classes. The degree of skin cancer is determined depending on classifications. According to findings, the system achieved a 0.10% False Positive Rate (FPR), 0.03% error and 0.98% accuracy, while previous methods like KNN, NB, RF and SVM have accuracies of 0.90%, 0.70%, 0.803% and 0.86% correspondingly, which is lesser than the proposed approach.
In most places, skin cancer, and its prevalence has risen substantially during the last generation to the extent that it has reached epidemic proportions [1]. The two most frequent types of skin cancer are Melanoma and Non-Melanoma Skin Cancers (NMSC). Melanoma is also known as Malignant Melanoma. In both men and women, melanoma is the 19th most frequent cancer. It is the most lethal type of skin cancer [2]. It's critical to detect various types of skin cancers because this will lead to the best treatment options [3]. It is the most prevalent cancer in males and the second most frequent cancer in women, trailing only breast cancer. Individuals who are white across the world are developing melanoma at an enhancing rate. Skin cancer is caused by genetic disposition, ultraviolet rays, organic carcinogens such as tar, oil products, and chemical fertilizers, as well as lead, immuno-suppression, gender, chronic inflammation, age and smoking[4]. The most prevalent cause of skin cancer is continuous exposure to sunlight, which accounts for 90% of all occurrences. Exposure to sunlight is the major risk factor causing sunburn. Avoiding sunlight exposure can lower the risk of skin cancer by reducing exposure to sunlight, as well as preventing the cumulative hazardous effects of sunlight. As an outcome, promoting preventive measures in the prevention of skin cancer is crucial [5].
To compile information from medical databases, machine learning based prediction algorithms were utilized to forecast the start of a variety of ailments and offer an early treatment option. Researchers extracted hidden patterns and relationships from massive amounts of data with many variables using a machine learning method that coordinates many statistical analyses and databases [6]. This subject has already been the subject of extensive manual and mechanical research. Due to the method's current unaffordable cost over a short period, it is no longer practical. On the other hand, the automatic system is not always dependable but is occasionally beneficial. When applying deep learning methods, it performs better than machine learning techniques [7]. Computer-based technology has made it possible to detect melanoma symptoms in a more pleasant, least expensive, and faster manner. Several non-invasive procedures are available to investigate skin cancer signs and intensity like melanoma and non-melanoma. Deep learning architectures can be utilized to address a broad range of classification issues due to their generality. It's becoming more popular as a strategy for multi-label classification, especially in the medical field [8]. The programme could help clinicians better spot cancer, offer initial therapy options, and provide multi-class categorization for 134 illnesses. Large amounts and diversity of data have been mainly related to recent advancements in Deep Learning (DL) models. Large volumes of data are essential in improving Machine Learning (ML) models' performance [9].
Artificial neural network approaches were addressed within this advanced subfield of machine learning. Algorithms that will aid in the prediction of melanoma with greater precision are built using DL techniques [10]. DL approaches are employed in various applications, including voice recognition, pattern matching and bioinformatics [11]. DL systems have delivered exceptional results in various applications when compared to older machine learning approaches [12]. Various machine learning algorithms have been used to detect diseases. But the condition of the disease diagnosis is more complex when detecting the disease. To address these challenges, the PNN classifier is presented as a method for determining the severity of skin cancer. The reason for using PNN in this system is that they are significantly faster than perceptron neural networks. The PNN classifier is fast and more accurate classifier than other back-propagation classifiers. The PNN is widely utilized for solving classification issues. Furthermore, these networks have the potential to outperform traditional classifiers like Multi-Layer Perceptron (MLP) networks in terms of accuracy [13]. And also it produces high accuracy compared to existing ML methods. It will also use to diagnose illness at an early stage and spare people from contracting it.
The main contributions of research works are given below.
 Skin cancer severity prediction model was designed using PNN classifier.
Skin cancer severity prediction model was designed using PNN classifier.
 For train modified PNN, the SMO algorithm was used to improve performance of classifier.
For train modified PNN, the SMO algorithm was used to improve performance of classifier.
 The flattening parameter of PNN classifier optimized using SMO optimization.
The flattening parameter of PNN classifier optimized using SMO optimization.
 A modified PNN classifier predicted four classes effectively. To demonstrate the performance of the proposed design, the results of the proposed technique were contrasted to those of numerous other techniques.
A modified PNN classifier predicted four classes effectively. To demonstrate the performance of the proposed design, the results of the proposed technique were contrasted to those of numerous other techniques.
The remainder of the text is organized as follows: section 2 presents numerous studies on previous intensity prediction methods for melanoma risk detection. Section 3 contains the proposed methodology of the severity prediction model. These obtained results are discussed in Section 4. Section 5 contains the conclusion of the proposed design.
Recently, various techniques utilized to diagnose the severity of skin cancer. In this section, some of the existing skin cancer prediction techniques used in deep learning techniques are reviewed below.
Seung Seog Han et al. [14] have developed a Deep Neural Network (DNN) Help Medical Practitioners Diagnose Skin Cancer and Identify Possible Treatments for 134 Skin Disorders. The technology helped clinicians better spot cancer, offer initial treatment options, as well as provide multi-class categorization for 134 ailments. The findings show that the system could be used as augmented intelligence to aid dermatologists in their diagnostic work. Overall, the algorithm performed similarly to that of dermatology residents in both malignancy and treatment predictions, but slightly worse than that of dermatologists. Mohammad Ali Kadampur and Sulaiman Al Riyaee et al. [15] suggested a cloud-based model-driven infrastructure for identifying dermal cell pictures for skin cancer detection. A design assists in the diagnosis of skin cancer with greater precision are constructed utilizing model-driven infrastructure in cloud, which uses DL approaches in its basic deployments. This model demonstrated how to make systems to categorize dermal cell pictures. The DL algorithms constructed were indeed evaluated on data sets, and a quantitative area under the Curve (AUC) of 99.77 % was obtained. Non-parametric methods, on either hand, do not rely on data being in a normally distributed format.
Chih-Wei Huang et al. [16] have introduced the DL prediction method for NMSC in EHR data. Algorithms based on DL that could predict the probability of advanced NMSC in Taiwanese persons. The convolution neural network (CNN) model was developed with all patient's conditions and drugs in mind. The specificity and sensitivity of the algorithm were assessed using the area under the receiver operating characteristic curve. The AUC of the model had a mean of 0.894, according to the results. The model's performance was seen with a specificity of 0.82, a PPV value of 0.57 and a sensitivity of 0.83. Hardik Nahata & Satya P. Singh et al. [17] has introduced utilizing DL for skin cancer detection and diagnosis. CNN has developed a skin cancer detection system which can distinguish skin-related cancer and aid in early detection. Different networking designs such as dense layers, convolutional layers, pooling layers and dropout layers were used to create and evaluate the model. Regarding rapid resolution, algorithm will employ transfer learning methods. Information from International Skin Imaging Collaboration (ISIC) competition records was used to evaluate and train the model. However large amounts of data were critical for enhancing the performance of ML methods. However, getting large amounts of data was either costly or time-consuming.
Kumar Abhishek et al. [18] developed automated ML techniques to identify skin decease via images that were approaching dermatologist-level precision. This method provided the first study to look at image-based clinical management decision prediction without forecasting diagnosis. This study also showed by simultaneously building a method to forecast seven-point criterion and skin disease detection enhances management predictive performance. For a collection of 100 dermoscopic photos, researchers analyzed the diagnostic accuracy of ensembles of automatic diagnosis prediction methods to 8 dermatologists' management decisions, but they did not employ a learning-based technique to directly predict management decisions. Rehan Ashraf et al. [19] developed a method for classifying skin cancer that is effective. Skin cancer was defined as the growth and distribution of abnormal cells in the physical body's skin. A DCNN-based approach for obtaining spatial information was developed in this paper as a method for skin cancer classification. Our proposed method's classification outcomes were presented to that state-of-the-art approaches utilizing a smaller number of factors/feature vectors. The experiments showed that the technique has an accuracy rate of roughly 93.29 per cent. The accurate study of skin lesions is, however, not unimportant even for seasoned staff.
Roman C. Maron et al. [20] have suggested a test on the resilience of neural networks in skin cancer categorization. The study's purpose was to develop a dermoscopic melanoma baseline for evaluating classifier robustness to OOD data. They use customized dermoscopic image collection and a set of visual alterations to create an OOD sturdiness test and examine the durability of four distinct CNN. They built an OOD robustness benchmark and evaluated the resilience of four different convolutional neural networks using a proprietary dermoscopic picture library and a series of image manipulations. The performance of the classifier validated CNN's flaws and served as a reference. Overall, this benchmark should help the creation of more powerful skin cancer classifiers by facilitating a more complete review procedure. Moreover, in dermatological such difficult test cases still were lacking. Md Shahin Ali et al. [21] developed a better approach for skin cancer identification using DCNNs and transfer learning methods. A deep Convolutional Neural Network (DCNN) system based on DL for reliably identifying malignant or benign skin infections was shown in this study. This DCNN approach was consistent against a variety of transfer learning methods, including ResNet, Mobile Net, VGG-16, Dense Net and Alex Net among others, to assess its efficiency. This technique was perhaps the most effective, with a training accuracy of 93.16 % and an assessment accuracy of 91.93 %. The DCNN model's ending research showed it was more reliable and robust than previous transfer learning methods. The processing time, on either hand, is not provided, which could raise the value of the findings.
Ankita Pramanik & Rivu Chakraborty et al. [22] suggested detecting cancerous lesions in dermatoscopic imagery with the DL prediction method. Using Dermatoscopic pictures, deep learning techniques may be utilized to automatically diagnose pigmented skin lesions. In this research, 16-layer DCNN was developed from the ground up. The architecture was validated without augmentation on dermatoscopic pictures from the Kaggle dataset collection. It had an efficiency of 87.58 per cent, which was significantly higher than previous work on the Kaggle dataset without augmentation. Yet, the overall process took a long time and the device took up a lot of space. Abhishek C. Salian et al. [23] developed DL methods that were used to categorize skin lesions. Recognizing lesions using skin scans is an important step in pre-diagnosis, supporting physicians and determining the patient's medical state. Only melanoma can be classified from a series of skin lesion photos, according to recent research. Employing Mobile nett, VGG-16, or their algorithm could reliably classify skin related lesions with above 80% reliability. Multiple DL topologies were employed to accurately classify skin lesions in contrast to earlier investigations. However, some skin blemishes might develop into cancerous tumours over time.
The Medical diagnostics issues for the essential aspects of the PNN-based approach were addressed by Izonin et al. [31]. The PNN topology was shown, and the process of how it works is detailed. There were two described algorithms for creating the output signal of these kinds of neural networks. Using both methods and a small sample of real medical data, the PNN operation was modelled. The fundamental task of quality prediction was completed. It has been shown that utilising an algorithm that describes the entire system of events significantly increases the accuracy of PNN operation. A hybrid classifier using PNN-based dimensionality reduction approach for biomedical engineering task was presented by Izonin et al. [32]. This technique uses a hybrid strategy that combines PNN, Ito decomposition, and a classifier for logistic regression. This method began by replacing the initial inputs with a set of probabilities calculated by utilizing PNN, which reduces the dimension of the input data space. The Ito decomposition method was then employed, and the resulting dataset was used to apply the classifier. Utilizing a genuine task, the provided strategy was evaluated. It has been demonstrated through experiments that adding PNN outputs to the initial inputs significantly improves the generalization capabilities of the Logistic Regression Classifier. A hybrid PNN-SVM (Probabilistic Neural Network-Support Vector Machine) high-precision method for the intelligent evaluation of alloy characteristics for additive manufacturing of biomedical implants was presented by Izonin et al. [33]. We have put forth a fresh method for increasing the dimensionality of the input data space using the outputs from the modified PNN topology's summation layer.
A system for accurate brain tumour categorization using MRI images was described by Guan et al. [34]. To prevent the network from over-fitting in this study, the brain MRI image was first pre-processed to enhance its visual quality and increase the number of sample images. The tumour proposals or locations were then obtained using an approach based on agglomerative clustering. Third, the backbone architecture receives upgraded input images and picture recommendations for the purpose of feature extraction. Fourth, based on a refinement network, high-quality image ideas or locations were attained. These improved recommendations were then passed to the head network to complete the desired classification task after being aligned to the same size. An automated method for locating brain tumours using magnetic resonance imaging was provided by Aamir et al. (MRI) [35]. First, pre-processing was done on brain MRI images to improve visual clarity. Second, they used two distinct deep learning models that have already been trained to extract significant features from images. The partial least squares (PLS) approach was then used to merge the obtained feature vectors into a hybrid feature vector. Third, agglomerative clustering was used to identify the primary tumour areas.
Based on above revealed article several significant challenges of skin cancer severity prediction model were non-parametric approaches were not constrained by the assumption that data distributed normally [14], slightly worse than that of dermatologists [15], costly and time-consuming [17], did not use a learning-based methodology to directly predict management decisions [18], The need of a thorough examination of skin lesions cannot be overstated [19], dermatology also lacks hard test sets [20], execution time was not mentioned [21]. Systems occupy huge storage [22]. To overcome these issues a modified Probabilistic Neural Network is proposed to predict skin cancer severity.
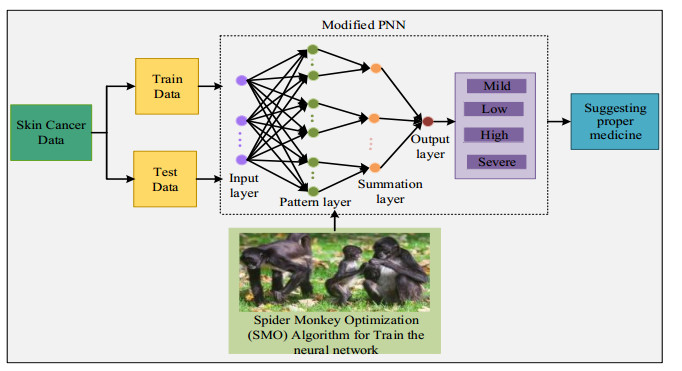
Modified PNN classifier based proposed for diagnosing skin cancer severity condition. In recent years, there are several people infected with skin cancer which is enlarged day to day over the world due to global warming. Therefore, the current technologies can be utilized to detect the disease in the initial stage, this can save people. There are many classification approaches commonly used to diagnose cancer disease. Many researchers have devised methods to detect a variety of diseases employing ML and DL methods, but the condition of disease diagnosis is more complicated than detecting sickness. Therefore, an effective skin cancer feature selection technique was derived in the initial phases of our research, which is presented in the first article. After selecting accurate features the ANFIS classifier was utilized to classify the extracted features to predict the skin cancer disease, which is presented in the second article. This paper mainly focuses on proposing an effective model to detect the severity condition of skin cancer disease utilizing the MPNN classifier. The architecture of the proposed MPNN classifier based disease severity detection model is shown in Figure 1.
The diagnosis model includes three phases in order to attain an effective disease detection like data feature selection, classification and pre-processing were achieved in our previous articles, that can predict disease is infected or not. Figure 1 illustrates the proposed architecture of the severity diagnosis model, it consists of two steps data testing and training. The extracted features of infected patient's data were used in the present design as input for the MPNN classifier. Moreover, SMO approach was used in train neural network. The classifier predicts four classes for analysing severity levels. Based on classes, doctors will suggest proper medicine for their severe condition.
The proposed design used modified PNN to detect cancer disease. The modified PNN is a form of neural network used to solve classification and pattern recognition challenges. The infected patients were identified in our previous article based on the ANFIS classifier. The severity level was analyzed in this paper, and the steps involved in the proposed methods will be briefly explained in the following sections.
The Bayesian classifier technique or assessment of probability distribution function was used to create a probabilistic neural network. The PNN classifier was fast and more accurate classifier than other back-propagation classifiers. The PNN is widely utilized for solving classification issues. PNN have several merits instead to using Back Propagation (BP) multilayer perceptron. In the Bayesian optimum method, input parameters must be classified into one of two classes. This algorithm does not require big data sets, can map each pattern optimally, and can address Back-Propagation difficulties. The statistical classification computing process, Parzen window assessment technique was utilized to attain conditional class probability. It can also establish hidden states right away using available training sets, without the need to train examples for attach weight. The pattern layer, output layer, summation layer and input layer are four layers that make up network. The input layer has same number of neurones as number of training sample parameter features. The pattern layer neurones have same number of training samples for categorization. Then, training samples were estimated based on connection among input and different pattern layers. The pattern layer's output can be estimated in each unit utilizing the following expression.
Each class corresponds to neurone in summation layer and summation layer's neurones were just linked to pattern layer of associated layer. As a result, input of summation layer components was only overlapped with own output in pattern layer units corresponding to its class. The outcome of summation layer components was directly proportional to a probability mass numbers of each class, depending on kernel function. All types of probability estimated values can be produced by normalizing output layer units. Simple threshold identification was used at the outputs decision-making layer of PNN with the purpose of picking neurone as system's output. This neurone has biggest subsequent density function in the predicted posterior distribution of every defect sequence. The neurones in the output layer were level of competition neurones, with each one functioning in one-to-one fault pattern. The amount of neurones in output layer determined using training set, which was same as number of defect types in training samples. All probability mass processes in summation layer feed into output layer neurones, which can be described as follows.
The function of PNN classification method is depending on Bayesian decision procedure, which is stated as follows. Assume labelled samples (z,y), label sample of z is z∈Rd and y∈{1,2,….12}, initially 12 features are given to classifier. Consider z belongs to the prior probability that kth class is hk, ck is impact of incorrectly identifying that sample and f1(z),fz(z),….,fk(z) is pdf of all populations. The Bayes theorem which is classifies number of unknown samples into ith class as shown in the following expression.
| hicifi(z1)>hjcjfj(z1),∀j≠i | (1) |
where, the probability density function is denoted as f1(z) of ith class assuming z. The samples for the training set is calculated based on utilizing the pdf is expressed as below.
| P(z1)=1Nσ∑Nj=1W(z1−xjσ) | (2) |
where, the input data is represented as z1∈R, the number of total training samples is considered as N, xj stands for jth sample, smoothing factor is written as σ and W stands for weight factor. Set of training samples a distribution estimator can be generally derived based on utilizing Parzen's approach. The probability distribution function of the univariate case was developed by Parzen's. P(z) Is represent as the multivariate pdf estimator, which is given as follows.
| P(z1,z2,…zd)=1Nσ1,σ2,…σd∑Nj=1W(z1−x1jσ1,z2−x2jσ2,…,zd−xdjσd) | (3) |
where, the standard deviation are σ1,σ2,σd which indicates the smoothing parameters. The interconnected neurons or units in the PNN are ordered in four layers.
Input Layer: The first one is the input layer, which contain 12 neurons in this proposed model, the dimension of the input is mentioned as neurons that allocates the pattern vector into the following neurons as expressed as below.
| z=[z1,..z12] | (4) |
Hidden Layer: The pattern layer, which has N neurones and assumes Ni of ith class for number of training data, accepts pattern z from input layer and allocates it to one of k classes. In Eq (3), [24] all smoothing parameters are almost similar to σ1=σ2=…σd as well as the weight factor is estimated utilizing the bell-shaped Gaussian function and the minimized expression is shown in Eq (3) in the standard equation of the pattern layer is given as below [25].
| ϕij(z)=1(2π)d/2×exp[−(z−xij)T(z−xij)2σ2] | (5) |
where, (z−xij) denoted as a function of ϕij, which indicates prospect of z which is equal to xij and jth data training vector is represent as xij in ith class includes jth training parameter. The smoothing parameter σ describes dispersion of Gaussian distribution and has range of 0 to 1.
Summation Layer: The summation layer, which has k neurones and determines highest probability of sequence z belonging to ith class, is as follows.
| Pi(z)=1Ni∑Nij=1ϕij(z) | (6) |
Output Layer: The decision layer is final layer and it assigns z class based on posterior probability.
| C(z)=argmaxi{Pi(z)},i=1,2,…,k | (7) |
where C(z) is class that belongs to z.
The SMO method is an optimization technique based on swarm intelligence. The position can be update according to Euclidean distance among potential solutions. Spider monkeys use postures and positions to communicate their intentions and observations, such as sexual receptivity and assault postures. They use particular call that mimics like horse's snivelling to communicate with one another over long distances. Every individual has distinct voice that allows another group members to readily recognize who is called. Spider monkeys can communicate across vast distances, allowing them to socialize, avoid enemies, share food, and gossip. They mostly employ visual and oral interaction to communicate with other members of the group. Because every stage includes a random component, it was unpredictable. The SMO approach relies on fission fusion structure of spider monkey.
The fission-fusion social method includes following key characteristics: Social Structure of Fission Fusion to prevent competition, animals live in groups of 40 to 50 monkeys that split into subdivisions for food hunting. The Global Leader (Female) is responsible of locating the group's food supply. These clusters are dispersed as smaller subgroups to go on its own with quest of food. Each day, Local Leader (Female) is responsible for directing subgroups and creating well-organized hunting route. These group members search for food sources and modify their stance based on distance to food supply. These group members interact with rest of group to keep social link strong in event of stagnation. The spider monkey's socialization inspired creation of stochastic optimization approach that mimics scavenging behaviour based on SM's fission-fusion social system (FFSS). In FFSS there are four key features are present.
1. Fission–fusion social animals are friendly and dwell in clusters of 40–50 people. The FFSS of swarm may reduce foraging rivalry between group mates by dividing group members into sub-groups to look for food.
2. For most circumstances female (global Leader) is in responsible of leading group and locating food supply. If she is unable to collect sufficient food for entire group, she divides it into smaller subgroups (varying in length from three to eight members) that hunt alone.
3. A female (local leader) is also intended to lead sub-groups and be decision-maker for every day's hunting route.
4. Individuals of such subgroups interact both inside and beyond subgroups relying on access food or need to preserve sovereign borders.
SMO is a collective repetitive hit and trial technique, similar to another population-based strategies. Global Leader Decision phase, Local Leader Decision phase, Local Leader Learning phase, Local Leader phase, Global Leader Learning phase and Global Leader phase are six steps of SMO process. These phases depict how a spider monkey modifies its position basis on previous events and behaviour of its neighbours. The following are the details of each phase of SMO algorithms:
Step 1: Initialization of the Population
Initialized residents of spider monkey is signified as N. The initial population illustrates D-dimensional vector as SMi(i=1,2…N). Consider all SMO as an optimal solution of concern. Here, SMi is initialized utilizing following expression.
| SMij=SMminj+U[0,1](SMmaxj−SMminj) | (8) |
In Eq (8), SMij is name of swarm's ith food supply, where U is consistently dispersed arbitrary integer as in interval [0, 1], and SMminj and SMmaxj are lowest and highest bounds of SMi in jth direction, correspondingly.
Step 2: Local Leader Phase (LLP)
The Local Leader Phase is the second stage of SMO. In this stage, spider monkey (SM) position can be update based on using global and local group members. The fitness function of new location and present position are compared these members utilizing greedy selection approach. The location can be update based on utilizing the following expression (9), [26] for ith SM of kth position.
| SMnewij=SMij+U[0,1](LLkj−SMij)+U[−1,1](SMrj−SMij) | (9) |
In Eq (9), jth dimension of ith solution is denoted as SMij, jth dimension of kth local leader location can be represented as LLkj. U[0,1] is consistently dispersed randomized integer as in region of (0, 1). The rth solutions, designated as SMrj like r≠i, is randomly chosen from kth group.
Step 3: Global Leader Phase (GLP)
The global leader phase is third stage. The following formula (10) used to modify rankings of Global Leader and Local Group Members depending on its previous experiences [26].
| SMnewij=SMij+U[0,1](GLj−SMij)+U[−1,1](SMrj−SMij) | (10) |
GLj corresponds to jth degree of GLP in equation (10), whereby j=1,2,…D is picked at random in within degree. The spider monkey (SM) can change its position that is predicted utilizing its fitness in this phase, depending on probabilities (probi). Likelihood can be calculated in variety of ways, but it is relation of fitness. The fitness of function represents its value and fitness computations must account for function value as demonstrated in formula (11), [27].
| probi=0.9×fitnessifitnessmax+0.1 | (11) |
Step 4: Global Leader Learning (GLL) Phase
In this phase, unscrupulous tactics were utilized to change SMO's global leadership role. The best-fitting answer was picked as global leader in present swarm. It also monitors whether global leader's position has changed and updates global limit count accordingly.
Step 5: Local Leader Learning (LLL) Phase
In this phase, position in local leader updated using conservative technique. The current spider monkey group's local leader chosen based on highly suited solution. It was examined whether status had been updated or not, as well as whether local limit count had been changed by location of local leader.
Step 6: Local Leader Decision (LLD) Phase
In LLD stage, choice can be made based on local leader's location, which is also known as local leader limit LLlimit if it is not modified up to barrier. If no changes occurs then initialize the location randomly in LL. The following expression (12) is used to decide the position of LL.
| SMnewij=SMij+U[0,1](GLj−SMij)+U[0,1](SMij−LLkj) | (12) |
The current aspect of SM drawn to global leader and repulses local leader, as seen in Eq (12).
Step 7: Global Leader Decision (GLD) Phase
Lastly, this stage takes judgement about Global Leader's location. The Global Leader Limit (GLlimit) determines if place has been changed up to limit and then this GLD creates tiny subgroups. For period, local leader utilizing LLL process for creating subgroups. The flow chart of SMO is shown as Figure 3.
For identifying the effective features, we employ a modified PNN model. SMO was employed to build PNN in proposed system. The weights in PNN also aren't "trained, " rather than allocated, and previous weights were not changed during training phase; instead, new angles were introduced into weight grids. Classifier was trained using 12 characteristics in this case. PNN offered a high level of fault tolerance and adaptability, but its operation was dependent on the network parameters chosen. Over confined design examples, smooth factor in PNN reflects entire sampling unit. As a result, least values of will provide the greatest results when classifying features, while large values of σ will do not totally deliver accurate results when obtaining classification process for multiple classes with no defined limits. As a result, significant challenge of PNN was parameter. The quantitative variation of smoothing parameter influences coefficient of similarity between design examples or modification in probability density distributed mechanism once training patterns examples have been obtained. As a result, the SMO approach was used to improve smoothing factor in speed up resolution speed of method, which can improve PNN predictive performance.
Training Phase:
The SMO algorithm was utilized in the training phase. The smoothing factor of a PNN is optimized using SMO. When SMO was used to enhance variable in PNN, σ=[σ1,σ2,…,σn] set is considered as smoothing factor and belongs to categories N. When there is spacing between sample material and example patterns 2σ.Therefore, σ can be estimated based on following equation.
| σ=g.dav[k] | (13) |
Step 1: Initialization
In step 1, SMO parameter were initialize the parameters. The spider monkey population size is considered as N.
| P={σ′1(t),σ′2(t),…σ′N(t)}(k=1,..N) | (14) |
Step 2: Evaluation of Fitness Function
According to equation (15), [27] each individual fitness value can be estimated. The fitness function of SMO was chosen using the following error function.
| E=∑Pi=1E=12∑Pi=1||d(xj)−y(xj)|| | (15) |
where, actual output is represented as y(xj) as well as desired output is represented as d(xj).
Step 3: Update the Position
According to expression (9) and (10) spider monkey position can be updated. As a result, new spider monkey was used as PNN smoothing factor.
Step 4: Termination
The final step is termination, when best solution is obtained process will be terminated.
Testing phase: The data will be tested in this testing phase with help of training phase. The final output from this neural network is classified patients skin cancer severity condition. Then, experimental analysis on proposed work was performed to study its performance in detail. The performance analysis is discussed briefly in following section. Table 1 shows the Pseudocode for the proposed model.
| Pseudocode |
| Input skin cancer infected data = D Data splitting { Training data Testing data Actual class } # Training HOA optimizer { Initialization = variable utilizing Eq. (14) Fitness function utilizing Eq. (15) Update solution Optimal solution } #Testing dataset } End Output: |
| Predict the severity level of skin cancer |
The goal of this procedure is to determine the severity of skin cancer diagnosis. The proposed Modified Probabilistic Neural Network (MPNN) is evaluated in this section. The testing was performed with help of python 3.8 software with RAM: 16GB, GPU: NVidia GeForce GTX 1650 and CPU: Intel core i5. PNN analyses information provided to see if it correctly diagnosed the severity of skin cancer. To boost the effectiveness and reliability of PNN optimum issue, optimization was used. The data was initially collected from [30], and it was split into two stages: training and testing. Before classification, the original data was needed to be improved through preprocessing. Because the raw data comprises numerous error data, thus in this proposed method adopted the preprocessing strategies from [28]. Then, these preprocessed data were given into the feature extraction strategy [28,29]. The extracted features of infected patients' data were used in the present model as the input of the modified PNN classifier. For analyzing severity degree, the classifier predicts four classifications. The first extracted data was taken and it consisted of testing and training were two aspects of the process. The extracted features of infected patients' data were used in the present model as the input of the modified PNN classifier. Here, the feature extracted data was divided into two different portions like the ratio of 80:20. Therefore, initially 80% of feature extracted data was provided as the input of the MPNN model. The pattern layer, output layer, summarization layer and input layer were all present in the modified PNN. The SMO method employed to train or enhance smoothening factor of PNN classifier. Once training was completed, the trained model was tested with the remaining 20% of feature extracted data. Finally, the output layer can detect four classes that were mild, low, high, and severe through the proposed classifier. Thus some simulation parameters were considered for this analysis which is provided in the following Table 2.
| Parameters | Values |
| MPNN | |
| Number of input nodes | N |
| Number of hidden nodes | 20 |
| Width of Gaussian function | 0.2 |
| R2 | 0.9755 |
| Train-test split | 80:20 |
| Batch size | 2048 |
| Epochs | 1000 |
| Optimizer | Adam |
| Learning rate | 10−3 |
| PSO | |
| Population size | 100, 80, 40, 20 |
| c1,c2 | 1.5 |
| wmin | 0.1 |
| wmax | 2 |
| Number of iterations | 1000 |
| FOA | |
| Randomization parameter α | 0.5 |
| wmin | 0.1 |
| wmax | 2 |
| Absorption coefficient γ | 1.0 |
| Population size | 20 |
| Max number of iterations | 1000 |
| BOA | |
| Population size | N |
| Weight factor Ω | 0.1 |
| Flying time factor H | 1.0 |
| Bat position X | 0.5 |
| Random Walk B | 0.2 |
| wmin | 0.1 |
| wmax | 2 |
| Max number of iterations | 1000 |
| SMO | |
| Population size | N |
| c1,c2 | 1.5 |
| wmin | 0.1 |
| wmax | 2 |
| Max number of iteration | 1000 |
Dataset Description: The dataset was collected from [30], which entirely comprises 34 features. Dermatology faces a serious challenge with the differential diagnosis of erythemato-squamous disorders. There weren't many differences between them other than the clinical characteristics of erythema and scaling. Psoriasis, seboreic dermatitis, lichen planus, pityriasis rosea, cronic dermatitis, and pityriasis rubra pilaris are the illnesses in this category. Typically, a biopsy was required for the diagnosis, but sadly, these diseases also share a lot of histological characteristics. Another challenge in making a differential diagnosis was that a disease may first resemble another disease while later developing its own distinctive symptoms. Twelve clinical features were used to evaluate patients at initially. Following that, skin samples were collected to assess 22 histological characteristics. An examination of the samples under a microscope yields the values of the histopathological traits. The following Table 3 shows the sample features in the dataset.
| age | erythema | scaling | definite | itching | koebner_phenomenon | polygonal_papules | follicular_papules | family_history | melanin_incontinence |
| 55 | 2 | 2 | 0 | 3 | 0 | 0 | 0 | 0 | 1 |
| 8 | 3 | 3 | 3 | 2 | 1 | 0 | 0 | 0 | 1 |
| 26 | 2 | 1 | 2 | 3 | 1 | 3 | 0 | 3 | 0 |
| 40 | 2 | 2 | 2 | 0 | 0 | 0 | 0 | 0 | 3 |
| 45 | 2 | 3 | 2 | 2 | 2 | 2 | 0 | 2 | 0 |
| 41 | 2 | 3 | 2 | 0 | 0 | 0 | 0 | 0 | 0 |
| 18 | 2 | 1 | 0 | 2 | 0 | 0 | 0 | 0 | 0 |
Figure 4 illustrates the convergence among the numbers of iteration vs fitness. The convergence analysis was done among the proposed as well as prior optimization algorithms. Here, blue line indices the applied optimal parameter selection algorithm of SMO, orange line indicates the Firefly optimization Algorithm (FOA) and gray line indicate the Bat Optimization Algorithm (BOA). When compared to the previous, the proposed shows less iterations. According to the SMO, the proposed model attained optimal parameters.
The suggested modified PNN technique was compared to some of existing approaches in terms of performance. KNN (K- Nearest Neighbour), RF (Random Forest), SVM (Support Vector Machine) and NB (Nave Bayesian) are some of known feature selection techniques utilized in comparative studies. The performance attained using these existing technique was compared with the proposed Modified PNN algorithm. Recall, specificity, accuracy, F1 score, precision, Negative Predictive Value (NPV), Error, Mathew Correlation Coefficient (MCC), False Negative Rate (FNR) and False Positive Rate (FPR) were among the performance measures utilized for comparison The comparative analysis employing previous and proposed DL methods is shown in Table 4.
| Performance Metrics (%) | MPNN | SVM | KNN | RF | NB |
| Accuracy | 98 | 86 | 90 | 83 | 70 |
| Recall | 97 | 82 | 84 | 69 | 61 |
| Error | 2 | 14 | 10 | 17 | 30 |
| Precision | 98 | 89 | 94 | 80 | 63 |
| F1 score | 97 | 89 | 81 | 79 | 63 |
| Specificity | 97 | 89 | 82 | 79 | 60 |
| MCC | 85 | 82 | 80 | 78 | 68 |
| FNR | 5 | 13 | 16 | 20 | 30 |
| FPR | 10 | 26 | 20 | 28 | 33 |
| NPV | 97 | 88 | 63 | 85 | 56 |
The above table contains the value obtained for various metrics using the proposed and existing algorithms. The value for performance metrics like FNR, error, NPV and FPR was smaller for the proposed algorithm compared to other performance metrics. The rest of the metric like F1 score, recall, specificity, accuracy, precision and MCC was greater for the proposed algorithm in comparison to conventional techniques. The graphical representation for this comparison investigation is given below.
The effectiveness of a classification method can be described using a confusion matrix. It can help you figure out which portions of your classification algorithm are accurate or erroneous. A confusion matrix is a valuable method for examining classification models. It gives you a clear picture of how well the model identified the classes based on the data you supplied, as well as how the classes were misclassified. Using confusion matrices important predictive analytics such as, specificity, recall, precision and accuracy are visualized. Confusion matrices are useful because they make it simple to compare values such as True Negatives, False Negatives, True Positives and False Positives. The proposed technique's confusion matrix is shown in Figure 5(a). For class 1 predicted label is 20, for class 2 predicted value is 8, for class 3 predicted value is 17 and for class 4 predicted value is 25.
The ROC curve is a performance indicator for identifying problems at different standard limits. The ROC is the likelihood curve, whereas AUC is a measurement of distinction. It demonstrates how the algorithm can differentiate among various classes. Plotting the true positive rate (TPR) against the false positive rate (FPR) yields the ROC curve. TPR is the proportion of all positive observations that should have been positive. There is no difference if AUC is less than 0.5. A rating of 0.7 to 0.8 is regarded acceptable, 0.8 to 0.9 is exceptional and higher than 0.9 is extraordinary. The proposed technique's ROC plot is shown in Figure 5(b). The ROC value for the proposed method was 0.98 and the AUC value was also 0.98 for the proposed classifier.
In Figure 6, the comparison approach of proposed accuracy metrics is given. The graph is plotted against different existing algorithms axis of X and obtained accuracy value axis of Y respectively. The accuracy value for the proposed MPNN classifier was 97% and seen to be in higher contrast to other existing systems such as SVM, KNN, RF, and NB whose values for accuracy were 90%, 93%, 86% and 70%. This comparison demonstrates that the suggested PNN classifier outperforms other current techniques. The proposed and existing accuracy metrics are compared in Figure 7. In this analysis also a graph is plotted against different existing algorithms on the axis of X and the precision amount is plotted on the axis of Y respectively. The proposed MPNN classifier has a precision value of 98%, which appears to be higher when compared to other classifiers on other existing systems such as SVM, KNN, RF, and NB whose values for precision were 89%, 94%, 80% and 63% respectively.
Figure 8 shows a comparison of proposed and previous recall metrics. The graph is plotted against different existing algorithms axis of X and obtained accuracy value axis of Y respectively. The accuracy value for the proposed MPNN classifier was 97% and is seen to be in higher contrast to other existing systems such as SVM, KNN, RF, and NB whose values for accuracy are 82%, 84%, 69% and 61%. This analysis proves that the proposed PNN classifier outperforms various current techniques. The proposed and existing error metrics are compared in Figure 9. In this analysis also a graph is plotted against different existing algorithms on the axis of X and the error amount is plotted on the axis of Y respectively. An error value for the proposed MPNN classifier is 3% and it is seen to be greater in comparison to other existing systems such as SVM, KNN, RF, and NB whose values for error were 10%, 7%, 14% and 30% respectively.
Figure 10 shows a comparison of proposed and previous specificity metrics. The graph is plotted against different existing algorithms' axis of X and obtained specificity value axis of Y respectively. The specificity value for the proposed MPNN classifier was 97% and it is seen to be greater in comparison to other existing systems such as SVM, KNN, RF, and NB whose values for specificity are 89%, 82%, 79% and 60%. This analysis proves that the proposed MPNN classifier outperforms various current techniques. The proposed and existing F1_Score metrics are compared in Figure 11. In this analysis also a graph is plotted against different existing algorithms on the axis of X and the F1_Score amount is plotted on the axis of Y respectively. The F1_Score value for the proposed MPNN classifier is 97% and it is seen to be greater on comparison of SVM, KNN, RF, and NB are examples of existing systems with F1_Score values of 89%, 81%, 79%, and 63% accordingly.
Figure 12 shows a comparison of proposed and previous NPV metrics. The graph is plotted against different existing algorithms axis of X and obtained NPV value axis of Y respectively. NPV for the proposed MPNN classifier was 97% and it is seen to be greater on comparison of SVM, KNN, RF, and NB are examples of existing systems with NPV values of 88%, 63%, 85%, and 56% respectively. This comparison demonstrates that the suggested MPNN classifier outperforms other current techniques. The proposed and existing FNR metrics are compared in Figure 13. In this analysis also a graph is plotted against different existing algorithms on the axis of X and FNR. In this analysis also a graph is plotted against different existing algorithms on the axis of X and the FNR amount is plotted on the axis of Y respectively. The FNR value for the proposed MPNN classifier is 5% and it is seen to be greater in comparison to other existing systems such as SVM, KNN, RF, and NB whose values for FNR were 13%, 16%, 20% and 30% respectively.
Figure 14 shows a comparison of proposed and previous FPR metrics. The graph is plotted against different existing algorithms axis of X and obtained FPR value axis of Y respectively. FPR for the proposed MPNN classifier is 10% and it is seen to be greater in comparison to other existing systems such as SVM, KNN, RF, and NB whose values for FPR were 26%, 20%, 28% and 33%. This comparison shows that the proposed MPNN classifier gives better performance compared to other existing approaches. The proposed and existing MCC metrics are compared in Figure 15. In this analysis also a graph is plotted against different existing algorithms on the axis of X and the MCC amount is plotted on the axis of Y discretely. The MCC value for the proposed MPNN classifier was 85% and it is seen to be greater in comparison to other existing systems such as SVM, KNN, RF, and NB whose values for MCC were 82%, 80%, 78% and 68% respectively. Considering the results of the full research, it is evident that the proposed MPNN classifier outperformed the previous approaches. So that the MPNN classifier is best suited for detecting skin cancer severity conditions.
This work presented a Modified Probabilistic Neural Network (PNN) classifier for diagnosing skin cancer severity conditions. Initially, the raw data was subjected to preprocessing strategies and after that, the effective features were extracted. Considering this idea, the modified PNN classifier technique was introduced. Here, the SMO technique was utilized for selecting the optimal weights in the neural network. This process comprises two phases such as testing and training. Then the feature extracted data was split into two phases with a ratio of 80:20. 80% of the data was considered for training purposes and once training was completed the trained model was tested by using the remaining 20% of data. After completed testing, the model produces four different severity conditions such as, mild, low, high, and severe. The proposed model was implemented on software to estimate its performance. The proposed MPNN method's efficiency was also verified and contrasted with existing approaches like SVM, KNN, RF and NB. According to the comparative analysis, the proposed model attained 98% accuracy. 82% of recall, 3% of error value, 98% of precision, 97% of f1_score, 97% of specificity, 85% of MCC, 5% of FNR, 10% of FPR and 97% of NPV. When compared with the prior methods the proposed technique attained better values than others. This method uses a numerical dataset for analyzing the severity condition. When compared through analyzing the severity condition through images it does not provide better diagnosis outcomes. Thus, in future, the image data will be taken for analyzing the severity conditions of cancer disease using advanced deep learning strategies.
All authors declare no conflicts of interest in this paper.
| [1] |
Putra TA, Rufaida SI and Leu JS (2020) Enhanced skin condition prediction through machine learning using dynamic training and testing augmentation. IEEE Access 8: 40536–40546. https://doi.org/10.1109/ACCESS.2020.2976045 doi: 10.1109/ACCESS.2020.2976045

|
| [2] | Nahata H and Singh SP (2020) Deep learning solutions for skin cancer detection and diagnosis. Machine Learning with Health Care Perspective, 159–182. Springer, Cham. https://doi.org/10.1007/978-3-030-40850-3_8 |
| [3] |
Mijwil MM (2021) Skin cancer disease images classification using deep learning solutions. Multimed Tools Appl 80: 26255–26271. https://doi.org/10.1007/s11042-021-10952-7 doi: 10.1007/s11042-021-10952-7

|
| [4] |
Jeihooni AK and Moradi M (2019) The effect of educational intervention based on PRECEDE model on promoting skin cancer preventive behaviors in high school students. J Cancer Educ 34: 796–802. https://doi.org/10.1007/s13187-018-1376-y doi: 10.1007/s13187-018-1376-y

|
| [5] |
Jeihooni AK and Rakhshani T (2019) The effect of educational intervention based on health belief model and social support on promoting skin cancer preventive behaviors in a sample of Iranian farmers. J Cancer Educ 34: 392–401. https://doi.org/10.1007/s13187-017-1317-1 doi: 10.1007/s13187-017-1317-1

|
| [6] | Mohapatra S, Abhishek NVS, Bardhan D, et al. (2021) Skin cancer classification using convolution neural networks. Advances in Distributed Computing and Machine Learning, 433–442. Springer, Singapore. https://doi.org/10.1007/978-981-15-4218-3_42 |
| [7] |
Maxwell A, Li R, Yang B, et al. (2017) Deep learning architectures for multi-label classification of intelligent health risk prediction. BMC bioinformatics, 18: 121–131. https://doi.org/10.1186/s12859-017-1898-z doi: 10.1186/s12859-017-1898-z

|
| [8] |
Han SS, Park I, Chang SE, et al. (2020) Augmented intelligence dermatology: deep neural networks empower medical professionals in diagnosing skin cancer and predicting treatment options for 134 skin disorders. J Investigat Dermatol 140: 1753–1761. https://doi.org/10.1016/j.jid.2020.01.019 doi: 10.1016/j.jid.2020.01.019

|
| [9] |
Kadampur MA and Riyaee SA (2020) Skin cancer detection: Applying a deep learning based model driven architecture in the cloud for classifying dermal cell images. Informatics in Medicine Unlocked 18: 100282. https://doi.org/10.1016/j.imu.2019.100282 doi: 10.1016/j.imu.2019.100282

|
| [10] | Nahata H and Singh SP (2020) Deep learning solutions for skin cancer detection and diagnosis. Machine Learning with Health Care Perspective, 159–182. Springer, Cham. https://doi.org/10.1007/978-3-030-40850-3_8 |
| [11] |
Pacheco AGC and Krohling A (2020) The impact of patient clinical information on automated skin cancer detection. Comput biol med 116: 103545. https://doi.org/10.1016/j.compbiomed.2019.103545 doi: 10.1016/j.compbiomed.2019.103545

|
| [12] |
Höhn J, Hekler A, Krieghoff-Henning E, et al. (2021) Integrating patient data into skin cancer classification using convolutional neural networks: systematic review. J Med Internet Res 23: e20708. https://doi.org/10.2196/20708 doi: 10.2196/20708

|
| [13] |
Bushehri SF and Zarchi MS (2019) An expert model for self-care problems classification using probabilistic neural network and feature selection approach. Appl Soft Comput 82: 105545. https://doi.org/10.1016/j.asoc.2019.105545 doi: 10.1016/j.asoc.2019.105545

|
| [14] |
Han SS, Park I, Chang SE, et al. (2020) Augmented intelligence dermatology: deep neural networks empower medical professionals in diagnosing skin cancer and predicting treatment options for 134 skin disorders. J Invest Dermatol 140: 1753–1761. https://doi.org/10.1016/j.jid.2020.01.019 doi: 10.1016/j.jid.2020.01.019

|
| [15] |
Kadampur MA and Riyaee SA (2020) Skin cancer detection: Applying a deep learning based model driven architecture in the cloud for classifying dermal cell images. Informatics in Medicine Unlocked 18: 100282. https://doi.org/10.1016/j.imu.2019.100282 doi: 10.1016/j.imu.2019.100282

|
| [16] | Huang CW, Nguyen AP, Wu CC, et al. (2021) Develop a Prediction Model for Nonmelanoma Skin Cancer Using Deep Learning in EHR Data. Soft Computing for Biomedical Applications and Related Topics, 11–18. Springer, Cham. https://doi.org/10.1007/978-3-030-49536-7_2 |
| [17] | Nahata H and Singh S (2020) Deep learning solutions for skin cancer detection and diagnosis. Machine Learning with Health Care Perspective, 2020,159–182. Springer, Cham. https://doi.org/10.1007/978-3-030-40850-3_8 |
| [18] |
Abhishek K, Kawahara J and Hamarneh G (2021) Predicting the clinical management of skin lesions using deep learning. Scientific reports 11: 1–14. https://doi.org/10.1038/s41598-021-87064-7 doi: 10.1038/s41598-021-87064-7

|
| [19] | Ashraf R, Kiran I, Mahmood T, et al. (2020) An efficient technique for skin cancer classification using deep learning. 2020 IEEE 23rd International Multitopic Conference (INMIC), 1–5. IEEE. https://doi.org/10.1109/INMIC50486.2020.9318164 |
| [20] |
Maron RC, Schlager JG, Haggenmüller S, et al. (2021) A benchmark for neural network robustness in skin cancer classification. Eur J Cancer 155: 191–199. https://doi.org/10.1016/j.ejca.2021.06.047 doi: 10.1016/j.ejca.2021.06.047

|
| [21] |
Ali MS, Miah MS, Haque J, et al. (2021) An enhanced technique of skin cancer classification using deep convolutional neural network with transfer learning models. Machine Learning with Applications 5: 100036. https://doi.org/10.1016/j.mlwa.2021.100036 doi: 10.1016/j.mlwa.2021.100036

|
| [22] | Pramanik A and Chakraborty R (2021) A Deep Learning Prediction Model for Detection of Cancerous Lesions from Dermatoscopic Images. Advanced Machine Learning Approaches in Cancer Prognosis, 395–423. Springer, Cham. https: //doi.org/10.1007/978-3-030-71975-3_15 |
| [23] | Salian AC, Vaze S, Singh P, et al. (2020) Skin lesion classification using deep learning architectures. 2020 3rd International conference on communication system, computing and IT applications (CSCITA), 168–173. IEEE. https://doi.org/10.1109/CSCITA47329.2020.9137810 |
| [24] |
Wang JS, Song JD and Gao J (2015) Rough set-probabilistic neural networks fault diagnosis method of polymerization kettle equipment based on shuffled frog leaping algorithm. Information 6: 49–68. https://doi.org/10.3390/info6010049 doi: 10.3390/info6010049

|
| [25] |
Chakravarthy SSR and Rajaguru H (2015) Lung cancer detection using probabilistic neural network with modified crow-search algorithm. Asian Pacific journal of cancer prevention: APJCP 20: 2159. https://doi.org/10.31557/APJCP.2019.20.7.2159 doi: 10.31557/APJCP.2019.20.7.2159

|
| [26] | Sharma H, Hazrati G and Bansal JC (2019) Spider monkey optimization algorithm. Evolutionary and swarm intelligence algorithms, 43–59. Springer, Cham. https://doi.org/10.1007/978-3-319-91341-4_4 |
| [27] |
Kumar S, Sharma B, Sharma VK, et al. (2020) Plant leaf disease identification using exponential spider monkey optimization. Sustainable computing: Informatics and systems 28: 100283. https://doi.org/10.1016/j.suscom.2018.10.004 doi: 10.1016/j.suscom.2018.10.004

|
| [28] |
Rajeshwari J and Sughasiny M (2022) Modified Filter Based Feature Selection Technique for Dermatology Dataset Using Beetle Swarm Optimization. EAI Endorsed Trans S, e2-e2. https://doi.org/10.4108/eetsis.vi.1998 doi: 10.4108/eetsis.vi.1998

|
| [29] |
Rajeshwari J and Sughasiny M (2022) Dermatology disease prediction based on firefly optimization of ANFIS classifier. AIMS Electronics and Electrical Engineering 6: 61–80. https://doi.org/10.3934/electreng.2022005 doi: 10.3934/electreng.2022005

|
| [30] | Dermatology Data set. Available from: https://archive.ics.uci.edu/ml/datasets/dermatology. |
| [31] | Izonin I, Tkachenko R, Ryvak L, et al. (2020) Addressing Medical Diagnostics Issues: Essential Aspects of the PNN-based Approach. IDDM, 209–218. |
| [32] |
Izonin I, Tkachenko R, Gregus M, et al. (2021) Hybrid Classifier via PNN-based Dimensionality Reduction Approach for Biomedical Engineering Task. Procedia Computer Science 191: 230–237. https://doi.org/10.1016/j.procs.2021.07.029 doi: 10.1016/j.procs.2021.07.029

|
| [33] |
Izonin I, Tkachenko R, Gregus M, et al. (2022) PNN-SVM Approach of Ti-Based Powder's Properties Evaluation for Biomedical Implants Production. CMC-COMPUT MATER CON 71: 5933–5947. https://doi.org/10.32604/cmc.2022.022582 doi: 10.32604/cmc.2022.022582

|
| [34] |
Guan Y, Aamir M, Rahman Z, et al. (2021) A framework for efficient brain tumor classification using MRI images. Math Biosci Eng 18: 5790–5815. https://doi.org/10.3934/mbe.2021292 doi: 10.3934/mbe.2021292

|
| [35] |
Aamir M, Rahman Z, Dayo ZA, et al. (2022) A deep learning approach for brain tumor classification using MRI images. Comput Electr Eng 101: 108105. https://doi.org/10.1016/j.compeleceng.2022.108105 doi: 10.1016/j.compeleceng.2022.108105

|
| Pseudocode |
| Input skin cancer infected data = D Data splitting { Training data Testing data Actual class } # Training HOA optimizer { Initialization = variable utilizing Eq. (14) Fitness function utilizing Eq. (15) Update solution Optimal solution } #Testing dataset } End Output: |
| Predict the severity level of skin cancer |
| Parameters | Values |
| MPNN | |
| Number of input nodes | N |
| Number of hidden nodes | 20 |
| Width of Gaussian function | 0.2 |
| R2 | 0.9755 |
| Train-test split | 80:20 |
| Batch size | 2048 |
| Epochs | 1000 |
| Optimizer | Adam |
| Learning rate | 10−3 |
| PSO | |
| Population size | 100, 80, 40, 20 |
| c1,c2 | 1.5 |
| wmin | 0.1 |
| wmax | 2 |
| Number of iterations | 1000 |
| FOA | |
| Randomization parameter α | 0.5 |
| wmin | 0.1 |
| wmax | 2 |
| Absorption coefficient γ | 1.0 |
| Population size | 20 |
| Max number of iterations | 1000 |
| BOA | |
| Population size | N |
| Weight factor Ω | 0.1 |
| Flying time factor H | 1.0 |
| Bat position X | 0.5 |
| Random Walk B | 0.2 |
| wmin | 0.1 |
| wmax | 2 |
| Max number of iterations | 1000 |
| SMO | |
| Population size | N |
| c1,c2 | 1.5 |
| wmin | 0.1 |
| wmax | 2 |
| Max number of iteration | 1000 |
| age | erythema | scaling | definite | itching | koebner_phenomenon | polygonal_papules | follicular_papules | family_history | melanin_incontinence |
| 55 | 2 | 2 | 0 | 3 | 0 | 0 | 0 | 0 | 1 |
| 8 | 3 | 3 | 3 | 2 | 1 | 0 | 0 | 0 | 1 |
| 26 | 2 | 1 | 2 | 3 | 1 | 3 | 0 | 3 | 0 |
| 40 | 2 | 2 | 2 | 0 | 0 | 0 | 0 | 0 | 3 |
| 45 | 2 | 3 | 2 | 2 | 2 | 2 | 0 | 2 | 0 |
| 41 | 2 | 3 | 2 | 0 | 0 | 0 | 0 | 0 | 0 |
| 18 | 2 | 1 | 0 | 2 | 0 | 0 | 0 | 0 | 0 |
| Performance Metrics (%) | MPNN | SVM | KNN | RF | NB |
| Accuracy | 98 | 86 | 90 | 83 | 70 |
| Recall | 97 | 82 | 84 | 69 | 61 |
| Error | 2 | 14 | 10 | 17 | 30 |
| Precision | 98 | 89 | 94 | 80 | 63 |
| F1 score | 97 | 89 | 81 | 79 | 63 |
| Specificity | 97 | 89 | 82 | 79 | 60 |
| MCC | 85 | 82 | 80 | 78 | 68 |
| FNR | 5 | 13 | 16 | 20 | 30 |
| FPR | 10 | 26 | 20 | 28 | 33 |
| NPV | 97 | 88 | 63 | 85 | 56 |
| Pseudocode |
| Input skin cancer infected data = D Data splitting { Training data Testing data Actual class } # Training HOA optimizer { Initialization = variable utilizing Eq. (14) Fitness function utilizing Eq. (15) Update solution Optimal solution } #Testing dataset } End Output: |
| Predict the severity level of skin cancer |
| Parameters | Values |
| MPNN | |
| Number of input nodes | N |
| Number of hidden nodes | 20 |
| Width of Gaussian function | 0.2 |
| R2 | 0.9755 |
| Train-test split | 80:20 |
| Batch size | 2048 |
| Epochs | 1000 |
| Optimizer | Adam |
| Learning rate | 10−3 |
| PSO | |
| Population size | 100, 80, 40, 20 |
| c1,c2 | 1.5 |
| wmin | 0.1 |
| wmax | 2 |
| Number of iterations | 1000 |
| FOA | |
| Randomization parameter α | 0.5 |
| wmin | 0.1 |
| wmax | 2 |
| Absorption coefficient γ | 1.0 |
| Population size | 20 |
| Max number of iterations | 1000 |
| BOA | |
| Population size | N |
| Weight factor Ω | 0.1 |
| Flying time factor H | 1.0 |
| Bat position X | 0.5 |
| Random Walk B | 0.2 |
| wmin | 0.1 |
| wmax | 2 |
| Max number of iterations | 1000 |
| SMO | |
| Population size | N |
| c1,c2 | 1.5 |
| wmin | 0.1 |
| wmax | 2 |
| Max number of iteration | 1000 |
| age | erythema | scaling | definite | itching | koebner_phenomenon | polygonal_papules | follicular_papules | family_history | melanin_incontinence |
| 55 | 2 | 2 | 0 | 3 | 0 | 0 | 0 | 0 | 1 |
| 8 | 3 | 3 | 3 | 2 | 1 | 0 | 0 | 0 | 1 |
| 26 | 2 | 1 | 2 | 3 | 1 | 3 | 0 | 3 | 0 |
| 40 | 2 | 2 | 2 | 0 | 0 | 0 | 0 | 0 | 3 |
| 45 | 2 | 3 | 2 | 2 | 2 | 2 | 0 | 2 | 0 |
| 41 | 2 | 3 | 2 | 0 | 0 | 0 | 0 | 0 | 0 |
| 18 | 2 | 1 | 0 | 2 | 0 | 0 | 0 | 0 | 0 |
| Performance Metrics (%) | MPNN | SVM | KNN | RF | NB |
| Accuracy | 98 | 86 | 90 | 83 | 70 |
| Recall | 97 | 82 | 84 | 69 | 61 |
| Error | 2 | 14 | 10 | 17 | 30 |
| Precision | 98 | 89 | 94 | 80 | 63 |
| F1 score | 97 | 89 | 81 | 79 | 63 |
| Specificity | 97 | 89 | 82 | 79 | 60 |
| MCC | 85 | 82 | 80 | 78 | 68 |
| FNR | 5 | 13 | 16 | 20 | 30 |
| FPR | 10 | 26 | 20 | 28 | 33 |
| NPV | 97 | 88 | 63 | 85 | 56 |