Simulation and numerical solution of fractional order Ebola virus model with novel technique

Ali Raza; Muhammad Farman; Ali Akgül; Muhammad Sajid Iqbal; Aqeel Ahmad; Ali Raza; Muhammad Farman; Ali Akgül; Muhammad Sajid Iqbal; Aqeel Ahmad

doi:10.3934/bioeng.2020017

AIMS Bioengineering

2020, Volume 7, Issue 4: 194-207. doi: 10.3934/bioeng.2020017

Previous Article Next Article

Research article

Simulation and numerical solution of fractional order Ebola virus model with novel technique

1.
Department of Mathematics and statistics, University of Lahore, Lahore-54590, Pakistan
2.
Art and Science Faculty, Department of Mathematics, Siirt University, 56100 Siirt, Turkey

Received: 07 May 2020 Accepted: 03 July 2020 Published: 06 July 2020

In this paper, nonlinear fractional order Ebola virus mathematical model is discussed for the complex transmission of the epidemic problems. We developed the fractional order Ebola virus transmission model for the treatment and control to reduce its effect on a population which play an important role for public health. Qualitative analysis has been made to verify the the steady state and uniqueness of the system is also developed for reliable results. Caputo fractional derivative operator ϕ_i ∈ (0,1] works to achieve the fractional differential equations. Laplace with Adomian Decomposition Methodsuccessfully solved the fractional differential equations. Ultimately, numerical simulations are also developed to evaluate the effects of the device parameter on spread of disease and effect of fractional parameter ϕ_i on obtained solution which can also be assessed by tabulated results.

Keywords:

Citation: Ali Raza, Muhammad Farman, Ali Akgül, Muhammad Sajid Iqbal, Aqeel Ahmad. Simulation and numerical solution of fractional order Ebola virus model with novel technique[J]. AIMS Bioengineering, 2020, 7(4): 194-207. doi: 10.3934/bioeng.2020017

Related Papers:

[1]	Norliyana Nor Hisham Shah, Rashid Jan, Hassan Ahmad, Normy Norfiza Abdul Razak, Imtiaz Ahmad, Hijaz Ahmad . Enhancing public health strategies for tungiasis: A mathematical approach with fractional derivative. AIMS Bioengineering, 2023, 10(4): 384-405. doi: 10.3934/bioeng.2023023
[2]	Rashid Jan, Imtiaz Ahmad, Hijaz Ahmad, Narcisa Vrinceanu, Adrian Gheorghe Hasegan . Insights into dengue transmission modeling: Index of memory, carriers, and vaccination dynamics explored via non-integer derivative. AIMS Bioengineering, 2024, 11(1): 44-65. doi: 10.3934/bioeng.2024004
[3]	Honar J. Hamad, Sarbaz H. A. Khoshnaw, Muhammad Shahzad . Model analysis for an HIV infectious disease using elasticity and sensitivity techniques. AIMS Bioengineering, 2024, 11(3): 281-300. doi: 10.3934/bioeng.2024015
[4]	Atta Ullah, Hamzah Sakidin, Shehza Gul, Kamal Shah, Yaman Hamed, Maggie Aphane, Thabet Abdeljawad . Sensitivity analysis-based control strategies of a mathematical model for reducing marijuana smoking. AIMS Bioengineering, 2023, 10(4): 491-510. doi: 10.3934/bioeng.2023028
[5]	Mehmet Yavuz, Waled Yavız Ahmed Haydar . A new mathematical modelling and parameter estimation of COVID-19: a case study in Iraq. AIMS Bioengineering, 2022, 9(4): 420-446. doi: 10.3934/bioeng.2022030
[6]	Fırat Evirgen, Fatma Özköse, Mehmet Yavuz, Necati Özdemir . Real data-based optimal control strategies for assessing the impact of the Omicron variant on heart attacks. AIMS Bioengineering, 2023, 10(3): 218-239. doi: 10.3934/bioeng.2023015
[7]	Ayub Ahmed, Bashdar Salam, Mahmud Mohammad, Ali Akgül, Sarbaz H. A. Khoshnaw . Analysis coronavirus disease (COVID-19) model using numerical approaches and logistic model. AIMS Bioengineering, 2020, 7(3): 130-146. doi: 10.3934/bioeng.2020013
[8]	Mariem Jelassi, Kayode Oshinubi, Mustapha Rachdi, Jacques Demongeot . Epidemic dynamics on social interaction networks. AIMS Bioengineering, 2022, 9(4): 348-361. doi: 10.3934/bioeng.2022025
[9]	Shital Hajare, Rajendra Rewatkar, K.T.V. Reddy . Design of an iterative method for enhanced early prediction of acute coronary syndrome using XAI analysis. AIMS Bioengineering, 2024, 11(3): 301-322. doi: 10.3934/bioeng.2024016
[10]	Adam B Fisher, Stephen S Fong . Lignin biodegradation and industrial implications. AIMS Bioengineering, 2014, 1(2): 92-112. doi: 10.3934/bioeng.2014.2.92

Abstract

1. Introduction

In 2014, an outbreak of Ebola virus (Ebola) decimated many people in Western Africa. With more than 16,000 clinically confirmed cases and approximately 70% mortality cases, this was the more deadly outbreak compared to 20 Ebola threats that occurred since 1976 [1]. In Africa, and particularly in the regions that were affected by Ebola outbreaks, people live close to the rain-forests, hunt bats and monkeys and harvest forest fruits for food [2], [3].

In [4] develop a SIR type model which, incorporates both the direct and indirect transmissions in such a manner that there is a provision of Ebola viruses with stability and numerical analysis is discussed. A number of mathematical models have been developed to understand the transmission dynamics of Ebola and other infectious diseases outbreak from various aspects [5], [6]. A commonly used model for characterising epidemics of diseases including Ebola is the susceptible-exposed-infectious-recovered (SEIR) model [7], and extensions to this basic model include explicit incorporation of transmission from Ebola deceased hosts [1], [8] or accounting for mismatches between symptoms and infectiousness [9], [10].

Many researchers and mathematicians have shown that fractional extensions of mathematical integer-order models are a very systematic representation of natural reality [11], [12], [13]. Recently, a non-integer-order idea is given by Caputo and Fabrizio [14]. The primary goal of this article is to use a fresh non-integer order derivative to study the model of diabetes and to present information about the diabetes model solution's uniqueness and existence using a fixed point theorem [15]. Atangana and Baleanu [16] then proposed another non-singular derivative version using the Mittag Leffler kernel function. In many apps in the actual globe, these operators have been successful [17], [18], [19]. The few existing works [4], [8], [9], [20] on the mathematical modeling tells transmission of the virus and spread of Ebola virus on the population of human. The classical settings of mathematical studies tells about spread of EVD, such as SI model, SIR model, SEIR model [4], SEIRD model, or SEIRHD model. World medical association invented medicines for Ebola virus. Quantitative approaches and obtaining an analysis of the reproduction number of Ebola outbreak were important modeling for EVD epidemics. Demographic data on Ebola risk factors and on the transmission of virus were studied through the household structured epidemic model [4], [21]. Predications, different valuable insights, personal and genomic data for EVD was reported and discovered through mathematical models [22], [23]. In [24], the authors observed spread that follows a fading memory process and also shows crossover behaviour for the EVD. They captured this kind of spread using differential operators that posses crossover properties and fading memory using the SIRDP model in [4]. They also analyzed the Ebola disease dynamic by considering the Caputo, Caputo-Fabrizio, and Atangana-Baleanu differential operators.

In this paper, we developed fractional order Ebola virus model by using the Caputo method of complex nonlinear differential equations. Caputo fractional derivative operator β ∈ (0,1] works to achieve the fractional differential equations. Laplace with Adomian Decomposition Methodsuccessfully solved the fractional differential equations. Ultimately, numerical simulations are also developed to evaluate the effects of the device parameter on spread of disease and effect of fractional parameter β on obtained solution which are also assessed by tabulated results.

2. Materials and method

2.1. Fractional order Ebola virus model

The classical model for Ebola virus model is given in [4], we developed the fractional order Ebola virus model in the followings equations

µ µ µ µ

$\begin{array}{l} D^{φ_{1}} S (t) = Π - (β_{1} I + β_{2} D + λ P) S - µ S \\ D^{φ_{2}} I (t) = (β_{1} I + β_{2} D + λ P) S - (µ + δ + γ) I \\ D^{φ_{3}} R (t) = γ I - µ R \\ D^{φ_{4}} D (t) = (µ + δ) I - b D \\ D^{φ_{5}} P (t) = σ + ξ I + α D - η P \end{array}$ (2.1)

with initial conditions

$S (0) = N_{1}, I (0) = N_{2}, R (0) = N_{3}, D (0) = N_{4}, P (0) = N_{5}$ (2.2)

Where S(t) represent the susceptible individuals, I(t) the individuals infected, R(t) the individuals recovered from the EVD, D(t) the individual that died with the Ebola virus and P(t) in the virus concentration in the environment. The susceptible human population is replenished by a constant recruitment at rate Pi. susceptible individuals S may acquire infection after effective contacts β₁ with infectious and β₂ is effective contact rate of deceased human individuals. They can also catch the infection through contact with a contaminated environment at rate λ. Infectious individuals I experience an additional death due to the disease at rate δ and they are recovered at rate γ. Deceased human individuals can be buried directly during funerals at rate b. Susceptible, infectious and recovered individuals die naturally at rate µ. η, ξ, α, represent the decay rate, shedding rate of infected, and shedding rate of deceased, respectively. The recruitment rate of the Ebola virus in the environment expressed as σ.

2.2. Equilibrium point and stability

Here system (2.1) is analyzed qualitatively analyzed for feasibility and numerical solution at disease free and endemic equilibrium point. For this purpose, we used

$D^{φ_{1}} S (t) = D^{φ_{2}} I (t) = D^{φ_{3}} R (t) = D^{φ_{4}} D (t) = D^{φ_{5}} P (t) = 0$ (2.3)

in system (1). For disease free equilibrium, we have E = (π/µ,0,0,0,0) and endemic equilibrium is

$E^{*} = (S^{*}, I^{*}, R^{*}, D^{*}, P^{*}),$

where

µ µ µ µ µ µ

$S^{*} = \frac{π}{µ R_{0}}; I^{*} = \frac{π (R_{0} - 1)}{(µ + δ + γ) R_{0}}; R^{*} = \frac{π γ (R_{0} - 1)}{µ (µ + δ + γ) R_{0}}; D^{*} = \frac{π (µ + δ) (R_{0} - 1)}{b (µ + δ + γ) R_{0}}$

µ µ

$P^{*} = \frac{π (b ξ + α δ + α µ) (R_{0} - 1)}{b η (µ + δ + γ) R_{0}}$

is endemic equilibria of the system (1). Where reproductive number is

µ µ µ µ

$R_{0} = \frac{η π (b β_{1} + β_{2} (µ + δ)) + λ π (b ξ + α δ + α µ)}{b η µ (µ + δ + γ)}$

Theorem. 1 There is a unique solution for the initial value problem given in system (2.1), and the solution remains in R⁵, x ≥ 0.

Proof: We need to show that the domain R⁵, x ≥ 0 is positively invariant. Since

µ

$\begin{array}{l} D^{φ_{1}} S (t) |_{S = 0} = Π \geq 0 \\ D^{φ_{2}} I (t) |_{I = 0} = (β_{1} I + β_{2} D + λ P) S \geq 0 \\ D^{φ_{3}} R (t) |_{R = 0} = γ I \geq 0 \\ D^{φ_{4}} D (t) |_{D = 0} = (µ + δ) I \geq 0 \\ D^{φ_{5}} P (t) |_{P = 0} = σ + ξ I + α D \geq 0 \end{array}$

Hence the solution lies in feasible domain, so the uniqueness and solution of the system exists.

2.3. Numerical analysis of the model

Consider the fractional-order Ebola virus model (2.1), by using Caputo definition with Laplace transform, we have

$\begin{array}{l} ℒ {D^{φ_{1}} S (t)} = Π ℒ {1} - β_{1} ℒ {I S} - β_{2} ℒ {D S} - λ ℒ {P S} - µ ℒ {S} \\ ℒ {D^{φ_{2}} I (t)} = β_{1} ℒ {I S} + β_{2} ℒ {D S} + λ ℒ {P S} - (µ + δ + γ) ℒ {I} \\ ℒ {D^{φ_{3}} R (t)} = γ ℒ {I} - µ ℒ {R} \\ ℒ {D^{φ_{4}} D (t)} = (µ + δ) ℒ {I} - b ℒ {D} \\ ℒ {D^{φ_{5}} P (t)} = σ ℒ {1} + ξ ℒ {I} + α ℒ {D} - η ℒ {P} \end{array}$ (2.4)

$\begin{array}{l} S^{φ_{1}} ℒ {S (t)} - S^{φ_{1} - 1} S (0) = Π ℒ {1} - β_{1} ℒ {I S} - β_{2} ℒ {D S} - λ ℒ {P S} - µ ℒ {S} \\ S^{φ_{2}} ℒ {I (t)} - S^{φ_{2} - 1} I (0) = β_{1} ℒ {I S} + β_{2} ℒ {D S} + λ ℒ {P S} - (µ + δ + γ) ℒ {I} \\ S^{φ_{3}} ℒ {R (t)} - S^{φ_{3} - 1} R (0) = γ ℒ {I} - µ ℒ {R} \\ S^{φ_{4}} ℒ {D (t)} - S^{φ_{4} - 1} D (0) = {µ + δ} ℒ {I} - b ℒ {D} \\ S^{φ_{5}} ℒ {P (t)} - S^{φ_{5} - 1} P (0) = σ ℒ {1} + ξ ℒ {I} + α ℒ {D} - η ℒ {P} \end{array}$ (2.5)

by using the initial conditions (2.2), we get

$\begin{matrix} ℒ {S (t)} = \frac{N_{1}}{S} + \frac{Π}{S^{φ_{1} + 1}} - \frac{β_{1}}{S^{φ_{1}}} ℒ {I S} - \frac{β_{2}}{S^{φ_{1}}} ℒ {D S} - \frac{λ}{S^{φ_{1}}} ℒ {P S} - \frac{µ}{S^{φ_{1}}} ℒ {S} \\ ℒ {I (t)} = \frac{N_{2}}{S} + \frac{β_{1}}{S^{φ_{2}}} ℒ {I S} + \frac{β_{2}}{S^{φ_{2}}} ℒ {D S} + \frac{λ}{S^{φ_{2}}} ℒ {P S} - \frac{µ + δ + γ}{S^{φ_{2}}} ℒ {I} \\ ℒ {R (t)} = \frac{N_{3}}{S} + \frac{γ}{S^{φ_{3}}} ℒ {I} - \frac{µ}{S^{φ_{3}}} ℒ {R} \\ ℒ {D (t)} = \frac{N_{4}}{S} + \frac{µ + δ}{S^{φ_{4}}} ℒ {I} - \frac{b}{S^{φ_{4}}} ℒ {D} \\ ℒ {P (t)} = \frac{N_{5}}{S} + \frac{σ}{S^{φ_{5} + 1}} + \frac{ξ}{S^{φ_{5}}} ℒ {I} + \frac{α}{S^{φ_{5}}} ℒ {D} - \frac{η}{S^{φ_{5}}} ℒ {P} \end{matrix}$ (2.6)

We have followings infinite series solution

$S = \sum_{k = 0}^{\infty} S_{k}, I = \sum_{k = 0}^{\infty} I_{k}, R = \sum_{k = 0}^{\infty} R_{k}, D = \sum_{k = 0}^{\infty} D_{k}, P = \sum_{k = 0}^{\infty} P_{k}$ (2.7)

The nonlinearity IS, DS and PS can be written as

$I S = \sum_{k = 0}^{\infty} A_{k}, D S = \sum_{k = 0}^{\infty} B_{k}, P S = \sum_{k = 0}^{\infty} C_{k}$ (2.8)

where A_k, B_k and C_k is called the Adomian polynomials. We have the followings results

$ℒ {S_{0}} = \frac{N_{1}}{S} + \frac{Π}{S^{φ_{1} + 1}}, ℒ {I_{0}} = \frac{N_{2}}{S}, ℒ {R_{0}} = \frac{N_{3}}{S}, ℒ {D_{0}} = \frac{N_{4}}{S}, ℒ {P_{0}} = \frac{N_{5}}{S} + \frac{σ}{S^{φ_{5} + 1}}$ (2.9)

Similarly, we have

$\begin{array}{l} ℒ {S_{1}} = - \frac{β_{1}}{S^{φ_{1}}} ℒ {A_{0}} - \frac{β_{2}}{S^{φ_{1}}} ℒ {B_{0}} - \frac{λ}{S^{φ_{1}}} ℒ {C_{0}} - \frac{µ}{S^{φ_{1}}} ℒ {S_{0}},... \\ ℒ {S_{k + 1}} = - \frac{β_{1}}{S^{φ_{1}}} ℒ {A_{k}} - \frac{β_{2}}{S^{φ_{1}}} ℒ {B_{k}} - \frac{λ}{S^{φ_{1}}} ℒ {C_{k}} - \frac{µ}{S^{φ_{1}}} ℒ {S_{k}} \end{array}$ (2.10)

$\begin{array}{l} ℒ {I_{1}} = \frac{β_{1}}{S^{φ_{2}}} ℒ {A_{0}} + \frac{β_{2}}{S^{φ_{2}}} ℒ {B_{0}} + \frac{λ}{S^{φ_{2}}} ℒ {C_{0}} - \frac{µ + δ + γ}{S^{φ_{2}}} ℒ {I_{0}},... \\ ℒ {I_{k + 1}} = \frac{β_{1}}{S^{φ_{2}}} ℒ {A_{k}} + \frac{β_{2}}{S^{φ_{2}}} ℒ {B_{k}} + \frac{λ}{S^{φ_{2}}} ℒ {C_{k}} - \frac{µ + δ + γ}{S^{φ_{2}}} ℒ {I_{k}} \end{array}$ (2.11)

$\begin{array}{l} ℒ {R_{1}} = \frac{γ}{S^{φ_{3}}} ℒ {I_{0}} - \frac{µ}{S^{φ_{3}}} ℒ {R_{0}},... \\ ℒ {R_{k + 1}} = \frac{γ}{S^{φ_{3}}} ℒ {I_{k}} - \frac{µ}{S^{φ_{3}}} ℒ {R_{k}} \end{array}$ (2.12)

$\begin{array}{l} ℒ {D_{1}} = \frac{µ + δ}{S^{φ_{4}}} ℒ {I_{0}} - \frac{b}{S^{φ_{4}}} ℒ {D_{0}},... \\ ℒ {D_{k + 1}} = \frac{µ + δ}{S^{φ_{4}}} ℒ {I_{k}} - \frac{b}{S^{φ_{4}}} ℒ {D_{k}} \end{array}$ (2.13)

$\begin{array}{l} ℒ {P_{1}} = \frac{ξ}{S^{φ_{5}}} ℒ {I_{0}} + \frac{α}{S^{φ_{5}}} ℒ {D_{0}} - \frac{η}{S^{φ_{5}}} ℒ {P_{0}},... \\ ℒ {P_{k + 1}} = \frac{ξ}{S^{φ_{5}}} ℒ {I_{k}} + \frac{α}{S^{φ_{5}}} ℒ {D_{k}} - \frac{η}{S^{φ_{5}}} ℒ {P_{k}} \end{array}$ (2.14)

We get the followings generalized form for analysis and numerical solution.

$ℒ {S_{k + 1}} = - \frac{β_{1}}{S^{φ_{1}}} ℒ {A_{k}} - \frac{β_{2}}{S^{φ_{1}}} ℒ {B_{k}} - \frac{λ}{S^{φ_{1}}} ℒ {C_{k}} - \frac{µ}{S^{φ_{1}}} ℒ {S_{k}}$ (2.15)

$ℒ {I_{k + 1}} = \frac{β_{1}}{S^{φ_{2}}} ℒ {A_{k}} + \frac{β_{2}}{S^{φ_{2}}} ℒ {B_{k}} + \frac{λ}{S^{φ_{2}}} ℒ {C_{k}} - \frac{µ + δ + γ}{S^{φ_{2}}} ℒ {I_{k}}$ (2.16)

$ℒ {R_{k + 1}} = \frac{γ}{S^{φ_{3}}} ℒ {I_{k}} - \frac{µ}{S^{φ_{3}}} ℒ {R_{k}}$ (2.17)

$ℒ {D_{k + 1}} = \frac{µ + δ}{S^{φ_{4}}} ℒ {I_{k}} - \frac{b}{S^{φ_{4}}} ℒ {D_{k}}$ (2.18)

$ℒ {P_{k + 1}} = \frac{ξ}{S^{φ_{5}}} ℒ {I_{k}} + \frac{α}{S^{φ_{5}}} ℒ {D_{k}} - \frac{η}{S^{φ_{5}}} ℒ {P_{k}}$ (2.19)

3. Results

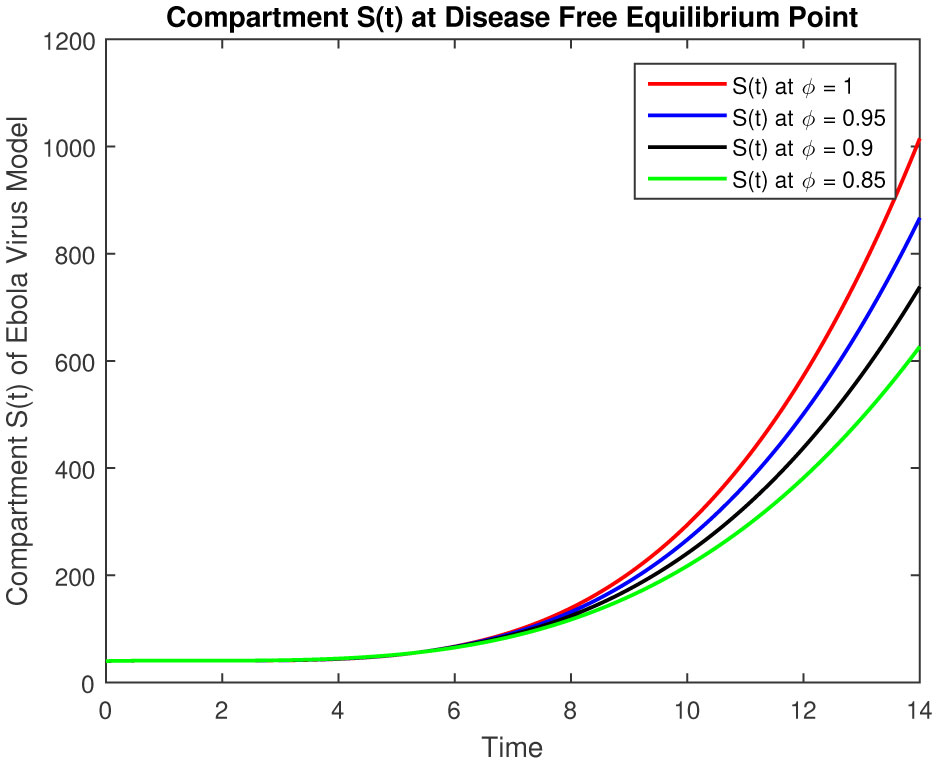
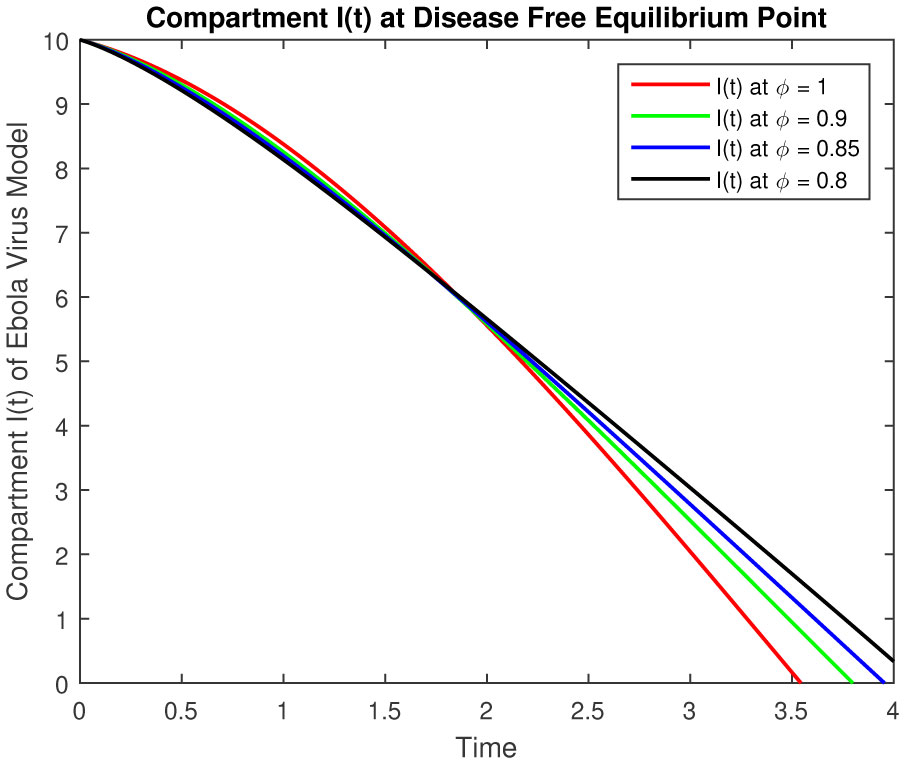
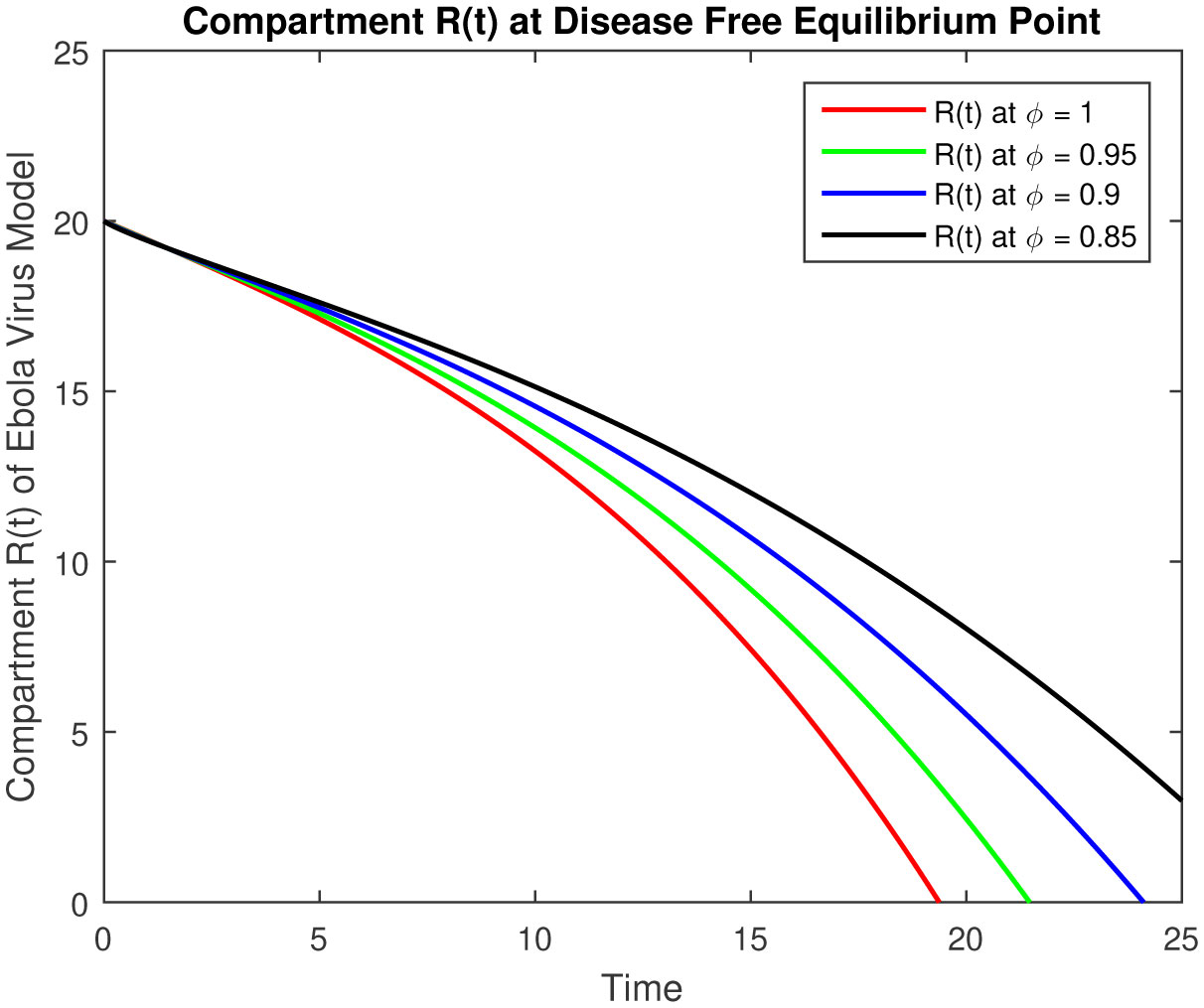
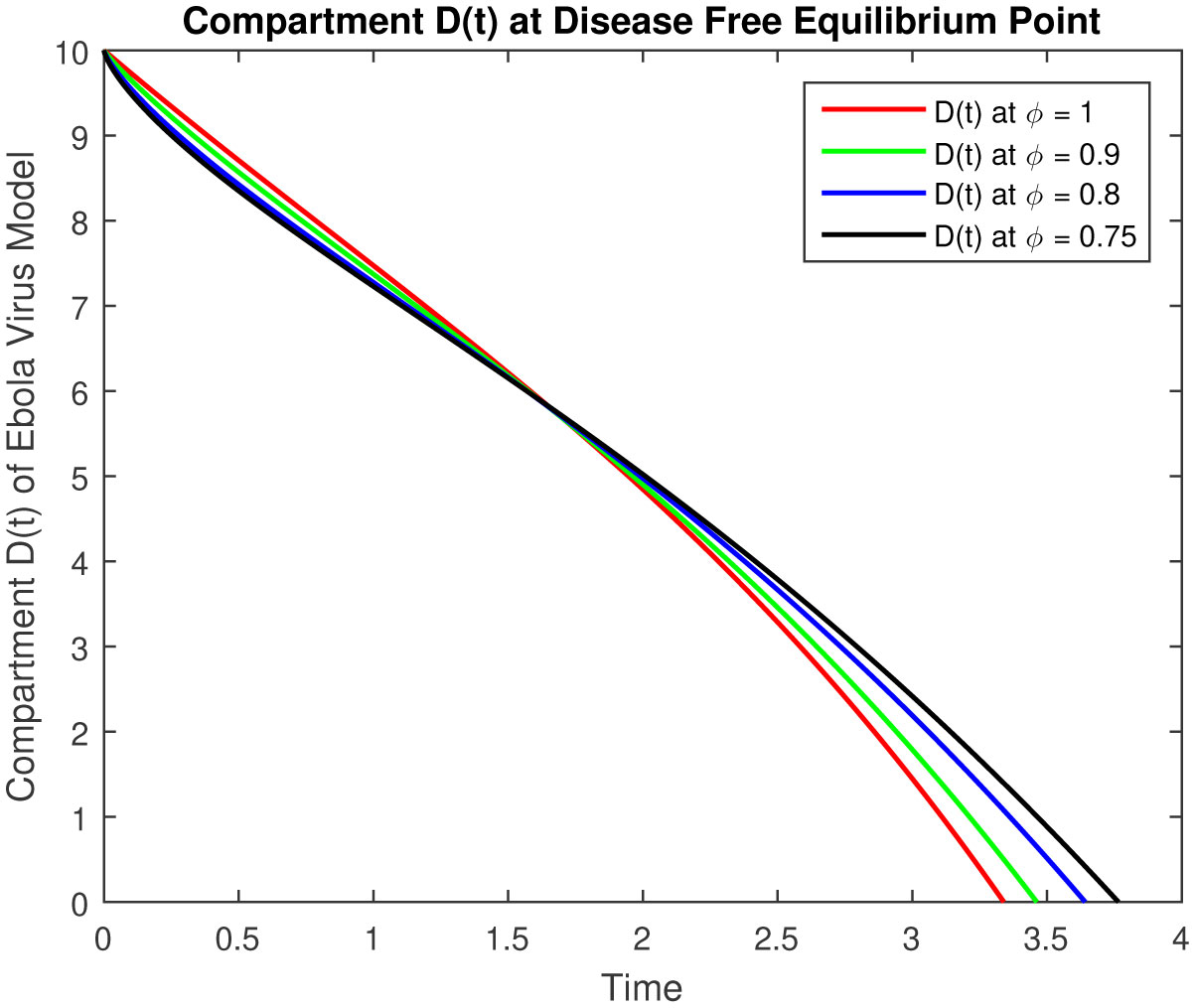
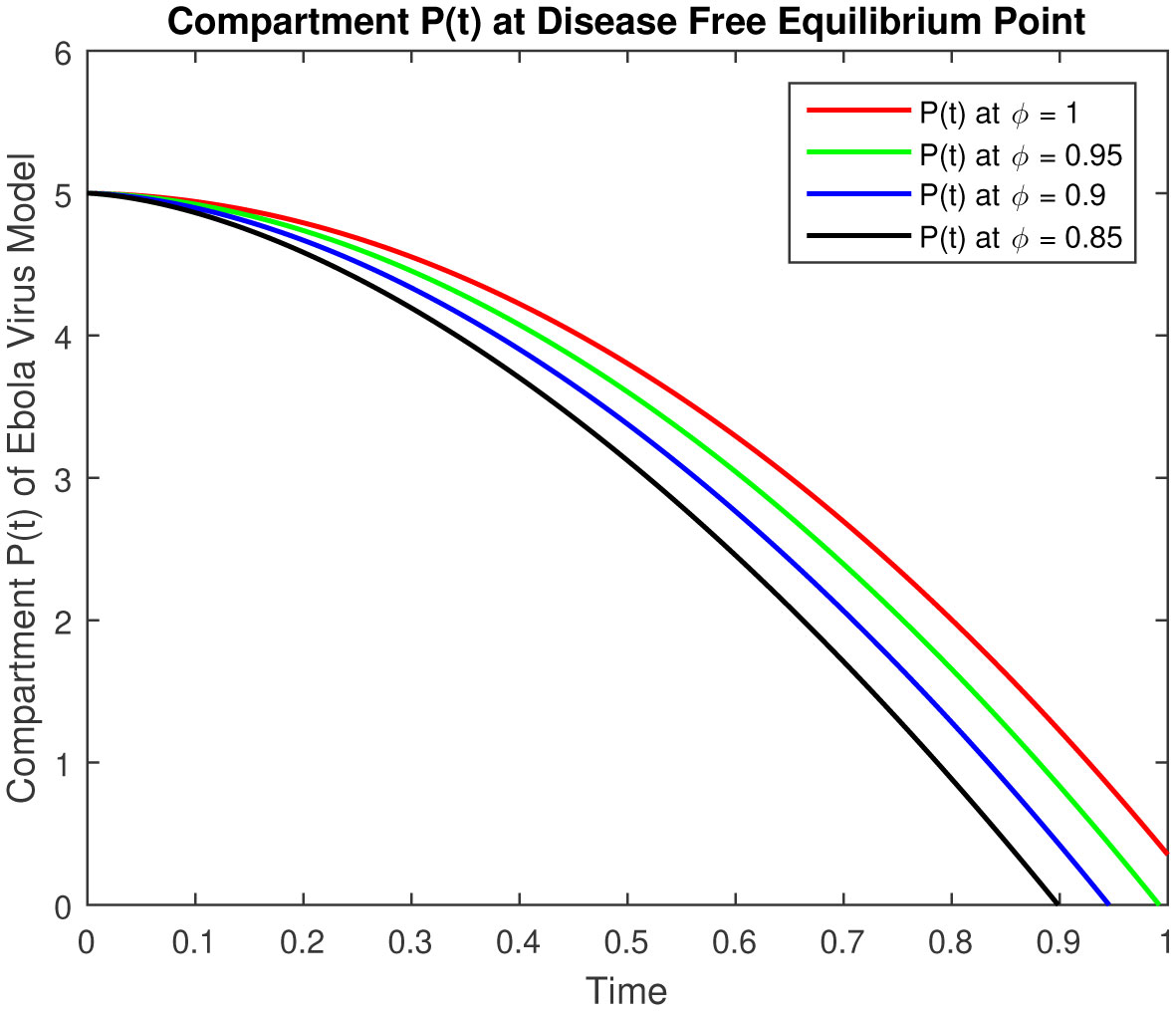
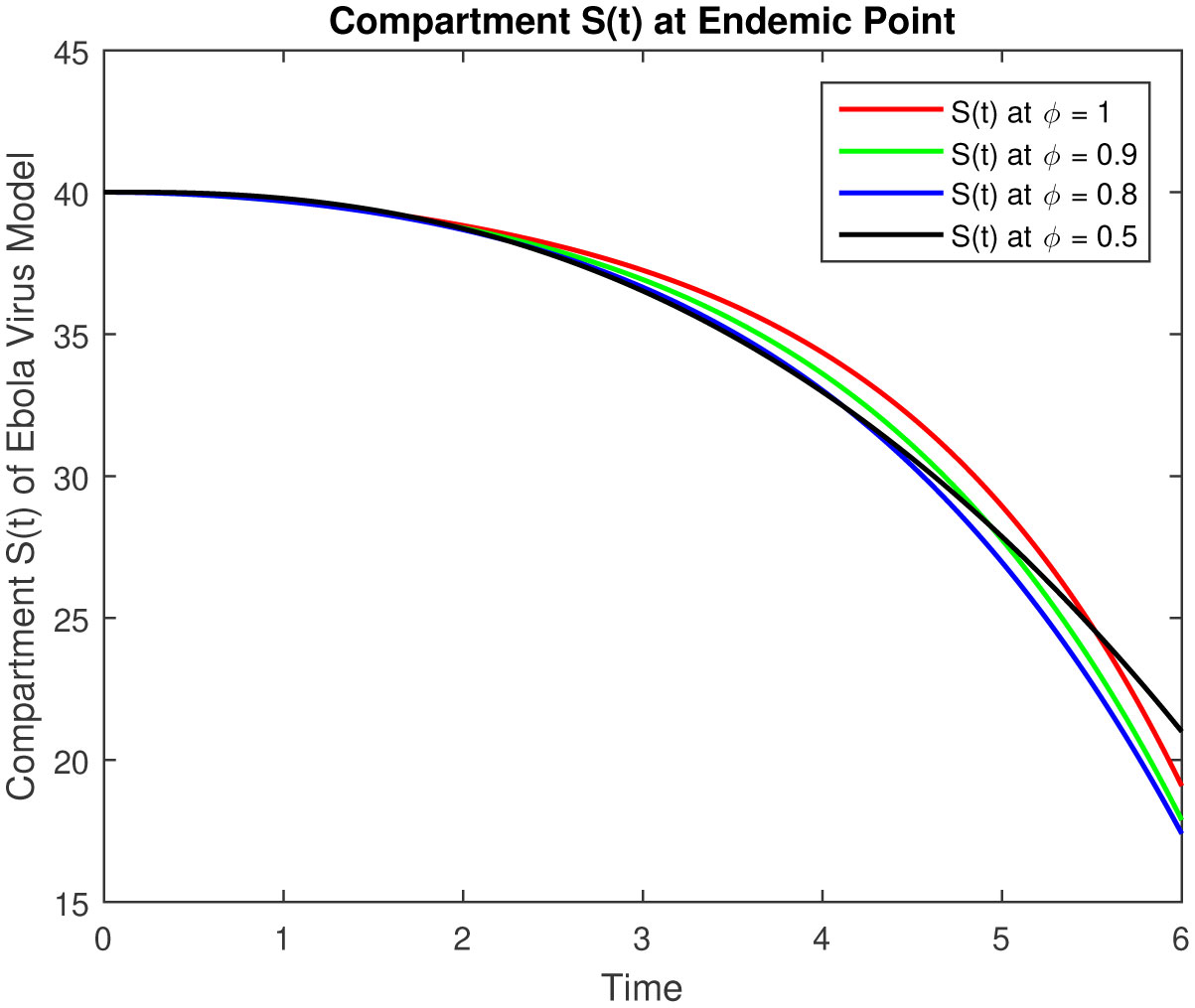
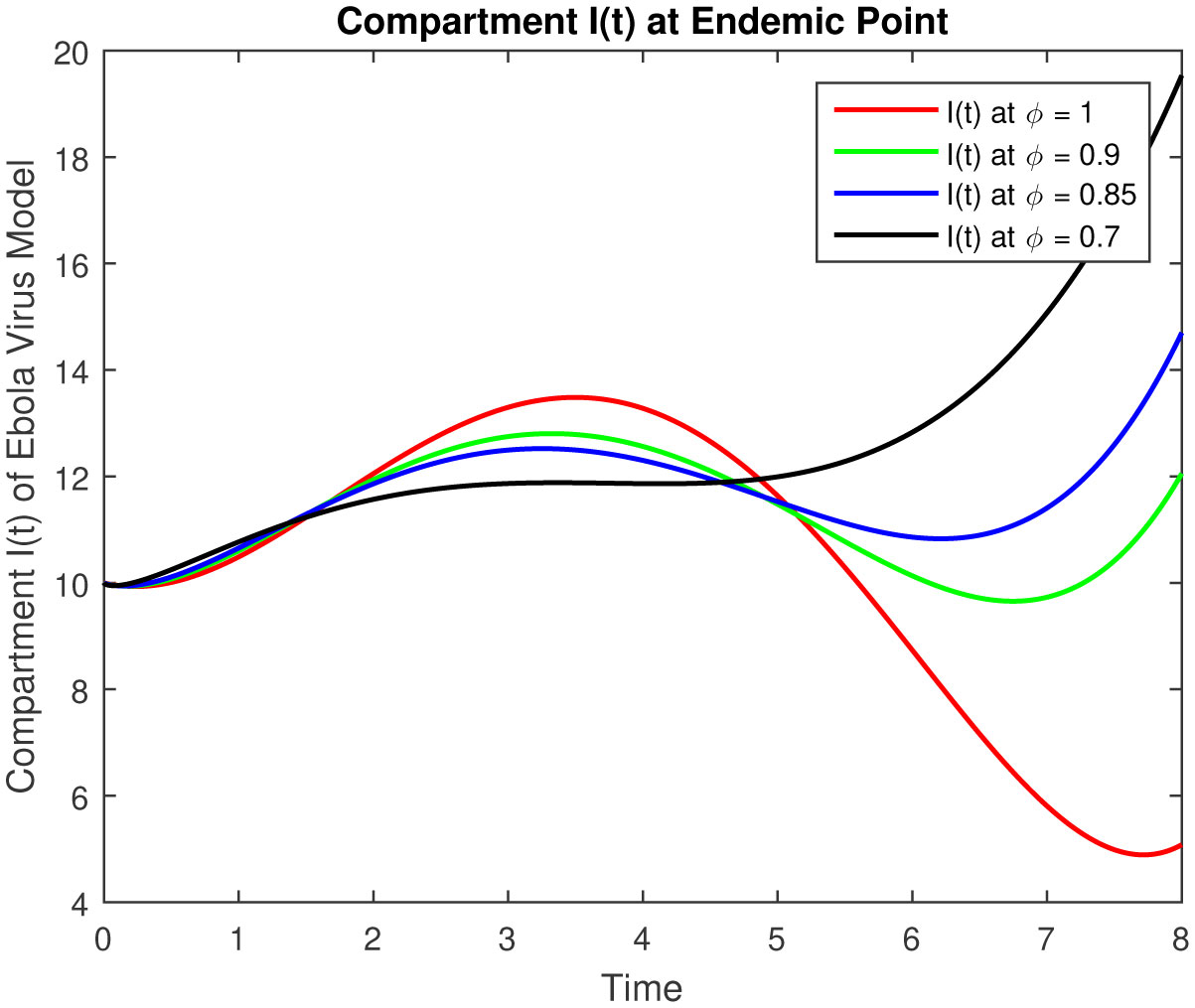
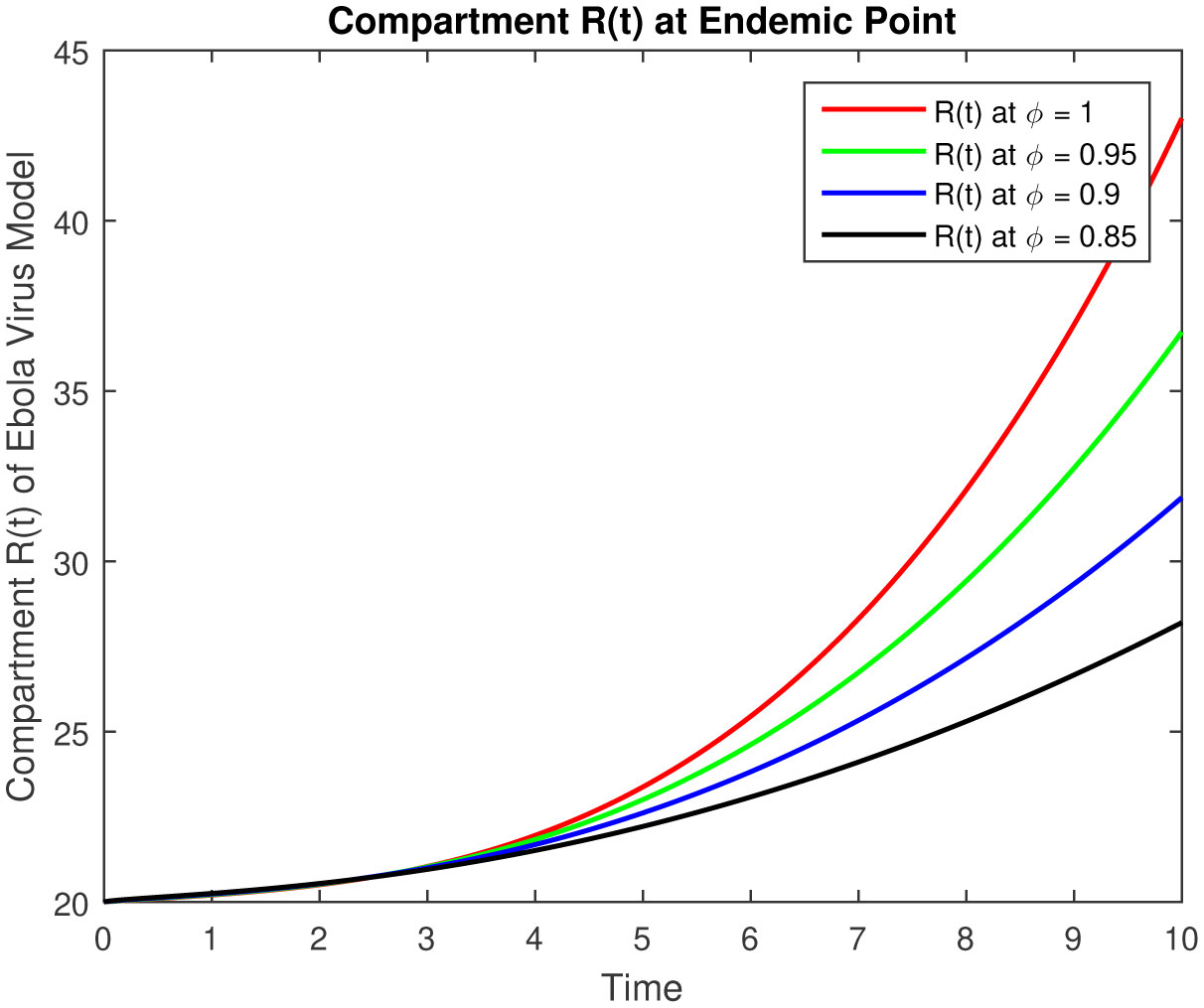
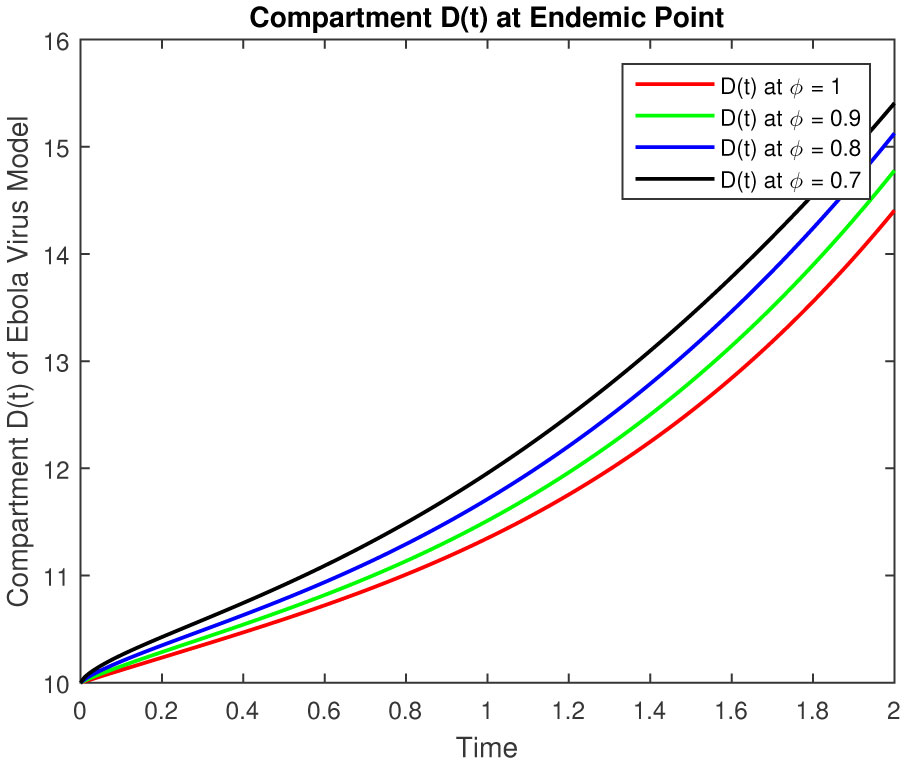
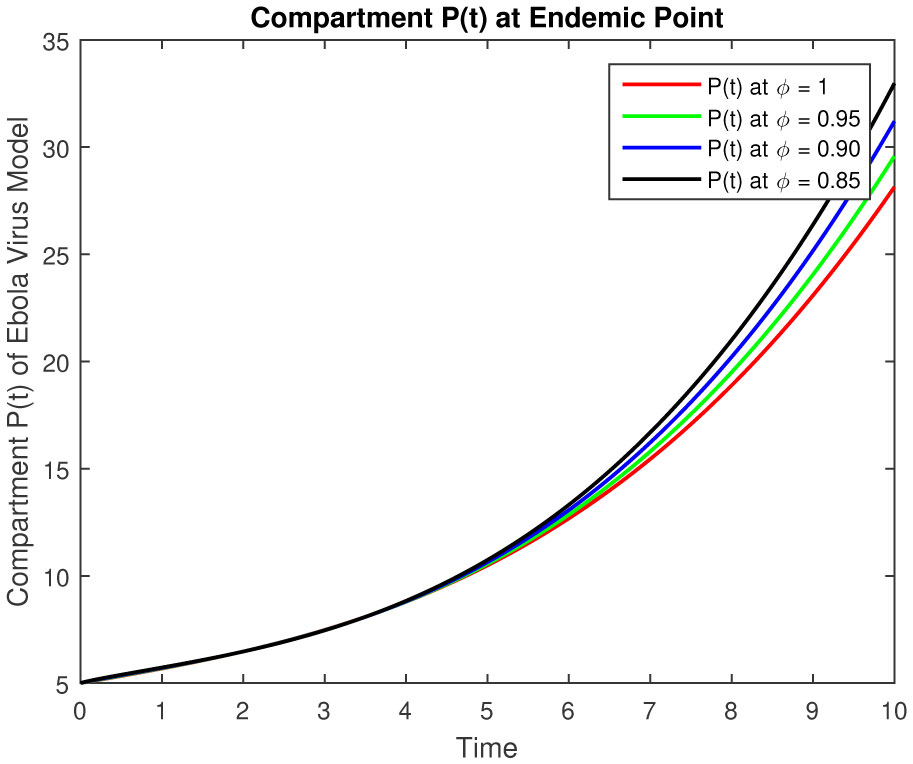
The results of fractional order model (2.1) is represented in followings tables and graphs.

Table 1. Numerical solution of S(t) with at different fractional values ϕ.

t	ϕ = 1	ϕ = 0.9	ϕ = 0.8	ϕ = 0.5
1	39.6912	39.5848	39.51	39.4383
1.5	39.3299	39.1117	39.0235	39.1181
3	37.2519	36.2268	36.264	37.5584
4.5	32.0652	29.2568	30.0105	34.514
6	19.0984	14.0068	17.2162	29.3074

| Show Table

DownLoad: CSV

Table 2. Numerical solution of I(t) with at different fractional values ϕ.

t	ϕ = 1	ϕ = 0.9	ϕ = 0.8	ϕ = 0.7
1	10.4879	10.6026	10.6542	10.7698
2	12.052	11.9378	11.8579	11.5689
4	13.2768	12.5387	12.2499	11.8581
6	8.7256	9.97166	10.5704	12.7973
8	5.0464	11.4457	13.7013	19.4353

| Show Table

DownLoad: CSV

Table 3. Numerical solution of R(t) with at different fractional values ϕ.

t	ϕ = 1	ϕ = 0.9	ϕ = 0.8	ϕ = 0.7
2	20.504	20.5195	20.5331	20.5414
4	21.952	21.8288	21.6815	21.509
6	25.448	24.6081	23.8154	23.076
8	32.096	29.4003	27.1489	25.2921
10	43	36.6889	31.8489	28.1877

| Show Table

DownLoad: CSV

Table 4. Numerical solution of D(t) with at different fractional values ϕ.

t	ϕ = 1	ϕ = 0.9	ϕ = 0.8	ϕ = 0.7
0.5	10.5931	10.6768	10.7803	10.9131
1	11.3486	11.5116	11.7127	11.9551
1.5	12.531	12.8083	13.1141	13.4308
2	14.4048	14.7773	15.124	15.4064

| Show Table

DownLoad: CSV

Table 5. Numerical solution of P(t) with at different fractional values ϕ.

t	ϕ = 1	ϕ = 0.95	ϕ = 0.9	ϕ = 0.85
1	5.67835	5.6959	5.68235	5.7302
2	6.4746	6.46707	6.45834	6.44629
4	8.788	8.62982	8.47227	8.30553
6	12.6746	12.1038	11.562	11.0225
8	18.8688	17.417	16.0958	14.8435
10	28.105	25.0658	22.3972	19.9683

| Show Table

DownLoad: CSV

Figure 1. Simulation of S(t) at different fractional values in time t.

DownLoad: Full-Size Img PowerPoint

Figure 2. Simulation of I(t) at different fractional values in time t.

DownLoad: Full-Size Img PowerPoint

Figure 3. Simulation of R(t) at different fractional values in time t.

DownLoad: Full-Size Img PowerPoint

Figure 4. Simulation of D(t) at different fractional values in time t.

DownLoad: Full-Size Img PowerPoint

Figure 5. Simulation of P(t) at different fractional values in time t.

DownLoad: Full-Size Img PowerPoint

Figure 6. Simulation of S(t) at different fractional values in time t.

DownLoad: Full-Size Img PowerPoint

Figure 7. Simulation of I(t) at different fractional values in time t.

DownLoad: Full-Size Img PowerPoint

Figure 8. Simulation of R(t) at different fractional values in time t.

DownLoad: Full-Size Img PowerPoint

Figure 9. Simulation of D(t) at different fractional values in time t.

DownLoad: Full-Size Img PowerPoint

Figure 10. Simulation of P(t) at different fractional values in time t.

DownLoad: Full-Size Img PowerPoint

4. Discussion

The objective of our work is to develop a scheme of epidemic fractional Ebola virus model with Caputo fractional derivative also numerical solutions have been obtained by using the Laplace with the Adomian Decomposition Method. The results of fractional order Ebola virus model is presented and convergence results of fractional-order model are also presented to demonstrate the efficacy of the process. The analytical solution of the fractional-order Ebola virus model consisting of the non-linear system of the fractional differential equation has been presented by using the Caputo derivative. To observe the effects of the fractional parameter on the dynamics of the fractional-order model (2.1), we conclude several numerical simulations varying the values of parameter given in [4]. These simulations reveal that a change in the value affects the dynamics of the model. The numerical solutions at classical as well as different fractional values by using Caputo fractional derivative can be seen in Figures 1–5 for disease free equilibrium. The rate of susceptible individuals and pathogens decreases by reducing the fractional values to acquire the desired value, whereas the other compartment starts decreasing by increasing the fractional values. The fractional-order model shows the convergence with theoretical contribution and numerical results. The fractional-order parameter values show the impact of increasing or decreasing the disease. Also, we can fix the parameter values where the rate of infection is decrease and the recover rate will increase for some values which are representing in figures and tables. These results can be used for disease outbreak treatment and analysis without defining the control parameters in the model based on fractional values. In general, approaches to fractional-order modeling in situations with large refined data sets and good numerical algorithms may be worth it. The simulation and numerical solutions at classical as well as different fractional values by using Caputo fractional derivative can be seen in Figures 6–10 for endemic equilibrium as well as in Tables 1–5. Results in both cases are reliable at fractional values to overcome the outbreak of this epidemic and meet our desired accuracy. Results discuss in [1], [5] for classical model, but our results are on fractional order model, fractional parameters easily use to adjust the control strategy without defining others parameters in the model. Another important feature that plays a critical role in the 2014 EVD outbreaks is traditional/cultural belief systems and customs. For instance, while some individuals in the three Ebola-stricken nations believe that there is no Ebola, control the population or harvest human organs. We conclude that depending on the specific data set, the fractional order model either converges to the ordinary differential equation model and fits data similarly, or fits the data better and outperforms the ODE model.

5. Conclusion

We develop a scheme of epidemic fractional Ebola virus model with Caputo fractional derivative for numerical solutions that have been obtained by using the Laplace with the Adomian Decomposition Method. In [24] the use of three different fractional operators on the Ebola disease model suggests that the fractional-order parameter greatly affects disease elimination for the non-integer case when decreasing α. We constructed a numerical solution for the Ebola virus model to show a good agreement to control the bad impact of the Ebola virus for the different period for diseases free and endemic equilibrium point as well. However, in this work, we introduced the qualitative properties for solutions as well as the non-negative unique solution for a fractional-order nonlinear system. It is important to note that the Laplace Adomian Decomposition Method is used for the Ebola virus fractional-order model differential equation framework is a more efficient approach to computing convergent solutions that are represented through figures and tables for endemic and disease-free equilibrium point. Convergence results of the fractional-order model are also presented to demonstrate the efficacy of the process. The techniques developed to provide good results which are useful for understanding the Zika Virus outbreak in our community. It is worthy to observe that fractional derivative shows significant changes and memory effects as compare to ordinary derivatives. This model will assist the public health planar in framing an Ebola virus disease control policy. Also, we will expand the model incorporating determinist and stochastic model comparisons with fractional technique, as well as using optimal control theory for new outcomes.

Conflict of interest

The authors declare no conflict of interest.

References

[1]	Agusto FB, Teboh-Ewungkem MI, Gumel AB (2015) Mathematical assessment of the effect of traditional beliefs and customs on the transmission dynamics of the 2014 Ebola outbreaks. BMC Med 13: 96. doi: 10.1186/s12916-015-0318-3
[2]	Amundsen SB (1998) Historical analysis of the Ebola virus: prospective implications for primary care nursing today. Clin Excell Nurse Pract 2: 343-351.
[3]	Baseler L, Chertow DS, Johnson KM, et al. (2017) The pathogenesis of Ebola virus disease. Annu Rev Pathol Mech Dis 12: 387-418. doi: 10.1146/annurev-pathol-052016-100506
[4]	Berge T, Lubuma JMS, Moremedi GM, et al. (2017) A simple mathematical model for Ebola in Africa. J Biol Dynam 11: 42-74. doi: 10.1080/17513758.2016.1229817
[5]	Agusto FB (2017) Mathematical model of Ebola transmission dynamics with relapse and reinfection. Math Biosci 283: 48-59. doi: 10.1016/j.mbs.2016.11.002
[6]	Mate SE, Kugelman JR, Nyenswah TG, et al. (2015) Molecular evidence of sexual transmission of Ebola virus. New Engl J Med 373: 2448-2454. doi: 10.1056/NEJMoa1509773
[7]	Althaus CL (2014) Estimating the reproduction number of Ebola virus (EBOV) during the 2014 outbreak in West Africa. doi: 10.1371/currents.outbreaks.91afb5e0f279e7f29e7056095255b288
[8]	Weitz JS, Dushoff J (2015) Modeling post-death transmission of Ebola: challenges for inference and opportunities for control. Sci Rep 5: 8751. doi: 10.1038/srep08751
[9]	Thompson RN, Hart WS (2018) Effect of confusing symptoms and infectiousness on forecasting and control of Ebola outbreaks. Clin Infect Dis 67: 1472-1474. doi: 10.1093/cid/ciy248
[10]	Hart WS, Hochfilzer LFR, Cunniffe NJ, et al. (2019) Accurate forecasts of the effectiveness of interventions against Ebola may require models that account for variations in symptoms during infection. Epidemics 29: 100371. doi: 10.1016/j.epidem.2019.100371
[11]	Singh J, Kumar D, Hammouch Z, et al. (2018) A fractional epidemiological model for computer viruses pertaining to a new fractional derivative. Appl Math Comput 316: 504-515.
[12]	Kumar D, Singh J, Baleanu D (2018) Analysis of regularized long-wave equation associated with a new fractional operator with Mittag–Leffler type kernel. Phys A 492: 155-167. doi: 10.1016/j.physa.2017.10.002
[13]	Farman M, Saleem MU, Ahmad A, et al. (2018) Analysis and numerical solution of SEIR epidemic model of measles with non-integer time fractional derivatives by using Laplace Adomian Decomposition Method. Ain Shams Eng J 9: 3391-3397. doi: 10.1016/j.asej.2017.11.010
[14]	Caputo M, Fabrizio M (2015) A new definition of fractional derivative without singular kernel. Prog Fract Differ Appl 1: 73-85.
[15]	Losada J, Nieto JJ (2015) Properties of a new fractional derivative without singular kernel. Prog Fract Differ Appl 1: 87-92.
[16]	Atangana A, Baleanu D (2016) New fractional derivatives with nonlocal and non-singular kernel: theory and application to heat transfer model. Therm Sci 20: 763-769. doi: 10.2298/TSCI160111018A
[17]	Saleem MU, Farman M, Ahmad A, et al. (2019) Stability analysis and control of fractional order diabetes mellitus model for artificial pancreas. Punjab Univ J Math 51: 85-101.
[18]	Jarad F, Abdeljawad T, Hammouch Z (2018) On a class of ordinary differential equations in the frame of Atangana–Baleanu fractional derivative. Chaos Soliton Fract 117: 16-20. doi: 10.1016/j.chaos.2018.10.006
[19]	Baleanu D, Jajarmi A, Hajipour M (2018) On the nonlinear dynamical systems within the generalized fractional derivatives with Mittag–Leffler kernel. Nonlinear Dynam 94: 397-414. doi: 10.1007/s11071-018-4367-y
[20]	Ndanguza D, Tchuenche JM, Haario H (2013) Statistical data analysis of the 1995 Ebola outbreak in the Democratic Republic of Congo. Afr Mat 24: 55-68. doi: 10.1007/s13370-011-0039-5
[21]	Rachah A, Torres DFM (2015) Mathematical modelling, simulation, and optimal control of the 2014 Ebola outbreak in West Africa. Discrete Dyn Nat Soc 2015: 842792. doi: 10.1155/2015/842792
[22]	Jiang S, Wang K, Li C, et al. (2017) Mathematical models for devising the optimal Ebola virus disease eradication. J Transl Med 15: 124. doi: 10.1186/s12967-017-1224-6
[23]	Chretien JP, Riley S, George DB (2015) Mathematical modeling of the West Africa Ebola epidemic . doi: 10.7554/eLife.09186
[24]	Muhammad Altaf K, Atangana A (2019) Dynamics of Ebola disease in the framework of different fractional derivatives. Entropy 21: 303. doi: 10.3390/e21030303

This article has been cited by:

1.	Aqeel Ahmad, Muhammad Farman, Ali Akgül, Nabila Bukhari, Sumaiyah Imtiaz, Mathematical analysis and numerical simulation of co-infection of TB-HIV, 2020, 27, 2576-5299, 431, 10.1080/25765299.2020.1840771
2.	Rana Muhammad Zulqarnain, Imran Siddique, Fahd Jarad, Rifaqat Ali, Thabet Abdeljawad, Ahmed Mostafa Khalil, Development of TOPSIS Technique under Pythagorean Fuzzy Hypersoft Environment Based on Correlation Coefficient and Its Application towards the Selection of Antivirus Mask in COVID-19 Pandemic, 2021, 2021, 1099-0526, 1, 10.1155/2021/6634991
3.	Waheed Ahmad, Mujahid Abbas, Effect of quarantine on transmission dynamics of Ebola virus epidemic: a mathematical analysis, 2021, 136, 2190-5444, 10.1140/epjp/s13360-021-01360-9
4.	Muhammad Farman, Aqeel Ahmad, Ali Akg黮, Muhammad Umer Saleem, Muhammad Naeem, Dumitru Baleanu, Epidemiological Analysis of the Coronavirus Disease Outbreak with Random Effects, 2021, 67, 1546-2226, 3215, 10.32604/cmc.2021.014006
5.	SHAHER MOMANI, R. P. CHAUHAN, SUNIL KUMAR, SAMIR HADID, A THEORETICAL STUDY ON FRACTIONAL EBOLA HEMORRHAGIC FEVER MODEL, 2022, 30, 0218-348X, 10.1142/S0218348X22400321
6.	Maryam Amin, Muhammad Farman, Ali Akgül, Mohammad Partohaghighi, Fahd Jarad, Computational analysis of COVID-19 model outbreak with singular and nonlocal operator, 2022, 7, 2473-6988, 16741, 10.3934/math.2022919
7.	Muhammad Farman, Ali Akg黮, Aqeel Ahmad, Dumitru Baleanu, Muhammad Umer Saleem, Dynamical Transmission of Coronavirus Model with Analysis and Simulation, 2021, 127, 1526-1506, 753, 10.32604/cmes.2021.014882
8.	Jie Liu, Peng Zhang, Hailian Gui, Tong Xing, Hao Liu, Chen Zhang, Resonance study of fractional-order strongly nonlinear duffing systems, 2024, 98, 0973-1458, 3317, 10.1007/s12648-024-03080-z
9.	Isaac K. Adu, Fredrick A. Wireko, Mojeeb Al-R. El-N. Osman, Joshua Kiddy K. Asamoah, A fractional order Ebola transmission model for dogs and humans, 2024, 24, 24682276, e02230, 10.1016/j.sciaf.2024.e02230
10.	Mohammed A. Almalahi, Khaled Aldowah, Faez Alqarni, Manel Hleili, Kamal Shah, Fathea M. O. Birkea, On modified Mittag–Leffler coupled hybrid fractional system constrained by Dhage hybrid fixed point in Banach algebra, 2024, 14, 2045-2322, 10.1038/s41598-024-81568-8
11.	Kamel Guedri, Rahat Zarin, Mowffaq Oreijah, Samaher Khalaf Alharbi, Hamiden Abd El-Wahed Khalifa, Artificial neural network-driven modeling of Ebola transmission dynamics with delays and disability outcomes, 2025, 115, 14769271, 108350, 10.1016/j.compbiolchem.2025.108350

Reader Comments

Your name:*

Email:*
© 2020 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

AIMS Bioengineering

Metrics

Article views(4478) PDF downloads(325) Cited by(10)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

Figures and Tables

Figures(10) / Tables(5)

AIMS Bioengineering

Simulation and numerical solution of fractional order Ebola virus model with novel technique

Related Papers:

Abstract

1. Introduction

2. Materials and method

2.1. Fractional order Ebola virus model

2.2. Equilibrium point and stability

2.3. Numerical analysis of the model

3. Results

4. Discussion

5. Conclusion

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Catalog

Abstract

1. Introduction

2. Materials and method

2.1. Fractional order Ebola virus model

2.2. Equilibrium point and stability

2.3. Numerical analysis of the model

3. Results

4. Discussion

5. Conclusion

References

AIMS Bioengineering

Simulation and numerical solution of fractional order Ebola virus model with novel technique

Related Papers:

Abstract

1. Introduction

2. Materials and method

2.1. Fractional order Ebola virus model

2.2. Equilibrium point and stability

2.3. Numerical analysis of the model

3. Results

4. Discussion

5. Conclusion

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog

Abstract

1. Introduction

2. Materials and method

2.1. Fractional order Ebola virus model

2.2. Equilibrium point and stability

2.3. Numerical analysis of the model

3. Results

4. Discussion

5. Conclusion

References