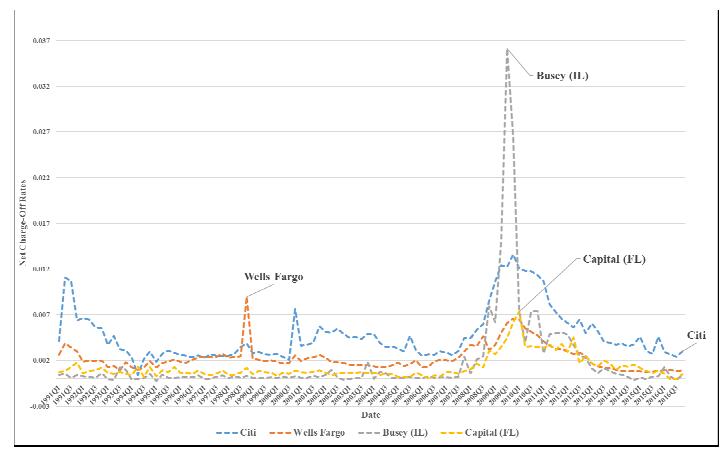
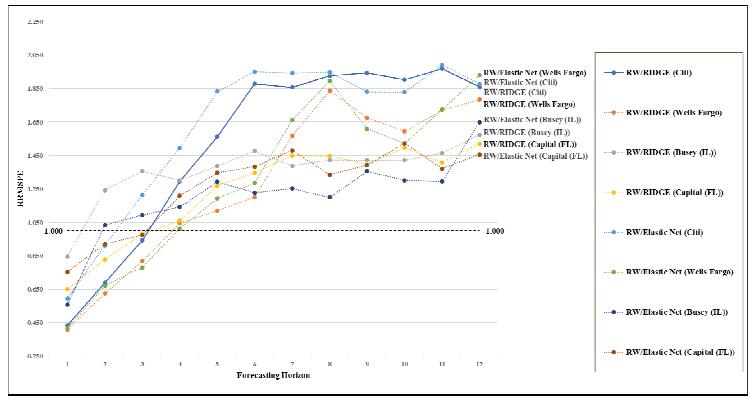
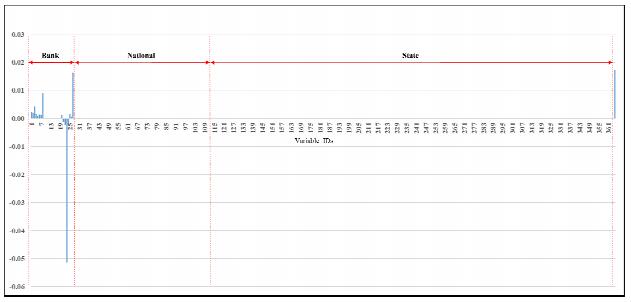
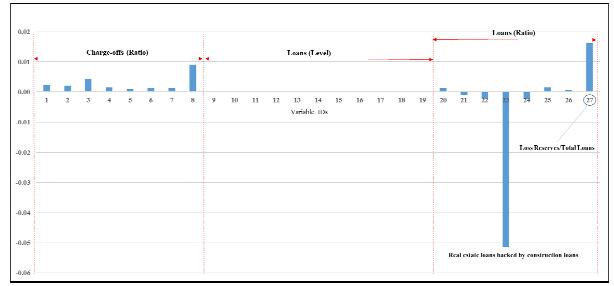
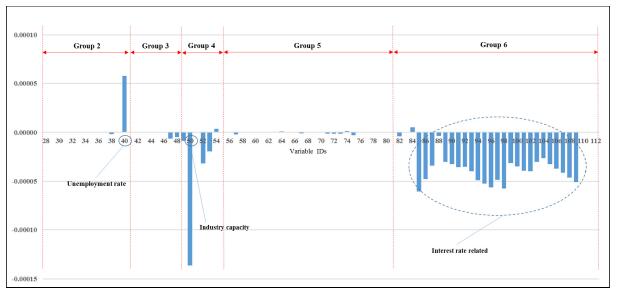
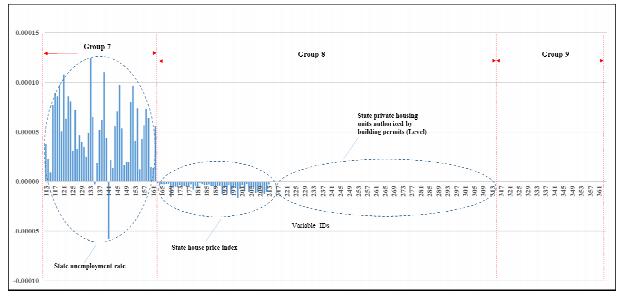
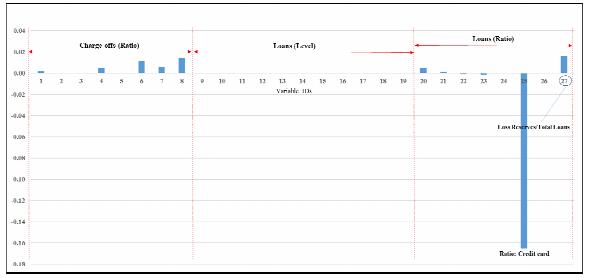
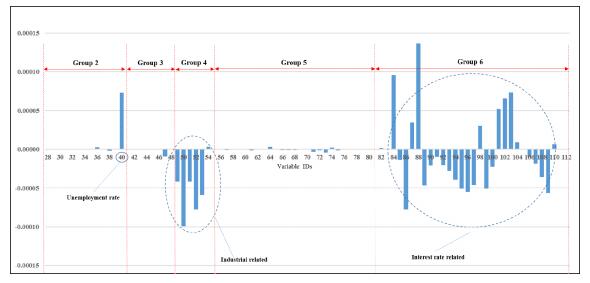
The purpose of this paper is to focus on the losses of two very big banks, Citigroup (Citi) and Wells Fargo & Company (Wells Fargo), and two very small banks, First Busey Corporation (Busey) and Capital City Bank Group (Capital), over the period 1991–2016. The federal government actually bailed out the two big banks, as measured by total assets, whereas neither of the two small banks required a bail out. Clearly, if one is able to use a variety of predictor variables to forecast accurately the losses of banks of various sizes, in different geographical locations, and operating a variety of business models, this may help identify potential causes of future banking problems and thereby lessen, if not eliminate, the need for future bailouts. This is important for both the banks and the bank regulatory authorities. In particular, those banks expected to suffer significant losses on loans may be in a position to increase their provisioning and thus loan loss allowances. If such banks are unable to take this type of action or other corrective action to address expected losses, regulatory action may become necessary in response to this situation. The motivation for our paper is this very issue: can one obtain accurate forecasts of losses, or the net charge-off rates, of banks? We provide an answer to this question by examining the four banks mentioned using several hundred predictor variables and several different forecast techniques.
1.
Introduction and statement of main results
Several important evolution equations arising in kinetic theory, mathematical physics and probability can be written in the form
where (X,Y,t):=(x1,...,xm,y1,...,ym,t)∈Rm×Rm×R=RN+1, N=2m, m≥1, and the coordinates X=(x1,...,xm) and Y=(y1,...,ym) are, respectively, the velocity and the position of the system. In its simplest form,
the equation in (1.1) was introduced and studied by Kolmogorov in a famous note published in 1934 in Annals of Mathematics, see [25]. In this case Kolmogorov noted that the equation in (1.1) is an example of a degenerate parabolic operator having strong regularity properties and he proved that the equation has a fundamental solution which is smooth off its diagonal. In fact, in this case the equation in (1.1) is hypoelliptic, see [24].
In kinetic theory, f represents the evolution of a particle distribution
subject to geometric restrictions and models for the interactions and collisions between particles. In this case the left-hand side in (1.1) describes the evolution of f under the action of transport, with the free streaming operator. The right-hand side describes elastic collisions through the nonlinear Boltzmann collision operator. The Boltzmann equation is an integro- (partial)-differential equation with nonlocal operator in the kinetic variable X. The Boltzmann equation is a fundamental equation in kinetic theory in the sense that it has been derived rigorously, at least in some settings, from microscopic first principles. In the case of so called Coulomb interactions the Boltzmann collision operator is ill-defined and Landau proposed an alternative operator for these interactions, this operator is now called the Landau or the Landau-Coulomb operator. This operator can be stated as in (1.1) with
where again A(f)=A(f)(X,Y,t) and B(f)=B(f)(X,Y,t) are nonlocal operators in the variable X. In this case the equation in (1.1) is a nonlinear, or rather quasilinear, drift-diffusion equation with coefficients given by convolution like averages of the unknown. As mentioned above the Landau equation is considered fundamental because of its close link to the Boltzmann equation for Coulomb interactions.
In the case of long-range interactions, the Boltzmann and Landau-Coulomb operators show local ellipticity provided the solution enjoys some pointwise bounds on the associated hydrodynamic fields and the local entropy. Indeed, assuming certain uniform in (Y,t)∈UY×I bounds on local mass, energy, and entropy, see [30,33], one can prove that
for some constant Λ≥1 and for (X,Y,t)∈UX×UY×I, i.e., under these assumptions the operator Q in (1.2) and in the Landau equation becomes locally uniformly elliptic. As a consequence, and as global well posedness for the Boltzmann equation and the construction of solutions in the large is an outstanding open problem, the study of conditional regularity for the Boltzmann and Landau equations has become a way to make progress on the regularity issues for these equations. We refer to [11,13,14,15,28,33,36,37] for more on the connections between Kolmogorov-Fokker-Planck equations, the Boltzmann and Landau equation, statistical physics and conditional regularity.
Based on the idea of conditional regularity one is lead to study the local regularity of weak solutions to the equation in (1.1) with
assuming that A is measurable, bounded and uniformly elliptic, and that B is bounded. In [20], see also [21,22,23] for subsequent developments, the authors extended, for equations as in (1.1) assuming (1.3), the De Giorgi-Nash-Moser (DGNM) theory, which in its original form only considers elliptic or parabolic equations in divergence form, to hypoelliptic equations with rough coefficients including the one in (1.1) assuming (1.3). [20] has spurred considerable activity in the field, see below for a literature review, as the results proved give the correct scale- and translation-invariant estimates for local Hölder continuity and the Harnack inequality for weak solutions.
In this paper we consider equations as in (1.1) with
subject to conditions on A which allow A to be a nonlinear function of ∇Xf. In this case we refer to the equations in (1.1) as nonlinear Kolmogorov-Fokker-Planck type equations with rough coefficients. Our contributions is twofold. First, we establish higher integrability (Theorem 1.1) and local boundedness (Theorem 1.2) of weak sub-solutions, weak Harnack and Harnack inequalities (Theorem 1.3), and Hölder continuity with quantitative estimates (Theorem 1.4), for the equation
Second, we establish existence and uniqueness, in certain bounded X, Y and t dependent domains, for a Dirichlet problem involving the equation in (1.5) also allowing for boundary data and a right hand side (Theorem 1.5). In the linear case, if A(X,Y,t) is a uniformly elliptic positive definite matrix with bounded measurable coefficients, then A(ξ,X,Y,t)=A(X,Y,t)ξ satisfies the hypothesis we impose on the symbol A, and in this case the equation in (1.5) reduces to the equation
Concerning regularity, our results therefore generalize [20,22,23], to nonlinear Kolmogorov-Fokker-Planck type equations with rough coefficients.
To the best of our knowledge, nonlinear equations of the form in (1.5) have so far not been investigated in the literature, and the purpose of this paper is to contribute to the regularity and existence theory for these equations. We believe that generalizations of the De Giorgi-Nash-Moser (DGNM) theory to nonlinear Kolmogorov-Fokker-Planck type equations with rough coefficients are relevant and interesting. We also believe that our treatment of the Dirichlet problem is new and enlightening.
1.1. The symbol A
We consider equations as in (1.5) subject to conditions on A. Concerning the symbol A our baseline assumption is that A belongs to the class M(Λ), where Λ∈[1,∞) is a constant. In our treatment of the Dirichlet problem we will need to impose stronger conditions on A and we will assume that A belongs to the class R(Λ). In the following ⋅ denotes the standard Euclidean scalar product in Rm.
Definition 1. Let Λ∈[1,∞). Then A is said to belong to the class M(Λ) if A=A(ξ,X,Y,t):Rm×Rm×Rm×R→Rm is continuous with respect to ξ, measurable with respect to X,Y and t, and
for almost every (X,Y,t)∈RN+1 and for all ξ∈Rm.
Definition 2. Let Λ∈[1,∞). Then A is said to belong to the class R(Λ) if A=A(ξ,X,Y,t):Rm×Rm×Rm×R→Rm is continuous with respect to ξ, measurable with respect to X,Y and t, and
for almost every (X,Y,t)∈RN+1 and for all ξ1,ξ2,ξ∈Rm.
Remark 1.1. Note that (1.8)-(iii) implies that A(0,X,Y,t)=0 for a.e. (X,Y,t)∈RN+1. Hence we deduce from (1.8)-(i),(ii) and (iii) that R(Λ)⊂M(Λ).
1.2. Dilations and group law
We will often use the notation (Z,t)=(X,Y,t)∈RN+1 to denote points. The natural family of dilations for our operators and equations, (δr)r>0, on RN+1, is defined by
for (X,Y,t)∈RN+1, r>0. Our classes of operators are closed under the group law
where (Z,t), (˜Z,˜t)∈RN+1. Note that
and hence
whenever (Z,t), (˜Z,˜t)∈RN+1. Given (Z,t)=(X,Y,t)∈RN+1 we let
Given r>0 and (˜Z,˜t)=(˜X,˜Y,˜t)∈RN+1, we let
We refer to Qr(˜Z,˜t) as a cylinder centered at (˜Z,˜t) and of radius r.
1.3. Statement of main results: regularity of weak solutions
We here state the regularity part of our results, Theorem 1.1–Theorem 1.4. These theorem are derived under the assumption that the symbol A belongs to the class M(Λ) introduced in Definition 1. For the notions of weak sub-solutions, super-solutions and solutions, we refer to Definition 3 below. For the definitions of function spaces used we refer to the bulk of the paper.
Theorem 1.1 (Higher integrability). Let (Z0,t0)=(X0,Y0,t0)∈RN+1,0<r1<r0≤1 and let u be a non-negative weak sub-solution to (1.5) in an open set of RN+1 containing Qr0(Z0,t0) in the sense of Definition 3 below. Then for any q∈[2,2+1/m) and s∈[0,1/3), we have*
*Ws,1Y denotes the fractional Sobolev space.
Here
where
for some constant c(m,Λ)≥1.
Theorem 1.2 (Local boundedness). Let (Z0,t0)=(X0,Y0,t0)∈RN+1,0<r∞<r0≤1 and let u be a non-negative weak sub-solution to (1.5) in an open set of RN+1 containing Qr0(Z0,t0) in the sense of Definition 3 below. Then for any p>0, there exists a constant c=c(m,Λ)≥1 and θ=θ(m)>1 such that
Theorem 1.3 (Harnack inequalities). Let u be a non-negative weak super-solution to (1.5) in an open set of RN+1 containing Q1 in the sense of Definition 3 below. Then there exists ζ>0 and c≥1, both depending only on m and Λ such that
where r0=1/20 and ˜Q−r0/2:=Qr0/2(0,0,−19r20/8). Furthermore, if u is a non-negative weak solution to (1.5) in an open set of RN+1 containing Q1, then
where ˜Q−r0/4:=Qr0/4(0,0,−19r20/8).
Theorem 1.4 (Hölder continuity). Let u be a weak solution to (1.5) in an open set of RN+1 containing Q2 in the sense of Definition 3 below. Then there exists α∈(0,1) and c≥1, both depending only on m and Λ such that
whenever (X1,Y1,t1),(X2,Y2,t2)∈Q1,(X1,Y1,t1)≠(X2,Y2,t2).
1.4. Statement of main results: existence and uniqueness for a Dirichlet problem
We here state the existence and uniqueness part of our results, Theorem 1.5. Throughout the paper we let UX⊂Rm be a bounded Lipschitz domain and let VY,t⊂Rm×R be a bounded domain with boundary which is C1,1-smooth, i.e., C1 with respect to Y as well as t. Let NY,t denote the outer unit normal to VY,t. We establish existence and uniqueness of weak solutions to a formulation of the Dirichlet problem
Here
∂K(UX×VY,t) will be referred to as the Kolmogorov boundary of UX×VY,t, and the Kolmogorov boundary serves, in our context, as the natural substitute for the parabolic boundary used in the context of the Cauchy-Dirichlet problem for uniformly elliptic parabolic equations. In particular, we study weak solutions in the sense of Definition 4. For the definition of the functional setting we refer to Section 2. We believe that the following result is of independent interest in particularly as we allow the symbol A to depend nonlinearly on ∇Xu.
Theorem 1.5 (Existence and uniqueness). Let (g,g∗)∈W(UX×VY,t)×L2Y,t(VY,t,H−1X(UX)) and assume that A belongs to the class R(Λ) introduced in Definition 2. Then there exists a unique weak solution u to the problem in (1.21) in the sense of Definition 4 below. Furthermore, there exists a constant c, depending only on m, Λ and UX×VY,t, such that
1.5. Known regularity results
As mentioned, the equation in (1.6), possibly also allowing for lower order terms, has attracted considerable attention in recent years. Anceschi-Cinti-Pascucci-Polidoro-Ragusa [2,12,34] proved local boundedness of weak sub-solutions of (1.6) and some versions thereof. Their approach is based on the Moser's iteration technique, the use of fundamental solutions and a Sobolev type inequality is crucial. It is worth noting that while the results in these papers are stated assuming only bounded and measurable coefficients, an implicit regularity assumption on the coefficients is imposed as the authors use a stronger notion of weak solutions assuming also (∂t+X⋅∇Y)u∈L2loc. It is unclear for what assumptions on the coefficients such weak solutions can be constructed. Bramanti-Cerutti- Manfredini-Polidoro-Ragusa [8,32,35] proved Lp estimates, interior Sobolev regularity and local Hölder continuity of weak solutions of (1.6) imposing additional assumptions on the coefficients beyond bounded, measurable and elliptic. In fact it was only recently that Golse-Imbert- Mouhot-Vasseur [20] proved local boundedness, Harnack inequality and local Hölder continuity of (true) weak solutions of (1.6) based on De-Giorgi and Moser's iteration technique. Still, it seems unclear to us how the authors actually resolve questions concerning the existence of weak solutions unless smooth coefficients are assumed qualitatively. However, subsequent developments have appeared in [22,23]. A weak Harnack inequality for weak super-solutions of (1.6) has been obtained by Guerand-Imbert [22] and this has been generalized by Anceschi-Rebucci [3]. In [23], Guerand-Mouhot revisited the theory for the linear equation in (1.6), also allowing for lower order terms, and gave lucid, novel and short proofs of the De Giorgi intermediate-value Lemma, weak Harnack and Harnack inequalities, and the Hölder continuity with quantitative estimates. [23] is an essentially self-contained account of the linear theory. Local Hölder continuity results are also proved in Wang-Zhang [38,39,40] for various linear analogues of (1.6). We emphasize that all results mentioned concern linear equations. Zhu [41] proved local boundedness and local Hölder continuity of weak solutions of (1.6) when the drift term ∂t+X⋅∇Y is replaced by ∂t+b(X)⋅∇Y for some nonlinear function b.
1.6. Known existence results
Boundary value problems for equations as in (1.6) but in non-divergence form were studied by Manfredini [31] who proved existence of strong solutions for the Dirichlet problem assuming Hölder continuous coefficients. Lanconelli-Lascialfari-Morbidelli [26,27] considered a quasilinear case, still in non-divergence form, allowing the coefficients to depend not only on (X,Y,t) but also the solution u, and as a function of (X,Y,t) the coefficients are assumed to be with Hölder continuous. In fact, functional analytic approaches to weak solutions to Kramers equation and Kolmogorov- Fokker-Planck equations have only recently been developed. Albritton-Armstrong-Mourrat- Novack [1] have developed a functional analytic approach to study well-posedness of Kramers equation, and its parabolic analogue
for suitable g∗. Equation (1.24) is often referred to as the kinetic Fokker-Planck equation. Litsgård-Nyström [29] studied existence and uniqueness results for the (linear) Dirichlet problem associated with (1.6), with rough coefficients A. In particular, in [29] Theorem 1.5 is proved in the case when A(ξ,X,Y,t)=A(X,Y,t)ξ. However, existence and uniqueness for (1.5) do not seem to have been studied in the literature so far. It is important to note that Theorem 1.5 states, similar to [29], the existence of a unique weak solution u to the problem in (1.21) in the sense of Definition 4 below. The latter is, as it assumes no knowledge of underlying traces, trace spaces and extension operators in the functional setting considered, a weaker formulation of the Dirichlet problem compared to what one usually aims for. Indeed, this is one way to formulate a weak form of the Dirichlet problem which circumvents a largely open problem in the context of kinetic Fokker-Planck equations, linear as well as non-linear, and that is the problem of a well defined trace operator and trace inequality. We refer to Section 6 for more.
1.7. Proofs
The regularity part of our results is modelled on the approach of Golse-Imbert-Mouhot-Vasseur [20] and the work of Guerand-Mouhot [23]. In fact, as can be seen from the very formulations of our regularity results, this part of our work is strongly influenced by [23] and armed with Theorem 1.1 and Theorem 1.2 we can to large extent refer to the corresponding arguments in [23] for the proofs of Theorem 1.3 and Theorem 1.4. The new difficulties in our case stem from the nonlinearity of A in ∇Xu. However, as we learn from the regularity theory for quasi-linear parabolic PDEs, see [16] for example, a careful development of the De Giorgi-Nash-Moser theory tends to be robust enough to handle the type of non-linearities considered in this paper. The higher integrability result in Theorem 1.1 is proved by combining the energy estimate in Lemma 3.1 with a Sobolev regularity estimate and here it is important that A has linear growth in ∇Xu. In particular, in the proof of Theorem 1.1 one is lead, after preliminaries and the use of an appropriate cut-off function, to conduct estimates for a (global) weak sub-solution u1 to the equation
where F1,F0 are in L2(RN+1) and u1,F1,F0 are supported in Qr0(0,0,0). To close the argument, as u1 is only a weak sub-solution, it seems important to replace it by a function which actually solves an equation. In particular, to make this operational one needs to construct a weak solution v to
such that v bounds u1 from above. One approach to Sobolev regularity estimates is then attempt to use an approach based on Bouchut [7] which implies a Sobolev embedding
To get hold of the H1/3X,Y,t(RN+1) norm of v one uses a result of Bouchut [7] which gives control of D1/3Yv, D1/3tv given energy estimates. To be able to bound u1 from above by v as in (1.26) one seems to need Theorem 1.5 and the comparison principle that we prove in Theorem 5.1 below. As the result of Bouchut [7] requires a solution which exists globally in time one can make this approach operational using Theorem 1.5 to prove Theorem 1.1 with the cylinders in (1.14) replaced by centered cylinders. An alternative approach to Sobolev regularity estimates, which in the end gives Theorem 1.1 as stated, is to first observe that if u1 satisfies (1.25), then one deduces that the weak formulation of (1.25) induces a positive distribution. One is therefore lead to prove estimates for v satisfying
where μ is now a positive measure. Due to the structure of g∗, Sobolev regularity estimates can then be deduced using a semi-classical approach via the fundamental solution associated to the linear equation (∂t+X⋅∇Y)f=ΔXf originally studied by Kolmogorov, see Lemma 10 in [23]. In the end, we follow this approach and here it is again important that A has linear growth in ∇Xu. Armed with the Sobolev regularity estimates the proofs of Theorem 1.1–Theorem 1.4 can be completed along the lines of the corresponding arguments in the linear case. Finally, to prove the existence and uniqueness result in Theorem 1.5 we use a variational approach and proceed along the lines of [1,4,29]. In particular, our argument is similar to the proof of Theorem 1.1 in [29].
1.8. Organization of the paper
In Section 2 we introduce the functional setting and the notion of weak solutions. Section 3 is devoted to a number of preliminary technical results to be used in the proofs of Theorem 1.1– Theorem 1.4. Theorem 1.1–Theorem 1.4 are proved in Section 4, and in the proof of Theorem 1.3 and Theorem 1.4 we for brevity mainly refer to the corresponding arguments in [23]. Theorem 1.5 is proved in Section 5. In Section 6 we mention a number of challenging problems for future research which we hope will inspire the community to look further into the topic of nonlinear Kolmogorov-Fokker-Planck type equations.
2.
The functional setting and weak solutions
2.1. Function spaces
We denote by H1X(UX) the Sobolev space of functions g∈L2(UX) whose distributional gradient in UX lies in (L2(UX))m, i.e.,
and we set
We let H1X,0(UX) denote the closure of C∞0(UX) in the norm of H1X(UX) and we recall, as UX is a bounded Lipschitz domain, that C∞(¯UX) is dense in H1X(UX). In particular, equivalently we could define H1X(UX) as the closure of C∞(¯UX) in the norm ||⋅||H1X(UX). Note that as H1X,0(UX) is a Hilbert space it is reflexive, hence (H1X,0(UX))∗=H−1X(UX) and (H−1X(UX))∗=H1X,0(UX), where ()∗ denotes the dual. Based on this we let H−1X(UX) denote the dual to H1X,0(UX) acting on functions in H1X,0(UX) through the duality pairing ⟨⋅,⋅⟩:=⟨⋅,⋅⟩H−1X(UX),H1X,0(UX). We let L2Y,t(VY,t,H1X,0(UX)) be the space of measurable function u:VY,t→H1X,0(UX) equipped with the norm
L2Y,t(VY,t,H−1X(UX)) is defined analogously. In analogy with the definition of H1X(UX), we let W(UX×VY,t) be the closure of C∞(¯UX×VY,t) in the norm
In particular, W(UX×VY,t) is a Banach space and u∈W(UX×VY,t) if and only if
Note that the dual of L2Y,t(VY,t,H1X,0(UX)), denoted by (L2Y,t(VY,t,H1X,0(UX)))∗, satisfies
and, as mentioned above,
Finally, the spaces L2Y,t,loc(VY,t,H1X,loc(UX)), L2Y,t,loc(VY,t,H−1X,loc(UX)), and Wloc(UX×VY,t) are defined in the natural way. The topological boundary of UX×VY,t is denoted by ∂(UX×VY,t). Let NY,t denote the outer unit normal to VY,t. We define a subset ∂K(UX×VY,t)⊂∂(UX×VY,t), the Kolmogorov boundary of UX×VY,t, as in (1.22). We let C∞K,0(¯UX×VY,t) and C∞X,0(¯UX×VY,t) be the set of functions in C∞(¯UX×VY,t) which vanish on ∂K(UX×VY,t) and {(X,Y,t)∈∂UXׯVY,t}, respectively. We let W0(UX×VY,t) and WX,0(UX×VY,t) denote the closure in the norm of W(UX×VY,t) of C∞K,0(¯UX×VY,t) and C∞X,0(¯UX×VY,t), respectively.
2.2. Weak solutions
We here introduce the notion of weak solutions.
Definition 3. Let g∗∈L2Y,t(VY,t,H−1X(UX)). A function u∈Wloc(UX×VY,t) is said to be a weak sub-solution (or super-solution) to the equation
if for every VX×VY×J⋐UX×VY,t, and for all non-negative ϕ∈L2Y,t(VY×J,H1X,0(VX)), we have
We say that u∈Wloc(UX×VY,t) is a weak solution to the Eq (2.3) if equality holds in (2.4) without a sign restriction on ϕ.
Note that if u is a weak sub-solution (or super-solution) of (2.3) in the sense of Definition 3 above, with g∗≡0, then
whenever ϕ∈C∞((t1,t2),C∞0(VX×VY)), is non-negative function. Furthermore, equality holds in (2.5) for every weak solution u of (2.3) without a sign restriction on ϕ.
Remark 2.1. Assume g∗≡0. (i) From Definition 3, it is clear that, if u is a weak sub-solution (resp. super-solution or solution) of (2.3) in UX×VY,t, then for any k∈R, the function v=(u−k) is also weak sub-solution (resp. super-solution or solution) of (2.3) in UX×VY,t.
(ii) Using the homogeneity property (iii) of A, it follows that, (a) for any c≥0, cu is a weak sub-solution (resp. super-solution or solution) of (2.3) in UX×VY,t, provided u is a weak sub-solution (resp. super-solution or solution) of (2.3) in UX×VY,t and (b) u is a weak solution of (2.3) in UX×VY,t if and only if −u is a weak solution of (2.3) in UX×VY,t.
2.3. The Dirichlet problem
Theorem 1.5 is a statement concerning existence and uniqueness of weak solutions to a formulation of the Dirichlet problem in (1.21). In particular, we study weak solutions in the following sense.
Definition 4. Consider (g,g∗)∈W(UX×VY,t)×L2Y,t(VY,t,H−1X(UX)). Given (g,g∗), u is said to be a weak solution to the problem in (1.21) if
and if
for all ϕ∈L2Y,t(VY,t,H1X,0(UX)) and where ⟨⋅,⋅⟩=⟨⋅,⋅⟩H−1X(UX),H1X,0(UX) is the duality pairing in H−1X(UX). If in (2.7), = is replaced by ≤(≥) whenever ϕ≥0, then u is said to be a weak sub- (super-) solution of (1.21) respectively.
3.
Technical lemmas
In this section we prove a number of technical results to be used in the proof of Theorem 1.1–Theorem 1.4. Throughout the rest of the paper, we use the notation s+:=max{s,0} for s∈R. Moreover, from Sections 3 and 4, we assume that the symbol A belongs to the class M(Λ) introduced in Definition 1.
Lemma 3.1. Let Z0=(X0,Y0,t0)∈RN+1, 0<r1<r0, be such that Qr0(Z0,t0)⋐UX×VY,t. Let u be a weak sub-solution of the Eq (1.5) in UX×VY,t in the sense of Definition 3. Then
where Qt(Z0,r):={(X,Y):(X,Y,t)∈Qr(Z0,t0)} for r>0, c=c(m,Λ)≥1 and
Proof. Let t1:=t0−r20 and t2:=t0. Considering l1, l2, such that t1<l1<l2<t2, we introduce for ϵ>0 the function θϵ∈W1,∞((t1,t2)) by
Let ψ∈[0,1] be smooth in Qr0(Z0,t0) such that ψ≡1 on Qr1(Z0,t0) and ψ≡0 outside Qr0(Z0,t0) satisfying
for some constant c=c(m)≥1.
Consider the function ϕ(X,Y,t)=2u(X,Y,t)ψ2(X,Y,t)θϵ(t). We intend to test (2.5) with ϕ and the following deductions are formal. However, as u is a weak sub-solution of the Eq (1.5) in UX×VY,t in the sense of Definition 3, we know that u∈Wloc(UX×VY,t) and as W(UX×VY,t) is defined as the closure of C∞(¯UX×VY,t) in the norm introduced in (2.1) our deduction can be made rigorous a posteriori. Testing (2.5) with ϕ(X,Y,t), letting ϵ→0, and then adding
on both sides of the resulting inequality, we deduce that
where
Using (1.7), (3.3) yields
Furthermore, using (1.7)-(i),(ii) we can continue the above estimate and conclude that
Using the properties of ψ and first letting l1→t1, and then letting l2→t2 in (3.5), we obtain
where c=c(m,Λ)≥1 and
Again using the properties of ψ and first letting l1→t1 in (3.5), then taking supremum over l2∈[t0−r21,t0) and noting that for such l2, ψ≡1, we also have
This completes the proof.
Lemma 3.2. Let u be a weak sub-solution of the Eq (1.5) in UX×VY,t in the sense of Definition 3. Let k∈R. Then (u−k)+ is also a weak sub-solution of the Eq (1.5) in UX×VY,t in the sense of Definition 3.
Proof. By Remark 2.1, it is enough to prove that u+ is a weak sub-solution of (1.5). Let ϵ>0 and ϕ∈L2Y,t(VY×J,H1X,0(VX)) be a non-negative test function in (2.4). Then u+(u++ϵ)ϕ∈L2Y,t(VY×J,H1X,0(VX)) is also a non-negative test function in (2.4). Using u+(u++ϵ)ϕ as a test function in (2.4), we obtain
Letting ϵ→0, we obtain
However, by (1.7)-(ii)
Hence,
This proves that u+ is a weak sub-solution.
The following result follows from [23,Lemma 10].
Lemma 3.3. Let f≥0 be locally integrable such that
where F1,F2∈L1∩L2(R2m×R−) and μ∈M1(R2m×R−) is a non-negative measure with finite mass in R2m×R− such that F1,F2 and μ have compact support, in the time variable, included in (−τ,0]. Then for any p∈[2,2+1/m) and σ∈[0,1/3) we have
and
for some constant c=c(τ).
The lemmas stated so far will be sufficient for our proof of Theorem 1.1 and Theorem 1.2.
3.1. Additional lemmas for the proofs of Theorem 1.3 and Theorem 1.4
Lemma 3.4 (Weak Poincaré inequality). Let ϵ∈(0,1) and σ∈(0,13). Then every non-negative weak sub-solution u of (1.5) in Q5 in the sense of Definition 3 satisfies
for some constant c=c(m,Λ)≥1, where Q−1:=Q1(0,0,−1) and uQ−1:=1|Q−1|∫Q−1u.
Proof. Using that u is a non-negative weak sub-solution of (1.5), Theorem 1.1 and the property 1.7-(i), the conclusion of the lemma follows from the lines of the proof of [23,Proposition 13,pages 8-10].
Lemma 3.5 (Intermediate value lemma). Let δ1,δ2∈(0,1) be given. Then there exists constants θ=c(m,Λ)(δ1δ2)10m+15, r0=120, and ν≥c(m,Λ)(δ1δ2)5m+8, such that the following holds. Let u:Q1→R be a weak sub-solution of (1.5) in Q5 in the sense of Definition 3, assume that u≤1 in Q12, and that
where Q−r0:=Qr0(0,0,−2r20). Then
Proof. Using Lemma 3.1, Lemma 3.2 and Lemma 3.4, the result follows from the lines of the proof of [23,Theorem 3,pages 11-12].
Lemma 3.6 (Measure to pointwise upper bound). Given δ∈(0,1) and r0=120, there exists a positive constant γ:=γ(δ)=c(m,Λ)δ2(1+δ−10m−16)>0 such that the following holds. Let u be a weak sub-solution of (1.5) in Q1 in the sense of Definition 3, assume that u≤1 in Q12 and that
where Q−r0:=Qr0(0,0,−2r20). Then
Proof. Using Remark 2.1, Theorem 1.2 and Lemma 3.5, the result follows by proceeding along the lines of the proof of [23,Lemma 16,page 12].
4.
Proof of Theorem 1.1–Theorem 1.4
In this section we prove Theorem 1.1–Theorem 1.4. We first note that since our class of operators is closed under the group law defined in (1.10), and by our definition of Qr0(Z0,t0), we can throughout the second without loss of generality assume that (Z0,t0)=0. Note that Qr0=Qr0(0,0)=VX×VY×J where VX=B(0,r0), VY=B(0,r30), J=(−r20,0), and where B(0,ρ) denotes the standard Euclidean ball with center at 0 and radius ρ in Rm.
4.1. Proof of Theorem 1.1
As discussed in subsection 1.7, since u is a weak sub-solution of (1.5), there exists a non-negative measure ˉμ such that
We define r2:=r0+r12. Let ϕ1∈[0,1] be smooth such that ϕ1≡1 in Qr1(Z0,t0) and ϕ1≡0 outside Qr2(Z0,t0) satisfying
for some constant c=c(m)≥1. Then we observe that v=uϕ1 is a weak solution of
where
By Lemma 3.3, we have
and
for some uniform constant c and for every q∈[2,2+1m) and s∈[0,13). Using (4.1), (1.7)-(i), Lemma 3.1 and that 0<r1<r0≤1, it follows that
where
Using (4.5) in (4.3), the estimate (1.15) follows. To obtain the estimate (1.16), let ϕ2∈[0,1] be smooth such that ϕ2≡1 in Qr2(Z0,t0) and ϕ2≡0 outside Qr0(Z0,t0) satisfying (4.1). Choosing ϕ2 as a test function in (4.2) and proceeding similarly as in the proof of energy estimate in Lemma 3.1, we get
where c1 is given by (4.6). The last estimate, combined with (4.4) and (4.5), yields the estimate (1.16).
4.2. Proof of Theorem 1.2
As mentioned, we can, without loss of generality, assume that (Z0,t0)=(0,0,0). For n∈N∪{0}, we define
and
By Lemma 3.2 we know that un is a weak sub-solution of (1.5). Thus applying Lemma 3.1 we obtain
where c=c(m,Λ)≥1 and
Now we will estimate the integral in the right hand side of (4.7). Let q=2+12m. By Hölder's inequality we have
Since kn>kn−1, we get un≤un−1. Using this fact, that 0<r∞<r0≤1, and Theorem 1.1, we get
for every n≥2, where we have used that
with cn−2,n−1 is as defined in (4.8).
Next, we observe that
Moreover,
Combining the preceding two estimates and using 0<r∞<r0≤1, we get
Using the estimates (4.10) and (4.11) in (4.9), we get
where we have also used that An−1≤An−2. Note that the latter is true since un−1≤un−2,rn−1<rn−2 and Tn−2<Tn−1 for every n≥2. Using (4.12) in (4.7), we obtain
where α=2−2q>1, since q>2. Therefore, defining Sn:=A2n, we get
where
Recursively we get
where we have used (4.7) and the estimate
Let
We observe that
Note that, by the property (ⅱ) in Remark 2.1, v is again a weak sub-solution of (1.5). Thus the estimate (4.13) holds by replacing u with v. This fact combined with γ<1 gives v≤12 a.e. in Qr∞. As a consequence we get
for some c=c(m,Λ)≥1 and θ=θ(m)>1. Now, arguing similarly as in the proof of [23,Proposition 12,pages 7-8], the result follows.
4.3. Proof of Theorem 1.3
Using Remark 2.1, Theorem 1.2 along with Lemma 3.6, and following the lines of the proof of [23,Theorem 5,pages 13-14], the result follows.
4.4. Proof of Theorem 1.4
Using Remark 2.1, Lemma 3.6, and following the lines of the proof of [23,Theorem 7,pages 14-15], the result follows.
5.
Proof of Theorem 1.5
The purpose of the section is to prove Theorem 1.5. As g∈W(UX×VY,t) we can in the following assume, without loss of generality, that g≡0.
In domains of the form UX×UY×I instead of UX×VY,t, one may attempt different approaches to prove Theorem 1.5, and perhaps the most natural first approach is to add the term ϵΔY to the operator and to instead consider the problem
Here ∂p(UX×UY×I) is now the (standard) parabolic boundary of UX×UY×I, i.e.,
The existence and uniqueness of weak solutions to (5.1) is classical and one easily deduces that
for some positive constant c, independent of ϵ. By the standard Poincaré inequality, applied on UX to uϵ(⋅,Y,t) with (Y,t) fixed, we have
Hence, using Cauchy-Schwarz we can conclude that
for a constant c which is independent of ϵ. The idea is then to let ϵ→0 and in this way construct a solution to the problem in (2.7). To make this operational, already in the linear case, A(ξ,X,Y,t)=A(X,Y,t)ξ, one seems to need some uniform estimates up to the Kolmogorov boundary ∂K(UX×UY×I) to get a solution in the limit. In addition, in the nonlinear case considered in this paper we also need to ensure that ∇Xuϵ→∇Xu pointwise a.e. as ϵ→0 and how to achieve this is even less clear. One approach is to try to adapt the techniques of Boccardo and Murat [6] but it seems unclear how to make this approach operational in our case due to the presence of the term ϵΔYuϵ in the approximating equation.
In this paper we will instead prove Theorem 1.5 by using a variational approach recently explored in Albritton-Armstrong-Mourrat-Novack [1] and Litsgård-Nyström [29]. We will prove that the solution to (1.21) can be obtained as the minimizer of a uniformly convex functional. The fact that a parabolic equation can be cast as the first variation of a uniformly convex integral functional was first discovered by Brezis-Ekeland [9,10] and for a modern treatment of this approach, covering uniformly elliptic parabolic equations of second order in the more general context of uniformly monotone operators, we refer to [4] which in turn is closely related to [19], see also [18].
5.1. Variational representation of the symbol
To make the approach operational we will use a variational representation of the mapping ξ↦A(ξ,X,Y,t), for each (X,Y,t)∈RN+1, that we learned from [4] and [5] and we refer to these papers for more background. Indeed, by [5,Theorem 2.9], there exists ˜A∈L∞loc(Rm×Rm×RN+1) satisfying the following properties, for Γ:=2Λ+1 and for each (X,Y,t)∈RN+1. First, the mapping
Second, the mapping
Third, for every ξ,η∈Rm, we have
and
Note that the choice of ˜A is in general not unique. Note also that (5.5) and (5.6) imply, in particular that
5.2. Setting up the argument
To ease the notation we will in the following at instances use the notation
and we let
Given an arbitrary pair (f,j) such that
we introduce
Using this notation, and given an arbitrary pair (f,f∗) such that
we set
where the infimum is taken with respect to the set
The condition
appearing in (5.14), should be interpreted as stating that
for all ϕ∈L2(VY,t,H1X,0(UX)). Finally, for g∗∈L2Y,t(VY,t,H−1X(UX)) fixed we introduce
5.3. J is uniformly convex on A(g∗)
Lemma 5.1. Let g∗∈L2Y,t(VY,t,H−1X(UX)) be fixed and let A(g∗) be the set introduced in (5.16). Then A(g∗) is non-empty.
Proof. Take f∈W0 and consider the equation
for dYdt-a.e. (Y,t)∈VY,t. By the Lax-Milgram theorem this equation has a (unique) solution v(⋅)=v(⋅,Y,t)∈H1X,0(UX) and
as f∈W0. In particular,
and hence A(g∗) is non-empty.
Lemma 5.2. The functional J introduced in (5.11) is uniformly convex on A(g∗).
Proof. Note that if (f,j)∈A(g∗) and (˜f,˜j)∈A(0), then (f+˜f,j+˜j)∈A(g∗) and (f−˜f,j−˜j)∈A(g∗). Consider (f,j)∈A(g∗). We first consider the term
We have
Recall that W0=W0(UX×VY,t) is the closure in the norm of W(UX×VY,t) of C∞K,0(¯UX×VY,t). In particular, there exists {fj}, fj∈C∞K,0(¯UX×VY,t) such that
and consequently
Using this we see that
However, using that fj∈C∞K,0(¯UX×VY,t) we see that
by the divergence theorem and the definition of the Kolmogorov boundary. Hence,
Using this, and observing that,
we can conclude that
over the set \mathcal{A}(g^\ast) . Hence it suffices to prove that
is uniformly convex over the set \mathcal{A}(g^\ast) . With (f, {\bf{j}})\in \mathcal{A}(g^*) and (\tilde f, \tilde {\bf{j}})\in \mathcal{A}(0) as above, (5.5) implies that
We also have
Thus
by using the (standard) Poincaré inequality. Hence {\mathcal J} is uniformly convex on \mathcal{A}(g^*) .
5.4. Correspondence between weak solutions and minimizers
As the functional {\mathcal J} is uniformly convex over \mathcal{A}(g^\ast) there exists a unique minimizing pair (f_1, {\bf{j}}_1)\in \mathcal{A}(g^\ast) such that
Note that
Moreover, by construction of \tilde A , see (5.7), we have
Lemma 5.3. There is a one-to-one correspondence between weak solutions in the sense of Eq (2.7) to {\mathcal L} u = g^\ast in U_X\times V_{Y, t} , such that u\in W_0 , and null minimizers of J[\cdot, g^\ast] .
Proof. To prove the lemma we need to prove that for every f \in W_{0} , we have
Indeed, the implication " \implies " is clear since if f solves {\mathcal L} u = g^\ast in the weak sense, then
Conversely, if J[f, g^\ast] = 0 , then f = f_1 and
Using (5.8), we see that the identity (5.27) implies that
and by the definition of the set \mathcal{A}(g^\ast) ,
Hence f_1 indeed solves
in the weak sense. I.e., we recover that f = f_1 is indeed a weak solution of {\mathcal L} u = g^\ast . In particular, the fact that there is at most one solution to {\mathcal L} u = g^* is clear.
5.5. An associated perturbed convex minimization problem
Using (5.26) and Lemma 5.3 we see that to complete the proof of Theorem 1.5 it remains to prove that
In order to do so, we introduce the perturbed convex minimization problem defined, for every f^* \in L_{Y, t}^2(V_{Y, t}, H_X^{-1}(U_X)) , by
As
we see that to prove (5.28) is suffices to prove that G(0) \le 0 .
Lemma 5.4. G is a convex, locally bounded from above and lower semi-continuous functional on L_{Y, t}^2(V_{Y, t}, H_X^{-1}(U_X)) .
Proof. For every pair (f, {\bf{j}}) \in \mathcal A(f^*+g^*) , we have
and thus
Hence
Taking the infimum over all (f, {\bf{j}}) satisfying the affine constraint (f, {\bf{j}}) \in \mathcal A(f^*+g^*) we obtain the quantity G(f^*) , i.e., G(f^*) can be expressed as
In particular, G(f^*) can be expressed as the infimum of
with respect to (f, {\bf{j}}) such that (f, {\bf{j}}) \in \mathcal A(f^*+g^*) . We now recall the argument in (5.21) and (5.22). In particular, given f\in W_0 there exists \{f_j\} , f_j\in C^\infty_{{\mathcal K}, 0}(\overline{U_X\times V_{Y, t}}) such that
and consequently
Using (5.21) and (5.22) we have
Obviously we get the same limit in (5.31) independent of what sequence \{f_j\} chosen as long as (5.30) holds. Now consider f, g\in W_0 and let \{f_j\} , f_j\in C^\infty_{{\mathcal K}, 0}(\overline{U_X\times V_{Y, t}}) , \{g_j\} , g_j\in C^\infty_{{\mathcal K}, 0}(\overline{U_X\times V_{Y, t}}) , be such that
Then
for all \tau\in [0, 1] . Hence
and we deduce that
In particular, we can conclude that the mapping
is convex on W_0 . Using this, and (5.5), we see that the expression in (5.29) is convex as a function of (f, f^*, {\bf{j}}) and this proves that G is convex. Furthermore, using (5.17)–(5.19) we can conclude that the infimum of the expression in (5.29) is finite, hence G(f^*) < \infty . In particular, the function G is locally bounded from above. These two properties imply that G is lower semi-continuous, see [17,Lemma 2.1 and Corollary 2.2].
5.6. The convex dual of G
We denote by G^* the convex dual of G , defined for every
as
Let G^{**} be the bidual of G . Since G is lower semi-continuous, we have that G^{**} = G (see [17,Proposition 4.1]), and in particular,
In order to prove that G(0) \le 0 , it therefore suffices to show that
To continue we note that we can rewrite G^*(h) as
where the supremum is taken with respect to
subject to the constraint
Furthermore, note that for every h \in L_{Y, t}^2(V_{Y, t}, H_{X, 0}^1(U_X)) , we have G^*(h) \in \mathbb R \cup \{+\infty\} .
Lemma 5.5. Consider h \in L_{Y, t}^2(V_{Y, t}, H_{X, 0}^1(U_X)) . Then
Proof. To prove the lemma we need to prove that (\partial_t+X\cdot\nabla_Y)h \in L_{Y, t}^2(V_{Y, t}, H_{X}^{-1}(U_X)) . Using that we take a supremum in the definition of G^\ast we can develop lower bounds on G^\ast by restricting the set with respect to which we take the supremum. Here, for f\in W_0 , we choose to restrict the supremum to (f, {\bf{j}}, f^*) where {\bf{j}} = {\bf{j}}_0 is a solution of \nabla_X\cdot {\bf{j}}_0 = g^* and f^* : = -(\partial_t+X\cdot\nabla_Y)f . Recall from (5.19) that such a {\bf{j}}_0 \in (L_{Y, t}^2(V_{Y, t}, L^2_X(U_X)))^m exists. With these choices for {\bf{j}} and f^* , the constraint (5.37) is satisfied, and we obtain that
Consider f\in C^\infty_{{\mathcal K}, 0}(\overline{U_X\times V_{Y, t}})\subset W_0 . Then, again arguing as in (5.21), (5.22),
Furthermore, restricting to f\in C^\infty_{0}({U_X\times V_{Y, t}})\subset C^\infty_{{\mathcal K}, 0}(\overline{U_X\times V_{Y, t}}) yields by the same argument that
Hence we have the lower bound
where the supremum now is taken with respect to f\in C_0^\infty(U_X\times V_{Y, t})\subset C^\infty_{{\mathcal K}, 0}(\overline{U_X\times V_{Y, t}}) . Moreover, as G^*(h) < +\infty , we have that
for every f\in C_0^\infty(U_X\times V_{Y, t}) fixed. Note that by replacing f with -f in the above argument we also obtain a lower bound. In particular,
where the supremum is taken over f \in C_0^\infty(U_X\times V_{Y, t}) such that ||f||_{L_{Y, t}^2(V_{Y, t}, H_{X, 0}^1(U_X))}\leq 1 . Using that C_0^\infty(U_X\times V_{Y, t}) is dense in L_{Y, t}^2(V_{Y, t}, H_{X, 0}^1(U_X)) we can conclude that
and this observation proves (5.38).
5.7. Bounding G^* from below
Lemma 5.5 gives at hand that in place of (5.35), we have reduced the matter to proving that
Furthermore, note that for \tilde h\in W\cap C_{X, 0}^\infty(\overline{U_X\times V_{Y, t}}) we have
As we are to establish a lower bound on G^* , we may restrict to taking the supremum over f^* such that
In Lemma 5.6 below we prove that
By combining this with (5.40) and (5.41) we see that
for all \tilde h \in W\cap C^\infty_{X, 0}(\overline{U_X\times V_{Y, t}}) . Furthermore, by the definitions of W , and L_{Y, t}^2(V_{Y, t}, H_{X, 0}^1(U_X)) , we can choose a sequence h_j\in W\cap C^\infty_{X, 0}(\overline{U_X\times V_{Y, t}}) such that
Hence the proof that G^*(h)\geq 0 , and hence the final piece in the proof of existence in Theorem 1.5, is to prove the following lemma.
Lemma 5.6.
Proof. To start the proof of the lemma we first note that we have, as f\in W_0 , that
and hence we can replace f^* by f^* - (\partial_t+X\cdot\nabla_Y)f in the variational formula (5.36) for G^* to get
where the supremum now is taken with respect to
subject to the constraint
Next using that f\in C^\infty_{{\mathcal K}, 0}(\overline{U_X\times V_{Y, t}}) , h\in C^\infty_{X, 0}(\overline{U_X\times V_{Y, t}}) , we have
Using the identity in the last display we see that
where the supremum still is with respect to (f, {\bf{j}}, f^*) as in (5.43) subject to (5.44). Now, by arguing exactly as in the passage between displays (3.23) and (3.26) in [29], using the properties of \tilde A , we can conclude that it suffices to prove that \tilde G^*(h)\geq 0 where
and where the supremum is taken with respect to all (\tilde f, {\bf{j}}, f^*, b) in the set
subject to the condition stated in [29], i.e., that
for some large but fixed \Gamma\geq 1 . However, this implies that \tilde f: = -h is an admissible function. With this choice of \tilde f , we then let {\bf{j}}: = A(-\nabla_X h, X, Y, t) \in (L_{Y, t}^2(V_{Y, t}, L^2_X(U_X)))^m and then
Using this we deduce that
where supremum now is taken with respect to b\in C^\infty_{{\mathcal K}, 0}(\overline{U_X\times V_{Y, t}}) . Using Lemma 5.7 below it follows that
The proof of the lemma is therefore complete.
Lemma 5.7. Assume that h\in W(U_X\times V_{Y, t})\cap C^\infty_{X, 0}(\overline{U_X\times V_{Y, t}}) . Then
Lemma 5.7 is Lemma 3.7 in [29] and in the next subsection we supply parts of the proof for completion.
5.8. Proof of Lemma 5.7
Let \psi(s)\in C^\infty(\mathbb R) be such that 0\leq \psi \leq 1 ,
|\psi'|\leq 2 and such that \sqrt{1-\psi^2}\in C^\infty(\mathbb R) . Based on \psi we introduce for r , 0\leq r < \infty
where we use the notation s^+: = \max\lbrace s, 0 \rbrace for s\in \mathbb R . As h is smooth, and U_X and V_{Y, t} are bounded domains, we have
Let, for any r\geq 0 ,
As in the proof of Lemma 3.7 in [29] it follows that
By construction, b_r vanishes on \partial_{\mathcal K}(U_X\times V_{Y, t}) . Together with (5.50), this yields that b_r\in W\cap C^\infty_{{\mathcal K}, 0}(\overline{U_X\times V_{Y, t}}) . Furthermore,
Letting r\to \infty we see that
5.9. The proof of Theorem 1.5
Retracing the argument we see by (5.26) and (5.28) that
Using Lemma 5.3 we can conclude that f_1 is the unique weak solution f_1\in W_0 to {\mathcal L} u = g^\ast in U_X\times V_{Y, t} in the sense of Eq (2.7). This completes the proof of existence and uniqueness part of Theorem 1.5. The quantitative estimate follows in the standard way.
5.10. A comparison principle
Assume that u\in W(U_X\times V_{Y, t}) is a weak sub-solution to the equation
By definition this means in particular that u\in W(U_X\times V_{Y, t}) . Given u we now let v\in W(U_X\times V_{Y, t}) be the unique weak solution to the problem
in the sense that
and in the sense that (2.7) holds for all \phi\in L_{Y, t}^2(V_{Y, t}, H_{X, 0}^1(U_X)) . By Theorem 1.5 v exists and is unique. We want to prove that u\leq v a.e. in U_X\times V_{Y, t} . To achieve this we let \epsilon > 0 be arbitrary and we use the test function \phi = (u-v-\epsilon)^+ . Then \phi is a non-negative admissible test function and \phi = 0 on \partial_{\mathcal K}(U_X\times V_{Y, t}) . Hence,
and
Subtracting these relations, we get
Using the property (1.8)- (ii) , we now first note that
Second, again using the definition of W(U_X\times V_{Y, t}) and that (v-u)\in W_0(U_X\times V_{Y, t}) , we see that we see that there exists a sequence \{f_j\} , f_j\in C_{{\mathcal K}, 0}^\infty(\overline{U_X\times V_{Y, t}}) such
as f_j = 0 on \partial_{\mathcal K}(U_X\times V_{Y, t}) . Hence, combining (5.57)–(5.59) we conclude that
Finally, using, for a.e. (Y, t)\in V_{Y, t} , the Poincaré inequality on U_X we deduce from (5.60) that
Hence (u-v-\epsilon)^+ = 0 a.e. in U_X\times V_{Y, t} and hence u\leq v+\epsilon a.e. in U_X\times V_{Y, t} . We can conclude that we have proved the following theorem.
Theorem 5.1. Let u\in W(U_X\times V_{Y, t}) be a weak sub-solution to the equation in (5.52) in the sense of Definition 4. Given u , let v\in W(U_X\times V_{Y, t}) be the unique weak solution to the problem in (5.53) in the sense of Definition 4. Then u\leq v a.e. in U_X\times V_{Y, t} . Similarly, if u\in W(U_X\times V_{Y, t}) is a weak super-solution to the equation in (5.52) in the sense of Definition 4, then v\leq u a.e. in U_X\times V_{Y, t} .
6.
Future research and open problems
In this paper we have initiated the study of weak solutions, and their regularity, for what we call nonlinear Kolmogorov-Fokker-Planck type equations. We believe that there are many directions to pursue in this field and in the following we formulate a number of problems.
Let p , 1 < p < \infty , be given and let A = A(\xi, X, Y, t): \mathbb R^m\times \mathbb R^m\times \mathbb R^m\times \mathbb R\to \mathbb R^m be continuous with respect to \xi , and measurable with respect to X, Y and t . Assume that there exists a finite constant \Lambda\geq 1 such that
for almost every (X, Y, t)\in \mathbb R^{N+1} and for all \xi\in\mathbb{R}^m . Given A and p we introduce the operator \mathcal{L}_{A, p} through
This defines a class of strongly degenerate nonlinear parabolic PDEs modelled on the classical PDE of Kolmogorov and the p -Laplace operator, and to our knowledge there is currently no literature devoted to these operators. The results established in this paper concern \mathcal{L}_{A, 2} assuming that A\in M(\Lambda) or A\in R(\Lambda) . We see a number of interesting research problems.
Problem 1: Establish existence and uniqueness of weak solutions to the Dirichlet problem
Problem 2: Prove higher integrability, local boundedness, Harnack inequalities and local Hölder continuity of weak solutions for the equation \mathcal{L}_{A, p}u = 0 in the case p\neq 2 . This is a challenging problem and the first step is probably to figure out how to replace the result of Bouchut [7], or the use of the fundamental solution constructed by Kolmogorov, in this case. The problem is already very interesting for the prototype
Problem 3: Consider the equation in (6.4). Prove bounds for \nabla_Xu and local Hölder continuity of \nabla_Xu . Note that this must be a difficult problem in the nonlinear setting due to the lack of ellipticity in the variable Y . Again, the right place to start is probably to (simply) consider the equation
where A(\xi) has linear growth, i.e., a nonlinear p = 2 case.
Finally, we discuss the very formulation of the Dirichlet problem. Consider the geometry of U_X\times V_{Y, t} and let \Gamma: = \partial U_X\times V_{Y, t} and
Using this notation \partial_{\mathcal K}(U_X\times V_{Y, t}) = \Gamma\cup \Sigma^- . Recall that W(U_X\times V_{Y, t}) is defined as the closure of C^\infty(\overline{U_X\times V_{Y, t}}) in the norm
Assuming u\in W(U_X\times V_{Y, t}) , it is relevant to define and study the trace of u to \Gamma\cup \Sigma^+\cup \Sigma_0\cup\Sigma^- . We let = B^{2, 2}_{1/2}(\partial U_X) denote the Besov space defined as the trace space of H_X^1(U_X) to \partial U_X (this space is often denoted H^{1/2}(\partial U_X) in the literature). It is well known, that if U_X is a bounded Lipschitz domain, then there exists a bounded continuous non-injective operator T:H_X^1(U_X)\to B^{2, 2}_{1/2}(\partial U_X) , called the trace operator, and a bounded continuous operator E: B^{2, 2}_{1/2}(\partial U_X)\to H_X^1(U_X) called the extension operator. The trace space of L_{Y, t}^2(V_{Y, t}, H_X^1(U_X)) on \Gamma is therefore L_{Y, t}^2(V_{Y, t}, B^{2, 2}_{1/2}(\partial U_X)) and
The trace to \Sigma^+\cup \Sigma_0\cup\Sigma^- is less clear. Indeed, recall that the space W_{X, 0}(U_X\times V_{Y, t}) is defined as the closure in the norm of W(U_X\times V_{Y, t}) of C_{X, 0}^\infty(\overline{U_X\times V_{Y, t}}) . In particular, given f\in W_{X, 0}(U_X\times V_{Y, t}) there exists \{f_j\} , f_j\in C_{X, 0}^\infty(\overline{U_X\times V_{Y, t}}) such that
and consequently,
Using this we see that
The first obstruction to a trace inequality is that (X, 1)\cdot N_{Y, t}{{\text{d}}} \sigma_{Y, t} is a signed measure on \Sigma^+\cup \Sigma_0\cup\Sigma^- . Assuming that f\in W_{0}(U_X\times V_{Y, t}) we deduce that
Hence, in this case
and we see that we can extract a subsequence of \{f_j\} converging in L^2(K, (X, 1)\cdot N_{Y, t}{{\text{d}}} \sigma_{Y, t}) whenever K is a compact subset of \Sigma^+ . At the expense of additional notation the roles of \Sigma^+ and \Sigma^- can be interchanged in this argument. This observation highlights the difficulty concerning the possibility of a trace inequality and concerning the identification of the trace space for W(U_X\times V_{Y, t}) . This explains why we in this paper, as in [29], have used the weaker formulation of the Dirichlet problem introduced.
Problem 4: What function space is the space of traces, to \Gamma\cup \Sigma^+\cup \Sigma_0\cup\Sigma^- , of W(U_X\times V_{Y, t}) ?
Conflict of interest
The authors declare no conflict of interest.














 DownLoad:
DownLoad: