Housing price dynamics and elasticities: Portugal's conundrum

1.   Introduction

Housing price increases in recent years have raised controversy and policy concerns in several European countries, with some experts warning that houses are overvalued (Read, 2022). Understanding the evolution of housing prices in relation to fundamentals is crucial to assessing risks and ensuring financial stability in the housing market. The price of housing is one of the most relevant components in the real estate sector, as it plays an essential role in the profitability of real estate investment projects and citizens' wealth. A significant change in housing prices, whether an increase or decrease, can significantly impact the real estate sector and, in turn, a country's economy. An increase in housing prices may cause an increase in future house price growth expectations, inducing the perception of the robustness of the banks' balance sheets and thus leading to a growth in mortgage credits. On the other hand, it could lead to an excessive housing supply.

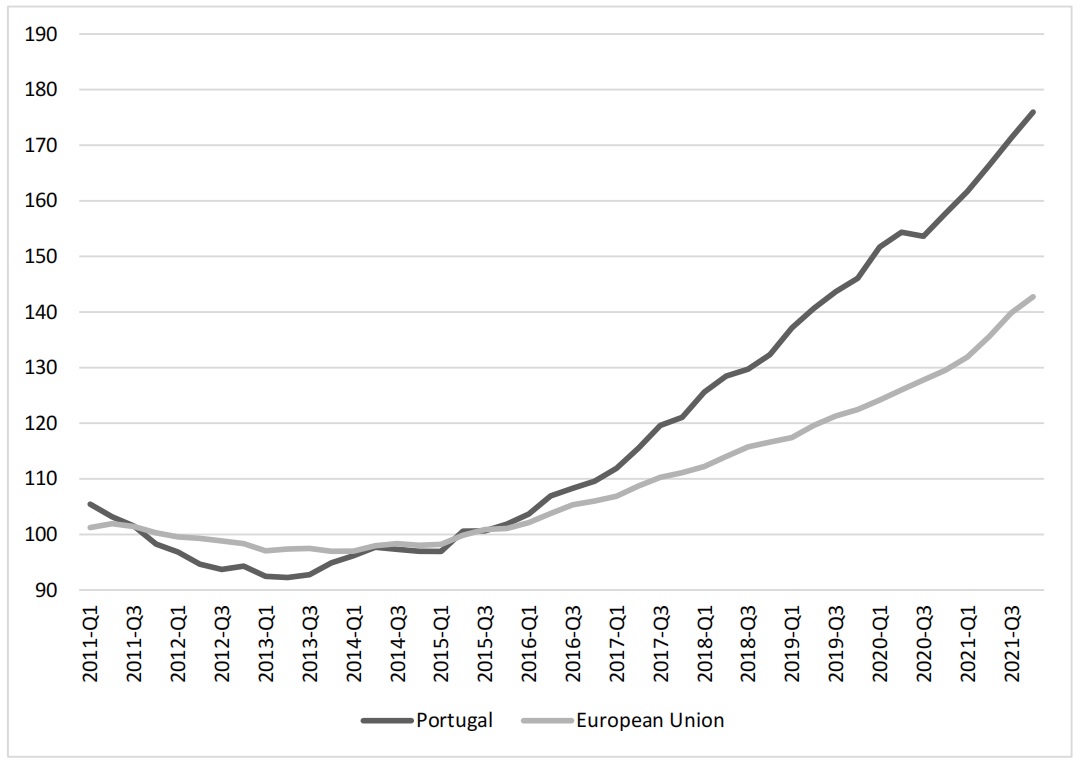
Portugal has been one of the European Union (EU) countries with the highest growth of housing prices in the last ten years, which has generated some protest and concern from citizens. According to a ranking developed by a financial firm (Sherlock, 2023), Portugal is the third most unaffordable housing market in the world (after Turkey and Iceland) in terms of the Price-to-Income ratio. As shown in Figure 1, housing prices in Portugal have grown more quickly than the average price in the EU.

Portugal's house price growth in the sample period was 67%, but the divergence in housing price growth between Portugal and the average EU house price from an equal base of 100 in 2015 reached 23.27% in the third quarter of 2021. Income has been studied as one of the major determinants in explaining the evolution of housing prices in many countries (Caldera & Johansson, 2013). However, when analyzing the evolution of the per capita gross domestic product (GDP), a proxy for income, as shown in Figure 2, we see that Portugal's GDP has followed the EU's average GDP.

Thus, it appears that housing price growth in Portugal has grown much more than the GDP growth, unlike in the EU, suggesting that, in Portugal, housing prices are not explained primarily by income. This motivates research into other fundamental factors that explain housing prices in Portugal in recent years. Understanding the main fundamentals in explaining housing prices will contribute to a better adjustment of housing policies and anticipation of potential impacts on the national economy, as well as on the stability of the financial system.

The causes of Portugal's abnormal housing price growth in the last decade are unknown. Although the conventional equilibrium housing price determinants have been previously estimated, we found a gap in the literature regarding the correlations between metropolitan elasticities and house price growth that we want to fill. We want to test if metropolitan areas with lower supply elasticity show higher housing price growth. If our hypothesis is confirmed, increasing the supply elasticity of the metropolitan areas more affected by abnormal housing price growth would help policymakers to make housing more affordable to the affected populations.

To study this hypothesis, we used panel data regressions to estimate the main determinants of housing prices at the national level referenced in the literature about stock-flow equilibrium models (aggregate income, construction costs, interest rates), and we include a determinant identified as evidence of speculative behavior in the housing market (the momentum effect). Afterward, we estimated the metropolitan areas' elasticities using time series regressions. We also studied the differences between the coastal and inner metropolitan areas. We found that, in Portugal, housing prices are inelastic to income, and the housing supply is inelastic, especially in coastal areas, where housing prices show higher growth. We did not find statistically significant correlations between house price growth, housing supply elasticities, and price-to-income elasticities. The momentum effect significantly affects all areas, suggesting that speculative forces drive the housing market. We conclude that the conventional equilibrium stock-flow model do not explain Portugal's housing market dynamics and suggest studying the effect of economic uncertainty and sentiment as the main drivers of the current situation.

This paper is organized as follows. The next section reviews the literature on housing price determinants and elasticities. Section three presents the data, tests, and econometric methodology. Section four shows the results, and section five concludes the study.

2.   Literature review

The literature about housing markets is abundant, although focusing on different approaches and methodologies, depending on whether the research is about an equilibrium or a dynamic process (Sims, 1980). Recent studies about housing price dynamics may include determinants such as disposable income, economic growth, interest rates, population, and economic policy uncertainty (Kishor & Marfatia, 2017; Balcilar et al., 2021b; Ngene & Gupta, 2023). These studies estimate house price predictors under autoregressive models, including multiperiod lagged housing prices as independent variables. Other factors, such as monetary policy surprises (Nyakabawo et al., 2018) and economic sentiment (Gupta et al., 2020; Balcilar et al., 2021a) have also positively impacted housing returns.

The stock-flow model of DiPasquale and Wheaton (1992) summarizes, in a theoretical model, the way real estate price determinants interact in a dynamic process to find a new equilibrium after a change in one of those determinants. The model includes income, interest rates, and construction costs as the main determinants of prices. We will review the existing literature about these determinants and related literature about the momentum effect that Case and Shiller (1989) identified as a dynamic explanatory variable of markets with speculative behavior.

Regarding the first variable of the stock-flow model, income, several European studies have used proxy income variables to determine housing prices, such as families' disposable income, salaries, or GDP (Belke & Keil, 2018; Taltavull, 2003). Cunha and Lobão (2022) studied the dynamics of housing prices in the Iberian market from 2011Q1 to 2021Q2, finding that coastal metropolitan areas have a higher price-to-income elasticity than inner metropolitan areas and that housing price growth was more significant in coastal metropolitan areas. Caldera and Johansson (2013) estimated the determinants of housing prices between 1980 and 2000 for 21 countries of the Organization for Economic Co-operation and Development (OECD), finding that in 13 European countries, housing prices were elastic to income, although in Germany and Ireland prices were inelastic to income. However, income proved significant and was relevant in determining housing prices. Cohen and Karpavičiūtė (2016) discovered that the GDP is one of the main factors that explain housing prices in Lithuania between 2001Q1 and 2014Q2, despite prices being inelastic to income. Oikarinen and Engblom (2016) studied the differences in housing price dynamics of 14 cities between 1988 and 2012, finding that the price-to-income elasticity was higher in large cities that normally have restrictions on the supply side due to scarcity of land, that is, cities with inelastic supply. In the USA, Case and Shiller (2003) showed that income was one of the fundamental factors in determining housing prices in metropolitan areas between 1985 and 2002. Holly et al. (2010) reached the same conclusion with panel data from 49 metropolitan areas between 1975 and 2003. Oikarinen et al. (2018) studied the dynamics of housing prices in 70 metropolitan areas between 1980Q1 and 2015Q2 and found that income is significant and determinant in explaining housing prices. However, housing prices were, on average, inelastic to aggregate income in the long term. Price-to-income elasticity was generally higher in metropolitan areas with more inelastic supply.

Regarding the second variable of the stock-flow model, interest rates, Tavares et al. (2014), in a study about Portugal, showed that interest rates significantly negatively affected housing prices between 2003T1 and 2011T4, as expected. Adams and Füss (2010) also found that interest rates negatively affected housing prices in 10 European countries. Turk (2015) reached the same result in a study of the housing prices in Sweden between 1980Q1 and 2015Q2. However, Belke and Keil (2018) later discovered that interest rates positively and significantly affected housing prices in German regions between 1995 and 2010, suggesting that interest rates follow economic cycles and thus should increase with housing prices. Jud and Winkler (2002) also discovered that interest rates positively influence housing prices in an investigation into price dynamics in 130 American metropolitan areas. Oikarinen et al. (2018) studied housing price dynamics in 70 metropolitan areas and confirmed that interest rates have a positive effect. Cunha and Lobão (2022) found the same results about the housing prices of the Iberian Peninsula, in Europe, between 2011Q1 and 2021Q2.

Regarding the third variable of the stock-flow model, construction costs, Adams and Füss (2010) found that construction costs positively affect housing prices in all countries analyzed and are statistically significant in most countries (USA, Spain, France, Netherlands, etc.). Li and Chand (2013), in a study of market fundamentals of housing prices in 29 Chinese provinces between 1998 and 2009, concluded that construction costs also positively affect the evolution of housing prices. In a study of about 70 American metropolitan areas, Oikarinen et al. (2018) also concluded that construction costs positively affect housing prices.

Regarding momentum, several empirical studies showed that housing prices tend to keep their dynamics for some periods, either increasing or decreasing, in the short run. Case and Shiller (1989) studied housing prices for resale in American metropolitan areas between 1970 and 1986 and found a positive momentum effect in the period, that is, housing prices from previous periods explain the movement in future housing prices, suggesting that housing prices do not seem efficient. They also found that the most recent quarter's lagged price has the largest weight in predicting housing prices, with momentum showing an exponential decay pattern. Later, Case and Shiller (1990) measured the price forecast and the excess returns in the housing market between 1970Q1 and 1986Q3 for the same metropolitan areas and confirmed again that the housing market appears inefficient, presenting a positive momentum effect. Beracha and Skiba (2011) follow Case and Shiller(1989, 1990) and confirm the existence of a momentum effect in the US residential market between 1983 and 2008 in 380 metropolitan areas. Oikarinen et al. (2018) also find a positive and statistically significant momentum effect in the US housing market. These authors show that the momentum effect is generally greater in metropolitan areas with a more inelastic supply. Dröes and Francke (2018) analyzed the determinants of the correlation of prices and turnover in European housing markets using a panel vector autoregressive model and discovered a positive and significant momentum effect between 1999 and 2013 in 16 European countries (Portugal included). Recently, Deng and Wong (2021) studied the momentum of the Hong Kong housing market, finding that the momentum effect at the metropolitan level was negative and insignificant, but at the aggregate market level, it was positive. Cunha and Lobão (2022) found a negative and significant momentum effect between 2011Q1 and 2021Q2 in Spain and Portugal's metropolitan areas and a mean reversion after five quarters. The research about the duration of the momentum effect is not consolidated.

Finally, regarding elasticities, the literature is more abundant. The first studies about the theme go back to Muth (1960) and Follain (1979) In the USA, who, using time series data with the ordinary least squares estimator, found that the supply elasticity was perfectly elastic in the long run. Later, Stover (1986), using cross-sectional data with the same estimator, confirmed the results of Muth (1960) and Follain (1979) in a study on the elasticity of supply of single-family housing in 61 American metropolitan areas between 1976 and 1981. Despite Stover's confirmations (1986) at the level of metropolitan areas in the US, there were significant differences in elasticities between metropolitan areas. From then on, Green et al. (2005) estimated the supply elasticities of 45 US metropolitan areas between 1979 and 1996, finding that elasticities varied between 29.9 (Dallas) and −0.3 (Miami). Goodman (2005) estimated the supply elasticity of 317 suburban areas in the 1970s, 1980s, and 1990s, finding that the suburban's supply is more elastic than the city centers' supply. Later, Paciorek (2013) investigated the supply elasticities of the ten most populated US metropolitan areas between 1984 and 2008 and concluded that supply is less elastic in coastal metropolitan areas than in the inner metropolitan areas. Duca (2020) recently found that coastal areas, where housing supply is often limited, present a substantial divergence in housing prices from the rest of the respective countries. In a study of 90 metropolitan areas of the UK, in Europe, Bramley (1993) found an average supply elasticity of 0.31 (inelastic), varying from 0.04 (Birmingham) to 0.86 (Northavon). The author concludes that the smallest values are found in city centers, and the highest values in growing metropolitan areas where there is land with building permits. Later, Meen (2005), confirmed the results of Bramley (1993), finding inelastic supply in 9 British regions between 1973Q3 and 2002Q4 to vary between 0.00 and 0.84. Cunha and Lobão (2021b) studied supply elasticities in Portugal's two most populated metropolitan areas from January 2011 to December 2019, finding that the housing supply in Lisbon was inelastic, although it was elastic in Porto. In Asia, Peng and Wheaton (1994) found an elastic housing supply in the Hong Kong property market. Later, Wang et al. (2012) studied the price elasticity of supply for 35 Chinese cities and reported an elastic supply varying between 2.8 and 5.6 between 1998 and 2009. Nevertheless, a recent study about the US housing market (Aastveit et al., 2023) has shown that the housing supply elasticities are declining, with monetary policy shocks having a stronger effect on house prices than in previous periods of housing price growth.

Regarding regional heterogeneity in housing markets, Tzeremes (2021) found strong heterogeneity among regions in housing prices, with asymmetry being one of the causes of the ripple effect on housing prices. Chowdhury et al. (2023) and Gabauer et al. (2024) showed that housing return shocks are transmitted between regions, with some regions acting as the main transmitter of the shocks, and Marfatia (2021) confirms that both national and regional factors can determine house price variations.

In summary, and according to the literature, the DiPasquale and Wheaton (1992) stock-flow model's three determinants are statistically significant in various studies of different countries and different periods, suggesting that it should explain the long run equilibrium prices of the housing market. Nevertheless, we also see in different studies that in the short run, momentum is found to be statistically significant, especially last quarter's lagged housing price. Finally, the literature shows that elasticities vary across areas and may affect the speed at which different housing markets move to new equilibriums. This leads us to the conclusion of Oikarinen et al. (2018) that housing market dynamics are different across metropolitan areas, and housing policies should consider local equilibrium models to predict housing prices.

We detect a gap in the literature regarding the correlation between abnormal housing price growth and metropolitan elasticities. If different metropolitan income and supply elasticities explain different housing price growth, policymakers could implement measures to increase the supply elasticity of the most affected metropolitan areas, thus improving affected populations housing affordability.

3.   Methodology and data

3.1.   Methodology

First, we are interested in estimating the housing price determinants' coefficients of Portugal's metropolitan areas under the DiPasquale and Wheaton (1992) stock-flow model, adapted to include the short-run dynamics (the momentum effect), namely the last quarter's lagged housing price, as proposed by Case and Shiller (1989). This combination of a stock-flow model with a dynamic factor has been used by several previous research papers about the same theme (DiPasquale & Wheaton, 1994; Quigley, 1999; Holly et al., 2010; Oikarinen et al., 2018). Therefore, and according to the previously mentioned research papers, Equation 1 represents the equilibrium equation of our study, with all the variables in the logarithmic format to stabilize variances:

where, HP — Median housing price per square meter; GDP — Product Gross Domestic; CC — Construction Cost Index; R — Mortgage Interest Rate; ${HP}_{i, t}$ — Last period median housing price per square meter; t — quarters from 2011Q1 to 2021Q4; i — Metropolitan area; ${\varepsilon }_{i, t}$ — Estimation errors from time t and metropolitan area i; ${\beta }_{0i}$, ${\beta }_{1}$, ${\beta }_{2}$, ${\beta }_{3}$ and ${\beta }_{4}$ — unknown coefficients to estimate.

The intercept coefficient has a "0" to account for fixed effects. The β1 coefficient is our estimation of interest, as it represents the price-to-income elasticity. The construction cost (CC) and the mortgage interest rate (R) coefficients do not have "i" because they are the same in all metropolitan areas. We consider these two as control variables.

Second, we want to understand the differences between coastal and inland metropolitan areas regarding the previously identified housing price determinants and respective supply elasticities. We divided the metropolitan areas into coastal and inner groups for that purpose. The coastal group is constituted by Alentejo Coast, Algarve, Alto Minho, Lisbon, Porto, Cávado, Oeste, Madeira, Azores, Aveiro, Coimbra and Leiria. The inner group is constituted by Alentejo Central, Alto Alentejo, Alto Tamega, Ave, Baixo Alentejo, Beira Baixa, Beiras e Serra Estrela, Douro, Lezíria do Tejo, Médio Tejo, Tâmega e Sousa, Terras de Trás-os-Montes, Viseu Dão Lafões. In Figure 3, we can observe the location of these metropolitan areas in Portugal.

We will estimate the supply elasticities for each metropolitan area with Equation 2, as has been used by previous studies cited in the literature review:

where: HQ — Housing stock; HP — Median housing price per square meter; t — quarters from 2011Q1 to 2021Q4; i — Metropolitan area; ${\alpha }_{0}$ — Constant; ${\alpha }_{1}$ — Estimated supply elasticity. ${\varepsilon }_{i, t}$ — Estimation errors from time t and metropolitan area i.

Finally, we will test the relationship between housing price growth, housing supply elasticities, and price-to-income elasticities at the national level by comparing the descriptive statistics of housing price growth to the β1 estimates and to the α1 estimates.

3.2.   Data

The quarterly data were taken from the Statistics Portugal database between 2011Q1 and 2021Q4. The 44-period observations of the 25 metropolitan areas add up to 1100 observations per variable, with a total sample of 5500 observations. The housing price (HP) variable is the quarterly median value of the bank appraisals (euros per square meter). Price determination using appraisals is of higher quality than the use of property tax assessment records but tends to be smoother than indices based on transaction records (Case and Wachter, 2005). This characteristic will produce prudent estimates for our independent variables. The metropolitan areas' gross domestic product (GDP) is measured in thousands of euros, interpolated to the quarter proportionally to the national quarterly GDP. Construction cost (CC) is the quarterly average construction cost index relative to the new dwellings (base 100 = 2015), being the same for all metropolitan areas. The mortgage interest rate (R) is the average effective quarterly interest rate, being the same for all metropolitan areas. Finally, housing stock (HQ) is the number of annual existing classic family accommodations linearly interpolated to quarterly numbers.

3.3.   Descriptive statistics

The descriptive statistics of the sample used for estimating Equation 1 are presented in Table 1 below.

In their original format, house prices and gross domestic product show some dispersion to the mean, reflecting the house price and economic differences between metropolitan areas. Construction cost and mortgage interest rates are the same in all metropolitan areas, having time as the only source of dispersion. All correlations (in logs) are statistically significant, with gross domestic product, construction cost, and lagged housing price positively correlated with housing price and the mortgage interest rate negatively correlated with housing price, as expected from the equilibrium model. The house price growth in the sample period can be seen in table 2, below.

The Porto metropolitan area had the highest house price growth (58, 34%), whereas Alto Alentejo had the lowest (−1.68%). The T-test shows that coastal metropolitan areas have higher house price growth than inner areas.

3.4.   Stationarity and cointegration tests

Table 3 presents the unit-root test to test the stationarity of the variables (in logs).

The null hypothesis is the existence of a unit root in the series (the non-stationarity of the series). We can observe that all p-values are less than 0.05, thus rejecting the null hypothesis. Therefore, we verify that all series are stationary.

Table 4 presents the Johansen cointegration test results (in logs).

The trace test rejects the null hypothesis of no cointegration, showing at least 4 cointegrating Equations. We can proceed with the estimation.

4.   Results

4.1.   National level estimation

In table 5, we present the estimates of Equation 1 with panel data at the national level, with three different econometric estimators: Ordinary least squares (OLS) pooled, OLS random effects (RE), and OLS fixed effects (FE). These are the commonly used estimators for estimating the panel data stock-flow model described in section 3.1. Although recent econometric advances, such as the mean group common correlated effects estimator, produce more accurate estimates in the presence of slope heterogeneity and cross-section dependence than the conventional OLS estimator, our purpose of this research is not to accurately estimate the housing price determinants of panel data, but to estimate the metropolitan areas elasticities and momentum effect, for which the conventional OLS estimator is robust.

We ran estimator consistency tests (F, Breusch-Pagan, Hausmann), with the three tests being rejected, concluding that the best estimator is the OLS-FE. Nevertheless, when estimating with the OLS-FE the econometric software fails to estimate the coefficients of construction cost (CC) and interest rate (R). We do not consider this a problem as these two variables have the same time series values in all cross-sections and, as such, were included as control variables. The housing price dynamics in this panel should be explained by price-to-income elasticity (GDP coefficient) and the momentum effect (HP_t-1 coefficient).

Although the GDP variable is statistically significant in our model, in line with all previous research, the estimated GDP coefficient was 0.112, which is lower than all previous estimations. An increase of 1% in GDP, on average, contributes to an increase of 0.112% in housing prices, ceteris paribus.

The momentum effect (price lagged in time) is statistically significant, also in line with the literature. However, the value of 0.760 means it is the most determinant factor of housing price dynamics. An increase of 1% in housing prices in the previous period, on average, contributes to a 0.760% increase in housing prices, ceteris paribus.

4.2.   Metropolitan areas estimation

In table 6, we present the estimates of Equation 1 with time series data at the metropolitan area level with the OLS estimator.

All metropolitan areas have significant estimates with adjusted R² greater than 0.7. Surprisingly, only seven out of the twenty-five metropolitan areas have their house prices determined by GDP. Only five areas have a construction cost (CC) that is statistically significant, and none of these is one of the seven that have a significant GDP. There are six areas with a statistically significant mortgage interest rate, some of which also have significant GDP or CC. The most important result of this estimation is the lagged price estimate: It is positive and statistically significant in all twenty-five metropolitan areas, showing that momentum is the most important determinant in the metropolitan areas' housing price dynamics, although varying according to location.

We are interested in analyzing these metropolitan areas grouped according to their locations. For that purpose, we split the sample according to the grouping shown in table 2 (section 3.2.) between coastal and inner areas. Table 7 estimates Equation 1 using panel data for coastal and inland metropolitan areas using OLS-FE.

Housing prices are inelastic to income but only statistically significant in inner metropolitan areas. This finding concerning coastal metropolitan areas contradicts DiPasquale and Wheaton's (1992) theoretical model and previous findings about the GDP as a determinant of housing prices. Momentum is statistically significant in explaining housing price dynamics in coastal and inland metropolitan areas. However, Coastal areas show a higher value (0.867 versus 0.486), in line with previous findings, suggesting that different supply elasticities between coastal and inner metropolitan areas could explain the longer inefficiency of the coastal housing markets regarding price adjustments.

4.3.   Housing supply elasticities

We want to verify if there are differences between coastal and inner metropolitan areas' housing supply elasticity. In table 8 we show the estimates of Equation 2, which represent the supply elasticity of each metropolitan area.

Observing table 8, we find that Portugal's housing supply, both at the metropolitan areas level and national level, is inelastic and statistically significant. Although the time series estimations show very similar housing supply among the 25 metropolitan areas (mean of 0.04), the estimation in panels produces slightly different and lower results, with the coastal metropolitan areas showing a non-significant housing supply and the inner metropolitan areas showing a housing supply elasticity above the national level estimate. These results seem to suggest a problem of lack of supply in Portugal, or a declining housing supply, confirming the results of Aastveit et al. (2023).

4.4.   Housing price growth versus Elasticities

To conclude our study, we measured the correlations between housing price growth and price elasticities of supply and income at the level of metropolitan areas to check if metropolitan areas with higher housing price growth have lower housing supply elasticity and higher price-to-income elasticity, as it would be expected from the literature. The results are presented in table 9, below.

The correlations are low and non-significant, meaning we cannot speculate that the abnormal housing price growth of the last decade is related to the housing supply elasticities or the price-to-income elasticities of Portugal's metropolitan areas.

4.5.   Discussion

We reject our hypothesis that, in Portugal, lower housing supply elasticity is correlated to higher housing price growth. Moreover, we cannot conclude that differences in income cause differences in housing price growth, rejecting the findings of several previous research papers about the determinants of housing prices based on the conventional equilibrium stock-flow model hypothesis. Momentum is the single most significant determinant of housing price dynamics, suggesting that the market is in disequilibrium.

These findings show that Portugal's housing market might be driven by speculative forces such as economic uncertainty (Kishor & Marfatia, 2017; Balcilar et al., 2021b; Ngene & Gupta, 2023), monetary policy surprises (Nyakabawo et al., 2018), and economic sentiment (Gupta et al., 2020; Balcilar et al., 2021a). Gray (2021) showed that the link between prices and income was disrupted in this century, probably due to liberalization, with increased price volatility. In a recent study about the English housing market, the same author (Gray, 2023) concludes that increased mortgage credit increases house prices in certain areas, which could create the conditions for future bubbles.

5.   Conclusions

Using a combination of time series and panel data, we studied Portugal's major determinants of housing price dynamics and elasticities according to the literature on housing prices. We estimated the housing price determinants and supply elasticity for the country's twenty-five metropolitan areas and the national level. Following previous literature, we further split the sample between coastal and inner metropolitan areas to find the differences between these two groups. We innovated by being the first study to estimate the correlations between housing price growth, the housing supply elasticity, and the price-to-income elasticity.

We found that the price-to-income elasticity at the national level is 0.112, a value lower than what was estimated in previous studies but higher in the inner metropolitan areas (0.302) than in coastal areas (non-significant). Considering that the housing price growth was much lower in inner areas (15.76%) than in coastal areas (34.01%), this result suggests that aggregate income has not been the main determinant of housing price growth in recent years. However, the momentum effect proved to be statistically significant and decisive in explaining housing prices in Portugal, with a 1% housing price growth in the last period leading to a 0.76% housing price increase in the current period. Momentum is positive and statistically significant in inner and coastal areas but higher in the latter. Policymakers should acknowledge that Portugal's housing market is in disequilibrium and that conventional equilibrium models do not explain current prices.

Furthermore, we analyzed the elasticity differences between inner and coastal areas to find if these differences could explain the housing price growth. We found an inelastic housing supply both at the national and metropolitan levels. Although inner and coastal areas have an inelastic supply, the former are less inelastic, probably because more building space is available. We wanted to know if the higher housing price growth registered in coastal areas could be related to the different housing supply elasticities and price-to-income elasticities. We did not find correlations with statistical significance between these three determinants, leaving us with a conundrum regarding the explanation of Portugal's housing price growth in the last decade, where neither aggregate income growth nor inelastic supply explains price growth.

In terms of limitations and future recommendation, we acknowledge that by studying a conventional equilibrium model with a single period autoregressive factor, we failed to capture the multiperiod autoregressive dynamic factors that drive housing prices when the market is in disequilibrium, which apparently is Portugal's housing market current situation. We did not study the effect of monetary policy on Portugal's housing prices as it was not the aim of this paper, but we include that theme as a suggestion for future research, as well as the study of economic uncertainty and sentiment.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of interest

All authors declare no conflicts of interest in this paper.