The impact of ESG performance on the credit risk of listed companies in Shanghai and Shenzhen stock exchanges

1.   Introduction

Human immunodeficiency virus (HIV) is the causative agent for acquired immunodeficiency syndrome (AIDS) which damages ability of body to fight against diseases and leave it open to attack from usual innocuous infections. Once the HIV virus enters in the body, it infects a large amount of $\text{CD4}^{+}$ T-cells and replicates quickly. During the initial stage of infection the blood contains high loads of HIV virus particles which propagates throughout the body. HIV viruses spread through bodily fluids, e.g., urine, spit, breast milk, blood, tears and so on. It is found in these fluids both as virus within infected immune cells and free virus particles. Without treatment, most of the HIV infected people will grow AIDS in ten to fifteen years of infection, while some people remain healthy longer than this even without treatment. The common signs and symptoms of AIDS are weight loss, skin rash, fever, white patches or sores in mouth, sores in throat, muscle weakness, breathing, mental changes and infection of the lining around the brain all occurring at the same time. Human body provides an ideal environment for many microbes, such as bacteria, viruses, and parasites, but the immune system prevents, limits their entry and growth to maintain finest health. Immune system is a system of biological structures, which is made up of proteins, tissues, organs, and special cells that work together to defend the body against microorganisms, disease, germs and other invaders. When the immune system of the body is destabilized, a number of different diseases, infections and cancers are allowed to grow in the human body. In humans, $\text{CD4}^{+}$ T-cells are the key target of HIV virus to kill and decreases the number of these cells increasingly throughout the course of the disease ^[1]. $\text{CD4}^{+}$ T-cells play a crucial role in the human immune system and normal amount of these cells in the blood of a healthy adults are 1000 per cubic millimeter approximately ^[2]. The destruction of these cells lies at the heart of the immunodeficiency that characterizes AIDS.

In many countries, the HIV/AIDS pandemic has reached the tipping point, with obvious and devastating economic and social consequences. HIV/AIDS becomes a macroeconomic challenge because of its wide economic effect, and strategies to combat the infection have immediate implications for important economic indicators including economic growth, income, and development. An approach that solely captures the key aggregate economic variables would overlook many of the microeconomic consequences of HIV/AIDS on living standards, which are important for public policy and influence the main aggregate economic variables, such as the accumulation of physical and human capital. Firstly, rising mortality reduces the number of employees in the economy, both intotal and across professions and skillsets. Production and administrative procedures become less efficient when employees become infected with HIV. Consumers seldom completely compensate for the loss of a breadwinner, leading to increased poverty and less access to education for children. Long term, HIV/AIDS impacts the development of both health and education. HIV/AIDS leads to a decline in wellbeing through increasing death and its economic consequences.

In recent years, several mathematical models have been proposed and analysed for the HIV infection and interaction of HIV with the immune system explaining various phenomena such as the models developed by McLean (1888–1990), Merrill (1989), Nowak et al. (1990) and Nowak Mc Lean (1991), etc. In 1889, Perelson ^[1] developed a model consisting three variables, i.e., the population of uninfected/infected T-cells and the free HIV virus particles. This model plays a fundamental role in mathematical modeling for human immune system and for understanding infection of HIV. later on, Perelson et al. ^[2] presented another model using four variables, i.e., the concentration of free virus particles, uninfected, actively infected and latently infected T-cells. This model demonstrated various clinical characteristics of AIDS such as the reduction of $\text{CD4}^{+}$ T-cells, the low levels and long latency time of free virus in the body. Ruan and Culshaw ^[3] reduced the model using three variables: free HIV virus particles, uninfected and infected T-cells. They introduced a discrete time delay model that shows the variation in time between the clearance of virus particles and infection of cells on a cellular level. Wang and Song ^[4] discussed the existence and stability aspects of the model. Mechee and Haitha ^[5] investigated about the application of Lie symmetry for HIV infected model and that model deal with initial value of nonlinear differential equation. The authors in ^[5] found uninfected T-cells in the host body with the help of Lie symmetry approach. Li and Xiao ^[6] studied the global dynamics of a virus immune system to demonstrate the HIV virus load and structured treatment interruptions. They also discussed sliding and global dynamics of the model that contains elimination rate of HIV and growth rate of the infection cells. Espindola et al. ^[7] worked on macrophages and its effect in HIV infection. They also analyzed the impact of Highly Active Anti-Retroviral Therapy (HAART) on HIV infection. Kinner et al. ^[8] studied the occurrence of HIV, Hepatitis-B and Hepatitis-C in older and young adults and concluded that it is lower in young adults than elder people and both of these are prisoners. Angulo et al. ^[9] demonstrated that the main path of HIV-1 infection is transmitted from mother to its kids. They also found polymorphisms Human Leukocyte Antigen class-B (HLA-B) that is concerned in HIV-1 infection. Theys et al. ^[10] studied HIV-1 impact on the host cell and their transmission. They also worked and found link between evolution of in host cell and fitness of host cell. Hallberge et al. ^[11] established a developed stage of knowledge on significance of HIV revelation between partners. They discussed that most of HIV infection is transferred from one infected person (female) to another person (male) and status of both are the main factor of this disease. Ransome et al. ^[12] analyzed the spread, cure and prevention of HIV infection in social relationship. They realized that social capital is important factor of HIV transmission from one to another person. Naidoo et al. ^[13] studied the care of Tuberculosis (TB) and their class in those people that already infected by HIV. Omondi et al. ^[14] considered a mathematical model of HIV infection and investigated the transmission between two kind of different ages. They also showed that males are less infected than their female partner by this infection. Sweileh et al. ^[15] discussed the global research activity on mathematical modeling of transmission and control of 23 selected infectious disease outbreak. Wu et al. ^[16] investigated the fractional-order HIV-1 infection model withuncertainty in the initial data. Ayele et al. ^[17] established an HIV/AIDS mathematical model that includes important compartments such as individuals who are aware and unaware of their susceptibility to the disease, undiagnosed HIV infections, diagnosed HIV infectious with and without AIDS symptoms, and people who have been treated for the disease. Aljahdaly et al. ^[18] introduced fractional-order into a mathematical model of HIV infection of healthy T-cells combining with the rate of multiply uninfected T-cells through mitosis and stem cell therapy. Sultanoglu et al. ^[19] used a mathematical model to analyse HIV transmission in Cyprus. Duro et al. ^[20] illustrated the $\text{CD4}^{+}$ T-cells monitoring in HIV infected peoples with the help of $\text{CD4}^{+}$ T-cells counts. They also found the chance of $\text{CD4}^{+}$ T-cells maintaining during viral suppression by using Kaplan-Meier technique. In open literature, various approximate analytical techniques, such as HAM, LADM, VIM and HPM, etc., are widely used for the solution of the models describing the real world phenomena. Khan et al.^[21] described the mathematical modeling and dynamics of a novel corona virus (2019-nCoV) solved numerically and presented many graphical results. Ongun ^[22] employed the laplace adomain decomposition method (LADM) to the model described in ^[3]. Merdan ^[23] applied homotopy perturbation method (HPM) to the model studied by Ongun for finding the approximate solution. Ghoreishi et al. ^[24] utilized the homotopy analysis method (HAM) and solved the governing model. Ali et al. ^[25] computed solution of HIV infected model by using Adomian decomposition method (ADM) that illustrate the solution of ODEs in term of infinite series components. Attaullah et al. ^[26] discussed the dynamical behaviour of HIV infection and show the influence of significant parameters involved in the model. They solved the model utilizing Galerkin method and compared the results with those obatained from RK4-method. Yuzbasi and Karacayir ^[27] considered a model of HIV infection and determined solution of the model by using exponential Galerkin method (EGM). They used a technique of residual correction. The purpose of this technique to reduce the error of solution. They also showed his result numerically and compared with numerous existing method. Attaullah and Sohaib ^[28] implemented two numerical schemes namely continuous GalerkinPetrov (cGP(2)) and Legendre Wavelet Collocation Method (LWCM).

1.1.   Main contributions

The main objectives of the present article is to extend the work of Ghoreishi et al. ^[24], which is based on HIV infection of $\text{CD4}^{+}$ T-cells. Therein, the production of new $\text{CD4}^{+}$ T-cells from thymus is considered as constant. But HIV may have the ability to infect these cells in bone marrow as well as in thymus ^[2]. For this reason we extend our work with the assumption that the production of new $\text{CD4}^{+}$ T-cells from thymus (source term) is a decreasing function of viral load ^[1,2,29]. We solved these models numerically utilizing Galerkin discretization schemes known as continuous Galerkin-Petrov method (see ^[26,28,30] for details information) and examined the influence of different parameters used in these models. Particularly, the cGP(2)-method is employed having the accuracy of 4th order in the discrete time points ^[26,28,30]. It is accurate and avoids the difficulties and massive computational work that commonly arise from traditional techniques, such as LADM, HPM, and HAM, etc. The results obtained by the proposed scheme are more reliable than the previous methods used for this model. Moreover, we have solved the model by using the Runge Kutta scheme of order four (RK4). By means of numerical experiments we compared the solutions of the RK4 scheme with the solutions obtained by the Galerkin discretization scheme with respect to accuracy. Graphical results are presented and discussed quantitatively to illustrate the solution. All the computations are performed by using a MATLAB code.

1.2.   Structures of the manuscript

The manuscript is organized as follows: Section 2 discusses the basic mathematical model for HIV infection. The details of the numerical methods employed in the model are described in Section 3. In Section 4, we demonstrated the results and discussion of the study. Section 5 introduces the comparison of the results achieved through the suggested schemes. Section 6 concludes the paper by outlining the future areas of research.

2.   Mathematical model

The model for HIV infection of $\text{CD4}^{+}$ T-cells described by Ghoreishi et al. ^[24] is

where $T(t), \; I(t)$ and $V(t)$ denote the concentration of healthy, infected $\text{CD4}^{+}$ T-cells and the free HIV virus particles at any time $t$, respectively.

The major parameter which shows the total number of HIV virus particles released by one cell during its lifetime is denoted by $N$. Since the model discussed here focuses on the population healthy $\text{CD4}^{+}$ T-cells and infected $\text{CD4}^{+}$ T-cells. Throughout the remainder of this study we will use the term healthy T-cells and infected T-cells to mean healthy $\text{CD4}^{+}$ T-cells and infected $\text{CD4}^{+}$ T-cells respectively. The initial values of dependent variables, parameter, constant and their explanation are given in Table 1.

Ghoreishi et al. ^[24] proposed a model with a constant source term of healthy T-cells $r_0$, where $r_0$ represents the production of new T-cells from thymus in uninfected individual. But HIV may have the ability to infect healthy T-cells in the bone marrow and in thymus and thus lead to reduced the supply rate of new healthy T-cells ^[2]. Therefore, instead of taking the production of new healthy T-cells from thymus is constant $r_0,$ we modified the model by taking the supply rate of these cells as a decreasing function of the viral load (for detail information see ^[2]) as follows:

where $\chi$ is constant. $\frac{ r_0\chi }{\chi+V}$ is a source term which represents the generation rate of new healthy T-cells from thymus. If $V = 0,$ then $r$ is a constant and $r$ will be decreased to half of its normal value if the viral load increases to the point $V = \chi.$ The initial values of dependent variables, parameter, constant and their explanation can be found in Table 1 and $\chi = 1 \text{mm}^{-3}$. We assumed that the dynamics of healthy T-cells, infected T-cells and free HIV virus particles populations are:

3.   The numerical methods for the HIV model

3.1.   Continuous Galerkin-Petrov method

The system of ODEs for HIV models (2.1)–(2.3) or (2.4)–(2.6) can considered as:

Find ${\bf{u}}:[0, t_{max}] to {\bf{V}} = {\mathbb R}^d$ such that

where ${\bf{u}}(t) = \left[T(t), \, I(t), \, V(t)\right]$ and ${\bf{F}}$ is the nonlinear right hand side vector valued function. At $t = 0$, $u_1(0) = T(0) = T_0, \; u_2(0) = I(0) = I_0$ and $u_3(0) = V(0) = V_0$, where $T_0, \; I_0$ and $V_0$ are the initial conditions given in Table 1.

In order to find the approximate solution of (3.1), we partitioned the time interval $I: = [0, t_{max}]$ into a number of small pieces $I_n : = (t_{n-1}, t_n)$, where $n\in\{1, \dots, N\}$ and

The symbol $\tau = t_n-t_{n}$ is used to represent the maximum time step size. For the derivation of the cGP-method, the system of equations in (3.1) is multiplied with a suitable test functions (see ^{[26,28,30,31]} for more details) and integrate over $I_n$. The discrete solution $ut|_{I_n}$ can be represent by the polynomial ansatz

where ${\bf{U}}_n^j$ are the members of the function space ${\bf{V}}$ and the basis functions $\phi_{n, j} \in {\mathbb P}_{k}(I_n)$ can be chosen as Lagrange basis functions w. r. t. the $k+1$ points $t_{n, j}\in I_n$ with the following assumption

where $\delta_{i, j}$ the usual Kronecker delta. We choose the points as $t_{n, 0} = t_{n-1}$ and $t_{n, 1}, \dots, t_{n, k}$ the ($k+1$)-quadrature points of Gauß-Lobatto formula on each time interval. In this way, the initial condition can be written as

The basis functions $\phi_{n, j}\in {\mathbb P}_{k}(I_n)$ of (3.2) are defined using the reference transformations (see ^{[26,28,30,31]} for more details). Similarly, the test basis functions $\psi h_i\in {\mathbb P}_{k-1}(\hat{I})$ are defined with appropriate choice in order to compute the coefficients (see ^{[26,28,30,31]} for details). Finally, the cGP($k$)-method reads:

where ${\bf{U}}_n^0 = {\bf{U}}_{n-1}^k$ for $n > 1$ and ${\bf{U}}_1^0 = {\bf{u}}_0$ for $n = 1$, are the initial values and $\alpha_{i, j}$ and $\beta_i$ are defined are

Once the above system is solved, the initial condition for the next time interval $\bar{I}_{n+1}$ is set to ${\bf{U}}_{n+1}^0 = {\bf{U}}_n^k$. For $k = 2$, the coefficients $\alpha_{i, j}$ and $\beta_{i, j}$ of the cGP($2$)-method are computed as follows.

3.1.1.   The cGP(2) method

Three-point Gauß-Lobatto formula (Simpson rule) is used to define the quadratic basis functions with weights $\hat {w}_0 = \hat {w}_2 = 1/3$, $\hat {w}_1 = 4/3$ and $\hat {t}_0 = -1$, $\hat {t}_1 = 0$, $\hat {t}_2 = 1$. Then, we get

Thus, the system to be solved for ${\bf{U}}_n^1, {\bf{U}}_n^2 \in {\bf{V}}$ from the known ${\bf{U}}_n^0 = {\bf{U}}_{n-1}^2$ becomes:

where ${\bf{U}}_n^0$ represents the initial condition at the current time interval.

3.2.   Classical explicit Runge-Kutta method

This method is very famous having order four developed by Kutta ^[32] (see ^[33] for more details). The Runge-Kutta method of order four is used to solve numerically the first order initial value problems. The detail information is given in Appendix-I.

4.   Numerical solutions

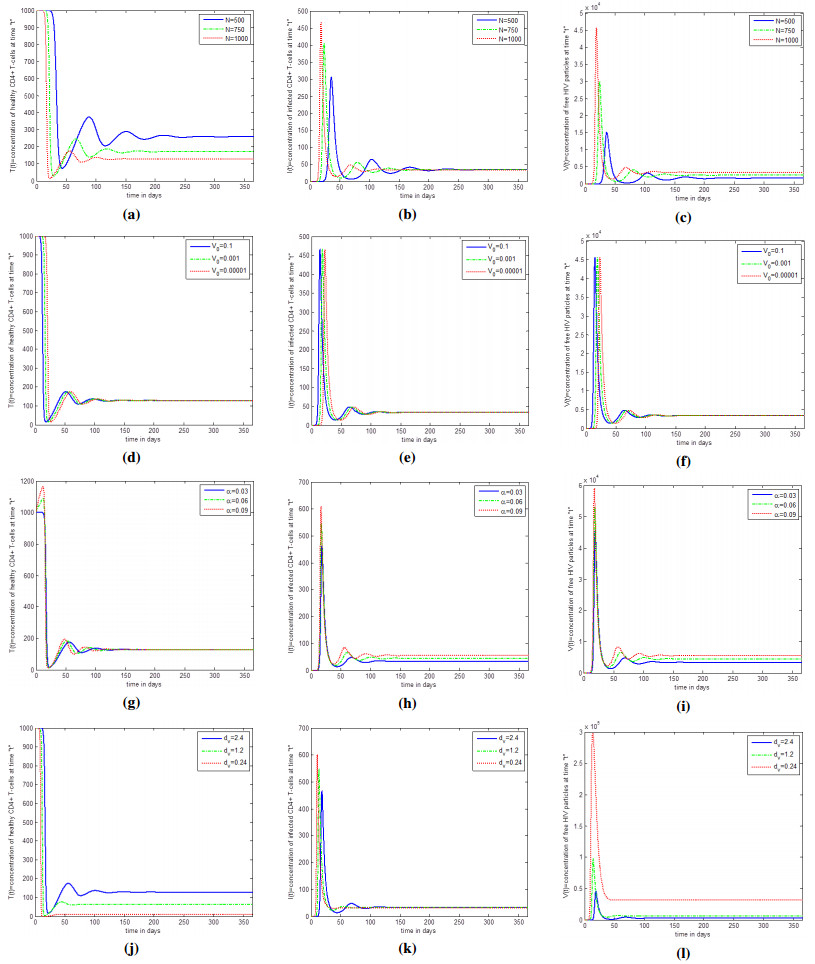
We implemented the cGP(2)-scheme to the proposed model and presented all the solutions graphically. The solution for different values of $N$ = 500,750 and 1000 in Figures 1a–1c is illustrated using the initial conditions and parameter values given in Table 1. In Figure 1a, for $N$ = 500, it is observed that the disease is characterized by a lag-phase in when there is no observable healthy T-cells depletion, followed by a stage in which the healthy T-cells clearly decrease. This stage is acute and symptomatic. Three to 6 weeks after initial infection, the HIV virus spreads throughout the body due to the burst of viral replication. About $50\%$ to $90\%$ of human beings will experience a nonspecific flu like syndrome during this acute phase. As the immune system has the ability to identify and fight against the external invaders to control the infection. Due to the killing of viral particles and cells response, the population size of T-cells again increasing after the initial decline. After 200 days the oscillations effectively disappear and the concentration of healthy T-cells remain constant. This is chronic infection phase. Figure 1b shows the changes in the amount of infected T-cells versus time after HIV infection. For $N$ = 500, we see that, the amount of infected T-cells remains small, approximately equal to zero in the first $25$ days indicating virus particles are in dormant stage. Three to 6 weeks after initial infection, the HIV virus spread throughout the body due to the burst of viral replication. The virus replicate and infect healthy T-cells, so the population size of infected T-cells increases rapidly, and attaining a maximum value approximately $300\text{mm}^{-1}$. Meanwhile, the immune system has the ability to identify and fight off against pathogen to control the infection, therefore the amount of infected T-cells again decreases and shows very small change from 60 to 90 days. After depletion, the population of infected T-cells again increases, the periodic change slows down and disappears after 180 days. Figure 1c represents the change in the population of virus particles versus time after HIV infection. Comparing the dynamics infected T-cells with HIV virus shows that the free virus follows considerably the same dynamics as the infected T-cells. As the value of $N$ increasing, they will infect larger amounts of healthy T-cells. Therefore, the amount of free HIV virus particles and infected T-cells increases, where as the number of healthy T-cells becoming smaller. We also observe that the equilibrium level of infected T-cells is approximately same, the equilibrium level of free HIV virus particles is becoming higher and the equilibrium level of healthy T-cells is becoming lower with increasing the value of $N$. Changing the initial value of HIV virus particles only affect the time from infection to depletion, e.g, increasing $V_0$, decreases the time to depletion as illustrated in Figures 1d–1f. Since the characteristic of the dynamics of infected T-cells and free HIV virus particles after infection is approximately same, so similar effects are seen if the initial condition of infected T-cells were changed. Figures 1g–1i show the effect of changing the growth rate $\alpha$, of healthy T-cells on the population dynamics of healthy T-cells, infected T-cells, and free HIV virus particles after infection. We concluded that, by increasing the values of $\alpha$, increases the population of healthy T-cells, infected T-cells, and virus particles. We also observed that the equilibrium level of infected T-cells and free HIV virus particles becomes higher, but the equilibrium level of healthy T-cells does not change with increasing $\alpha$. Decreasing the death rate of virus particles $d_V,$ decreases the number of healthy T-cells, and also speeds up the depletion. While the population of virus particles and infected T-cells increases, the time for the growth of viruses and infected T-cells also decreases. Moreover, the equilibrium level of infected T-cells does not change, the equilibrium level of virus particles becomes higher, and the equilibrium level of healthy T-cells changes downward. Also, the oscillations effectively disappear in each case, as shown in Figures 1j–1l clearly.

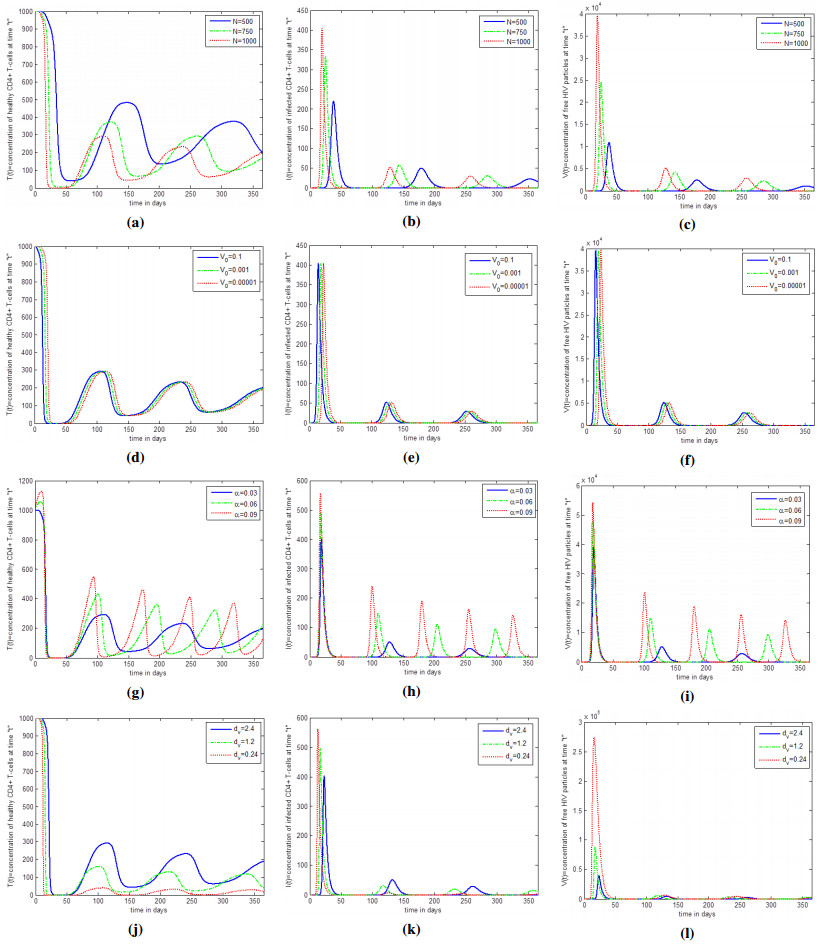
Numerical solution of the model modified is represented in Figures 2a–2l, where the source term $r_0$ of healthy T-cells replaced by $r(V),$ using the other parameter values given in Table 1 with $\chi = 1 \text{mm}^{-3}$. Here the production rate of new healthy T-cells from thymus is a monotonically decreasing function of viral load depending on the population of virus particles $V.$ Figure 2a shows the dynamics of healthy T-cells after infection by HIV virus particles. For $N$ = 500, we see that, decreasing in the population of healthy T-cells is now more gradual than in Figure 1a. Generally, most of the HIV infected peoples have a more gradual depletion in their healthy T-cells concentration ^[34]. After the initial depletion, the amount of healthy T-cells is again increases and show damped oscillatory behavior. As the value of $N$ increases the concentration as well as time to depletion of healthy T-cells decreases. In case of constant source term the dynamics of healthy T-cells again increase after the initial decline and the periodic change becomes slowdown and effectively disappear after 230 days which is complete accordance with Figure 1a. Figure 2b represents the change in the concentration of infected T-cells versus time after infection. For $N$ = 500, we observe that the amount of infected T-cells increases and reach to maximum value approximately 225mm$^{-3}$ and then decreases due to cells response and killing of virus particles. The oscillation in the population of infected T-cells can be seen even after 365 days while in case of constant source term the oscillation disappear after 150 day approximately. The time for growth in the amount of infected T-cells decreases but the population of these T-cells increases by increasing the value of $N$. Comparison of the dynamics of free HIV virus particles with infected T-cells shows that the free virus particles follows considerably the same dynamics as the infected T-cells as illustrated in Figure 2c. Figures 2d–2f show the change in the population dynamics of healthy T-cells, infected T-cells and free HIV virus particles by changing the value of initial viral load $V_0.$ As the value of $V_0$ decreases then the time for depletion of healthy T-cells also decreases as well as the time for growth in the concentration of free HIV virus particles and infected T-cells decreases. Moreover, the dynamics of healthy T-cells, infected T-cells and free HIV virus particles show the damped oscillatory behaviour, while in case of constant source term the population of healthy T-cells, infected T-cells and free HIV virus show no change by increasing the initial viral load after 100 days approximately. When the growth rate of healthy T-cells $\alpha$ increases the concentration of healthy T-cells show the same behaviour as in case of constant source term initially but after the initial decline the oscillation disappear after 100 days approximately. The oscillation even shown after 365 days incase of source term depending on the virus particles. Figures 2h–2i demonstrate the change in the growth rate of infected T-cells and free HIV virus particles after infection whenever the value of $\alpha$ increases the amount of free HIV virus particles and infected T-cells increases but after some time decreases rapidly. Furthermore, we observe that the time for oscillation in the concentration of HIV virus particles and infected T-cells decreases. But there is no oscillation in case of constant source term after 100 days only the equilibrium level of infected T-cells and free HIV virus becoming higher with increasing the value of $\alpha.$ In Figures 2j–2l we have shown the variation in the death rate of virus particles on the population dynamics of healthy T-cells, infected T-cells and free HIV virus particles respectively.

5.   Comparison of the CGP(2)-Method with RK4 Method

In this section, we applied the RK4 method to the proposed model and obtained the numerical solution using the initial conditions and parameters values given in Tables 1. In order to validate our proposed scheme, we compared the results of the cGP(2)-method with those obtained from the RK4 method concerning the achieved accuracy. Comparison of the numerical results obtained by both techniques are presented in Table 2–4 for $T(t)$, $I(t)$ and $V(t)$. The comparison clearly reveals that the presented time discretization cGP(2)-method yields the results of the model with fairly good accuracy. Additionally, we presented these results graphically. Figures 2a–2c represent the graphical out puts of both techniques. From the graphical results, it can be seen that the cGP(2) method solutions match the RK4 method solutions very well. Finally in Table 5, we provide the absolute errors between the numerical results of the cGP(2) method and RK4 method. From Table 5, we conclude that the presented scheme provides highly accurate result as compare to traditional methods e.g., HAM, HPM, LADM and so on. Tables 2–5 and Figures 2a–2c clearly expose that the proposed technique provides the results of the proposed model in a reasonably good agreement with RK4, using only eleven iterations for the given time interval. This shows that the numerical approximations to the solutions of the HIV model are reliable and confirm the power and ability of the Galerkin time discretization cGP(2)-method for computing the solutions of other nonlinear systems.

6.   Conclusions and future recommendations

In this paper, two forms of the HIV model have been studied. In the first form, the supply rate of new healthy T-cells $r_0$ from thymus is constant, whereas in the other form, we modified the model by considering the source term of healthy T-cells as a monotonically decreasing function depending on the concentration of viral load. We have implemented the cGP(2)-method to solve the time-dependent ODE systems of both these HIV models and studied the influence of different key parameters involved in the models on the population dynamics of healthy T-cells, infected T-cells, and free HIV virus particles for each case. Figures 1a–1l show the graphical output of the extended model. From the models discussed in this paper, we concluded that $N$, the number of viruses produced by infected T-cells during their life time, is the major parameter that affects the population of healthy T-cells. Figure 2a shows the dynamics of healthy T-cells after infection by HIV virus particles. For $N$ = 500, we observed that the decrease in the population of healthy T-cells is now more gradual than in Figure 1a. As the value of $N$ increases, the concentration as well as the time to depletion of healthy T-cells decrease and then show a periodic change. In the case of constant source terms, the dynamics of healthy T-cells again increases after the initial decline. The periodic change in the amount of healthy T-cells becomes slow and effectively disappears after 230 days, approximately, as shown in Figure 1a. The oscillation in the population of infected T-cells can be seen even after 365 days, while in the case of constant source term, the oscillation disappears after approximately 150 days. A comparison of the dynamics of free HIV virus particles with infected T-cells shows that the free virus follows considerably the same behaviour as the infected T-cells as shown in Figures 2b–2c. When the growth rate of healthy T-cells $\alpha$ increases the concentration of healthy T-cells shows the same behaviour as in the case of a constant source term initially, but after the initial decline, the oscillation disappears after approximately 100 days. The oscillation is even shown after 365 days in the case of the source term depending on the virus particles. Furthermore, we observe that the time for oscillation in the concentration of infected T-cells and free HIV virus particles decreases. But there is no oscillation in the case of constant source term; after 100 days, only the equilibrium level of infected T-cells and free HIV virus particles becomes higher with increasing the value of $\alpha.$ Moreover, we solved the model with a variable source term by using the RK4 method and compared the results obtained by both methods. Tables 2–5 and Figures 3a–3c show that the cGP(2)-method solutions for the model are very close to the RK4 method solutions. From the comparison, we concluded that the proposed scheme is effective and reliable for obtaining the numerical solution of nonlinear real-world problems.

In the future, we plan to develop a model for HIV infection with a cure and vaccination rate and show the influence of COVID-19 on the dynamics of the HIV virus. These basic and applied studies can be expected to benefit each other as more is learned about HIV and how it affects people. This knowledge can then be used to come up with more effective ways to stop the virus from hurting people.

Acknowledgments

The authors Ramzi Drissi and Attaullah would like to thank the Deanship of Scientific Research at Umm Al-Qura University for supporting this work by Grant Code (22UQU4350518DSR01). The author Wajaree Weera would like to thank the Department of Mathematics, Faculty of Science, Khon Kaen University, Fiscal Year 2022.

Conflict of interest

The authors declare that they have no conflicts of interest.

Appendix-I

A.   Runge-Kutta method of order four (RK-4 method)

The Runge-Kutta method of order four is used to solve numerically the first order initial value problems. Let

is the initial value problem with the initial condition $y(a) = \alpha$, let $N > 0$ be an integer and set $h = \frac{b-a}{N}$ is the step size. Partition the whole interval into $N$ subinterval with mesh points ${t_i = a+ih}$, for $i = 0, 1, 2, \cdots, N-1$. Then the Runge-Kutta method of order four is described as

where

The Runge Kutta method of order four (RK-4) agrees with the Taylor series method up to terms of $\mathcal{O}(h^4)$. This method can be extended to solve a system of $n$ first-order differential equations. The generalization of the method as follows.

Let

be the nth-order system of first-order initial value problems with the initial conditions

Use the notation $y_i^j,$ for each $i = 0, 1, 2, \cdots, N$ and $j = 1, 2, \cdots, n,$ to denote an approximation to $y^j(t_i).$ That is, $y_i^j$ approximates the $jth$ solution $y^(t)$ of (A.4) at the $ith$ mesh points $t_i.$ For the initial condition, set

Suppose that the values $y_i^1, \; y_i^2, \cdots, y_i^n$ have been computed. We obtain $y_{i+1}^1, \; y_{i+1}^2, \cdots, y_{i+1}^n$ by first calculating

for each $j = 1, 2, \cdots, n;$ and then

for each $j = 1, 2, \cdots, n.$ The values $k_1^1, k_1^2, \cdots, k_1^n$, must be computed before any of the terms of the form $k_2^j$ can be determined. For more questions regarding reference style, please refer to the Citing Medicine.