A portfolio selection using the intuitionistic fuzzy analytic hierarchy process: A case study of the Tehran Stock Exchange

1.   Introduction

Nowadays, investing in the stock market (SM) has attracted the attention of many investors, especially beginner investors. The stock market is influenced by many direct and indirect factors. Investing in the SM provides an opportunity for money to diversify risk with potential returns, hence most people tend to invest in the stock market (Narang et al., 2022; Ren et al., 2017; Zeleny & Cochrane, 1973). In the world of capital, there are always people and institutions who are faced with excess capital, and on the other hand, some people need these funds to carry out their activities. The function of the capital market is to transfer funds from savers to those who need funds. The existence of an active capital market is a sign of the development of a country (Elton & Graber, 1995). Choosing the optimal portfolio to achieve maximum profit, while the risk is low, has always been the concern of financial market investors. Therefore, one of the most important challenges that organizations face today is to decide on the prioritization of projects in a portfolio so that this prioritization is optimal as well as strategic. Financial experts believe in the principle of not putting all your eggs in one basket". This popularized concept leads to portfolio selection (PS) (Zhao et al., 2021; Li et al., 2018). In modern portfolio theory (MPT), how to choose the combination of return and risk in the decision to invest in securities is a fundamental problem (Marasović & Babić, 2011; De Minguel et al., 2009). A decision- maker (DM) has many criteria for selecting stocks, and the criteria depend on factors related to each other. The main concern of the manager or decision- maker is to compare these factors and prioritize them. Evaluating the performance of the investment portfolio and ranking them is important so that stock traders can make the necessary decisions about holding, selling, or buying the shares of these companies at the appropriate time (Ren et al., 2017).

It is very natural for potential investors to look for the best market performance, where there are stocks and portfolios performing better than others. On the other hand, it becomes more difficult for investors obtaining new portfolios in uncertain environments (Narang et al., 2022; Dincher, 2015). The subject of PS is not a new one for researchers (Paur, 2020; Chen et al., 2017; Shroff et al., 2011). In modern finance, PS has been an important issue since the 1950s (Markowitz, 1952). American economist Markowitz, taking into account the portfolio theory, used mathematical methods to apply the multi-objective optimization model and created the first model for portfolio optimization in 1952, which received the Nobel Prize in Economics for his contributions (Jin et al., 2021). In fact, he developed a mean-variance model (M-V) to explain how to achieve the best balance between return and risk by choosing the right portfolio of securities (Bernal et al., 2021). In today's global economy, with the globalization of financial markets, which has created an uncertain environment for investment, it has become very difficult to make investment decisions. Models have been presented to solve this problem and, over time, the defects of each have been identified and other models have replaced them. The tools that are often used to make financial decisions are usually based on statistical and econometric models. These tools have shortcomings that make it difficult to add quality criteria and check them during the decision-making process (Marqués, 2020; Cohon, 2004). In practice, decision- makers' judgments are often uncertain and cannot be expressed by precise numerical values. Therefore, to face the complexities of such decision-making issues, it is necessary to use new interdisciplinary approaches. In general, considering the uncertainty that prevails in the stock exchange and also considering the different tendencies and preferences of investors, finding a way to choose a suitable set of projects through which uncertainty and different preferences can be overcome is necessary (Tumsekcali, 2021; Tandon et al., 2019; Xu & Liao, 2014; Zadeh, 1965). Fuzzy set theory is one of the powerful tools for dealing with the ambiguity created by financial markets and investors' behavior, which is used to describe fuzzy environments, including many aspects of financial markets, such as the unpredictable behavior of financial managers. This study used MCDM approaches for PS. The multi-criteria approach is a tool for calculating the weight of evaluation criteria and ranking the options available in these issues, and one of the main features of the method is the inclusion of quantitative measures(Bektur, 2021; Zelani & Cochrane, 1973). The process of decision-making is a complex mental program that aims to solve problems by considering multiple aspects and determining the most desirable outcome (Sheikh & Senfi, 2024). In MCDM problems, a DM or DMs must rank or select alternatives that are associated with some intangible or conflicting attributes (Haseli et al., 2019; Zavadskas et al., 2018). A general MCDM problem can be expressed in the form of a decision matrix (M × N), where M is the number of options and N represents the number of decision criteria (Marqués, 2020). To overcome the problem, the theory of fuzzy sets was introduced, and then classical AHP was developed into fuzzy AHP (FAHP), in which each pairwise comparison is described as a fuzzy number (Rajaprakash et al., 2015; Van Laarhoven & Pedrycz, 1983). Considering that factors such as doubt or uncertainty are not defined in classical sets and even fuzzy sets, it is necessary to use intuitionistic fuzzy sets (IFSs), in which, in addition to the degree of membership and non-membership, a factor of uncertainty is also used(Ayyildiz & TaskinGumus, 2021; Tumsekcali et al., 2021).

The intuitionistic fuzzy analytic hierarchy process (IFAHP) methodology enhances the traditional analytic hierarchy process (AHP) by incorporating intuitionistic fuzzy logic to handle uncertainties and vagueness in decision-making processes. In traditional AHP, decisions are made based on pairwise comparisons of criteria and alternatives using crisp values. However, real-world decision-making often involves subjective judgments and imprecise information that cannot be accurately represented by crisp values. This is where intuitionistic fuzzy logic comes into play in IFAHP. Intuitionistic fuzzy logic allows decision-makers to express their hesitancy and uncertainty by considering not only the degree of membership of an element in a set (as in fuzzy logic) but also the degree of non-membership. This additional dimension of information enables a more comprehensive representation of decision-makers' preferences and uncertainties. In IFAHP, the pairwise comparisons in the AHP process are conducted using intuitionistic fuzzy numbers to capture the uncertainty and vagueness in decision-makers' judgments. These intuitionistic fuzzy numbers consist of three components: the degree of membership ($\mu_{A}$), the degree of non-membership ($\nu_{A}$), and the degree of hesitation ($\pi_{A}$). By incorporating intuitionistic fuzzy logic into the AHP framework, IFAHP provides decision-makers with a more flexible and robust methodology to handle complex decision-making scenarios where uncertainties and vagueness play a significant role. This integration allows for a more realistic representation of decision-makers' preferences and uncertainties, ultimately leading to more informed and reliable decision outcomes. Traditional methods often struggle to capture the full spectrum of uncertainties inherent in financial markets, leaving decision-makers grappling with incomplete information and hesitancies. Addressing this crucial gap, our research explores the transformative potential of intuitionistic fuzzy sets (IFS) in revolutionizing financial decision-making processes. Our study aimed to not only showcase the capabilities of IFS in handling uncertainty but also to highlight the innovative value they bring to the financial decision-making landscape. By extending the traditional fuzzy set framework to incorporate degrees of membership, non-membership, and hesitancy, IFS provide decision-makers with a more nuanced and comprehensive toolset for analyzing and managing uncertainties in financial contexts. The primary objective of our work was to demonstrate how the application of IFS can enhance decision-making accuracy, risk assessment, and overall performance in financial markets. By bridging the gap between traditional fuzzy sets and the complex uncertainties of financial environments, our research contributes to a deeper understanding of how advanced mathematical frameworks can empower decision-makers to navigate volatile markets with confidence and precision. Through a detailed examination of the innovative value of IFS in financial decision-making, our study seeks to provide a roadmap for researchers to leverage this cutting-edge approach to address existing challenges and unlock new opportunities in the ever-evolving financial landscape. By shedding light on the transformative potential of IFS, we aim to pave the way for a more robust and effective decision-making framework that can drive success and resilience in today's dynamic financial markets. IFAHP offers several advantages over traditional portfolio selection methods, such as the mean-variance model. The advantages of IFAHP over traditional portfolio selection methods are:

● Handling Uncertainty: IFAHP, with its intuitionistic fuzzy logic, can effectively handle uncertainties and vagueness in decision-making, which are common in portfolio selection due to market fluctuations and incomplete information. Traditional methods like mean-variance optimization may struggle to account for such uncertainties adequately.

● Subjectivity: IFAHP allows decision-makers to express their subjective judgments and preferences more comprehensively through intuitionistic fuzzy numbers. This subjective input can lead to more personalized and realistic portfolio selections compared to traditional methods that rely solely on objective data and assumptions.

● Flexibility: IFAHP is more flexible in accommodating different decision criteria and preferences, making it suitable for a wide range of portfolio selection scenarios. Traditional methods may be more rigid and limited in their ability to adapt to changing investment objectives or constraints.

● Transparency: IFAHP provides a transparent decision-making process by explicitly capturing decision-makers' hesitancy and uncertainty through intuitionistic fuzzy numbers. This transparency can enhance stakeholders' understanding and acceptance of the selected portfolio compared to traditional methods that may seem black-and- white in nature.

The limitations of IFAHP compared to traditional portfolio selection methods are:

● Complexity: The integration of intuitionistic fuzzy logic in IFAHP adds complexity to the decision-making process, requiring a good understanding of fuzzy logic principles and additional computational efforts. Traditional methods like mean-variance optimization may be simpler and more straightforward to implement.

● Data Requirements: IFAHP may require more detailed and nuanced input data, such as subjective judgments in the form of intuitionistic fuzzy numbers, which could be challenging to elicit and analyze compared to the quantitative data typically used in traditional portfolio selection methods.

● Computational Intensity: The computation involved in IFAHP, especially when dealing with a large number of criteria and alternatives, can be more intensive compared to traditional methods. This increased computational burden may limit the scalability of IFAHP for large portfolio selection problems.

Intuitionistic fuzzy sets provide a framework for handling uncertainty in financial decision-making by allowing decision-makers to express not only the degree of membership of an element in a set but also the degree of non-membership and hesitancy. Here's how IFS effectively handle uncertainty in financial decision-making:

● Representation of Uncertainty: Traditional fuzzy sets only consider the degree of membership of an element in a set, but IFS extend this concept by incorporating the degree of non-membership and hesitancy. In financial decision-making, where uncertainty is prevalent, this additional information allows decision-makers to better capture the nuances of uncertainty and make more informed decisions.

● Flexibility in Decision-Making: IFS offer a more flexible and nuanced approach to decision-making by allowing decision-makers to express their uncertainty and hesitancy in a more granular way. This flexibility is particularly useful in financial decision-making, where factors such as market volatility, changing economic conditions, and incomplete information can introduce significant uncertainty.

● Risk Management: In financial decision-making, managing risk is crucial. IFS provide a more comprehensive framework for risk assessment and management by considering not only the possibilities of outcomes but also the uncertainties associated with these outcomes. This allows decision-makers to assess and mitigate risks more effectively.

● Handling Incomplete Information: Financial markets are complex and dynamic, making it challenging to have complete information for decision-making. IFS can handle incomplete or imprecise information effectively by allowing decision-makers to express their uncertainty and hesitancy regarding the available data. This is particularly valuable in financial decision-making, where decisions are often made based on imperfect information.

● Aggregation of Expert Opinions: In financial decision-making, it is common to have inputs from multiple experts or sources. IFS can aggregate these diverse opinions by capturing not only the degree of agreement but also the degree of disagreement and hesitancy among experts. This allows decision-makers to consider a wide range of perspectives and make more robust decisions.

● Quantification of Uncertainty: IFS provide a quantitative framework for representing uncertainty, allowing decision-makers to assign numerical values to the degree of membership, non-membership, and hesitancy. This quantification enables decision-makers to perform calculations, comparisons, and analyses that take into account the uncertainties inherent in financial decision-making.

By incorporating intuitionistic fuzzy sets into financial decision-making processes, decision-makers can better navigate the complexities and uncertainties of the financial markets, leading to more informed, robust, and effective decision-making strategies. Since the problem of portfolio evaluation and selection is an MCDM problem and the current methods do not have the necessary efficiency to solve this problem, we incorporate here innovative and combined methods for extracting the solution of the problem. Therefore, in this article, in order to evaluate and choose the stock portfolio, we examine the listed companies in the Tehran Stock Exchange and select six companies that are more suitable for investment than others. According to the Tehran Stock Exchange, where the existing price charts are available based on the performance of the companies, it is observed that Kaghazsazi Kavehstock, with a profit limit of 100%, is in an important support range and the profitability is rising. Laabiran stock has recorded very good profitability growth in recent years and is technically in a good range. Also, the stock price of Daro Jabra Ben Hayyan has successfully broken the dynamic resistance and is expected to have good fundamental conditions, so it can be one of the significant options for investment. Also, the shares of Daro Luqman, Bourse Kala Iran, and Pashme Shishe Iran companies are in the range of potential support and profitability compared to other companies admitted to the Tehran Stock Exchange and can be good options that are suggested for long-term investment (https://nezarat.com/training/best-stock-long-term-buying, 2022; https://nabzebourse.com/, 2022). The selection of the Tehran Stock Exchange (TSE) as the focus of analysis was based on several factors:

● Market Dynamics: The Tehran Stock Exchange is one of the largest and most active stock exchanges in the Middle East region. Analyzing stocks listed on the TSE can provide insights into the dynamics of the Iranian stock market, including trends, volatility, and investor sentiment.

● Diversification: Investing in stocks from different markets, such as the TSE, can help diversify a portfolio and reduce overall risk. By including TSE-listed stocks in the analysis, investors can gain exposure to a different market and potentially benefit from diversification.

● Economic Considerations: The performance of stocks listed on the TSE can be influenced by the broader economic conditions and geopolitical factors specific to Iran. Analyzing TSE-listed stocks can provide valuable information on the economic outlook and investment opportunities in the country.

As for the specific stocks analyzed on the Tehran Stock Exchange, the selection may be based on various criteria, such as market capitalization, sector representation, liquidity, and historical performance. Here are some common reasons for selecting specific stocks for analysis:

● Market Capitalization: Including stocks with different market capitalizations (large-cap, mid-cap, small-cap) can provide a diversified view of the market and cater to different investment preferences.

● Sector Representation: Analyzing stocks from various sectors (e.g., finance, technology, healthcare) can help assess sector-specific trends and opportunities, as well as manage sector-specific risks.

● Liquidity: Stocks with higher liquidity are often preferred for analysis as they are easier to buy and sell, reducing transaction costs and enhancing portfolio flexibility.

● Historical Performance: Selecting stocks with a track record of consistent performance or growth may be of interest to investors seeking long-term investment opportunities.

Overall, the rationale behind selecting the Tehran Stock Exchange and specific stocks for analysis may vary based on investment objectives, risk tolerance, and the need for diversification and exposure to a specific market or sector. Conducting thorough research and analysis on the chosen stocks can help investors make informed decisions and optimize their investment portfolios. So in order to evaluate and choose the stock portfolio, for the first time, we have examined a combination of fuzzy theory and MCDM under the name of IFAHP.

2.   Related work

Choosing and managing the stock portfolio are the main areas of financial decision- making. The existence of uncontrollable variables has affected the decision-making process in general, and this is of great importance for investors, who are actually the final DMs for allocating their budget to financial assets in the investment portfolio. Identifying the factors involved in the investor's decision-making, measuring these factors, and determining how they affext the selection of the portfolio are the fundamental problems for financial analysts. Considering that the basis of the work of many organizations today is project-oriented, they are faced with the problem of choosing a project portfolio. Optimum decision-making is important to solve this problem in organizations because a wrong decision in this case can cause many negative results for the organization. Therefore, it is better to use decision-making such as the MCDM methods to manage the principled problem solving (PPS) (Souza et al., 2022; Stanitsas et al., 2021). Fuzzy techniques are one of the main mathematical models that are currently available to support decision theory. Therefore, one of the best solutions is to apply the principles and techniques of the hierarchical analysis process in the prioritization and selection of projects in a portfolio. Among the best MCDM methods that can be used in making decisions for investing in portfolios and efficient management is the use of AHP, ELECTRE, VIKOR, and TOPSIS.

In the literature, there are several approaches to managing and building a portfolio. There are also some performance evaluation studies using MCDM methods, and we will mention a few of them. For example, Gupta et al. (2023) aimed to construct an investment portfolio (IP) of 100 listed companies in the National Stock Exchange of India (NSE) using non-parametric methods, which reduced risks while maximizing returns. Utilizing theD'Agostino-Pearson (DP) omnibus test, companies with non-normal distributions were selected, and financial beta was used to assess return and risk. The TOPSIS and Bayes portfolio model were employed for multi-criteria decision-making and selecting profitable, low-risk stocks for the portfolio. Narang et al. (2022), in a study of an integrated two-stage framework, merges the Heronian mean operator and combined compromise solution (CoCoSo) method for stock selection. The CoCoSo-H model boosted decision flexibility and accuracy, which was validated via an NSE stock selection case study. Portfolios, optimized with particle swarm optimization, showcase the model's superior performance and stability. Rasoulzadeh et al. (2022) proposed a novel integrated Markowitz and cross data envelopment analysis (DEA) model utilizing intuitionistic fuzzy numbers for optimal portfolio selection. Their study on 50 Tehran Stock Exchange enterprises demonstrates model efficiency and constraint coverage, validated through NSGA-II optimization, showcasing superior effectiveness compared to existing methods. Vasquez et al. (2022) used the AHP-TOPSIS approach for stock portfolio selection after analyzing the performance of the Colombian market during the period of 2012-2017. Yu et al. (2021) built an intuitionistic fuzzy multi-objective linear programming model for the portfolio selection problem, and Javaherian et al. (2021) created a new DEA model consisting of intuitionistic fuzzy data. Cheng et al. (2021) used the decision tree method based on MCDM methods considering the basic characteristics for stock selection. Furthermore, Peng et al. (2021) applied the ELECTRE I method to select the best portfolio. Considering the importance of the issue, we intend to describe how to evaluate and prioritize the portfolio of companies admitted to the stock exchange using one of the MCDM techniques under IFAHP. Leung et al. (2021) studied a decentralized robust portfolio optimization using multiagent systems. Initially, decentralized robust portfolio optimization is defined as two distributed minimax optimization challenges within a Markowitz return-risk framework. Cooperative-competitive multiagent systems were created and utilized to address these problems. Also it is demonstrated that these multiagent systems can achieve agreements on expected stock prices and convergence in investment allocations through interactions within and between groups. The article presents experimental findings using stock data from four major markets to support the effectiveness of multiagent systems for decentralized robust portfolio optimization. Furthermore, Leung and Wang (2020) focused on utilizing collaborative neurodynamic optimization for portfolio selection. They formulated the classic Markowitz mean-variance (MV) framework and its variant, mean conditional value-at-risk (CVaR), as minimax and biobjective portfolio selection challenges. Neurodynamic techniques were employed to tackle these optimization tasks. Multiple neural networks collaborate to define the efficient frontier using particle swarm optimization (PSO)-based weight optimization. The study demonstrates the effectiveness and attributes of collaborative neurodynamic strategies in addressing portfolio optimization issues through experiments with stock data from four major markets. As stated, each of the researchers mentioned in this article have used a different approach in MCDM to optimize and choose the portfolio. In this study we also used the intuitionistic fuzzy approach of IFAHP to evaluate and choose the best portfolio for investment.

3.   Preliminaries of IFS and intuitionistic fuzzy AHP

The AHP is a decision-making method first developed by Saaty (Saaty, 1980). Today, this process is used in management science to determine priorities in MCDM. In fact, it solves the problem by breaking down a complex problem into a multi-level hierarchical structure of goals, criteria, sub -criteria, and alternatives. Thereafter, it provides a relative scale for displaying judgments. AHP seems to be insufficient to investigate preferences in today's uncertain decision-making situations. To overcome this issue, fuzzy set theory was introduced and fuzzy AHP (FAHP) was developed in which judgments are made in pairs (Rajaprakash et al., 2015). Fuzzy logic, which Zadeh introduced in 1965, is suitable for both qualitative evaluation and subjective judgment of decision-making issues. Considering that factors such as doubt or uncertainty are not defined in classical sets and even fuzzy sets, the use of IFS is essential, in which, in addition to the degree of membership and non-membership, the degree of uncertainty is addressed. Therefore, AHP and conventional FAHP were gradually developed to intuitionistic fuzzy conditions, which fill this gap and have the ability to convert qualitative measures into quantitative ones using verbal variables (Rajaprakash et al., 2015). In the process of intuitionistic fuzzy hierarchical analysis, the pairwise comparison matrix is shown as triangular intuitionistic fuzzy numbers. A triangular intuitionistic fuzzy number (TIFN) and a trapezoidal fuzzy number are both fuzzy numbers (Deng et al., 2022). While Zadeh's (1965) theory only defined a function for membership, Atanasov proposed IFS theory, which is a generalized model of fuzzy set theory. Also, Atanasov added a third parameter for uncertainty in IFS. One of the most widely used fuzzy sets for defining linguistic criteria, which has attracted the attention of DMs today, is IFS. In this section, we will discuss the basic definitions of IFSs to understand the implementation of IFAHP, and we will start by introducing some basic concepts and definitions related to IFSs.

Definition 1: Suppose the value function $X$ from the set of propositions is defined as follows: $X(A) = < \mu_{A}(x), \nu_{A}(x) >$. Thus the function $X:A\rightarrow [0, 1]$ is the value function that gives us the "degree of correctness" and "degree of incorrectness" of each statement in the set of X.

Definition 2: Let us fix a set $X$ to be a nonempty set, where $A\subset X$ is a subset of $X$. The intuitionistic fuzzy set (IFS) is defined as follows: $X(A) = \{(x, \mu_{A}(x), \nu_{A}(x))\mid x\in X\}$ where $\mu_{A}(x)\rightarrow [0, 1]$ and $\nu_{A}(x)\rightarrow [0, 1]$ denote the membership function and the non-membership function, respectively; and for every $x \in X, 0\leq \mu_{A}(x)+\nu_{A}(x)\leq 1$ holds (Tumsekcali et al., 2021; Ilbahar et al., 2020).

Definition 3: Fuzzy logic is a special case of intuitionistic fuzzy logic where $\mu_{A}(x)+\nu_{A}(x) = 1$ and then, $X(A) = < \mu_{A}(x), 1-\mu_{A}(x) >$.

Definition 4: For each IFS (Dabiri & Safari, 2016), $\pi_A$ is defined as $\pi_{A}(x) = 1- \mu_{A}(x)-\nu_{A}(x)$. It is called the hesitation degree or degree of non-determinacy (uncertainty) of $x \in A$ or $x \notin A$.

Definition 5: $A$ is a finite set of alternatives (Xu & Liao, 2014; Saaty, 1986)as follows: $A = \{A_1, A_2, …A_m \}$; $C$ is a set of $n$ criteria as follows: $C = \{C_1, C_2, …C_n \}$, and $w$ is a vector that defines the weight of criteria as follows: $w = \{w_1, w_2, …w_n \}$ where $w_i \geq 0$ for $i = 1, 2, …, n$ and $\sum_{i = 1}^{n}w_i = 1$.

Definition 6: $A$ is an intuitionistic fuzzy set in $X$ with membership function $\mu_{A} (x)$ and non-membership function (Souza et al., 2021, 2022; Ayyildiz et al., 2021) $\nu_{A} (x)$ as follows: For $l\leq m \leq u$ that $l$ and $u$ are lower and upper values of the support of $A$, respectively, $m$, $m_1$, and $m_2$ are the modal values. When $l = m = u$, the triangular fuzzy number reduces to a crisp number and the trapezoidal fuzzy number reduces to a triangular fuzzy number when $m_{1} = m_{2}$. Therefore,

$\mu_{A}(x) = \begin{pmatrix} \frac{x-l}{m-l}, & x \in [l, m] \\ \frac{u-x}{u-m}, & x \in [m, u] \\ 0, & otherwise \end{pmatrix}$ and $\nu_{A}(x) = \begin{pmatrix} 0, & x \in [-\infty, l]\\ \frac{x-l}{m_1 -l}, & x \in [l, m_1] \\ 1, & x \in [m_1, m_2] \\ \frac{u-x}{u-m_2}, & x \in [m_2, u] \\ 0, & x\in [u, +\infty] \end{pmatrix}$

4.   Pairwise comparison matrix

Pairwise comparison is an important strategy for distinguishing and checking the degree of similarity of each reference pair. In order to compare the desired pairs, we form a matrix called the pairwise comparison matrix (PCM) (Zhang et al, 2014). One of the fundamental tools in MCDM approaches, especially in the intuitionistic fuzzy hierarchical process, is the pairwise comparison matrix that simply compares two factors and is used to calculate the relative priorities of criteria, or sub-criteria, or options. A pairwise comparison matrix is as follows:

$A = (a_{ij})_{n\times n} \begin{pmatrix} a_{11} & a_{12} & ......&a_{1n} \\ a_{21} & a_{22} & ......&a_{2n} \\... & ... & ...... & ... \\ a_{n1} & a_{n2} & ......&a_{nn} \end{pmatrix}.$ In fuzzy methods, this matrix is used in which $a_{ii} = 1, a_{ij} = 1/a_{ji}$ for $i\neq j$ (Sepehrian et al., 2021).

Definition 7: Intuitionisticfuzzy preference relation in matrix $R$ is $R = (r_{ij})_{n\times n}$, where $r_{ij} = (\mu_{ij}, \nu_{ij})$ for $i, j = (1, 2, …n)$.

Here, the multiplicative consistents are as follows when $i\leq t\leq k$ and $i, k \in [1, 2, …, n]$ :

and

Definition 8: For any $r_{ij} = (\mu_{ij}, \nu_{ij})$ and $r_{tl} = (\mu_{tl}, \nu_{tl})$ in $X$, $\mu_{ij}$ is the degree of membership, $\nu_{ij}$ is the degree of non-membership, and its operations are given as follows:

5.   Motivations for the research

In the realm of financial decision-making, the ever-present challenges of uncertainty, complexity, and volatility underscore the critical need for innovative tools that can enhance decision-making processes. Traditional methods often fall short in capturing the multifaceted uncertainties that characterize financial markets, leading to suboptimal decisions and missed opportunities. Motivated by this pressing need, our research delves into the realm of intuitionistic fuzzy sets (IFS) to unlock their transformative potential in revolutionizing financial decision-making. The motivation behind our study stems from the recognition of the limitations of conventional decision-making approaches in effectively managing the intricate uncertainties present in financial environments. By embracing the advanced mathematical framework of IFS, which extends beyond traditional fuzzy sets to incorporate degrees of membership, non-membership, and hesitancy, we aim to provide decision-makers with a more nuanced and robust toolset for navigating the complexities of financial markets.Our research is driven by the desire to empower decision-makers with a comprehensive and innovative approach to handling uncertainty, thereby enabling more informed, accurate, and resilient financial decisions. By shedding light on the unique capabilities of IFS in addressing the challenges of incomplete information, risk assessment, and expert opinion aggregation, we seek to bridge the gap between theoretical advancements and practical applications in financial decision-making. Through a detailed exploration of the motivations behind our research, we aim to highlight the transformative value of IFS in enhancing decision-making processes and driving performance in dynamic financial landscapes. By unveiling the untapped potential of intuitionistic fuzzy sets, our study sets the stage for a paradigm shift in how decision-makers approach and navigate uncertainties in financial decision-making, ultimately paving the way for more effective and informed strategies in today's complex financial markets.

6.   Methodology

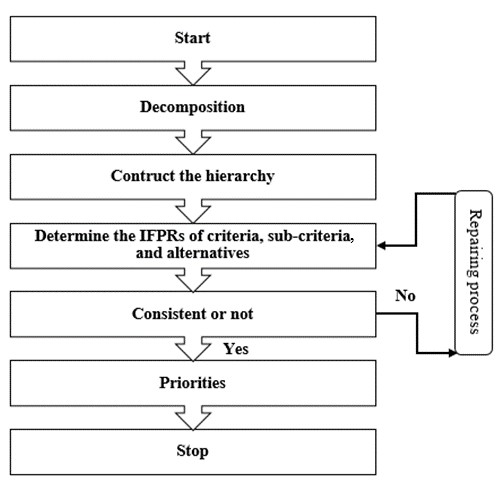
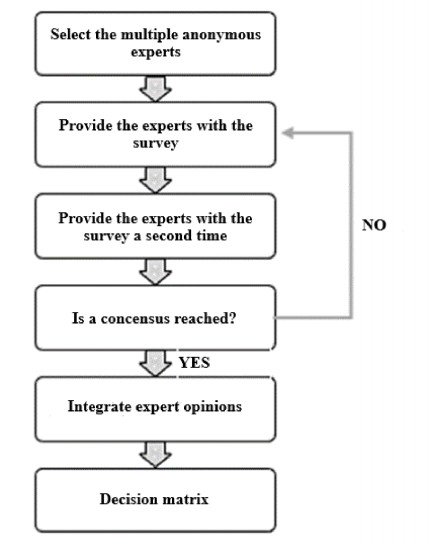
A four-level hierarchical benchmark structure was developed in this study to improve on the traditional methods. This new model for choosing the best option is called IFAHP, and its structure includes objective, criteria, sub-criteria, and alternatives. The weights of the criteria are determined by IFAHP using expert evaluations for each level. A modified Delphi method (Tumsekcali et al., 2021) was used to collect experts' opinions, the steps of which can be seen in Figure 1:

Considering that a DM is faced with multiple factors and ambiguity to choose a portfolio, MCDM can provide a solution. Therefore, in the following, we will explain how to choose the best portfolio using the IFAHP approach, which has high accuracy and speed, and can analyze the information well to give us the best option.

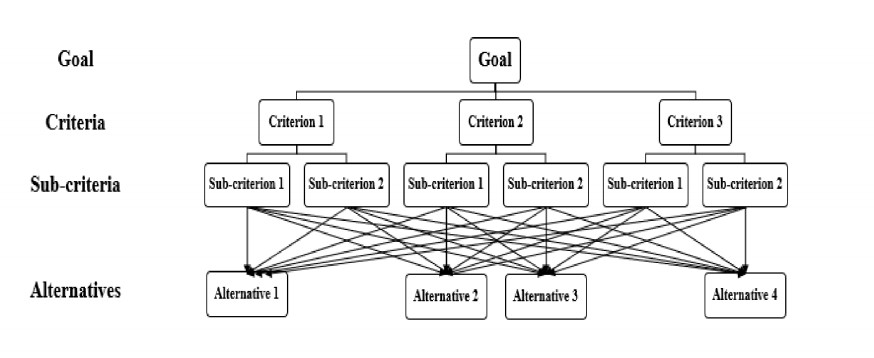
The IFAHP decision problem is hierarchically structured in four different levels. The highest level of this hierarchical structure expresses the overall goal and the lowest level represents the possible alternatives. The intermediate levels form the decision criteria and sub-criteria, respectively. The hierarchy (Tumsekcali et al., 2021) is shown in Figure 2 as follows:

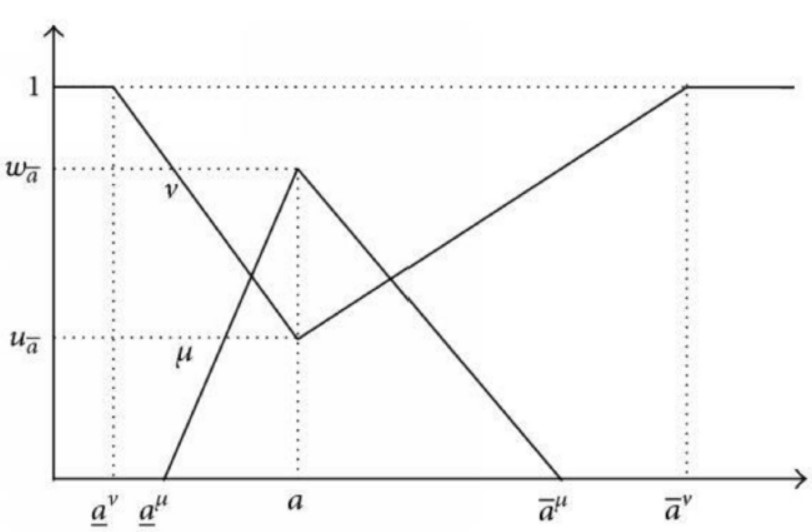
The intuitionistic fuzzy preference programming (IFPP) model is used to calculate the weights of criteria and sub-criteria. The weights of the criteria are combined with the weights of their corresponding sub-criteria to produce the final weights for ranking. A graphical representation (Deng et al., 2022) is depicted in Figure 3.

The steps of the IFAHP method, which is based on a combination method for evaluation and selection, are as follows:

Step 1: To construct the hierarchy of the considered problem based on Figure 2, first we identify the objective, criteria, sub-criteria, and alternatives of the decision- making problem. Then go to the next step.

Step 2: Before running the IFAHP, determine the intuitionistic fuzzy preference relations using the linguistic terms in Table 1 (Ilbahar et al., 2022) and then construct the pairwise comparison matrix $R$ through pairwise comparisons between each criterion and sub-criterion.

The intuitionistic fuzzy judgment matrix $R$ is generated using pairwise comparisons.

$R = (R_{ij}^{k})_{n\times n} = \begin{pmatrix} R_{11}^{k} & R_{12}^{k} & ...... & R_{1n}^{k} \\ R_{21}^{k} & R_{22}^{k} & ...... & R_{2n}^{k} \\... & ... & ...... & ... \\ R_{n1}^{k} & R_{n2}^{k} & ...... & R_{nn}^{k} \end{pmatrix}, k \in K\; where \; R_{ij}^{k} = (\mu_{ij}^{k}, \nu_{ij}^{k})$

After the linguistic terms in these pairwise comparison matrices are converted to intuitionistic fuzzy values (IFVs) values, alternatives are also compared under each criterion or sub-criterion and intuitionistic preference relations are constructed for them.

Step 3: At this stage, the matrix $\overline{R}$ must be formed. We use the following relationships to determine the degree of membership and non-membership in this matrix. Let $\overline{r}_{ik} = r_{ik}$ for $k = i+1$ and $\overline{r}_{ik} = (\overline{\mu}_{ki}, \overline{\nu}_{ki})$ for $k < i$ where

and

Step 4: We get the distance between $R$ and $\overline{R}$ according to the following formula:

where $\pi_{ij}(x_i, x_j) = 1-\mu_{ij}(x_i, x_j)-\nu_{ij}(x_i, x_j)$, and $\pi_{ij}(x_i, x_j) = 1-\mu_{ij}(x_i, x_j)-\nu_{ij}(x_i, x_j)$, and $\overline{\pi}_{ij}(x_i, x_j) = 1-\overline{\mu}_{ij}(x_i, x_j)-\overline{\nu}_{ij}(x_i, x_j)$. The relationship is compatible if this distance is $0.1$ and we have:

We can also show the compatibility of relationships using the method provided by Saaty to measure the degree of compatibility for a preferred relationship (Tumsekcali et al., 2021). If all of the relations are of acceptable consistency, go to Step 5; otherwise, to repair these inconsistencies, inconsistent intuitionistic fuzzy preference relations must be returned to DMs for reevaluation until they are acceptable.

Step 5: Calculate IFAHP criteria weights. The geometric mean method is used to compute the intuitionistic fuzzy priority weights.

The priority vector for the weights is as follows:

Step 6: Repeat Steps 1–5 to determine the weight of each main criterion and sub-criterion related to this main criterion. Using the following mathematical function introduced by Szmidt and Kacprzyk in 2009 (Szmidt & Kacprzyk, 2009) to rank IFVs, rank all overall weights from lowest to highest and then select the best alternative.

The lower the value of $\rho(\alpha)$, it indicates more reliability and that option has a higher priority.

Step 7: End.

The schematic diagram is shown in Figure 4 for the developed of the IFAHP method.

7.   Case study

Here, we will choose a portfolio of the following companies to find the best stocks to invest in as a real case situation. In order to choose the stocks to buy, one must first carefully examine and analyze the companies, the history of activities and the future of the industry related to their activities, and other basic matters, in order to choose the best stocks for them. According to the information from the stock exchange organization in recent years, the companies whose shares are significant in the Tehran Stock Exchange, and are technically and fundamentally suitable for long-term investment, are (https://nabzebourse.com/, 2022):

● Daro Luqman (Deluqma)

● Daro Jabra Ben Hayyan (Dejaber)

● Bourse Kala Iran (Kala)

● Kaghazsazi Kaveh (Chekaveh)

● Pashme Shishe Iran (Kapshir)

● Laabiran (Shelaab)

The growing stocks of the above companies are given in Table 2.

Companies admitted to the stock exchange are introduced with a symbol, consisting of abbreviations, to have a more uniform identity. Therefore, you can find the symbol of these companies here (https://nabzebourse.com/, 2022). Identifying the best portfolio for investment cannot be based on guesswork, and we must look for assets that will experience price growth in the future. Therefore, using fundamental analysis, it is possible to check the past performance of companies and choose stocks of companies that are more stable for long-term investment.

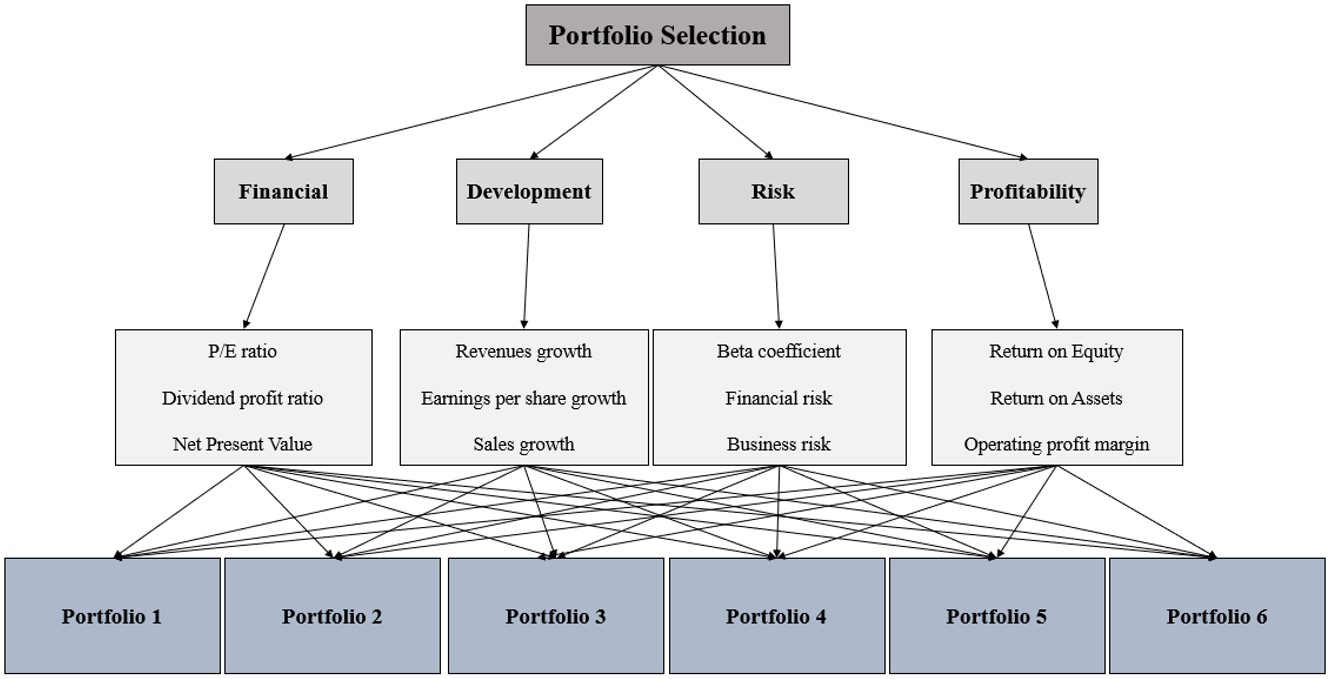
In the financial market and for choosing a portfolio, the most important factors that should be considered are: price to earnings ratio (P/E R), dividend profit ratio (DPR), net present value (NPV), revenues growth (RG), earnings per share growth (ESG), sales growth (SG), beta coefficient, financial risk, business risk, return on equity, return on assets, and operating profit margin (OPM). In order to prioritize the portfolio of companies, we consider each of the desired stocks hypothetically as one of the alternatives and implement the IFAHP technique on them to finally find the best option for investment.

A set of 4 criteria and 12 sub-criteria (for each criterion, we choose 3 sub-criteria) is used to evaluate 6 alternatives (Table 3), which is shown by the following hierarchical diagram (Figure 5):

First, criteria and sub-criteria should be compared in pairs. Therefore, we create the pairwise comparison matrix $R$ for the desired criteria and sub-criteria, and we will follow the next steps.

Step 1: We will form a matrix of paired importance of criteria relative to each other and calculate the fallowing pairwise comparison matrix $R$ for the criteria (Table 4).

Step 2: After calculating the distance using the formula (9) and considering that $d(R, \overline{R}) < 0.1$, the compatibility of the pairwise importance matrix of the criteria is proved. Therefore, there is no need to return to experts and restore relations, and we go to the next step.

Step3: We will calculate the weight of the criteria after establishing the stability of the intuitive preference relations and we obtain the weights (Table 5) of the criteria using formula (11) for use in the next steps.

Step 4: Forming the matrix of paired importance of sub-criteria with respect to each other and calculate their weights. In this part, we obtain the pairwise comparison matrix for the sub-criteria. We calculate the compatibility of the sub-criteria pairwise importance matrix using the formula (9) and conclude the compatibility of the relationships. Then we calculate the weight of each (Table 6) using formula (11), which can be seen in Tables 7-10. Therefore, we go to the next step.

Step 5: We will form the matrix of the pairwise preference relationship of the alternatives compared to the sub-criteria to apply the proposed IFAHP method, and evaluate the six portfolios that we consider as alternatives with each of the determined criteria and sub-criteria. The results are obtained, which are shown in Table 11.

Step 6: We will calculate the weight of the alternative options on the criteria $C_i (i = 1, 2, 3, 4)$ and sub-criteria in the intuitionistic fuzzy environment (see Tables 12–15). At this stage, using formula (11), we calculate the weight of each of the portfolios that are considered as alternative options on the criteria and sub-criteria as follows. Finally, we sum up all the weights with respect to each alternative using the following relationship: $\omega_{i} = \oplus_{j = 1}^{n} (\omega_{j} \otimes \omega_{ij})$. Here $n$ is the number of sub-criteria. We calculate the value of $\rho (\alpha)$ for the obtained weights using the equation (13) and the following final weights are obtained for the alternatives based on the fourth criterion:

Based on the final weight obtained in Table 17, the following results are obtained: $\omega_5 > \omega_2 > \omega_3 > \omega_6 > \omega_1 > \omega_4$. This means $A_5 > A_2 > A_3 > A_6 > A_1 > A_4$. These results show that, according to the financial, development, risk and profitability criteria, portfolio 5 has the highest weight and therefore has the highest priority. After that, portfolio 2 is the second best option. In general, based on the total results obtained, portfolio 5 can be considered the best option and portfolio 4 the worst option for investment.

Step 7: End.

8.   Discussion

The research sheds light on the significant impact of employing the IFAHP approach in decision-making concerning investment portfolios. By amalgamating quantitative and qualitative criteria, the approach enhances decision-making accuracy, empowering decision-makers to make well-informed choices that result in more dependable investment decisions. Furthermore, through the application of multi-criteria decision-making techniques using IFAHP, decision-makers can prioritize investment portfolios more effectively, aiding in the selection of companies with growth potential and suitability for investment, ultimately boosting portfolio performance. The research underscores the efficiency of the IFAHP approach in evaluating investment options accurately, considering crucial criteria in financial markets, which can lead to strategic and successful investment decisions. Recommendations for future research include exploring the impact of various criteria on investment outcomes and conducting sensitivity analysis to ensure the approach's robustness, paving the way for further advancements in financial decision-making methodologies.

Overall, the study's findings significantly contribute to the field by providing a practical and effective method for decision-makers to navigate the complexities of investment decisions. By empowering decision-makers to make informed and strategic choices in selecting investment portfolios, the research offers insights that can enhance financial performance and risk management.

The research conducted on the application of the IFAHP in prioritizing investment portfolios offers significant impact and insights for decision-makers in the financial industry. By showcasing the effectiveness of the IFAHP approach in handling both quantitative and qualitative criteria with speed and accuracy, the authors provide a valuable tool for navigating the complexities of investment decision-making. The key impact and insights of the research can be summarized as follows:

● Enhanced Decision-making Accuracy: The research demonstrates how the IFAHP approach can enhance decision-making accuracy by effectively incorporating both quantitative and qualitative criteria in the evaluation of investment portfolios. Decision-makers can leverage this method to make informed choices based on a comprehensive set of criteria, leading to more reliable investment decisions.

● Improved Portfolio Prioritization: Through the application of multi-criteria decision-making techniques using IFAHP, the research offers insights into how DMs can prioritize investment portfolios based on key criteria essential for long-term investment success. This approach enables decision-makers to identify and select companies with growth potential and suitability for investment, enhancing portfolio performance.

● Efficient Evaluation of Investment Options: The research highlights how the IFAHP approach enables decision-makers to compare investment options with high accuracy, considering various important criteria in financial markets. This efficiency in evaluating and prioritizing investment opportunities can lead to more strategic and successful investment decisions.

● Recommendations for Future Research: The study provides valuable recommendations for future research, such as exploring the impact of different criteria on investment outcomes and conducting sensitivity analysis to ensure the robustness of the approach. These suggestions pave the way for further advancements in utilizing IFAHP and similar methodologies in financial decision-making.

Overall, the research on the application of the IFAHP approach in prioritizing investment portfolios contributes significantly to the field by offering a practical and effective method for decision-makers to navigate the complexities of investment decisions. The insights provided by the study can empower DMs to make informed and strategic choices in selecting investment portfolios, ultimately leading to improved financial performance and risk management. One limitation of the study is the reliance on historical financial data, which may not fully capture the dynamic nature of financial markets. Despite this limitation, the research provides valuable insights into the advantages of IFS in financial decision-making and sets the stage for further exploration in this area such as:

● Incorporating Real-time Data Analysis: Future research could focus on integrating real-time data analysis techniques with the IFAHP approach to enable decision-makers to make timely and informed investment decisions in dynamic market conditions. This could involve developing algorithms that can process and analyze streaming financial data to enhance the accuracy and relevance of portfolio prioritization.

● Exploring Sector-specific Applications: Researchers could explore the application of the IFAHP method in specific sectors or industries to understand how different criteria and variables impact investment decisions within distinct market segments. This sector-specific analysis could provide valuable insights for decision-makers looking to optimize portfolio selection strategies in specialized areas.

● Integration of Machine Learning Algorithms: Future studies could investigate the integration of machine learning algorithms with the IFAHP approach to enhance the predictive capabilities of investment portfolio prioritization. By leveraging machine learning models for pattern recognition and trend analysis, decision-makers can gain deeper insights into market dynamics and make more informed investment choices.

● Risk Management and Portfolio Optimization: Researchers could delve into how the IFAHP method can be utilized for effective risk management and portfolio optimization strategies. Future studies could explore the integration of risk assessment models with the IFAHP approach to help decision-makers identify and mitigate potential risks associated with investment portfolios.

● Comparative Analysis of Decision-making Methods: A comparative analysis of different decision-making methods, including IFAHP, Analytic Hierarchy Process (AHP), and other multi-criteria decision-making techniques, could provide valuable insights into the strengths and limitations of each approach. This comparative study could help decision-makers choose the most suitable method for their specific investment decision needs.

● Exploring Behavioral Finance Aspects: Future research could delve into the behavioral finance aspects of decision-making in investment portfolio prioritization. By considering the psychological biases and heuristics that influence investor behavior, researchers can develop frameworks that incorporate behavioral finance principles into the IFAHP method for more accurate decision-making outcomes.

By exploring these solid future research directions, the authors can further enhance the application of the IFAHP approach in prioritizing investment portfolios and contribute to the advancement of decision-making processes in the financial industry.

In comparing IFAHP with the recently developed best worst method (BWM), full consistency method (FUCOM), and depth image based rendering (DIBR) methods, it is evident that each approach offers unique strengths and applications. IFAHP stands out for its integration of AHP with intuitionistic fuzzy sets, making it suitable for decision-making under uncertainty and subjective assessments. BMW utilizes biogeography-based optimization with mutation for global optimization tasks, while FUCOM excels in fuzzy clustering through competitive learning without requiring labeled data. DIBR, focusing on deep learning and convolutional neural networks (CNNs) for image recognition, is ideal for tasks like object detection. The choice among these methods depends on the specific problem domain and requirements, considering factors such as uncertainty handling, optimization needs, clustering objectives, or image recognition tasks. By understanding the distinct methodologies and strengths of IFAHP, BMW, FUCOM, and DIBR, researchers can make informed decisions about which approach best aligns with their specific application requirements. Whether the priority lies in handling uncertainty, optimizing global solutions, performing fuzzy clustering, or tackling image recognition tasks, each method offers a tailored set of tools and techniques to address diverse challenges. Ultimately, the choice among these methods should be guided by a thorough assessment of the problem context, ensuring that the selected approach is well-suited to deliver effective and efficient solutions in the target domain. Therefore, according to the purpose of the research that the decision should be made in an ambiguous environment, the IFAHP approach has been chosen.

9.   Conclusions

Nowadays, due to the growing trend of capital market and economy, DMs have encountered many criteria and variables when choosing an investment portfolio, which causes confusion. One of the powerful tools to deal with the uncertainty created by financial markets and investor behavior for DMs can be integrated MCDM techniques. Also, in selecting portfolios, the criteria are not only quantitative, but we are faced with many qualitative criteria that cannot be measured and weighted in many decision-making methods. So here we have used the IFAHP with new hybrid approach. The intuitive fuzzy analytical hierarchy process has high speed and accuracy in decision-making for quantitative and qualitative criteria. One of the important features of this approach is that it can fill this gap and use verbal variables to consider quantitative equivalents for qualitative variables, thereby easily calculating the weight of criteria and prioritizing options.

In order to apply this approach in prioritizing the portfolio of companies, after reviewing the listed companies in the Tehran Stock Exchange, we have focused on companies that were prone to growth during the period of our research and were a more suitable option for long-term investment. Finally, by multi-criteria decision-making, and focusing on the technique of IFAHP, considering hypothetical alternatives, we evaluated and prioritized the portfolio of companies based on important criteria that were the basis for choosing the best option for investing in financial markets. In addition to this approach, the decision-maker can compare the options available for investment with high accuracy and evaluate them based on several criteria that are important in financial markets to measure stocks, and ultimately choose the right portfolio for a reliable investment. Considering the capabilities that the introduced approach has for multi-criteria decision-making issues, it is recommended to use it as a useful tool for evaluating the performance and ranking of the portfolio of companies based on other criteria in addition to the criteria mentioned herein, and also such cases in future researches. Another suggestion for future work is to examine the importance and impact of different criteria on the final result to ensure the effectiveness of the approach and its sensitivity analysis.

Use of AI tools declaration

The authors declare that they have not used artificial intelligence (AI) tools in the creation of this article.

Conflict of interest

The authors declare that there are no conflicts of interest.