1. Introduction
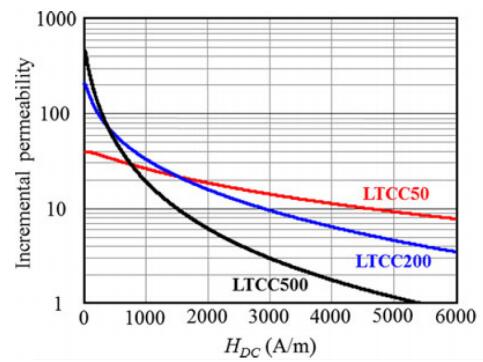
With the expansion of electrical circuits and electronic devices, the desire to minimize the size of devices has increased. In portable instruments such as laptop and mobile chargers, enhancing efficiency, downsizing and increasing their lifetime is particularly important. Various methods are proposed to increase the efficiency of the converters, especially in low power applications [1,2,3]. In these converters, the inductor allocates a large amount of converter size which affects their performance. Therefore, the circuit efficiency can be increased and the converter size can be reduced by minimizing the size and optimizing the inductor's performance [4]. In recent years, various structures of specific and nonlinear inductors have been discussed to optimize converter performance, reduce losses, and increase the efficiency and inductor density [5,6,7]. However, these methods have some disadvantages like, including using additional circuits for increasing efficiency [8]. LTCC (Low Temperature Co-fired Ceramics) inductors are introduced as new alternative to increases the inductance value and its efficiency relaying on the type of applied materials and the specific structure [9]. Also, the rate of the inductance reduction (in the full load current) is lower than the usual commercial inductors. This paper aims to improve the performance of the inductor (or increasing the inductance) by reducing the size and volume. If a specific inductance is required, inductor volume reduces by increasing the inductance density. It is clear that that with the same size, the proposed inductor can be applied in higher power applications. The magnetic materials used in the LTCC inductors are the green material types with the commercial names of ESL40010, ESL40011, ESL40012 which have a permeability coefficient of 50,200, and 500, respectively (behavior of these materials is shown in Figure 1) [10].
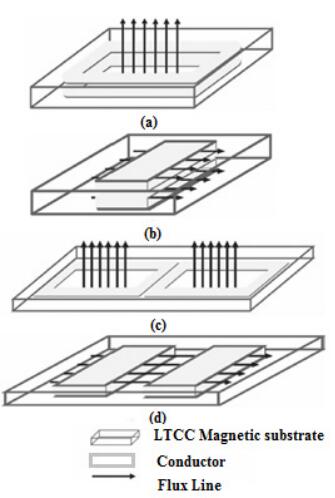
LTCC inductors are divided according to the types of structure and the location of the winding. There are three major types of winding: Spiral, solenoid, and toroidal. Since it is very difficult to reach the isolated and symmetrical windings in a toroidal form at LTCC, this type of winding is not used. The types of windings under the layers are also divided vertically and horizontally. Therefore, there are four general structures of spiral winding shape, vertical direction (SV), spiral winding shape, horizontal direction (SH), solenoid winding shape, vertical direction (NV) and solenoid winding shape, horizontal direction (NH), which can be seen in Figure 2 [11].
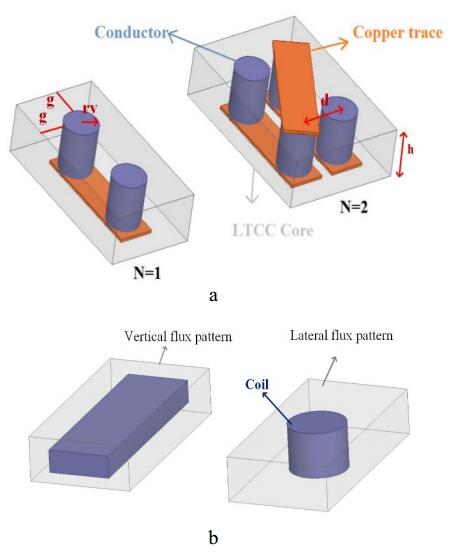
Figure 3a shows LTCC inductor with turn number of N = 1 and N = 2. In Figure 3 rv is the conductor radius, d is the distance between two parallel paths, g determines the size of the core, and h is the core thickness. The maximum rv, g and h are determined based on the maximum output dc current, inductor footprint and the amount of required inductance respectively. Note that this footprint should be equal to the active part of the circuit. In this inductor, the base size and the value of inductor is obtained according to the following equations [12]:
The effect of size variation of each part of LTCC inductor was discussed in detail in [13]. For instance, inductor increases by increasing parallel turn number from N = 1 to N = 2; but from N = 2 to N = 3 there is not much change. The inductance increases by increasing core thickness to a certain range. However, above that range, the increase in core thickness does not make any significant differences in the inductor. Size and radius of the conductor make a significant change in the inductance value which increases by decreasing the conductor size. However, the radius of the conductor cannot be lowered from a certain range according to the maximum amount of current.
Moreover, the various structures of LTCC inductor could be distinguished based on vertical and lateral flux patterns. In vertical flux pattern, the flux is perpendicular to the inductor's core while in lateral flux pattern, flux is parallel to the core surface [14]. Figure 3b shows the structure of the two inductors with vertical and lateral flux patterns. The flux density in vertical flux inductor is limited by the core thickness, and by reducing inductor thickness, the inductor value would be reduced. However, in lateral flux, flux density is not limited by the thickness of the core. Therefore, it is better to use a lateral flux inductor to reach higher inductance in a limited thickness and size [15].
The inductor size is the main problem in increasing power density. Also, increasing inductor size for achieving a higher quality is not an appropriate solution, because it is aimed at minimizing the size. This paper uses an integration of two methods of inverse coupling and multi-permeability inductors, each of which is a method for increasing the power density and the inductance value. With a similar size and a normal inverse coupling inductor, the proposed hybrid LTCC inductor reaches power density of 735 (W/in3) and inductance of 310 nH in low currents (which is 90 nH higher than the normal inverse coupled inductor) [15].
2. Problem definition
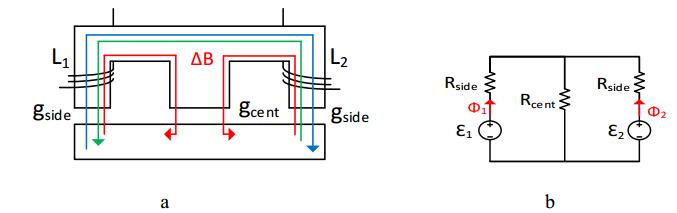
As noted earlier, since a large amount of DC energy needs to be stored in the inductor, the small size of the inductor is a major problem in increasing the power and the inductance density. The uses of multiphase converter with an inverse-coupled inductor as well as multi-permeability inductor are among the methods in which the power and inductance density can be increased. Inverse coupling increases inductor power density through cancelling DC flux effect which leads to size minimization. By increasing the amount of flux cancellation, it is no longer necessary for the inductor to store large amounts of DC energy [16]. In Figure 4, a normal inductor is shown with air gap. As it can be observed, the generated fluxes in two legs cancel each other which leads to inductor's size reduction. Φ1 and Φ2 are DC fluxes generated in two legs; given equation (3), they are limited by Rside and Rcent which are indicative of gside and gcent reluctance [15]. With the flux cancellation, the inductor's working range increases. The flux cancellation effect is investigated in two states of vertical and lateral flux patterns. As noted earlier, the inductor with lateral flux has more inductance density than vertical flux with similar thickness. This paper presents a method based on lateral flux; however, for investigating inductor's behavior, vertical flux inductor would be investigated, too.
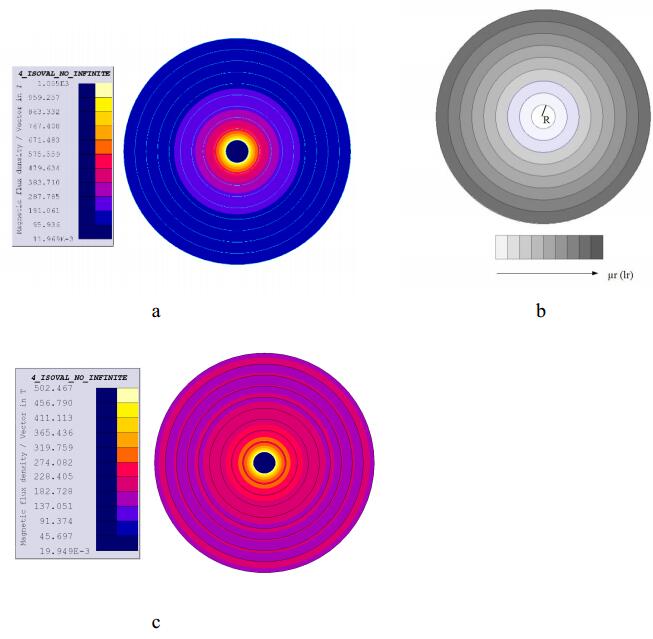
In a multi-permeability method, several types of materials with different permeability such as LTCC50, LTCC200 and LTCC500 are used. As it can be seen in Figure 5a flux density around the conductor is high in single permeability inductor while flux density decreases farther away. This non-uniformity of inductor flux causes improper use of the inductor core [17,18]. By using multi-permeability inductor and inductor layering, most core points can be used optimally in a way that there are different permeabilities in different layers. An inductor that has different permeability at various distances from the conductor is shown in Figure 5b. In this inductor, higher permeability material is selected as the layers become more distant from the conductor. The results of this inductor is shown in Figure 5c where a more uniform flux is produced at the core. This flux uniformity causes better use of the core and increasing the inductance density [19,20,21].
2.1. Multi-permeability inverse-coupled inductor with vertical flux pattern (Mhttps://www.aimspress.com/aimspress-data/electreng/2018/3/PICI-VFP)
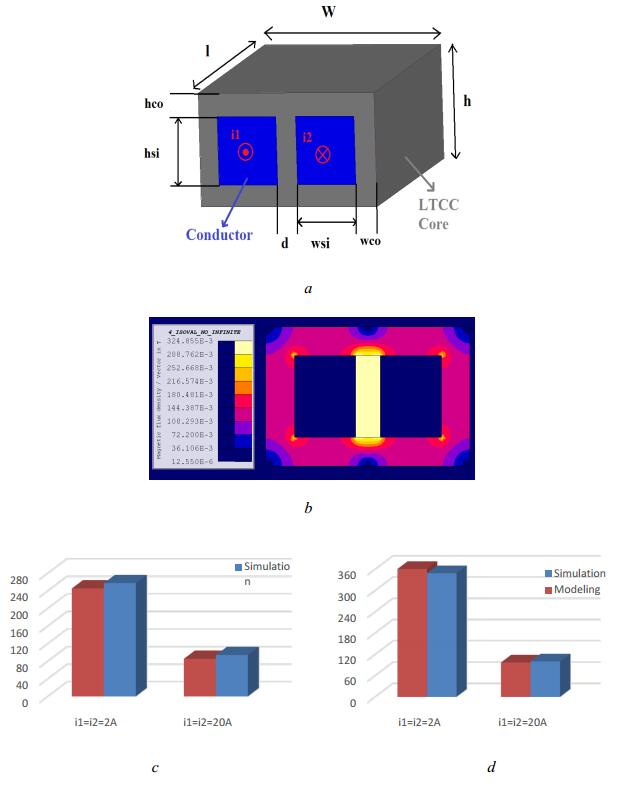
Figure 6a shows the structure of inverse-coupled inductor with the vertical flux pattern (ICI-VFP) along with its various constituent parameters. Figure 6b shows the flux density of various parts in FEA 2D FLUX simulation. As it can be observed, the flux density is divided into two central and side sections with different values. Therefore, this inductor could be modeled as Figure 4 and given this model; the inductor is obtained from the following equations:
In which μout1 and μout2 are the permeability of materials used in the structure of the inductor core. This inductor is investigated in two states:
State 1: the normal ICI-VFP is used with a single permeability material of ESL40011. In this structure, the inductance value changes from around 260 nH to 93 nH by changing current from 2 A to 20 A.
State 2: for better use of the core, the ICI-VFP is used in multi-permeability form. Since the core in non-center (two sides) parts has lower flux density, a material with higher permeability of ESL40012 is used in this section. Also, ESL40011 is used for the core center. In this structure, the inductance value changes from around 340 nH to 96 nH by changing current from 2 A to 20 A. By smoothing flux, magnetic core is better used which leads to increment of inductance value in high and low currents. Figure 6c and Figure 6d shows the flux in FEA software simulation and modeling results in two states with the parameters of Table 1. the currents are defined as I1 = I2 = 2 A and I1 = I2 = 20 A. During modeling, the permeability should be obtained from the material's working point and its B-H curve (see Figure 1).
Table 1. Parameters of ICI-VFP.
| Wsi |
Wco |
hsi |
hco |
d |
l |
Conductor type |
| 1.5 mm |
0.7 mm |
2 mm |
0.7 mm |
0.6 mm |
19.5 mm |
Silver 7740 |
2.2. Multi-permeability inverse-coupled inductor with lateral flux pattern (Mhttps://www.aimspress.com/aimspress-data/electreng/2018/3/PICI-LFP)
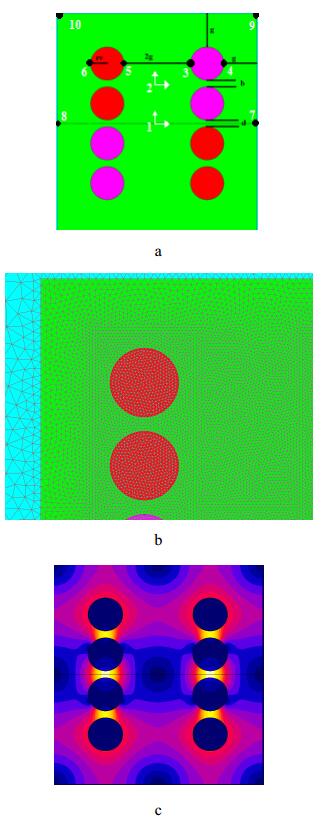
There are various structures for inversed-coupled inductor with lateral flux pattern (ICI-LFP) in [15]. Given the fact that there should be a parameter for controlling the inverse coupling, the two turns- two phases structure (see Figure 7a) is the best structure because the flux cancellation takes place in most directions. Figure 7c shows the distribution of lateral flux structure. The noticeable difference in vertical flux is that the flux distribution which is in the core, cannot be modeled like Figure 3.
The various parameters of lateral flux structure are determined according to the trends specified in the introduction section. Radius rv is obtained based on the maximum current and d is obtained according to the coupling coefficient between two phases. In Figure 6a the distance between the two conductors is the value of b, g value which is specified according to the circuit footprint. Based on Figure 7a, in this inductor, the circuit footprint value is obtained according to the following equation:
Before presenting the simulation results, the design and simulation procedure of the Flux software is explained in the manuscript. In fact, the simulation of the inductor is conducted in three major steps:
(1) Plotting the structure of the inductor in Flux software
(2) Meshing each part of the inductor
(3) Determining the kind of material used in each part
For instance, in the first step, the coordinates of the specified points should be found according to Figure 7a To do this, zero is defined as the origin of the coordinates. In fact, other the coordinates of other points could be specified through the defined zero origin, but the coordinate width of (d/2 + 2rv + b/2) is chosen for the system. Then point 3 and point 4 are defined with coordinates of (b/2+ rv, g) and (b/2 + rv, g + 2rv) respectively. Point 5 and point 6 are doublets of point 3 and point 4 against point 2. Then a circle with radius of r is formed between point 3 and point 4 another circle with the same radius is formed between point 5 and point 6. By transferring these two circle faces by b + 2rv mm against point 2 another two circle faces are also formed. Then points 7, 8, 9, 10 are added to simulation and straight lines are drawn between them. Next a symmetry transformation was made and the first phase was transferred by this transformation therefore, the second phase is formed.
After drawing the inductor, mesh points are assigned to each point for meshing. Figure 7b shows inductor's meshing. As it can be seen, in points near the coil conductors has better meshing accuracy than other points.
After meshing, different regions of inductor are specified. Generally these kinds of inductors have three types. Coil conductor that is in positive direction (red parts in Figure 7a) and in negative direction (magenta parts in Figure 7a) characteristic of the material of the Inductor's core are specified for different parts of the core based on Figure 1. And finally the air around inductor that has relative premeablity of 1 is specified. At last the converter which the inductor is used in is designed. After finishing all these steps the simulation is run.
Flux density of various parts of the core with the simulation by FLUX FEA Software is shown in Figure 7c with the parameters given in Table 2.
Table 2. Parameters of ICI-LFP.
| rV |
g |
d |
b |
I |
| 1 mm |
2 mm |
0.5 mm |
0.4 mm |
20 A |
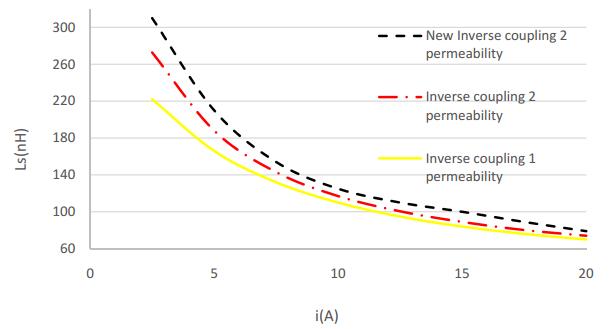
Figure 10 shows the variation of inverse coupled inductor by changing current from 2 A to 20 A with different structures (Single permeability core (Shttps://www.aimspress.com/aimspress-data/electreng/2018/3/PICI-LFP), double permeability core (Dhttps://www.aimspress.com/aimspress-data/electreng/2018/3/PICI-LFP) and proposed structure).
For a Shttps://www.aimspress.com/aimspress-data/electreng/2018/3/PICI-LFP core structure with ESL40011, the inductors values are 222 nH and 70 nH for 2 A and 20 A current respectively.
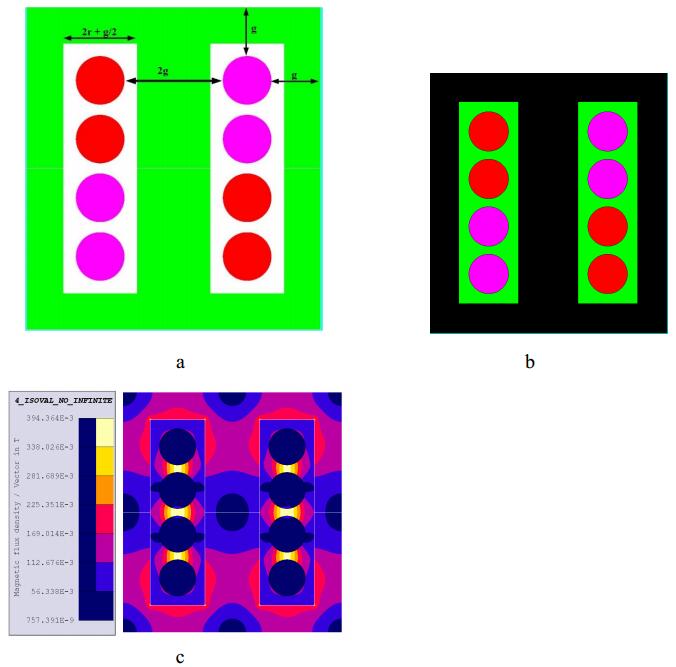
For a multi-permeability core structure, Figure 8a shows the parameters related to the inductor footprint and the different parts of the core. Due to the flux density of the different parts, g/2 distances are separated from the conductor and a material with a different permeability is in this section (white part in Figure 8a). These distances are selected due to the flux diffusion of the single- permeability inverse inductor (It is not optimized).
For the first multi-permeability core structure, ESL40011 is used in the near conductor layers and ESL40012 is used in the farther parts. The structure type and flux densities of different parts of the inductor's core are brought in Figure 8b and Figure 8c respectively. In those parts of the core which are farther from the conductor and have lower flux density, a material with higher permeability coefficient (ESL40012) is used. In the areas near to the conductor with higher flux density, a material with lower permeability coefficient (ESL40011) is used. This causes more smooth flux distribution in the core which increases inductance. According to Figure 10 the inductance value in a similar volume to Shttps://www.aimspress.com/aimspress-data/electreng/2018/3/PICI-LFP increases. The inductance values are 272 nH and 74 nH for 2 A and 20 A current, respectively.
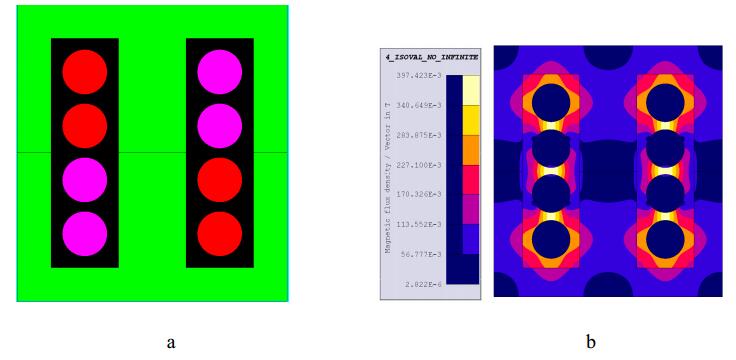
As it is clear in the Figure 7c flux distribution is a fundamental problem for a Shttps://www.aimspress.com/aimspress-data/electreng/2018/3/PICI-LFP. This problem could be solved by employing multi-permeability method. In some parts of the core that are close to the conductor, a higher permeability material is used and a lower permeability material is used in farther points. By doing this, the flux closes its path to a higher permeability material and therefore, the magnetic path for flux in this type of Dhttps://www.aimspress.com/aimspress-data/electreng/2018/3/PICI-LFP decreases which leads to reluctance reduction and inductance increment. Figure 9 shows the new structure and simulation of the Dhttps://www.aimspress.com/aimspress-data/electreng/2018/3/PICI-LFP in a similar volume to other discussed lateral flux inductors, in FEA FLUX. In this inductor, in areas close to the conductor ESL40012 and in the farther parts ESL40011 is used. According to Figure 10 the inductance value in a similar volume with Shttps://www.aimspress.com/aimspress-data/electreng/2018/3/PICI-LFP, increases. The inductance values are 320 nH and 79 nH for 2 A and 20 A current respectively.
According to the mentioned analysis, the inductance value in proposed structure is more than other strategies in both low and high current. However, this increment is greater in lower currents.
3. Discussion
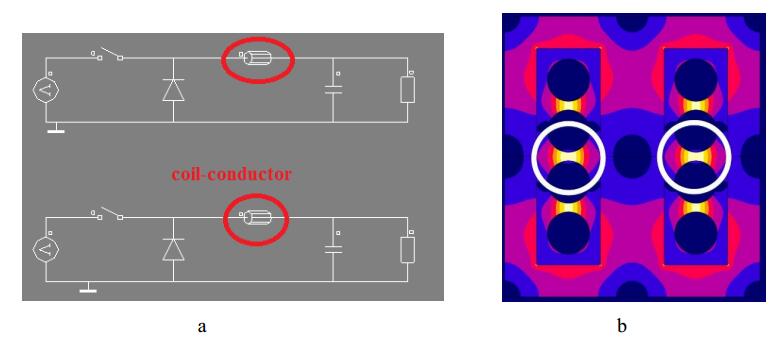
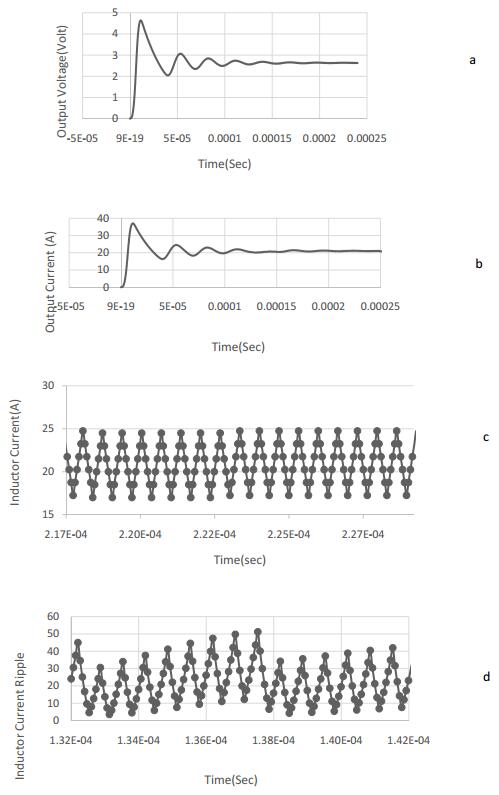
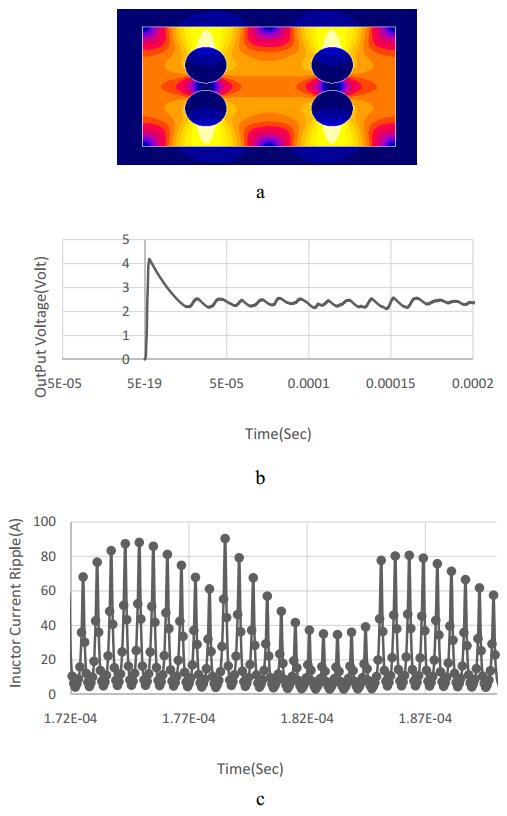
In this section, for observing the performance of the double-phase Dhttps://www.aimspress.com/aimspress-data/electreng/2018/3/PICI-LFP, buck converter of Figure 11a is implemented. For each phase, 5 V input voltage, 2.5 V output voltage, 1.5 MHz switching frequency, and 20 A current are considered in FEA FLUX software. This converter is simulated in 5000 steps with a range of 0.1 switching periods. Figure 11b shows the flux distribution in Dhttps://www.aimspress.com/aimspress-data/electreng/2018/3/PICI-LFP. It is noteworthy that by increasing the current, only the points marked with a white circle will saturate and the other points will not reach its saturation level until the current is much higher than 20 A. This is due to the inverse coupling of the inductor. Figure 12a and Figure 12b shows the output voltage and output current of this converter respectively, and Figure 12c represents the inductor's current ripple in 20 A output current which is around 7.5 A.
The results which has been shown until now is for the inductor's normal mode work points, but if inductor's current goes up (about 25 A or more), the inductance will decline greatly and the current ripple rises. It's worth mentioning that the current ripple is variable. So that in constant output current, the inductor's ripple is variable. Figure 12d shows the inductor current ripple in saturation mode for output current of 25 A.
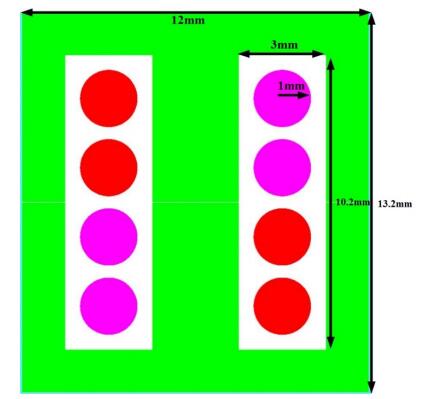
Given the dimensions of the inductor in Figure 13 for a comparison between the first Dhttps://www.aimspress.com/aimspress-data/electreng/2018/3/PICI-LFP and the new Dhttps://www.aimspress.com/aimspress-data/electreng/2018/3/PICI-LFP and observing the occupied regions by each material (ESL40011, ESL40012) in the new Dhttps://www.aimspress.com/aimspress-data/electreng/2018/3/PICI-LFP core structure, the volume for each material is calculated as follows (ESL40012 white section near the conductor, ESL40011 green part away from the conductor):
Inductor volume: 13.2×12×1.8 = 285.12mm3
Core volume: (285.12)-(8×πr2×1.8) = 239.88mm3
ESL40012 volume: 2×(10.2×3-4πr2)×1.8 = 64.92mm3
ESL40011 volume: 13.2×12-2(10.2×3) = 174.96mm3
According to the above calculations, in the new Dhttps://www.aimspress.com/aimspress-data/electreng/2018/3/PICI-LFP structure, ESL40012 occupies only 23% of the total inductor volume and 27% of the core volume. This reduction in the use of ESL40012 also includes a reduction in losses for obvious reasons. Also, as seen in the Figure 10 in addition to reducing the area used by a higher permeability material, the inductance also increased about 100 nH.
In order to compare the performance of this inductor in the buck converter, the normal two turns LTCC inductor with the same value as the Dhttps://www.aimspress.com/aimspress-data/electreng/2018/3/PICI-LFP in the same converter condition is simulated. Figure 14a shows the flux distribution in this inductor. As it is clear in the figure, under the same switching and load conditions, most points of the inductor will saturate. Figure 14b shows output voltage of the converter and Figure 14c displays inductor's current waveform. Due to the saturation of the inductor, the output DC voltage is inappropriate and inductor's current ripple is so high.
According to [15], a normal inversed coupled inductor with lateral flux pattern for a typical 46 W buck converter is designed with the features of 5 V input, 1.2 V output and 1.5 MHz frequency. In this converter, considering the use of IRF6633 and IRF6619 MOSFET switches and LM27222 driver, and also 5.5 mm thickness for the converter's active layer and inductor thickness of 1.8 mm, power density is 680 (w/in3). However, by using the new structure of double- phase Dhttps://www.aimspress.com/aimspress-data/electreng/2018/3/PICI-LFP, the thickness of the inductor could be reduced up to 30%, as a result of which power density would increase up to 735 (W/in3). In addition, with similar volume, the inductance density increases by increasing inductance in high and low currents, too. For the normal ICI-LFP, inductance density in low currents is 8 μH/in3, but in the new Dhttps://www.aimspress.com/aimspress-data/electreng/2018/3/PICI-LFP, inductance density in low currents increases up to 17.8 μH/in3.
4. Conclusion
This paper investigated inverse coupled inductor with vertical and lateral flux patterns in multi-permeability state. Three different structures in the lateral flux inverse coupled inductor are considered. In the first structure, normal double-phase inverse coupling inductor is discussed; in the second one, double-phase double-permeability inverse coupling inductor is considered; and ultimately, in the third one, a new structure of double-phase double-permeability inverse coupling inductor is addressed. The inductors of the second and third structures in low currents are remarkably greater than normal inverse coupling inductor, which causes improvement of the inductor performance in low currents. The inductor value also increases in higher currents, but this increment is not as much as low currents. Finally, the converter is designed in FEA FLUX and MATLAB. The performance of this inductor is investigated in a 5 V to 2.5 V buck converter at 1.5 MHz switching frequency. The significant point in these lateral flux pattern inductors is that the inductor value is almost the same as vertical flux pattern with the half thickness size. Finally, by using this inductor, flux density increases up to 17.8 μH/in3 and power density increases up to 735 (w/in3).
Conflict of interest
The authors declare no conflict of interests in this paper.









 DownLoad:
DownLoad: