1.
Introduction
A significant problem in achieving the required level of accuracy of modern computing complexes and systems is the detection of coarse measurements (outliers) in the time series of data at the preprocessing stage. The proper detection and removal of outliers from measurement data is a necessary step in any scientific application to obtain the most accurate final result. This problem inevitably arises when solving problems in which the initial data is measurement data. Examples of such problems are transmitting time over long distances [1] and comparing remote time scales [2] using satellites, positioning using global navigation satellite systems (GNSS) [3], determining the Earth's rotation parameters [4], very long baseline radio interferometry (VLBI) signal processing [5], and others. The sequential least-squares wavelet and cross-wavelet analyses of VLBI time series performed in [6] make it possible to obtain accurate instantaneous frequency information along with phase differences in the time-frequency domain, as well as to investigate the components of temperature time series at antennae locations.
It should also be noted that the Global Geodetic Observing System (GGOS) provides measurements of the time-varying gravity, rotation, and shape of the Earth using geodetic and gravimetric instruments located on the ground and in space. These measurements need to be accurate to better than a part per billion in order to advance our understanding of the underlying processes that are causing the Earth's rotation, gravity, and shape to change. Mass transport in the global water cycle, sea level and climate change, and crustal deformation associated with geohazards are examples of particularly demanding applications of geodetic and gravimetric measurements with sub-mm accuracy [7]. On the one hand, it is impossible to achieve such accuracy without equipping the colocation sites with new-generation measuring instruments of VLBI, GNSS, and satellite laser ranging systems (SLR). On the other hand, even the availability of state-of-the-art equipment does not relieve the necessity of improved models and methods for both post- and pre-processing of the measurement data received from GNSS receivers forming a global network [8].
As noted in [9], outlier detection and trend detection are two sides of the same coin. The relationship between these two problems is obvious: an incorrectly found trend leads to incorrectly found outliers, and vice versa. The problem of detecting outliers is closely related to the problem of searching for an unknown trend in the data series (see, e.g., [9]). The detection of outliers depends on the solution to this problem: if the trend is determined incorrectly, knowingly accurate data can be rejected while inaccurate one can be left for further processing.
In measurement data processing theory, an outlier is defined as an observation that is at an abnormal distance from other values in a random sample from the population. The uncertainty of this definition lies in how to distinguish anomalous observations from the general data set. The well-known definition of outliers by V. Barnett and T. Lewis states them as being "an observation (or subset of observations) which appears to be inconsistent with the remainder of that set of data" [10]. However, the concepts of "inconsistent" and "remainder" are vague. Various algorithms have been proposed to detect outliers in accordance with our intuition (see [9]). An overview of the different approaches together with the classification of outlier types is given in [11].
The trend detection problem has long been known and is often solved by choosing a polynomial of a given degree that approximates the measurement data in RMS (root-mean-square) norm. Polynomial coefficients are found by the least squares (LS) method as a solution to the system of linear equations, and detection of rough measurements is carried out on the basis of the subsequent analysis of deviations of measured data from the values of the found polynomial. However, with this approach to the problem, the data remaining after the removal of the found outliers, as a rule, do not coincide with the original data set by which the trend was built, whereas the iterative process of sequential redefinition of the trend at a predetermined deviation level may lead to an infinite computational loop. To avoid this looping, it is common practice to reduce the outlier detection level, which can result in the loss of knowingly "good" data.
Some trend-building methods rely on regression techniques and machine learning. An example is the least absolute shrinkage and selection operator (LASSO) used for modeling the relationship between a dependent variable (which may be a vector) and one or more explanatory variables, by fitting the regularized least squares model (see [12]). Trained LASSO model can produce sparse coefficients due to the use of the regularization term. LASSO regression is widely used in feature selection tasks. For example, in the field of compressed sensing, it is used to effectively identify relevant features associated with the dependent variable from a few observations with a large number of features. LASSO regression is also used to overcome multicollinearity of feature vectors in the training data set. For more details, see [13]. The application of the method in medicine can be seen, for example, in [14], as well as in references ibid.
Among the numerous trend-detecting methods are those applied to irregularly distributed data, such as in seismology and marine seismic data. Least-squares spectral analysis (LSSA) was introduced by Vaniček in 1969 [15] to analyze unequally spaced time series. It estimates a frequency spectrum based on the least-squares fit of sinusoids to the entire time series by accounting for measurement errors, trends, and constituents of known forms. Subsequently, scholars have developed various versions of this method. One of them, the anti-leakage least-squares spectral analysis (ALLSSA), is an iterative method based on LSSA and proposed in [16]. Further development of this method to regularize data series was presented in articles [17,18] which also showed its robust performance on synthetic and marine seismic data examples (for details and additional references see ibid.).
A large number of works are devoted to the study of the spatial movement of the Earth's surface in order to identify land subsidence that threatens the human environment. Compared with the traditional leveling and global positioning system (GPS) measurement methods, the interferometric synthetic aperture radar (InSAR) technique can obtain a wide spatial range of information about the deformation of the Earth's surface with millimeter accuracy [19]. The output of InSAR processing is a collection of time series representing the ground displacements of measurement points (MPs) on the surface during the observed period. InSAR has been used for monitoring natural hazards such as landslides, earthquakes, volcanic activity, and ground subsidence [20], as well as for monitoring man-made structures such as dams, buildings [21], and bridges [22], and anthropogenic activities such as the pumping or injection of fluids. Various methods are used to process InSAR time series. For example, in [23] a processing InSAR time series method was proposed, using a convolutional neural network that can distinguish different ground motion features and detect nonlinear deformation signals on a large scale without human intervention. In [24], the authors performed a spatiotemporal analysis of land subsidence in Beijing using the InSAR method based on 47 TerraSAR-X SAR images from 2010 to 2015. Distinct variations in land sediment were identified in the study areas. Numerous examples of the application of InSAR time series processing can be found in the references of the articles above.
Overviews of trend-building methods applied to different research areas can also be found in [25,26,27,28]. These describe approaches and methods for modeling trends in geodetic time series, in time series of observations of the chemical composition of the atmosphere, in the series of physiological data in the medical field, as well as systematized methods for building a trend based on data in the social sphere in order to identify extraordinary events and incidents.
In [29], a new absolutely convergent algorithm for detection of coarse measurements in data with removed trends was proposed. A modification of this algorithm, leading to an optimal solution with a minimum number of rejected data, was proposed in [30], and a fast algorithm with O(NlogN) arithmetic operations performed by it to find the optimal solution was given in [31]. The author in [32] proposed a new trend-detection method in which the trend is searched in the power polynomial class, while the polynomials in the L2 norm are not fitted to all observational data but to their subset, called reference values, which are selected from these data through a convergent iterative process. One of the advantages of the proposed method is that the trend search procedure does not require a priori threshold values, which are usually used to eliminate outliers; all measurement data remain in processing until the trend is determined. The method was approved on the data obtained from GNSS receivers, as well as on the SLR measurement data obtained from the AJISAI geodetic satellite (EGS) [31]. The purpose of this article is to extend the applicability of the previously proposed trend detection method into two additional functional classes, which will make it possible to extend further investigations into many physical processes based on observed data.
The article includes examples of building a trend for noisy data with outliers generated using computer simulation. In the examples below, the trend search is carried out for three functional classes: power polynomials (see Section 6), trigonometric functions with a given set of frequencies (Section 9), and harmonic functions with unknown frequencies, amplitudes, and phases (Section 10). The peculiarity of the trend search in the last class of harmonic signals is that the desired harmonics depend nonlinearly on unknown frequencies and, for their search, the traditional least squares method does not lead to a system of linear equations. In this case, the values of unknown frequencies are sought by the conjugate gradients method combined with the MS method (see below). The results of numerical calculations are given.
2.
Problem setting
The results yj=y(tj) of observations (measurements) of a certain random value Y(t), formed by measuring devices at time points {tj}Nj=1, in many cases can be represented in the form of a one-dimensional time series:
where fj=f(tj) is a trend function dictated by the physical process under consideration and usually unknown; z – is an unknown average; ξ j=ξ (tj) is a centered random variable with an unknown distribution, which may contain outliers, resulting from adverse effects of external factors on the measurements [33]. The challenge is to find fj.
It is clear that this problem does not have a unique solution due to the lack of clear criteria when searching for a trend and the impact of outliers on the result of its search, as well as due to the absence of a strict definition of the concept "rough measurement" or "outlier". The trend detection strategy presented in this paper is based on the MS method, developed by the author, as well as on the search for optimal solution algorithms.
3.
Optimal solution for data with removed trend
As mentioned above, trend and outlier detection problems are tightly coupled. To find a trend, we first need to find outliers and eliminate them from the values of series (1); after that, we need to find the desirable trend by adjusting some functions to the remaining values treated as reference ones. On the other hand, to detect outliers, it is necessary to know the trend. Initially, neither trend nor outliers are known. Both trend and outlier problems are found through iterations as described below. This Section describes the statement of the outlier detection problem for detrended data series, which is solved during search trend iterations (see Section 6).
If the trend fj is known, we can remove it from the time series (1):
with ˆyj=yj−fj. The task of detecting outliers in series (2) is usually to find a set YL={ˆyj1,...,ˆyjL} of L numbers (length L) for which the following conditions are met:
where σ YL and σmax are SD (standard deviation) and its preset threshold value, respectively; Δ is a parameter defining an outlier detection threshold (e.g., Δ=3σmax); Lmin is a specified parameter that limits the length of the search set from below (for example, Lmin=10); below we consider 1<Lmin<N. Values ˆyj not included in YL are considered outliers in series (2), and corresponding values yj – as outliers in series (1). The latter are removed from further processing. Often, conditions (3)–(5) are the only ones when searching coarse measurements in a series (2), while no additional conditions are imposed on the parameter L. Problem (2)–(5) is usually solved by iterations, which, as mentioned above, can lead to endless looping or loss of knowingly "good" data (for examples, see [29]).
In [30,31,32], the set YL search problems were formulated, where the conditions (3)–(5) are supplemented by two selection conditions: Of all possible sets satisfying (3)–(5), the set of maximum length Λ (the number of outliers is minimal) is selected as the desired set, and if there are several such sets, the set with the lowest SD value is selected. This solution was called optimal and designated YΛ,opt. The algorithms described in the above-listed works are guaranteed to lead to an optimal solution, if only it exists. However, their application to data containing a not-excluded trend can lead to an unreasonably large number of detected outliers or to the absence of a solution at all, when all measurement data will be detected as outliers. Therefore, our task is to build a suitable approximation ˜fj of an unknown trend and subtract it from the series (1). For this, we associate the concept of "suitable" with the requirement to maximize the number of data of series (1) remaining after the removal of outliers. Commonly, the trend is searched among the functions from some manifold chosen by the researcher depending on the physical problem being solved. In some cases, it can be power polynomials, in others it can be a class of trigonometric, rational functions, etc. Outliers in the measurement data can essentially distort the trend found. Below, we set out an approach to the trend-detection problem in noisy data, based on the minimizing sets method, which allows us to minimize the impact of outliers. We give a sequential exposition of the method for the class of power polynomials. Also, we will demonstrate the capabilities of the method when searching for a trend in other functional classes.
In the case of power polynomials, the trend is approximated by functions of the form
where n∈N and →a={a0,...,an−1,an}∈Rn+1 are the degree and coefficients of the polynomial, respectively; xj=(tj−t1)/(tN−t1). The trend detection, in this case, is based on the fitting to reference values of series (1) of a polynomial (6), the degree and coefficients of which are sought through iterations (see Section 6).
Trend fitting is performed to L reference values, which are also searched through iterations. The L value is set in advance to satisfy the inequality L⩽N−−Nout, which is a necessary condition for outliers not to be included in the final set of reference values at the end of the iterative procedure.1 Because the number Nout of outliers is unknown, the parameter L in the below discussed algorithm (see Section 6) is set to be guaranteed to be smaller than the possible value of the quantity N−−Nout so that the above inequality is fulfilled.
1 In Section 7, we will waive this restriction.
4.
Definition of a minimizing set of given length L
Let us define a minimizing set consisting of L numbers of series (2), which plays an important role in the trend detection process.
Let YL={ˆyj1,...,ˆyjL} be a set of L values of the series (2). Denote zYL and σ YL the average and SD values for it, respectively. We have:
Definition 1. For a given value L and a given sequence {ˆyj}Nj=1, the set of values
at which the value σ 2YL determined by (8) reaches a minimum, we call the minimizing set of length L. The corresponding values of the average and SD for this set are denoted by zYL,min and σYL,min, respectively.
According to this definition, we have
The minimum in (10) is searched throughout all possible sets of length L composed of the numerical series {ˆyj}Nj=1. Note that the number of possible sets of length L that can be selected from the series (2) is equal to the number CLN of combinations of N elements taken L at a time. It follows that the algorithm for finding the minimizing set YL,min, based on the enumeration of all kinds of sets, as a rule, is not feasible in a reasonable time on any modern computer, even with relatively small values of N. For example, with N = 100, the number of sets of length L = 80 is of the order of 1021. To avoid global brute force when searching the minimizing set YL,min, we note that its composition is determined up to a permutation of the numbers {ˆyj∗1,...,ˆyj∗L} and does not depend on the arrangement of the numbers in the series (2). This means that when searching the minimizing set, we can arrange the numbers of the series (2) in any order. Let us arrange them in ascending order so that after renumbering (keeping the same notation for the numbers of series (2) and considering them different), the inequalities will be fulfilled:
Let us formulate an assertion that radically reduces the number of sets to be examined.
Assertion 1. Let YL,min={ˆyj∗1,...,ˆyj∗L} be a minimizing set of length L for a given sequence {ˆyj}Nj=1 and
Then, the interval (ymin,ymax) does not contain values ˆyj that do not belong to the set YL,min.
See [32] for proof.
Without limiting generality, we consider the numbers ˆyj∗1,...,ˆyj∗L to be in ascending order, that is ˆyj∗1<...<ˆyj∗L. By virtue of (11), the indices j∗1,…,j∗L also follow in ascending order: j∗1<...<j∗L.
The following assertion is true.
Assertion 2. The ascending set of indices j∗1,...,j∗L in the minimizing set YL,min={ˆyj∗1,...,ˆyj∗L} contains all consecutive integers from j∗1 to j∗L.
Proof. Suppose the opposite: Let there be some index j0 such that j∗1<j0<j∗L, but j0∉{j∗1, ..., j∗L}. Then, the inequalities ˆyj∗1<ˆyj0<ˆyj∗L are satisfied for the number ˆyj0 but ˆyj0∉YL,min. This contradicts Assertion 1. It follows that the set of indices j∗1,j∗2,...,j∗L in YL,min coincides with the set of indices j∗1,j∗1+1,...,j∗1+L−1:
Therefore, instead of a global enumeration of all possible sets (with a total number of order CLN), it is enough to search YL,min among the sets {ˆyk, ..., ˆyk+L−1} consisting of segments of length L of an ordered series (2), varying only one parameter k, subject to the condition 1⩽k⩽N−L+1. The total number of such sets is (N−L+1).
5.
The minimizing set search algorithm
Thus, to find the minimizing set of length L, it is enough to consider N−−L+1 sets
and select from them the one for which the SD value is minimal. The formulas below minimize the number of arithmetic operations in the search of YL,min.
Denote Y(k,L)={ˆyk, ..., ˆyk+L−1} a set of numbers corresponding to a pair (k,L), and z(k,L) and σ (k,L) as the arithmetic mean and SD value of the set Y(k,L), respectively:
The values z(k,L) and σ2(k,L) during the search YL,min can be calculated according to the diagram shown in Figure 1 (in which z(k,L) are shown only):
First, using formulas (12) and (13), the values z(1,L) and σ2(1,L) are calculated; then, by formulas
the values {z(2,L) and σ2(2,L)} →, …, →{z(N−L+1,L) and σ2(N−L+1,L)} are successively calculated with the simultaneous selection of the smallest from the numbers:
The set YL,min={ˆym,ˆym+1,...,ˆym+L−1}, for which the SD is minimal, will be the desired minimizing set of length L for the ascending series {ˆyj}. As mentioned above, the same set will also be the minimizing set for the disordered series (2). Let us estimate the number of elementary operations needed to find it. Since the calculation of the values z(1,L) and σ2(1,L) requires 4L + 2 operations, and for each (N−L) the transitions in → direction (see Figure 1)–10, the total number of arithmetic operations when searching for the set YL,min in the ordered series (2) is estimated by the value 4L+2 +10(N−−L) ⩽ 10N.
In order to estimate the number of operations required to find the minimizing set in the unordered series (2), it is necessary to take into account the ordering costs, which are estimated by the value O(Nlog N) (see [34]).
Thus, we have proved the validity of the following assertion.
Assertion 3. For any (unordered) time series (2), a minimizing set YL,min of length L can be found in most O(Nlog N) arithmetic operations.
6.
Trend detection algorithm in power polynomial class
This section describes the trend-search algorithm using the MS method. Our immediate goal is to find a set of reference values, as a subset of the numbers of the series (1), used to fit the desired trend to them. Suppose that the subset we are looking for and denoted as YL,ref consists of L reference values: YL,ref = {yj1,...,yjL}, where L is not yet defined. As mentioned above, in order to obtain a proper approximation of the trend, the set of reference values should not contain outliers. This requires that the inequality L⩽N−−Nout be fulfilled, in which the parameter Nout, the number of outliers in series (1), is unknown.
Suppose that the number of outliers in series (1) does not exceed some value Nmaxout known a priori2. (For example, if it is known in advance that the number of outliers cannot exceed 10% of the total number of measurements, then we can set Nmaxout=0,1N.) Then, the number of "correct" values in a series yj that can be considered as reference ones is not lower than the value N−Nmaxout, and the problem is to find them.
2 In the next Section 7, we will abandon this assumption.
Below, we consider L to be fixed and associated with the number of reference values of series (1) used to build the trend.
Consider the following algorithm ([32]), containing two iterative cycles: external, by n, and internal, by s. Iterations over s will be marked with the superscript "s" in parentheses. Reference values chosen from the series (1) are marked with the flagj function, which takes values 1, if yj is considered as a reference value, or 0 otherwise.
Step 0. n = 0. Assume L=N−Nmaxout.
Step 1. n++3; Assume s = 0; (0)j=1, j=1,…,N. (Reference values are all numbers of the series (1): Y(0)N,ref = {y1,...,yN}.)
3 n incremented by 1.
Step 2. Using the least squares method, we find the coefficients →a(s)={a(s)0,...,a(s)n} of the polynomial of degree n:
where Pn,j(→a) is the polynomial defined by equation (6). The functional Φ(s)(→a) defined by equation (17) is calculated on L reference values Y(s)L,ref of series (1) found in the previous iteration4.
4 If s = 0, then reference values are all numbers of the series (1).
Step 3. We form the differences ˆy(s)j:
where Pn,j(→a(s)) is a polynomial with coefficients found in Step 2.
Step 4. For the series {ˆy(s)j}Nj=1 defined in (18), we find a minimizing set Y(s)L,min={ˆy(s)j∗(s)1,...,ˆy(s)j∗(s)L} of length L using the algorithm described in Section 5; using formulas (9) and (10), we can calculate the corresponding values of mean zY(s)L,min and SD σY(s)L,min.
Step 5. We redefine the reference points to find the polynomial at the next iteration (Step 2), marking them with the function flag(s+1)j:
At that Y(s+1)L,ref = {yj∗(s)1,...,yj∗(s)L}.
Step 6. s++. Increment the iteration counter s by 1 and go to Step 2.
We perform the sequence of Steps 2 to 6 until the convergence of the sequence σY(s)L,min, s = 0, 1, 2, ..., which always takes place (see Assertion 4).
After achieving convergence of the s-iterations (Steps 2–6), we proceed to Step 7 to find the optimal solution.
Step 7. Let the convergence of s-iterations be achieved at s=smax. In this case, the indices in both sets Y(smax)L,min and Y(smax)L,ref coincide up to permutation. The desired trend approximation ˜fn,j corresponding to the degree n of the polynomial is equal to ˜fn,j=Pn,j(→a(smax)).
Next, we find the optimal solution YΛ,opt={ˆyk1,...,ˆykΛ} for the series ˆy(smax)j=yj−Pn,j(→a(smax)), j= 1,…,N, using any of the algorithms described in [30,31,32]. As a result, the outliers will be the numbers yj of the series (1), for which j∉{k1,...,kΛ}. The resulting number of outliers detected is equal to Nout=N−−Λ.
If it turns out that Nout≤Nmaxout, then the solution is considered to be found, and the search process ends; at that, the desired trend is ˜fj=Pn,j(→a(smax)). Otherwise, if Nout>Nmaxout, then we transit to Step 1, at which we increase the polynomial degree by 1. The process (Steps 1–7) continues until a solution is found or n exceeds a preset value (e.g., 10). In the latter case, it will probably be necessary to select another functional class to search for a trend.
Example 1. We will generate synthetic noisy data using a computer simulation by the formula:
Here, j=1...N, randomj are pseudo-random numbers evenly distributed on the segment [0, 1]. The first term on the right side (20) models the trend, the second models the white noise, and the third models outliers at points j, multiples of 13, 43, or 113 (Figure 2). Suppose N=1250, then the number of modeled outliers is 134. Next, we set σ max=0.6,Δ=1.8, Lmin=10 and will search for the trend and outliers in accordance with the algorithm described above, putting Nmaxout=140; at L=N−Nmaxout=1110.
The calculation results for this example are presented in Table 1, in which n is the degree of the polynomial; smax is the number of s-iterations performed until convergence; Λ is the length of the optimal solution found; and Nout is the number of outliers detected.
As can be seen from Table 1, the minimum polynomial order at which the maximum length Λ of the optimal solution is reached equals 7. Therefore, a 7th-degree polynomial can be chosen as a suitable trend approximation.
The values P7,j(→a(0)) of the 7th-degree polynomial, constructed over all reference values without performing the above iterations (s = 0), are shown in Figure 2 (solid blue line). The corresponding polynomial differences ˆyj=yj−P7,j(→a(0)) are shown in Figure 3. It can be seen that the values ˆyj are distributed unevenly relative to 0, which indicates the inaccuracy of the constructed polynomial trend, since the reference values contain outliers.
The optimal solution found for the obtained series ˆyj has the length Λ = 1067 (number of outliers = 183). Trend refinement occurs as a result of multiple repeats of Steps 2–6 of the above iterative procedure.
Figure 4 shows the values P7,j(→a(4)) of the found polynomial of the 7th-degree (blue line), approximating the data set over L = 1110 reference values found after achieving convergence at the 4th iteration (smax = 4) of the above iteration process (Step 2–6). The corresponding differences ˆyj=yj−˜fj, where ˜fj=P7,j(→a(4)), are shown in Figure 5. It can be seen that the values ˆyj are evenly distributed relative to 0. The optimal solution found for the obtained series ˆyj has a length Λ = 1116, while the number of detected outliers = 134, their positions being marked with white circles.
Note that in the example considered, the trend was modeled by a function that does not belong to the class of power polynomials.
7.
Refine trend search strategy
As mentioned above, in order for the trend detection strategy described in the previous section to give an adequate result, it is necessary that the inequality L⩽N−Nout is fulfilled. The task of this section is to choose an L at which this inequality holds true. We cannot choose an L either too small or too large; otherwise, this will result in a distorted trend approximation ˜fj. Since Nout is unknown a priori, we cannot specify L to run a trend-search algorithm. To overcome this obstacle, we will use the L selection strategy proposed in [35]. Note that each value L corresponds to the optimal solution of length Λ depending on L (Λ = Λ(L)) obtained after removing from the series (1) trend, built on the L reference values. The L selection strategy proposed in [35] is based on searching the maximum of the length function Λ(L). By applying the algorithm discussed in Section 6, we can find a length sequence Λ(N), Λ(N−1),..., Λ(Lmin) for optimal solutions corresponding to the sequence of different L, starting with L = N and further decreasing L by 1. Then, we can find the maximum of this sequence denoted as Λ∗:
Next, from all possible values of L for which the equality Λ(L)=Λ∗ is fulfilled, we choose the maximum that we designate as L*:
It corresponds to the optimal solution YΛ∗,opt={ˆyj1,...,ˆyjΛ∗} of length Λ∗, at which the number of outliers detected is equal to N – Λ∗.
Let us test this strategy presented by equations (21) and (22) on the data from Example 1, expressed by equation (20). We will approximate the trend with a 7th-degree polynomial (n = 7). As a result, we find the sequence Λ(N), Λ(N−1), … plotted in Figure 6. The maximum value Λ∗=1118; the values of L at which this maximum is achieved are all numbers in the range L∈[1109,1129], the maximum of them is equal to L∗=1129. The reference values of the original series found at L∗=1129 can be used as reference ones for building a polynomial trend.
8.
Convergence of s-iterations in the trend search algorithm
The question of convergence of iterations described in the trend search algorithm (see Section 6) is formulated in the following statement.
Assertion 4. The sequence σY(s)L,min of SD values calculated in the trend-search algorithm decreases monotonically at s = 0.1, ...:
and therefore converges.
For proof, see [32].
Remark. The monotonic decreasing of the sequence σY(s)L,min of SD values calculated in the trend-search algorithm may be violated during real calculations due to insufficient calculation accuracy. It may happen that calculations with 64 bits do not provide the necessary calculation accuracy. The situation is usually corrected by switching to a 128-bit grid.
9.
Trend detection in the trigonometric polynomial class
The idea of the method described for finding a trend in a power polynomial class can also be implemented for other functional classes. Consider a periodic with period N function defined on a homogeneous grid Ω={xj=hj,j=0,±1,±2,..,Nh=l} that describes the sequence of measurements of a signal coming from a technical device:
As known, the function f(j) can be expanded into a discrete Fourier series into a sum of trigonometric functions:
The trend search for such a signal can be carried out in the form of an n-th-order polynomial
in which the coefficients ak, bk are searched by the least squares method from the condition of the minimum functional, similar to (17), where Pn,j(→a) should be replaced by Тn,j(→a,→b). The trend-search algorithm, in this case, is no different from the polynomial trend-search algorithm described above.
The convergence of s-iterations (see Assertion 4) for a given class of functions also takes place, as proved by literally word-for-word repetition of the proof of Assertion 4.
Example 2. Consider a computer simulation of the wave packet in the form of the product of the Gaussian function by a sinusoid:
where j = 1...N. The first two terms on the right side simulate a trend in the form of a wave packet and additive white noise, respectively. The third term simulates outliers at points j that are multiples of 13, 17, and 43.
Figure 7 shows the values of this function at N = 500 (orange diamonds) and the values T12,j(→a(0),→b(0)) of trigonometric polynomial (24) of the 12th order, plotted over all reference points, i.e., without performing the s-iterations (s = 0) (blue circles). Figure 8 shows the differences ˆyj=yj−T12,j(→a(0),→b(0)). It can be seen that the residuals contain a non-deleted trend component, which leads to an unreasonably large number of rejected measurement results when finding the optimal solution.
Figure 9 shows the values T12,j(→a(2),→b(2)) of the trigonometric polynomial of the 12th order (blue circles), constructed over L = 450 reference values found after achieving convergence at the second iteration (smax=2) of the above iteration process (see Section 6).
The differences ˆyj=yj−T12,j(→a(2),→b(2)) shown in Figure 10 are evenly distributed relative to 0, which indicates a satisfactory approximation of the trend.
10.
Trend detection in harmonic function class
Consider the problem of finding a trend in data representing a superposition of unknown harmonic signals, on which noise and outliers are superimposed:
Here, ak,bk,νk are the unknown parameters to be defined. An unknown parameter is also the number n of harmonics representing the signal under study.
The fundamental difference between this representation and decomposition (24) is its nonlinear dependence on unknown parameters νk, the search for which cannot be reduced to solving a system of linear equations. The search for reference values is carried out in accordance with the algorithm described above when searching for a polynomial trend, while it is necessary to replace Pn,j(→a) by Hn,j(→a, →b, →ν) in the expression (17) for the functional. The search for the minimum of the functional (see Step 2, Section 6), obtained as a result of such a replacement, is carried out by the conjugate gradients method.
Example 3. Figure 11 shows the result of a computer simulation of the harmonic signal generated by the formula
where j=1,...,N=5700. On the signal represented by the first term on the right side of equation (27), additive white noise (the second term) and outliers (the third term added to the previous two at points j, multiples of 13, 23, or 113) are superimposed.
A fragment of this signal in enlarged form is shown in Figure 12.
As a result of the search, the frequency of the signal was determined (see Table 2).
The detected trend is shown in Figure 13. The maximum value of the relative error of the found trend compared to the exact one is 0.008.
Example 4. Figure 14 shows the result of a computer simulation of a superposition of five harmonics:
where . On the signal represented by the first five terms on the right side of equation (28), additive white noise (the penultimate term) and outliers (the last term added to the previous ones at j, multiples of 13, 23, and 113) are superimposed.
Table 3 shows the frequencies found by the conjugate gradients method implemented in the trend-search algorithm described above. Figure 15 shows the found trend (blue line). The maximum value of the relative error of the found trend compared to the exact one is 0.006. The lower value of the relative bias found in the case of five harmonics compared to the case of one harmonic is explained by different levels of modeled additive white noise. In the case of one harmonic, it is 34% of the carrier level; in the case of five harmonics, it is 6% [see formulae (27), (28)].
11.
Conclusions
The developed method of minimizing sets allows us to find the appropriate approximations of the trend in the numerical series of noisy data containing outliers. The trend search can be carried out in various functional classes, such as power polynomials, trigonometric functions with a given set of frequencies, and harmonic functions with unknown frequencies, amplitudes, and phases, which is confirmed by the considered numerical examples. High efficiency of the trend detection method in noisy series of measurement data has been demonstrated. In the case of harmonic noisy signals, harmonic frequencies were found using the conjugate gradients method combined with the minimizing sets method. The relative error of the frequencies found in the considered examples did not exceed the magnitude . After constructing a trend and subtracting it from the values of the original data series, the robust algorithms are used to search for outliers, which are guaranteed to lead to an optimal solution with a minimum number of rejected measurements.
The method can be effectively applied in solving numerous applied and fundamental problems in various scientific and technical fields such as space geodesy, gravimetry, and astrometry, as well as in the tasks of exploring near and deep space, Earth's remote sensing, and others. The choice of the functional class for the trend search is chosen by the researcher, taking into account the specifics of the problem being solved.
Finding a trend in other functional classes, such as the class of fractional rational functions used in Padé approximations, requires more research. Some problems concerning the prediction of stationary processes can be solved using the harmonic functions discussed above. At the same time, additional studies are also required to predict quasi-stationary time series, such as satellite GNSS orbits and Earth rotation parameters. In the future, the priority area of research is the use of the proposed method to solve problems with real measurement data.
Acknowledgments
The author thanks the anonymous reviewers for their comments that significantly improved the presentation of the paper.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Conflict of interest
The author declares no conflict of interest.
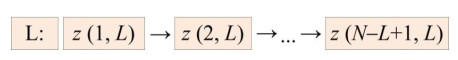









 DownLoad:
DownLoad: