Extreme values in SIR epidemic models with two strains and cross-immunity

1.   Introduction

Recently, a number of theoretical studies have focused on the mathematical modeling of coexistence of different pathogens or strains of a disease in a population of individuals; without any claim to an exhaustive enumeration, multiple pathogens or strains of a disease are usually involved in the spread of an important variety of human diseases, such as chlamydia trachomatis ^[1], hantavirus/arenavirus pulmonary syndromes ^[2,3], HIV-AIDS ^[4,5], influenza ^[6], nosocomial pathogens ^[7], tuberculosis ^[8,9], and viral respiratory tract diseases –including respiratory syncytial virus, human parainfluenza virus and human metapneumovirus– ^[10], to name a few. A special case of coexistence is related to the competition between two or more infectious agents interacting to increase or decrease each other's infectiousness, when each agent confers immunity and protection against infection by the others.

Epidemics in competition have been studied extensively from deterministic and stochastic perspectives under a variety of assumptions, including two-strain SI-models with total cross immunity and vertical transmission ^[3], SIR- and SIS-models with finite population size and two pathogen strains ^[1,11,12], SIR- and SIS-models with multiple pathogens and a population of variable size ^[13,14] and related variants with various levels of competition and isolation ^[6], among others. Unlike these references where a susceptible becomes infective of a certain type $k$ only when it is contacted by type-$k$ infectives, Ball and Clancy ^[15] assume that, on becoming infected, each newly infective may choose its type at random from a set of several different types of infective, this choice being made independently of other events.

In this paper, the aim is to define new probabilistic descriptors of the stochastic SIR-model with two strains analyzed by Kendall and Saunders ^[11]; see Appendix A for its deterministic counterpart. The strains in ^[11] are assumed to be perfectly distinguishable and instantly diagnosed; each strain of the disease confers immunity against the second strain, which implies that the epidemic will die out almost surely in a finite time since the population is assumed to be finite and there are no births, deaths or immigrations. It is the purpose of this paper to extend the algorithmic results in ^[16] to two strains by characterizing extreme value distributions and the final size of the epidemic in terms of iterative procedures for the corresponding mass functions, Laplace-Stieltjes transforms and related expected values. To that end, we take advantage of the sparsity on the infinitesimal generators arising when analyzing global outbreaks and outbreaks of each strain of the disease; therefore, the mathematical formulation is closely related to well-known matrix-analytic techniques existing in the literature for analyzing level-dependent quasi-birth-death (LD-QBD) processes (see e.g. ^[17,18]) and first-passage arguments applied to absorbing continuous-time Markov chains (CTMCs).

LD-QBD processes can be seen as CTMCs in two dimensions, the level and the phase, verifying that the process only jumps across either adjacent levels or the same level in one transition. By conveniently labeling states, this results in a tridiagonal-by-blocks structure for the underlying infinitesimal generator. For these processes, a number of general-purpose algorithmic procedures can be found in the literature in order to compute several performance measures such as stationary distributions (see ^{[17, Section 2]} and ^{[18, Chapter 10]}), first-passage times and hitting probabilities (see ^{[17, Sections 3-4]} and ^{[19, Section 2.1]}), maximum levels ^{[19, Section 2.2]}, and perturbation properties ^[19], among others. LD-QBD processes are specially relevant in epidemic modeling due to the fact that events such as infections and recoveries occur one at a time in continuous time. The work presented in this paper is part of our ongoing study on extreme value properties in a variety of epidemic models analyzed in terms of LD-QBD processes, including a SEIR stochastic model with limited resources ^[20], SIS models with heterogeneous contacts ^[21], the general stochastic model with infective and susceptible immigrants ^[22], multi-type SIS models ^[19,23] and maximum clonal sizes ^[24], among others.

The paper proceeds as follows. Section 2 provides the mathematical description of the SIR-model with two strains and cross-immunity, and outlines a first LD-QBD process allowing us to describe the dynamics of the strains during an outbreak. Sections 3.1 and 3.2 discuss extreme values and the final size of the epidemic during a global outbreak and during the outbreaks of each strain, respectively. Section 4 is devoted to an application of our analytical/algorithmic results to the spread of antibiotic-sensitive and antibiotic-resistant bacterial strains in a hospital ward. Section 5 collects our thoughts and conclusions.

2.   The two-strain SIR-model with total cross-immunity

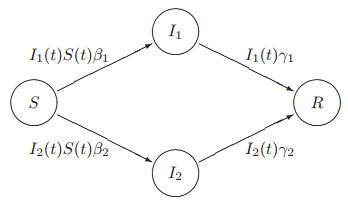
The interest is in a multi-type SIR epidemic model for the spread of two strains of a disease, termed type-$1$ and type-$2$, among an homogeneously mixed population of $N$ individuals; see Figure 1. At time $t$, the population consists of $S(t)$ susceptibles, $I_k(t)$ type-$k$ infectives, for $k\in\{1, 2\}$, and $R(t)$ recovered individuals, in such a way that $R(t) = N-S(t)-I_1(t)-I_2(t)$ due to the assumption that there are no births, deaths or migrations. For $k\in\{1, 2\}$, a type-$k$ infective makes infectious contacts at random points of a Poisson process with rate $\beta_k > 0$ during its infectious period, which follows an exponentially distributed recovery time with expected value $\gamma_k^{-1}$, and the individuals contacted at successive contacts are selected independently and uniformly from the individuals remaining susceptibles at those contact epochs. It is assumed that suffering from one type of infectious disease shall provide immunity against the other; this means that, for $k\in\{1, 2\}$, any type-$k$ infective cannot be infected by any type-$k'$ infective, with $k'\neq k$, during its infectious period, and it acquires immunity against both infectious diseases after its infectious period expires. Further, infectious periods and contact processes are assumed to be mutually independent.

Under the assumption of initial numbers of $I_1(0) = I_2(0) = 1$ infectives and $S(0) = N-2$ susceptibles, the two-strain SIR-model with cross-immunity may be formulated as a time-homogeneous CTMC $\mathcal{X} = \{X(t) = (I(t), J(t), R(t)): t\geq 0\}$, where $I(t) = I_1(t)+I_2(t)$ is the total number of infectives and $J(t) = I_2(t)$ is the number of type-$2$ infectives at time $t$, which is defined on the finite state space $\mathcal{S} = \cup_{i = 0}^N l(i)$ with levels

where $\delta_{a, b}$ denotes the Kronecker's delta, $l(0, 0) = \{(0, 0, r): r\in\{2, ..., N\}\}$, $l(i, j) = \{(i, j, r): r\in\{1, ..., N-i\}\}$ if $i\in\{1, ..., N-1\}$ and $j\in\{0, i\}$, and $l(i, j) = \{(i, j, r): r\in\{0, ..., N-i\}\}$ if $i\in\{2, ..., N\}$ and $j\in\{1, ..., i-1\}$. The process $\mathcal{X}$ is uniquely specified by the infectious contact rates $\beta_k > 0$ and recovery rates $\gamma_k > 0$, for $k\in\{1, 2\}$, in such a way that states in $l(0, 0)$ are absorbing——amounting to the ultimate extinction of both strains of the disease——and the class $\cup_{i = 1}^N l(i)$ consists of transient states. More concretely, the non-null infinitesimal rates $q_{(i, j, r), (i', j', r')}$ of $\mathcal{X}$ are given by

for states $(i, j, r), (i', j', r')\in\mathcal{S}$, with $q_{(i, j, r), (i, j, r)} = -q_{(i, j, r)}$ and

For later use, we now specify the structured form of the infinitesimal generator $\bf{Q}$ of $\mathcal{X}$, which is seen in Section 3.1 to be the keystone to derive algorithmic solutions for the final size of the epidemic and the extreme value distribution during a global outbreak. To that end, states in $\mathcal{S}$ are labeled in lexicographical ordering and, consequently, the infinitesimal generator ${\bf Q}$ has the block-tridiagonal form

where ${\bf 0}_{a\times b}$ is the null matrix of dimension $a\times b$, and the cardinalities of $l(i)$ and $\cup_{i = 1}^N l(i)$ are denoted by $L(i)$ and $L'$, respectively; i.e., $L(i) = 2(N-i)+(i-1)(N-i+1)$ if $i\in\{0, 1, ..., N\}$, and $L' = 6^{-1}N(N-1)(N+7)$. Sub-matrices ${\bf T}_0$ and ${\bf T}$ in Eq. (2.1) are given by

and entries $q_{(i, j, r), (i', j', r')}$ of ${\bf Q}_{i, i'}$ are related to transitions from the state $(i, j, r)\in l(i)$ to the state $(i', j', r')\in l(i')$, with $i'\in\{i-1, i, i+1\}$; see Appendix B for a concrete specification of the sub-matrices ${\bf Q}_{i, i'}$, for integers $i'\in\{i-1, i, i+1\}$.

Remark 1. Expressions for ${\bf Q}_{i, i'}$, with $i'\in\{i-1, i, i+1\}$, are inherently linked to the initial state of $\mathcal{X}$. In deriving expressions for ${\bf Q}_{i, i'}$ for any initial state $X(0) = (i_1+i_2, i_2, 0)$ with $i_1, i_2\in\{1, ..., N-2\}$ and $i_1+i_2\in\{2, ..., N-1\}$, we may first write the state space $\mathcal{S}$ from the levels

where the subsets $l(i, j)$ are specified as follows:

${(ⅰ)}$ For $i\in\{0, ..., i_1+i_2-2\}$ and $j\in\{\max\{0, i-(i_1-1)\}, ..., \min\{i_2-1, i\}\}$, the subset $l(i, j)$ has the form $\{(i, j, r): r\in\{i_1+i_2-i, ..., N-i\}\}$.

${(ⅱ)}$ For $i\in\{i_1, ..., N-1\}$ and $j\in\{\max\{0, i-(N-i_2)\}, ..., \min\{i_2-1, i-i_1\}\}$, the subset $l(i, j)$ has the form $\{(i, j, r): r\in\{i_2-j, ..., N-i\}\}$.

${(ⅲ)}$ For $i\in\{i_2, ..., N-1\}$ and $j\in\{\max\{i_2, i-(i_1-1)\}, ..., \min\{N-i_1, i\}\}$, the subset $l(i, j)$ has the form $\{(i, j, r): r\in\{i_1-(i-j), ..., N-i\}\}$.

${(ⅳ)}$ For $i\in\{i_1+i_2, ..., N\}$ and $j\in\{\max\{i_2, i-(N-i_2)\}, ..., \min\{N-i_1, i-i_1\}\}$, the subset $l(i, j)$ has the form $\{(i, j, r): r\in\{0, ..., N-i\}\}$.

Although these specifications for $l(i, j)$ result in a cumbersome procedure, general-purpose expressions for ${\bf Q}_{i, i'}$ can be then derived in a similar manner to the case $X(0) = (2, 1, 0)$ (Appendix B), and our results in Section 3 can be conveniently adapted for any initial state $X(0) = (i_1+i_2, i_2, 0)$ of $\mathcal{X}$ with $i_1, i_2\in\{1, ..., N-2\}$ and $i_1+i_2\in\{2, ..., N-1\}$.

3.   Extreme values during an outbreak

In this section, we focus on extreme values of the two-strain SIR-model with cross-immunity during a global outbreak (Section 3.1), which is related to the LD-QBD process $\mathcal{X}$ and its absorption in states of $l(0)$, and during the outbreak corresponding to the type-$k$ strain (Section 3.2), with $k\in\{1, 2\}$.

3.1.   Global outbreaks

A global outbreak begins when the population is seen to contain one type-$1$ infective, one type-$2$ infective and $N-2$ susceptible individuals. The disease spreads from the infectives to the susceptible individuals at rates $\beta_k$, with $k\in\{1, 2\}$, in such a way that new type-$k$ infectives try to infect other susceptibles and then recover in accordance to the model description in Section 2. The global outbreak is said to end when no infectives remain.

Remark 2. In terms of $\mathcal{X}$, the process $\mathcal{X}$ will reach states of level $l(0)$, starting from the initial state $X(0) = (2, 1, 0)$, and the epidemic will always die out. Specifically, the random length $T = \inf\{t\geq 0: I(t) = 0\}$ of a global outbreak can be seen as the time till absorption of $\mathcal{X}$ into the set $l(0)$ of absorbing states. Therefore, starting from numbers $I_1(0) = I_2(0) = 1$ of infectives and $S(0) = N-2$ of susceptibles, the length $T$ of the outbreak can be thought of as a continuous phase-type (PH) random variable of order $L'$ and representation $({ {{ α}}}, {\bf T})$, where the row vector ${ {{ α}}}$ records the initial probabilities of $\mathcal{X}$ on the class $\cup_{i = 1}^N l(i)$ of transient states; see ^{[18, Definition 2.3.1]}. By using a lexicographical ordering of states (Appendix B), it is seen that the $3(N-1)$th entry of ${ {{ α}}}$ corresponds to the initial state $X(0) = (2, 1, 0)$ and consequently ${ {{ α}}} = {\bf e}_{L'}(3(N-1))$, where ${\bf e}_a(b)$ is a row vector of order $a$ such that all entries are equal to $0$, except for the $b$th entry which is equal to $1$.

Since the absorption into the set $l(0)$ occurs with probability one, the matrix ${\bf T}$ is nonsingular and the inverse $-{\bf T}^{-1}$ is a nonnegative matrix of expected sojourn times spent in transient states before absorption; see ^{[18, Theorem 2.4.3]}. The following result allows us to evaluate the distribution of the final epidemic size by using the matrix $-{\bf T}^{-1}$.

Theorem 3.1. Under the assumption of initial numbers $I_1(0) = I_2(0) = 1$ of infectives and $S(0) = N-2$ of susceptibles, the mass function $\{P(r) = P(R(\infty) = r | X(0) = (2, 1, 0)): r\in\{2, ..., N\}\}$ of the final epidemic size is specified by

Proof. Since the process $\mathcal{X}$ is Markovian, it is enough to point out that the matrix ${\bf T}$ is stable (see ^{[18, Remark 2.4.5]}) and the transition function

of the LD-QBD process $\mathcal{X}$ has the form

where ${\bf I}_a$ denotes the identity matrix of order $a$. This implies that $\lim_{t\to\infty}e^{{\bf T}t} = {\bf 0}_{L'\times L'}$ and that the time-dependent probabilities $P(r; t) = P(X(t) = (0, 0, r) | X(0) = (2, 1, 0))$ are given by

for integers $r\in\{2, ..., N\}$. Then, Eq. (3.1) is easily derived from the limit result $P(r) = \lim_{t\to\infty}P(r; t)$.

In analyzing extreme values during a global outbreak, we define the random variable $X_{\max}$ as the maximum number of individuals simultaneously infected by the disease –regardless of the strain– during the interval $[0, T)$, and we let $T_{\max}$ denote the time to reach the random integer $X_{\max}$ for the first time; i.e., in terms of $\mathcal{X}$ it is clear that $X_{\max} = \max\{I(t): t\in [0, T)\}$ corresponds to the maximum level visited by the process $\mathcal{X}$ before its absorption into states of $l(0)$, and $T_{\max} = \inf\{t\geq 0: I(t) = X_{\max}\}$ is a suitably defined first-passage time.

In order to characterize the joint distribution of $(X_{\max}, T_{\max})$, we proceed in two steps. We first derive the marginal distribution of $X_{\max}$ in terms of the probability mass function $\{P_{(2, 1, 0)}(x) = P(X_{\max} = x | X(0) = (2, 1, 0)): x\in\{2, ..., N\}\}$^*; and we then determine expressions for the restricted Laplace-Stieltjes transforms

It is clear that $P_{(2, 1, 0)}(x) = 0$ if $x\in\{0, 1\}$, provided that $X(0) = (2, 1, 0)$.

for integers $x\in\{2, ..., N\}$ and $Re(\theta)\geq 0$. To that end, we introduce the notation $P_{(i, j, r)}(x)$ and $\varphi_{(i, j, r)}(\theta; x)$, for states $(i, j, r)\in\mathcal{S}\setminus l(0)$ and integers $x\in\{i, i+1, ..., N\}$, by adapting the definition of $P_{(2, 1, 0)}(x)$ and $\varphi_{(2, 1, 0)}(\theta; x)$ to an arbitrary time $t$. More concretely, $P_{(i, j, r)}(x)$ and $\varphi_{(i, j, r)}(\theta; x)$ are linked, respectively, to the maximum number of individuals simultaneously infected by the disease during the residual global outbreak, and the time to reach this number for the first time, provided that $(i, j, r)$ is the current state of $\mathcal{X}$ at time $t$; note that $P_{(i, j, r)}(x)$ and $\varphi_{(i, j, r)}(\theta; x)$ depend on the event $\{X(t) = (i, j, r)\}$ only in terms of $(i, j, r)$, since the LD-QBD process $\mathcal{X}$ is time-homogeneous.

For the initial state $X(0) = (2, 1, 0)$, we express

for $x\in\{2, ..., N\}$, where $F_{\max}(x; (2, 1, 0)) = P(X_{\max}\leq x | X(0) = (2, 1, 0))$, and we observe that, for a fixed integer $x\in\{2, ..., N\}$, the function $F_{\max}(x; (2, 1, 0))$ is equivalent to the probability that, starting from state $(2, 1, 0)$, the LD-QBD process $\mathcal{X}$ reaches the level $l(0)$ of absorbing states, but avoiding visits to states of the sub-class $\cup_{i = x+1}^N l(i)$ of transient states. This probability is related to an absorbing LD-QBD process $\overline{\mathcal{X}}(x)$ defined on the state space $\overline{\mathcal{S}}(x) = \{0\}\cup\bigcup_{i = 1}^x l(i)\cup\{x+1\}$, where $0$ and $x+1$ are absorbing states and states in $\cup_{i = 1}^x l(i)$ are assumed to be transient. To be concrete, the infinitesimal generator of the auxiliary process $\overline{\mathcal{X}}(x)$ has the structured form

where $\overline{L}(x)$ is the cardinality of the sub-class $\cup_{i = 1}^x l(i)$ (i.e., $\overline{L}(x) = 6^{-1}x(3N(x+3)-(2x^2+3x+7))$), the column vectors ${\bf t}_0(x)$ and ${\bf t}_{x+1}(x)$ are given by

and the column vectors ${\bf 1}_a$ and ${\bf 0}_a$ are the unit vector and the null vector of order $a$, respectively. The sub-matrix ${\bf T}(x)$ is block-tridiagonal and has the following form:

Next we state two results allowing us to derive the marginal distribution of $X_{\max}$ in a recursive manner; their proofs mostly repeat arguments of ^{[25, Section 2.1]}, and they are thus omitted.

Theorem 3.2. Under the assumption of initial numbers $I_1(0) = I_2(0) = 1$ of infectives and $S(0) = N-2$ of susceptibles, the probability distribution function of $X_{\max}$ is given by $F_{\max}(x; (2, 1, 0)) = {\bf e}_{\overline{L}(x)}(3(N-1))(-{\bf T}^{-1}(x)){\bf t}_0(x)$ if $x\in\{2, ..., N\}$, and $0$ if $x\in\{0, 1\}$.

The perceptive reader may notice that there is more information in Algorithm 3.3. For instance, we have that, for a fixed integer $x\in\{2, ..., N\}$, the matrix $-{\bf T}^{-1}(x)$ records expected total times spent in states of $\cup_{i = 1}^x l(i)$ until absorption, and the entries of the column vector $-{\bf T}^{-1}(x){\bf t}_0(x)$ contain probabilities that the absorption into state $0$ occurs in a finite time; note that these properties are established by observing that the matrix ${\bf T}(x)$ is stable and $\int_0^{\infty}e^{{\bf T}(x) t}{\bf t}_0(x)dt = -{\bf T}^{-1}(x){\bf t}_0(x)$. This means that, in the setting of a residual global outbreak, the column vector

consists of the probabilities $P_{(i, j, r)}(x)$, for current states $(i, j, r)\in\mathcal{S}\setminus l(0)$ and integers $x\in\{i, ..., N\}$. Moreover, taking into account that the last iteration in Step 1 yields $-{\bf T}^{-1}(N)$ (i.e., $-{\bf T}^{-1}$), the expected length of a global outbreak and the final size of the epidemic can be computed by adding an additional step, as follows:

Step 2: $E[T | X(0) = (2, 1, 0)]: = {\bf e}^T_{\overline{L}(x)}(3(N-1))(-{\bf T}^{-1}(x)){\bf 1}_{\overline{L}(x)}$;

            $r: = 1$;

            while $r < N$,

                  $r: = r+1$;

                  $P(r): = {\bf e}^T_{\overline{L}(x)}(3(N-1))(-{\bf T}^{-1}(x)){\bf T}_0 {\bf e}^T_{N-1}(r-1)$.

Another algorithm similar to Algorithm 3.3 for the probability distribution function $\{F_{\max}(x; (2, 1, 0)): x\in\{2, ..., N\}\}$ can be derived by using an alternative labeling of states; for details, see Appendix C.

In order to characterize the joint distribution of $(X_{\max}, T_{\max})$, we notice that

It is therefore seen that the marginal distribution of $T_{\max}$ has a discrete contribution on $\{T_{\max} = 0\}$ and a continuous contribution on $\{T_{\max} > 0\}$, which are linked to the sets $\{X_{\max} = 2\}$ and $\{X_{\max} = x\}$, for $x\in\{3, ..., N\}$, of sample paths, respectively; in particular, the former is derived from Algorithm 3.3, and the latter shall be characterized (Algorithm 3.4) in terms of restricted Laplace-Stieltjes transforms $\varphi_{(2, 1, 0)}(\theta; x)$.

For integers $x\in\{3, ..., N\}$, the probability law of $T_{\max}$ on $\{X_{\max} = x\}$ is defined on $\{T_{\max} > 0\}$ and is related to those sample paths of the LD-QBD process $\mathcal{X}$ satisfying that the first visit to states of level $l(x)$ occurs before the first access to $l(0)$ in such a way that, after the first visit to $l(x)$, the process $\mathcal{X}$ does not leave the set $\cup_{i = 1}^x l(i)$ until its absorption into states of $l(0)$. Therefore, by conditioning on each possible state $(x, j, r)\in l(x)$ visited by $\mathcal{X}$ at time $t = U(x)$ of the first passage, we express

for $Re(\theta)\geq 0$ and integers $x\in\{3, ..., N\}$, where $\phi_{(2, 1, 0)}(\theta; (x, j, r))$ is the restricted Laplace-Stieltjes transform of the first-passage time $U(x)$ to level $l(x)$ on the set $\{X(U(x)) = (x, j, r)\}$ of sample paths, provided that $X(0) = (2, 1, 0)$.

In evaluating $\varphi_{(2, 1, 0)}(\theta; x)$ in Eq. (3.3), we define –similarly to $\phi_{(2, 1, 0)}(\theta; (x, j, r))$– the restricted Laplace-Stieltjes transforms $\phi_{(i', j', r')}(\theta; (x, j, r))$ by replacing the initial state $(2, 1, 0)$ by the current state $(i', j', r')$ visited by the process $\mathcal{X}$ at an arbitrary time $t$, and we condition on the first transition of $\mathcal{X}$ occurring from the current state $(i', j', r')$. Starting at $(i', j', r')$, the first state visited by $\mathcal{X}$ may be any accessible state of $l(i'-1)\cup l(i'+1)$, whence we write down

${(ⅰ)}$ For current states $(i', j', r')\in \cup_{i = 1}^{x-2} l(i)$,

${(ⅲ)}$ For current states $(x-1, j', r')\in l(x-1)$,

By multiplying (3.4) and (3.5) by $(\theta +q_{(i', j', r')}) P_{(x, j, r)}(x)$, for states $(i', j', r')\in \cup_{i = 1}^{x-2} l(i)$) and $(\theta +q_{(x-1, j', r')}) P_{(x, j, r)}(x)$, for states $(x-1, j', r')\in l(x-1)$, respectively, and summing on states $(x, j, r)\in l(x)$, we derive the matrix equality

for integers $x\in\{3, ..., N\}$ and column vectors ${ {{ φ}}}_{i'}(\theta; x)$ of restricted Laplace-Stieltjes transforms $\varphi_{(i', j', r')}(\theta; x)$ with states $(i', j', r')\in l(i')$ and $i'\in\{1, ..., x-1\}$. The column vector ${\bf b}(x)$ consists of sub-vectors ${\bf b}_{j'}(x)$, for $j'\in\{0, ..., x-1\}$, where

Note that, in the case $x = N$, these expressions become ${\bf b}_{j'}(N) = 0$, for $j'\in\{0, N-1\}$, and

for $j'\in\{1, ..., N-2\}$. Then, by taking derivatives in Eq. (3.6) with respect to $\theta$ at point $\theta = 0$, and noting that the column vector

contains the $n$th moment of $T_{\max}$ on the set $\{X_{\max} = x\}$ of sample paths (i.e., $E[T_{\max}^n 1\{X_{\max} = x\} | X(0) = (i, j, r)]$ for states $(i, j, r)\in l(i)$ with $i\in\{1, ..., x-1\}$, and integers $x\in\{3, ..., N\}$), we may characterize the moments of the random time $T_{\max}$ on $\{X_{\max} = x\}$ as the unique solution to the system of linear equations

for $i\in\{1, ..., x-1\}$ and $n\geq 1$.

This results in Algorithms 3.4 and 3.5, from which the column vectors ${ {{ φ}}}_i(\theta; x)$ and ${\bf m}_i^{(n)}(x)$ can be computed in an efficient and unified manner by applying block-Gaussian elimination to Eqs. (3.6)-(3.7), respectively.

It should be noted that, in Algorithm 3.5, sub-vectors ${\bf m}^{(0)}_{i}(x) = { {{ φ}}}_{i}(\theta; x)|_{\theta = 0}$ containing probabilities $P_{(i, j, r)}(x)$, for states $(i, j, r)\in l(i)$, are evaluated as a prerequisite for computing ${\bf m}^{(n)}_{i}(x)$ in terms of the $(n-1)$th restricted moments of $T_{\max}$ on the set $\{X_{\max} = x\}$ of sample paths. Therefore, a joint implementation of Algorithms 3.4 and 3.5 leads us to the following expression for the expectation of the random time $T_{\max}$ to reach the maximum number $X_{\max}$ for the first time:

3.2.   Type-$k$ outbreaks

Provided that initially the population contains one type-$1$ infective, one type-$2$ infective and $N-2$ susceptibles, a type-$k$ outbreak is said to end when no type-$k$ infectives remain, for $k\in\{1, 2\}$. Extreme values in a type-$k$ outbreak are then related to the length $T(k) = \inf\{t\geq 0: I_k(t) = 0\}$ of the type-$k$ outbreak, the maximum number $X_{\max}(k) = \max\{I_k(t): t\in [0, T(k))\}$ of individuals simultaneously type-$k$ infected during the type-$k$ outbreak, and the random time $T_{\max}(k) = \inf\{t\geq 0: I_k(t) = X_{\max}(k)\}$ to reach the maximum number $X_{\max}(k)$ for the first time. It is worth noting that, depending on how both strains of the disease interact during the outbreak, the end of a global outbreak might correspond to either the end of a type-$k$ outbreak or the end of a type-$k'$ outbreak, for $k'\neq k$. Thus, the survival of the strain of type $k'$ amounts to the event $\{T(k) < T(k')\}$ –equivalently, $\{T = T(k')\}$– in such a way that, during the residual interval $[T(k), T)$, the surviving population behaves as the standard SIR-model ^[16,26] with initial numbers $I_{k'}(T(k))$ of infectives and $S(T(k))$ of susceptible individuals.

Without any loss of generality, we from now on consider the case $k = 2$ and observe that, in terms of $\mathcal{X}$, the length $T(2)$ of a type-$2$ outbreak is equivalent to the random time to reach states of the subset $\cup_{i = 0}^{N-1}l(i, 0)$. The analytical treatment of $T(2)$ and $(X_{\max}(2), T_{\max}(2))$ can be therefore reduced to Theorems 3.1-3.2 and Algorithms 3.3-3.5 by using a suitably chosen labeling of states. More concretely, we may use the LD-QBD process $\mathcal{Y} = \{Y(t): t\geq 0\}$ with $Y(t) = (J(t), I(t), R(t))$ instead of $X(t) = (I(t), J(t), R(t))$, which is defined on the state space $\mathcal{S}^* = \cup_{j = 0}^{N-1}l^*(j)$, where levels are now specified by

with $l^*(j, 0) = \{(j, j, r): r\in\{1+\delta_{0, j}, ..., N-j\}\}$ and $l^*(j, i) = \{(j, i, r): r\in\{\delta_{0, j}, ..., N-i\}\}$, for $i\in\{j+1, ..., N-\delta_{0, j}\}$; note that absorbing states of $\mathcal{X}$ are now states within the sub-level $l^*(0, 0)$. The associated infinitesimal generator ${\bf Q}^*$ of $\mathcal{Y}$ has the structured form

where $K(j)$ and $K'$ denote the respective cardinalities of $l^*(j)$ and $\mathcal{S}\setminus l^*(0)$ (i.e., $K(j) = 2^{-1}(N-1)(N+2)$ if $j = 0$, and $2^{-1}(N-j)(N-j+3)$ if $j\in\{1, ..., N-1\}$, and $K' = 6^{-1}N(N-1)(N+4)$) and

Sub-matrices ${\bf Q}^*_{j, j'}$ record transition rates related to jumps of the process $\mathcal{Y}$ from states of level $l^*(j)$ to states in $l^*(j')$, with $j'\in\{j-1, j, j+1\}$, and diagonal entries of ${\bf Q}^*_{j, j}$ are given by $-q_{(i, j, r)}$, for states $(j, i, r)\in l^*(j)$ with $j\in\{0, ..., N-1\}$; expressions for these sub-matrices are readily specified from Section 2, and they are thus omitted.

It is important to note that, provided that $I_1(0) = I_2(0) = 1$ and $S(0) = N-2$ are the initial conditions, the length $T(2)$ of a type-$2$ outbreak is a PH random variable of order $K'$ and representation $({ {{ α}}}^*, {\bf T}^*)$ with the vector ${ {{ α}}}^* = {\bf e}_{K'}(2)$ of initial probabilities. Moreover, by adapting our arguments in Section 3.1 to the LD-QBD process $\mathcal{Y}$, it is seen that the joint distribution of $(X_{\max}(2), T_{\max}(2))$ can be characterized by means of the conditional probabilities (Algorithm D.1)

(equivalently, $F^*_{\max}(x; (1, 2, 0)) = P(X_{\max}(2)\leq x | Y(0) = (1, 2, 0))$) and the restricted Laplace-Stieltjes transforms (Algorithms D.2-D.3)

for integers $x\in\{1, ..., N-1\}$ and $Re(\theta)\geq 0$. For the sake of brevity, we present Algorithms D.1-D.3 in Appendix D, but with no detailed proof.

4.   Numerical experiments and discussion

Recently, Cen et al. ^[27], and Lipsitch et al. ^[7] have discussed a deterministic model for the spread of two strains of a single bacterial species in a hospital ward; see Appendix A. These strains are either antibiotic-sensitive (AS) or antibiotic-resistant (AR). We propose here a stochastic version of this model with total cross-immunity by assuming that the infection of a patient by one bacterial strain provides immunity against the other. Initially the hospital ward accommodates one infective colonized by the AS bacteria, one infective colonized by the AR bacteria and $N-2$ susceptible patients. It is assumed that patients cannot be discharged from the hospital ward and, consequently, the entire group of $N$ patients remains under study during the outbreak. Two antimicrobial agents –referred as drug A and drug B– are routinely provided to patients in the ward, irrespectively of these patients being or not infected by bacteria. Drug A is assumed to be effective against the AS bacteria with per-capita treatment rate $\tau_A > 0$, and drug B is effective against both bacterial strains with per-capita treatment rate $\tau_B > 0$.

We let $S(t)$, $I_1(t)$, $I_2(t)$ and $R(t)$ be the respective numbers of susceptible patients, infectives colonized by the AS bacterial strain, infectives colonized by the AR bacterial strain and recovered patients in the hospital ward at time $t$. Infections of type $1$ and of type $2$ (Section 2) are therefore associated with the AS and AR bacterial strains, respectively, and the resulting two-strain SIR-model is specified by the infection rates $\beta_1 = N^{-1}\beta$ and $\beta_2 = (1-c)N^{-1}\beta$, and the recovery rates $\gamma_1 = \tau_A+\tau_B+\gamma_0$ and $\gamma_2 = \tau_B+\gamma_0$, where $\beta > 0$ is the per-capita primary transmission rate, $\gamma_0 > 0$ is the per-capita clearance rate of the bacteria and $c\in[0, 1)$ is the fitness cost of a bacterial strain resistant to drug A. It should be noted that clinical and epidemiological research has demonstrated that antibiotic resistance often carries a fitness cost, expressed in terms of reduced competitive ability or virulence, and translated here into the reduced growth rate $(1-c)\beta_1$ for resistant bacteria. This cost of resistance is highly variable as it is thought to be influenced by a wide variety of factors such as basic cellular functions, biochemical effects of specific resistance mutations and the underlying genetic mechanism of resistance; for related work, see ^[28] and references therein. Because we do not deal with observations from strains of a particular bacteria, we assume values $c\in\{0.25, 0.5, 0.75\}$ in our numerical results to predict generic properties of the model.

Our numerical experiments (Tables 1-3, Figures 2-10) are linked to a hospital ward with $N = 20$ patients, and values $\beta^{-1} = 1 \ day$, $\tau_A^{-1} = 5 \ days$, $\gamma_0^{-1} = 45 \ days$, and three scenarios which are defined from the choices $\tau_B^{-1} = 10 \ days$ (scenario 1), $15 \ days$ (scenario 2) and $20 \ days$ (scenario 3). Note that these values correspond to realistic selections in Lipsitch et al. ^{[7, Table 1, Figure 2]}. For easy of presentation, we use here the notation $T(AS)$ and $T(AR)$ instead of $T(1)$ and $T(2)$, and we replace $(X_{\max}(1), T_{\max}(1))$ and $(X_{\max}(2), T_{\max}(2))$ by $(X_{\max}(AS), T_{\max}(AS))$ and $(X_{\max}(AR), T_{\max}(AR))$, respectively.

In Tables 1-2, we list values of the expected length $E[T]$ of a global outbreak and the expectation $E[R(\infty)]$ of the final size distribution, as well as their counterparts $E[T(AR)]$ and $E[T(AS)]$ for the AR and AS bacterial strains, and the mean numbers $E[R(T(AR))]$ and $E[R(T(AS))]$ of recovered patients at the end of AR and AS bacteria outbreaks. Figures 2-4 plot the mass functions of the final size $R(\infty)$ of the epidemic, and of the numbers $R(T(AR))$ and $R(T(AS))$. Based on Table 1, we may classify scenarios 1-3 and values $c\in\{0.25, 0.5, 0.75\}$ of the fitness cost according to the degree of co-circulation of the AS and AR bacterial strains during the outbreak. To be concrete, we may estimate the degree of co-circulation, relative to the resistant strain in terms of the ratio $(E[T(AR)])^{-1}E[T(AS)]$, in such a way that scenarios 2 and 3 with $c = 0.25$ are related to a low degree (i.e., $\hbox{ratio}\leq 0.30$), scenario 1 with $c = 0.75$ is associated with a high degree (i.e., $\hbox{ratio} > 0.50$), and other selections in our examples yield medium degrees of co-circulation of strains (i.e., $0.30 < \hbox{ratio}\leq 0.50$); more particularly, scenario 1 with $c = 0.75$ ($\hbox{ratio} = 0.61632$) implies a coexistence of both strains more lasting in time, whereas scenario 3 with $c = 0.25$ ($\hbox{ratio} = 0.25405$) leads to an early extinction of sensitive bacteria and, consequently, a large residual outbreak of the AR bacterial strain. It is also observed that, as intuition tells us, the mean length $E[T]$ of a global outbreak (respectively, the expectation $E[R(\infty)]$ of the final epidemic size) and the mean lengths $E[T(AR)]$ and $E[T(AS)]$ of AR and AS bacteria outbreaks (respectively, the mean numbers $E[R(T(AR))]$ and $E[R(T(AS))]$ of recovered patients at the end of the AR and AS bacteria outbreaks) increase when the effectiveness of drug B decreases (i.e., with increasing values of $\tau^{-1}_B$) since drug B affects both recovery rates $\gamma_1$ and $\gamma_2$. On the other hand, increasing values of the fitness cost $c$ lead to decreasing mean lengths $E[T]$ and $E[T(AR)]$, and decreasing mean numbers $E[R(\infty)]$ and $E[R(T(AR))]$, whereas $E[T(AS)]$ and $E[R(T(AS))]$ increase with increasing values of $c$. Indeed, increasing values of $c$ can lead to smaller expected numbers $E[R(T(AR))]$ of recoveries, in comparison with its sensitive counterpart over larger outbreaks; more concretely, it is observed in scenario 1 (Tables 1-2) that $E[R(T(AR))] < E[R(T(AS))]$ whereas $E[T(AR)] > E[T(AS)]$ in the case $c = 0.75$, and values $c\in\{0.25, 0.5\}$ yield the inequalities $E[R(T(AR))] > E[R(T(AS))]$ and $E[T(AR)] > E[T(AS)]$. This apparently contradictory behavior relates to the non-linear form of the infection rates (i.e., $I_1(t)S(t)\beta_1$ and $I_2(t)S(t)\beta_2$) and can be explained by noting that higher values of the fitness cost $c$ result in smaller values of the rate $\beta_2$ governing infections by the AR bacterial strain. This implies that the number $I_2(t)$ of patients colonized by the AR bacterial strain decreases and, consequently, it is seen that the number $I_1(t) (N-I_1(t)-I_2(t)-R(t))$ of contact processes generating new patients colonized by the AS bacterial strain increases. Thus, a longer AS bacterial outbreak is expected (Table 1) when the fitness cost $c$ is large enough, which is closely related to the fact that scenario 1 with $c = 0.75$ yields the highest degree of coexistence of strains in our examples; as a result, the number $E[R(T(AS))]$ of recovered patients at the end of an AS bacteria outbreak increases (Table 2).

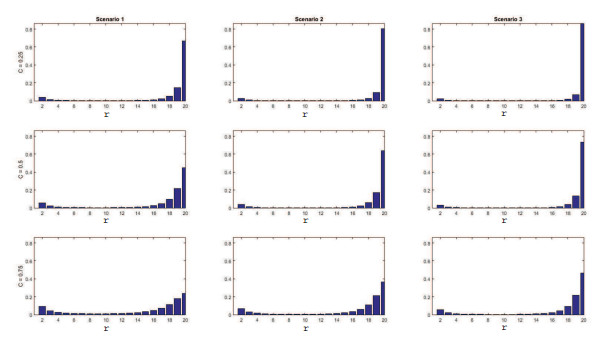
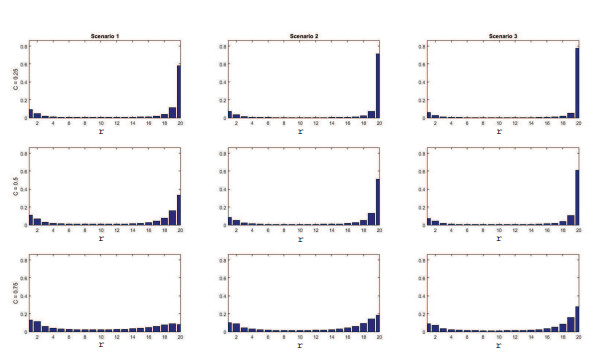
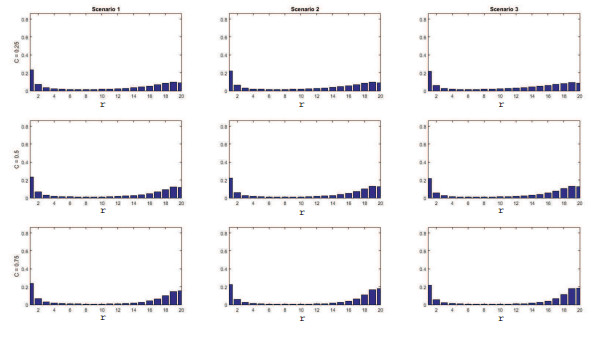
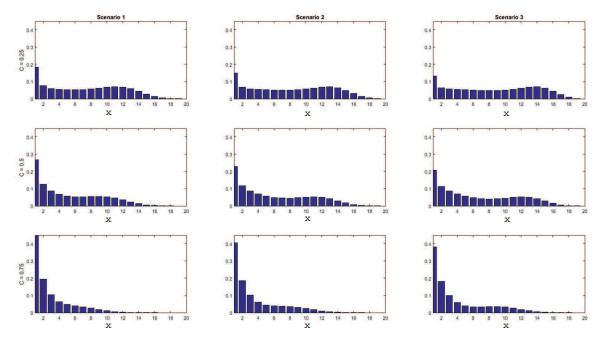
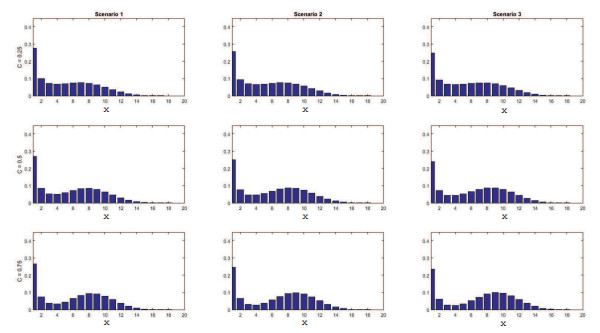
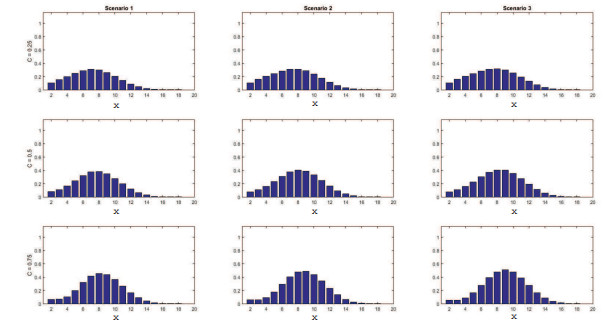
Figure 2 allows us to study the severity of the epidemic in terms of the mass function of the final epidemic size $R(\infty)$. It is observed that the most likely event to occur during the global outbreak is the colonization by the bacteria of all patients, regardless of the bacterial strain. More particularly, this occurs with a significant probability which increases as the fitness cost $c$ and/or the effectiveness of drug B decrease; in our examples, the maximum probability of this event corresponds to scenario 3 and the selection $c = 0.25$, and is greater than $0.8$. It is also seen (Figure 3) that similar remarks can be made for the mass function of the random number $R(T(AR))$ of recovered patients at the extinction time $T(AR)$ of the AR bacterial strain. Regarding to the number $R(T(AS))$ of recovered patients at the end of an AS bacterial outbreak, the most likely events (Figure 4) amount to either the extinction of the AS bacterial strain before a patient is newly colonized by the AS bacterial strain, or the colonization of almost all patients present in the hospital ward.

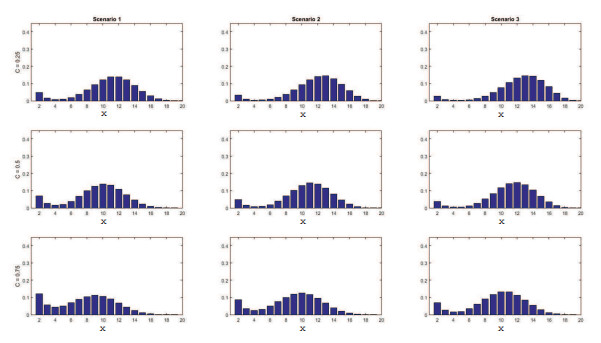
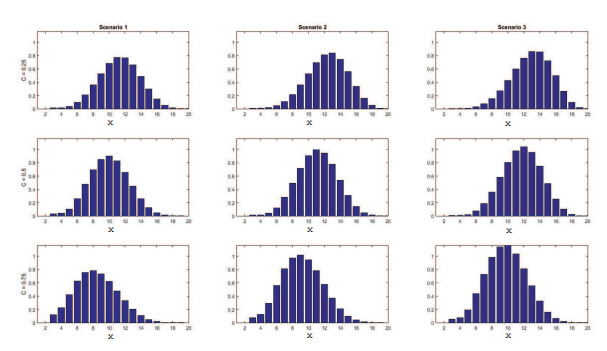
In Table 3, the focus is on the mean times $E[T_{\max}]$, $E[T_{\max}(AR)]$ and $E[T_{\max}(AS)]$ to reach the maximum numbers $X_{\max}$, $X_{\max}(AR)$ and $X_{\max}(AS)$ of patients simultaneously colonized by the bacteria, and by the AR and AS bacterial strains, respectively; in Figures 5-7, we plot the mass functions of the maximum numbers $X_{\max}$, $X_{\max}(AR)$ and $X_{\max}(AS)$. Similarly to Tables 1-2, Table 3 shows that $E[T_{\max}]$, $E[T_{\max}(AR)]$ and $E[T_{\max}(AS)]$ increase when the effectiveness of drug B decreases. It is however seen that $E[T_{\max}]$, $E[T_{\max}(AR)]$ and $E[T_{\max}(AS)]$ do not have a monotone behavior as a function of the fitness cost $c$, which is closely related to the non-linear effect of the contact rates and the bimodal distribution of $X_{\max}$, $X_{\max}(AR)$ and $X_{\max}(AS)$. It is observed that the marginal distribution of $X_{\max}$ (Figure 5) is a bimodal distribution with two peaks (modes) of different heights. The first peak amounts to the smallest value of $X_{\max}$ (i.e., the event $\{X_{\max} = 2\}$), regardless of the scenario and magnitude of $c$, and its height (i.e., the probability $P_{(2, 1, 0)}(2)$) becomes higher with increasing values of the fitness cost $c$, and decreases when the effectiveness of drug B decreases. The second peak corresponds to an intermediate integer $x'\in\{2, ..., N\}$, which increases with increasing values of $\tau^{-1}_B$ and, on the contrary, decreases with increasing values of $c$, whereas smaller heights (i.e., $P_{(2, 1, 0)}(x')$) are related to smaller values of $\tau^{-1}_B$ and bigger values of $c$ (i.e., the choice $(c, \tau^{-1}_B) = (0.75, 10)$ in Figure 5). The maximum numbers $X_{\max}(AR)$ and $X_{\max}(AS)$ have mostly bimodal distributions (Figures 6-7), with a single exception in the case of $X_{\max}(AR)$ for the pair $(c, \tau^{-1}_B) = (0.75, 10)$. Unlike the first peak of $X_{\max}$ which has a very moderate height, the first peak in the mass functions of $X_{\max}(AR)$ and $X_{\max}(AS)$ is notably more significant than the second one.

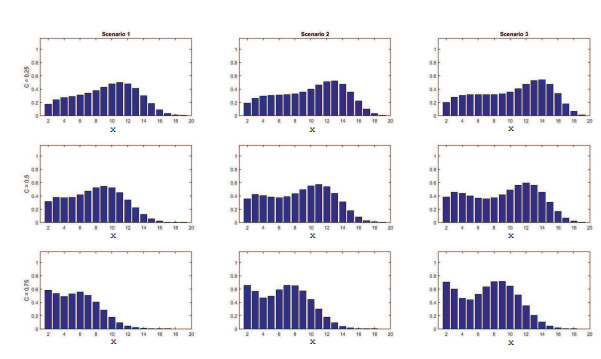
Figure 8 (respectively, Figures 9-10) illustrates the joint distribution of the random vector $(X_{\max}, T_{\max})$ (respectively, $(X_{\max}(AR), T_{\max}(AR))$ and $(X_{\max}(AS), T_{\max}(AS))$) in terms of the restricted expectations $E[T_{\max} 1\{X_{\max} = x\} | X(0) = (2, 1, 0)]$, for integers $x\in \{2, ..., N\}$ (respectively, $E[T_{\max}(AR) 1\{X_{\max}(AR) = x\} |X(0) = (2, 1, 0)]$ and $E[T_{\max}(AS) 1\{X_{\max}(AS) = x\} | X(0) = (2, 1, 0)]$, for integers $x\in \{1, ..., N-1\}$). Looking at $E[T_{\max} 1\{X_{\max} = x\} | X(0) = (2, 1, 0)]$ and $E[T_{\max}(AS) 1\{X_{\max}(AS) = x\} | X(0) = (2, 1, 0)]$ as a function of $x$, it is seen that they have a single peak at intermediate integers $x_0\in \{2, ..., N\}$ and $x_0^{AS}\in \{1, ..., N-1\}$, which increase with increasing values of $\tau^{-1}_B$ and decrease with increasing values of $c$. Then, it is observed that increasing values of $\tau^{-1}_B$ increase the maximum expectations $E[T_{\max} 1\{X_{\max} = x_0\} | X(0) = (2, 1, 0)]$ and $E[T_{\max}(AS) 1\{X_{\max}(AS) = x_0^{AS}\} | X(0) = (2, 1, 0)]$. For the AS bacterial strain, the maximum expectation $E[T_{\max}(AS) 1\{X_{\max}(AS) = x_0^{AS}\} | X(0) = (2, 1, 0)]$ is always seen to be an increasing function of $c$; with the exception of the pair $(c, \tau^{-1}_B) = (0.75, 10)$, this is also observed for $E[T_{\max} 1\{X_{\max} = x_0\} | X(0) = (2, 1, 0)]$ in our examples. For the AR bacterial strain, the behavior of $E[T_{\max}(AR) 1\{X_{\max}(AR) = x\} | X(0) = (2, 1, 0)]$ is strongly influenced by the existence of either a single peak (for smaller values of $c$) or two peaks (for moderate and higher values of $c$).

For the sake of completeness, Table 4 lists the maximum numbers $x_{\max}^*$, $x_{\max}^*(AR)$ and $x_{\max}^*(AS)$ of patients colonized by bacteria during the outbreak, and the times $t_{\max}^*$, $t_{\max}^*(AR)$ and $t_{\max}^*(AS)$ to reach these numbers in the deterministic model (Appendix A). In agreement with the stochastic results, the maximum numbers $x_{\max}^*$, $x_{\max}^*(AR)$ and $x_{\max}^*(AS)$ of colonized patients, as well as their respective times $t_{\max}^*$, $t_{\max}^*(AR)$ and $t_{\max}^*(AS)$, increase when the effectiveness of drug B decreases, for a fixed value of $c$. Identical monotone behavior as a function of $c$ is observed for $x_{\max}^*(AS)$ and $t_{\max}^*(AS)$, and their stochastic counterparts $E[X_{\max}(AS)]$ and $E[T_{\max}(AS)]$, regardless of the effectiveness of drug B. On the contrary, the dynamics of $x_{\max}^*$, $t_{\max}^*$, $x_{\max}^*(AR)$ and $t_{\max}^*(AR)$ with increasing values of $c$ do not agree with those of their stochastic counterparts. For example, the time $t_{\max}^*(AR)$ to reach the maximum number of patients simultaneously colonized by resistant bacteria decreases as a function of the fitness cost $c$ in scenarios 1-2, and it is observed to be a nonmonotone function of $c$ in scenario 3; on the contrary, $E[T_{\max}(AR)]$ behaves in the opposite direction showing to be a nonmonotone function of $c$ in scenarios 1-2 and an increasing function of $c$ in scenario 3.

5.   Conclusion

This paper focuses on two issues concerning the SIR-model with two strains analyzed by Kendall and Saunders ^[11]. The first issue relates to the derivation of the joint distribution of the random vector $(X_{\max}, T_{\max})$, which describes the maximum number of individuals simultaneously infected by the disease during an outbreak, and the time to reach this maximum number for the first time. Two specialized versions of $(X_{\max}, T_{\max})$ are studied when the interest is in type-$k$ infectives, for $k\in\{1, 2\}$, and $(X_{\max}(k), T_{\max}(k))$ is related to an outbreak of type $k$, which is said to end when no type-$k$ infectives remain. The second issue concerns the use of absorbing LD-QBD processes allowing us to formulate the maximum numbers $X_{\max}$ and $X_{\max}(k)$ as maximum levels visited by these processes before absorption, and the random times $T_{\max}$ and $T_{\max}(k)$ as suitably defined first-passage times. Since analytical formulas for the maximum level visited by an absorbing LD-QBD process before its absorption and the time to reach this maximum level are not available, we present algorithmic solutions for the mass functions of $X_{\max}$ and $X_{\max}(k)$, and the joint distributions of $(X_{\max}, T_{\max})$ and $(X_{\max}(k), T_{\max}(k))$ in terms of restricted Laplace-Stieltjes transforms and related moments.

Our approach uses matrix algebra and exploits the specific matrix structure of the underlying infinitesimal generators, from which we characterize the random length of an outbreak of the disease and the random length of an outbreak of type $k$ as continuous PH random variables, and we derive appropriate expressions for the mass function of the final epidemic size $R(\infty)$, and the number $R(T(k))$ of recovered individuals at the end of a type-$k$ outbreak. We illustrate the approach by means of applying extreme values in the two-strain SIR-model (Kendall and Saunders ^[11]) to the spread of antibiotic-sensitive and antibiotic-resistant bacterial strains in a hospital ward.

Unlike the studies presented by Cen et al. ^[27] and Lipsitch et al. ^[7] where the focus is on deterministic models, we demonstrate that Markov chain models can be helpful for understanding the transmission of antibiotic-resistant bacteria in a hospital; since the concepts of final epidemic size and peak epidemic values are widely used to describe the severity of a disease, we show how the initially susceptible patients are severely affected by the spread of the bacterial strains. More particularly, it is seen that stochastic effects, due to the random nature of infectious events in hospitals, can cause important deviations from the deterministic solution. In general, deterministic models are much easier to analyze compared to stochastic models, and parameter estimation methods are better developed in the deterministic case than in the stochastic setting; in contrast, stochastic models are commonly preferable when studying a closed community with small population size, which is the case in Section 4. We refer the reader to the survey by Britton ^[29] for a more detailed discussion on situations where a deterministic model is insufficient. For the bacterial transmission model, a remarkable advantage of the stochastic model is related to the bimodal distribution of the final epidemic size $R(\infty)$ (Figure 2) and the bimodal distribution of the maximum number $X_{\max}$ of infectives during a global outbreak (Figure 5) –and its variants for resistant and sensitive strains (Figures 3-4 and 6-7)–, which discourage the use of the deterministic values $r^*(\infty)$ and $x^*_{\max}$, and even the summary statistics $E[R(\infty)]$ and $E[X_{\max}]$ of these random variables. Other stochastic measures, such as $E[T_{\max} 1\{X_{\max} = x\} | X(0) = (2, 1, 0)]$ (Figure 8) – and its versions for resistant and sensitive strains (Figures 9-10)–, do not have any deterministic counterpart to be compared with.

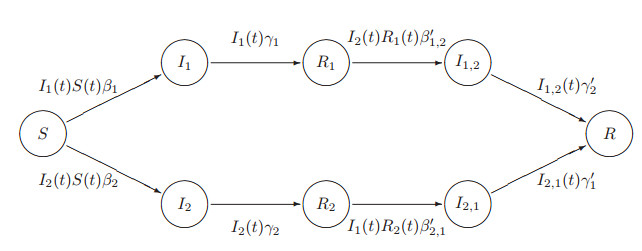
As a last remark, we note that the techniques developed here can be applied to other epidemic models with similar jumps in their dynamics. For instance, in the case of partial cross-immunity, the two-strain SIR-model is modeled through the compartmental diagram of Figure 11, where individuals are divided in susceptible ($S$), infected by the strain of type $1$ with no previous infection history ($I_1$), infected by the strain of type $2$ with no previous infection history ($I_2$), recovered by the type-$1$ strain ($R_1$), recovered by the type-$2$ strain ($R_2$), infected by the strain of type $2$ previously infected by the strain of type $1$ ($I_{1, 2}$), infected by the strain of type $1$ previously infected by the strain of type $2$ ($I_{2, 1}$), and permanently recovered and immune to both strains ($R$). Specifically, a susceptible individual becomes infected of type $k$ with rate $I_k(t)S(t)\beta_k$, for $k\in\{1, 2\}$; an infective of type $k$ with no previous infection history becomes recovered by the type-$k$ strain with rate $I_k(t)\gamma_k$, for $k\in\{1, 2\}$; an individual recovered by the type-$k$ strain becomes infected by the strain of type $k'$ with rate $I_{k'}(t)R_k(t)\beta'_{k, k'}$, for $k, k'\in\{1, 2\}$ with $k'\neq k$; and an infective of type $k$ previously infected by the strain of type $k'$ becomes permanently recovered at rate $I_{k', k}(t)\gamma'_k$, for $k, k'\in\{1, 2\}$ with $k'\neq k$. It should be straightforward to adapt the approach in Sections 3.1-3.2 to analyze extreme values by observing that the random length of a global outbreak amounts to the absorption time of the LD-QBD process $\mathcal{X}' = \{X'(t): t \geq 0\}$ with $X'(t) = (I(t), J(t), I_1(t), I_2(t), R_1(t), R_2(t), R(t))$, where $I(t) = I_1(t)+I_{2, 1}(t)+I_2(t)+I_{1, 2}(t)$ is the total number of infectives and $J(t) = I_2(t)+I_{1, 2}(t)$ is the total number of type-2 infectives, since the ultimate extinction of the disease is equivalent to the absorption of $\mathcal{X}'$ into any state $(i, j, i_1, i_2, r_1, r_2, r)$ with $i = 0$ (i.e., $i = j = i_1 = i_2 = 0$). Extreme values during an outbreak of the type-$k$ strain are then related to the absorption into any state $(j, i, i_1, i_2, r_1, r_2, r)$ with $j = 0$ (i.e., $j = i_2 = 0$) for the modified version $\mathcal{Y}' = \{Y'(t): t\geq 0\}$ with $Y'(t) = (J(t), I(t), I_1(t), I_2(t), R_1(t), R_2(t), R(t))$, in the special case $k = 2$.

6.   Acknowledgements

The authors thank two anonymous referees whose comments and suggestions led to improvements in the manuscript. They also thank Dr. Martín López-García (University of Leeds) for his help in the numerical treatment of systems of differential equations. This work is supported by the Ministry of Economy, Industry and Competitiveness (Government of Spain), Project MTM2014-58091-P.

7.   Conflict of interest

The authors declare no competing interests.

Appendix A

Kendall and Saunders ^{[11, Section 3]} generalize the deterministic general epidemic model ^[26] to a two-strain model with total cross-immunity by considering the set of equations

where $s^*(t)$ denotes the number of susceptibles and $i_k^*(t)$ is the number of infectives of type $k$ at time $t$; since the total population remains constant, the number $r^*(t)$ of removals is given by $r^*(t) = N-s^*(t)-i_1^*(t)-i_2^*(t)$. The deterministic versions of the random variables $X_{\max}$ and $T_{\max}$, as well as the final epidemic size $R(\infty)$ in Section 3.1, can be readily evaluated from these equations as the absolute maximum value $x_{\max}^*$ of the trajectory of infectives $i_1^*(t)+i_2^*(t)$ and its instant $t_{\max}^*$ of occurrence, and the number $r^*(\infty)$ of removals at the end of the outbreak. In a similar manner, for an outbreak of the type-$k$ strain with $k\in\{1, 2\}$, the deterministic counterparts of $X_{\max}(k)$, $T_{\max}(k)$ and $R(T(k))$ are given by the absolute maximum value $x_{\max}^*(k)$ of the number $i_k^*(t)$ of type-$k$ infectives and its instant $t_{\max}^*(k)$ of occurrence, and the number $r^*(t^*(k))$ of removals when an outbreak of the type-$k$ strain (with length $t^*(k)$) ends.

The above differential equations do not appear to be explicitly soluble. Therefore, under the initial conditions $i_1^*(0) = i_2^*(0) = 1$ and $s^*(0) = N-2$, they are numerically solved in Section 4 by using MATLAB algorithms for suitably defined infection rates $\beta_k$ and removal rates $\gamma_k$, for $k\in\{1, 2\}$; for convenience, the values $x^*_{\max}(1)$, $t_{\max}^*(1)$, $x^*_{\max}(2)$ and $t_{\max}^*(2)$ are denoted in Table 4 by $x^*_{\max}(AS)$, $t_{\max}^*(AS)$, $x^*_{\max}(AR)$ and $t_{\max}^*(AR)$, respectively.

Appendix B

Under the lexicographical ordering of states, sub-matrices ${\bf Q}_{i, i-1}$, ${\bf Q}_{i, i}$ and ${\bf Q}_{i, i+1}$ in Eq. (2.1) are specified as follows:

${(ⅰ)}$ For $i\in\{1, ..., N-1\}$, the sub-matrix ${\bf Q}_{i, i-1}$ has dimension $L(i)\times L(i-1)$ and has the form

and ${\bf Q}_{N, N-1}$ is given by

with

where ${\bf U}_k = ({\bf 0}_k, {\bf I}_k)$.

${(ⅱ)}$ For $i\in\{1, ..., N-1\}$, the sub-matrix ${\bf Q}_{i, i}$ is a diagonal matrix of order $L(i)$ and is specified by ${\bf Q}_{i, i} = diag({\bf Q}_{(i, 0)}^{(i, 0)}, {\bf Q}_{(i, 1)}^{(i, 1)}, ..., {\bf Q}_{(i, i)}^{(i, i)})$ with

In the case $i = N$, it is seen that ${\bf Q}_{N, N} = diag(-q_{(N, 1, 0)}, ..., -q_{(N, N-1, 0)})$.

${(ⅲ)}$ For $i\in\{1, ..., N-2\}$, the sub-matrix ${\bf Q}_{i, i+1}$ has dimension $L(i)\times L(i+1)$ and has the form

with

where the matrix ${\bf V}_k$ is given by

In the case $i = N-1$, the sub-matrix ${\bf Q}_{N-1, N}$ has the form

Appendix C

For convenience, we let $G_{\max}(x; (s, i, j))$ be the conditional probability $P(X_{\max}\leq x | (S(0), I(0), J(0)) = (s, i, j))$, which means that the probability distribution function $F_{\max}(x; (i, j, r))$ in Section 3.1 corresponds to $G_{\max}(x; ((N-i-r, i, j))$, for states $(i, j, r)\in\mathcal{S}$ and integers $x\in\{2, 3, ..., N\}$.

In the algorithm below, we use $G_{\max}(N; (s, i, j)) = 1$ and derive, starting with $x = 2$, the conditional probabilities $G_{\max}(x; (s, i, j))$, for states $(i, j, N-i-s)\in\mathcal{S}\setminus l(0)$, by iteration in the number of susceptibles. Specifically, the conditional probabilities $G_{\max}(x; (s, i, j))$, for states $(i, j, N-i-s)\in\mathcal{S}\setminus l(0)$, are characterized as the unique solution to the following system of linear equations:

${(ⅰ)}$ For $x\in\{2, ..., N-1\}$ and $(s, i, j)\in\{(s', 1, j'): s'\in\{1, ..., N-2\}, j'\in\{0, 1\}\}$,

${(ⅱ)}$ For $x\in\{2, ..., N-1\}$ and $(s, i, j)\in\{(s', x, j'): s'\in\{1, ..., N-x-1\}, j'\in\{0, ..., x\}\}\cup\{(N-x, x, j'): j'\in\{1, ..., x-1\}\}$,

${(ⅲ)}$ For $x\in\{3, ..., N-1\}$ and $(s, i, j)\in\{(s', i', j'): s'\in\{1, ..., N-x\}, i'\in\{2, ..., x-1\}, j'\in\{0, ..., i'\}\}\cup\{(s', i', j'): s'\in\{N-x+1, ..., N-3\}, i'\in\{2, ..., N-s'-1\}, j'\in\{0, ..., i'\}\}\cup\{(N-2, 2, 1)\}$,

Note that, similarly to (3.4)-(3.5), Eqs. (5.1)-(5.3) are derived by conditioning on the first transition of $\mathcal{X}$ occurring from the current state $(i, j, N-i-s)$.

Appendix D

The proof of Algorithm D.1 mostly uses our arguments in Section 3.1 and is therefore based on an iterative computation of the matrix $(-{\bf T}^*(x))^{-1}$, where the entries of ${\bf T}^*(x)$ are the infinitesimal rates for transitions between states of the class $\cup_{j = 1}^x l^*(j)$ of transient states; specifically, for integers $x\in\{1, ..., N-1\}$ the square matrix ${\bf T}^*(x)$ of order $\overline{K}(x) = 6^{-1}x(3N(N+3)-(x+1)(3N-x+4))$ has the structured form (3.2) with sub-matrices ${\bf Q}_{i, i'}$ replaced by ${\bf Q}^*_{j, j'}$. The column vector ${\bf t}^*_{0}(x)$ in Algorithm D.1 is specified by

For $x\in\{1, ..., N-1\}$, the restricted Laplace-Stieltjes transforms $\varphi^*_{(1, 2, 0)}(\theta; x)$ and related moments $E[T^n_{\max}(2) 1\{X_{\max}(2) = x\} | Y(0) = (1, 2, 0)]$ are characterized as the unique solutions to the systems of linear equations (3.6) and (3.7), respectively, where the sub-matrices ${\bf Q}^*_{j, j'}$ and column vectors ${ {{ φ}}}^*_j(\theta; x)$ and ${\bf m}_j^{*(n)}(x)$ are now playing the role of ${\bf Q}_{i, i'}$, ${ {{ φ}}}_i(\theta; x)$ and ${\bf m}_i^{(n)}(x)$ in (3.6)-(3.7); more particularly, the entries of ${ {{ φ}}}^*_j(\theta; x)$ and ${\bf m}_j^{*(n)}(x)$ are given by $\varphi^*_{(j, i, r)}(\theta; x)$ and $E[T^n_{\max}(2) 1\{X_{\max}(2) = x\} | Y(0) = (j, i, r)]$, where these restricted Laplace-Stieltjes transforms and related moments are defined –in a similar manner to $\varphi^*_{(1, 2, 0)}(\theta; x)$ and $E[T^n_{\max}(2) 1\{X_{\max}(2) = x\} | Y(0) = (1, 2, 0)]$– by assuming that $(j, i, r)$ is the current state of the LD-QBD process $\mathcal{Y}$ at an arbitrary time. In Eq. (3.6), ${\bf b}(x)$ should be appropriately replaced by a column vector ${\bf b}^*(x)$ consisting of sub-vectors ${\bf b}^*_j(x)$, for $j\in\{x, ..., N\}$, with

and ${\bf b}^*_N(x) = 0$. Then, an appeal to Algorithms D.2-D.3 with ${\bf m}^{*(0)}_j(x) = { {{ φ}}}_j(\theta; x)|_{\theta = 0}$, for $j\in\{1, ..., x-1\}$ and $x\in\{2, ..., N-1\}$, yields an iterative computation of $E[T^n_{\max}(2) | Y(0) = (1, 2, 0)] = {\bf e}_{K(1)}(N)\sum_{x = 2}^{N-1}{\bf m}_1^{*(n)}(x)$.