The Within-Host dynamics of malaria infection with immune response

1.   Introduction

Rice is a staple food in Indonesia, which is one of the largest rice producers in the world. According to BPS-Statistics Indonesia, rice production touched 54.60 million tons in 2019 ^[1]. Polished rice is the primary product of rice, of which rice bran is the main by-product, followed by rice husk and germ. Rice bran consists of 8-12 percent of the by-product from the rice milling process ^[2].

Rice bran is used mainly as animal feed in Indonesia. There are not many studies on bioactivity, especially using animal model of diseases. Several studies show the potency of rice bran as food, especially as a functional ingredient, due to its beneficial bioactive compound content. The active bioactive compounds of rice bran are γ-oryzanol, polyphenols, phytosterols, tocopherols, tocotrienols, adenosine, ferulic acid, and adenosine, which can function as antioxidants and chemopreventive agents, with properties of lowering blood pressure and regulating cholesterol synthesis ^[3,4,5,6] Further, in some pigmented rice cultivars, rice bran is the part where the pigment is concentrated. The well-known pigmented rice in Indonesia is black rice. Black rice bran has a higher total phenolic content (TPC), anthocyanins, flavonoids, and antioxidant activity than polished red and white rice bran ^[7].

Solid-state fermentation (SSF) is known to enhance the bioactive compounds of rice bran ^[8]. This method uses solid media for microbial growth. The advantages of SSF are avoidance of lipid hydrolysis, minimum water requirements, low risk of contamination, and high yield of fermentation product ^[9]. Earlier studies and our own showed that SSF, by using Rhizopus oligosporus, can increase TPC and antioxidant activity ^[10,11]. Further, our results showed that SSF with R. oligosporus offers the optimum fermentation conditions for rice bran in Inpari 30 and Cempo Ireng for 72 hours at 30 ℃ ^[11].

The non-volatile compounds in rice bran have been studied in varieties of Calrose, Dixiebelle, and Neptune ^[12,13]. 453 compounds were found, consisting of amino acids, carbohydrates, vitamins and cofactors, lipids, nucleotides, peptides, secondary metabolites, and xenobiotics. Other studies have shown that fermentation treatment affects the number and diversity of bioactive compounds of rice bran ^[14]. Based on these findings, the non-volatile compounds of fermented and non-fermented rice bran may differ between rice varieties. Research has not been carried out on the non-volatile compounds in fermented and non-fermented bran, especially for rice bran varieties in Indonesia. Therefore, the purpose of this study was to analyze and compare non-volatile compounds of fermented and non-fermented rice bran of two varieties -i.e., Inpari 30 (IPR30) and Cempo Ireng (CI)- and their blood pressure lowering activity, by using a spontaneously hypertensive animal model. The IPR30 cultivar, another Ciherang cultivar (white rice) widely consumed in Indonesia and CI black rice cultivar, a variety of local pigmented rice planted in Bogor-West Java, Indonesia, were studied in this regard.

2.   Materials and methods

2.2.   Rice bran preparation

The sample used in this study was brown rice IPR30 obtained from Indonesian Center for Rice Research, Indonesian Agency for Agricultural Research and Development, Ministry of Agriculture, Subang, West Java, Indonesia and paddy CI from the local farmer in Bogor, West Java, Indonesia. Paddy of CI was de-hulled by a Rice Machine-THU (Satake, Japan) to obtain brown rice. Two types of brown rice were polished by mini rice mill processing (Satake Grain Testing Mill, Hiroshima, Japan) as described previously ^[11]. The samples were divided into non-fermented IPR30 rice bran (IPRNF), fermented IPR30 rice bran (IPRF), non-fermented CI rice bran (CINF), and fermented CI rice bran (CIF).

2.2.   Rice bran fermentation

R. oligosporus were obtained from the Indonesian Culture Collection, Research Center for Biology, the Indonesian Institute of Science, Cibinong, Indonesia. The R. oligosporus were asseverated on potato dextrose agar media. The preparation of the culture and fermentation process followed the method used in a previous study ^[11]. The fermented and non-fermented samples were freeze-dried using a freeze-dryer (Labconco, USA) before further analysis.

2.3.   Sample extraction

Sample extraction was done as described by ^[15,16], with modifications. Samples were dissolved in distilled water with 20% (w/v). The solutions were centrifuged (5223 x g, 10 minutes, 4 ℃) and then extracted by the solid phase extraction method. For every five mL of supernatant, one ml of lidocaine (internal standard) was added, resulting in 2.0083 µM of lidocaine in the supernatant. Thereafter, six ml of solution two was inserted into the cartridge (Oasis HLB 12 mL). Samples were vacuumed to remove their water and salt content. Samples were then eluted with methanol 5% and 1.5 mL were collected for analysis. For the animal study, the water extract of fermented RB was used by an oral single dose experiment.

2.4.   Analysis of non-volatile compounds

Non-volatile compounds were analyzed using Ultra performance liquid chromatography-tandem mass spectrometry (UPLC-MS/MS), as described in ^[12] with modifications. The liquid chromatography instrument used in this study was Waters ACQUITY UPLC H-Class System with C18 column (1.8 µm, 2.1 × 100 mm) at 50 ℃, while the mass spectrometry was Xevo G2-S quadrupole time-of-flight mass spectrometry (QToF-MS/MS) with electrospray ionization spray (ESI) system. For MS, the ion positive mode was used between 70-1000 m/z. Before injection, samples were filtered with a 0.2 µm syringe filter. Five µL of the sample was injected with mobile phase (A), 0.1% formic acid in water and (B), 0.1% formic acid in methanol (0% B to 70% B for 4 minutes, 70-98% B for 0.5 minutes, 98% B for 0.9 minutes). The observed injection flow rate was 0.2 mL per minute for 23 minutes. Masslynx v4.1 was used to identify the non-volatile compounds in the sample. The non-volatile compound data were then cross-checked with MassBank, Human Metabolome Database (HMDB) and Kyoto Encyclopedia of Genes and Genomes (KEGG) data ^[13]. The relative concentration of non-volatile compounds in the sample were determined by comparing the percentage area between sample and internal standard (lidocaine), based on the concentration of internal standard. The relative concentration was then converted into ppm units.

2.5.   Animal experiment

The male SHRSP/Izumo strain (Japan SLC, Shizuoka, Japan) was used in these studies. The rats were housed in individual stainless-steel cages in a controlled atmosphere (temperature, 23 ± 2 ℃; humidity, 50 ± 10%; 12 h light-dark cycle) as per a previous study ^[4]. The Animal Research-Animal Care Committee approved the experimental plan for the present study of Tohoku University (2016AgA-024). The entire experiment was conducted following the guidelines issued by this committee and Japanese governmental legislation (2005). The water extract of fermented RB (CI and IPR30, 72 h fermentation) was used to determine the BP-lowering effect in SHRSP. The number of animals used in this study, concentration of the sample in the treated group, and control were similar to our previous study ^[11]. The blood pressure measurement was by the tail-cuff method with a BP meter as described in the previous study ^[4].

2.6.   Statistical analysis

The data are described as the mean ± SD. One way analysis of variance using SPSS version 22.0 was performed by two-way analysis (SPSS, Inc., Chicago, IL, USA) followed by Duncan's multiple range test for blood pressure study. The categorization of non-volatile compounds based on their relative concentration was analyzed by principal component analysis (PCA) with XLSTAT 2019.

3.   Results and discussion

3.1.   Non-volatile compounds of rice bran

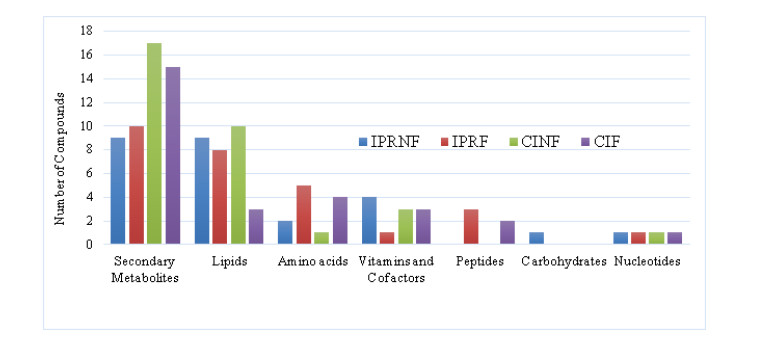
The non-volatile compounds of fermented and non-fermented rice bran of Inpari 30 and Cempo Ireng are presented in Supplementary Table 1. These were classified into 36 secondary metabolites, 16 lipids, 8 amino acids, 7 vitamins and cofactors, 3 peptides, one carbohydrate, and one nucleotide (Figure 1). Fermentation of Inpari 30 and Cempo Ireng rice bran produced new compounds that were not found in the non-fermented samples.

Figure 1.  Non-volatile compounds of rice bran. Inpari 30 non-fermented (IPRNF); Inpari 30 fermented (IPRF); Cempo Ireng non-fermented (CINF); and Cempo Ireng fermented (CIF).

DownLoad: Full-Size Img PowerPoint

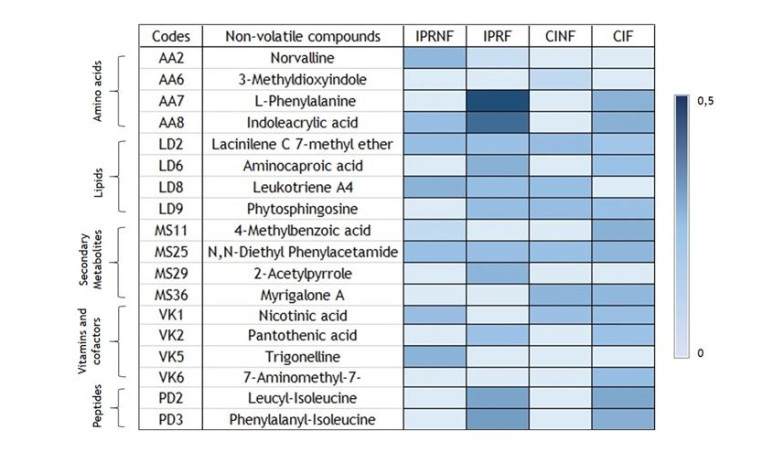
The highest concentration of secondary metabolites found in IPRNF consisted of n, n-diethyl phenylacetamide (MS25), while in IPRF rice bran, the contents were dominated by 2-acetylpyrrole (MS29) and momilactone B (MS7). A study on n, n-diethyl phenylacetamide has shown that it can be used as an insect repellent ^[17] and 2-acetylpyrrole has hepatoprotective properties ^[18]. Several studies have shown momilactone B exhibiting inhibitory activities on α-amylase and α-glucosidase, as well as anti-cancer activities by increasing apoptosis in cancer cells ^[19,20]. In CINF rice bran, the dominant secondary metabolites were myrigalone A (MS36), kojic acid (MS9) and 4-methylbenzoic acid (MS11). Myrigalone A has been known to show antibacterial properties and kojic acid is a chelating agent produced during aerobic fungal fermentation ^[21].

The most abundant compounds from the lipid in IPRNF and IPRF were leukotriene A4 (LD8) and aminocaproic acid (LD6). The dominant lipid compounds in CINF and CIF were lacinilene C 7-methyl ether (LD2) and phytosphingosine (LD9) respectively. Lacinilene C 7-methyl ether is known to have antibacterial properties ^[22]. Phytosphingosine has shown anti-inflammatory and antibacterial properties in skin disorders, besides playing a role in transcription activation in peroxisome proliferator-activated receptor ^[23,24].

Amino acids with the highest concentration found in IPRNF and IPRF were norvaline (AA2) and l-phenylalanine (AA7) respectively. Norvaline is a byproduct of branched-chain amino acid synthesis, which can also act as arginase inhibitor ^[25]. L-phenylalanine is involved in neurotransmitters, hormones, and skin pigment synthesis in humans ^[26]. The highest concentration of amino acids in CINF and CIF were 3-methyldioxyindole (AA6) and indoleacrylic acid (AA8) respectively. Indoleacrylic acid has been known to be produced during tryptophan degradation.

The dominant compounds found in the vitamins and cofactors group in IPRNF and IPRF were trigonelline (VK5) and pantothenic acid (VK2) respectively. Trigonelline is found only in IPRNF rice bran and is involved in treating diabetes by lowering the blood glucose level, increasing insulin sensitivity, and decreasing lipid peroxidation ^[27]. Pantothenic acid is synthesized by R. oligosporus from β-alanine and pantoic acid ^[28]. The dominant compound in the vitamins and cofactors in CINF and CIF were nicotinic acid (VK1) and 7-aminomethyl-7-carbaguanine (VK6), respectively. Nicotinic acid prevents atherosclerosis by increasing high-density lipoprotein, and decreasing triglyceride level and oxidative stress ^[29].

Non-volatile compounds from the peptide group were detected only in the fermented samples. The most abundant peptide found in IPRF and CIF were phenylalanyl-isoleucine (PD3) and leucyl-isoleucine (PD2), respectively. According to an earlier study, Leucyl-isoleucine increases monocytes and platelet level in rats and stimulates AMPK phosphorylation ^[30,31].

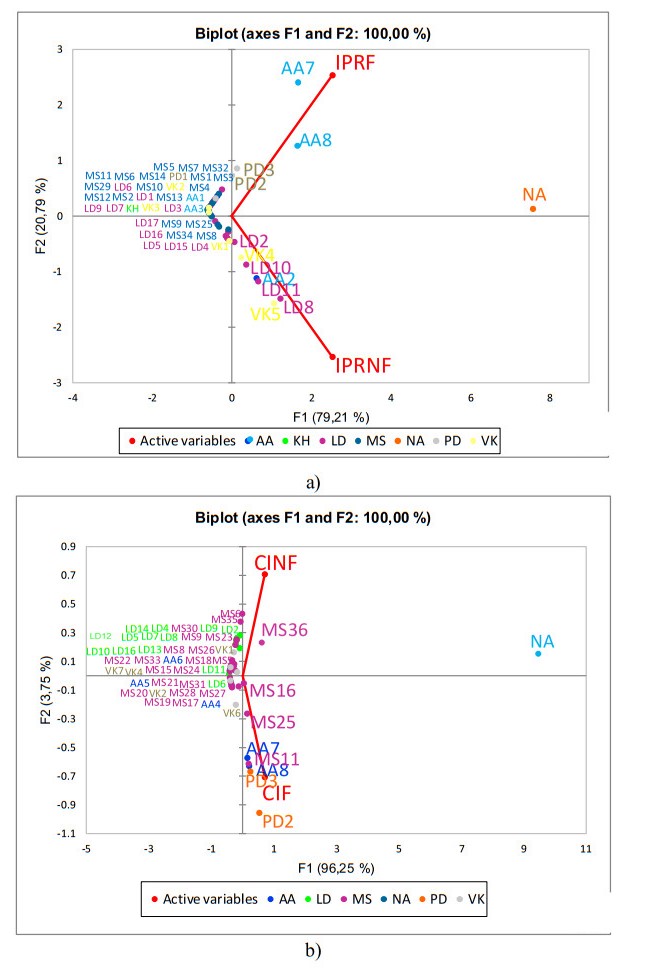
3.2.   Principle component analysis

Principal component analysis (PCA) was applied to compare the differences of quantum in non-volatile compounds among the samples. The PCA of non-volatile compounds is shown in Figure 2. Non-fermented rice bran samples (IPRNF and CINF) were located in a quadrant different from fermented rice bran (IPRF and CIF), indicating that fermentation influenced non-volatile compound production. Adenosine (NA) generally was found the most in non-volatile compounds across all the samples. In the fermented sample of Inpari 30, the level of n, n-diethyl phenylacetamide (MS25), indoleacrylic acid (AA8), and l-phenylalanine (AA7) were higher, compared to non-fermented rice bran. Other major non-volatile compounds found in IPRNF samples were leukotriene A4 (LD8) and trigonelline (VK5).

On the other hand, fermentation of the Cempo Ireng variety showed an increase in quercetin (MS15), isorhamnetin 7-glucoside (MS16), isorhamnetin (MS17), and nicotinic acid (VK1) levels. In Cempo Ireng samples, the non-volatile compounds with the highest concentration after adenosine were different. In CINF, it was myrigalone A (MS36), while CIF leucyl-isoleucine (PD2) and phenylalanyl-isoleucine (PD3) showed similar concentrations. These compounds are likely to have originated from arachidonic acid, nicotinic acid and nicotinamide, phenylalanine, tryptophan, and dipeptide metabolism. The major non-volatile compounds from each classification from PCA analysis are summarized in Figure 3. The list of non-volatile compounds and its statistical analyses shown in Supplementary Table 1 (Supplementary data).

Adenosine is a compound necessary for production of energy within the body, and is created from purine metabolism. As a phytochemical found in rice bran, adenosine has the effect of lowering blood pressure, helps to treat hyperlipidemia, increases insulin activity, and preventing hypertension in the stroke-prone spontaneously hypertensive rat (SHRSP) ^[5]. In humans, adenosine has neuromodulator and neuroprotective functions, reduces epilepsy, and regulates the sleep cycle ^[32,33,34].

Several studies of these compounds have shown them to have beneficial effects for the body, which includes lowering blood pressure, improving the immune and digestive systems, as well as having neuromodulator, neuroprotective, chemo preventive and antidiabetic properties. Further, other studies have also found that these bioactive compounds play a part in preventing gastric ulcer and improving hormone and melanin synthesis ^{[26,27,30,32]}.

Figure 2.  PCA plot non-volatile compounds of a) Inpari 30 (IPR) and b) Cempo Ireng (CI) (Fermented, F; and Non-Fermented, NF). The list of non-volatile compounds and its codes can be seen in Supplementary Table 1.

DownLoad: Full-Size Img PowerPoint

Figure 3.  Summary of major non-volatile compounds (ppm). Inpari 30 non-fermented (IPRNF); Inpari 30 fermented (IPRF); Cempo Ireng non-fermented (CINF); and Cempo Ireng fermented (CIF).

DownLoad: Full-Size Img PowerPoint

3.3.   Proposed metabolic pathway of non-volatile compounds of rice bran

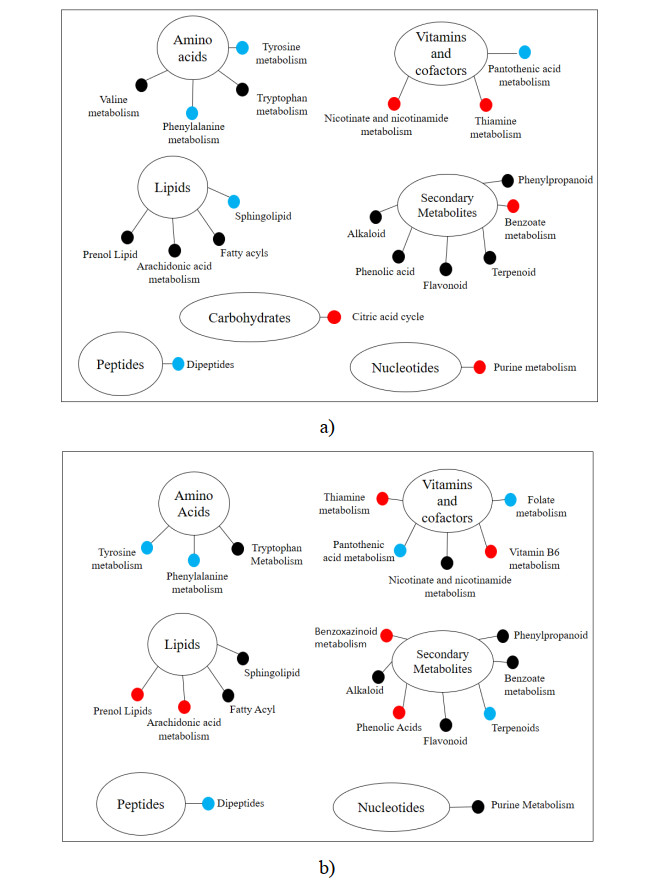
The proposed metabolic pathways found in rice bran are shown in Figure 4. Previous studies shown that rice bran has contained non-volatile compounds (12-14). Our study carried out non-volatile compound of fermented and non-fermented rice bran varieties in Indonesia. Pathways related to the compounds in the fermented and non-fermented Inpari 30 rice bran were the metabolism of valine and the citric acid cycle, respectively. Folate metabolism was found in fermented Cempo Ireng rice bran, while pentatonic acid, vitamin B6, and benzoxazinoid metabolism were found in non-fermented Cempo Ireng rice bran. Fermented versions of both fermented Inpari 30 and Cempo Ireng rice bran produced compounds from the metabolism of tyrosine, phenylalanine, pantothenic acid and dipeptide that was not detected in the non-fermented samples.

Figure 4.  Proposed metabolic pathways of non-volatile compound of rice bran (a) Inpari 30 and (b) Cempo Ireng. (blue dots) fermented rice bran, (red dots) non-fermented rice bran, and (black dots) fermented and non-fermented rice bran.

DownLoad: Full-Size Img PowerPoint

Non-volatile compounds in fermented Inpari 30 and Cempo Ireng rice brans were identified as metabolic pathways from tyrosine, phenylalanine, pantothenic acid, folic acid, dipeptide, terpenoid, and sphingolipid. The presence of dipeptide and amino acid compounds indicated that the samples were attributed to rice bran protein degradation by R. oligosporus-synthesized protease ^[35]. Similarly, metabolites of pantothenic and folic acid were also utilized by fungi, as they are components necessary for fungal metabolic activities ^[36]. Comparatively, compounds from sphingolipid metabolism are commonly found in fungal plasma membrane ^[37]. Fungi sphingolipids known to be involved in hyphal morphogenesis are produced during sphingolipid metabolism with serine and palmitoyl-CoA as its precursor ^[38,39], similar to the terpenoid found in fermented rice bran produced by the fungal mevalonate pathway ^[40].

3.4.   Effect of fermented rice bran on blood pressure

This study also investigated whether fermented RB showed any blood pressure-lowering effects after administration of a single oral dose (40 mg/kg body weight) (Table 1). Twelve-week-old male SHRSP with a systolic blood pressure (sBP) of approximately 170 mmHg, were used in this study. The result showed that there was similar sBP of the control group before and after administration. The sBP showed a significant decrease after 6h administration of IPRF (p < 0.05), compared to the control group. A blood pressure lowering activity was also found as sBP was decreasing from 2 h after administration until the end of the study. This study was consistent with the previous study by using Inpari 30 fermented RB ^[11]. Further, this study also showed evidence of adenosine as one of the identified bioactive compounds in rice bran ^[5].

Table 1.  Time course of systolic blood pressure (mm/Hg) of fermented rice bran^a.

Group	0 h	2 h	4 h	6 h
Control	172.3 ± 13.1	172.0 ± 8.1	161.3 ± 6.5	168.0 ± 3.0
CIF	176.8 ± 9.1	175.3 ± 2.9	165.3 ± 13.3	166.8 ± 8.5
Change b (%)	-	+1.9	+2.4	−0.7
IPRF	171.3 ± 5.0	152.3 ± 14.3	142.0 ± 12.4	141.5 ± 12.2*
Change b (%)	-	−12.9	−13.6	−18.7
Note: a Values are given as means ± SD, n = 4. *A significantly different (p < 0.05) versus Control after statistical analysis by one-way analysis of variance using SPSS version 22 software (SPSS, Inc., Chicago, IL, USA) followed by Duncan's multiple range test.

---

 | Show Table

DownLoad: CSV

This study strengthened the proposition that IPRF is a good source of functional ingredient that can be effective in decreasing hypertension in an animal model of metabolic syndrome-related diseases. Future studies are required to specify the IPRF mechanism of blood pressure-lowering activity and other functionalities in relation to metabolic diseases.

4.   Conclusions

Different rice varieties and fermentation processes influence the concentration and types of non-volatile compounds in rice bran. Adenosine was found to have the greatest concentration of non-volatile compound in rice bran. Fermentation of rice bran samples from IPR30 and CI varieties generated compounds from tyrosine, phenylalanine, pentatonic acid, dipeptide, sphingolipid and terpenoid metabolism, which were not found in the non-fermented rice bran. Fermentation of rice bran can produce and enhance non-volatile compounds as anti-hypertensive effect in an animal model of hypertension. Further, this study found adenosine to be a useful marker for non-volatile compounds in rice bran.

Acknowledgments

We would like to thank to the Ministry Research and Technology/BRIN RI for research funding. The partial of the research was supported by a grant from the collaboration research of JSPS and DIKTI RI.

Conflict of interest

All authors declare no conflict of interest.

Table Supplementary 1.  Non-volatile compounds detected in rice bran of Inpari 30 and Cempo Ireng by using UPLC-MS/MS.

Compounds	Codes	HMDB ID	Relative Concentrations (ppm)				Effects	References
			Inpari 30		Cempo Ireng
			Non-fermented	Fermented	Non-fermented	Fermented
(Amino acids)
Meta-tyrosine	AA1	0059720	ND	0.0266*	ND	ND	Immunoprotective	[41]
							Reduces metastasis	[42]
Norvaline	AA2	0013716	0.0253*	0.0008*	ND	ND	Arginase inhibitor	[31]
N-Acetyltryptophan	AA3	0013713	ND	0.0039*	ND	ND	Antioxidant	[43]
1H-Imidazole-1-acetic acid	AA4	0029736	ND	ND	ND	0.0033*	-	-
L-DOPA	AA5	0000181	ND	ND	ND	0.0050*	Treatment of Parkinson Dissease (by increasing dopamine levels in brain)	[44]
3-Methyldioxyindole	AA6	0004186	ND	ND	0.0011 ± 0.0003	ND	-	-
L-Phenylalanine	AA7	0000159	ND	0.2413 ± 0.2051a	ND	0.0360 ± 0.0080b	Neurotransmitter synthesis, hormones and pigments synthesis	[26]
Indoleacrylic acid	AA8	0000734	0.0115*a	0.1806 ± 0.1412b	ND	0.0395 ± 0.0011a	Improves the instentines functions	[45]
(Carbohydrates)
Succinic acid	KH	0000254	0.0002*	ND	ND	ND	Antioxidant, Imrpove the immune and nervous functions	[46]
(Lipids)
Cincassiol B	LD1	0036855	ND	0, 0208*	ND	ND	-	-
Lacinilene C 7-methyl ether	LD2	0036456	0.0129 ± 0.0015	0.0058*	0.0134*	0.0023*	Antimicrobial	[22]
Valdiic acid	LD3	0040980	ND	0.0088 ± 0.0108	ND	ND	-	-
Prostaglandin C1(1-)	LD4	0062756	0.0102 ± 0.0029	ND	0.0090 ± 0.0017	ND	-	-
10-Oxo-11-octadecen-13-olide	LD5	0029786	0.0041*	ND	0.0109*	ND	-	-
Aminocaproic acid	LD6	0001901	ND	0.0390*	ND	0.0037*	Antifibrinolytic	[47]
L-Octanoylcarnitine	LD7	0000791	ND	0.0180*	0.0091 ± 0.0052	ND	-	-
Leukotriene A4	LD8	0029016	0.0352 ± 0.0288	0.0131 ± 0.0063	0.0110*	ND	The parent molecule for the biosynthesis of all leukotrienes	[48]
Phytosphingosine	LD9	0004610	ND	0.0126*b	0.0114 ± 0.0031a	0.0049 ± 0.0042b	● Anti-inlammatory and antibacterial in skin disorders	[31]
							● Activates the transcription activity on PPAR	[23]
(Ent-2alpha, 3beta, 15beta, 16beta)-15, 16-Epoxy-2, 3-kauranediol	LD10	0038688	0.0201 ± 0.0099b	ND	0.0019*a	ND	-	-
Dehydroabietic acid	LD11	0031127	0.0263*	ND	ND	ND	● Anti-inflammatory in obese people	[49]
							● Activates the SIRT1 enzymes	[50]
13, 14-Dihydro-15-keto-PGE2	LD12	0002776	ND	ND	0.0010*	ND	Increases the growth of pancreatic celss	[51]
3-hydroxyundecanoyl carnitine	LD13	0061637	ND	ND	0.0102 ± 0.0031	ND	-	-
Leukotriene C4	LD14	0001198	0.0095*	ND	ND	ND	Lipid mediator for inflammation	[52]
5-Hexyltetrahydro-2-furanoctanoic acid	LD15	0029018	0.0105*	ND	0.0021*	ND	-	-
(Z)-13-Oxo-9-octadecenoic acid	LD16	0029796	0.0094*	0.0072*	ND	ND	-	-
(Nucleotides)
Adenosine	NA	0000050	0.0838 ± 0.1053	0.4323 ± 0.1236	0.2119 ± 0.0142	0.3007 ± 0.1602	● Neuromodulator	[34]
							● Neuroprotective	[33]
							● Reduces epilepsy	[32]
							● Regulates the sleep cycle	[53]
							● Lowering blood pressure	[5]
(Secondary Metabolites)
Cohumulone	MS1	0033981	ND	0.0052*	ND	ND	Aldo keto reductase inhibitors	[54]
3-O-Methylmethyldopa	MS2	0142154	ND	0.0022 ± 0.0005	ND	ND	-	-
2, 6-Dimethoxy-4-propylphenol	MS3	0036226	ND	0.0007 ± 0.0001	ND	ND	-	-
Alpha-curcumene	MS4	0059878	ND	0.0017±0.0004	ND	ND	● Antimicrobial	[55]
							● Induced apoptosis	[56]
Cuscohygrine	MS5	0030290	ND	0.0033*	0.0051*	0.0028*	-	-
3-Tert-butyl-4-hydroxyanisole	MS6	0059925	ND	0.0015*	0.0184*	ND	The building blocks of butylated hydroxyanisole (BHA)	[57]
Momilactone B	MS7	0036749	ND	0.0153*	ND	ND	● α-Amylase and α-Glucosidase inhibitors	[20]
							● Cancer chemopreventive	[19]
2-Indolecarboxylic acid	MS8	0002285	0.0024*	ND	0.0023*	ND	Antioxidant	[58]
Kojic acid	MS9	0032923	0.0061 ± 0.0016	ND	0.0103 ± 0.0010	ND	● Tyrosinase inhibitors	[59]
							● Immunomodulator	[9]
L-1, 2, 3, 4-Tetrahydro-beta-carboline-3-carboxylic acid	MS10	0035665	0.0008*	ND	ND	ND	-	-
4-Methylbenzoic acid	MS11	0029635	0.0010*a	ND	ND	0.0385 ± 0.0103b	-	-
2-Methylhippuric acid	MS12	0011723	0.0006*	ND	ND	ND	-	-
Momilactone A	MS13	0036748	0.0020*	ND	ND	ND	● α-Amylase and α-Glucosidase inhibitors	[20]
Coumarin	MS14	0001218	0.0009*	ND	ND	ND	● Antimicrobial	[60)
							● Acetylcholinesterase (AChE) inhibitor	[61]
Quercetin	MS15	0005794	ND	ND	0.0050 ± 0.0031	0.0057 ± 0.0028	● Antioxidant	[62]
							● Decreases activation of dendytic celss for the treatment of inflammation, autoimmunity and transplantation	[61]
							● Antiviral activity against dengue fever	[63]
							● Lowering blood pressure in people with hypertension	[64]
							● Reduces symptoms of non-alcoholic fatty liver dissease	[65]
Isorhamnetin 7-glucoside	MS16	0029479	ND	ND	0.0089 ± 0.0050	0.0165 ± 0.0009	Antioxidant	[66]
Isorhamnetin	MS17	0002655	ND	ND	0.0048*	0.0121*	Treats cerebral vascular complications associated with diabetes	[67]
2-Hydroxy-2-phenylpropanoic acid	MS18	0142137	ND	ND	0.0045 ± 0.0007a	0.0029 ± 0.0013b	-	-
2-Phenylpropionaldehyde dimethyl acetal	MS19	0032468	ND	ND	ND	0.0055 ± 0.0022	-	-
Naringenin	MS20	0002670	ND	ND	ND	0.0037*	● Hepatoprotector	[68]
							● Reduces TNF- α production	[69]
							● Anti-hyperglycemia	[70]
							● Cardioprotective	[71]
							● Antiviral activity against dengue fever	[72]
							● Inhibits the proliferation and migration of prostate cancer cells	[73]
Phenprocoumon	MS21	0015081	ND	ND	ND	0.0058*	● Anticoagulant	[74]
Isovanillic acid	MS22	0060003	ND	ND	0.0042 ± 0.0011	ND	● Antibacterial	[75]
							● Antioxidant	[76]
							Antimicrobial	[60]
2, 6-Dimethoxybenzoic acid	MS23	0029273	ND	ND	0.0106*	ND	-	-
Benzoic acid	MS24	0001870	ND	ND	0.0009 ± 0.0003	ND	Inhibits the growth of resistant bacteria	[77]
N, N-diethyl phenylacetamide	MS25	0032635	0.0090*	0.0096*	0.0066*	0.0263*	Mosquitos repellent	[17]
Oryzalide B	MS27	0037592	ND	ND	ND	0.0053 ± 0.0032	Antibacterial	[78]
Acetylvalerenolic acid	MS28	0035687	ND	ND	ND	0.0045*	-	-
	MS29	0035882	ND	0.0309	ND	ND	Hepatoprotector	[18]
Dimboa-glc	MS30	0029710	ND	ND	0.0089 ± 0.0056	ND	-	-
2-Decylfuran	MS31	0032215	ND	ND	ND	0.0015	-	-
Piperenol A triacetate	MS32	0041535	ND	0.0129*	ND	ND	-	-
Ginsenoyne G	MS33	0039589	ND	ND	0.0025	ND	-	-
Acetylpterosin C	MS34	0030764	0.0053*	ND	ND	ND	-	-
1, 3, 11-Tridecatriene-5, 7, 9-triyne	MS35	0034294	ND	ND	0.0160	ND	-	-
Myrigalone A	MS36	0037245	ND	ND	0.0278*	0.0256*	Antibacterial	[79]
(Vitamins dan cofactors)
Nicotinic acid	VK1	0001488	0.0114 ± 0.0007	ND	0.0060 ± 0.0025	0.0076 ± 0.0009	Increases HDL cholesterol and lowers triglycerides for the treatment of atherosclerosis	[29]
Pantothenic acid	VK2	0000210	ND	ND	ND	0.0028 ± 0.0010	Substrates for the synthesis of coenzyme A and ACP (acyl carrier protein)	[80]
2-Hydroxypyridine	VK3	0013751	0.0008*	ND	ND	ND	-	-
4-Methyl-5-thiazoleethanol	VK4	-	0.0175 ± 0.0014	ND	0.0066 ± 0.0021	ND	-	-
Trigonelline	VK5	0000875	0.0344 ± 0.0247	ND	ND	ND	● Increases cell sensitivity to anticancer and apoptotic drugs	[81]
							● Prevents gastric ulcer induced by indomethacin	[82]
							● Lowering blood sugar and lipid as well as increasing insulin sensitivity for diabetes
							● Inhibits neurons loss in hypocampus	[83]
7-Aminomethyl-7-carbaguanine	VK6	0011690	ND	ND	ND	0.0132*	-	-
Pyridoxal	VK7	0001545	ND	ND	0.0066 ± 0.0021	ND	● Cofactors in various amino acids metabolism	[84]
							● Maintains the nervous systems in infants	[85]
(Peptides)
Leucyl-valine	PD1	0028942	ND	0.0222 ± 0.0162	ND	ND	Increases the expression of glutathione peroxidase, antioxidants and cell protection agents	[86]
Leucyl-isoleucine	PD2	0028932	ND	0.0653 ± 0.0436	ND	0.0596 ± 0.0263	Increases the stimulation of AMPK phosphorylation (5'-AMP protein kinase), monocytes, and platelets	[30]
Note: The presentation of the relative value data for the compounds comes from the calculation of the average relative area of the compound from 3 replications ± deviation standard; ND = Not Detected; * = compound obtained only in 1 replication; Numbers on the same line with different letters indicate significant differences (p < 0.05).

---

 | Show Table

DownLoad: CSV