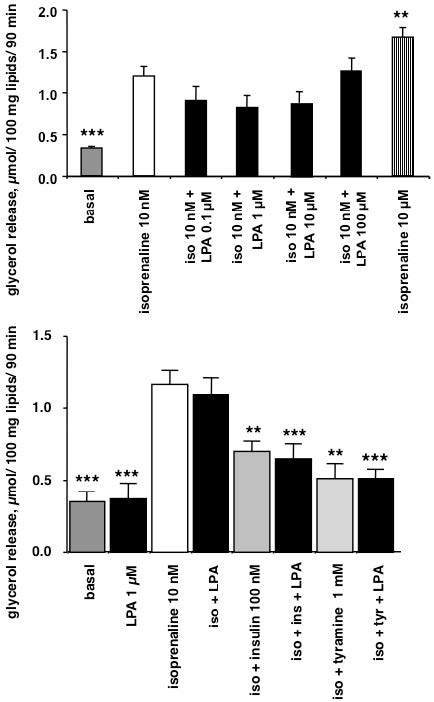
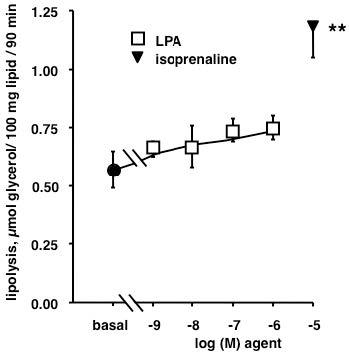
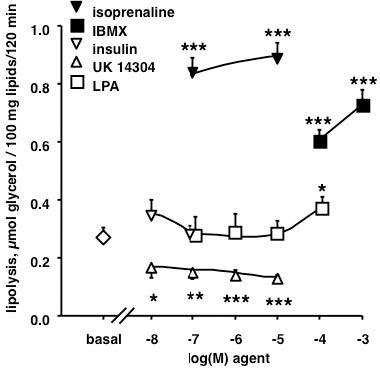
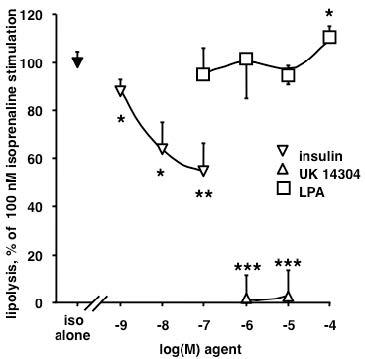
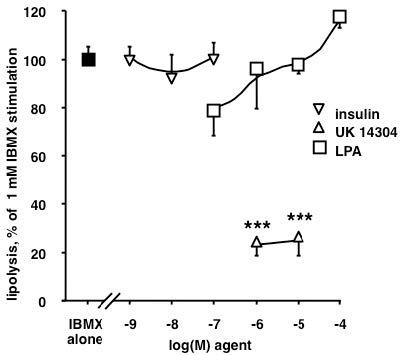
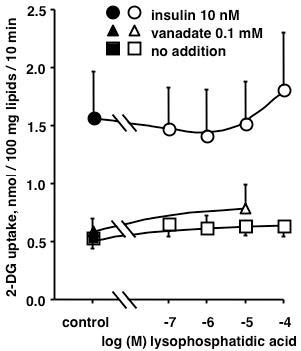
Lysophosphatidic acid (LPA) is a bioactive phospholipid that activates cell proliferation, differentiation and migration via the activation of its membrane-bound receptors (LPAR 1 to 6) expressed in various tissues and organs. Adipose tissue produces LPA, which, in turn, increases preadipocyte proliferation, mainly through the stimulation of LPA1R. However, while LPA plasma levels increase with obesity, only few studies have investigated the acute autocrine properties of LPA on mature adipocytes. We therefore assessed the lipolytic and antilipolytic effects of LPA on human adipocytes. Here, we show that, in human subcutaneous adipocytes, LPA (0.1–10 µM) did not mimic insulin effects in human adipocytes, i.e. lipolysis inhibition and glucose uptake activation. By contrast, supramicromolar doses of the phospholipid slightly activated lipolysis, and the effect of 100 µM LPA was additive to the β-adrenergic stimulation of lipolysis by isoprenaline. Moreover, LPA did not alter the activity of primary amine oxidase, an enzyme highly expressed in human adipose cells. Our observations indicate that, although rapid and direct, LPA impact on triglyceride storage in mature adipocytes is less pronounced than its ability to stimulate proliferation in preadipocytes.
1.
Introduction
Deep learning has significantly succeeded in image recognition, image segmentation and target detection. However, deep learning models often require a large amount of labeled data to train, and labeling the data will take more time. Some scholars propose zero-shot learning. Zero-shot learning uses the model obtained from the seen classes to infer the unseen class of samples, which can largely reduce the labeling of samples [1,2]. Zero-shot learning mimics the process of human cognition of new things. For example, a person knows an animal, like a horse, through pictures and their linguistic descriptions; when knowing about the linguistic description of zebras, zebras look like horses and have black and white stripes on its body, then the person can still recognize zebras by this linguistic description when seeing zebras even though he or she has never seen a zebra [3]. In zero-shot learning, semantic features are needed in addition to using sample features. Semantic features are linguistic descriptions of the samples, such as the color, size and other characteristics. Word vectors extracted by Word2Vec [4] are usually used as semantic features. In zero-shot learning, the model is trained by the seen class samples with semantic features to find the relationship between semantic features and the seen class samples, and then transfers the model to unseen class samples to infer the categories of the unseen class samples.
There are two categories of zero-shot learning: generalized zero-shot learning and conventional zero-shot learning. The test set contains only the unseen class samples for conventional zero-shot learning. While for generalized zero-shot learning, the test set contains not only the unseen class samples but also the seen class samples. In zero-shot learning, there are many approaches devoted to finding the relationship between the training set samples and the training set semantic features, such as mapping the training set samples to the semantic feature space, mapping the semantic features to the sample space [5], mapping the semantic features and samples to the common space [6,7] and mapping the semantic features and samples to each other's space [8]. However, the training set contains only the seen class samples, and the classes in the training set are not the same as those in the unseen class, which can lead to the inaccurate classification of the unseen class samples when the classification models are used in the test set.
To address these problems, some scholars use generative models, such as Variational Autoencoder (VAE) [9] and Generative Adversarial Network (GAN) [10], to generate the unseen class pseudo samples, and input them to the classifier for training, which can alleviate the problem of inaccurate classification of samples in the unseen classes. It has been proposed in the literature [11,12] that the use of VAE and GAN leads to the problems of posterior collapse and training instability, and the use of Wasserstein Auto-Encoder (WAE) and Wasserstein Generative Adversarial Network (WGAN) to generate pseudo samples can alleviate this problem. However, the unseen class samples generated by these methods are easily biased to the features of the seen class samples, leading to inaccurate classification results when classifying the real unseen class samples. To address these problems, we propose the following methods:
1) Different from the above generation models, we use autoencoder to generate the unseen class samples. To make the sample features in the latent space more distinguishable and representative, a classifier is used for the sample features in the latent space.
2) In order to reduce the unseen class pseudo sample features that are biased to the seen class sample features, we propose new sample features and use them together with unseen class semantic features for cross-reconstruction loss function.
3) The proposed method is validated for three datasets, AWA1, AWA2 and aPY and have good results.
The structure of this paper is organized as follows. First, we thoroughly review the related works in Section 2. The proposed method is illustrated in Section 3. In Section 4, we discuss the experiments, and we conclude the paper in Section 5.
2.
Related works
For zero-shot learning, embedding-based zero-shot learning is a common approach. However, embedding-based zero-shot learning can produce domain shift problems and misclassification in unseen class samples [13].
There are three solutions to alleviate the unseen class samples that are easily misclassified into the seen classes in zero-shot learning: calibrated stacking, generative models and detection of the unseen class samples. Calibrated stacking [14] added a calibrated term to the classifier so that the score of the seen class is reduced during classification, and the score of the unseen class samples can be increased. The calibrated stacking equation is as follows:
where $ \gamma $ is the calibrated factor and the indicator function. $ \mathbb{I}[\cdot ] $ indicates whether $ c $ belongs to a seen class, if $ c $ is a seen class, the value of the indicator function is 1, otherwise the value of the indicator function is 0. The classifier of APN [15] used class embedding and added calibrated stacking in the classifier to alleviate misclassification of the unseen class samples.
The method of generative models is to use generative models to generate pseudo samples substitute real unseen class samples [16]. The training set and pseudo samples are used in training the classifier, so that the unseen class samples can avoid bias to the seen classes. Multi-modal Feature Fusion algorithm (MFF) [17] used visual principal component features to compensate for the lack of descriptive information using only semantic features, and then combined GAN and VAE to generate high-quality pseudo-samples. Cross- and Distribution Aligned VAE (CADA-VAE) [18] was the VAE method. The latent space distributional alignment and cross-alignment were used to ensure the alignment between the two different modalities of sample features and semantic features. To make the generated samples close to the real samples, Over-Complete Distribution using Conditional Variational Autoencoder (OCD-CVAE) [19] used over-complete distribution to generate pseudo samples. Chen et al. [12] proposed to use WAE to generate pseudo samples and used an aggregated posterior distribution in the latent space to align the manifold structure of the sample features and the semantic features. f-CLSWGAN [20] used WGAN to generate pseudo samples and used a classifier to make the generated pseudo samples more discriminative. Based on f-CLSWGAN, Adaptive Bias-Aware GAN (ABA-GAN) [21] proposed adaptive adversarial loss and domain loss functions to make the generated pseudo samples more meaningful and to distinguish the seen classes from the unseen classes. Li et al. [11] used WGAN to generate pseudo samples and used multimodal cyclic loss function and bi-directional autoencoder. In response to the fact that GAN is not easy to train, and the pseudo samples generated by VAE are of low quality, Dual VAEGAN [22] used a combination of GAN and VAE.
Detection of samples of the unseen class. This method first distinguishes whether the samples belong to the seen classes or the unseen classes and then classifies the samples into specific class. GatingAE [3] first used the latent space and the cross-reconstruction space to detect samples belonging to the unseen class, and then used a linear classifier to classify the samples in the seen classes and a nearest neighbor classifier for the samples belonging to the unseen classes. Chen et al. [23] proposed determining whether a sample belongs to the seen class or the unseen class by calculating the cosine similarity between the latent space features of the samples and the mean value of each class. However, the models in these methods are obtained by training the samples from the seen classes; when migrating to the samples from the unseen classes, the classification results of the samples from the unseen classes are still biased to the seen classes.
Cao et al. [24] achieved recognition of zero shot traffic signs using autoencoder. Different from the literature [24], we use autoencoder to generate the unseen samples to alleviate the misclassification of the unseen class samples. To prevent the generated unseen class samples biased towards the features of seen class samples and improve the classification accuracy of the unseen class samples, we add the information of both unseen class semantic features and the proposed sample features.
3.
The proposed method
3.1. Definition of zero-shot classification
In zero-shot learning, the training set can be denoted as $ S = \{{X}_{S}, {A}_{S}, {Y}_{S}\} $, and the unseen class can be denoted as $ U = \{{X}_{U}, {A}_{U}, {Y}_{U}\} $, where $ X $ denotes sample features, $ A $ denotes semantic features and $ Y $ denotes labels. For conventional zero-shot learning, the class of $ {X}_{U} $ is predicted by the classifier: $ {X}_{U}\to {Y}_{U} $; for generalized zero-shot learning, the class of $ X $ is predicted by the classifier: $ X\to {Y}_{S}\cup {Y}_{U} $.
3.2. Zero-shot learning via visual-semantic aligned autoencoder
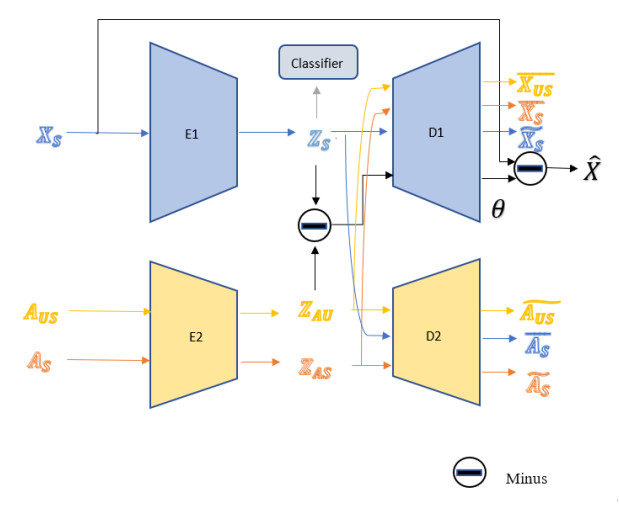
In this study, we use autoencoder to generate the pseudo samples of unseen classes, and the model is shown in Figure 1. In the Figure 1, E1 and E2 represent the encoder, D1 and D2 represent the decoder. The sample features and semantic features are encoded to obtain the same dimensional latent space features.
According to the autoencoder, for the training set, the generated sample features $ \widetilde {{X}_{S}} $ and the semantic features of the seen classes $ \widetilde {{A}_{S}} $ need to approximate the input features $ {X}_{S} $ and $ {A}_{S} $.Assuming that there are $ m $ samples, the reconstruction loss function can be written as:
We use the lowercase $ {x}_{si} $, $ \widetilde {{x}_{si}} $, $ {a}_{si} $ and $ {a}_{si} $ to denote one sample feature in $ {X}_{S} $, one generate sample feature in $ \widetilde {{X}_{S}} $, one semantic feature in $ {A}_{S} $ and one generated semantic feature in $ \widetilde {{A}_{S}} $ respectively. We want these two modality features to be aligned in the latent space. We use $ {Z}_{S} $ to represent the sample features of the latent space and $ {Z}_{AS} $ to represent the seen class semantic features of the latent space.
In Eq (2), we use the lowercase $ {z}_{Si} $ to denote one sample feature in $ {Z}_{S} $, and use the $ {z}_{ASi} $ to denote one seen class semantic feature in $ {Z}_{AS} $. In addition to the reconstruction loss function shown in Eq (1), zero-shot learning contains two different modalities, sample features and semantic features. Aligning different modalities can reduce the domain shift problem [25]. Inspired by GatingAE [3], Chen et al. [12], CADA-VAE [18] and Discriminative Cross-Aligned Variational Autoencoder(DCA-VAE) [25], we use the cross-reconstruction loss function. The features $ \overline {{X}_{S}} $ and $ \overline {{A}_{S}} $ are obtained by passing the semantic features and sample features of the latent space through D2 and D1 decoders, respectively, the cross-reconstruction loss function is as follows:
Here, $ \overline {{x}_{si}} $ denotes one feature in $ \overline {{X}_{S}} $, and $ \overline {{a}_{si}} $ denotes one feature in $ \overline {{A}_{S}} $. Although we can use Eqs (1), (2) and (3) to train the model and then to generate samples of the unseen classes, Eqs (1), (2) and (3) only contains samples of the seen classes and semantic features, which will lead to the pseudo samples being biased to the seen classes. To address this problem, we add the unseen class semantic features $ {A}_{US} $ to the model and propose new sample features $ \widehat{X} $.
The unseen class semantic features $ {A}_{US} $ can be obtained by the following method. The sample features of the training set are mapped to the semantic feature space using the following equation:
$ {||\cdot ||}_{F} $ in Eq (4) denotes Frobenius norm. The mapping matrix $ W $ is obtained as follows:
where $ I $ in Eq (5) represents the unit matrix and $ \alpha $ denotes an adjustable parameter. The sample features in the training set are then mapped to the semantic feature space through the mapping matrix $ W $ and find the nearest unseen class semantic features, which constitute $ {A}_{US} $.
After obtaining $ {A}_{US} $, we input $ {A}_{US} $ to the autoencoder to obtain the generated unseen class semantic features $ \widetilde {{A}_{US}} $, and the reconstruction loss between $ \widetilde {{A}_{US}} $ and $ {A}_{US} $ is:
Here, we use $ {a}_{usi} $ to denote one unseen class semantic feature in $ {A}_{US} $ and $ \widetilde {{a}_{usi}} $ to denote one generated unseen class semantic feature in $ \widetilde {{A}_{US}} $. Except the reconstruction loss for $ {A}_{US} $. We also want to align different modalities between the unseen class semantic features and sample features, but there is a lack of unseen class samples in the training set. In this paper, we take the following approach to get the cross-reconstruction loss function: Find the difference between the unseen class semantic features and the seen class sample features in the latent space, the difference represents the relationship between the unseen class semantic features and the seen class sample features in the latent space. Then, pass the difference through the decoder D1 to get $ \mathrm{\theta } $. We use $ {Z}_{S} $ and $ {Z}_{AU} $ to represent the latent features of the seen class sample features and the latent features of the unseen class semantic features. The formula is as follows:
Then subtract $ \theta $ from the sample features of the training set to obtain the feature $ \widehat{X} $:
The cross-reconstruction loss function for unseen class semantic features can be written as:
$ \beta $ in the above equation is an adjustable parameter. $ \widehat{{x}_{i}} $ denotes one feature in $ \widehat{X} $, $ \overline {{x}_{usi}} $ denotes one feature obtained by passing one unseen class semantic feature through the decoder D1. The reason for using the feature $ \widehat{X} $ instead of $ {X}_{S} $ is that $ \widehat{X} $ can reduce the information of the seen class samples in the loss function, which can alleviate the similarity between the unseen class pseudo samples and the seen class samples.
To better find the relationship between the semantic features of unseen classes and the training set samples in Eq (7), and also make the sample features in the latent space distinguishable and representative, the sample features of the latent space are classified using the cross-entropy loss function:
$ \widetilde {{y}_{si}} $ in Eq (10) is the predicted label and $ {y}_{si} $ is the true label of the sample features of the latent space.
Combining Eqs (1), (2), (3), (6), (9) and (10), the objective function is:
3.3. Zero-shot classification
After the model is trained according to Eq (11), the samples are generated with the sample features $ {X}_{S} $ and semantic features $ {A}_{US} $. For generalized zero-shot classification, all the generated seen class samples and unseen class samples need to be input to the classifier for training. For conventional zero-shot classification, only the generated unseen class samples need to be input to the classifier for training.
4.
Experiments
4.1. Datasets and parameter settings
Three datasets, AWA1, AWA2 and aPY, are used in our study.
1) AWA1 [26]: The seen class contains 40 categories, and the unseen class contains 10 categories. The number of samples in the seen class is 19832, the number of samples in the unseen class is 5685 and the dimension of the semantic features is 85.
2) AWA2 [27]: The seen class contains 40 categories, and the unseen class contains 10 categories. The number of samples in the seen class is 23527, the number of samples in the unseen class is 7913 and the dimension of the semantic features is 85.
3) aPY [28]: The seen class contains 20 categories, and the unseen class contains 12 categories. The number of samples in the seen class is 5932, the number of samples in the unseen class is 7924, and the dimension of the semantic features is 64.
The sample features and semantic features used in our study are taken from the literature [27]. Following the literature [12], the input dimension of encoder E1 is 2048 dimensions, the output of the first layer is 512 dimensions, and the dimension of the latent space is 128; the dimension of the output of the first layer of encoder E2 is 128.The dimension of the output of the first layer of decoder D1 is 256 and the dimension of output is 2048; the dimension of output of the first layer of decoder D2 is 256. We use the Adam algorithm for optimization, the learning rate is 0.001 and the batch size is 256.
4.2. The results of zero-shot classification
We use the evaluation criteria proposed in the literature [27]. For the conventional zero-shot classification, only the accuracy of classification needs to be calculated:
For generalized zero-shot classification, not only the classification accuracy of the seen class and the unseen class should be calculated, but also the harmonic mean. Assuming that the classification accuracy of the samples of seen classes is denoted as $ {acc}_{tr} $ and the classification accuracy of the samples of unseen classes is denoted as $ {acc}_{ts} $, the harmonic mean can be written as:
The generalized zero-shot classification results and the conventional zero-shot classification results are shown in Tables 1 and 2, where the results of Semantic Autoencoder (SAE) [8], Direct Attribute Prediction (DAP) [26], Indirect Attribute Prediction (IAP) [26] and Structured Joint Embedding (SJE) [29] are from the literature [27]. In Table 1, "ts" represents the classification results of unseen classes and "tr" represents the classification results of the seen classes. From Table 1, the proposed method is 1% less than CADA-VAE [18] for the AWA1 dataset. For the AWA2 dataset, the proposed method is 0.5% better than Chen et al. [23]. For the aPY dataset, the proposed method is 3.1% higher than DAP [26], while it is 4.9% higher than the generative model Chen et al. [12]. The accuracy of the proposed method on unseen class is higher than other methods.
Table 2 shows the conventional zero-shot classification results. For the AWA1 dataset, the proposed method is slightly lower than f-CLSWGAN [20] and Li et al. [11], which used the GAN model. For the aPY dataset, the method in this paper is slightly lower than the method of Zhang et al. [31] and more accurate than the other methods. The accuracy of the method in this paper is higher than the other methods on the AWA2 dataset.
4.3. The influence of parameters
The parameters involved in the model are $ \alpha $, $ \beta $ and the dimensionality of the latent space, where we denote the dimensionality of the latent space as $ d $. The effects of taking different values of $ \alpha $, $ \beta $ and $ d $ on the generalized zero-shot classification and the conventional zero-shot classification are shown in Figures 2, 3 and 4.
Figure 2 shows the effects of the parameter $ \alpha $ on the zero-shot classification results. The parameter $ \alpha $ is used to prevent overfitting. Taking the values of $ \alpha $ as 0.1, 1, 10 and 100. It can be seen from Figure 2 that the classification results of the aPY dataset are decreasing and then increasing as $ \alpha $ keeps increasing. The results of the AWA2 dataset on the conventional zero-shot classification are increasing all the time, while the values of the generalized zero-shot classification are decreasing and then increasing. The results of AWA1 dataset on the conventional zero-shot classification is decreasing and then increasing, and the harmonic mean is always increasing.
The values of $ \beta $ are taken as 0.001, 0.01, 0.1 and 1. $ \beta $ is used to regulate the relationship between the training set samples and the generated unseen class semantic features, and the value of $ \beta $ is taken small because the training set samples are not the real unseen class samples. From Figure 3, the accuracy of conventional zero-shot classification on the aPY dataset is almost unaffected by the value of $ \beta $, but the value in the generalized zero-shot classification decreases with increasing of $ \beta $. The classification accuracy of AWA1 and AWA2 on conventional zero-shot classification is also almost unaffected by the value of $ \beta $, but the harmonic mean value increases and then decreases with increasing of $ \beta $.
Figure 4 shows the effects of dimension $ d $ on the zero-shot classification results, with $ d $ taking values of 64,128 and 256. For the aPY dataset, the accuracy of conventional zero-shot classification increases first and then decreases as $ d $ increases, the harmonic mean value keeps decreasing. For the AWA1 dataset, the results increase and then decrease with increasing $ d $, except for the classification results of the seen classes. For the AWA2 dataset, most of the zero-shot classification results show a trend of increasing and then decreasing with increasing $ d $.
4.4. tSNE
Figure 5 shows the tSNE for generalized zero-shot classification of the aPY dataset, where (a) and (b) denote the training set samples and unseen class samples, respectively, and (c) and (d) are the generated training set samples and unseen class samples.
For the training set samples, the distribution between the generated samples and the original samples is almost the same, and the generated samples are more dispersed between different categories and more concentrated within classes than the original samples. For the unseen class samples, there are more samples presenting orange color in the original samples, while in the generated samples, since $ {A}_{US} $ is chosen for generating the unseen class samples in this paper, it will lead to the number of some classes will be more and the number of some other classes will be less in the generated samples. Except for the inconsistent number of samples, most of the generated samples are similar to the distribution of the real samples.
4.5. Ablation experiments
The ablation experiments are divided into the following cases: a. Only Eq (1) is retained as the loss function of the model. b. Add $ {L}_{latent-recon} $ to Eq(1). c. $ {L}_{cross-recon1}\ne 0 $ on the basis of b. d. $ {L}_{classifier}\ne 0 $ on the basis of c; e. Based on d, the second term in $ {L}_{cross-recon2} $ is not 0; f. Based on e, $ {L}_{recon2}\ne 0 $. The proposed method is to add the first term in $ {L}_{cross-recon2} $, on the basis of f. The harmonic mean H and the accuracy acc of the conventional zero-shot classification are shown in Table 3.
As can be seen in Table 3, most of the classification results are increased as the term increased in the loss function. However, for the AWA1 dataset when changing from e to f, the accuracy does not change for the conventional zero-shot classification, and the harmonic mean decreases slightly. The proposed method does not increase particularly much in the conventional zero-shot classification compared to other methods, especially in the aPY dataset, and for aPY dataset, the method b is larger than other methods except the proposed method. For AWA2 when changing from b to c, the results decreases, especially in harmonic mean. The seen class information increased when we add the $ {L}_{cross-recon1} $ and the accuracy of the unseen classes decreases. However, for generalized zero-shot classification, the proposed method can provide some information about the unseen classes when training the model, and reduce the similarity between the generated unseen class samples and the seen class samples.
By replacing $ \widehat{X} $ in the loss function $ {L}_{cross-recon2} $ with $ {X}_{S} $, the results are shown in Table 4 numbered as (1), and the results of the proposed model numbered as (2). From Table 4, when $ {X}_{S} $ is used instead of $ \widehat{X} $, the results of zero-shot classification are all decreased, especially for generalized zero-shot classification. This is because the loss function contains more information about the samples of the seen classes, making the results easily biased to the seen classes.
5.
Conclusions
In this study, an autoencoder approach is used for generating samples of unseen classes in zero-shot learning. For the problem that the generated unseen class sample features are always biased to the seen class features, we add the semantic features of the unseen class with the proposed new sample features to the cross-reconstruction loss function. This can reduce the information of the seen class samples and make the generated unseen class samples closer to the real unseen class samples, and improve the classification accuracy of the unseen class samples. The experimental results on three datasets verify that the proposed method can achieve good results.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Conflict of interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad: