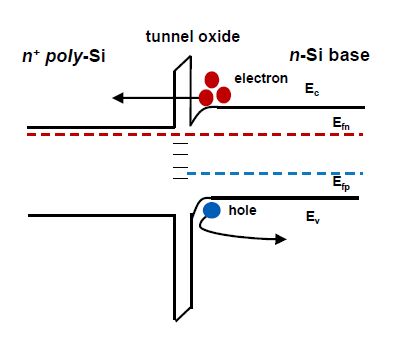
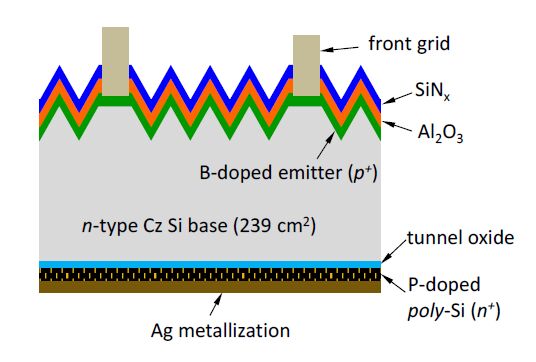
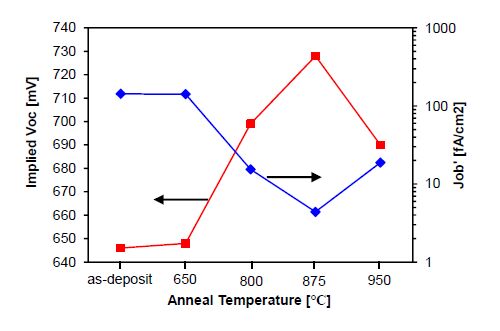
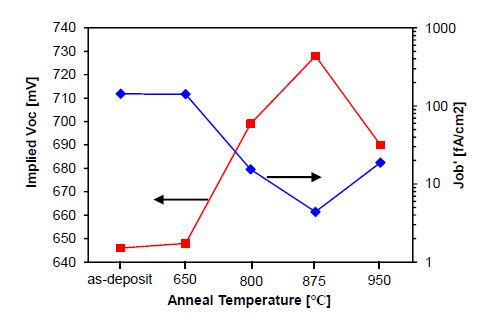
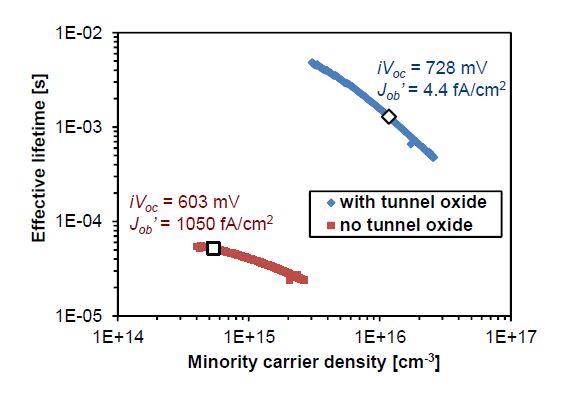
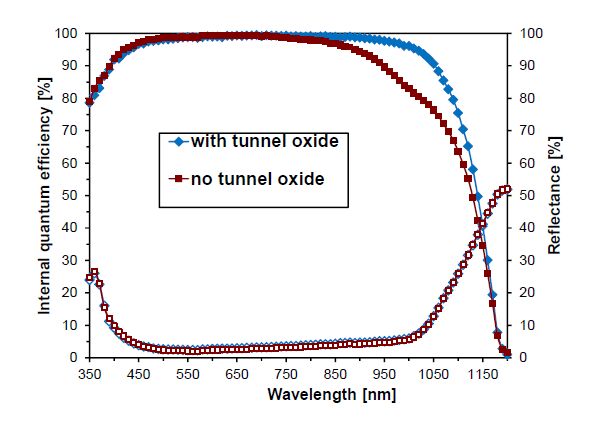
Carrier-selective contact with low minority carrier recombination and efficient majority carrier transport is mandatory to eliminate metal-induced recombination for higher energy conversion efficiency for silicon (Si) solar cells. In the present study, the carrier-selective contact consists of an ultra-thin tunnel oxide and a phosphorus-doped polycrystalline Si (poly-Si) thin film formed by plasma enhanced chemical vapor deposition (PECVD) and subsequent thermal crystallization. It is shown that the poly-Si film properties (doping level, crystallization and dopant activation anneal temperature) are crucial for achieving excellent contact passivation quality. It is also demonstrated quantitatively that the tunnel oxide plays a critical role in this tunnel oxide passivated contact (TOPCON) scheme to realize desired carrier selectivity. Presence of tunnel oxide increases the implied Voc (iVoc) by ~ 125 mV. The iVoc value as high as 728 mV is achieved on symmetric structure with TOPCON on both sides. Large area (239 cm2) n-type Czochralski (Cz) Si solar cells are fabricated with homogeneous implanted boron emitter and screen-printed contact on the front and TOPCON on the back, achieving 21.2% cell efficiency. Detailed analysis shows that the performance of these cells is mainly limited by boron emitter recombination on the front side.
1.
Introduction
The (conventional) vector space is based on two basic operations, which are vector addition and scalar multiplication. Under these two operations, some required axioms are needed to extend the concepts of finite-dimensional Euclidean space $ \mathbb{R}^{n} $. Usually, there are eight axioms are provided in the real vector space. However, some spaces cannot satisfy all of the axioms in vector space. In this case, the weak concept of a so-called near vector space will be studied in this paper. We provide three well-known spaces that cannot be the (conventional) vector spaces. However, they can be checked to be near vector spaces.
● Let $ {\cal I} $ be the space of all bounded and closed intervals in $ \mathbb{R} $. The interval addition and scalar multiplication of intervals can be treated as the vector addition and scalar multiplication. An interval which subtracts itself may not provide a zero element in $ {\cal I} $. In this case, we cannot consider the concept of an inverse element in $ {\cal I} $. This says that $ {\cal I} $ cannot be a (conventional) vector space by referring to Example 2.1. However, it is not difficult to check that $ {\cal I} $ is a near vector space, which will be presented in the context of this paper.
● Let $ {\cal F}_{cc}(\mathbb{R}) $ be the space of all fuzzy numbers in $ \mathbb{R} $. The fuzzy number addition and scalar multiplication of fuzzy numbers can be treated as the vector addition and scalar multiplication. A fuzzy number which subtracts itself may not provide a zero element in $ {\cal F}_{cc}(\mathbb{R}) $. In this case, we cannot consider the concept of an inverse element in $ {\cal F}_{cc}(\mathbb{R}) $. This says that $ {\cal F}_{cc}(\mathbb{R}) $ cannot be a (conventional) vector space as according to Subsection 2.1.
● Let $ U $ be a (conventional) vector space, and let $ {\cal P}(U) $ be a collection of all subsets of $ U $. The collection $ {\cal P}(U) $ is also called a hyperspace. The set addition and scalar multiplication of sets can be treated as the vector addition and scalar multiplication. A set which subtracts itself may not provide a zero element in $ {\cal P}(U) $. In this case, we cannot consider the concept of an inverse element in $ {\cal P}(U) $. This says that $ {\cal P}(U) $ cannot be a (conventional) vector space as according to Subsection 2.2.
The main issue of the above three spaces is that the concept of an inverse element is not available. Therefore, in this paper, a concept of a so-called null set will be adopted for the purpose of playing the role of a zero element in the so-called near vector space that can include the space consisting of all bounded and closed intervals in $ \mathbb{R} $, the space consisting of all fuzzy numbers in $ \mathbb{R} $, and the hyperspace consisting of all subsets of $ \mathbb{R} $.
We can also attach a norm to this near vector space to form a so-called near normed space, which is a completely new concept with no available related references for this topic. The readers may just refer to the monographs [1,2,3,4,5] on topological vector spaces and the monographs [6,7,8] on functional analysis.
Based on the concept of a null set, we can define the concept of almost identical elements in near vector space. The norm which is defined in near vector space is completely different from the conventional norm defined in vector space, since the so-called near normed space involves the null set and almost identical concept. The triangle inequality is still considered in near normed space. The concepts of limit and class limit of a sequence in near normed space will be defined. For this setting, we can similarly define the concept of a Cauchy sequence, which can be used to define the completeness of a near normed space. A near normed space that is also complete is called a near Banach space. The main purpose of this paper is to establish the so-called near fixed point in near Banach space, where the near fixed point is based on the almost identical concept. The near fixed point theorems in the normed interval space, the space of fuzzy numbers and the hyperspace have been studied by Wu [9,10,11]. This work will consider the general near normed space such that the near fixed point theorems established in this paper will extend the results obtained by Wu [9,10,11].
In Sections 2 and 3, the concepts of a near vector space and near normed space are proposed, where some interesting properties are derived in order to study the near fixed point theorem. In Section 4, the concept of a Cauchy sequence in near normed space will be defined. Also, the so-called near Banach space will be defined based on the concept of a Cauchy sequence. In Section 5, we present the near fixed point theorem and the Meir-Keeler type of near fixed point theorem that are established using the almost identical concept in near normed space. In Section 6, we present the near fixed point in the space of fuzzy numbers in $ \mathbb{R} $. In Section 7, we present the near fixed point in the hyperspace.
2.
Near vector spaces
Let $ U $ be a universal set such that it is endowed with the vector addition and scalar multiplication as follows:
● (Vector addition). Given any $ x, y\in U $, the vector addition $ x\oplus y $ is in $ U $.
● (Scalar multiplication). Given any $ \alpha\in\mathbb{R} $ and $ x\in U $, the scalar multiplication $ \alpha x $ is in $ U $.
In this case, we also say that $ U $ is a universal set over $ \mathbb{R} $. It is clear that the (conventional) vector space $ V $ over $ \mathbb{R} $ is a universal set over $ \mathbb{R} $ satisfying eight axioms. In the conventional vector space over $ \mathbb{R} $, the additive inverse element of $ v\in V $ is denoted by $ -v $, and it can also be shown that $ -v = (-1)v $, which means that the inverse element $ -v $ is equal to the scalar multiplication $ (-1)v $. In this paper, we are not going to consider the concept of an inverse element. However, we still adopt $ -x = (-1)x $ for convenience. In other words, when we write $ -x $, it just means that $ x $ is multiplied by the scalar $ -1 $, since we are not going to consider the concept of an inverse element in the universal set $ U $ over $ \mathbb{R} $.
For any $ x $ and $ y $ in the universal set $ U $ over $ \mathbb{R} $, the substraction $ x\ominus y $ is defined by
Recall that $ -y $ means the scalar multiplication $ (-1)y $. On the other hand, given any $ x\in U $ and $ \alpha\in\mathbb{R} $, we remark that
in general, unless this law $ \alpha (\beta x) = (\alpha\beta)x $ holds true for any $ \alpha, \beta\in\mathbb{R} $. However, in this paper, this law will not be assumed to be true, since $ U $ is not a vector space over $ \mathbb{R} $. Next, we present a space that cannot have the concept of an inverse element.
Example 2.1. Let $ {\cal I} $ be the family of all bounded and closed intervals in $ \mathbb{R} $. The vector addition and scalar multiplication are given below.
● (Vector addition). Given any two bounded closed intervals $ [A, B] $ and $ [C, D] $, their vector addition is given by
● (Scalar multiplication). Given any $ k\in\mathbb{R} $ and $ [A, B]\in {\cal I} $, the scalar multiplication is given by
Before introducing the inverse element, we need to point out the zero element. It is clear to see that $ [0, 0] $ is the zero element of $ {\cal I} $, since we have
However, the problem is that $ [A, B] $ cannot have an inverse element. The main reason is that we cannot find an interval $ I\in {\cal I} $ satisfying
This also says that the family $ {\cal I} $ is not a (conventional) vector space. On the other hand, we cannot have the following equality
for any $ I\in {\cal I} $ and $ \alpha, \beta\in\mathbb{R} $. This shows another reason why the family $ {\cal I} $ is not a (conventional) vector space.
Definition 2.2. Let $ U $ be a universal set over $ \mathbb{R} $. The following set
is called the null set of $ U $. Many other terminologies are also given below:
● The null set $ \Psi $ is said to satisfy the neutral condition when
where $ -\psi $ means $ (-1)\psi $, since the concept of an inverse element is not considered in $ U $.
● The null set $ \Psi $ is said to be closed under the condition of the vector addition when we have
● The element $ \theta\in U $ is said to be a zero element when we have
Example 2.3. Continued from Example 2.1, we are going to present the null set of the family $ {\cal I} $. Given any $ [A, B]\in {\cal I} $, we have
It is clear to see that the null set $ \Psi $ of $ {\cal I} $ is given by
Definition 2.4. Let $ U $ be a universal set over $ \mathbb{R} $. We say that $ U $ is a near vector space over $ \mathbb{R} $ when the following conditions are satisfied.
● For any $ x\in U $, the equality $ 1x = x $ holds true.
● For any $ x, y, z\in U $ and $ \alpha\in\mathbb{R} $, the identity $ x = y $ implies the following identities
● (Commutative law). For any $ x, y\in U $, the following equality
holds true.
● (Associative Law). For any $ x, y, z\in U $, the following equality
holds true.
It is clear to see that any (conventional) vector space over $ \mathbb{R} $ is also a near vector space over $ \mathbb{R} $. However, the converse is not true. Although the family $ {\cal I} $ of all bounded and closed intervals as shown in Example 2.1 is not a (conventional) vector space, it is easy to check that $ {\cal I} $ is a near vector space over $ \mathbb{R} $. Next, we define the concept of an almost identical element.
Definition 2.5. Let $ U $ be a near vector space over $ \mathbb{R} $ with the null set $ \Psi $. Any two elements $ x $ and $ y $ in $ U $ are said to be almost identical when any one of the following conditions is satisfied:
● We have $ x = y $;
● There exists $ \psi\in\Psi $ such that
● There exist $ \psi_{1}, \psi_{2}\in\Psi $ such that
We also write $ x\stackrel{\Psi}{ = }y $ to indicate that $ x $ and $ y $ are almost identical.
Remark 2.6. In this paper, when we plan to study some properties using the concept $ x\stackrel{\Psi}{ = }y $, it is enough to just consider the third case, i.e.,
since the same arguments are still valid for the first and second cases.
Regarding the binary relation $ \stackrel{\Psi}{ = } $ in Definition 2.5, given any $ x\in U $, we consider the following set
We also define the following family
The proof of the following proposition is left for the readers.
Proposition 2.7. Let $ U $ be a near vector space over $ \mathbb{R} $ with the null set $ \Psi $. Suppose that the null set $ \Psi $ is closed under the condition of the vector addition. In other words, we have
Then, the binary relation $ \stackrel{\Psi}{ = } $ in Definition 2.5 is an equivalence relation.
The above proposition also says that, when the null set $ \Psi $ is not closed under the condition of the vector addition, the binary relation $ \stackrel{\Psi}{ = } $ is not necessarily an equivalence relation. Therefore, given any $ y\in [x] $, we may not have $ [y] = [x] $, unless the binary relation $ \stackrel{\Psi}{ = } $ is an equivalence relation.
Suppose that the null set $ \Psi $ is closed under the condition of the vector addition. Then Proposition 2.7 says that the sets defined in (2.1) form the equivalence classes. We also have that $ y\in [x] $ implies $ [x] = [y] $, which says that the family of all equivalence classes forms a partition of the whole universal set $ U $. Even though in this situation, the space $ [U] $ is still not a (conventional) vector space, since not all of the axioms taken in the (conventional) vector space are not necessarily to be satisfied in $ [U] $. For example, we consider the near vector space $ {\cal I} $ over $ \mathbb{R} $ from Example 2.1. The quotient space $ [{\cal I}] $ cannot be a (conventional) vector space. The reason is that
since
Therefore, we need to seriously study the so-called near vector space.
2.1. Near vector space of fuzzy numbers
Let $ U $ be a topological space. The fuzzy subset $ \tilde{A} $ of $ U $ is defined by a membership function $ \xi_{\tilde{A}}:U\rightarrow [0, 1] $. The $ \alpha $-level set of $ \tilde{A} $ is denoted and defined by
for all $ \alpha\in (0, 1] $. The $ 0 $-level set $ \tilde{A}_{0} $ is defined as the closure of the set $ \{x\in U:\xi_{\tilde{A}}(x) > 0\} $.
Now, we take $ U = \mathbb{R} $. Let $ \odot $ denote any of the four basic arithmetic operations $ \oplus, \ominus, \otimes, \oslash $ between two fuzzy subsets $ \tilde{A} $ and $ \tilde{B} $ in $ \mathbb{R} $. The membership function of $ \tilde{A}\odot\tilde{B} $ is defined by
for all $ z\in\mathbb{R} $. More precisely, the membership functions are given by
where $ \tilde{A}\ominus\tilde{B}\equiv \tilde{A}\oplus (-\tilde{B}) $.
Definition 2.8. Let $ U $ be a real topological vector space. We denote by $ {\cal F}_{cc}(U) $ the set of all fuzzy subsets of $ U $ such that each $ \tilde{A}\in {\cal F}_{cc}(U) $ satisfies the the following conditions:
● $ \xi_{\tilde{A}}(x) = 1 $ for some $ x\in U $;
● The membership function $ \xi_{\tilde{A}}(x) $ is upper semicontinuous and quasi-concave;
● The $ 0 $-level set $ \tilde{A}_{0} $ is a compact subset of $ U $.
In particular, if $ U = \mathbb{R} $ then each element of $ {\cal F}_{cc}(\mathbb{R}) $ is called a fuzzy number.
For $ \tilde{A}\in {\cal F}_{cc}(\mathbb{R}) $, it is well-known that, for each $ \alpha\in [0, 1] $, the $ \alpha $-level set $ \tilde{A}_{\alpha} $ is a bounded closed interval in $ \mathbb{R} $, and it is also denoted by
We say that $ \tilde{1}_{a} $ is a crisp number with a value of $ a $ when the membership function of $ \tilde{1}_{a} $ is given by
It is clear that each $ \alpha $-level set of $ \tilde{1}_{a} $ is a singleton $ \{a\} $ for $ \alpha\in [0, 1] $. Therefore, the crisp number $ \tilde{1}_{a} $ can be identified with the real number $ a $. In this case, we can identify the inclusion $ \mathbb{R}\subset {\cal F}_{cc}(\mathbb{R}) $. For convenience, we also write $ \lambda\tilde{A}\equiv\tilde{1}_{\lambda}\otimes\tilde{A} $.
Let $ \tilde{A} $ and $ \tilde{B} $ be two fuzzy numbers with
It is well known that
and
For $ \lambda\in\mathbb{R} $, we also have
Given any $ \tilde{A}\in {\cal F}_{cc}(\mathbb{R}) $, we have
This says that each $ \alpha $-level set $ (\tilde{A}\ominus\tilde{A})_{\alpha} $ can be treated as an "approximated real zero number" with symmetric uncertainty $ \tilde{A}_{\alpha}^{U}-\tilde{A}_{\alpha}^{L} $. We can also see that the real zero number has the highest membership degree of $ 1 $ given by $ \xi_{\tilde{A}\ominus\tilde{A}}(0) = 1 $. In this case, we can say that $ \tilde{A}\ominus\tilde{A} $ is a fuzzy zero number.
The space $ {\cal F}_{cc}(\mathbb{R}) $ cannot be a (conventional) vector space over $ \mathbb{R} $ since we cannot identify the inverse elements of any elements in $ {\cal F}_{cc}(\mathbb{R}) $. It is not hard to check that the space $ {\cal F}_{cc}(\mathbb{R}) $ of fuzzy numbers is a near vector space over $ \mathbb{R} $ by treating the vector addition as the fuzzy addition $ \tilde{A}\oplus\tilde{B} $ and the scalar multiplication as $ \lambda\tilde{A} = \tilde{1}_{\lambda}\otimes\tilde{A} $. Then, the null set $ \Psi $ of the near vector space $ {\cal F}_{cc}(\mathbb{R}) $ is given by
Therefore, given any $ \tilde{\psi}\in\Psi $, there exists $ \tilde{A}\in{\cal F}_{cc}(\mathbb{R}) $ satisfying $ \tilde{\psi} = \tilde{A}\ominus\tilde{A} $. Equivalently, from (2.5), we see that $ \tilde{\psi}\in\Psi $ if and only if $ \tilde{\psi}_{\alpha}^{U}\geq 0 $ and $ \tilde{\psi}_{\alpha}^{L} = -\tilde{\psi}_{\alpha}^{U} $ for all $ \alpha\in [0, 1] $, i.e.,
where the bounded closed interval $ \tilde{\psi}_{\alpha} $ is an "approximated real zero number" with symmetric uncertainty $ \tilde{\psi}_{\alpha}^{U} $. In other words, each $ \tilde{\psi}\in\Psi $ is a fuzzy zero number. It is also clear that the crisp number $ \tilde{1}_{\{0\}} $ with a value of $ 0 $ is in $ \Psi $. We also see that $ \tilde{1}_{\{0\}} $ is a zero element of $ {\cal F}_{cc}(\mathbb{R}) $, since we have
for any $ \tilde{A}\in {\cal F}_{cc}(\mathbb{R}) $.
Remark 2.9. It is not hard to check that the null set $ \Psi $ is closed under the condition of the vector addition (i.e., fuzzy addition) and satisfies the neutral condition.
Given any two $ \tilde{A} $ and $ \tilde{B} $ in $ {\cal F}_{cc}(\mathbb{R}) $, the definition says
By considering the $ \alpha $-level sets, for any $ \alpha\in [0, 1] $, we have
which says
Let $ K_{\alpha} = (\tilde{\psi}^{(2)})_{\alpha}^{U}-(\tilde{\psi}^{(1)})_{\alpha}^{U} $. Then, we have
Therefore, we obtain
Therefore $ \tilde{A}\stackrel{\Psi}{ = }\tilde{B} $ means that the $ \alpha $-level sets $ \tilde{A}_{\alpha} $ and $ \tilde{B}_{\alpha} $ are essentially identical differing with symmetric uncertainty $ K_{\alpha} $ for $ \alpha\in [0, 1] $.
2.2. Near vector structure in hyperspace
Let $ U $ be a (conventional) vector space, and let $ {\cal P}(U) $ be a collection of all subsets of $ U $. Given any $ A, B\in {\cal P}(U) $, the set addition of $ A $ and $ B $ in $ \mathbb{R} $ is defined by
and the scalar multiplication in $ {\cal P}(U) $ is defined by
where $ \lambda $ is a constant in $ \mathbb{R} $. The substraction between $ A $ and $ B $ is denoted and defined by
Then, we have the following properties:
● $ \lambda (A\oplus B) = \lambda A\oplus \lambda B $ for $ \lambda\in\mathbb{R} $;
● $ \lambda_{1}(\lambda_{2}A) = (\lambda_{1}\lambda_{2})A $ for $ \lambda_{1}, \lambda_{2}\in\mathbb{R} $;
● Let $ A $ be a convex subset of $ U $. If $ \lambda_{1} $ and $ \lambda_{2} $ have the same sign, then we have
In $ {\cal P}(U) $, the set addition $ A\oplus B $ can be treated as the vector addition and $ \lambda A $ can be treated as the scalar multiplication. Let $ \theta_{U} $ be the zero element of $ U $. It is clear that the singleton $ \{\theta_{U}\} $ can be regarded as the zero element of $ {\cal P}(U) $, since we have
Since $ A\ominus A\neq\{\theta_{U}\} $, it means that $ A\ominus A $ is not the zero element of $ {\cal P}(U) $. In other words, the additive inverse element of $ A $ in $ {\cal P}(U) $ does not exist. Therefore, the space $ {\cal P}(U) $ cannot be a (conventional) vector space over $ \mathbb{R} $, since we cannot identify the inverse elements of any elements in $ {\cal P}(U) $. It is not hard to check that $ {\cal P}(U) $ is a near vector space over $ \mathbb{R} $. In this case, the null set of $ {\cal P}(U) $ is given by
Remark 2.10. It is not hard to check that the null set $ \Psi $ is closed under the condition of the vector addition (i.e., set addition) and satisfies the neutral condition.
3.
Near normed spaces
Let $ U $ be a near vector space over $ \mathbb{R} $ with the null set $ \Psi $. We are going to endow a norm to the space $ U $. Because we do not have an elegant structure in $ U $ like in the (conventional) vector space, many kinds of so-called near normed spaces are proposed below.
Definition 3.1. Let $ U $ be a near vector space over $ \mathbb{R} $ with the null set $ \Psi $, and let $ \parallel\cdot\parallel:U\rightarrow \mathbb{R}_{+} $ be a nonnegative real-valued function defined on $ U $.
● The function $ \parallel\cdot\parallel $ is said to satisfy the null condition when
● The function $ \parallel\cdot\parallel $ is said to satisfy the null super-inequality when
● The function $ \parallel\cdot\parallel $ is said to satisfy the null sub-inequality when
● The function $ \parallel\cdot\parallel $ is said to satisfy the null equality when
Definition 3.2. Let $ U $ be a near vector space over $ \mathbb{R} $ with the null set $ \Psi $. Given a nonnegative real-valued function $ \parallel\cdot\parallel:U\rightarrow \mathbb{R}_{+} $ defined on $ U $, we consider the following conditions:
(i) $ \parallel\alpha x\parallel = |\alpha |\parallel x\parallel $ for any $ x\in U $ and $ \alpha\in\mathbb{R} $;
(i') $ \parallel\alpha x\parallel = |\alpha |\parallel x\parallel $ for any $ x\in U $ and $ \alpha\in\mathbb{R} $ with $ \alpha\neq 0 $.
(ii) $ \parallel x\oplus y\parallel\leq\parallel x\parallel +\parallel y \parallel $ for any $ x, y\in U $.
(iii) $ \parallel x\parallel = 0 $ implies $ x\in\Psi $.
Many kinds of near normed spaces are defined below.
● $ (U, \parallel\cdot\parallel) $ is said to be a near pseudo-seminormed space when conditions ($ \; {\rm{i}}\; ' $) and (ii) are satisfied.
● $ (U, \parallel\cdot\parallel) $ is said to be a near seminormed space when conditions (i) and (ii) are satisfied.
● $ (U, \parallel\cdot\parallel) $ is said to be a near pseudo-normed space when conditions ($ \; {\rm{i}}\; ' $), (ii) and (iii) are satisfied.
● $ (U, \parallel\cdot\parallel) $ is said to be a near normed space when conditions (i)–(iii) are satisfied.
Remark 3.3. Suppose that the norm $ \parallel\cdot\parallel $ satisfies the null condition. Then, we have the following observations.
● We want to claim that the norm $ \parallel\cdot\parallel $ also satisfies the null sub-inequality. Indeed, using the triangle inequality, it follows that
● We want to claim that $ \Psi $ is closed under the condition of the scalar multiplication. Indeed, using conditions (i) and (iii) in Definition 3.2, it follows that
● We want to claim that $ \Psi $ is closed under the condition of the vector addition. Indeed, using condition (ii) in Definition 3.2, it follows that
which implies $ \psi_{1}\oplus\psi_{2}\in\Psi $.
Example 3.4. Continued from Examples 2.1 and 2.3, we define the norm $ \parallel\cdot\parallel:{\cal I}\rightarrow \mathbb{R}_{+} $ on $ {\cal I} $ by
It is easy to check that the family $ ({\cal I}, \parallel\cdot\parallel) $ is a near normed space such that the norm $ \parallel\cdot\parallel $ satisfies the null equality and null condition.
Let $ (U, \parallel\cdot\parallel) $ be a near pseudo-seminormed space. In general, we cannot have the following equality
The reason is that we do not assume the laws
for $ x, y\in U $ and $ \alpha, \beta\in\mathbb{R} $. It also says that, in general, we cannot obtain the following equality
Therefore, we propose the following definition.
Definition 3.5. Let $ (U, \parallel\cdot\parallel) $ be a near pseudo-seminormed space. The norm $ \parallel\cdot\parallel $ is said to satisfy the symmetric condition when
Next, we are going to provide the sufficient conditions to guarantee that the norm is able to satisfy the symmetric condition.
Proposition 3.6. Let $ (U, \parallel\cdot\parallel) $ be a near pseudo-seminormed space. Suppose that the norm $ \parallel\cdot\parallel $ satisfies the null equality. Then, this norm $ \parallel\cdot\parallel $ satisfies the symmetric condition.
Proof. We first have
Using the null equality, we obtain
Using the associative and commutative laws, we also have
where $ \psi_{1} = x\oplus (-x)\in\Psi $ and $ \psi_{1} = y\oplus (-y)\in\Psi $. Using the null equality two times, we obtain
Finally, using condition ($ \; {\rm{i}}\; ' $) in Definition 3.2, it follows that
Combining the above equalities, we obtain
This completes the proof.
Let $ U $ be a near vector space over $ \mathbb{R} $. Then, the following equality
does not hold true in general, since $ U $ does not have the elegant structure like the conventional vector space. However, if $ (U, \parallel\cdot\parallel) $ is a near pseudo-seminormed space, we can have the following interesting results.
Proposition 3.7. Let $ (U, \parallel\cdot\parallel) $ be a near pseudo-seminormed space. Suppose that the norm $ \parallel\cdot\parallel $ satisfies the null equality. Given any $ x, y, z\in U $, we have
and
However, in general without using the norm, we have
and
Proof. Let $ \psi_{1} = x\ominus x\in\Psi $ and $ \psi_{2} = y\ominus y\in\Psi $. Then, we have
By adding $ z\ominus (x\oplus y) $ on both sides, we obtain
Let $ \psi_{3} = (x\oplus y)\ominus (x\oplus y)\in\Psi $. Then, we obtain
Since the norm $ \parallel\cdot\parallel $ satisfies the null equality, we have
Now, we also have
Let $ \psi_{4} = (x\ominus y)\ominus (x\ominus y)\in\Psi $, and add $ z\ominus (x\ominus y) $ on both sides. Then, we obtain
Using the null equality, we can similarly obtain the desired result by taking the norm $ \parallel\cdot\parallel $ on both sides. This completes the proof.
Proposition 3.8. Let $ (U, \parallel\cdot\parallel) $ be a near pseudo-normed space. Suppose that the norm $ \parallel\cdot\parallel $ satisfies the null super-inequality. Given any $ x, z, y_{1}, \cdots, y_{m}\in U $, we have
Proof. Since $ y_{j}\oplus (-y_{j}) = y_{j}\ominus y_{j} = \psi_{j}\in\Psi $ for $ j = 1, \cdots, m $, using the null super-inequality for $ m $ times, we have
Using the commutative and associative laws, we also have
Using (3.1), the proof is complete.
Proposition 3.9. We have the following properties.
(i) Let $ (U, \parallel\cdot\parallel) $ be a near pseudo-normed space. Given any $ x, y\in U $,
(ii) Let $ (U, \parallel\cdot\parallel) $ be a near pseudo-seminormed space. Suppose that the norm $ \parallel\cdot\parallel $ satisfies the null equality. Given any $ x, y\in U $,
(iii) Let $ (U, \parallel\cdot\parallel) $ be a near pseudo-seminormed space. Suppose that the norm $ \parallel\cdot\parallel $ satisfies the null super-inequality and null condition. Given any $ x, y\in U $,
Proof. To prove Part (i), for $ \parallel x\ominus y\parallel = 0 $, we have $ x\ominus y\in\Psi $, i.e., $ x\ominus y = \psi_{1} $ for some $ \psi_{1}\in\Psi $. Let $ \psi_{2} = y\ominus y\in\Psi $, and add $ y $ on both sides. Then, we obtain
which says that $ x\stackrel{\Psi}{ = }y $.
To prove Part (ii), the definition says that $ x\stackrel{\Psi}{ = }y $ implies
Using the null equality, it follows that
To prove Part (iii), we first note that the null set $ \Psi $ is closed under the condition of the vector addition from Remark 3.3. For $ x\stackrel{\Psi}{ = }y $, we have
Let $ \psi_{3} = y\ominus y\in\Psi $, and add $ -y $ on both sides. Then, we obtain
Using the null super-inequality and (3.2), it follows that
This completes the proof.
Example 3.10. We are going to define a norm in $ {\cal F}_{cc}(\mathbb{R}) $. Given any $ \tilde{A}\in {\cal F}_{cc}(\mathbb{R}) $, we define
We first claim that $ \parallel\cdot\parallel $ satisfies the null condition. In other words, we want to check that
Suppose that $ \parallel \tilde{A}\parallel = 0 $. Then, we have $ |\tilde{A}_{\alpha}^{L}+\tilde{A}_{\alpha}^{U}| = 0 $ for all $ \alpha\in [0, 1] $, which also says that $ \tilde{A}_{\alpha}^{L} = -\tilde{A}_{\alpha}^{U} $ for all $ \alpha\in [0, 1] $. This shows that $ \tilde{A}\in\Psi $. On the other hand, suppose that $ \tilde{A}\in\Psi $. Then, we have $ \tilde{A}_{\alpha}^{L} = -\tilde{A}_{\alpha}^{U} $ for all $ \alpha\in [0, 1] $, which says that $ \parallel \tilde{A}\parallel = 0 $.
Using (2.4), we have
Using (2.2), we also have
This shows that $ ({\cal F}_{cc}(\mathbb{R}), \parallel\cdot\parallel) $ is a near normed space such that the null condition is satisfied.
Furthermore, we can show that the null equality is also satisfied. Given any $ \tilde{\psi}\in\Psi $, it means that $ \tilde{\psi}_{\alpha}^{L} = -\tilde{\psi}_{\alpha}^{U} $ for all $ \alpha\in [0, 1] $. Therefore, we have
which shows that the null equality is indeed satisfied.
Example 3.11. Let $ (U, \parallel\cdot\parallel_{U}) $ be a (conventional) normed space. We consider the hyperspace $ {\cal P}(U) $ in the normed space $ (U, \parallel\cdot\parallel_{U}) $. We want to define a norm $ \parallel\cdot\parallel $ in $ {\cal P}(U) $ such that $ ({\cal P}(U), \parallel\cdot\parallel) $ is a near normed space. Given any $ A\in {\cal P}(U) $, we define
Let $ \theta_{U} $ be the zero element in the normed space $ (U, \parallel\cdot\parallel_{U}) $. We want to claim that $ \parallel A\parallel = 0 $ if and only if $ A = \{\theta_{U}\}\in\Psi $. Suppose that $ A = \{\theta_{U}\} $. Then, we have$ \parallel A\parallel = 0 $. On the other hand, suppose that $ \parallel A\parallel = 0 $. Then, we have $ \parallel a\parallel_{U} = 0 $ for all $ a\in A $, which says that $ A = \{\theta_{U}\} $.
Now, we have
and
This shows that $ ({\cal P}(U), \parallel\cdot\parallel) $ is indeed a near normed space.
4.
Cauchy sequences
Let $ (U, \parallel\cdot\parallel) $ be a near pseudo-seminormed space. Since the symmetric condition is not necessarily satisfied, we can define many concepts of limits based on $ \parallel\cdot\parallel $. For a sequence $ \{x_{n}\}_{n = 1}^{\infty} $ in $ U $, since
in general, many concepts of limits are proposed below.
Definition 4.1. Let $ (U, \parallel\cdot\parallel) $ be a near pseudo-seminormed space.
● A sequence $ \{x_{n}\}_{n = 1}^{\infty} $ in $ U $ is said to $ \triangleright $-converge to $ x\in U $ when we have the following limit
● A sequence $ \{x_{n}\}_{n = 1}^{\infty} $ in $ U $ is said to $ \triangleleft $-converge to $ x\in U $ when we have the following limit
● A sequence $ \{x_{n}\}_{n = 1}^{\infty} $ in $ U $ is said to converge to $ x\in U $ when we have the following limit
Remark 4.2. We have the following observations.
● Suppose that the norm $ \parallel\cdot\parallel $ satisfies the null equality. Then, Proposition 3.6 says that the symmetric condition is satisfied, i.e.,
This also means that the above three concepts of convergence are equivalent.
● Suppose that the sequence $ \{x_{n}\}_{n = 1}^{\infty} $ is simultaneously $ \triangleright $-convergent and $ \triangleleft $-convergent. It says that there exists $ x, y\in U $ such that we have the following limits
However, in this situation, $ x $ is not necessarily equal to $ y $.
Let $ U $ be a near vector space over $ \mathbb{R} $ with the null set $ \Psi $. Suppose that the null set $ \Psi $ is closed under the condition of the vector addition. Then, Proposition 2.7 says that the binary relation $ \stackrel{\Psi}{ = } $ in Definition 2.5 is an equivalence relation, which also says that the classes defined in (2.1) form the equivalence classes. In this case, we have many interesting results as follows.
Proposition 4.3. Let $ (U, \parallel\cdot\parallel) $ be a near pseudo-normed space with the null set $ \Psi $ such that $ \Psi $ is closed under the condition of the vector addition.
(i) Suppose that the norm $ \parallel\cdot\parallel $ satisfies the null super-inequality. Then, we have the following results.
● If the sequence $ \{x_{n}\}_{n = 1}^{\infty} $ in $ (U, \parallel\cdot\parallel) $ $ \triangleleft $-converges to $ x $ and $ \triangleright $-converges to $ y $, then $ [x] = [y] $.
● If the sequence $ \{x_{n}\}_{n = 1}^{\infty} $ in $ (U, \parallel\cdot\parallel) $ converges to $ x $ and $ y $ simultaneously, then $ [x] = [y] $.
(ii) Suppose that the norm $ \parallel\cdot\parallel $ satisfies the null equality. If the sequence $ \{x_{n}\}_{n = 1}^{\infty} $ in $ (U, \parallel\cdot\parallel) $ converges to $ x\in U $, then, given any $ y\in [x] $, the sequence $ \{x_{n}\}_{n = 1}^{\infty} $ also converges to $ y $.
Proof. To prove Part (i), suppose that the sequence $ \{x_{n}\}_{n = 1}^{\infty} $ $ \triangleleft $-converges to $ x $ and $ \triangleright $-converges to $ y $. Then, we have the following limits
Using Proposition 3.8, we obtain
which implies
This shows that $ \parallel x\ominus y\parallel = 0 $. By Definition 3.2, it follows that $ x\ominus y\in\Psi $, i.e., $ x\stackrel{\Psi}{ = }y $. Since the binary relation $ \stackrel{\Psi}{ = } $ is an equivalence relation by Proposition 2.7, we obtain $ [x] = [y] $, which shows the first case. The second case by assuming that $ \{x_{n}\}_{n = 1}^{\infty} $ converges to $ x $ and $ y $ simultaneously can be similarly obtained.
To prove Part (ii), given any $ y\in [x] $, we have
Using Proposition 3.6, the symmetric condition is satisfied. Therefore, we obtain
which says that
This completes the proof.
Inspired by Part (ii) of Proposition 4.3, we propose the following concept of a limit.
Definition 4.4. Let $ (U, \parallel\cdot\parallel) $ be a near pseudo-seminormed space. When a sequence $ \{x_{n}\}_{n = 1}^{\infty} $ in $ U $ converges to some $ x\in U $, the equivalence class $ [x] $ is called the class limit of the sequence $ \{x_{n}\}_{n = 1}^{\infty} $. In this case, we also write
Remark 4.5. Suppose that $ [x] $ is a class limit of the sequence $ \{x_{n}\}_{n = 1}^{\infty} $. Then, for $ y\in [x] $, it is not necessarily that the sequence $ \{x_{n}\}_{n = 1}^{\infty} $ converges to $ y $, unless the norm $ \parallel\cdot\parallel $ satisfies the null equality as given by Part (ii) of Proposition 4.3.
The uniqueness of the class limit is shown below.
Proposition 4.6. Let $ (U, \parallel\cdot\parallel) $ be a near pseudo-normed space. Suppose that the norm $ \parallel\cdot\parallel $ satisfies the null super-inequality. Then, the class limit is unique.
Proof. Suppose that the sequence $ \{x_{n}\}_{n = 1}^{\infty} $ is convergent with two class limits $ [x] $ and $ [y] $. It means
Using (4.1), we have
which says that $ \parallel x\ominus y\parallel = 0 $. Using Part (i) of Proposition 3.9, we obtain $ x\stackrel{\Psi}{ = }y $, i.e., $ [x] = [y] $. This completes the proof.
In the near pseudo-seminormed space $ (U, \parallel\cdot\parallel) $, the symmetric condition is not necessarily satisfied. Therefore, we can propose many different concepts of a Cauchy sequence and completeness as follows.
Definition 4.7. Let $ (U, \parallel\cdot\parallel) $ be a near pseudo-seminormed space, and let $ \{x_{n}\}_{n = 1}^{\infty} $ be a sequence in $ U $.
● $ \{x_{n}\}_{n = 1}^{\infty} $ is called a $ \ltimes $-Cauchy sequence when, given any $ \epsilon > 0 $, there exists an integer $ N $ such that $ n > m > N $ implies $ \parallel x_{n}\ominus x_{m}\parallel < \epsilon $.
a. If every $ \ltimes $-Cauchy sequence in $ U $ is convergent, we say that $ U $ is $ \ltimes $-complete.
b. If every $ \ltimes $-Cauchy sequence in $ U $ is $ \triangleright $-convergent, we say that $ U $ is $ (\ltimes, \triangleright) $-complete.
c. If every $ \ltimes $-Cauchy sequence in $ U $ is $ \triangleleft $-convergent, we say that $ U $ is $ (\ltimes, \triangleleft) $-complete.
● $ \{x_{n}\}_{n = 1}^{\infty} $ is called a $ \rtimes $-Cauchy sequence when, given any $ \epsilon > 0 $, there exists an integer $ N $ such that $ n > m > N $ implies $ \parallel x_{m}\ominus x_{n}\parallel < \epsilon $.
a. If every $ \rtimes $-Cauchy sequence in $ U $ is convergent, we say that $ U $ is $ \rtimes $-complete.
b. If every $ \rtimes $-Cauchy sequence in $ U $ is $ \triangleright $-convergent, we say that $ U $ is $ (\rtimes, \triangleright) $-complete.
c. If every $ \rtimes $-Cauchy sequence in $ U $ is $ \triangleleft $-convergent, we say that $ U $ is $ (\rtimes, \triangleleft) $-complete.
● $ \{x_{n}\}_{n = 1}^{\infty} $ is called a Cauchy sequence when, given any $ \epsilon > 0 $, there exists an integer $ N $ such that $ m, n > N $ with $ m\neq n $ implies $ \parallel x_{n}\ominus x_{m}\parallel < \epsilon $ and $ \parallel x_{m}\ominus x_{n}\parallel < \epsilon $.
a. If every Cauchy sequence in $ U $ is convergent, we say that $ U $ is complete.
b. If every Cauchy sequence in $ U $ is $ \triangleright $-convergent, we say that $ U $ is $ \triangleright $-complete.
c. If every Cauchy sequence in $ U $ is $ \triangleleft $-convergent, we say that $ U $ is $ \triangleleft $-complete.
Remark 4.8. Suppose that $ \parallel\cdot\parallel $ satisfies the symmetric condition, i.e.,
Then all of the concepts of a Cauchy sequence are equivalent, and all of the concepts of completeness are equivalent.
Remark 4.9. It is clear to see that if $ \{x_{n}\}_{n = 1}^{\infty} $ is a Cauchy sequence then $ \{x_{n}\}_{n = 1}^{\infty} $ is both a $ \ltimes $-Cauchy sequence and $ \rtimes $-Cauchy sequence.
Remark 4.10. From Remark 4.9, we have the following observations.
● If $ U $ is complete, then it is also $ \ltimes $-complete and $ \rtimes $-complete.
● If $ U $ $ \triangleright $-complete, then it is also $ (\ltimes, \triangleright) $-complete and $ (\rtimes, \triangleright) $-complete.
● If $ U $ is $ \triangleleft $-complete, then it is also $ (\ltimes, \triangleleft) $-complete and $ (\rtimes, \triangleleft) $-complete.
Proposition 4.11. Let $ (U, \parallel\cdot\parallel) $ be a near pseudo-seminormed space. Suppose that the norm $ \parallel\cdot\parallel $ satisfies the null super-inequality. Then, we have the following properties.
(i) Every convergent sequence is a Cauchy sequence.
(ii) Suppose that the norm $ \parallel\cdot\parallel $ satisfies the null condition. Then, every simultaneously $ \triangleright $-convergent and $ \triangleleft $-convergent sequence is a Cauchy sequence.
(iii) Given any fixed $ x\in U $, suppose that the following conditions are satisfied:
● The sequence $ \{x_{n}\}_{n = 1}^{\infty} $ $ \triangleright $-converges to $ x $.
● The sequence $ \{y_{n}\}_{n = 1}^{\infty} $ $ \triangleleft $-converges to $ x $.
Then, the sequence $ \{x_{n}\ominus y_{n}\}_{n = 1}^{\infty} $ is a Cauchy sequence satisfying
Proof. To prove Part (i), let $ \{x_{n}\}_{n = 1}^{\infty} $ be a convergent sequence. Therefore, by the definition of convergence, given any $ \epsilon > 0 $, we have
for a sufficiently large $ n $. Using Proposition 3.8, we obtain
and
for sufficiently large $ n $ and $ m $. This shows that $ \{x_{n}\}_{n = 1}^{\infty} $ is a Cauchy sequence.
To prove Part (ii), we first note that the null set $ \Psi $ is closed under the condition of the vector addition from Remark 3.3. Assume that the sequence $ \{x_{n}\}_{n = 1}^{\infty} $ simultaneously $ \triangleright $-converges to $ x $ and $ \triangleleft $-converges to $ y $. Then, Part (i) of Proposition 4.3 says that $ x\stackrel{\Psi}{ = }y $, which also implies $ \parallel x\ominus y\parallel = 0 $ by Part (iii) of Proposition 3.9. Given any $ \epsilon > 0 $, we also have
for a sufficiently large $ n $. Since $ \parallel x\ominus y\parallel = 0 $, using Proposition 3.8, we obtain
and
for a sufficiently large $ n $ and $ m $. This shows that $ \{x_{n}\}_{n = 1}^{\infty} $ is a Cauchy sequence.
To prove Part (iii), the assumption says that
Therefore, given any $ \epsilon > 0 $, we have
for a sufficiently large $ n $. Let $ z_{n} = x_{n}\ominus y_{n} $. Then, we have
which shows that
for a sufficiently large $ n $ and $ m $ by using (4.3). We can similarly obtain $ \parallel z_{m}\ominus z_{n}\parallel < \epsilon $. This shows that the sequence $ \{z_{n}\}_{n = 1}^{\infty} $ is a Cauchy sequence. Using Proposition 3.8 and (4.2), we obtain
This completes the proof.
Many different kinds of near Banach spaces can also be proposed as follows.
Definition 4.12. Let $ (U, \parallel\cdot\parallel) $ be a near pseudo-seminormed space. Different kinds of near Banach spaces are defined below.
● If $ U $ is complete, then it is called a near pseudo-semi-Banach space.
● If $ U $ is $ \triangleright $-complete, then it is called a near $ \triangleright $-pseudo-semi-Banach space.
● If $ U $ is $ \triangleleft $-complete, then it is called a near $ \triangleleft $-pseudo-semi-Banach space.
● If $ U $ is $ \ltimes $-complete, then it is called a near $ \ltimes $-pseudo-semi-Banach space.
● If $ U $ is $ (\ltimes, \triangleright) $-complete, then it is called a near $ (\ltimes, \triangleright) $-pseudo-semi-Banach space.
● If $ U $ is $ (\ltimes, \triangleleft) $-complete, then it is called a near $ (\ltimes, \triangleleft) $-pseudo-semi-Banach space.
● If $ U $ is $ \rtimes $-complete, then it is called a near $ \rtimes $-pseudo-semi-Banach space.
● If $ U $ is $ (\rtimes, \triangleright) $-complete, then it is called a near $ (\rtimes, \triangleright) $-pseudo-semi-Banach space.
● If $ U $ is $ (\rtimes, \triangleleft) $-complete, then it is called a near $ (\rtimes, \triangleleft) $-pseudo-semi-Banach space.
Definition 4.13. Different kinds of near Banach spaces are defined below.
● Let $ (U, \parallel\cdot\parallel) $ be a near seminormed space. If $ U $ is complete, then it is called a near semi-Banach space. According to the different kinds of completeness in Definition 4.12, the other kinds of near Banach spaces can be similarly defined.
● Let $ (U, \parallel\cdot\parallel) $ be a near pseudo-normed space. If $ U $ is complete, then it is called a near pseudo-Banach space. According to the different kinds of completeness in Definition 4.12, the other kinds of near Banach spaces can be similarly defined.
● Let $ (U, \parallel\cdot\parallel) $ be a near normed space. If $ U $ is complete, then it is called a near Banach space. According to the different kinds of completeness in Definition 4.12, the other kinds of near Banach spaces can be similarly defined.
Example 4.14. Continued from Example 3.4, we want to claim that the near normed space $ ({\cal I}, \parallel\cdot\parallel) $ is complete. In other words, we want to claim that $ ({\cal I}, \parallel\cdot\parallel) $ is a near Banach space. We first have
Therefore, the norm $ \parallel\cdot\parallel $ satisfies the symmetric condition. Let $ \{[A_{n}, B_{n}]\}_{n = 1}^{\infty} $ be a Cauchy sequence in the space $ ({\cal I}, \parallel\cdot\parallel) $. Therefore, given any $ \epsilon > 0 $, for a sufficiently large $ n $ and $ m $, we have
Let $ C_{n} = A_{n}+B_{n} $. Then, the expression (4.4) says that $ \{C_{n}\}_{n = 1}^{\infty} $ is a Cauchy sequence in $ \mathbb{R} $. The completeness of $ \mathbb{R} $ says that there exists $ C\in\mathbb{R} $ satisfying $ |C_{n}-C| < \epsilon $ for a sufficiently large $ n $. In this case, we can define a closed interval $ [A, B] $ satisfying $ A+B = C $. Therefore, we obtain
for a sufficiently large $ n $. This says that the sequence $ \{[A_{n}, B_{n}]\}_{n = 1}^{\infty} $ is convergent, since the norm $ \parallel\cdot\parallel $ satisfies the symmetric condition. This shows that $ ({\cal I}, \parallel\cdot\parallel) $ is a near Banach space.
Example 4.15. Continued from Example 3.10, we want to claim that the near normed space of fuzzy numbers $ ({\cal F}_{cc}(\mathbb{R}), \parallel\cdot\parallel) $ is complete. Suppose that $ \{\tilde{A}^{(n)}\}_{n = 1}^{\infty} $ is a Cauchy sequence in $ ({\cal F}_{cc}(\mathbb{R}), \parallel\cdot\parallel) $. By definition, we have
We write
Then, we have
For each fixed $ \alpha\in [0, 1] $, we define
Let $ f_{n}(\alpha) = C_{\alpha}^{(n)} $. Using (4.5), we have
According to the properties of fuzzy numbers, the function $ f_{n} $ is continuous on $ [0, 1] $. In this case, we consider a sequence of continuous functions $ \{f_{n}\}_{n = 1}^{\infty} $ on $ [0, 1] $. Then (4.6) says that the sequence of functions $ \{f_{n}\}_{n = 1}^{\infty} $ satisfies the Cauchy condition for uniform convergence. By referring to Apostol [12,Theorem 9.3], it follows that $ \{f_{n}\}_{n = 1}^{\infty} $ converges uniformly to a limit function $ f(\alpha)\equiv C_{\alpha} $ on $ [0, 1] $. In other words, for sufficiently large $ n $, we have
Since each $ f_{n} $ is continuous on $ [0, 1] $, it follows that the limit function $ f(\alpha)\equiv C_{\alpha} $ is continuous on $ [0, 1] $ according to Apostol [12,Theorem 9.2]. The continuity of $ C_{\alpha} $ on $ [0, 1] $ allows us to find a fuzzy number $ \tilde{A} $ satisfying
Therefore, for a sufficiently large $ n $, we have
This shows that the sequence $ \{\tilde{A}^{(n)}\}_{n = 1}^{\infty} $ is convergent. Therefore, we conclude that $ ({\cal F}_{cc}(\mathbb{R}), \parallel\cdot\parallel) $ is a near Banach space of fuzzy numbers.
Example 4.16. Continued from Example 3.11, we further assume that $ (U, \parallel\cdot\parallel_{U}) $ is a (conventional) Banach space. Then, we want to claim that the near normed space $ ({\cal P}(U), \parallel\cdot\parallel) $ is complete. Suppose that $ \{A_{n}\}_{n = 1}^{\infty} $ is a Cauchy sequence in $ ({\cal P}(U), \parallel\cdot\parallel) $. Let $ \mathfrak{A} $ be a collection of all sequences generated by the sequence $ \{A_{n}\}_{n = 1}^{\infty} $. More precisely, each element in $ \mathfrak{A} $ is a sequence $ \{a_{n}\}_{n = 1}^{\infty} $ with $ a_{n}\in A_{n} $ for all $ n $. We want to claim that each sequence (each element) in $ \mathfrak{A} $ is convergent. Since $ \{A_{n}\}_{n = 1}^{\infty} $ is a Cauchy sequence, by definition, we have
which says that
which says $ \parallel a_{n}-a_{m}\parallel_{U} < \epsilon $ for any sequence $ \{a_{n}\}_{n = 1}^{\infty} $ with $ a_{n}\in A_{n} $ for all $ n $ in the uniform sense; that is to say, $ \epsilon $ is independent of $ a_{n} $ and $ a_{m} $. Using the completeness of $ (U, \parallel\cdot\parallel_{U}) $, we see that each sequence $ \{a_{n}\}_{n = 1}^{\infty} $ is convergent to some $ a\in U $ such that
where the uniform sense meas that $ \parallel a_{n}-a\parallel_{U} < \epsilon $ such that $ \epsilon $ is independent of $ a_{n}\in A_{n} $ and $ a $ for a sufficiently large $ n $. Indeed, if $ \epsilon $ is dependent on $ a_{n} $ and $ a $, then
says that $ \epsilon $ is dependent on $ a_{n} $ and $ a_{m} $, which is a contradiction.
We can define a subset $ A $ of $ U $ that collects all of the limit points of each sequence in $ \mathfrak{A} $. Then, we want to show $ \parallel A_{n}\ominus A\parallel\rightarrow 0 $ as $ n\rightarrow \infty $. Given any $ x\in A_{n}-A $, we have $ x = a_{n}-a $ for some $ a_{n}\in A_{n} $ and $ a\in A $. Since $ a $ is a limit point of some sequence $ \{\hat{a}_{n}\}_{n = 1}^{\infty} $ in $ \mathfrak{A} $, for $ m > n > N $, using (4.8), we have
where $ \epsilon $ is independent of $ a_{n} $ and $ \hat{a}_{m} $ according to (4.8). Since $ \parallel \hat{a}_{m}-a\parallel_{U}\rightarrow 0 $ as $ m\rightarrow \infty $ in the unform sense according to (4.9), it follows that $ \parallel a_{n}-a\parallel_{U}\rightarrow 0 $ as $ n\rightarrow \infty $ in the uniform sense. Therefore, we obtain
This shows that the sequence $ \{A_{n}\}_{n = 1}^{\infty} $ is convergent. Therefore, we conclude that $ ({\cal P}(U), \parallel\cdot\parallel) $ is a near Banach space.
5.
Near fixed point theorems
Let $ T:U\rightarrow U $ be a function from a universal set $ U $ into itself. Any point $ x\in U $ is called a fixed point when we have $ T(x) = x $. Recall that $ ({\cal I}, \parallel\cdot\parallel) $ presented in Example 3.4 is not a (conventional) normed space. Therefore, we are not able to study the fixed point of contractive mappings defined on $ ({\cal I}, \parallel\cdot\parallel) $ into itself. In this paper, we shall study the so-called near fixed point that is defined below.
Definition 5.1. Let $ U $ be a near vector space over $ \mathbb{R} $ with a null set $ \Psi $, and let $ T:U\rightarrow U $ be a function defined on $ U $ into itself. A point $ x\in U $ is called a near fixed point of $ T $ when we have $ T(x)\stackrel{\Psi}{ = }x $.
In the sequel, we shall consider three different contractions to study the near fixed point theorem.
5.1. Contraction on near pseudo-seminormed space
We are going to propose the concept of a contraction on a near pseudo-seminormed space. Under some suitable conditions, we can obtain the near fixed point theorem based on near Banach space.
Definition 5.2. Let $ (U, \parallel\cdot\parallel) $ be a near pseudo-seminormed space, and let $ T:(U, \parallel\cdot\parallel)\rightarrow (U, \parallel\cdot\parallel) $ be a function from $ (U, \parallel\cdot\parallel) $ into itself. The function $ T $ is called a contraction on $ U $ when there exists a real number $ 0 < \alpha < 1 $ such that the inequality
is satisfied for any $ x, y\in U $.
Given any initial element $ x_{0}\in U $, we can generate an iterative sequence $ \{x_{n}\}_{n = 1}^{\infty} $ using the composition of function $ T $ given by
The main goal of this paper is to show that the sequence $ \{x_{n}\}_{n = 1}^{\infty} $ in $ U $ can converge to a near fixed point.
Theorem 5.3. (Near fixed point theorem). Let $ (U, \parallel\cdot\parallel) $ be a near pseudo-Banach space with the null set $ \Psi $. Suppose that the following conditions are satisfied.
● The norm $ \parallel\cdot\parallel $ satisfies the null equality.
● The null sets $ \Psi $ is closed under the condition of the vector addition and satisfies the neutral condition.
● The function $ T:(U, \parallel\cdot\parallel)\rightarrow (U, \parallel\cdot\parallel) $ is a contraction on $ U $.
Then $ T $ has a near fixed point $ x\in U $ satisfying $ T(x)\stackrel{\Psi}{ = }x $. Moreover, the near fixed point $ x $ is obtained by the following limit
where the sequence $ \{x_{n}\}_{n = 1}^{\infty} $ is generated according to (5.1). We also have the following properties.
(a) There is a unique equivalence class $ [x] $ such that, for any $ x^{*}\not\in [x] $, $ x^{*} $ cannot be a near fixed point. If $ x^{*} $ is a near fixed point of $ T $, then we have $ [x^{*}] = [x] $, i.e., $ x\stackrel{\Psi}{ = }x^{*} $.
(b) Every point $ x^{*} $ in the equivalent class $ [x] $ is also a near fixed point of $ T $ such that the following equalities
are satisfied.
Proof. Proposition 3.6 says that the norm $ \parallel\cdot\parallel $ satisfies the symmetric condition. Using Proposition 2.7, we also see that the family of all sets $ [x] $ forms the equivalence classes. Given any initial element $ x_{0}\in U $, we are going to show that the sequence $ \{x_{n}\}_{n = 1}^{\infty} $ generated by (5.1) is a Cauchy sequence. Now, we have
Given any two integers $ n $ and $ m $ satisfying $ n < m $, we obtain
Since $ 0 < \alpha < 1 $, it follows that
which shows that $ \{x_{n}\}_{n = 1}^{\infty} $ is a Cauchy sequence. Since the norm $ \parallel\cdot\parallel $ satisfies the symmetric condition and the near normed space $ (U, \parallel\cdot\parallel) $ is complete, there exists $ x\in U $ satisfying
Next, we want to claim that any point $ x^{*} $ in the equivalence class $ [x] $ is a near fixed point. We first have
Since the norm $ \parallel\cdot\parallel $ satisfies the null equality, we have
Using Proposition 3.8, we also have
The the neutral condition says that $ -\psi_{1}\in\Psi $. Since the norm $ \parallel\cdot\parallel $ satisfies the null equality, we have
Using Proposition 3.7, we also have
which says that
Combining (5.5)–(5.7), we obtain
Using (5.4), we also obtain
Now, we have
and
Combining (5.8)–(5.10), we obtain
which implies $ \parallel x^{*}\ominus T(x^{*})\parallel = 0 $ as $ m\rightarrow \infty $ by using (5.3). Using Part (i) of Proposition 3.9, we obtain
Now, we assume that $ x^{\circ}\not\in [x] $ is another near fixed point $ x^{\circ} $ of $ T $, i.e., $ x^{\circ}\stackrel{\Psi}{ = } T(x^{\circ}) $. Since $ x\stackrel{\Psi}{ = } T(x) $, we have
for some $ \psi_{i}\in\Psi $, $ i = 1, \cdots, 4 $. Now, we have
We can similarly obtain
Therefore, we obtain
Since $ 0 < \alpha < 1 $, it forces $ \parallel x^{\circ}\ominus x\parallel = 0 $, i.e., $ x^{\circ}\stackrel{\Psi}{ = }x $ by Part (i) of Proposition 3.9, which contradicts $ x^{\circ}\not\in [x] $. This shows that any $ x^{\circ}\not\in [x] $ cannot be the near fixed point of $ T $. Equivalently, if $ x^{\circ} $ is a near fixed point of $ T $, then we must have $ x^{\circ}\in [x] $. This completes the proof.
5.2. Weakly strict contraction on near pseudo-normed space
We are going to propose the concept of a weakly strict contraction on a near pseudo-seminormed space. Under some suitable conditions, we can obtain the near fixed point theorem based on a near $ \ltimes $-Banach space and near $ \rtimes $-Banach space.
Definition 5.4. Let $ (U, \parallel\cdot\parallel) $ be a near pseudo-normed space. A function
is called a weakly strict contraction on $ U $ when the following conditions are satisfied:
● $ x\stackrel{\Psi}{ = }y $ implies $ \parallel T(x)\ominus T(y)\parallel = 0 $;
● $ x\stackrel{\Psi}{\neq}y $ implies $ \parallel T(x)\ominus T(y)\parallel < \parallel x\ominus y\parallel $.
Part (i) of Proposition 3.9 says that $ x\stackrel{\Psi}{\neq}y $ implies $ \parallel x\ominus y\parallel\neq 0 $. Therefore, the second condition of the weakly strict contraction is well-defined. In other words, when we consider the weakly strict contraction, the space $ (U, \parallel\cdot\parallel) $ should be assumed to be a near pseudo-normed space rather than a near pseudo-seminormed space.
Proposition 5.5. Let $ (U, \parallel\cdot\parallel) $ be a near pseudo-normed space. Suppose that the norm $ \parallel\cdot\parallel $ satisfies the null super-inequality and null condition. If $ T $ is a contraction on $ U $, then it is also a weakly strict contraction on $ U $.
Proof. Since $ T $ is a contraction on $ U $, we have
for $ 0 < \alpha < 1 $. We consider the following two cases.
● Suppose that $ x\stackrel{\Psi}{ = }y $. Part (iii) of Proposition 3.9 says that $ \parallel x\ominus y\parallel = 0 $, which implies
i.e., $ \parallel T(x)\ominus T(y)\parallel = 0 $.
● Suppose that $ x\stackrel{\Psi}{\neq}y $. Then, we have
since $ 0 < \alpha < 1 $.
This completes the proof.
Theorem 5.6. (Near fixed point theorem). Let $ (U, \parallel\cdot\parallel) $ be a near pseudo $ \ltimes $-Banach space $ ($resp. near pseudo $ \rtimes $-Banach space$) $ with the null set $ \Psi $. Suppose that the following conditions are satisfied.
● The null set $ \Psi $ satisfies the neutral condition.
● The norm $ \parallel\cdot\parallel $ satisfies the null super-inequality and null condition.
● The function $ T:(U, \parallel\cdot\parallel)\rightarrow (U, \parallel\cdot\parallel) $ is a weakly strict contraction on $ U $.
If $ \{T^{n}(x_{0})\}_{n = 1}^{\infty} $ forms a $ \ltimes $-Cauchy sequence $ ($resp. $ \rtimes $-Cauchy sequence$) $ for some $ x_{0}\in U $, then $ T $ has a near fixed point $ x\in U $ satisfying $ T(x)\stackrel{\Psi}{ = }x $. Moreover, the near fixed point $ x $ is obtained by the following limit
We further assume that the norm $ \parallel\cdot\parallel $ satisfies the null equality. Then, we also have the following properties.
(a) There is a unique equivalence class $ [x] $ such that, for any $ x^{*}\not\in [x] $, $ x^{*} $ cannot be a near fixed point. If $ x^{*} $ is a near fixed point of $ T $, then we have $ [x^{*}] = [x] $, i.e., $ x\stackrel{\Psi}{ = }x^{*} $.
(b) Every point $ x^{*} $ in the equivalent class $ [x] $ is also a near fixed point of $ T $ such that the following equalities
are satisfied.
Proof. Since $ (U, \parallel\cdot\parallel) $ is a near $ \ltimes $-Banach space, using the $ \ltimes $-completeness, the $ \ltimes $-Cauchy sequence $ \{T^{n}(x_{0})\}_{n = 1}^{\infty} $ says that there exists $ x\in U $ satisfying
Therefore, given any $ \epsilon > 0 $, there exists an integer $ N $ such that
Since $ T $ is a weakly strict contraction on $ U $, we consider the following two cases.
● For $ T^{n}(x_{0})\stackrel{\Psi}{ = }x $, using Part (iii) of Proposition 3.9, the weakly strict contraction says that
● For $ T^{n}(x_{0})\stackrel{\Psi}{\neq}x $, using (5.15), the weakly strict contraction says that
The above two cases show that
Using Proposition 3.8, we obtain
Using (5.14) and (5.16), we also obtain
which says that $ \parallel x\ominus T(x)\parallel = 0 $, i.e., $ T(x)\stackrel{\Psi}{ = }x $ by using Part (i) of Proposition 3.9. This shows that $ x $ is a near fixed point.
Similarly, when $ (U, \parallel\cdot\parallel) $ is assumed to be a near $ \rtimes $-Banach space and $ \{T^{n}(x_{0})\}_{n = 1}^{\infty} $ is assumed to be a $ \rtimes $-Cauchy sequence, the above arguments are still valid to show that $ x $ is a near fixed point.
Now, we further assume that the norm $ \parallel\cdot\parallel $ satisfies the null equality. Proposition 3.6 says that the norm $ \parallel\cdot\parallel $ satisfies the symmetric condition. Since $ x $ is a near fixed point, in the sequel, we shall claim that each point $ x^{*} $ in the class $ [x] $ is also a near fixed point of $ T $. For any $ x^{*}\in [x] $, we first note $ x^{*}\stackrel{\Psi}{ = }x $, which says that
Then, we have
Using (5.14), we obtain
Therefore, given any $ \epsilon > 0 $, there exists an integer $ N $ such that
Since $ T $ is a weakly strict contraction on $ U $, we consider the following two cases.
● For $ T^{n}(x_{0})\stackrel{\Psi}{ = }x^{*} $, using Part (iii) of Proposition 3.9, the weakly strict contraction says that
● For $ T^{n}(x_{0})\stackrel{\Psi}{\neq}x^{*} $, using (5.19), the weakly strict contraction says that
The above two cases show that
Using Proposition 3.8, we have
Using (5.18) and (5.20), we also obtain
which says that $ \parallel x^{*}\ominus T(x^{*})\parallel = 0 $, i.e., $ T(x^{*})\stackrel{\Psi}{ = }x^{*} $ by using Part (i) of Proposition 3.9. This shows that $ x^{*} $ is a near fixed point for any point $ x^{*}\in [x] $.
Suppose that $ x^{\circ}\not\in [x] $ is another near fixed point of $ T $. Then, we have
Since we also have $ T(x)\stackrel{\Psi}{ = }x $, it follows that
for some $ \psi_{i}\in\Psi $ for $ i = 1, 2, 3, 4 $. On the other hand, we have
We can similarly obtain
Therefore, we have
This contradiction shows that any $ x^{\circ}\not\in [x] $ cannot be the near fixed point of $ T $. Equivalently, if $ x^{\circ} $ is a near fixed point of $ T $, then we must have $ x^{\circ}\in [x] $. This completes the proof.
5.3. Weakly uniformly strict contraction on near pseudo-normed space
We are going to propose the concept of a weakly uniformly strict contraction on a near pseudo-normed space. Under some suitable conditions, we can obtain the near fixed point theorem based on the near $ \rtimes $-Banach space and near $ \ltimes $-Banach space. The concept of a weakly uniformly strict contraction was proposed by Meir and Keeler [13].
Definition 5.7. Let $ (U, \parallel\cdot\parallel) $ be a near pseudo-normed space with the null set $ \Psi $. A function
is called a weakly uniformly strict contraction on $ U $ when the following conditions are satisfied
● $ x\stackrel{\Psi}{ = }y $ implies $ \parallel T(x)\ominus T(y)\parallel = 0 $;
● given any $ \epsilon > 0 $, there exists $ \delta > 0 $ such that
for any $ x\stackrel{\Psi}{\neq}y $.
Part (i) of Proposition 3.9 says that $ x\stackrel{\Psi}{\neq}y $ implies $ \parallel x\ominus y\parallel\neq 0 $. Therefore, the second condition of the weakly uniformly strict contraction is well-defined. In other words, when we consider the weakly uniformly strict contraction, the space $ (U, \parallel\cdot\parallel) $ should be assumed to be a near pseudo-normed space rather than a near pseudo-seminormed space.
Remark 5.8. Since the second condition implies
it says that if $ T $ is a weakly uniformly strict contraction on $ U $, then $ T $ is also a weakly strict contraction on $ U $.
Lemma 5.9. Let $ (U, \parallel\cdot\parallel) $ be a near pseudo-normed space with the null set $ \Psi $, and let
be a weakly uniformly strict contraction on $ U $. Suppose that the norm $ \parallel\cdot\parallel $ satisfies the null super-inequality and null condition. Then, for any $ x\in U $, the sequence $ \{\parallel T^{n}(x)\ominus T^{n+1}(x)\parallel\}_{n = 1}^{\infty} $ is decreasing and satisfying
Proof. Let $ T^{n}(x) = a_{n} $ and $ b_{n} = \parallel a_{n}\ominus a_{n+1}\parallel $ for all $ n $. We consider the following two cases.
● For $ [a_{n-1}]\neq [a_{n}] $, we have
● For $ [a_{n-1}] = [a_{n}] $, we have
The above two cases show that the sequence $ \{b_{n}\}_{n = 1}^{\infty} $ is indeed decreasing.
Suppose that $ a_{k}\stackrel{\Psi}{\neq}a_{k+1} $ for all $ k\geq 1 $. Since the sequence $ \{b_{n}\}_{n = 1}^{\infty} $ has been proven to be decreasing, we assume $ b_{n}\downarrow\epsilon > 0 $, i.e., $ b_{n}\geq\epsilon > 0 $ for all $ n $. Then, there exists $ \delta > 0 $ satisfying $ \epsilon\leq b_{k} < \epsilon +\delta $ for some $ k $, i.e.,
Therefore, we have
which contradicts $ b_{k+1}\geq\epsilon $. This contradiction says that $ a_{k}\stackrel{\Psi}{ = }a_{k+1} $ for some $ k\geq 1 $. Therefore, we can now assume that $ k $ is the first index in the sequence $ \{a_{n}\}_{n = 1}^{\infty} $ satisfying $ a_{k-1}\stackrel{\Psi}{ = }a_{k} $. Then, we want to claim that $ b_{k-1} = b_{k} = b_{k+1} = \cdots = 0 $. Since $ a_{k-1}\stackrel{\Psi}{ = }a_{k} $, Part (iii) of Proposition 3.9 says that
We also have
which says that $ a_{k}\stackrel{\Psi}{ = }a_{k+1} $ by Part (ii) of Proposition 3.9. Using the similar arguments, we can also obtain $ b_{k+1} = 0 $ and $ a_{k+1}\stackrel{\Psi}{ = }a_{k+2} $. Therefore, the sequence $ \{b_{n}\}_{n = 1}^{\infty} $ is decreasing to zero. This completes the proof.
Theorem 5.10. (Meir-Keeler type of near fixed point theorem). Let $ (U, \parallel\cdot\parallel) $ be a near pseudo $ \rtimes $-Banach space or near pseudo $ \ltimes $-Banach space with the null set $ \Psi $. Suppose that the following conditions are satisfied.
● The null sets $ \Psi $ satisfies the neutral condition.
● The norm $ \parallel\cdot\parallel $ satisfies the null super-inequality and null condition.
● The function $ T:(U, \parallel\cdot\parallel)\rightarrow (U, \parallel\cdot\parallel) $ is a weakly uniformly strict contraction on $ U $.
● There exists $ x_{0}\in U $ satisfying
Then $ T $ has a near fixed point satisfying $ T(x)\stackrel{\Psi}{ = }x $. Moreover, the near fixed point $ x $ is obtained by the following limit
We further assume that the norm $ \parallel\cdot\parallel $ satisfies the null equality. Then, we also have the following properties.
(a) There is a unique equivalence class $ [x] $ such that, for any $ x^{*}\not\in [x] $, $ x^{*} $ cannot be a near fixed point. If $ x^{*} $ is a near fixed point of $ T $, then we have $ [x^{*}] = [x] $, i.e., $ x\stackrel{\Psi}{ = }x^{*} $.
(b) Every point $ x^{*} $ in the equivalent class $ [x] $ is also a near fixed point of $ T $ such that the following equalities
are satisfied.
Proof. Using Theorem 5.6 and Remark 5.8, we remain to show that if $ T $ is a weakly uniformly strict contraction, then $ \{T^{n}(x_{0})\}_{n = 1}^{\infty} $ forms both a $ \rtimes $-Cauchy sequence and $ \ltimes $-Cauchy sequence.
Let $ a_{n} = T^{n}(x_{0}) $ and $ b_{n} = \parallel a_{n}\ominus a_{n+1}\parallel $. Suppose that $ \{T^{n}(x_{0})\}_{n = 1}^{\infty} = \{a_{n}\}_{n = 1}^{\infty} $ is not a $ \rtimes $-Cauchy sequence. Then, there exists $ \epsilon > 0 $ such that, given an integer $ N $, there exist $ n > m\geq N $ satisfying $ \parallel a_{m}\ominus a_{n}\parallel > 2\epsilon $. Since $ T $ is a weakly uniformly strict contraction on $ U $, the definition says that there exists $ \delta > 0 $ such that
Let $ \eta = \min\{\delta, \epsilon\} $. We are going to claim that
We consider the following two cases.
● If $ \eta = \delta $, it is clear to see that (5.25) implies (5.26).
● If $ \eta = \epsilon $, it means that $ \epsilon < \delta $. Therefore, we have
which also says that (5.25) implies (5.26)
For $ n > m\geq N $, we have
Therefore, using Part (iii) of Proposition 3.9, we obtain
From (5.24), we have
Lemma 5.9 says that the sequence $ \{b_{n}\}_{n = 1}^{\infty} $ is decreasing to zero. Therefore, we can find an integer $ N $ satisfying $ b_{N} < \eta/3 $. Then, for $ m\geq N $, we obtain
For $ k $ with $ m < k\leq n $, Proposition 3.8 says that
We want to show that there exists $ k $ with $ m < k\leq n $ satisfying
Let $ \gamma_{k} = \parallel a_{m}\ominus a_{k}\parallel $ for $ k = m+1, \cdots, n $. Then, (5.27) implies
and (5.29) implies
Let $ k_{0} $ be an index satisfying
Then, we have
From (5.32) and (5.33), we also see that $ m+1\leq k_{0} < n $, which says that $ k_{0} $ is well defined. Since $ k_{0} $ is an integer, we also have $ k_{0}+1\leq n $. By the definition of $ k_{0} $, it means that $ k_{0}+1 $ does not satisfy (5.34), i.e.,
which also says that $ a_{m}\stackrel{\Psi}{\neq}a_{k_{0}+1} $ by using Part (iii) of Proposition 3.9. Therefore, from (5.36), the expression (5.31) will be sound if we can show that $ \gamma_{k_{0}+1} < \epsilon +\eta $. Suppose that this is not true, i.e.,
From (5.30), we have
Therefore, we have
This contradiction says that (5.31) is sound.
Using (5.26), we see that (5.31) implies
Therefore, we obtain
which contradicts (5.31). This contradiction shows that the sequence $ \{T^{n}(x)\}_{n = 1}^{\infty} $ is a $ \rtimes $-Cauchy sequence.
We can similarly prove that the sequence $ \{T^{n}(x)\}_{n = 1}^{\infty} $ is a $ \ltimes $-Cauchy sequence. This completes the proof.
Example 5.11. Continued from Example 4.15, suppose that the function
is a contraction on $ {\cal F}_{cc}(\mathbb{R}) $. Using Theorem 5.3, the contraction $ T $ has a near fixed point $ \tilde{x}\in {\cal F}_{cc}(\mathbb{R}) $ satisfying $ T(\tilde{x})\stackrel{\Psi}{ = }\tilde{x} $. Moreover, the near fixed point $ \tilde{x} $ is obtained by the following limit
in which the sequence $ \{\tilde{x}_{n}\}_{n = 1}^{\infty} $ is generated according to $ (5.1) $. We also have the following properties.
(a) There is a unique equivalence class $ [\tilde{x}] $ such that, for any $ \tilde{x}^{*}\not\in [\tilde{x}] $, $ \tilde{x}^{*} $ cannot be a near fixed point. If $ \tilde{x}^{*} $ is a near fixed point of $ T $, then we have $ [\tilde{x}^{*}] = [\tilde{x}] $, i.e., $ \tilde{x}\stackrel{\Psi}{ = }\tilde{x}^{*} $.
(b) Every point $ \tilde{x}^{*} $ in the equivalent class $ [\tilde{x}] $ is also a near fixed point of $ T $ such that the following equalities
are satisfied.
Example 5.12. Continued from Example 4.15, suppose that the function
is a weakly uniformly strict contraction on $ {\cal F}_{cc}(\mathbb{R}) $. Theorem 5.10 says that $ T $ has a near fixed point satisfying $ T(\tilde{x})\stackrel{\Psi}{ = }\tilde{x} $. Moreover, the near fixed point $ \tilde{x} $ is obtained by the following limit
We also have the same properties (a) and (b) given in Example 5.11.
6.
Conclusions
The so-called near vector space, which extends the concept of a vector space, is considered in this paper. The main issue of a near vector space is that it lacks the additive inverse elements. Three well-known space near vector spaces are the space of all bounded and closed intervals in $ \mathbb{R} $, the space of all compact and convex subsets of a topological space, and the space of all fuzzy numbers in $ \mathbb{R} $. We see that these three spaces do not own the concept of additive inverse elements. Therefore, the so-called null set is introduced to play the role of zero element.
Based on the null set, a so-called near normed space is proposed, which just endows a norm to a near vector space. Furthermore, the concept of completeness is then introduced to propose the so-called near Banach space. Therefore, under these settings, we are able to establish the near fixed point theorems in near Banach space. In the future research, many advanced topics regarding the fixed point theorems can be hopefully established in near vector space.
Conflict of interest
The author declares that he has no conflict of interest.













 DownLoad:
DownLoad: