Advanced financial market forecasting: integrating Monte Carlo simulations with ensemble Machine Learning models

1.   Introduction

In the ever-evolving landscape of financial markets, the quest for more accurate and dynamic forecasting models has always been at the forefront of both academic research and practical applications. The intricate and volatile nature of financial markets demands sophisticated tools that can not only predict future trends, but also assess associated risks with a high degree of precision. This paper presents an integrated approach that combines the strengths of ML (ML) models with the robust scenario analysis capabilities of Monte Carlo simulations, setting a new benchmark in the field of financial forecasting and risk assessments.

Historically, financial forecasting relied on statistical and econometric models, which, while foundational, often struggled to fully grasp the complexities inherent in financial data. The advent of ML heralded a paradigm shift, offering models capable of deciphering non-linear relationships and processing vast, multidimensional datasets. This transition is critically examined in the early sections of the paper, emphasizing the evolution from linear time-series analyses to advanced ML techniques such as Random Forest (Kumar and Thenmozhi, 2006), Support Vector Machines, and neural networks, specifically LSTM networks(Deep, 2023a).

While ML models have significantly enhanced market prediction capabilities, they are not without limitations. Challenges such as overfitting and the inherently non-stationary nature of financial data necessitate further advancements. This paper responds to these challenges by integrating ML models with Monte Carlo simulations, which is a method traditionally used in finance for risk assessment and derivative pricing. This integration is not only innovative but also pragmatically essential, particularly in capturing the dynamic and stochastic nature of financial markets.

The core methodology of this study involves an ensemble of ML models, including Random Forest Regression, LSTM Networks, Linear Regression, and Sentiment Analysis, all fine-tuned through reinforcement learning for dynamic weight adjustment. The base model is presented in our previous work titled "A Multifactor Analysis Model for Stock Market Prediction" (Deep, 2023a). These models are then seamlessly integrated with Monte Carlo simulations, which are employed for both risk assessment and the dynamic calculation of beta, a measure of systematic risk. This fusion results in a robust tool that enhances both predictive accuracy and risk evaluation, significantly advancing the field of financial forecasting.

Furthermore, the paper explores quantitative analyses, employing a variety of risk-reward ratios such as Sharpe, Sortino, Treynor, Calmar, Sterling, and Rachev ratios. These analyses provide a comprehensive view of the risk-reward profiles for selected stocks and the SPY Exchange-Traded Fund (ETF), demonstrating the practical application of the proposed methodologies.

In conclusion, this paper not only presents an innovative approach to financial forecasting but also sets a new standard in the integration of ML with traditional financial modeling techniques. The methodologies and analyses detailed herein offer invaluable insights for investors, financial analysts, and academics, paving the way for more informed and effective financial decision-making in an increasingly complex market environment.

2.   Literature review

2.1.   Evolution of financial forecasting models

Financial forecasting has evolved over the past few decades, transitioning from traditional statistical models to more sophisticated ML techniques. Early methods, such as time-series analyses and econometric models, were rooted in linear assumptions and often struggled with the complexities of financial data. Di Persio et al. (2023) presented a hybrid approach that combined Generalized AutoRegressive Conditional Heteroskedasticity (GARCH) models with recurrent neural networks (RNNs), including LSTM and Gated recurrent unit (GRU), for improved volatility forecasting, essential for implementing risk parity strategies in multi-asset portfolios (Di Persio et al., 2023). The advent of ML models, such as Random Forest, Support Vector Machines, and neural networks, marked a paradigm shift (Nokeri, 2021). These models are capable of capturing non-linear relationships and handling large, multi-dimensional datasets, making them particularly suited for analyzing financial markets characterized by their dynamic and chaotic nature.

2.2.   ML in market prediction

ML models, particularly deep learning algorithms like LSTM networks, have shown significant promise in predicting financial market trends.As indicated by recent research (Fang and George, 2017), neural networks offer promising avenues for overcoming the limitations of classical models in accurately pricing financial derivatives under conditions of high volatility. These models excel in identifying patterns in historical data, which is essential for forecasting future market movements. However, their performance can be hindered by overfitting and the non-stationary nature of financial data.

2.3.   Monte Carlo simulations in finance

Monte Carlo simulations have been a staple in financial modeling, primarily for risk assessment and derivative pricing (Glasserman, 2004). Their stochastic nature allows for the exploration of a vast number of scenarios, making them ideal to assess the probability distribution of potential outcomes. However, integrating these simulations with ML models for an enhanced predictive accuracy is a relatively new area of exploration.

2.4.   Beta calculation and financial risk

The calculation of beta, which is a measure of systematic risk, is crucial in financial risk management. Traditional linear regression methods used for calculating beta often oversimplify the dynamic relationship between an individual asset and the market. Recent research by (Heymans and Brewer, 2023) highlighted the significance of considering volatility spillover effects in beta calculations. They proposed an enhanced approach to constructing efficient portfolios by integrating traditional market beta measures with an analysis of volatility spillovers among stocks. Using intraday stock returns and a residual-based test (aggregate shock model) framework, their study demonstrated that portfolios with stocks that exhibit minimal spillover effects tend to have reduced overall volatility. This insight, supported by their experimental approach involving Monte Carlo simulations, aligns with the need for more sophisticated techniques in systematic risk assessment, further emphasizing the relevance of dynamic and nuanced methods in beta calculations.

2.5.   Integrating ML with monte Carlo Simulations

The integration of ML models with Monte Carlo simulations represents a novel approach in financial forecasting and risk assessments. This integration leverages the predictive power of ML and the scenario analysis strength of Monte Carlo simulations, thus aiming to provide a more robust and adaptive forecasting tool. Such integration is especially pertinent in the context of rapidly evolving financial markets, where traditional models may fail to capture the full spectrum of market dynamics.

This literature review provides a comprehensive overview of the current state of financial forecasting models, highlighting both the advancements and the gaps in existing methodologies. It underscores the potential of integrating ML models with Monte Carlo simulations to create a more dynamic, adaptive, and accurate tool for financial market forecasting and risk assessments, setting the foundation for the proposed study in this field.

3.   Methodology

This study creates innovations in financial market forecasting and risk assessments by integrating Monte Carlo simulations with a composite of ML models, which are augmented by reinforcement learning for a dynamic weight adaptation. The methodology is segmented into distinct components: the assembly of ensemble ML models, the application of Monte Carlo simulations, their integration, data sourcing and preprocessing, and the experimental framework.

3.1.   Ensemble ML models

We employ an ensemble of diverse ML models (Deep, 2023a), each bringing a unique perspective to financial data analyses:

● Random Forest Regression: Random Forest Regression is an ensemble learning method that constructs a composite model from numerous decision trees. Each tree independently estimates the target variable, with the final output being an aggregated mean of all tree predictions. To mitigate overfitting, a penalty term $\lambda$ for the number of trees $B$ is introduced. This adjustment balances predictive performance with the model complexity. The modified mathematical representation of the Random Forest model is as follows:

where $R(x)$ is the Random Forest prediction, $T_b(x; \Theta_b)$ represents the prediction of the $b$-th decision tree, $B$ is the number of trees, and $\lambda$ is the penalty term. The inclusion of $\lambda$ ensures a balance between the bias and the variance, maintaining the model's robustness while avoiding undue complexity.

The penalty term in a Random Forest model might not work effectively when it is either too small or too large. If the penalty term is too small, it may not effectively prevent overfitting, as the model could still grow to be too complex by including too many trees, each fitting closely to the training data. Conversely, if the penalty term is too large, it may overly simplify the model by discouraging the inclusion of enough trees, potentially leading to underfitting where the model cannot capture the underlying patterns in the data. The key is finding a balance that optimizes the model complexity without compromising the predictive accuracy.

● Long Short-Term Memory (LSTM) Networks: LSTM networks are specialized deep learning models for processing sequences, thus capturing long-term dependencies in time-series data. The core of an LSTM unit is formulated as follows:

where $\sigma$ is the sigmoid function, and $W$ and $b$ are the weights and biases of the model, respectively.

● Addressing Non-Stationarity in Financial Data: This is a critical aspect for predictive modeling of financial time series data. To tackle non-stationarity, we incorporate adaptive mechanisms in our ML models, especially in LSTM networks.

– Adaptive Mechanisms for Non-Stationary Data: We use online learning algorithms and rolling window analyses. These methods enable continual model updates and adaptation, capturing recent market trends and dynamics.

– Rolling Window Analysis for LSTM Models: The LSTM models are adapted to use a rolling window analysis, which dynamically adjusts the window size based on the market volatility and trends. The LSTM's formulation in this context is as follows:

where $W$ is the rolling window size, $\Theta$ represents the LSTM model parameters, and $x_t$ is the input at time $t$.

– Responding to Market Volatility: In addition to the rolling window analysis, our models incorporate mechanisms for adjusting their learning rate and parameters in response to the observed market volatility, ensuring sensitivity to market shifts and emergent patterns.

● Linear Regression: A linear regression provides a baseline for predictions and interpretability. It models the relationship between a dependent variable $y$ and independent variables $x$ as follows:

where $\beta$ are coefficients, and $\epsilon$ is the error term.

● Sentiment Analysis: A sentiment analysis employs Natural Language Processing (NLP) to analyze textual data, extracting market sentiment. The sentiment score $S$ for a document $d$ can be formulated as follows:

where $\text{Polarity}(t)$ represents the sentiment polarity of term $t$.

● Support Vector Regression (SVR): SVR is derived from support vector machines, and is optimized for regression tasks. It finds a hyperplane in a multi-dimensional space that best fits the data points, effectively managing non-linear and high-dimensional data. The objective function of SVR is as follows:

and is subject to the following:

where $w$ is the weight vector, $b$ is the bias, and $\xi, \xi^*$ are slack variables. SVR is used for its ability to handle non-linear patterns in financial time series data.

The ensemble is dynamically weighted using a reinforcement learning algorithm, optimizing the predictive performance based on market conditions (Deep, 2023b). The weight adjustment can be modeled as a reinforcement learning problem, where the reward function is aligned with the prediction accuracy.

3.2.   Dynamic weight adjustment in reinforcement learning

Our approach innovatively leverages a dynamic weight adjustment mechanism amongst an ensemble of ML models through a reinforcement learning strategy (Deep, 2023b). This approach is pivotal to optimize the predictive accuracy of individual stocks such as Apple Inc (AAPL), Amazon.com Inc (AMZN), Google/Alphabet Inc Class C (GOOG), Microsoft Corp (MSFT), and NVIDIA Corp (NVDA), tailoring the weight distribution to the unique patterns and volatilities of each stock.

We have adopted the Advantage Actor-Critic (A2C) algorithm, which is a policy gradient method distinguished for its robustness in continuous and complex action spaces that aligns well with the multifaceted nature of financial markets. The A2C algorithm assists in assigning dynamic weights to various models within the ensemble, with adjustments based on their real-time performance. This dynamic weighting is particularly crucial in financial forecasting, where market conditions are in constant flux, and the relevance of specific predictive models can shift rapidly.

The reward function within our Reinforcement Learning (RL) framework plays a critical role, designed to evaluate and provide feedback on the effectiveness of weight adjustments in terms of their impact on the portfolio performance. It serves as a performance indicator, rewarding the agent for effective weight choices and penalizing it for suboptimal selections, thus guiding the agent towards more profitable decision-making pathways.

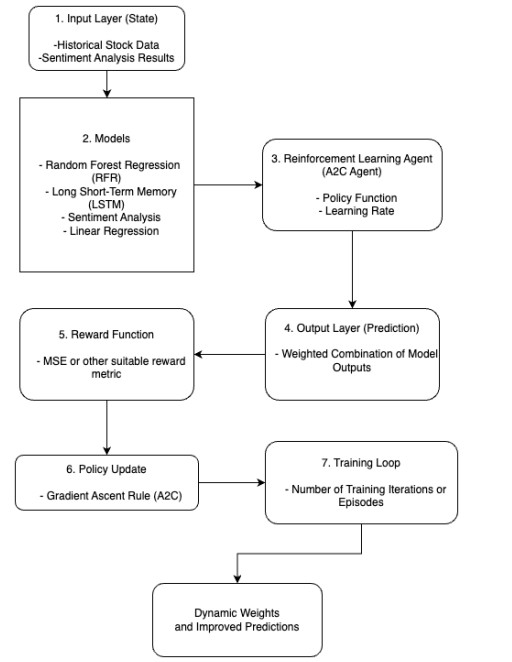
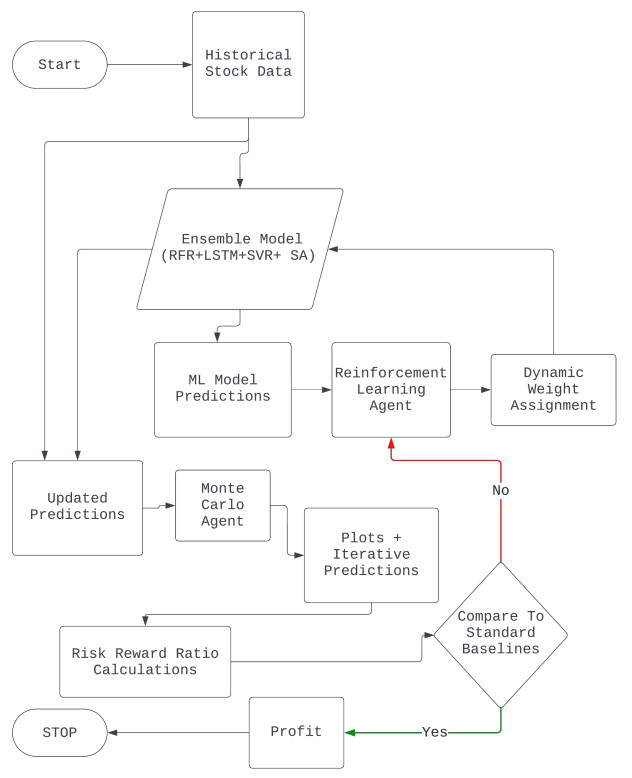
As illustrated in the accompanying flowchart (Figure 2), the architecture of our RL model shows the process from the data input to the final prediction output. Historical stock data and sentiment analysis results act as inputs to our ensemble of models. The outputs from these models inform the RL agent, which then dynamically adjusts the weights of each model. This process is iterative, allowing for continuous learning and adaptation, which is essential for maintaining the accuracy of predictions in response to new market information and emerging trends.

In refining the ensemble model predictions for each stock, we ensure that the RL agent's strategy is not static but evolves based on the ongoing market performance feedback. By doing so, our model remains agile, adjusting to the market dynamics and potentially leading to more informed and lucrative trading strategies. This system's flexibility and responsiveness represent a significant advancement in the application of ML techniques to financial market forecasting.

3.2.1.   Balancing exploration and exploitation

In reinforcement learning, balancing exploration and exploitation is a key challenge. A way to handle this is to employ an epsilon-greedy strategy (Huang, 2018), allowing for both the exploration of new strategies and the exploitation of known profitable ones, which is essential in the dynamic financial market environment. This method selects random actions with a probability of $\epsilon$ and the best-known action with a probability of $1 - \epsilon$, ensuring adaptability to new market trends.(Paavai Anand, 2021)

3.2.2.   Enhanced reward function

Guiding the learning process, the reward function in our model is augmented to include an exploration term. The enhanced reward function is formulated as:

where Accuracy is the predictive accuracy, $N$ is the total number of model selections, $n_i$ is the number of times the $i^{th}$ model has been selected, and $\epsilon$ controls the exploration-exploitation trade-off.

3.2.3.   Implementation

The reinforcement learning agent in our model continuously evaluates the performance of each model in the ensemble, adjusting their weights according to the enhanced reward function. This iterative and ongoing process allows the ensemble to effectively adapt to evolving market conditions.

3.3.   Monte Carlo simulations

Monte Carlo simulations are utilized for two primary tasks:

● Risk Assessment: A risk assessment includes the simulation of numerous potential future market scenarios, providing probabilistic insights. Key risk metrics such as Value at Risk (VaR) and Conditional Value at Risk (CVaR) are calculated using the following:

where $F^{-1}$ is the inverse cumulative distribution function, and $\alpha$ is the confidence level. (Jäckel, 2002)

● Beta Calculations: Beta Calculations include an estimation of beta values under various simulated market conditions. Beta $\beta$ is calculated as the covariance of the asset's returns with the market returns over the variance of the market returns:

where $r_a$ and $r_m$ are the returns of the asset and the market, respectively.

3.4.   Integration of Monte Carlo Simulations with ensemble models

The integration is a key innovation, with the ensemble model outputs feeding into Monte Carlo simulations. This synergistic approach allows the simulations to assess risks based on predicted market dynamics and refine future ensemble predictions through a feedback loop.

4.   Data sources and preprocessing

4.1.   Data acquisition

Our primary dataset for this study was acquired from Yahoo Finance. It is comprised of historical stock prices, including daily Open, High, Low, Close (OHLC) values, Adjusted Close prices, and trading volumes. The dataset spans from January 1, 2010, to November 10, 2023, covering a broad range of market conditions.

4.2.   Data structure

Each record in the dataset corresponds to a trading day and includes the following fields:

● Date: The date of trading.

● Open: The opening price of the stock for the trading day.

● High: The highest price of the stock during the trading day.

● Low: The lowest price of the stock during the trading day.

● Close: The closing price of the stock at the end of the trading day.

● Adj Close: The closing price adjusted for dividends and stock splits.

● Volume: The number of shares traded during the trading day.

4.3.   Preprocessing techniques

The preprocessing of this dataset involved several steps to ensure the data quality and prepare it for analysis:

1. Data Cleaning: We first checked for missing values and inconsistencies in the dataset. Missing data points were imputed using linear interpolation to maintain the continuity of the time series.

2. Data Standardization: To compare features on a common scale, we standardized the data. The standardization process was performed using the following formula:

where $x$ is the original value, $\mu$ is the mean, and $\sigma$ is the standard deviation of the feature across the dataset (Zhou, 2012).

3. Adjustment for Stock Splits and Dividends: The "Adjusted Close" price was used for all analyses involving stock prices, as it accounts for any stock splits and dividend distributions, ensuring a true reflection of the stock's value over time.

4. Volume Normalization: The trading volume was normalized to ensure comparability across different trading days and stocks. This normalization helps to analyze volume changes relative to the stock's usual trading activity.

5. Time Series Decomposition: Given the time series nature of the data, we performed a seasonal decomposition to identify and account for underlying trends, seasonal patterns, and residuals in the stock prices.

These preprocessing steps were critical to transform raw financial data into a standardized and analytically useful format, laying the foundation for subsequent data analyses and model training.

Here is the associated algorithm of the data preprocessing:

4.4.   Experimental setup

The integrated model undergoes rigorous testing in a controlled environment, utilizing backtesting with historical market data. The performance metrics include the predictive accuracy, the effectiveness of risk assessments (including Value at Risk (VaR), Conditional Value at Risk (CVaR), and beta values), and comparative analyses against both standalone ensemble models and conventional risk assessment methodologies.

The methodology is designed to provide a nuanced, adaptable, and precise tool for financial market analyses. This integration of ML with Monte Carlo simulations represents a significant step forward in financial forecasting, not only in predictive accuracy, but also in understanding and managing associated risks.

5.   Monte Carlo simulations for risk assessment and beta calculations

5.1.   Risk assessment with Monte Carlo simulations

The utilization of Monte Carlo simulations in this study is a critical step towards enhancing the robustness of financial risk assessments. These simulations enable the exploration of a vast array of market scenarios, thus providing a deep probabilistic understanding of potential future market behaviors. By generating numerous potential market conditions based on historical volatility and trends, the simulations create a comprehensive platform for assessing risk. This approach is particularly valuable in quantifying the potential losses under adverse market conditions. The key risk metrics calculated for each scenario, namely VaR and CVaR, offer a quantified and insightful view of the market risk. This information is crucial to evaluate the risk profiles of various assets and investment strategies, especially under extreme market conditions.

5.2.   Beta calculations using Monte Carlo simulations

In parallel, Monte Carlo simulations play a vital role in the dynamic calculation of beta values, which is a measure of systematic risk. Traditional methods of calculating the beta often rely on linear assumptions, which may not fully capture the intricacies of market movements and asset behaviors. In contrast, the simulations employed in this study model the relationship between individual asset returns and overall market returns across a range of scenarios. This method yields a spectrum of beta values, providing a more detailed and realistic understanding of the systematic risk associated with different assets under varied market conditions. Furthermore, the study conducts a comparative analysis, juxtaposing the beta values obtained through Monte Carlo simulations against those derived from traditional linear regression methods. This comparison is instrumental in illustrating the superiority of a scenario-based approach in accurately capturing the true risk profile of assets.

5.3.   Integration with ensemble ML models

The crux of this research lies in the seamless integration of Monte Carlo simulations with the ensemble ML models. The predictive outputs of the ensemble models, which encompass the anticipated asset prices and market trends, serve as crucial inputs for the simulations. This convergence allows for risk assessments that are intricately aligned with the forecasted market conditions, resulting in a more precise and relevant evaluation of future risks. Moreover, a unique feedback loop is established where the outcomes of the Monte Carlo simulations, particularly the risk metrics and beta calculations, inform and refine the ensemble models. This integration ensures that the predictive models are continuously enhanced by comprehensive and up-to-date risk assessments, thus improving their overall accuracy and reliability.

5.4.   Advanced risk measures

In addition to traditional risk metrics, an additional path would be to incorporate advanced risk measures, such as Expected Shortfall (ES), to provide a more comprehensive risk assessment. At a confidence level $\alpha$, ES is defined as follows:

where $VaR_\gamma$ represents the Value at Risk at confidence level $\gamma$. This measure offers a more nuanced view of the tail risk than VaR by averaging the worst $(1-\alpha)%$ of the loss distribution.

5.5.   Algorithm

5.6.   Context-Aware sentiment analysis

To further improve the sentiment analysis, we can perhaps adopt a context-aware approach using Bidirectional Encoder Representations from Transformers (BERT) embeddings. For a document $d$, the context-aware sentiment score $Sc(d)$ is calculated as follows:

where $E(d)$ denotes the BERT embeddings for document $d$, $W$ and $b$ are trainable parameters, and $\text{softmax}$ provides the probability distribution over the sentiment classes. This method leverages deep learning to capture the nuanced sentiment of financial news and reports, enhancing the predictive accuracy of market movements.

5.7.   Conclusions

This innovative methodology, which combines Monte Carlo simulations for risk assessment and beta calculations with dynamic ensemble ML models, marks a significant advancement in the field of financial market forecasting. The approach transcends traditional forecasting techniques by not only enhancing the predictive accuracy, but by also providing a detailed and realistic assessment of the risks associated with financial market investments. The dynamic range of risk metrics and beta values generated through this integrated method offers invaluable insights for effective risk management and informed investment decision-making in complex and rapidly evolving financial markets.

6.   Model validation through in-sample and out-of-sample analysis

A critical aspect of evaluating the effectiveness and reliability of predictive models in financial forecasting is through rigorous model validation. This process involves analyzing the model's performance on both in-sample and out-of-sample data sets. In-sample data refers to the portion of data used during the model training phase, thus offering insights into the model's learning capability. Conversely, out-of-sample data, which the model has not previously encountered during training, provides a genuine test of the model's predictive power and generalization ability.

6.1.   In-sample vs. out-of-sample performance metrics

The table below presents a comparative analysis of the in-sample and out-of-sample performance metrics for our ensemble ML models applied to the SPY Exchange-Traded Fund (ETF) and selected major stocks such as AAPL, AMZN, GOOG, MSFT, and NVDA. The metrics include the Mean Absolute Error (MAE), Mean Squared Error (MSE), and Root Mean Squared Error (RMSE), offering a multidimensional perspective on the model accuracy and error magnitude.

6.2.   Interpretation and implications

The table illustrates that for all considered assets, the out-of-sample performance metrics closely align with the in-sample metrics. This closeness indicates that our ensemble ML models possess great generalization capabilities, which are essential to adapt to unseen market conditions. Notably, the slight improvements in the out-of-sample metrics for some assets suggest that the models are not overfitting to the training data, which is a common pitfall in financial modeling where the models perform well on historical data but fail to predict future market movements accurately.

For investors and traders, these findings are invaluable. In particular, the out-of-sample performance provides a realistic expectation of how the model might perform in real-world trading scenarios, thus serving as a crucial tool for risk assessment and decision-making. A model that demonstrates strong predictive capabilities across both in-sample and out-of-sample data sets instills confidence in its use for forecasting future market trends, identifying potential investment opportunities, and evaluating trades with a higher probability of success.

6.3.   Hypothesis for high values for SPY and NVDA

The augmented volatility and market sensitivity inherent to Nvidia Corporation (NVDA) and SPDR S & P 500 ETF Trust (SPY) substantially contribute to the elevated MAE, MSE, and RMSE observed in both the in-sample and out-of-sample analyses. This phenomenon is attributed to several key factors unique to these assets and their market behaviors, which are detailed as follows:

1. Volatility: NVDA, which is situated within the dynamic technology sector, is exposed to rapid technological advancements, regulatory changes, and competitive forces. This volatility fosters significant price fluctuations, complicating predictive model accuracy and elevating the error metrics.

2. Market Sensitivity: The SPY ETF, which mirrors the S & P 500 index, reflects the performance of a wide array of the largest U.S. publicly traded companies. Its broad market exposure heightens its sensitivity to macroeconomic indicators, interest rate shifts, and geopolitical events, thus increasing the complexity of accurate price prediction and corresponding error metrics.

3. Sector-Specific Risks: As a constituent of the technology sector, NVDA is subject to distinct challenges, including shifts in the consumer demand, innovation cycles, and a competitive landscape. These factors introduce unpredictability into the stock price movements, detracting from model predictive precision.

4. Scale of Price Movements: Both NVDA and SPY have experienced pronounced price movements within the analysis timeframe, with larger price shifts leading to greater absolute errors as minor percentage inaccuracies manifest in significant absolute value discrepancies.

5. Economic and Market-wide Events: The analysis period may have included significant economic or broad market events, affecting the overall market and technology stocks in particular. Such events can cause sudden and marked market movements, thus complicating the predictions and potentially increasing the error metrics for assets such as NVDA and SPY.

These elements collectively highlight the challenges in predicting the price movements for NVDA and SPY, resulting in higher MAE, MSE, and RMSE values. For investors and traders, these metrics serve as indicators of the prediction model's accuracy and reliability, suggesting caution in relying on model predictions for these assets, especially for short-term trading decisions. This may lead investors to either adjust their risk management strategies or diversify their investment portfolios to mitigate the impact of the prediction inaccuracies.

6.4.   Value for investment strategies

The validation of our models through in-sample and out-of-sample analyses underlines their potential to enhance the investment strategies. By leveraging these validated models, investors can gain insights into the likely future movements of the SPY ETF and other significant stocks, thus enabling more informed investment decisions. Whether for short-term trading or long-term investment planning, the ability to accurately predict market trends and asset performance is a substantial advantage.

In conclusion, the meticulous validation of our ensemble ML models through in-sample and out-of-sample analyses plays a pivotal role in reinforcing their applicability and reliability in financial forecasting. For investors and traders, the insights derived from these analyses are instrumental in navigating the complexities of the financial markets, thus optimizing investment portfolios, and enhancing the strategic execution of trades.

7.   Quantitative analysis of risk-reward ratios for SPY ETF

This section presents a comprehensive quantitative analysis of the SPY Exchange-Traded Fund (ETF), emphasizing the evaluation of various risk-reward ratios. The analysis utilizes historical price data, with a particular focus on 'Adjusted Close' prices, to account for dividends and stock splits.

7.1.   Data preprocessing

The initial step involved the preparation of the SPY ETF historical price data for the analysis. This process included loading the data from a CSV file, converting date strings into a datetime format, and setting these dates as the dataframe index for efficient data manipulation. The "Adjusted Close" prices, which are crucial for an accurate representation of returns, were exclusively used in subsequent calculations.

7.2.   Calculation of daily returns

Daily returns, which are pivotal in financial analysis, were computed as the percentage change in the Adjusted Close prices from one day to the next. This measure serves as a fundamental indicator of the ETF's daily price volatility.

7.3.   Statistical measures

Several key statistical measures were calculated to assess the risk and performance of the SPY ETF:

● Mean Daily Return: $\bar{r} = \frac{1}{N} \sum_{i = 1}^{N} r_i$, where $r_i$ denotes the daily return and $N$ the number of observations.

● Standard Deviation: $\sigma = \sqrt{\frac{1}{N-1} \sum_{i = 1}^{N} (r_i - \bar{r})^2}$, quantifying the volatility of daily returns.

● Downside Standard Deviation: $\sigma_{\text{downside}} = \sqrt{\frac{1}{N-} \sum_{r_i < 0} (r_i - \bar{r})^2}$, focusing on the volatility of negative returns to evaluate downside risk.

7.4.   Risk-reward ratios

The analysis proceeded with the calculation of various risk-reward ratios, each providing unique insights into the investment's performance and risk characteristics:

1. Sharpe Ratio: Defined as $\frac{\bar{R} - R_f}{\sigma}$, where $\bar{R}$ is the annualized mean return, $R_f$ the risk-free rate, and $\sigma$ the annualized standard deviation. This ratio measures excess return per unit of total risk (Sharpe, 1998).

2. Sortino Ratio: Calculated as $\frac{\bar{R} - R_f}{\sigma_{\text{downside}}}$, it focuses on downside risk, making it particularly relevant for risk-averse investors (Sortino and Van Der Meer, 1991).

3. Treynor Ratio: Given by $\frac{\bar{R} - R_f}{\beta}$, with $\beta$ representing the portfolio's market risk. For the SPY ETF, $\beta$ is assumed to be 1.

4. Calmar Ratio: This ratio is computed as $\frac{\bar{R}}{\text{Max Drawdown}}$, offering insights into the investment's performance relative to its maximum drawdown.

5. Sterling Ratio: Defined as $\frac{\bar{R}}{\text{Average Annual Drawdown} - 0.10}$, it emphasizes consistent performance over average drawdown.

6. Rachev Ratio: Reflects the balance between potential gains and losses through the ratio of the right tail factor to the left tail factor of returns.(Stoyanov et al., 2007)

7.5.   Algorithm

Algorithm 3 presents the associated algorithm that shows the workflow.

7.6.   Results and interpretation

The computed ratios elucidate the risk-reward profile of the SPY ETF. High values of the Sharpe and Sortino ratios indicate superior risk-adjusted returns, appealing to both general and risk-averse investors. The Treynor, Calmar, and Sterling ratios provide further insights into the ETF's performance relative to the market risk, drawdowns, and consistency, respectively. The Rachev Ratio offers a unique perspective on the balance between the potential for high returns and the risk of significant losses. Collectively, these metrics furnish a multifaceted understanding of the SPY ETF's investment characteristics.

8.   Comparative analysis of risk-reward ratios for selected stocks

8.1.   Methodology

The analysis involved calculating several key risk-reward ratios for five major stocks: Apple (AAPL), Amazon (AMZN), Google (GOOG), Microsoft (MSFT), and Nvidia (NVDA). These ratios include the Sharpe, Sortino, Treynor, Calmar, Sterling, and Rachev Ratios.

8.2.   Results

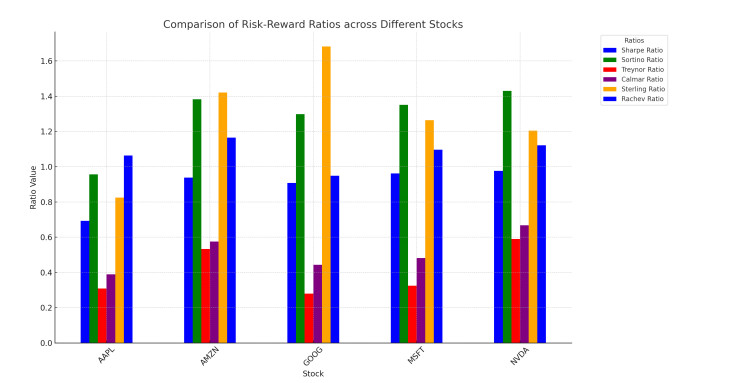
The computed ratios were visualized in a comparison chart and summarized in a table.

8.3.   Discussion

The analysis revealed several insights into the risk-reward profiles of the selected stocks:

● Sharpe Ratio: This indicates the excess return per unit of total risk. NVDA exhibited the highest Sharpe Ratio, suggesting better risk-adjusted returns compared to the others, with AAPL showing the lowest.

● Sortino Ratio: This focuses on the downside risk. NVDA and AMZN led in this metric, implying efficient returns per unit of bad risk.

● Treynor Ratio: This measures excess returns per unit of market risk. NVDA demonstrated the highest efficiency in earning excess returns relative to market risk.

● Calmar Ratio: This relates the return to maximum drawdown risk. NVDA had the highest ratio, indicating an improved performance per unit of historical drawdown risk.

● Sterling Ratio: This measures the average return over the average drawdown. GOOG led in this ratio, suggesting an improved average performance relative to its drawdowns.

● Rachev Ratio: This compares the potential for gains versus losses. AMZN and NVDA showed an improved balance between potential gains and losses.

In conclusion, the analysis suggests that NVDA has a particularly strong risk-reward profile, excelling in multiple ratios. GOOG showed strength in the Sterling Ratio, while AMZN leds in the Rachev Ratio. Despite lower ratings in some ratios, AAPL maintained a balanced risk-reward profile. These findings are crucial for investors to consider the trade-offs between risk and return in their investment strategies.

9.   Integration of traditional risk-reward ratios for enhanced risk assessment

9.1.   Rationale

While our reinforcement learning model demonstrates significant potential in forecasting stock market trends, integrating traditional risk-reward ratios provides a complementary risk assessment. These ratios, namely Sharpe, Sortino, Treynor, Calmar, Sterling, and Rachev, offer established metrics to gauge the risk-adjusted performance of stocks.

9.2.   Methodology

We calculated these ratios for the stocks analyzed in our reinforcement learning model (AAPL, AMZN, GOOG, MSFT, NVDA) (Deep, 2023b). The computation involved historical price data analyses to derive the daily returns and the subsequent risk-reward ratios.

9.3.   Integration with reinforcement learning model

The integration of these ratios with our model's predictions offers a dual-layered assessment: one that encompasses traditional risk measures and another that leverages advanced reinforcement learning techniques. This approach provides a comprehensive view, combining the strength of established financial metrics with cutting-edge ML models.

9.4.   Results

The calculated risk-reward ratios for each stock are presented in Table 3. Then these ratios are juxtaposed with the predictions made by our reinforcement learning model, offering insights into the risk profiles of the stocks under varying market conditions.

9.5.   Conclusions

The fusion of traditional risk-reward ratios with advanced reinforcement learning predictions, embodies a holistic approach to financial market analysis. This methodology not only enhances the robustness of our predictions but also provides crucial risk insights, making it a valuable tool for investors and financial analysts.

10.   Monte Carlo simulation of SPY ETF

10.1.   Objective

The objective of this Monte Carlo simulation is to project potential future price paths for the SPY Exchange-Traded Fund (ETF) over a one-year horizon. By employing a probabilistic approach, this simulation aims to elucidate the range of possible outcomes and inherent volatility of the ETF, offering valuable insights for investors and portfolio managers.

10.2.   Methodology

The simulation is based on the historical mean and standard deviation of the ETF's daily returns, employing a random walk hypothesis. The formula for each simulated price path is given by the following:

where $P_{t}$ is the price at time $t$, and $r_{t}$ is the daily return, which is randomly sampled from a normal distribution with the historical mean and standard deviation.

10.3.   Implementation

The dataset containing the daily prices of the SPY ETF is prepared for analysis through a series of preprocessing steps. Initially, the data, structured with columns for Open, High, Low, Close, Adjusted Close, and Volume, is loaded. Dates are parsed to ensure the temporal accuracy and set as the index of our dataset to facilitate time-series analysis. This process is critical to chronologically align the data, setting the foundation for subsequent calculations and analyses.

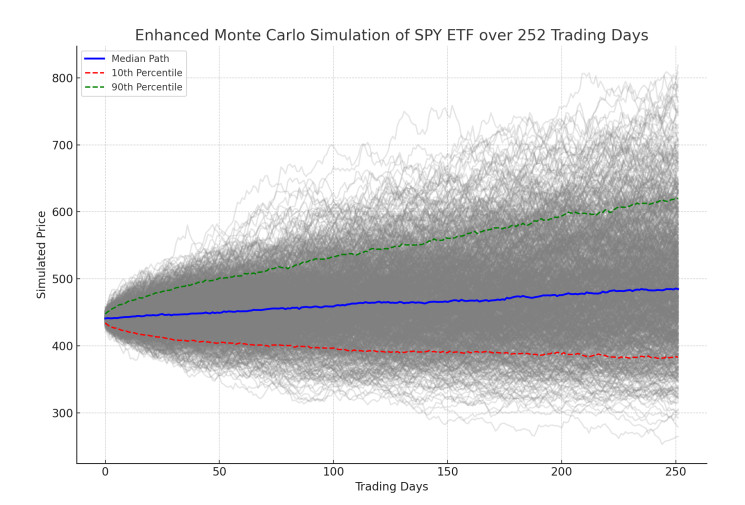
10.4.   Results

The simulation generated 1,000 potential price paths for the SPY ETF. The results were visualized in a plot, highlighting the median, 10th, and 90th percentile paths. The plot is shown in Figure 4.

The median path (50th percentile) represents the most probable outcome, while the 10th and 90th percentiles provide a sense of the potential range of outcomes. This visualization helps to assess the risk and variability associated with the ETF over the next year.

10.5.   Limitations of the Monte Carlo simulation

While Monte Carlo simulations offer valuable insights, they are inherently limited by certain assumptions. Chief among these is the assumption of a normal distribution of returns. Financial markets often exhibit fat tails and skewness, deviating from normality, which can lead to underestimating the probability of extreme events.

Moreover, the simulation does not account for structural changes in the market, regulatory shifts, geopolitical crises, or unforeseen global events that can cause significant deviations from historical patterns. The model's inability to incorporate these black swan events means that the range of outcomes, while broad, may not fully capture the extremes of what could happen in atypical circumstances.

The Monte Carlo simulation provides a valuable tool to visualize and assess the range of potential future scenarios for the SPY ETF. While it offers insightful projections, it's important to remember that these are based on historical trends and are not predictive of the future market behavior.

11.   Beta analysis of the SPY ETF relative to the DJIA

11.1.   Introduction

Relative to a benchmark index, the beta of an ETF quantifies its volatility in comparison to the market. A beta greater than 1 indicates higher volatility than the market, while a beta less than 1 indicates lower volatility. This section details the calculation of the beta of the SPY ETF relative to the Dow Jones Industrial Average (DJIA).

11.2.   Methodology

The beta is calculated using a linear regression model, where the daily returns of the SPY ETF are regressed against the daily returns of the DJIA. The mathematical model is given by the following:

where $\text{Return}_{\text{SPY}}$ and $\text{Return}_{\text{DJIA}}$ are the daily returns of the SPY ETF and the DJIA, respectively, $\alpha$ is the intercept, $\beta$ is the slope (beta), and $\varepsilon$ is the error term.

11.3.   Data processing and regression analysis

The beta calculation is implemented in Python. Historical data for the SPY ETF and the DJIA are merged based on common dates, and the daily returns are calculated. Then the regression analysis is performed using the 'statsmodels' library.

11.4.   Results

The key findings from the regression analysis are as follows:

● Beta Value: The calculated beta of the SPY ETF relative to the DJIA is approximately 0.363.

● Interpretation: This suggests that the SPY ETF is less volatile than the DJIA. For every 1% change in the DJIA, the SPY ETF is expected to change by about 0.363% in the same direction.

● R-squared Value: The R-squared value is approximately 0.421, indicating that about 42.1% of the variation in the SPY ETF's returns can be explained by the returns of the DJIA.

● Statistical Significance: The p-value for the beta coefficient is significantly low, indicating a statistically significant relationship between the returns of the SPY ETF and the DJIA.

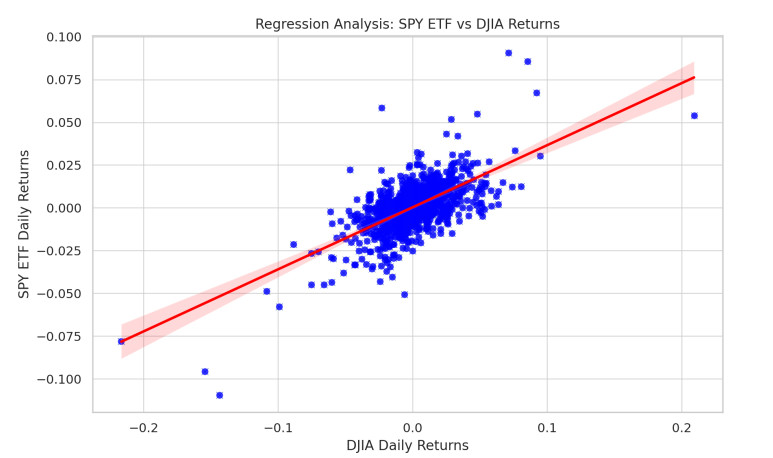
11.5.   Visualization of the regression

The relationship between the daily returns of the SPY ETF and the DJIA is visualized through a scatter plot with a regression line. The following plot demonstrates this relationship:

The beta value, derived from the slope of the regression line, provides a quantitative measure of the SPY ETF's volatility relative to the DJIA. This metric is crucial for investors to understand the risk profile of the ETF in relation to broader market movements.

11.6.   Insights

The beta analysis of the SPY ETF, conducted relative to the DJIA, provides critical insights that are integral to the overarching theme of this paper. This section serves to underscore the significance of this analysis within the broader context of financial market forecasting and risk assessment.

11.6.1.   Grounding financial forecasts with quantitative risk measures

The calculation of the beta offers a quantitative foundation to assess the systematic risk associated with the SPY ETF compared to the broader market. This measure is essential not only for understanding the volatility of the ETF, but also for grounding the more complex risk assessments facilitated by the integration of ML models and Monte Carlo simulations. By quantifying the ETF's market-related risk, the beta analysis complements the sophisticated risk assessment methodologies discussed throughout the paper, thus providing a cohesive approach to financial forecasting.

11.6.2.   SPY ETF as a case study

It is important to note that while this research prominently features the SPY ETF in this section and its beta analysis relative to the DJIA, the methodologies and insights presented are not confined to this specific ETF or benchmark index. The SPY ETF serves as a case study or example to illustrate the application and effectiveness of the proposed integrated approach. In practice, this methodology can be applied to any stock listed on a comparable market, with the choice of benchmark index (e.g., DJIA for a broad market representation or NASDAQ for technology stocks) depending on the specific sector or market segment under analysis. This versatility underscores the adaptability and relevance of the integrated forecasting model across various financial contexts.

11.6.3.   Integrating beta analysis with ML ensemble predictions for investment Decisions

A key aspect of this research is the integration of a traditional beta analysis with advanced ML ensemble predictions. The beta value acts as a grounding factor, providing a measure of systematic risk that complements the predictive insights generated by the ensemble of ML models. This combination enables a holistic view of both the potential returns and associated risks of investment options. In the context of executing potential trades or investments, the integration of beta analysis with ML predictions offers a robust framework for informed decision-making, enhancing the potential for optimized investment outcomes.

11.6.4.   Implications for investors and financial analysts

For investors and financial analysts, the insights derived from the beta analysis, particularly when combined with the advanced predictive capabilities of the ML ensemble, are invaluable for strategic investment planning. This integrated approach facilitates a more informed assessment of risk-return profiles, aiding to the portfolio management and asset allocation decisions. By providing a comprehensive analysis that balances traditional risk measures with cutting-edge predictive analytics, the research empowers investors to navigate the complexities of the financial markets with a greater confidence and strategic insight.

In conclusion, the integration of a beta analysis with ML ensemble predictions represents a significant advancement in financial forecasting and risk assessments. This approach not only enhances the accuracy and reliability of financial market analyses, but also provides a pragmatic framework for applying these insights to real-world investment decisions. The versatility of the methodology, exemplified through the case study of the SPY ETF, demonstrates its applicability across a wide range of stocks and market conditions, offering a valuable tool for investors seeking to optimize their investment strategies in an ever-evolving market landscape.

12.   Conclusions

In this paper, we have unveiled a pioneering approach to financial market forecasting and risk assessment, merging the analytical prowess of ML models with the stochastic depth of Monte Carlo simulations. This fusion represents a significant leap forward in financial analytics, effectively marrying the precision of modern computational techniques with the rigor of traditional financial analyses.

Our journey commenced with a detailed review of the evolution of financial forecasting models, tracing their trajectory from linear time-series methods to advanced ML algorithms. The cornerstone of our research is the novel amalgamation of a diverse array of ML models—encompassing Random Forest, LSTM networks, and sentiment analysis—with the intricate scenario-based analysis offered by Monte Carlo simulations. This unique blend not only elevates the accuracy of predicting financial market trends but also provides a richer, more detailed perspective on the risk factors.

The empirical analysis, focusing on the SPY Exchange-Traded Fund (ETF) and prominent stocks such as AAPL, AMZN, GOOG, MSFT, and NVDA, employed various risk-reward ratios to evaluate the efficacy of our integrated model. The results underscored the superiority of our approach over conventional methodologies, offering a more comprehensive risk-reward assessment and insight into the market dynamics.

This research stands out for its ability to synthesize the predictive accuracy with intricate risk assessments, delivering a powerful tool that is poised to transform decision-making in financial markets. Its implications extend far beyond mere predictive modeling, providing investors, analysts, and policymakers with a dynamic, multifaceted framework to navigate the complexities of today's financial landscapes. By striking a balance between pursuing returns and managing risks, this integrated model serves as a beacon for informed, strategic decision-making in the fast-paced, ever-evolving realm of financial markets.

In summation, our study not only challenges the existing paradigms in financial forecasting, but also sets a new standard for integrating computational intelligence with financial risk assessment. It paves the way for future research and applications, promising to reshape our understanding and approach to financial market analyses in the data-driven age.

13.   Technologies and libraries used

This research project extensively utilized a variety of technologies and open-source libraries, pivotal in achieving the analytical and computational objectives set forth. Below is a summary of the key technologies and libraries that played an integral role in the project:

1. Python: The core programming language used for this project. Python's versatility and extensive support for data analysis and ML made it an ideal choice (VanRossum and Drake, 2010).

2. PyTorch and TensorFlow: These two open-source ML libraries were used for building and training various deep learning models. PyTorch offered dynamic computation graphs that are useful for iterative model adjustments, while TensorFlow provided scalability and deployment features (Paszke et al., 2019) (Abadi et al., 2016).

3. Scikit-learn: This library was instrumental for implementing various ML algorithms. It provided efficient tools for data mining and data analysis, which were essential in preprocessing data and evaluating the model performance (Pedregosa et al., 2011).

4. Pandas: Used for data manipulation and analysis, Pandas offered powerful data structures like DataFrames, making the handling of large financial datasets more efficient (pandas development team, 2020).

5. Matplotlib: This plotting library was used to visualize data and results. It helped in creating a range of graphs and plots to effectively present data patterns and insights (Hunter, 2007).

The combination of these technologies and libraries formed the backbone of the research, enabling the successful execution of complex computational tasks, data analysis, model training, and validation. Additionally, their open-source nature added to the collaborative and progressive spirit of this research endeavor.

14.   Future work

Looking forward, there are several avenues for future research stemming from this study:

1. Real-Time Data Analysis: Implementing and testing the model with real-time financial data to understand its live market performance and responsiveness.

2. Diverse Asset Classes: Expanding the model's scope to include commodities, foreign exchange, and cryptocurrencies for a comprehensive tool adaptable to various market segments.

3. Advanced ML Techniques: Exploring newer ML techniques like deep reinforcement learning and generative adversarial networks to enhance predictive accuracy and adaptability.

4. Incorporating Advanced Risk Measures: Future research directions will focus on incorporating advanced risk measures and leveraging the latest advancements in natural language processing to enhance the model's capabilities.

5. Expected Shortfall and Spectral Risk Measures: These measures provide a more comprehensive view of risk, especially in the tails of the distribution. Expected Shortfall, for instance, offers insight into the expected loss in extreme market conditions, defined at a confidence level $\alpha$ as $ES_\alpha = \frac{1}{1 - \alpha} \int_{\alpha}^{1} VaR_\gamma d\gamma$, where $VaR_\gamma$ is the Value at Risk at confidence level $\gamma$.

6. Context-Aware Sentiment Analysis Using BERT: To further enhance the sentiment analysis component of the model, implementing context-aware sentiment analysis with BERT embeddings will be considered. This approach, which calculates the sentiment score as $Sc(d) = \text{softmax}(W \cdot E(d) + b)$, can significantly improve the understanding of complex financial narratives by capturing the nuanced sentiment of textual data.

7. Global Market Analysis: Applying the model to global financial markets to test its robustness and scalability across different economic conditions and regulatory environments.

8. Integration with Economic Indicators: Incorporating macroeconomic indicators and global economic trends for a more holistic market view.

While this research marks a significant advancement in financial forecasting and risk assessments, the evolving nature of financial markets and technological advancements present continuous opportunities for further explorations and enhancements of this integrated approach.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgement

I express my sincere gratitude to Dr. Svetlozar Rachev from Texas Tech University Mathematical Finance Program for his invaluable guidance and insights into the available literature on the Rachev ratio and other risk-reward ratios. His expertise significantly contributed to the depth and accuracy of this research.

Conflict of interest

As the author of this paper, Ⅰ, Akash Deep, disclose a potential conflict of interest. The methodologies and insights from this research, particularly those concerning "Advanced Financial Market Forecasting: Integrating Monte Carlo Simulations with Ensemble ML Models", may be applied in the operations of DeepAI-Finance, a startup Ⅰ have co-founded. This declaration is made in the spirit of transparency and to maintain the integrity of the research, which has been conducted independently and based solely on academic principles, separate from the business interests of DeepAI-Finance.

Funding

This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors. The work was conducted independently by the author, Akash Deep, without any external financial support.

Code Repository

Github Link : ML-Finance-Monte-Carlo-RRR.