Listen to the radio and go on field trips: A study on farmers' attributes to opt for extension methods in Northwest Ethiopia

1.   Introduction

In nonlinear chemical reaction systems, the three-molecule autocatalytic model shows abundant dynamical behaviors, many abundant research results have been obtained ^{[1,2,3,4,5,6,7]}. In 1979, Schnakenberg proposed a typical three-molecule autocatalytic reaction-diffusion model ^[8]. In ^[9], the authors studied the one-dimensional static Turing bifurcation of Schnakenberg model. In ^[10,11,12], the authors introduced the relevant research background of reaction-diffusion Schnakenberg system. However, most references ^{[13,14,15,16]} focus on whether the constant equilibrium solution has Turing instability, but pay little attention to whether the periodic solutions of system may also suffer from Turing instability. Therefore, by applying the theoretical methods in ^[17,18], we study the Turing instability of Hopf bifurcating periodic solutions for the Schnakenberg model.

On the basis of the Schnakenberg model ^[8], We introduce self-diffusion and cross-diffusion coefficients, and establish reaction-diffusion Schnakenberg model with cross-diffusion and self-diffusion:

where $\Omega$ is a open bounded domain in n-dimensional Euclidean space, and its boundary $\partial \Omega$ is smooth. $\Delta$ is Laplace operator. The parameters $a, b, {{d}_{11}}, {{d}_{12}}, {{d}_{21}}, {{d}_{22}}$ are all positive constants. $u = u(x, t)$ and $v = v(x, t)$ indicate the concentrations of chemicals at position $x\in \Omega$ and time $t > 0$, respectively, and the initial concentrations ${{u}_{*}}(x), {{v}_{*}}(x)$ are nonnegative functions. ${{d}_{11}}, {{d}_{22}}$ denote self-diffusion coefficients of $u$ and $v$, respectively. ${{d}_{12}}, {{d}_{21}}$ represent cross-diffusion coefficients of $u$ and $v$, respectively. Simultaneously, we suppose that ${{d}_{11}}{{d}_{22}}-{{d}_{12}}{{d}_{21}} > 0$ holds.

2.   Hopf bifurcation and stability of periodic solutions for the ODE system and perturbed system

2.1.   Stability of periodic solutions for the ODE system

We consider the corresponding zero-dimensional dynamic system of system (1.1)

The equilibrium $\left({{u}_{0}}, {{v}_{0}} \right)$ of system (2.1) satisfies

with ${{u}_{0}} = a+b, {{v}_{0}} = \frac{b}{{{\left(a+b \right)}^{2}}}$. By straightforward computation, we know $\left({{u}_{0}}, {{v}_{0}} \right)$ is the only equilibrium of system (2.1). For convenience, setting $\mu : = a+b$, then $\left({{u}_{0}}, {{v}_{0}} \right) = \left(\mu, \frac{b}{{{\mu }^{2}}} \right)$. In the following, for the three-molecule autocatalytic Schnakenberg model, we discuss the stability of its Hopf bifurcating periodic solutions by taking $\mu$ as parameter.

Theorem 2.1. Let $\mu _{0}^{H} = \sqrt[3]{b+\sqrt{{{b}^{2}}+\frac{1}{27}}}+\sqrt[3]{b-\sqrt{{{b}^{2}}+\frac{1}{27}}}$, for the ODEs (2.1), the following statements are true:

(1) At ${{\left(\mu, \frac{b}{{{\mu }^{2}}} \right)}^{T}}$, system (2.1) is unstable for $\mu \in \left(0, \mu _{0}^{H} \right)$, while locally asymptotically stable for $\mu \in \left(\mu _{0}^{H}, +\infty \right)$.

(2) At $\lambda = \mu _{0}^{H}$, system has a family of periodic solutions ${{\left({{u}_{T}}(t), {{v}_{T}}(t) \right)}^{T}}$ bifurcating from ${{\left(\mu, \frac{b}{{{\mu }^{2}}} \right)}^{T}}$. Supercritical Hopf bifurcation of system (2.1) occurs at ${{\left(\mu, \frac{b}{{{\mu }^{2}}} \right)}^{T}}$, and the bifurcating periodic solutions are stable.

Proof. The Jacobian matrix of system (2.1) at ${{\left(\mu, {{v}_{\mu }} \right)}^{T}}$ is $J\left(\mu \right) = \left(\begin{matrix} -1+\frac{2b}{\mu } & {{\mu }^{2}} \\ -\frac{2b}{\mu } & -{{\mu }^{2}} \\ \end{matrix} \right).$ The characteristic equation of $J\left(\mu \right)$ is

with

The eigenvalue $\lambda \left(\mu \right)$ of $J\left(\mu \right)$ is given by

When $\mu \ge 2b$, all the eigenvalues of $J\left(\mu \right)$ have strict negative real parts, according to the stability theory, the equilibrium ${{\left(\mu, \frac{b}{{{\mu }^{2}}} \right)}^{T}}$ is locally asymptotically stable. When $0 < \mu < 2b$, ${T}'\left(\mu \right) = -2\mu -\frac{2b}{{{\mu }^{2}}} < 0$, then $T\left(\mu \right)$ is monotonically decreasing for $0 < \mu < 2b$. Since $\underset{\mu \to 0}{\mathop{\lim }}\, T\left(\mu \right) = +\infty, \; T\left(2b \right) = -4b-\frac{1}{2b} < 0$, then $T\left(\mu \right)$ has only zero point $\mu _{0}^{H}\in (0, 2b)$, namely, $T\left(\mu _{0}^{H} \right) = 0$. For any $\mu \in \left(\mu _{0}^{H}, 2b \right)$, we have $T\left(\mu \right) < 0$, then system (2.1) is locally asymptotically stable at ${{\left(\mu, \frac{b}{{{\mu }^{2}}} \right)}^{T}}$, while for any $\mu \in \left(0, \mu _{0}^{H} \right)$, system (2.1) is unstable at ${{\left(\mu, \frac{b}{{{\mu }^{2}}} \right)}^{T}}$. When $\mu = \mu _{0}^{H}$, $J\left(\mu \right)$ has a pair of pure imaginary roots $\lambda = \pm i{{\omega }_{0}}$ with ${{\omega }_{0}} = \mu$. Let $\text{ }\lambda \left(\mu \right) = \alpha \left(\mu \right)\pm i\omega \left(\mu \right)$ be the roots of Eq (2.2) near $\mu = \mu _{0}^{H}$, then we have

According to Poincaré-Andronov-Hopf bifurcation theorem, system (2.1) experiences a Hopf bifurcation at $\mu = \mu _{0}^{H}$.

Next, we study the properties of Hopf bifurcating periodic solutions of system (2.1). Here, we still use the notations and computation in ^[20] to deduce the expression of cubic term coefficient ${{c}_{1}}(\mu _{0}^{H})$ in the norm form. By ^[21], we can rewrite the Poincaré normal form of the abstract form of system (2.1) in the small neighborhood of ${{p}_{0}}$ as follows:

Let the eigenvector of $J\left(\mu _{0}^{H} \right)$ corresponding to the eigenvalue $i{{\omega }_{0}}$ be $q = {{\left({{a}_{0}}, {{b}_{0}} \right)}^{T}}$ satisfying

Define inner product in ${{X}_{\mathbb{C}}}$:

where ${{U}_{i}} = {{\left({{u}_{i}}, {{v}_{i}} \right)}^{T}}\in {{X}_{\mathbb{C}}}, i = 1, 2$. Note that $\langle \lambda {{U}_{1}}, {{U}_{2}} \rangle = \bar{\lambda }\langle {{U}_{1}}, {{U}_{2}} \rangle$, denote the adjoint operator of $J\left(\mu _{0}^{H} \right)$ by ${{J}^{*}}\left(\mu _{0}^{H} \right)$, then the eigenvector of ${{J}^{*}}\left(\mu _{0}^{H} \right)$ corresponding to the eigenvalue $-i{{\omega }_{0}}$ be ${{q}^{*}} = {{\left(a_{0}^{*}, b_{0}^{*} \right)}^{T}}\in {{X}^{\mathbb{C}}}$ satisfying

Therefore, ${{q}^{*}} = {{\left(a_{0}^{*}, b_{0}^{*} \right)}^{T}} = {{\left(\frac{-1-i\mu _{0}^{H}}{2\mu _{0}^{H}l\pi }, \frac{-i}{2l\pi } \right)}^{T}}$. Performing the spatial decomposition $X = {{X}^{c}}\oplus {{X}^{s}}$, where ${{X}^{c}} = \left\{ zq+\bar{z}\bar{q}|z\in \mathbb{C} \right\}, {{X}^{s}} = \left\{ u\in X| < {{q}^{*}}, u > = 0 \right\}$, then for any $U = {{\left(u, v \right)}^{T}}\in X$, there exist $z\in \mathbb{C}$ and $\omega = \left({{\omega }_{1}}, {{\omega }_{2}} \right)\in {{X}^{s}}$ such that ${{\left(u, v \right)}^{T}} = zq+\bar{z}\bar{q}+{{\left({{\omega }_{1}}, {{\omega }_{2}} \right)}^{T}}$. Thus, system (2.3) can be transformed into the following system with $\left(z, \omega \right)$ as the coordinate:

with

Writing ${{F}_{0}}$ as

here, $Q, C$ is a symmetric multilinear form. For convenience, denoting ${{Q}_{XY}} = Q\left(X, Y \right), {{C}_{XYZ}} = C\left(X, Y, Z \right)$, we calculate ${{Q}_{qq}}$, ${{Q}_{q\bar{q}}}$ and ${{C}_{qq\bar{q}}}$, where

here, denoting $f(u, v) = a-u+{{u}^{2}}v, \quad g(u, v) = b-{{u}^{2}}v$, with

here, all the partial derivatives of $f(u, v)$ and $g(u, v)$ are evaluated at the bifurcation point ${{\left(\mu _{0}^{H}, \frac{b}{\mu {{_{0}^{H}}^{2}}} \right)}^{T}}$,

Let

from (2.5) and (2.6), we can obtain

Because system (2.4) has normal manifold, which can be written as follows

By (2.7), (2.8) and $J\left(\mu _{0}^{H} \right)\omega +H\left(z, \bar{z}, \omega \right) = \frac{d\omega }{dt} = \frac{\partial \omega }{\partial z}\frac{dz}{dt}+\frac{\partial \omega }{\partial \bar{z}}\frac{d\bar{z}}{dt}$, we have

By calculation, we have

we can also get ${{H}_{20}} = 0, {{H}_{11}} = 0$, this implies ${{\omega }_{20}} = {{\omega }_{11}} = 0$, then

Thus, we have

The real part and imaginary part of ${{c}_{1}}(\mu _{0}^{H})$ are as follows

By $\operatorname{Re}{{c}_{1}}\left(\mu _{0}^{H} \right) < 0$, we know that the Hopf bifurcating periodic solutions of system (2.1) are stable at $\mu = \mu _{0}^{H}$. Additionally, because transversality condition ${{\left. \frac{d\alpha \left(\mu \right)}{d\mu } \right|}_{\mu = \mu _{0}^{H}}} < 0$, so the direction of Hopf bifurcation is subcritical. □

2.2.   Hopf bifurcation and stability of periodic solutions for the perturbed system

We introduce the following perturbed system model on the basis of ODEs (2.1)

here, $\varepsilon$ is sufficiently small such that $\left(\begin{matrix} 1+\varepsilon {{d}_{11}} & \varepsilon {{d}_{12}} \\ \varepsilon {{d}_{21}} & 1+\varepsilon {{d}_{22}} \\ \end{matrix} \right)$ is reversible. System (2.10) is equivalent to the following system

where

Then at $\left(\mu, {{v}_{\mu }} \right)$, the Jacobian matrix of system (2.11) is

with

The characteristic equation corresponding to the jacobian matrix $J(\mu, \varepsilon)$ is

where

Notice that $H(\mu _{0}^{H}, 0) = T\left(\mu _{0}^{H} \right) = 0$ and ${{\partial }_{\mu }}H(\mu, \varepsilon) = {T}'\left(\mu _{0}^{H} \right)\ne 0$. According to the implicit function existence theorem, there exist a sufficiently small ${{\varepsilon }_{0}} > 0$ and a continuously differentiable function $\mu _{\varepsilon }^{H} = {{\mu }^{H}}\left(\varepsilon \right)$ such that when $\varepsilon \in \left(-{{\varepsilon }_{0}}, {{\varepsilon }_{0}} \right)$, $H(\mu _{\varepsilon }^{H}, \varepsilon) = 0$ and ${{\mu }^{H}}\left(0 \right) = \mu _{0}^{H}$ hold. Let $\lambda \left({{\mu }_{\varepsilon }} \right) = \beta ({{\mu }_{\varepsilon }})\pm i\omega ({{\mu }_{\varepsilon }})$ be the characteristic root of Eq 2.14, then when $\mu \to {{\mu }_{\varepsilon }}$, we have

By ^[18], we have the following lemma.

Lemma 2.1. Assume $\mu$ is sufficiently close to $\mu _{\varepsilon }^{H}$, $T$ is the minimum positive period of the stable periodic solution $\left({{u}_{T}}(t), {{v}_{T}}(t) \right)$ of system (2.1) bifurcating from $\left(\mu, {{v}_{\mu }} \right)$, then there exists ${{\varepsilon }_{1}} > 0$ such that for any $\varepsilon \in \left(-{{\varepsilon }_{1}}, {{\varepsilon }_{1}} \right)$, system (2.10) has a periodic solution $\left({{u}_{T}}(t, \varepsilon), {{v}_{T}}(t, \varepsilon) \right)$ depending on $\varepsilon$. Its minimum positive period is $T\left(\varepsilon \right)$, simultaneously, it satisfies

1) When $\varepsilon \to 0$, $\left({{u}_{T}}(t, \varepsilon), {{v}_{T}}(t, \varepsilon) \right)\to \left({{u}_{T}}(t), {{v}_{T}}(t) \right)$ and $T\left(\varepsilon \right)\to T$.

2) $T(\varepsilon) = \frac{2\pi }{\omega \left(\mu _{\varepsilon }^{H} \right)}\left(1+\left(\frac{{\beta }'\left(\mu _{\varepsilon }^{H} \right)\operatorname{Im}\left({{c}_{1}}\left(\mu _{\varepsilon }^{H} \right) \right)}{\omega \left(\mu _{\varepsilon }^{H} \right)\operatorname{Re}\left({{c}_{1}}\left(\mu _{\varepsilon }^{H} \right) \right)}-\frac{{\omega }'\left(\mu _{\varepsilon }^{H} \right)}{\omega \left(\mu _{\varepsilon }^{H} \right)} \right)\left(\mu -\mu _{\varepsilon }^{H} \right)+O\left({{\left(\mu -\mu _{\varepsilon }^{H} \right)}^{2}} \right) \right.$ with

Theorem 2.2. Suppose that $\mu$ is sufficiently close to $\mu _{\varepsilon }^{H}$, $\left({{u}_{T}}(t), {{v}_{T}}(t) \right)$ is the stable periodic solution of system (2.1), then when $\varepsilon \to 0$, we have

with

Proof. According to Lemma 2.1, we have

If $\mu \to \mu _{\varepsilon }^{H}$, then $O\left(\mu -\mu _{\varepsilon }^{H} \right)\to 0$, so the sign of ${T}'(\varepsilon)$ is mainly determined by the sign of the first two at $\varepsilon = 0$. Next, we calculate the expressions of ${{\left. \frac{d\mu _{\varepsilon }^{H}}{d\varepsilon } \right|}_{\varepsilon = 0}}$ and ${{\left. \frac{d\omega \left(\mu _{\varepsilon }^{H} \right)}{d\varepsilon } \right|}_{\varepsilon = 0}}$.

At $\mu = \mu _{\varepsilon }^{H}$, by (2.15), we can derive

Differentiating (2.17) with $\varepsilon$, we have

with

According to (2.16),

Differentiating it with $\mu$, we know

When $\mu \to \mu _{\varepsilon }^{H}$, $H\left(\mu _{\varepsilon }^{H}, \varepsilon \right) = 0$ and ${{\partial }_{\lambda }}D\left(\mu _{\varepsilon }^{H}, \varepsilon \right) = \frac{1}{N(\varepsilon)}{D}'\left(\mu _{\varepsilon }^{H} \right)$. Hence,

From $\omega \left(\mu _{\varepsilon }^{H} \right) = \sqrt{D\left(\mu _{\varepsilon }^{H}, \varepsilon \right)}$ and $D\left(\mu _{\varepsilon }^{H}, \varepsilon \right) = \frac{D\left(\mu _{\varepsilon }^{H} \right)}{N(\varepsilon)}$, differentiating them with $\varepsilon$, we can obtain

When $\varepsilon = 0$, we get

Thus, according to (2.22) and (2.23), we have

where $b(\mu _{0}^{H})$ is defined in (2.19). From (2.21) and (2.24), we can obtain

By (2.18), (2.20) and (2.25), we can deduce

At last, substituting (2.19) into (2.26), we can obtain

with

□

3.   Turing instability of spatially homogeneous Hopf bifurcating periodic solutions

In this section, applying the theory elaborated in ^[17], we study stable spatially homogeneous Hopf bifurcating periodic solutions of system (2.1) will become Turing unstable in reaction-diffusion system (1.1) with cross-diffusion. According to the previous discussion, we give the following theorem.

Theorem 3.1. Suppose that $\mu$ is sufficiently close to ${{\mu }_{0}}$, $\left({{u}_{T}}(t), {{v}_{T}}(t) \right)$ is stable spatially homogeneous Hopf bifurcating periodic solution of system (2.1) bifurcating from $\left(\mu, {{v}_{\mu }} \right)$. If ${T}'(0) < 0$ and $\Omega$ is large enough, then $\left({{u}_{T}}(t), {{v}_{T}}(t) \right)$ will become Turing unstable in system (1.1) with cross-diffusion.

Proof. Assume that the stable periodic solution of system (2.1) is $\left({{u}_{T}}(t), {{v}_{T}}(t) \right)$ with minimum positive period $T$, then the linearized system of (1.1) evaluated at $\left({{u}_{T}}(t), {{v}_{T}}(t) \right)$ is

where $D: = \left(\begin{array}{*{35}{l}} {{d}_{11}} & {{d}_{12}} \\ {{d}_{21}} & {{d}_{22}} \\ \end{array} \right)$, $\Delta$ is Laplace operator, the Jacobian matrix of system (2.1) at $\left({{u}_{T}}(t), {{v}_{T}}(t) \right)$ is ${{J}_{T}}(t): = \left(\begin{matrix} -1+2{{u}_{T}}(t){{v}_{T}}(t) & {{u}_{T}}^{2}(t) \\ -2{{u}_{T}}(t){{v}_{T}}(t) & -{{u}_{T}}^{2}(t) \\ \end{matrix} \right)$. Setting ${{\beta }_{n}}$ and ${{\eta }_{n}}\left(x \right)$ be the eigenvalue and eigenfunction of $-\Delta$ in $\Omega$ with Neumann boundary condition. Let ${{(\phi, \varphi)}^{T}} = {{(h(t), g(t))}^{T}}\underset{n = 0}{\overset{\infty }{\mathop \sum }}\, {{k}_{n}}{{\eta }_{n}}\left(x \right)$, then

in which, $\tau : = {{\beta }_{n}}\ge 0, n\in {{\mathbb{N}}_{0}}: = \{0, 1, 2\cdots \}$. Assume ${{d}_{11}} = {{d}_{12}} = {{d}_{21}} = {{d}_{22}} = 0$, then system (3.2) can be rewritten as

Let $\Phi (t)$ be the fundamental solution matrix of system (3.3) satisfying $\Phi (0) = {{I}_{2}}$. Denote ${{\lambda }_{i}}, i = 1, 2$ as the eigenvalue of $\Phi (T)$, the corresponding characteristic function is ${{\left({{N}_{i}}, {{M}_{i}} \right)}^{T}}$, i.e.,

then ${{\lambda }_{i}}$ is the Floquet multiplier corresponding to the periodic solution $\left({{u}_{T}}(t), {{v}_{T}}(t) \right)$ of system (3.2). Define

apparently,

In system (2.1), differentiating with $t$, we have

Then 1 is the eigenvalue of $\Phi (T)$, the corresponding eigenvector is ${{\left({{{{u}'}}_{T}}(0), {{{{v}'}}_{T}}(0) \right)}^{T}}$. We might as well assume ${{\lambda }_{1}} = 1$, ${{\left({{\phi }_{1}}(t), {{\psi }_{1}}(t) \right)}^{T}} = {{\left({{{{u}'}}_{T}}(t), {{{{v}'}}_{T}}(t) \right)}^{T}}$. Since $\left({{u}_{T}}(t), {{v}_{T}}(t) \right)$ is stable, then $\left| {{\lambda }_{2}} \right| < 1$. Let $\Phi (t, \tau)$ be the fundamental solution matrix of system (3.2), and $\Phi (0, \tau) = I$, namely,

For sufficiently small $\tau$, $\Phi (t, \tau)$ is continuously differentiable with respect to $t$ and $\tau$, and $\Phi (t, 0) = \Phi (t)$. Define mapping $\mathcal{L}:[0, +\infty)\times \mathcal{C}\times {{\mathcal{C}}^{2}}\to {{\mathcal{C}}^{2}}$, where $\mathcal{C}: = \mathbb{R}\oplus i\mathbb{R}$, we have

clearly, $\mathcal{L}\left(0, {{\lambda }_{i}}, {{\left({{N}_{i}}, {{M}_{i}} \right)}^{T}} \right) = {{(0, 0)}^{T}}$ and

here, ${{\mathcal{L}}_{{{\delta }_{i}}}}$ is the Fréchet derivative of $\mathcal{L}$ with respect to ${{\delta }_{i}}$, and ${{\mathcal{L}}_{{{\left({{n}_{i}}, {{m}_{i}} \right)}^{T}}}}$ is the Fréchet derivative of $\mathcal{L}$ with respect to ${{\left({{n}_{i}}, {{m}_{i}} \right)}^{T}}$. Setting ${{\lambda }_{i}}$ is the single eigenvalue of $\Phi (T)$, then we have

where $Ker$ represents the kernel of ${{\lambda }_{i}}I-\Phi (T)$, and $Rank$ represents the range of ${{\lambda }_{i}}I-\Phi (T)$, then ${{\mathcal{L}}_{\left({{\delta }_{i}}, {{\left({{n}_{i}}, {{m}_{i}} \right)}^{T}} \right)}}\left(0, {{\lambda }_{i}}, {{\left({{N}_{i}}, {{M}_{i}} \right)}^{T}} \right), i = 1, 2$ is an isomorphic mapping. By the implicit function theorem, there exist ${{\tau }_{1}} > 0$, $\tau \in \left(-{{\tau }_{1}}, {{\tau }_{1}} \right)$ and continuously differentiable functions ${{\delta }_{i}}(\tau), {{n}_{i}}(\tau), {{m}_{i}}(\tau)$ such that

where ${{\delta }_{i}}(\tau), i = 1, 2$ are the Floquet multipliers corresponding to $\left({{u}_{T}}(t), {{v}_{T}}(t) \right)$. Define

by $\Phi (0, \tau) = I$ and (3.5), we can obtain

From (3.4) and (3.6), we have

Specifically, by (3.5), we have

By the definition of ${{\left({{\phi }_{1}}(t, \tau), {{\psi }_{1}}(t, \tau) \right)}^{T}}$ in (3.5), we can obtain

Differentiating (3.8) with respect to $\tau$ and setting $\tau = 0$, we have

here, ${{\phi }_{1\tau }}: = {{\partial }_{\tau }}{{\phi }_{1}}, {{\psi }_{1\tau }}: = {{\partial }_{\tau }}{{\psi }_{1}}$. On the other hand, from (3.4) and (3.5), we can derive

Differentiating (3.10) with $\tau$, we get

In (3.11), setting $\tau = 0$, from (3.6)and ${{\delta }_{1}}(0) = {{\lambda }_{1}} = 1$, we have

According to Lemma 2.1, $\left({{u}_{T}}(t, \varepsilon), {{v}_{T}}(t, \varepsilon) \right)$ is the periodic solution of system (2.10), that is,

Differentiating (3.13) with respect to $\varepsilon$ and setting $\varepsilon = 0$, we have

where ${{\partial }_{t}}{{u}_{T}}(t, 0) = {{\phi }_{1}}(t), {{\partial }_{t}}{{v}_{T}}(t, 0) = {{\psi }_{1}}(t)$. Since $\left({{u}_{T}}(t, \varepsilon), {{v}_{T}}(t, \varepsilon) \right)$ is the periodic solution with period $T\left(\varepsilon \right)$, thus,

In (3.15), differentiating with respect to $\varepsilon$ and setting $\varepsilon = 0, t = 0$, then

here, ${{u}_{T}}(t, 0) = {{u}_{T}}(t), {{v}_{T}}(t, 0) = {{v}_{T}}(t), T(0) = T$. Define

From (3.9), (3.12), (3.14) and (3.16), we have

Let $\Gamma (t) = \Phi (t){{\left({{Y}_{1}}, {{Y}_{2}} \right)}^{T}}$ be the general solution of (3.17), where any vector ${{\left({{Y}_{1}}, {{Y}_{2}} \right)}^{T}}\in {{\mathbb{R}}^{2}}$. Since ${{\left({{\phi }_{1}}(0), {{\psi }_{1}}(0) \right)}^{T}}$ and ${{\left({{\phi }_{2}}(0), {{\psi }_{2}}(0) \right)}^{T}}$ are linearly independent, then there exit constants ${{\gamma }_{1}}$ and ${{\gamma }_{2}}$ so that

Substituting (3.19) into (3.18), we can obtain ${{{\delta }'}_{1}}(0)+{T}'(0) = 0$. Assume that ${T}'(0) < 0$, which is equivalent to ${{{\delta }'}_{1}}(0) > 0$, if $\Omega$ is large enough so that the minimum positive eigenvalue of $-\Delta$ is small enough, then there exists at least one eigenvalue ${{\beta }_{n}}$ of $-\Delta$ such that $\delta_{1} (\tau) = \delta_{1} \left({{\beta }_{n}} \right) > 1$. Thus, $\left({{u}_{T}}(t), {{v}_{T}}(t) \right)$ becomes Turing unstable in reaction-diffusion system (1.1) with cross-diffusion. □

4.   Numerical simulations

In this section, we shall select several groups of data for numerical simulations to support theoretical analysis. In system (1.1), Fix parameters $a = 0.1823, b = 0.5$, initial values ${{u}_{0}} = 0.6+0.01\cos x, {{v}_{0}} = 1+0.01\sin x$, then the equilibrium is $\left(0.6823, 1.074 \right)$, $\mu _{0}^{H} = 0.6823278$, $\operatorname{Re}{{c}_{1}}\left(\mu _{0}^{H} \right) = -0.5 < 0$, $\operatorname{Im}{{c}_{1}}\left(\mu _{0}^{H} \right) = -0.0270945 < 0$. According to Theorem 2.1, system (2.1) produces a spatially homogeneous Hopf bifurcating periodic solution ${{\left({{u}_{T}}(t), {{v}_{T}}(t) \right)}^{T}}$ at the equilibrium, which is stable and subcritical. By calculation, we can obtain

For different diffusion coefficients, Turing instability of system (1.1) at the periodic solution ${{\left({{u}_{T}}(t), {{v}_{T}}(t) \right)}^{T}}$ is different. Hence, we give diffusion coefficients in four cases and carry out corresponding numerical simulations.

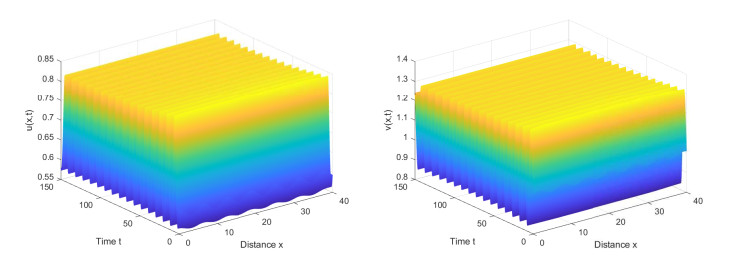
(1) If we select ${{d}_{11}} = 1, {{d}_{22}} = 1, {{d}_{12}} = {{d}_{21}} = 0$, at this moment, Turing instability of ${{\left({{u}_{T}}(t), {{v}_{T}}(t) \right)}^{T}}$ does not exist in system (1.1) (Figure 1). That is, the same diffusion rates will not cause Turing instability of periodic solution (^[19]).

(2) If we select ${{d}_{11}} = 0.05, {{d}_{22}} = 2, {{d}_{12}} = {{d}_{21}} = 0$, then

According to Theorem 3.1, system (1.1) is Turing unstable at periodic solution ${{\left({{u}_{T}}(t), {{v}_{T}}(t) \right)}^{T}}$. Through simulation simulation, it can be observed that the stable periodic solution produces Turing bifurcation (Figure 2), which is consistent with the theoretical analysis.

(3) If we choose ${{d}_{11}} = {{d}_{22}} = 1, {{d}_{21}} = 0.2, {{d}_{12}} = 1.05$, from Theorem 3.1, we have

then system (1.1) is Turing unstable at periodic solution ${{\left({{u}_{T}}(t), {{v}_{T}}(t) \right)}^{T}}$. Through simulation simulation, it can be verified that the stable periodic solution generates Turing bifurcation (Figure 3). Therefore, cross-diffusion causes the stable periodic solution of system (1.1) to become Turing unstable. self-diffusion induces Turing instability of periodic solution.

(4) If we choose ${{d}_{11}} = 0.5, {{d}_{12}} = 1.5, {{d}_{21}} = 0.6, {{d}_{22}} = 4$, then

By Theorem 3.1, we can derive that diffusion causes the stable periodic solution of system (1.1) to become Turing unstable (Figure 4). This conforms to the theoretical analysis.

5.   Conclusions

In this paper, a three-molecule autocatalytic Schnakenberg model with cross-diffusion is considered. From both theoretical and numerical perspectives, we investigated how cross-diffusion causes the Turing instability of spatially homogeneous Hopf bifurcating periodic solutions.

The theoretical results indicate that in the Schnakenberg model, when the parameters satisfy certain conditions and $\Omega$ is sufficiently large, once the instability of periodic solutions induced by diffusion occurs, new and rich spatiotemporal patterns may emerge. For the reaction-diffusion Schnakenberg model, we can derive the precise conditions of diffusion rates, under which the periodic solutions may experience the instability caused by diffusion.

By numerical simulations, the Turing instability of periodic solution ${{\left({{u}_{T}}(t), {{v}_{T}}(t) \right)}^{T}}$ can be observed. Figure 1 shows that without cross-diffusion coefficients, the identical self-diffusion coefficients will not cause the stable periodic solution to produce Turing bifurcation. Figures 2 and 4 illustrate that with appropriate diffusion coefficients, the stable periodic solution of system (1.1) generates Turing instability. Figure 3 indicates that if we select appropriate cross-diffusion coefficients, even for the models with identical self-diffusion rates, cross-diffusion can also cause stable periodic solution to produce Turing bifurcation. Thus, the Turing instability of stable periodic solution ${{\left({{u}_{T}}(t), {{v}_{T}}(t) \right)}^{T}}$ is actually induced by cross-diffusion.

Conflict of interest

The authors declare there is no conflicts of interest.