1.
Introduction
Helmholtz and Burgers' equations play an important role in various streams of applied physics. The Helmholtz equation frequently occurs in the study of physical phenomena involving elliptic partial differential equations (PDEs) such as wave and diffusion, magnetic fields, seismology, electromagnetic radiation, transmission, vibrating lines, acoustics, and geosciences. This equation is actually derived from the wave equation. The Helmholtz equation is a transformed form of the acoustic wave equation. It is utilized in a stream of seismic wave propagation and imaging. This equation plays a significant role in estimations of acoustic propagation in shallow water at low frequencies and characteristics of geodesic sea floor [1]. Mathematically, the eigenvalue problem for the Laplace operator is called the Helmholtz equation expressed by elliptic type linear PDE ∇2ϑ=−k2ϑ, where ∇2 denotes the Laplacian differential operator, k2 signifies the eigenvalue, and ϑ is the eigen function. When this equation is used in respect of waves, k is termed as the wave number which measures the spatial frequency of waves. For the first time, Samuel and Thomas [2] suggested the Helmholtz equation with fractional order. Recently, Prakash et al. [3] presented the solution of the space-fractional Helmholtz equation with the q-homotopy analysis transform method (q-HATM). More recently, Shah et al. [4] examined the fractional Helmholtz equation also.
On the other hand, the Burgers' equations [5,6,7] characterize the nonlinear diffusion phenomenon through the simplest PDEs. Burgers' equations occur mainly in the mathematical model of turbulence, fluid mechanics, and approximation of flow in viscous fluids [5,8,9]. The coupled Burgers' equations in one-dimensional form are described as a sedimentation and/or evolution model of scaled volume concentrations in fluid suspensions. More literature about coupled Burgers' equations can be found in previous works [10,11]. In view of the development of the fractional calculus approach, the Burgers' equation with a fractional derivative was first presented in [12]. After that, many authors investigated the solution for fractional Burgers' equations in past decades using approximate analytical methods (see, for example, [13,14,15,16,17,18,19,20,21,22,23]).
From the past decade, the concept of local fractional calculus and local fractional derivatives developed in the work of Yang [24,25] has been a centre of attraction among researchers. Further, many authors investigated the equations and models appearing in fractal media through various local fractional methods, for instance, local fractional homotopy perturbation method (LFHPM) for handling local fractional PDEs (LFPDEs) [26,27], local fractional Tricomi equation arising in fractal transonic flow [28], local fractional Klein-Gordon equations [29], local fractional heat conduction equation [30], local fractional wave equation in fractal strings [31], local fractional Laplace equation [32], system of LFPDEs [33], and fractal vehicular traffic flow [34], etc. In this sequence, the 2D local fractional Helmholtz equation (LFHE) was introduced in [35]. Recently, the LFHE was solved by local fractional variational iteration method [36], local fractional series expansion method [37]. The local fractional Helmholtz and coupled Helmholtz equations were handled successfully by Baleanu and Jassim [38,39,40] through various local fractional methods. In recent years, the local fractional coupled Burgers' equations (LFCBEs) were also investigated for solutions through various techniques that can be found in [41,42,43,44,45].
The 2D local fractional coupled Helmholtz equations (LFCHEs) suggested in [38] are given as follows:
subject to the initial conditions:
where ϑ1(γ,τ) and ϑ2(γ,τ) are unknown local fractional continuous functions, and ℵ1(γ,τ) and ℵ2(γ,τ) are the nondifferentiable source terms.
The system of nonlinear coupled Burger's equations with local fractional derivatives can be described as:
subject to the initial conditions:
where ξ1, ξ2, μ1, and μ2 denote real constants, ρ and η specify arbitrary constants that depend on parameters of the system, ϑ1(γ,τ) and ϑ2(γ,τ) are local fractional continuous functions, and γ lies in the computational domain Ω.
The key purpose of this work is to establish a new coupling of local fractional homotopy analysis method (LFHAM) [43,46] and local fractional natural transform (LFNT) [47], named as local fractional natural homotopy analysis method (LFNHAM) throughout in this paper. The second goal of the paper is to explore the solutions for the LFCHEs and the LFCBEs by utilizing the newly suggested combination LFNHAM. Moreover, the numerical simulations have also been presented for the obtained solutions of LFCHEs and LFCBEs for the fractal order σ=ln2/ln3 of a local fractional derivative by using MATLAB. The originality and novelty of the paper lie in the fact that the LFCHEs and LFCBEs have never been solved by using this newly suggested combination LFNHAM. In addition, convergence and uniqueness of the LFNHAM solution are also examined for the LFNHAM solution of general LFPDE in view of Banach's fixed point theory.
The notable aspect of the LFNHAM as compared to others is that it offers an extended degree of freedom for analysis and the main ingredient is an auxiliary parameter ℏ≠0 to ensure the convergence of the acquired series solution. Furthermore, a more appropriate choice of an initial guess & effortless creation of deformation equations are the interesting attributes of this method. The LFNHAM is surely beneficial as it combines two powerful algorithms to attain the solutions for nonlinear LFDEs. The LFNHAM generates a convergent series solution that revolves around a convergence parameter without involving linearization, perturbation, or descretization phenomena. In addition, the LFNHAM also minimizes the numerical work unlike other conventional methods while still giving extremely precise results. The LFNHAM provides a more general solution as compared to LFHPM, local fractional Adomian decomposition method (LFADM) and local fractional natural homotopy perturbation method (LFNHPM) and assimilates their consequences as a special case. In addition, it does not involve the computation of complicated Adomian or He's polynomials. But there is also a point of demerit with this technique. The implementation of LFNHAM can be difficult in the situation of non-evaluation of the LFNT of a function. This work checks the LFNHAM solution regarding uniqueness and convergence for the first time and the error analysis of the LFNHAM solution is also discussed. These points surely illustrate the reliability and validity of the proposed method. The other aspect of the LFNHAM is that the coupling of LFNT with LFHAM performs fast-tracked calculations in comparison to LFHAM and consequently consumes less time and less computer memory.
Moreover, the LFNT possesses two important attributes, scale property and unit-preserving property, and hence can be utilized to handle LFPDEs without exerting new frequency range. In the light of these facts, the LFNT which possesses the linearity feature, also possesses the feature of linearity of functions, and hence does not involve the changing of units. This transform performs operation similarly as the local fractional Laplace transform (LFLT) and local fractional Sumudu transform (LFST). By virtue of these facts, the LFNT may be used to analyze some complex problems of science and engineering that may be handled hardly with other integral transforms.
The rest portion of the paper is organized as follows: Section 2 presents definitions and formulae for the local fractional derivative and LFNT. Section 3 illustrates the computational procedure for the suggested scheme LFNHAM. The convergence and uniqueness of the LFNHAM solution is discussed in Section 4. Sections 5 and 6 are devoted to the implementation of the LFNHAM to the LFCHEs and LFCBEs, respectively. In Section 7, numerical simulations have been performed in respect of a fractal value. At the end, Section 8 presents the epilogue.
2.
Preliminaries
The section presents a quick view of some definitions and formulae which have been utilized in this work.
2.1. Local fractional integral (LFI) and local fractional derivative (LFD)
Definition 2.1.1. [24,25] Let (l1,l2) be the interval and Δt=max{Δt0,Δt1,Δt2,Δt3,...} be a partition of (l1,l2) with (tj,tj+1), j=0,...,N−1, t0=l1, tN=l2 with Δtj=tj+1−tj. Now, the LFI of ϑ(γ) is formulated as
Definition 2.1.2. [24,25] The Mittag-Leffler function is given as
Definition 2.1.3. [24,25] The fractal sine and cosine functions are given by
Definition 2.1.4. [24,25] The LFD of ϑ(γ)∈Cσ(l1,l2) of order σ at γ=γ0 is presented as
where Δσ(ϑ(γ)−ϑ(γ0))≅Γ(σ+1)(ϑ(γ)−ϑ(γ0)).
The local fractional partial derivative of ϑ(γ,τ)∈Cσ(l1,l2) of order σ was provided by Yang [24,25] as follows:
where Δσ(ϑ(γ,τ)−ϑ(γ,τ0))≅Γ(σ+1)(ϑ(γ,τ)−ϑ(γ,τ0)).
The LFIs and LFDs of special functions used in this study and described in [24,25] are given as follows:
where γσ signifies a Cantor function.
2.2. Local fractional natural transform (LFNT)
For the first time, Khan & Khan [48] suggested a new integral transform called N-transform. Some years later, Belgacem and Silambarasan [49,50,51] changed its name to Natural transform and also presented a comprehensive study regarding its applications. This transform performs operation similarly as the Laplace and Sumudu transforms.
Definition 2.2.1. [47] The LFNT of the function ϑ(γ,τ) of order σ is defined as
and the corresponding inverse LFNT LFN−1σ is formulated as
where sσ and uσ signify the LFNT variables and ρ denotes a real constant. The integral in the definition of inverse LFNT is taken along sσ=ρ in the complex plane sσ=xσ+iyσ. It is notable that the LFNT converges to LFLT for u=1 and to LFST for s=1.
Some properties of the LFNT are being mentioned here:
Proposition 2.2.2. [47] The LFNT of a LFD is defined by
For q=1,2 and 3, the following expressions are generated
Proposition 2.2.3. [47] The linearity property of the LFNT is defined by
where ˉϑ1,σ(γ,s,u) and ˉϑ2,σ(γ,s,u) denote the LFNT of ϑ1(γ,τ) and ϑ2(γ,τ), respectively.
Theorem 2.2.4. (Local fractional convolution). If LFNσ{ϑ1(γ,τ)}=ˉϑ1,σ(γ,s,u) and LFNσ{ϑ2(γ,τ)}=ˉϑ2,σ(γ,s,u), we have
where
Some useful formulae for LFNT are listed in Table 1 [47].
3.
LFNHAM: Computational procedure
To explain the basic idea of LFNHAM, the following LFPDE is taken here
where Lσ≡∂qσ∂τqσ denotes the linear local fractional differential operator (LFDO) of order qσ i.e., ∃ a number δ>0 such that ‖Lσϑ‖⩽δ‖ϑ‖, Pσ specifies the linear fractional differential operator of general nature in γ and τ. Here, it is also assumed that Pσ is bounded i.e., |Pσ(ϑ−ϑ∗)|⩽λ|ϑ−ϑ∗|. Qσ denotes the nonlinear differential operator which is Lipschitz continuous with ξ>0 fulfilling the criteria |Qσ(ϑ−ϑ∗)|⩽ξ|ϑ−ϑ∗|, γ and τ are independent variables, ϑ(γ,τ) and ω(γ,τ) denote local fractional unknown function and nondifferentiable source term, respectively.
Now, the suggested computational approach recommends the implementation of the LFNT operator PNϵ on Eq (3.1)
Using the property of LFNT for LFDs, it follows
After simplification, we get
Now on account of Eq (3.5), the nonlinear operator is constituted as
where κ∈[0,1] is an embedding parameter, φ(γ,τ;κ) symbolizes the local fractional unknown function of γ,τ and κ, and the symbol LFNσ represents the LFNT operator.
Now utilizing the traditional approach of LFHAM [43,46] and basic methodology of HAM [52,53,54], the zeroth-order deformation equation is developed in this way:
where ℏ≠0 is a convergence regulation parameter and ϑ0(γ,τ) symbolizes an initial guess for ϑ(γ,τ).
It is observed that LFNHAM makes easy the choice of auxiliary parameters, linear operator, and initial guess. The following equations stand firmly for κ=0 and κ=1 in this manner
Hence, when κ takes values from 0 to 1, φ(γ,τ;κ) deviates from ϑ0(γ,τ) to ϑ(γ,τ). Next, the Taylor's series expansion of φ(γ,τ;κ) about κ generates
where
The convergence controller ℏ≠0 promptly provides the convergence of the series solution (3.9). Thus the series given by Eq (3.9) converges at κ=1 with appropriate pick of ϑ0(γ,τ). Thus, we have
Equation (3.11) provides a relationship between ϑ0(γ,τ) and the exact solution ϑ(γ,τ) through the terms ϑμ(γ,τ),(μ=1,2,3,...), that will be calculated in upcoming steps. Eq (3.11) provides the solution of Eq (3.1) in the form of a series.
The vectors are constituted as
Now, the μth-order deformation equation is framed as
Operating the inverse of LFNT on Eq (3.13), we get
In Eq (3.14), the value of ℜμ(ϑμ−1(γ,τ)) can be written in a new look as
where the value of χμ is presented as
In Eq (3.15), P′μ denotes homotopy polynomial suggested in [55] in functioning of LFHAM [43,46], and is formulated as
where
Putting the value of ℜμ(ϑμ−1) from Eq (3.15) in Eq (3.14) transforms the Eq (3.14) as follows:
From Eq (3.19), the components ϑμ(γ,τ) can be evaluated for μ⩾1 and the LFNHAM solution is presented in the following way:
The significant aspect of the LFNHAM is the auxiliary parameter ℏ≠0 which guarantees the convergence of the series solution of Eq (3.1).
Theorem 3.1. If a constant 0<ℵ<1 can be estimated such that ‖ϑμ+1(γ,τ)‖⩽ℵ‖ϑμ(γ,τ)‖ for each value of μ. Moreover, if the truncated series ∑Nμ=0ϑμ(γ,τ) is assumed as an approximate solution ϑ then the maximum absolute truncated error is computed as
Proof. The maximum absolute truncated error is computed in this way:
This finishes the proof.
In the upcoming Section 4, we establish the convergence and uniqueness of the LFNHAM solution.
4.
Uniqueness and convergence analyses of LFNHAM solution
Theorem 4.1. (Uniqueness theorem). The attainment of solution by implementation of LFNHAM for the LFPDE (3.1) is unique, wherever 0<ρ<1, where
Proof. The solution of nonlinear LFPDE (3.1) is obtained as
where
Let ϑ(γ,τ) and ϑ∗(γ,τ) be two distinct possible solutions for Eq (3.1), then we acquire
Utilization of the local fractional convolution theorem for LFNT in Eq (4.4) gives
Now, with the help of mean value theorem (MVT) of LFI calculus [56,57], inequality (4.5) transforms in the following form
where \rho = \left({1 + \hbar } \right) + \hbar \, \left({\lambda + \xi } \right)\, \varsigma . (4.7)
Since 0 < \rho < 1 , therefore \left| {\vartheta - {\vartheta ^ * }\, } \right| = 0 , which provides \vartheta = {\vartheta ^ * } . This ensures the aspect of uniqueness of the solution of Eq (3.1).
Theorem 4.2. (Convergence theorem). Suppose \Xi is a Banach space and \Theta :\Xi \to \Xi is a nonlinear mapping. Assume that
Then Banach's fixed point theory [58,59] suggests the existence of a fixed point for \Theta . Moreover, the sequence constructed by LFNHAM converges to the fixed points of \Theta with arbitrary choices of {\omega _0}, \, \, {\vartheta _0} \in \Xi and
Proof. It is presumed that \left({\Pi \left[\Omega \right]\, , \, \left\| {\, .\, } \right\|} \right) , where \Pi \left[\Omega \right] signifies the Banach space of continuous functions on real line interval \Omega holding the sup norm. Now, it is sufficient to prove that \left\{ {\, {\vartheta _{{l_2}}}} \right\} is a Cauchy sequence in the Banach space \Xi .
Now, consider
Employing the local fractional convolution theorem for LFNT in Eq (4.10), we have
Now, application of MVT of LFI calculus [56,57] reduces the inequality (4.11) in the following form
Assume {l_1} = {l_2} + 1 , then it produces
Utilizing the triangular inequality, we have
Since 0 < {{\rlap{-} \lambda }} < 1 , thus 1 - {{{\rlap{-} \lambda }} ^{{l_1} - {l_2} - 1}} < 1 , then
But \left\| {\, {\vartheta _1} - {\vartheta _0}} \right\| < \infty , thus \left\| {\, {\vartheta _{{l_1}}} - {\vartheta _{{l_2}}}} \right\| \to 0 as n \to \infty , hence \left\{ {\, {\vartheta _{{l_2}}}} \right\} is a Cauchy sequence in \Pi \left[\Omega \right] and so \left\{ {\, {\vartheta _{{l_2}}}} \right\} is convergent. This ensures the convergence of the solution \vartheta \left({\gamma, \, \tau } \right) of LFPDE (3.1). Hence the theorem. □
5.
Application of LFNHAM for LFCHEs
In this section, LFNHAM is implemented for deriving the solutions for LFCHEs.
The following LFCHEs on Cantor set are investigated
subject to the fractal initial conditions:
where {\vartheta _1}\, \left({\gamma, \, \tau } \right) and {\vartheta _2}\, \left({\gamma, \, \tau } \right) represent the local fractional continuous functions.
On account of the initial conditions (5.3) and algorithm of LFNHAM, the initial guess are written as
Employing the LFNT operator {}^{LF}{N_\sigma } on Eqs (5.1) and (5.2), we get
Now, the implementation of formula of LFNT for local fractional derivatives yields
After rearranging the terms, we get
Now, further simplification in view of initial condition (5.3) reduces Eqs (5.9) and (5.10) in the following way
Now in view of Eqs (5.11) and (5.12), the nonlinear operators are formed as:
where \kappa is an embedding parameter and {\varphi _1}\left({\gamma, \tau; \kappa } \right) & {\varphi _2}\left({\gamma, \tau; \kappa } \right) are real valued functions of \gamma, \tau and \kappa .
Now using the steps of the LFHAM [43,46] and basic methodology of HAM [52,53,54], \mu \, th -order deformation equations are constructed as follows:
In Eqs (5.15) and (5.16), the terms {\Re _\mu }\left({{\vartheta _{1, \, (\mu - 1)}}\left({\gamma, \, \tau } \right)} \right) and {\Re _\mu }\left({{\vartheta _{2, \, (\mu - 1)}}\left({\gamma, \, \tau } \right)} \right) are expressed as
Now implementing the LFNHAM and using Eqs (5.15) to (5.18), we have
On account of Eqs (5.19) and (5.20) for \mu = 1 , we have
Using initial guess values (5.4) and further simplification reduces Eqs (5.21) and (5.22) in this way
By means of Eqs (5.19) and (5.20) for \mu = 2 , we have
Utilizing the values provided by Eqs (5.23) and (5.24) in Eqs (5.25) and (5.26), we obtain
Following the similar procedure, we obtain the rest of the values for {\vartheta _{1, \mu }}\left({\gamma, \, \tau } \right) and {\vartheta _{2, \mu }}\left({\gamma, \, \tau } \right) for \mu \geqslant 3 .
Setting the convergence-control parameter \hbar = - 1 , we attain the following values
and so on.
Hence, the solutions of Eqs (5.1) and (5.2) are obtained as
Similarly, we have
Finally, the solutions of the coupled Helmholtz Eqs (5.1) & (5.2) are expressed as
Thus, the LFNHAM solutions are in complete agreement with the solutions obtained by Yang and Hua [60].
6.
Application of LFNHAM for LFCBEs
In this portion, the LFNHAM is executed for deriving the solutions for LFCBEs.
subject to the fractal initial conditions:
where {\vartheta _1}\, \left({\gamma, \, \tau } \right) and {\vartheta _2}\, \left({\gamma, \, \tau } \right) are local fractional continuous functions.
In view of initial conditions (6.3) and LFNHAM, the initial guess are expressed as
Employing the LFNT operator {}^{LF}{N_\sigma } on Eqs (6.1) and (6.2), we get
Now, employing the formula of LFNT for LFDs yields
After rearranging the terms, we get
Now, further simplification in view of initial conditions (6.3) reduces Eqs (6.9) and (6.10) as follows:
Now in view of Eqs (6.11) and (6.12), the nonlinear operators are formed as
where \kappa \in \left[{0, \, 1} \right] is an embedding parameter and {\varphi _1}\left({\gamma, \tau; \kappa } \right) & {\varphi _2}\left({\gamma, \tau; \kappa } \right) are real valued functions of \gamma, \tau , and \kappa .
Performing the steps of the LFNHAM, \mu \, th -order deformation equations are formed as
In Eqs (6.15) and (6.16), the terms {\Re _\mu }\left({{\vartheta _{1, \, (\mu - 1)}}\left({\gamma, \, \tau } \right)} \right) and {\Re _\mu }\left({{\vartheta _{2, \, (\mu - 1)}}\left({\gamma, \, \tau } \right)} \right) are computed as
where {P_{\mu - 1}} , {P'_{\mu - 1}} , {P''_{\mu - 1}} denote the homotopy polynomials [55] and are formulated as
and
On account of LFNHAM and Eqs (6.15)–(6.18), we have
Taking into account the set of iterative schemes (6.24) & (6.25) and initial conditions (6.3), the iterative terms for various values of \mu are computed as follows:
Proceeding in the similar way, we get the remaining values for {\vartheta _{1, \mu }}\left({\gamma, \, \tau } \right) and {\vartheta _{2, \mu }}\left({\gamma, \, \tau } \right) for \mu \geqslant 4 .
Setting the convergence-control parameter \hbar = - 1 , we attain the following values
and so on.
Proceeding in the same way, the rest of the terms of {\vartheta _{1, \mu }}\left({\gamma, \, \tau } \right) and {\vartheta _{2, \mu }}\left({\gamma, \, \tau } \right) for \mu \geqslant 4 are evaluated in a smooth manner, and finally the local fractional series solutions are obtained.
Hence, the solutions of Eqs (6.1) and (6.2) are obtained as
Similarly,
The solutions of LFCHEs and LFCBEs acquired by implementing the LFNHAM are the general form of solutions as compared to the LFADM, LFHPM, and LFNHPM. It is noteworthy that the LFNHAM solution transforms to the LFNHPM solution for \hbar = - 1 . The computational results validate the reliability and accuracy of the proposed method to achieve solutions for LFCHEs and LFCBEs. Moreover, the solutions of LFCHEs are in excellent match with the solutions obtained by Yang and Hua [60]. These facts authenticate the reliability of the solutions obtained by LFNHAM. Conclusively, the suggested hybrid framework can be employed to a variety of local fractional models occurring in a fractal medium.
7.
Numerical simulation
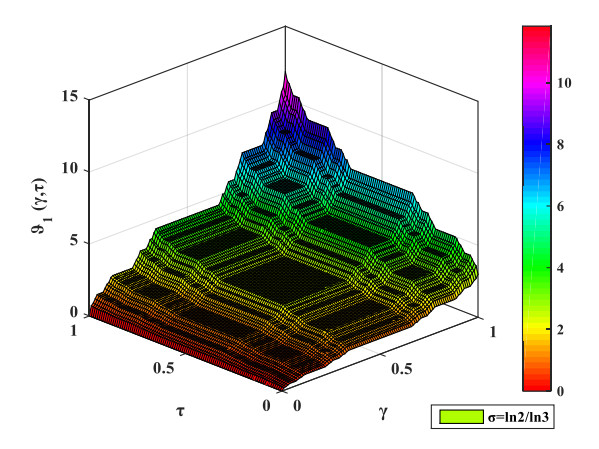
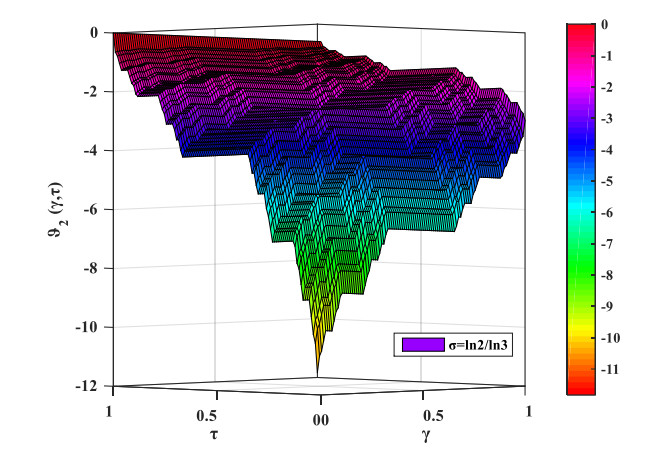
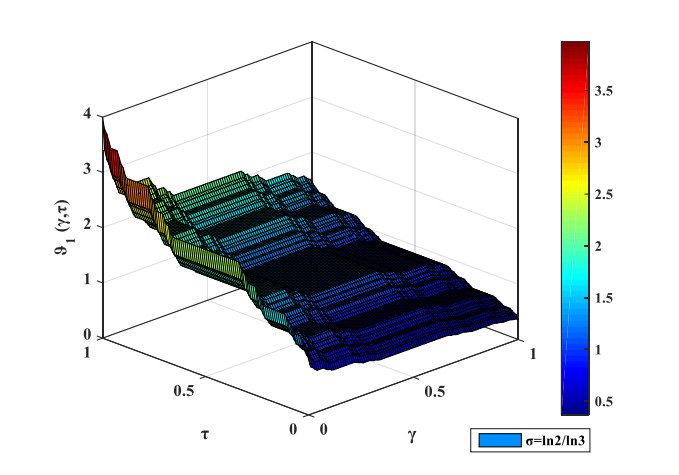
In this segment, the numerical simulations are presented for the solutions of the LFCHEs and LFCBEs under fractal initial conditions obtained via LFNHAM. The 3D plots for solutions of LFCHEs and LFCBEs have been generated for the fractal order \sigma = \ln 2/\ln 3 . Here, all the 3D plots on the Cantor sets have been prepared with the aid of MATLAB software. Figures 1 and 2 depict the 3D surface graphics of coupled solutions {\vartheta _1}\left({\gamma, \, \tau } \right) and {\vartheta _2}\left({\gamma, \, \tau } \right) for the LFCHEs. Similarly, Figures 3 and 4 show the 3D surface graphics of coupled solutions {\vartheta _1}\left({\gamma, \, \tau } \right) and {\vartheta _2}\left({\gamma, \, \tau } \right) for LFCBEs. Here, \gamma and \tau have been taken in the closed interval of 0 to 1. The nature of {\vartheta _1}\left({\gamma, \, \tau } \right) and {\vartheta _2}\left({\gamma, \, \tau } \right) have been explored with respect to \gamma and \tau . The fractal solutions of the LFCHEs and LFCBEs show interesting characteristics for \sigma = \ln 2/\ln 3 . The graphical presentation demonstrates that the computed solutions for the LFCHEs and LFCBEs are consistently dependent on the fractal order \sigma . Furthermore, the 3D figures drawn on Cantor sets indicate that the coupled solutions {\vartheta _1}\left({\gamma, \, \tau } \right) and {\vartheta _2}\left({\gamma, \, \tau } \right) are of fractal nature.
8.
Conclusions
In this paper, the LFNHAM is proposed for computation of solutions for LFCHEs and LFCBEs on Cantor sets. The local fractional series solutions for LFCHEs and LFCBEs have been depicted in terms of Mittag-Leffler function. The 3D plots are presented for solutions of LFCHEs and LFCBEs by using the MATLAB software. It is clearly observed from the surface graphics of the solutions that the figures plotted on the Cantor set for the functions {\vartheta _1}\left({\gamma, \, \tau } \right) and {\vartheta _2}\left({\gamma, \, \tau } \right) are of fractal nature. The computational results authenticate the reliability and accuracy of the implemented method to obtain solutions for LFCHEs and LFCBEs. The combination of LFHAM and LFNT performs faster calculations than LFHAM. The convergence and uniqueness of the LFNHAM solution for a general LFPDE is also discussed in view of Banach's fixed point theory. In a nutshell, the suggested hybrid approach in connection with LFNT can be employed to such types of local fractional models appearing in a fractal media.
Acknowledgments
The authors are very grateful to the referees for constructive comments and suggestions towards the improvement of this paper. This research received no external funding.
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad: