Modeling the COVID-19 epidemic in Bolivia

Antonio N. Bojanic; Alejandro Jordán; Antonio N. Bojanic; Alejandro Jordán

doi:10.3934/bdia.2020004

Big Data and Information Analytics

2020, Volume 5, Issue 1: 47-57. doi: 10.3934/bdia.2020004

Previous Article Next Article

Research article

Modeling the COVID-19 epidemic in Bolivia

Antonio N. Bojanic ^{1
,
,},
Alejandro Jordán ²

1.
Economics Department, Tulane University, 6823 St. Charles Ave., New Orleans, LA 70118, USA
2.
Sam M. Walton College of Business, University of Arkansas, Fayetteville, AR 72701, USA

Received: 21 August 2020 Accepted: 15 October 2020 Published: 27 October 2020

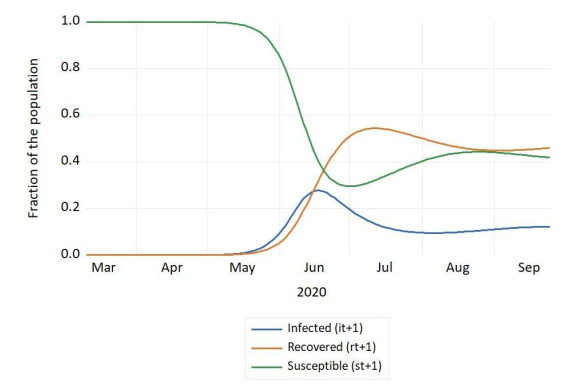
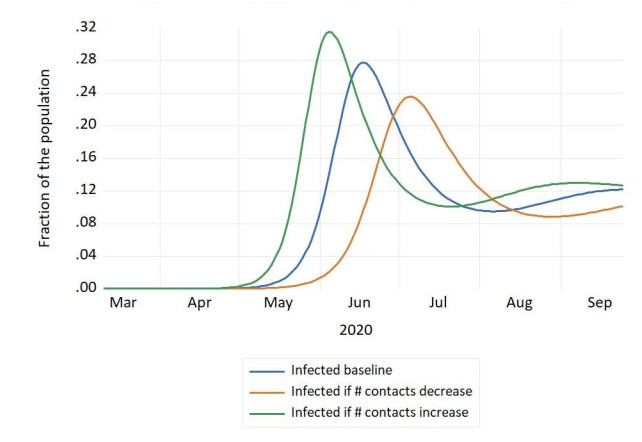
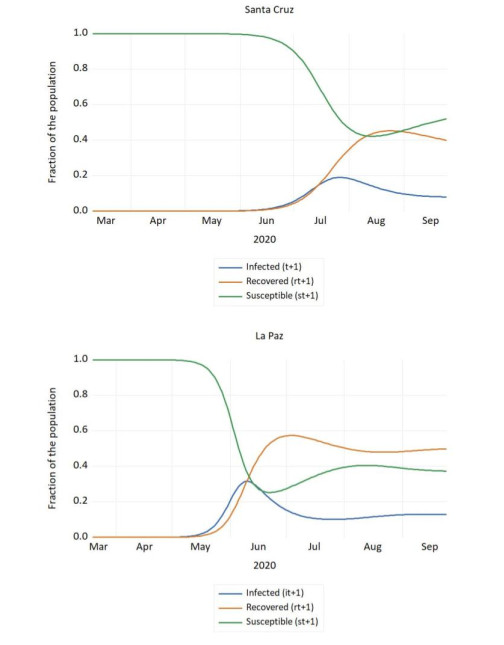
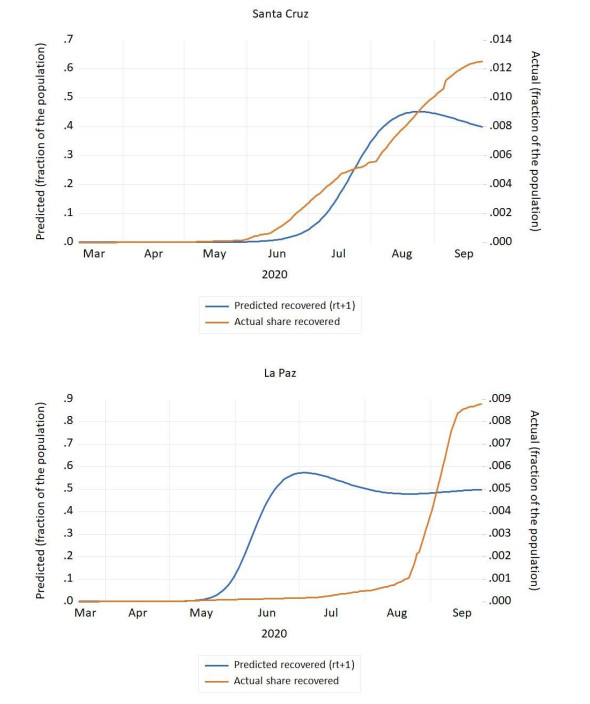
The first cases of COVID-19 appeared in Bolivia on March 10. Since then and until September 24,132,618 people have been infected, 7765 have died, and 92,101 have recovered; the virus has spread throughout the country, but the departments of Santa Cruz, La Paz, and Cochabamba account for the overwhelming percentage of infected, recovered and dead. We analyze the spread of the virus utilizing a SIR model. We find that a maximum fraction of infected individuals occurs on June 17, when around 28% of the population is infected; when the epidemic begins to subside, 54% of the population is in the recovered category, indicating that more than half of the population will have been infected by COVID-19 during some period of the epidemic. There is an uptick in the number of susceptible individuals after July 1, highlighting that the relaxing of mitigation measures might have happened too soon.

Keywords:

Citation: Antonio N. Bojanic, Alejandro Jordán. Modeling the COVID-19 epidemic in Bolivia[J]. Big Data and Information Analytics, 2020, 5(1): 47-57. doi: 10.3934/bdia.2020004

Related Papers:

[1]	Rahat Zarin, Usa Wannasingha Humphries, Amir Khan, Aeshah A. Raezah . Computational modeling of fractional COVID-19 model by Haar wavelet collocation Methods with real data. Mathematical Biosciences and Engineering, 2023, 20(6): 11281-11312. doi: 10.3934/mbe.2023500
[2]	Biplab Dhar, Praveen Kumar Gupta, Mohammad Sajid . Solution of a dynamical memory effect COVID-19 infection system with leaky vaccination efficacy by non-singular kernel fractional derivatives. Mathematical Biosciences and Engineering, 2022, 19(5): 4341-4367. doi: 10.3934/mbe.2022201
[3]	Somayeh Fouladi, Mohammad Kohandel, Brydon Eastman . A comparison and calibration of integer and fractional-order models of COVID-19 with stratified public response. Mathematical Biosciences and Engineering, 2022, 19(12): 12792-12813. doi: 10.3934/mbe.2022597
[4]	Salma M. Al-Tuwairqi, Sara K. Al-Harbi . Modeling the effect of random diagnoses on the spread of COVID-19 in Saudi Arabia. Mathematical Biosciences and Engineering, 2022, 19(10): 9792-9824. doi: 10.3934/mbe.2022456
[5]	Saima Akter, Zhen Jin . A fractional order model of the COVID-19 outbreak in Bangladesh. Mathematical Biosciences and Engineering, 2023, 20(2): 2544-2565. doi: 10.3934/mbe.2023119
[6]	Hamdy M. Youssef, Najat A. Alghamdi, Magdy A. Ezzat, Alaa A. El-Bary, Ahmed M. Shawky . A new dynamical modeling SEIR with global analysis applied to the real data of spreading COVID-19 in Saudi Arabia. Mathematical Biosciences and Engineering, 2020, 17(6): 7018-7044. doi: 10.3934/mbe.2020362
[7]	Abdon ATANGANA, Seda İǦRET ARAZ . Piecewise derivatives versus short memory concept: analysis and application. Mathematical Biosciences and Engineering, 2022, 19(8): 8601-8620. doi: 10.3934/mbe.2022399
[8]	Hardik Joshi, Brajesh Kumar Jha, Mehmet Yavuz . Modelling and analysis of fractional-order vaccination model for control of COVID-19 outbreak using real data. Mathematical Biosciences and Engineering, 2023, 20(1): 213-240. doi: 10.3934/mbe.2023010
[9]	Tao Chen, Zhiming Li, Ge Zhang . Analysis of a COVID-19 model with media coverage and limited resources. Mathematical Biosciences and Engineering, 2024, 21(4): 5283-5307. doi: 10.3934/mbe.2024233
[10]	Jiajia Zhang, Yuanhua Qiao, Yan Zhang . Stability analysis and optimal control of COVID-19 with quarantine and media awareness. Mathematical Biosciences and Engineering, 2022, 19(5): 4911-4932. doi: 10.3934/mbe.2022230

Abstract

1. Introduction

Covid-19 is a pandemic infections which globally has caused damage to human lives and also effect other lining things. This coronavirus has been a terrible epidemic for mankind around the globe. The transmission of COVID-19 has significant negative effects on the lives of all people, and the many people have died from the virus. The first attack of these viruses occurred on last days of 2019. Symptoms of unfamiliar conditions of lungs, coughing, fever, tiredness and breathing problems were seen in the people of Wuhan, China. The healthy territory of China as well as its Central Infections Control (CDC) quickly reconsidered the cause of such signs, a viral virus from the population of Coronaviruses, and it was named as COVID-19 by the World Health Organization (WHO) ^[1,2,3].

For the investigation of the new coronavirus in terms of predictions and infectivity, the authors in ^[4] established a deep analysis algorithm and found that bat and minks are the main sourced of the said virus. Mostly, mathematical models have had an important role in modeling the direct transmission between humans in the outbreak. As demonstrated in the literature, many people were infected in Wuhan and had no contact with other people, but the virus spread very rapidly in the whole province and China ^[5]. The infected people have a long incubation period, they are not aware of the symptoms and don not know the quarantine time. This infection can easily spread to other people, and many researchers have documented models of COVID-19 ^[6,7,8,9,10]. Several researchers have developed the COVID-19 time delay models and studied by different aspects. Most of them modified the said models by the application of fractional operators such as Power and Mittag-Leffler law ^{[11,12,13,14,15,16,17,18]}.

In this article, we have re-considered the COVID-19 mathematical model ^[19], which has not been investigated under novel piecewise derivative and integrals operators. The considered model has ten agents, namely: Susceptible $\mathbb{S}$ , Infectious $\mathbb{I}$ , Diagnosed $\mathbb{D}$ , Ailing $\mathbb{A}$ , Recognized $\mathbb{R}$ , Infectious Real $\mathbb{I}_r$ , Threatened $\mathbb{T}$ , Recovered Diagnosed $\mathbb{H}_d$ , Healed $\mathbb{H}$ , and Extinct population $\mathbb{E}$ . The COVID-19 model has the following form:

$\begin{eqnarray} \begin{split}& \dot{\mathbb{S}} = -(\alpha\mathbb{I}+\beta\mathbb{D}+\gamma\mathbb{A}+\delta\mathbb{R})\mathbb{S}\\& \dot{\mathbb{I}} = -(\epsilon+\zeta+\lambda)\mathbb{I}+(\alpha\mathbb{I}+\beta\mathbb{D}+\gamma\mathbb{A}+\delta\mathbb{R})\mathbb{S}\\& \dot{\mathbb{D}} = -(\eta+\rho)\mathbb{D}+\epsilon\mathbb{I}\\& \dot{\mathbb{A}} = -(\theta+\mu+\kappa)\mathbb{A}+\zeta\mathbb{I}\\& \dot{\mathbb{R}} = -(\nu+\xi)\mathbb{R}+\eta\mathbb{D}\theta\mathbb{A}\\& \dot{\mathbb{I}_r} = (\alpha\mathbb{I}+\beta\mathbb{D}+\gamma\mathbb{A}+\delta\mathbb{R})\mathbb{S}\\& \dot{\mathbb{T}} = -(\sigma+\tau)\mathbb{T}+\mu\mathbb{A}+\nu\mathbb{R}\\& \dot{\mathbb{H}_d} = \rho\mathbb{D}\xi\mathbb{R}+\sigma\mathbb{T}\\& \dot{\mathbb{H}} = \lambda\mathbb{I}+\rho\mathbb{D}+\kappa\mathbb{A}+\xi\mathbb{R}+\sigma\mathbb{A}\\& \dot{\mathbb{E}} = \tau\mathbb{T}, \end{split} \end{eqnarray}$

(1.1)

where the used parameters in the model with descriptions are given in Table 1.

Table 1. Parameters and their description in model 1.1.

Parameter	Description
$\alpha, \beta, \gamma, \delta$	transfer rates from Susceptible class to infectious,
	Diagnosed, Ailing and Recognized stages, respectively
$\epsilon$	Rates of detecting related to Asymptomatic person and
$\theta$	detecting rate of Symptomatic individuals
$\zeta, \eta_1$	Rates of Awareness and Non-awareness classes from being infected
$\mu$	Rate at which Un-detected class transfers to Threaten class
$v$	Rate at which Detected classes transfer to Threaten class
$\tau$	Death rate of Threaten individuals, transfer to Extinct class
$\lambda, \kappa, \xi, \sigma, \rho$	Rates of Recovery from five Compartments

| Show Table

DownLoad: CSV

Modern calculus (MC) has attracted more interest from researchers and scientists in the last 20 years ^[20,21]. MC, compared to traditional integer-order models, gives novel, accurate, and deeper information on the complicated activity of several infectious disease mathematical models ^{[22,23,24,25]}. Because of genetic properties and memory behaviors, integer order problems are not superior to MC problems. Many types of integer order equations are used in mathematical models of the real world. The real phenomena are analyzed for a higher degree of choices and precision by applying the fractional differential equations. Several researchers have done enough work in MC, and the authors in ^[26] used the Mittag-Leffler derivative and investigated the fractional infectious disease model. In ^[27], the authors used Atangana-Baleanu-Caputo fractional derivative and studied a mathematical model of Covid-19. The authors in ^[28] applied the Caputo-Fabrizio operator along with double Laplace transform and found the series solution for the fractional biological model. The scholars in ^[29] applied a novel fractional order Lagrangian scheme to show the motion of a beam on nanowire. Liaqat et al. ^[30], established a new scheme to obtain the approximate and exact solution in the sense of Caputo fractional partial differential equation along with variable. Odibat and Baleanu ^[31] studied a novel system of fractional differential equations involving generalized fractional Caputo operator. Different disease models have been investigated by researchers by using the fractional operators such as ^{[32,33,34,35,36]}. By using various operators to solve a variety of issues from the real world, significant work in the area of fractional calculus has been documented by numerous mathematicians and academics ^{[37,38,39,40,41,42,43,44]}.

A novel operator for piecewise derivative and integrals was presented by Atangana and Araz ^[45]. The piecewise derivative is divided into two sub intervals: The first interval solution is found out in the sense of Caputo while the second intervals solution is under the ABC derivative. As the time of crossover behavior is not mentioned by the power or Mittag-Leffler law and therefore it is well defined in the piecewise derivative. In order to overcome these challenges, one of the unique ways of piecewise derivative has been proposed in ^[45]. A new window of cross-over behaviors using these operators has been studied by researchers. Several applications of the aforesaid fractional operators are investigated in the literature by different researchers ^{[46,47,48,49]}. Inspired by the above novel operator, we investigate the model taken from ^[19] under the framework of piecewise Caputo and Atangana-Baleanu operator as follows:

$\begin{eqnarray} \begin{cases} {_0^{PCABC}}{{\bf D}_t^{\upsilon}}\mathbb{S}(t) = -(\alpha\mathbb{I}+\beta\mathbb{D}+\gamma\mathbb{A}+\delta\mathbb{R})\mathbb{S}, \\ {_0^{PCABC}}{{\bf D}_t^{\upsilon}}\mathbb{I}(t) = -(\epsilon+\zeta+\lambda)\mathbb{I}+(\alpha\mathbb{I}+\beta\mathbb{D}+\gamma\mathbb{A}+\delta\mathbb{R})\mathbb{S}, \\ {_0^{PCABC}}{{\bf D}_t^{\upsilon}}\mathbb{D}(t) = -(\eta+\rho)\mathbb{D}+\epsilon\mathbb{I}, \\ {_0^{PCABC}}{{\bf D}_t^{\upsilon}}\mathbb{A}(t) = -(\theta+\mu+\kappa)\mathbb{A}+\zeta\mathbb{I}, \\ {_0^{PCABC}}{{\bf D}_t^{\upsilon}}\mathbb{R}(t) = -(\nu+\xi)\mathbb{R}+\eta\mathbb{D}\theta\mathbb{A}, \\ {_0^{PCABC}}{{\bf D}_t^{\upsilon}}{\mathbb{I}_r} = (\alpha\mathbb{I}+\beta\mathbb{D}+\gamma\mathbb{A}+\delta\mathbb{R})\mathbb{S}\\ {_0^{PCABC}}{{\bf D}_t^{\upsilon}}{\mathbb{T}} = -(\sigma+\tau)\mathbb{T}+\mu\mathbb{A}+\nu\mathbb{R}\\ {_0^{PCABC}}{{\bf D}_t^{\upsilon}}{\mathbb{H}_d} = \rho\mathbb{D}\xi\mathbb{R}+\sigma\mathbb{T}\\ {_0^{PCABC}}{{\bf D}_t^{\upsilon}}{\mathbb{H}} = \lambda\mathbb{I}+\rho\mathbb{D}+\kappa\mathbb{A}+\xi\mathbb{R}+\sigma\mathbb{A}\\ {_0^{PCABC}}{{\bf D}_t^{\upsilon}}{\mathbb{E}} = \tau\mathbb{T}. \end{cases} \end{eqnarray}$

(1.2)

In more detail we can write Eq (1.2) as

$\begin{eqnarray} {^{CABC}_0} {{\bf D}_t^{\upsilon}}(\mathbb{S}(t)) = \left\{\begin{split}& {^{C}_0} {{\bf D}_t^{\upsilon}}(\mathbb{S}(t)) = ^C{\mho}_1(\mathbb{S}, \mathbb{I}, \mathbb{D}, \mathbb{A}, \mathbb{R}, \mathbb{I}_r, \mathbb{T}, \mathbb{H}_d, \mathbb{H}, \mathbb{E}, t), \ \ 0 < t\leq t_{1}, \\& {^{ABC}_0} {{\bf D}_t^{\upsilon}}(\mathbb{S}(t)) = ^{ABC}{\mho}_1(\mathbb{S}, \mathbb{I}, \mathbb{D}, \mathbb{A}, \mathbb{R}, \mathbb{I}_r, \mathbb{T}, \mathbb{H}_d, \mathbb{H}, \mathbb{E}, t), \ \ t_1 < t\leq T, \end{split}\right. \\ {^{CABC}_0} {{\bf D}_t^{\upsilon}}(\mathbb{I}(t)) = \left\{\begin{split}& {^{C}_0} {{\bf D}_t^{\upsilon}}(\mathbb{I}(t)) = ^C{\mho}_2(\mathbb{S}, \mathbb{I}, \mathbb{D}, \mathbb{A}, \mathbb{R}, \mathbb{I}_r, \mathbb{T}, \mathbb{H}_d, \mathbb{H}, \mathbb{E}, t), \ \ 0 < t\leq t_1, \\& {^{ABC}_0} {{\bf D}_t^{\upsilon}}(\mathbb{I}(t)) = ^{ABC}{\mho}_2(\mathbb{S}, \mathbb{I}, \mathbb{D}, \mathbb{A}, \mathbb{R}, \mathbb{I}_r, \mathbb{T}, \mathbb{H}_d, \mathbb{H}, \mathbb{E}, t), \ \ t_1 < t\leq T, \end{split}\right. \\ {^{CABC}_0} {{\bf D}_t^{\upsilon}}(\mathbb{D}(t)) = \left\{\begin{split}& {^{C}_0} {{\bf D}_t^{\upsilon}}(\mathbb{D}(t)) = ^C{\mho}_3(\mathbb{S}, \mathbb{I}, \mathbb{D}, \mathbb{A}, \mathbb{R}, \mathbb{I}_r, \mathbb{T}, \mathbb{H}_d, \mathbb{H}, \mathbb{E}, t), \ \ 0 < t\leq t_1, \\& {^{ABC}_0} {{\bf D}_t^{\upsilon}}(\mathbb{D}(t)) = ^{ABC}{\mho}_3(\mathbb{S}, \mathbb{I}, \mathbb{D}, \mathbb{A}, \mathbb{R}, \mathbb{I}_r, \mathbb{T}, \mathbb{H}_d, \mathbb{H}, \mathbb{E}, t), \ \ t_1 < t\leq T, \end{split}\right.\\ {^{CABC}_0} {{\bf D}_t^{\upsilon}}(\mathbb{A}(t)) = \left\{\begin{split}& {^{C}_0} {{\bf D}_t^{\upsilon}}(\mathbb{A}(t)) = ^C{\mho}_4(\mathbb{S}, \mathbb{I}, \mathbb{D}, \mathbb{A}, \mathbb{R}, \mathbb{I}_r, \mathbb{T}, \mathbb{H}_d, \mathbb{H}, \mathbb{E}, t), \ \ 0 < t\leq t_1, \\& {^{ABC}_0} {{\bf D}_t^{\upsilon}}(\mathbb{A}(t)) = ^{ABC}{\mho}_4(\mathbb{S}, \mathbb{I}, \mathbb{D}, \mathbb{A}, \mathbb{R}, \mathbb{I}_r, \mathbb{T}, \mathbb{H}_d, \mathbb{H}, \mathbb{E}, t), \ \ t_1 < t\leq T, \end{split}\right. \\ {^{CABC}_0} {{\bf D}_t^{\upsilon}}(\mathbb{R}(t)) = \left\{\begin{split}& {^{C}_0} {{\bf D}_t^{\upsilon}}(\mathbb{R}(t)) = ^C{\mho}_5(\mathbb{S}, \mathbb{I}, \mathbb{D}, \mathbb{A}, \mathbb{R}, \mathbb{I}_r, \mathbb{T}, \mathbb{H}_d, \mathbb{H}, \mathbb{E}, t), \ \ 0 < t\leq t_1, \\& {^{ABC}_0} {{\bf D}_t^{\upsilon}}(\mathbb{R}(t)) = ^{ABC}{\mho}_5(\mathbb{S}, \mathbb{I}, \mathbb{D}, \mathbb{A}, \mathbb{R}, \mathbb{I}_r, \mathbb{T}, \mathbb{H}_d, \mathbb{H}, \mathbb{E}, t), \ \ t_1 < t\leq T, \end{split}\right.\\ {^{CABC}_0} {{\bf D}_t^{\upsilon}}(\mathbb{I}_r(t)) = \left\{\begin{split}& {^{C}_0} {{\bf D}_t^{\upsilon}}(\mathbb{I}_r(t)) = ^C{\mho}_6(\mathbb{S}, \mathbb{I}, \mathbb{D}, \mathbb{A}, \mathbb{R}, \mathbb{I}_r, \mathbb{T}, \mathbb{H}_d, \mathbb{H}, \mathbb{E}, t), \ \ 0 < t\leq t_1, \\& {^{ABC}_0} {{\bf D}_t^{\upsilon}}(\mathbb{I}_r(t)) = ^{ABC}{\mho}_6(\mathbb{S}, \mathbb{I}, \mathbb{D}, \mathbb{A}, \mathbb{R}, \mathbb{I}_r, \mathbb{T}, \mathbb{H}_d, \mathbb{H}, \mathbb{E}, t), \ \ t_1 < t\leq T, \end{split}\right. \end{eqnarray}$

(1.3)

$\begin{eqnarray} {^{CABC}_0} {{\bf D}_t^{\upsilon}}(\mathbb{T}(t)) = \left\{\begin{split}& {^{C}_0} {{\bf D}_t^{\upsilon}}(\mathbb{T}(t)) = ^C{\mho}_7(\mathbb{S}, \mathbb{I}, \mathbb{D}, \mathbb{A}, \mathbb{R}, \mathbb{I}_r, \mathbb{T}, \mathbb{H}_d, \mathbb{H}, \mathbb{E}, t), \ \ 0 < t\leq t_1, \\& {^{ABC}_0} {{\bf D}_t^{\upsilon}}(\mathbb{T}(t)) = ^{ABC}{\mho}_7(\mathbb{S}, \mathbb{I}, \mathbb{D}, \mathbb{A}, \mathbb{R}, \mathbb{I}_r, \mathbb{T}, \mathbb{H}_d, \mathbb{H}, \mathbb{E}, t), \ \ t_1 < t\leq T, \end{split}\right.\\ {^{CABC}_0} {{\bf D}_t^{\upsilon}}(\mathbb{H}_d(t)) = \left\{\begin{split}& {^{C}_0} {{\bf D}_t^{\upsilon}}(\mathbb{H}_d(t)) = ^C{\mho}_8(\mathbb{S}, \mathbb{I}, \mathbb{D}, \mathbb{A}, \mathbb{R}, \mathbb{I}_r, \mathbb{T}, \mathbb{H}_d, \mathbb{H}, \mathbb{E}, t), \ \ 0 < t\leq t_1, \\& {^{ABC}_0} {{\bf D}_t^{\upsilon}}(\mathbb{H}_d(t)) = ^{ABC}{\mho}_8(\mathbb{S}, \mathbb{I}, \mathbb{D}, \mathbb{A}, \mathbb{R}, \mathbb{I}_r, \mathbb{T}, \mathbb{H}_d, \mathbb{H}, \mathbb{E}, t), \ \ t_1 < t\leq T, \end{split}\right.\\ {^{CABC}_0} {{\bf D}_t^{\upsilon}}(\mathbb{H}(t)) = \left\{\begin{split}& {^{C}_0} {{\bf D}_t^{\upsilon}}(\mathbb{H}(t)) = ^C{\mho}_9(\mathbb{S}, \mathbb{I}, \mathbb{D}, \mathbb{A}, \mathbb{R}, \mathbb{I}_r, \mathbb{T}, \mathbb{H}_d, \mathbb{H}, \mathbb{E}, t), \ \ 0 < t\leq t_1, \\& {^{ABC}_0} {{\bf D}_t^{\upsilon}}(\mathbb{H}(t)) = ^{ABC}{\mho}_9(\mathbb{S}, \mathbb{I}, \mathbb{D}, \mathbb{A}, \mathbb{R}, \mathbb{I}_r, \mathbb{T}, \mathbb{H}_d, \mathbb{H}, \mathbb{E}, t), \ \ t_1 < t\leq T, \end{split}\right.\\ {^{CABC}_0} {{\bf D}_t^{\upsilon}}(\mathbb{E}(t)) = \left\{\begin{split}& {^{C}_0} {{\bf D}_t^{\upsilon}}(\mathbb{E}(t)) = ^C{\mho}_{10}(\mathbb{S}, \mathbb{I}, \mathbb{D}, \mathbb{A}, \mathbb{R}, \mathbb{I}_r, \mathbb{T}, \mathbb{H}_d, \mathbb{H}, \mathbb{E}, t), \ \ 0 < t\leq t_1, \\& {^{ABC}_0} {{\bf D}_t^{\upsilon}}(\mathbb{E}(t)) = ^{ABC}{\mho}_{10}(\mathbb{S}, \mathbb{I}, \mathbb{D}, \mathbb{A}, \mathbb{R}, \mathbb{I}_r, \mathbb{T}, \mathbb{H}_d, \mathbb{H}, \mathbb{E}, t), \ \ t_1 < t\leq T. \end{split}\right. \end{eqnarray}$

We considered the dynamics in terms of piecewise fractional operators. The piecewise operators discuss the crossover and abrupt dynamics very well. Therefore, we treated the said model under the two fractional operators in different intervals. For each operator the qualitative analysis is provided on each subinterval. The UH stability is applied for stability analysis of the system. The system is investigated for approximate solution with the piecewise term and also the fractional parameters in the last expression of the system. This gives the choice for any dynamics of integer order as well as rational values.

2. Preliminaries

Here we present some definitions regarding Caputo and $ABC$ fractional as well as piecewise derivatives and also integrals.

Definition 2.1. The definition of ${ABC}$ operator of function ${\bf K}(t)$ with condition ${\bf K}(t)\in\mathcal{H}^1(0, T)$ is :

$\begin{eqnarray} ^{ABC}{_0 D}_{t}^\upsilon ({\bf K}(t)) = \frac{ABC(\upsilon)}{1-\upsilon}\int_0^t\frac{d}{d\vartheta}{\bf K}(\vartheta){E}_\upsilon\bigg[\frac{-\upsilon\bigg(t-\vartheta\bigg)^\upsilon}{1-\upsilon}\bigg]d\vartheta. \end{eqnarray}$

(2.1)

One can replace ${E}_\upsilon\bigg[\frac{-\upsilon}{1-\upsilon}\bigg(t-\vartheta\bigg)^{\vartheta}\bigg]$ by ${E}_1 = \exp\bigg[\frac{-\upsilon}{1-\upsilon}\bigg(t-\vartheta\bigg)\bigg]$ in (2.1) and obtain the Caputo-Fabrizio operator.

Definition 2.2. Consider ${\bf K}(t)\in P[0, T]$ , and then the $\mathbb{ABC}$ integral is:

$\begin{eqnarray} ^{{ABC}}{_0{I}}_{t}^\upsilon {\bf K}(t) = \frac{1-\upsilon}{{ABC}(\upsilon)}{\bf K}(t)+\frac{\upsilon}{{ABC}(\upsilon)\Gamma(\upsilon) }\int_0^t {\bf K}(\vartheta)(t-\vartheta)^{\upsilon-1}d\vartheta. \end{eqnarray}$

(2.2)

Definition 2.3. The Caputo operator of function ${\bf K}(t)$ is

$\begin{eqnarray*} ^C_0{D}^\upsilon_t {\bf K}(t) = \frac{1}{\Gamma(1-\upsilon)}\int_0^t {\bf K}^{'}(\vartheta)(t-\vartheta)^{n-\upsilon-1}d\vartheta. \end{eqnarray*}$

Definition 2.4. Suppose ${\bf K}(t)$ is piecewise differentiable. Then, the piecewise derivative with Caputo and ABC operators ^[26] is

$\begin{eqnarray*} ^{PCABC}_{0}{D}_{t}^\upsilon {\bf K}(t) = \left\{\begin{split}& ^C_{0}{D}_{t}^\upsilon {\bf K}(t), \ \ 0 < t\leq t_1, \\& ^{ABC}_{0}{D}_{t}^\upsilon {\bf K}(t) \ \ t_1 < t\leq T, \end{split} \right. \end{eqnarray*}$

where $^{PCABC}_{0}{D}_{t}^\upsilon$ represents piecewise differential operator, where Caputo operator is in interval $0 < t\leq t_1$ and $ABC$ operator in interval $t_1 < t\leq T$ .

Definition 2.5. Suppose ${\bf K}(t)$ is piecewise integrable, and then piecewise derivative with Caputo and ABC operators ^[26] is

$\begin{eqnarray*} ^{PCABC}_{0}{I}_{t}{\bf K}(t) = \left\{\begin{split}& \frac{1}{\Gamma{\upsilon}}\int_{t_1}^t {\bf K}(\vartheta)(t-\vartheta)^{\upsilon-1}d(\vartheta), \ \ 0 < t\leq t_1, \\& \frac{1-\upsilon}{ABC{\upsilon}}{\bf K}(t)+\frac{\upsilon}{ABC{\upsilon}\Gamma{\upsilon}}\int_{t_1}^t{\bf K}(\vartheta) (t-\vartheta)^{\upsilon-1}d(\vartheta) \ \ t_1 < t\leq T, \end{split}\right. \end{eqnarray*}$

where $^{PCABC}_{0}{I}_{t}^\upsilon$ represents piecewise integral operator, where Caputo operator is in interval $0 < t\leq t_1$ and $ABC$ operator in interval $t_1 < t\leq T$ .

3. Existence and uniqueness

The existence and the uniqueness results of the suggested model in the piecewise notion are found in this part. We shall now determine whether a solution exists for the hypothetical piecewise derivable function as well as its specific solution attribute. In order to do this, we may use the system (1.3) and can also write the following by way of more explanation:

$\begin{eqnarray*} ^{\mathrm{P}CABC}_0{{\bf D}}^\upsilon_t\mathcal{W}(t) = \mathcal{N}(t, \mathcal{W}(t)), \ \ 0 < \upsilon\leq 1 \end{eqnarray*}$

$\begin{eqnarray} \mathcal{W}(t) = \left\{\begin{split}& \mathcal{W}_0+\frac{1}{\Gamma(\upsilon)}\int_0^t \mathcal{N}(\vartheta, \mathcal{W}(\vartheta))(t-\vartheta)^{\upsilon-1}d\vartheta, \ 0 < t\leq t_1\\& \mathcal{W}(t_1)+\frac{1-\upsilon}{ABC{(\upsilon)}}\mathcal{N}(t, \mathcal{W}(t))+\frac{\upsilon}{ABC{(\upsilon)}\Gamma(\upsilon)}\int_{t_1}^t (t-\vartheta)^{\upsilon-1}\mathcal{N}(\vartheta, \mathcal{W}(\vartheta))d(\vartheta), \ \ t_1 < t\leq T, \end{split}\right. \end{eqnarray}$

(3.1)

where

$\begin{equation} \mathcal{W}(t) = \left\{\begin{split}& {\mathbb{S}}(t)\\& \mathbb{I}(t)\\& \mathbb{D}(t)\\& \mathbb{A}(t)\\& \mathbb{R}(t)\\& \mathbb{I}_r(t)\\& \mathbb{T}(t)\\& \mathbb{H}_d(t)\\& \mathbb{H}(t)\\& \mathbb{E}(t) \end{split} \right., \ \ \ \mathcal{W}_0 = \left\{\begin{split}& {\mathbb{S}}_0\\& \mathbb{I}_0\\& \mathbb{D}_0\\& \mathbb{A}_0\\& \mathbb{R}_0\\& \mathbb{I}_{r(0)}\\& \mathbb{T}_0\\& \mathbb{H}_{d(0)}\\& \mathbb{H}_0\\& \mathbb{E}_0 \end{split} \right., \ \ \ \mathcal{W}_{t_1} = \left\{\begin{split}& {\mathbb{S}}_{t_1}\\& \mathbb{I}_{t_1}\\& \mathbb{D}_{t_1}\\& \mathbb{A}_{t_1}\\& \mathbb{R}_{t_1}\\& \mathbb{I}_{r(t_1)}\\& \mathbb{T}_{t_1}\\& \mathbb{H}_{d(t_1)}\\& \mathbb{H}_{t_1}\\& \mathbb{E}_{t_1} \end{split} \right., \ \ \ \mathcal{N}(t, \mathcal{W}(t)) = \left\{\begin{split} {\mho}_i = \left\{\begin{split}& ^{C}{\mho}_i(\mathbb{S}, \mathbb{I}, \mathbb{D}, \mathbb{A}, \mathbb{R}, \mathbb{I}_r, \mathbb{T}, \mathbb{H}_d, \mathbb{H}, \mathbb{E}, t)\\& ^{ABC}{\mho}_i(\mathbb{S}, \mathbb{I}, \mathbb{D}, \mathbb{A}, \mathbb{R}, \mathbb{I}_r, \mathbb{T}, \mathbb{H}_d, \mathbb{H}, \mathbb{E}, t) \end{split} \right. \end{split} \right., \end{equation}$

(3.2)

where $i = 1, 2, 3..., 10.$ Take $0 < t\leq \mathbb{T} < \infty$ and the Banach space ${E}_1 = {C}[0, \mathbb{T}]$ with a norm

$\|\mathcal{W}\| = \max\limits_{t\in [0, \mathbb{T}]}|\mathcal{W}(t)|.$

We assume the following growth condition:

${\bf{(C1)}}$ $\exists$ $\mathcal{L}_{\mathcal{W}} > 0$ ; $\forall$ $\mathcal{N}, \ \bar{\mathcal{W}}\in {E}$ we have

$|\mathcal{N}(t, \mathcal{W})-\mathcal{N}(t, \bar{\mathcal{W}})|\leq \mathcal{L}_{\mathcal{N}}|\mathcal{W}-\bar{\mathcal{W}}|,$

${\bf{(C2)}}$ $\exists$ $C_{\mathcal{N}} > 0$ & $M_{\mathcal{N}} > 0,$ ;

$|\mathcal{N}(t, \mathcal{W}(t))|\leq C_{\mathcal{N}}|\mathcal{W}|+M_{\mathcal{N}}.$

If $\mathcal{N}$ is piece-wise continuous on $(0, t_1]$ and $[t_1, T]$ on $[0, \mathcal{T}]$ , also satisfying $(C2)$ , then (1.3) has $\geq 1$ solution.

Proof. Let us use the Schauder theorem to define a closed sub-set as $\mathfrak{B}$ and $E$ in both subintervals of $[0, \mathscr{L}]$ .

${B} = \{\mathcal{W}\in {E}:\ \|\mathcal{W}\|\leq {R}_{1, 2}, \ {R}_{1, 2} > 0\},$

Suppose $\mathscr{L}: \mathfrak{B} \rightarrow \mathfrak{B}$ and using (4.8) as

$\begin{eqnarray} \mathscr{L}(\mathcal{W}) = \left\{\begin{split}& \mathcal{W}_0+\frac{1}{\Gamma(\upsilon)}\int_0^{\mathrm{t}_1} \mathcal{N}(\vartheta, \mathcal{W}(\vartheta))(\mathrm{t}-\vartheta)^{\upsilon-1}d\vartheta, \ 0 < \mathrm{t}\leq \mathrm{t}_1\\& \mathcal{W}(\mathrm{t}_1)+\frac{1-\upsilon}{ABC{(\upsilon)}}\mathcal{N}(\mathrm{t}, \mathcal{W}(\mathrm{t}))+\frac{\upsilon}{ABC{(\upsilon)}\Gamma{(\upsilon)}}\int_{\mathrm{t}_1}^\mathrm{t} (\mathrm{t}-\vartheta)^{\upsilon-1}\mathcal{N}(\vartheta, \mathcal{W}(\vartheta))d(\vartheta), \ \ \mathrm{t}_1 < \mathrm{t}\leq T. \end{split}\right. \end{eqnarray}$

(3.3)

Any $\mathcal{W}\in {B}$ , we have

$\begin{eqnarray*} \label{p6} |\mathscr{L}(\mathcal{W})(t)|&\leq& \left\{\begin{split}& |\mathcal{W}_0|+\frac{1}{\Gamma(\upsilon)}\int_0^{\mathrm{t}_1} (\mathrm{t}-\vartheta)^{\upsilon-1}|\mathcal{N}(\vartheta, \mathcal{W}(\vartheta))|d\vartheta, \\& |\mathcal{W}_(t_1)|+\frac{1-\upsilon}{ABC{(\upsilon)}}|\mathcal{N}(t, \mathcal{W}(t))|+\frac{\upsilon}{ABC{(\upsilon)}\Gamma{(\upsilon)}}\int_{\mathrm{t}_1}^\mathrm{t} (\mathrm{t}-\vartheta)^{\upsilon-1}|\mathcal{N}(\vartheta, \mathcal{W}(\vartheta))|d(\vartheta), \end{split}\right.\\ &\leq& \left\{\begin{split}& |\mathcal{W}_0|+\frac{1}{\Gamma(\upsilon)}\int_0^{\mathrm{t}_1} (\mathrm{t}-\vartheta)^{\upsilon -1}[C_\mathcal{N} |\mathcal{W}|+M_\mathcal{N}]d\upsilon, \\& |\mathcal{W}_(\mathrm{t}_1)|+\frac{1-\upsilon}{ABC{(\upsilon)}}[C_\mathcal{N} |\mathcal{W}|+M_\mathcal{N}]+\frac{\upsilon}{ABC{(\upsilon)}\Gamma{(\upsilon)}}\int_{\mathrm{t}_1}^\mathrm{t} (\mathrm{t}-\vartheta)^{\upsilon-1}[C_\mathcal{N} |\mathcal{W}|+M_\mathcal{N}]d(\upsilon), \end{split}\right.\\ &\leq& \left\{\begin{split}& |\mathcal{W}_0|+\frac{{\bf T}^\upsilon}{\Gamma(\upsilon+1)}[C_H |\mathcal{W}|+M_\mathcal{N}] = R_1, \ 0 < \mathrm{t}\leq \mathrm{t}_1, \\& |\mathcal{W}_(t_1)|+\frac{1-\upsilon}{ABC{(\upsilon)}}[C_\mathcal{N} |\mathcal{W}|+M_\mathcal{N}]+\frac{\upsilon (T-{\bf T})^\upsilon}{ABC{(\upsilon)}\Gamma{(\upsilon) +1}}[C_\mathcal{N} |\mathcal{W}|+M_\mathcal{N}]d(\upsilon) = R_2, \ \mathrm{t}_1 < \mathrm{t}\leq T, \end{split}\right.\\ &\leq& \left\{\begin{split}& R_1, \ 0 < \mathrm{t}\leq \mathrm{t}_1, \\& R_2, \ \mathrm{t}_1 < \mathrm{t}\leq T. \end{split}\right. \end{eqnarray*}$

As determined by the previous equation, $\mathcal{W}\in {{\bf B}}$ . Therefore, $\mathscr{L}({{\bf B}})\subset {{\bf B}}$ . Thus, it demonstrates that $\mathscr{L}$ is closed and complete. In order to further demonstrate the complete continuity, we also write by using $\mathrm{t}_i < \mathrm{t}_j \in [0, \mathrm{t}_1]$ as the initial interval in the sense of Caputo, consider

$\begin{eqnarray} |\mathscr{L}(\mathcal{W})(\mathrm{t}_j)-\mathscr{L}(\mathcal{W})(\mathrm{t}_i)|& = &\bigg |\frac{1}{\Gamma(\upsilon)}\int_0^{\mathrm{t}_j} (\mathrm{t}_j-\vartheta)^{\upsilon-1} \mathcal{N}(\vartheta, \mathcal{W}(\vartheta))d\vartheta-\frac{1}{\Gamma(\upsilon)}\int_0^{t_i}(\mathrm{t}_i-\vartheta)^{\upsilon-1}\mathcal{N}(\vartheta, \mathcal{W}(\vartheta))d\vartheta\bigg|\\ &\leq& \frac{1}{\Gamma(\upsilon)}\int_0^{t_i} [(t_i-\vartheta)^{\upsilon-1}-(\mathrm{t}_j-\vartheta)^{\upsilon-1}] |\mathcal{N}(\vartheta, \mathcal{W}(\vartheta))|d\vartheta\\ &+&\frac{1}{\Gamma(\upsilon)}\int_{t_i}^{t_j} (t_j-\vartheta)^{\upsilon-1}|\mathcal{N}(\vartheta, \mathcal{W}(\vartheta))|d\vartheta\\ &\leq&\frac{1}{\Gamma(\upsilon )}\bigg[\int_0^{t_i}[(t_i-\vartheta)^{\upsilon-1}-(t_j-\vartheta)^{\upsilon-1}]d\vartheta +\int_{t_i}^{t_j} (t_j-\vartheta)^{\upsilon-1}d\vartheta\bigg](C_{H}|\mathcal{W}|+M_{\mathcal{N}})\\ &\leq&\frac{(C_{\mathcal{N}}\mathcal{W}+M_{\mathcal{N}})}{\Gamma(\upsilon+1)}[t_j^{\vartheta}-t_i^\upsilon+2(t_j-t_i)^\upsilon]. \end{eqnarray}$

(3.4)

Next (3.4), we obtain $t_i\rightarrow t_j$ , and then

$|\mathscr{L}(\mathcal{W})(t_j)-\mathscr{L}(\mathcal{W})(t_i)|\rightarrow 0, \ \text{as}\ t_i\rightarrow t_j.$

So, $\mathscr{L}$ is equi-continuous in $[0, t_1]$ . Consider $t_i, t_j \in [t_1, T]$ in $ABC$ sense as

$\begin{eqnarray} |\mathscr{L}(\mathcal{W})(t_j)-\mathscr{L}(\mathcal{W})(\mathrm{t}_i)|& = &\bigg |\frac{1-\upsilon}{ABC(\upsilon)}\mathcal{N}(t, \mathcal{W}(t))+\frac{\upsilon}{ABC{(\upsilon)}\Gamma(\upsilon)}\int_{t_1}^{\mathrm{t}_j} (\mathrm{t}_j-\vartheta)^{\upsilon-1} \mathcal{N}(\vartheta, \mathcal{W}(\vartheta))d\vartheta, \\ &-&\frac{1-\upsilon}{ABC(\upsilon)}\mathcal{N}(t, \mathcal{W}(t))+\frac{(\upsilon)}{ABC{(\upsilon)}\Gamma(\upsilon)}\int_{\mathrm{t}_1}^{\mathrm{t}_i} (\mathrm{t}_i-\vartheta)^{\upsilon-1}\mathcal{N}(\vartheta, \mathcal{W}(\vartheta))d\vartheta\bigg|\\ &\leq& \frac{\upsilon}{ABC{(\upsilon)}\Gamma(\upsilon)}\int_{t_1}^{t_i} [(t_i-\vartheta)^{\upsilon-1}-(t_j-\vartheta)^{\upsilon-1}] |\mathcal{N}(\vartheta, \mathcal{W}(\vartheta))|d\vartheta\\ &+&\frac{\upsilon}{ABC{(\upsilon)}\Gamma(\upsilon)}\int_{t_i}^{t_j} (t_j-\vartheta)^{\upsilon-1}|\mathcal{N}(\vartheta, \mathcal{W}(\vartheta))|d\vartheta\\ &\leq&\frac{\upsilon}{ABC{(\upsilon)}\Gamma(\upsilon)}\bigg[\int_{t_1}^{t_i}[(t_i-\vartheta)^{\upsilon-1}-(t_j-\vartheta)^{\upsilon-1}]d\vartheta\\ &+&\int_{t_i}^{t_j} (t_j-\vartheta)^{\upsilon-1}d\upsilon\bigg](C_{\mathcal{N}}|\mathcal{W}|+M_{\mathcal{N}})\\ &\leq&\frac{\upsilon(C_{\mathcal{N}}\mathcal{W}+M_{\mathcal{N}})}{ABC{(\upsilon)}\Gamma(\upsilon+1)}[t_j^\upsilon-t_i^\upsilon+2(t_j-t_i)^\upsilon]. \end{eqnarray}$

(3.5)

If $t_i\rightarrow \mathrm{t}_j$ , then

$|\mathscr{L}(\mathcal{W})(\mathrm{t}_j)-\mathscr{L}(\mathcal{W})(t_i)|\rightarrow 0, \ \text{as}\ t_i\rightarrow t_j.$

So, the operator $\mathscr{L}$ shows its equi-continuity in $[\mathrm{t}_1, T]$ . Thus, $\mathscr{L}$ is an equi-continuous map. Based on the Arzelà-Ascoli result, $\mathscr{L}$ is continuous (completely), uniformly continuous, and bounded. The Schauder result shows that problem (1.3) has at least one solution in the subintervals.

Further, if $\mathscr{L}$ is a contraction mapping with $(C1)$ , then the suggested system has unique solution. As $\mathscr{L}: {{\bf B}}\rightarrow {{\bf B}}$ is piece-wise continuous, consider $\mathcal{W}$ and $\bar{\mathcal{W}} \in {B}$ on $[0, t_1]$ in the sense of Caputo as

$\begin{eqnarray} \|\mathscr{L}(\mathcal{W})-\mathscr{L}(\bar{\mathcal{W}})\|& = &\max\limits_{t\in [0, t_1]}\bigg|\frac{1}{\Gamma(\upsilon)}\int_0^t (t-\vartheta)^{\upsilon-1}\mathcal{N}(\vartheta, \mathcal{W}(\vartheta))d\vartheta- \frac{1}{\Gamma(\upsilon)}\int_0^t (t-\vartheta)^{\upsilon-1}\mathcal{N}(\vartheta, \bar{\mathcal{W}}(\vartheta))d\vartheta\bigg|\\ &\leq& \frac{{\bf T}^\upsilon}{\Gamma(\upsilon+1)}L_\mathcal{N}\|\mathcal{W}-\bar{\mathcal{W}}\|. \end{eqnarray}$

(3.6)

From (3.6), we have

$\begin{eqnarray} \|\mathscr{L}(\mathcal{W})-\mathscr{L}(\bar{\mathcal{W}})\|\leq \frac{{\bf T}^\upsilon}{\Gamma(\upsilon+1)}L_\mathcal{N}\|\mathcal{W}-\bar{\mathcal{W}}\|. \end{eqnarray}$

(3.7)

As a result, $\mathscr{L}$ is a contraction. As a result, the issue under consideration has only one solution in the provided sub interval in light of the Banach result. Also $\mathrm{t}\in[\mathrm{t}_1, T]$ in the sense of the $ABC$ derivative as

$\begin{eqnarray} \|\mathscr{L}(\mathcal{W})-\mathscr{L}(\bar{\mathcal{W}})\|\leq \frac{1-\upsilon}{ABC(\upsilon)}L_\mathcal{N}\|\mathcal{W}-\bar{\mathcal{W}}\|+\frac{\upsilon({{\bf T}-T}^\upsilon)}{ABC(\upsilon)\Gamma(\upsilon+1)}L_{\mho}\|\mathcal{W}-\bar{\mathcal{W}}\|. \end{eqnarray}$

(3.8)

$\begin{eqnarray} \|\mathscr{L}(\mathcal{W})-\mathscr{L}(\bar{\mathcal{W}})\|\leq L_\mathcal{N}\bigg[\frac{1-\upsilon}{ABC(\upsilon)}+\frac{\upsilon(T-{\bf T})^\upsilon}{ABC(\upsilon)\Gamma{(\upsilon+1)}}\bigg]\|\mathcal{W}-\bar{\mathcal{W}}\|. \end{eqnarray}$

(3.9)

This is why $\mathscr{L}$ is a contraction. As a result, the issue under consideration has a singleton solution in the provided sub interval in light of the Banach result. So, with (3.7) and (3.9), the suggested problem has unique solution on each sub-interval.

4. Stability analysis

Here, we prove the H-U stability and different forms for our considered model.

Definition 4.1. Our proposed model (1.1) is U-H stable, if for each $\alpha > 0$ , and the inequality

$\begin{eqnarray} \left|^{PCABC}{\bf D}_{t}^{\upsilon}\Theta(t)-{\mho}(t, \Theta(t))\right| < \alpha, for\; \; all, t\in\mathcal{T}, \end{eqnarray}$

(4.1)

unique solution $\overline{\Theta}\in Z$ exists with a constant $\mathcal{H} > 0$ ,

$\begin{eqnarray} \left|\left|\Theta-\overline{\Theta}\right|\right|_{Z}\leq\mathcal{H}\alpha, for\; \; all, t\in\mathcal{T}, \end{eqnarray}$

(4.2)

In addition, if we take the increasing function $\Phi:[0, \infty)\rightarrow R^{+}$ , then the above inequality can be written as

$\begin{eqnarray*} \left|\left|\Theta-\overline{\Theta}\right|\right|_{Z}\leq\mathcal{H}\Phi(\alpha), at\; every, t\in\mathcal{T}, \end{eqnarray*}$

if $\Phi(0) = 0$ , then the obtained solution is generalized U-H stable.

Definition 4.2. Our considered model 1.2 is U-H Rassias stable if, $\Psi:[0, \infty)\rightarrow R^{+}$ , for each $\alpha > 0$ , and inequality

$\begin{eqnarray} \left|^{PCABC}{\bf D}_{t}^{\upsilon}\Theta(t)-{\mho}(t, \Theta(t))\right| < \alpha \Psi(t), for\; all, t\in\mathcal{T}, \end{eqnarray}$

(4.3)

unique solution $\overline{\Theta}\in Z$ with constant $\mathcal{H}_{\Psi} > 0$ , so that

$\begin{eqnarray} \left|\left|\Theta-\overline{\Theta}\right|\right|_{Z}\leq\mathcal{H}_{\Psi}\alpha\Psi(t), t\in\mathcal{T}. \end{eqnarray}$

(4.4)

If $\Psi:[0, \infty)\rightarrow R^{+}$ is exist, for the above inequality, then

$\begin{eqnarray} \left|^{PCABC}{\bf D}_{t}^{\upsilon}\Theta(t)-{\mho}(t, \Theta(t))\right| < \Psi(t), t\in\mathcal{T}, \end{eqnarray}$

(4.5)

then there exist a unique solution $\overline{\Theta}\in Z$ with constant $\mathcal{H}_{\Psi} > 0$ , such that

$\begin{eqnarray} \left|\left|\Theta-\overline{\Theta}\right|\right|_{Z}\leq\mathcal{H}_{\Psi}\Psi(t), t\in\mathcal{T}. \end{eqnarray}$

(4.6)

then the obtained solution is generalized U-H Rassias stable.

Remark 1. Suppose a function $\phi\in C(\mathcal{T})$ does not depend upon $\Theta\in\mathcal{Z}$ , and $\phi(0) = 0$ . Then,

$\begin{eqnarray*} \label{c4} \left|\phi(t)\right|&\leq&\alpha, t\in \mathcal{T}\\ ^{PCABC}{\bf D}_{t}^{\upsilon}\Theta(t)& = &{\mho}\left(t, \Theta(t)\right)+\phi(t), t\in\mathcal{T}. \end{eqnarray*}$

Lemma 4.2.1. Consider the function

$\begin{eqnarray} ^{PCABC}_0{{\bf D}}^\varrho_t \Theta(t) = {\mho}(t, \Theta(t)), \ \ 0 < \varrho\leq 1. \end{eqnarray}$

(4.7)

The solution of (4.7) is

$\begin{eqnarray} \Theta(t) = \left\{\begin{split}& \Theta_0+\frac{1}{\Gamma(\upsilon)}\int_0^t {\mho}(\vartheta, \Theta(\vartheta))(t-\vartheta)^{\upsilon-1}d\vartheta, \ 0 < t\leq t_1\\& \Theta(t_1)+\frac{1-\upsilon}{ABC{(\upsilon)}}{\mho}(t, \Theta(t))+\frac{\upsilon}{ABC{(\upsilon)}\Gamma(\upsilon)}\int_{t_1}^t (t-\vartheta)^{\upsilon-1}{\mho}(\vartheta, \Theta(\vartheta))d(\vartheta), \ \ t_1 < t\leq T, \end{split}\right. \end{eqnarray}$

(4.8)

$\begin{eqnarray} \left|\left|F(\Theta)-F(\overline{\Theta})\right|\right|\leq\left\{\begin{split}& \frac{\mathcal{T}_{1}^{\upsilon}}{\Gamma{(\upsilon+1)}}\alpha, t\in\mathcal{T}_{1}\\& \left[\frac{(1-\upsilon)\Gamma{(\upsilon)}+(T_{2}^{\upsilon})}{ABC(\upsilon)\Gamma{(\upsilon)}}\right]\alpha = \Lambda\alpha, t\in\mathcal{T}_{2}. \end{split}\right. \end{eqnarray}$

(4.9)

Theorem 1. In light of lemma (4.2.1), if the condition $\frac{L_{f}\mathcal{T}^{\upsilon}}{\Gamma(\upsilon)} < 1$ holds, then the solution of our considered model (1.2) is H-U as well as generalized H-U stable.

Proof. Suppose $\Theta\in Z$ is the solution of (1.2), and $\overline{\Theta}\in Z$ is a unique solution of (1.2). Then we have

Case:1 for $t\in\mathcal{T}$ , we have

$\begin{eqnarray} \begin{split}& \left|\left|\Theta-\overline{\Theta}\right|\right| = \sup\limits_{t\in\mathcal{T}}\left|\Theta-\left(\Theta_{\circ}+\frac{1}{\Gamma(\upsilon)}\int_{0}^{t_{1}}(t_{1}-\vartheta)^{\upsilon-1}{\mho}\left(\vartheta, \overline{\Theta}(\vartheta)\right)d\vartheta\right)\right|\\& \leq\sup\limits_{t\in\mathcal{T}}\left| \Theta-\left(\Theta_{\circ}+\frac{1}{\Gamma(\upsilon)}\int_{0}^{t_{1}}(t_{1}-\vartheta)^{\upsilon-1}{\mho}\left(\vartheta, \overline{\Theta}(\vartheta)\right)d\vartheta\right)\right|\\& +\sup\limits_{t\in\mathcal{T}}\left| +\frac{1}{\Gamma(\upsilon)}\int_{0}^{t_{1}}(t_{1}-\vartheta)^{\upsilon-1}{\mho}\left(\vartheta, \Theta(\vartheta)\right)d\vartheta-\frac{1}{\Gamma(\upsilon)}\int_{0}^{t_{1}}(t_{1}-\vartheta)^{\upsilon-1}{\mho}\left(\vartheta, \overline{\Theta}(\vartheta)\right)d\vartheta\right|\\& \leq\frac{\mathcal{{T}_{1}}^{\upsilon}}{\Gamma(\upsilon+1)}\alpha+\frac{L_{f}\mathcal{{T}_{1}}}{\Gamma(\upsilon+1)}\left|\left|\Theta-\overline{\Theta}\right|\right|. \end{split} \end{eqnarray}$

(4.10)

On further simplification

$\begin{eqnarray} \left|\left|\Theta-\overline{\Theta}\right|\right| &\leq&\left(\frac{\frac{\mathcal{{T}_{1}}}{\Gamma(\upsilon+1)}}{1-\frac{L_{f}\mathcal{{T}_{1}}}{\Gamma(\upsilon+1)}}\right)\alpha \end{eqnarray}$

(4.11)

Case:2

$\begin{eqnarray*} \left|\left|\Theta-\overline{\Theta}\right|\right| &\leq&\sup\limits_{t\in\mathcal{T}}\left|\Theta-\left[\Theta(t_{1})+\frac{1-\upsilon}{{ABC}(\upsilon)}\left[{\mho}\left(t, \Theta(t)\right), \right] \right.\right.\\ &+&\left.\left.\frac{\upsilon}{ABC(\upsilon)\Gamma(\upsilon)}\left[\int_{t_{1}}^{t}(t-\vartheta)^{\upsilon-1}{\mho}\left(\vartheta, \overline{\Theta}(\vartheta) \right)d(\vartheta)\right]\right]\right|\\ &+&\sup\limits_{t\in\mathcal{T}}\frac{1-\upsilon}{{ABC}(\upsilon)}\left|{\mho}\left(t, \Theta(t)\right) -{\mho}\left(t, \overline{\Theta}(t), \right)\right|\\ &+&\sup\limits_{t\in\mathcal{T}}\frac{\upsilon}{{ABC}(\upsilon)\Gamma(\upsilon)}\int_{t_{1}}^{t}(t-\vartheta)^{\upsilon-1}\left|{\mho}\left(\vartheta, \Theta(\vartheta)\right) -{\mho}\left(\vartheta, \overline{\Theta}(\vartheta)\right)\right|ds. \end{eqnarray*}$

By further simplification and using $\Lambda = \left[\frac{(1-\upsilon)\Gamma(\upsilon)+T_{2}^{\upsilon}}{ABC(\upsilon)\Gamma(\upsilon)}\right],$ we have

$\begin{eqnarray} \left|\left|\Theta-\overline\Theta\right|\right|_{Z}\leq\Lambda\alpha+\Lambda{L_{f}}\left|\left|\Theta-\overline\Theta\right|\right|_{Z} \end{eqnarray}$

(4.12)

We have

$\begin{eqnarray*} \left|\left|\Theta-\overline\Theta\right|\right|_{Z}\leq\left(\frac{\Lambda}{1-\frac{\Lambda} {L_{f}}}\right)\alpha\left|\left|\Theta-\overline\Theta\right|\right|_{Z}. \end{eqnarray*}$

we use

$\begin{eqnarray*} \mathcal{H} = \max\left\{\left(\frac{\frac{\mathcal{T}_{1}}{\Gamma(\upsilon+1)}}{1-\frac{L_{f}\mathcal{T}_{1}}{\Gamma(\upsilon+1)}}\right), \frac{\Lambda}{1-\frac{\Lambda L_{f}}{1-M_{f}}}\right\} \end{eqnarray*}$

Now, from Eqs (4.11) and (4.12), we have

$\begin{eqnarray*} \label{c33} \left|\left|\Theta-\overline\Theta\right|\right|_{Z}\leq\mathcal{H}\alpha, at\; \; each\; t\in \mathcal{T}. \end{eqnarray*}$

Therefore, the solution of model (1.2) is H-U stable. Also, if we replace $\alpha$ by $\Phi(\alpha)$ , then from (4.13),

$\begin{eqnarray*} \label{c34} \left|\left|\Theta-\overline\Theta\right|\right|_{Z}\leq\mathcal{H}\Phi(\alpha), at\; \; each\; t\in \mathcal{T}. \end{eqnarray*}$

Now, $\Phi(0) = 0$ shows that the solution of our proposed model (1.2) is generalized H-U stable.

We give the following remark to conclude the Rassias stability results and also the generalized form.

Remark 2. Suppose a function $\phi\in C(\mathcal{T})$ does not depend upon $\Theta\in\mathcal{Z}$ , and $\phi(0) = 0$ . Then,

$\begin{eqnarray*} \label{c44} \left|\phi(t)\right|&\leq&\Psi(t)\alpha, t\in \mathcal{T}\\ ^{PCABC}\mathcal{D}_{t}^{\upsilon}\Theta(t)& = &{\mho}\left(t, \Theta(t)\right)+\phi(t), t\in\mathcal{T}\\ \int_{0}^{t}\Psi(\vartheta)ds&\leq& C_{\Psi}\Psi(t), t\in \mathcal{T}. \end{eqnarray*}$

Lemma 4.2.2. Solution to the model

$\begin{eqnarray*} \label{c5} ^{PCABC}\mathcal{D}_{t}^{\upsilon}\Theta(t)& = &{\mho}\left(t, \Theta(t)\right)+\phi(t), \\ \Theta(0) = \Theta_{\circ}, \end{eqnarray*}$

hold the relation given below:

$\begin{eqnarray} \left|\left|F(\Theta)-F(\overline{\Theta})\right|\right|\leq\left\{\begin{split}& \frac{\mathcal{T}_{1}^{\upsilon}}{\Gamma{(\upsilon+1)}}C_{\Psi}\Psi(t)\alpha, t\in\mathcal{T}_{1}\\& \left[\frac{(1-\upsilon)\Gamma{(\upsilon)}+(T_{2}^{\upsilon})}{ABC(\upsilon)\Gamma{(\upsilon)}}\right]C_{\Psi}\Psi(t)\alpha = \Lambda C_{\Psi}\Psi(t)\alpha, t\in\mathcal{T}_{2}. \end{split}\right. \end{eqnarray}$

(4.13)

where $\mathcal{H}_{f, \Psi, \Lambda} = \Lambda\mathcal{H}_{f, \Psi}$ .

With the help of remark 2, one can get Eq (4.7).

Theorem 2. The solution of model (4.13) is H-U-R stable if the following conditions hold:

$\left.H_{1}\right)$ For each $\Theta, v\in\mathcal{Z}$ and a constant $C_{\Phi} > 0$ , we get

$\begin{eqnarray*} \left|\Phi(\Theta)-\Phi(v)\right|\leq C_{\Phi}\left|\Theta-v\right|, \end{eqnarray*}$

$\left.H_{2}\right)$ For each $\Theta, v, \overline{\Theta}, \overline{v}\in\mathcal{Z}$ and constant $L_{f} > 0, 0 < M_{f} < 1$ , we get

$\begin{eqnarray*} \left|{\mho}(t, \Theta, v)-{\mho}(t, \overline{\Theta}, \overline{v})\right|\leq L_{f}\left|\Theta-\overline{\Theta}\right|+M_{f}\left|v-\overline{v}\right| \end{eqnarray*}$

$\begin{eqnarray*} M_{f}& < &1. \end{eqnarray*}$

Proof. We prove these results in two cases.

Case:1 for $t\in\mathcal{T}$ , we have

$\begin{eqnarray*} \left|\left|\Theta-\overline{\Theta}\right|\right|& = &\sup\limits_{t\in\mathcal{T}}\left|\Theta-\left(\Theta_{\circ}+\frac{1}{\Gamma(\upsilon)}\int_{0}^{t_{1}}(t_{1}-\vartheta)^{\upsilon-1}{\mho}\left(\vartheta, \overline{\Theta}(\vartheta)\right)d\vartheta\right)\right|\\ &\leq&\sup\limits_{t\in\mathcal{T}}\left| \Theta-\left(\Theta_{\circ}+\frac{1}{\Gamma(\upsilon)}\int_{0}^{t_{1}}(t_{1}-\vartheta)^{\upsilon-1}{\mho}\left(\vartheta, \overline{\Theta}(\vartheta)\right)d\vartheta\right)\right|\\ &+&\sup\limits_{t\in\mathcal{T}}\left| +\frac{1}{\Gamma(\upsilon)}\int_{0}^{t_{1}}(t_{1}-\vartheta)^{\upsilon-1}{\mho}\left(\vartheta, \Theta(\vartheta)\right)d\vartheta\right.\\ &-&\left.\frac{1}{\Gamma(\upsilon)}\int_{0}^{t_{1}}(t_{1}-\vartheta)^{\upsilon-1}{\mho}\left(\vartheta, \overline{\Theta}(\vartheta)\right)d\vartheta\right|\\ &\leq&\frac{\mathcal{T}_{1}^{\upsilon}}{\Gamma(\upsilon+1)}C_{\Phi}\Phi(t)\alpha+\frac{L_{f}\mathcal{{T}_{1}}}{\Gamma(\upsilon+1)}\left|\left|\Theta-\overline{\Theta}\right|\right|. \end{eqnarray*}$

On further simplification

$\begin{eqnarray} \left|\left|\Theta-\overline{\Theta}\right|\right| &\leq&\left(\frac{C_{\Phi}\Phi(t)\frac{\mathcal{T}_{1}}{\Gamma(\upsilon+1)}}{1-\frac{L_{f}\mathcal{T}_{1}}{\Gamma(\upsilon+1)}}\right)\alpha \end{eqnarray}$

(4.14)

Case:2

By further simplification and using $\Lambda = \left[\frac{(1-\upsilon)\Gamma(\upsilon)+T_{2}^{\upsilon}}{ABC(\upsilon)\Gamma(\upsilon)}\right],$ we have

$\begin{eqnarray} \left|\left|\Theta-\overline\Theta\right|\right|_{Z}\leq\Lambda C_{\Phi}\Phi(t)\alpha+\Lambda{L_{f}}\left|\left|\Theta-\overline\Theta\right|\right|_{Z} \end{eqnarray}$

(4.15)

We have

$\begin{eqnarray*} \left|\left|\Theta-\overline\Theta\right|\right|_{Z}\leq\left(\frac{\Lambda C_{\Phi}\Phi(t)}{1-\frac{\Lambda} {L_{f}}}\right)\alpha\left|\left|\Theta-\overline\Theta\right|\right|_{Z}. \end{eqnarray*}$

We use

$\begin{eqnarray*} \mathcal{H}_{\Lambda, C_{\Phi}} = \max\left\{\left(\frac{\frac{\mathcal{T}_{1}}{\Gamma(\upsilon+1)}}{1-\frac{L_{f}\mathcal{T}_{1}}{\Gamma(\upsilon+1)}}\right), \frac{C_{\Phi}\Phi(t)\Lambda}{1-\frac{\Lambda L_{f}}{1-M_{f}}}\right\} \end{eqnarray*}$

Now, from Eqs (4.14) and (4.15), we have

$\begin{eqnarray*} \label{c3} \left|\left|\Theta-\overline\Theta\right|\right|_{Z}\leq\mathcal{H}_{\Lambda, C_{\Phi}}\alpha, at\; \; each\; t\in \mathcal{T} \end{eqnarray*}$

So, the solution of model (1.2) is H-U-R stable.

Remark 3. Suppose a function $\phi\in C(\mathcal{T})$ does not depend upon $\Theta\in\mathcal{Z}$ , and $\phi(0) = 0$ ; then,

$\begin{eqnarray*} \left|\phi(t)\right|\leq\Psi(t), t\in\mathcal{T}; \end{eqnarray*}$

Theorem 3. In light of $H_{1}$ , $H_{2}$ , Remark 3 and 2, the solution of model 1.2 is generalized H-U-R stable, if $M_{f} < 1$ .

Where

$\left.H_{1}\right)$ For each $\Theta, v\in\mathcal{Z}$ and constant $C_{\Phi} > 0$ , we get

$\begin{eqnarray*} \left|\Phi(\Theta)-\Phi(v)\right|\leq C_{\Phi}\left|\Theta-v\right| \end{eqnarray*}$

and

$\left.H_{2}\right)$ For each $\Theta, v, \overline{\Theta}, \overline{v}\in\mathcal{Z}$ and constant $L_{f} > 0, 0 < M_{f} < 1$ , we get

$\begin{eqnarray*} \left|{\mho}(t, \Theta, v)-{\mho}(t, \overline{\Theta}, \overline{v})\right|\leq L_{f}\left|\Theta-\overline{\Theta}\right|+M_{f}\left|v-\overline{v}\right| \end{eqnarray*}$

Proof. We obtained our results in two cases:

Case 1: for $t\in\mathcal{T}$ , we have

$\begin{eqnarray*} \left|\left|\Theta-\overline{\Theta}\right|\right|& = &\sup\limits_{t\in\mathcal{T}}\left| \Theta-\left(\Theta_{\circ}+\frac{1}{\Gamma(\upsilon)}\int_{0}^{t_{1}}(t_{1}-\vartheta)^{\upsilon-1}{\mho}\left(\vartheta, \overline{\Theta}(\vartheta)\right)d\vartheta\right)\right|\\ &\leq&\sup\limits_{t\in\mathcal{T}}\left| \Theta-\left(\Theta_{\circ}+\frac{1}{\Gamma(\upsilon)}\int_{0}^{t_{1}}(t_{1}-\vartheta)^{\upsilon-1}{\mho}\left(\vartheta, \overline{\Theta}(\vartheta)\right)d\vartheta\right)\right|\\ &+&\sup\limits_{t\in\mathcal{T}}\left| +\frac{1}{\Gamma(\upsilon)}\int_{0}^{t_{1}}(t_{1}-\vartheta)^{\upsilon-1}{\mho}\left(\vartheta, \Theta(\vartheta)\right)d\vartheta-\frac{1}{\Gamma(\upsilon)}\int_{0}^{t_{1}}(t_{1}-\vartheta)^{\upsilon-1}{\mho}\left(\vartheta, \overline{\Theta}(\vartheta)\right)d\vartheta\right|\\ &\leq&\frac{\mathcal{T}_{1}^{\upsilon}}{\Gamma(\upsilon+1)}C_{\Phi}\Phi(t)\alpha+\frac{L_{f}\mathcal{{T}_{1}}}{\Gamma(\upsilon+1)}\left|\left|\Theta-\overline{\Theta}\right|\right|. \end{eqnarray*}$

On further simplification

(4.16)

Case 2:

$\begin{eqnarray*} \left|\left|\Theta-\overline{\Theta}\right|\right| &\leq&\sup\limits_{t\in\mathcal{T}}\left|\Theta-\left[\Theta(t_{1})+\frac{1-\upsilon}{{ABC}(\upsilon)}\left[{\mho}\left(t, \Theta(t)\right) \right] \right.\right.\\ &+&\left.\left.\frac{\upsilon}{ABC(\upsilon)\Gamma(\upsilon)}\left[\int_{t_{1}}^{t}(t-\vartheta)^{\upsilon-1}{\mho}\left(\vartheta, \overline{\Theta}(\vartheta) \right)d(\vartheta)\right]\right]\right|\\ &+&\sup\limits_{t\in\mathcal{T}}\frac{1-\upsilon}{{ABC}(\upsilon)}\left|{\mho}\left(t, \Theta(t)\right) -{\mho}\left(t, \overline{\Theta}(t), \right)\right|\\ &+&\sup\limits_{t\in\mathcal{T}}\frac{\upsilon}{{ABC}(\upsilon)\Gamma(\upsilon)}\int_{t_{1}}^{t}(t-\vartheta)^{\upsilon-1}\left|{\mho}\left(\vartheta, \Theta(\vartheta)\right) -{\mho}\left(\vartheta, \overline{\Theta}(\vartheta)\right)\right|ds. \end{eqnarray*}$

By further simplification and using $\Lambda = \left[\frac{(1-\upsilon)\Gamma(\upsilon)+T_{2}^{\upsilon}}{ABC(\upsilon)\Gamma(\upsilon)}\right],$ we have

$\begin{eqnarray} \left|\left|\Theta-\overline\Theta\right|\right|_{Z}\leq\Lambda C_{\Phi}\Phi(t)\alpha+\Lambda{L_{f}}\left|\left|\Theta-\overline\Theta\right|\right|_{Z} \end{eqnarray}$

(4.17)

We have

$\begin{eqnarray*} \left|\left|\Theta-\overline\Theta\right|\right|_{Z}\leq\left(\frac{\Lambda C_{\Phi}\Phi(t)}{1-\Lambda L_{f}}\right)\left|\left|\Theta-\overline\Theta\right|\right|_{Z}. \end{eqnarray*}$

We use

Now, from Eqs (4.16) and (4.17), we have

$\begin{eqnarray*} \left|\left|\Theta-\overline\Theta\right|\right|_{Z}\leq\mathcal{H}_{\Lambda, C_{\Phi}}, at\; \; each\; t\in \mathcal{T} \end{eqnarray*}$

So the solution of the model (1.2) is generalized H-U-R stable.

5. Numerical Scheme for the fractional piecewise COVID-19 model

In this section we derive the numerical scheme for the following Covid-19 model (1.2).

$\begin{eqnarray} \begin{cases} {_0^{PCABC}}{{\bf D}_t^{\upsilon}}\mathbb{S}(t) = -(\alpha\mathbb{I}+\beta\mathbb{D}+\gamma\mathbb{A}+\delta\mathbb{R})\mathbb{S}, \\ {_0^{PCABC}}{{\bf D}_t^{\upsilon}}\mathbb{I}(t) = -(\epsilon+\zeta+\lambda)\mathbb{I}+(\alpha\mathbb{I}+\beta\mathbb{D}+\gamma\mathbb{A}+\delta\mathbb{R})\mathbb{S}, \\ {_0^{PCABC}}{{\bf D}_t^{\upsilon}}\mathbb{D}(t) = -(\eta+\rho)\mathbb{D}+\epsilon\mathbb{I}, \\ {_0^{PCABC}}{{\bf D}_t^{\upsilon}}\mathbb{A}(t) = -(\theta+\mu+\kappa)\mathbb{A}+\zeta\mathbb{I}, \\ {_0^{PCABC}}{{\bf D}_t^{\upsilon}}\mathbb{R}(t) = -(\nu+\xi)\mathbb{R}+\eta\mathbb{D}\theta\mathbb{A}, \\ {_0^{PCABC}}{{\bf D}_t^{\upsilon}}\mathbb{I}_r(t) = (\alpha\mathbb{I}+\beta\mathbb{D}+\gamma\mathbb{A}+\delta\mathbb{R})\mathbb{S}, \\ {_0^{PCABC}}{{\bf D}_t^{\upsilon}}\mathbb{T}(t) = -(\sigma+\tau)\mathbb{T}+\mu\mathbb{A}+\nu\mathbb{R}, \\ {_0^{PCABC}}{{\bf D}_t^{\upsilon}}\mathbb{H}_d(t) = \rho\mathbb{D}\xi\mathbb{R}+\sigma\mathbb{T}, \\ {_0^{PCABC}}{{\bf D}_t^{\upsilon}}\mathbb{H}(t) = \lambda\mathbb{I}+\rho\mathbb{D}+\kappa\mathbb{A}+\xi\mathbb{R}+\sigma\mathbb{A}, \\ {_0^{PCABC}}{{\bf D}_t^{\upsilon}}\mathbb{E}(t) = \tau\mathbb{T}, \end{cases} \end{eqnarray}$

(5.1)

By applying the piece-wise integral to the Caputo and AB derivative, we obtain

$\begin{eqnarray} \mathbb{S}(t)& = &\begin{cases} \mathbb{S}(0)+\frac{1}{\Gamma{(\upsilon)}}\int_{0}^{t_{1}}(t-\rho)^{{\upsilon-1}{c}}{\mho}_{1}(t, \mathbb{S})d{\rho}\ \ 0 < t\leq t_1, \\ \mathbb{S}(t_{1})+\frac{1-\upsilon}{AB(\upsilon)}{\mho}_{1}(t, \mathbb{S})d{\rho}+ \frac{\upsilon}{AB(\upsilon)\Gamma{(\upsilon)}}\int_{t_{1}}^{t}(t-\rho)^{\upsilon-1}{\mho}_{1}(t, \mathbb{S})d{\rho}\ \ t_1 < t\leq T \end{cases} \\ \mathbb{I}(t)& = &\begin{cases} \mathbb{I}(0)+\frac{1}{\Gamma{(\upsilon)}}\int_{0}^{t_{1}}(t-\rho)^{{\upsilon-1}{c}}{\mho}_{2}(t, \mathbb{I})d{\rho}\ \ 0 < t\leq t_1, \\ \mathbb{I}(t_{1})+\frac{1-\upsilon}{AB(\upsilon)}{\mho}_{2}(t, \mathbb{I})d{\rho} +\frac{\upsilon}{AB(\upsilon)\Gamma{(\upsilon)}}\int_{t_{1}}^{t}(t-\rho)^{\upsilon-1}{\mho}_{2}(t, \mathbb{I})d{\rho}\ \ t_1 < t\leq T \end{cases}\\ \mathbb{D}(t)& = &\begin{cases} \mathbb{D}(0)+\frac{1}{\Gamma{(\upsilon)}}\int_{0}^{t_{1}}(t-\rho)^{{\upsilon-1}{c}}{\mho}_{3}(t, \mathbb{D})d{\rho}\ \ 0 < t\leq t_1, \\ \mathbb{D}(t_{1})+\frac{1-\upsilon}{AB(\upsilon)}{\mho}_{3}(t, \mathbb{D})d{\rho} +\frac{\upsilon}{AB(\upsilon)\Gamma{(\upsilon)}}\int_{t_{1}}^{t}(t-\rho)^{\upsilon-1}{\mho}_{3}(t, \mathbb{D})d{\rho}\ \ t_1 < t\leq T \end{cases} \\ \mathbb{A}(t)& = &\begin{cases} \mathbb{A}(0)+\frac{1}{\Gamma{(\upsilon)}}\int_{0}^{t_{1}}(t-\rho)^{{\upsilon-1}{c}}{\mho}_{4}(t, \mathbb{A})d{\rho}\ \ 0 < t\leq t_1, \\ \mathbb{A}(t_{1})+\frac{1-\upsilon}{AB(\upsilon)}{\mho}_{4}(t, \mathbb{A})d{\rho} +\frac{\upsilon}{AB(\upsilon)\Gamma{(\upsilon)}}\int_{t_{1}}^{t}(t-\rho)^{\upsilon-1}{\mho}_{4}(t, \mathbb{A})d{\rho}\ \ t_1 < t\leq T \end{cases} \\ \mathbb{R}(t)& = &\begin{cases} \mathbb{R}(0)+\frac{1}{\Gamma{(\upsilon)}}\int_{0}^{t_{1}}(t-\rho)^{{\upsilon-1}{c}}{\mho}_{5}(t, \mathbb{R})d{\rho}\ \ 0 < t\leq t_1, \\ \mathbb{R}(t_{1})+\frac{1-\upsilon}{AB(\upsilon)}{\mho}_{5}(t, \mathbb{R})d{\rho} +\frac{\upsilon}{AB(\upsilon)\Gamma{(\upsilon)}}\int_{t_{1}}^{t}(t-\rho)^{\upsilon-1}{\mho}_{5}(t, \mathbb{R})d{\rho}\ \ t_1 < t\leq T \end{cases} \\ \mathbb{I}_r(t)& = &\begin{cases} \mathbb{I}_r(0)+\frac{1}{\Gamma{(\upsilon)}}\int_{0}^{t_{1}}(t-\rho)^{{\upsilon-1}{c}}{\mho}_{6}(t, \mathbb{I}_r)d{\rho}\ \ 0 < t\leq t_1, \\ \mathbb{I}_r(t_{1})+\frac{1-\upsilon}{AB(\upsilon)}{\mho}_{6}(t, \mathbb{I}_r)d{\rho} +\frac{\upsilon}{AB(\upsilon)\Gamma{(\upsilon)}}\int_{t_{1}}^{t}(t-\rho)^{\upsilon-1}{\mho}_{6}(t, \mathbb{I}_r)d{\rho}\ \ t_1 < t\leq T \end{cases} \\ \mathbb{T}(t)& = &\begin{cases} \mathbb{T}(0)+\frac{1}{\Gamma{(\upsilon)}}\int_{0}^{t_{1}}(t-\rho)^{{\upsilon-1}{c}}{\mho}_{7}(t, \mathbb{T})d{\rho}\ \ 0 < t\leq t_1, \\ \mathbb{T}(t_{1})+\frac{1-\upsilon}{AB(\upsilon)}{\mho}_{7}(t, \mathbb{T})d{\rho} +\frac{\upsilon}{AB(\upsilon)\Gamma{(\upsilon)}}\int_{t_{1}}^{t}(t-\rho)^{\upsilon-1}{\mho}_{7}(t, \mathbb{T})d{\rho}\ \ t_1 < t\leq T \end{cases} \\ \mathbb{H}_d(t)& = &\begin{cases} \mathbb{H}_d(0)+\frac{1}{\Gamma{(\upsilon)}}\int_{0}^{t_{1}}(t-\rho)^{{\upsilon-1}{c}}{\mho}_{8}(t, \mathbb{H}_d)d{\rho}\ \ 0 < t\leq t_1, \\ \mathbb{H}_d(t_{1})+\frac{1-\upsilon}{AB(\upsilon)}{\mho}_{8}(t, \mathbb{H}_d)d{\rho} +\frac{\upsilon}{AB(\upsilon)\Gamma{(\upsilon)}}\int_{t_{1}}^{t}(t-\rho)^{\upsilon-1}{\mho}_{8}(t, \mathbb{H}_d)d{\rho}\ \ t_1 < t\leq T \end{cases} \\ \mathbb{H}(t)& = &\begin{cases} \mathbb{H}(0)+\frac{1}{\Gamma{(\upsilon)}}\int_{0}^{t_{1}}(t-\rho)^{{\upsilon-1}{c}}{\mho}_{9}(t, \mathbb{H})d{\rho}\ \ 0 < t\leq t_1, \\ \mathbb{H}(t_{1})+\frac{1-\upsilon}{AB(\upsilon)}{\mho}_{9}(t, \mathbb{H})d{\rho} +\frac{\upsilon}{AB(\upsilon)\Gamma{(\upsilon)}}\int_{t_{1}}^{t}(t-\rho)^{\upsilon-1}{\mho}_{9}(t, \mathbb{H})d{\rho}\ \ t_1 < t\leq T \end{cases} \\ \mathbb{E}(t)& = &\begin{cases} \mathbb{E}(0)+\frac{1}{\Gamma{(\upsilon)}}\int_{0}^{t_{1}}(t-\rho)^{{\upsilon-1}{c}}{\mho}_{10}(t, \mathbb{R})d{\rho}\ \ 0 < t\leq t_1, \\ \mathbb{E}(t_{1})+\frac{1-\upsilon}{AB(\upsilon)}{\mho}_{10}(t, \mathbb{E})d{\rho} +\frac{\upsilon}{AB(\upsilon)\Gamma{(\upsilon)}}\int_{t_{1}}^{t}(t-\rho)^{\upsilon-1}{\mho}_{10}(t, \mathbb{E})d{\rho}\ \ t_1 < t\leq T \end{cases} \end{eqnarray}$

(5.2)

At $t = t_{n+1}$

$\begin{eqnarray*} \mathbb{S}(t)& = &\begin{cases} \mathbb{S}(0)+\frac{1}{\Gamma{(\upsilon)}}\int_{0}^{t_{1}}(t-\rho)^{{\upsilon-1}{c}}{\mho}_{1}(t, \mathbb{S})d{\rho}\ \ 0 < t\leq t_1, \\ \mathbb{S}(t_{1})+\frac{1-\upsilon}{AB(\upsilon)}{\mho}_{1}(t, \mathbb{S})d{\rho}+ \frac{\upsilon}{AB(\upsilon)\Gamma{(\upsilon)}}\int_{t_{1}}^{t_{n+1}}(t-\rho)^{\upsilon-1}{\mho}_{1}(t, \mathbb{S})d{\rho}\ \ t_1 < t\leq T \end{cases} \nonumber\\ \mathbb{I}(t)& = &\begin{cases} \mathbb{I}(0)+\frac{1}{\Gamma{(\upsilon)}}\int_{0}^{t_{1}}(t-\rho)^{{\upsilon-1}{c}}{\mho}_{2}(t, \mathbb{E})d{\rho}\ \ 0 < t\leq t_1, \\ \mathbb{I}(t_{1})+\frac{1-\upsilon}{AB(\upsilon)}{\mho}_{2}(t, \mathbb{I})d{\rho} +\frac{\upsilon}{AB(\upsilon)\Gamma{(\upsilon)}}\int_{t_{1}}^{t_{n+1}}(t-\rho)^{\upsilon-1}{\mho}_{2}(t, \mathbb{I})d{\rho}\ \ t_1 < t\leq T \end{cases}\\ \mathbb{D}(t)& = &\begin{cases} \mathbb{D}(0)+\frac{1}{\Gamma{(\upsilon)}}\int_{0}^{t_{1}}(t-\rho)^{{\upsilon-1}{c}}{\mho}_{3}(t, \mathbb{I})d{\rho}\ \ 0 < t\leq t_1, \\ \mathbb{D}(t_{1})+\frac{1-\upsilon}{AB(\upsilon)}{\mho}_{3}(t, \mathbb{D})d{\rho} +\frac{\upsilon}{AB(\upsilon)\Gamma{(\upsilon)}}\int_{t_{1}}^{t_{n+1}}(t-\rho)^{\upsilon-1}{\mho}_{3}(t, \mathbb{D})d{\rho}\ \ t_1 < t\leq T \end{cases} \nonumber\\ \mathbb{A}(t)& = &\begin{cases} \mathbb{A}(0)+\frac{1}{\Gamma{(\upsilon)}}\int_{0}^{t_{1}}(t-\rho)^{{\upsilon-1}{c}}{\mho}_{4}(t, \mathbb{A})d{\rho}\ \ 0 < t\leq t_1, \\ \mathbb{A}(t_{1})+\frac{1-\upsilon}{AB(\upsilon)}{\mho}_{4}(t, \mathbb{A})d{\rho} +\frac{\upsilon}{AB(\upsilon)\Gamma{(\upsilon)}}\int_{t_{1}}^{t_{n+1}}(t-\rho)^{\upsilon-1}{\mho}_{4}(t, \mathbb{A})d{\rho}\ \ t_1 < t\leq T \end{cases} \nonumber\\ \mathbb{R}(t)& = &\begin{cases} \mathbb{R}(0)+\frac{1}{\Gamma{(\upsilon)}}\int_{0}^{t_{1}}(t-\rho)^{{\upsilon-1}{c}}{\mho}_{5}(t, \mathbb{R})d{\rho}\ \ 0 < t\leq t_1, \\ \mathbb{R}(t_{1})+\frac{1-\upsilon}{AB(\upsilon)}{\mho}_{5}(t, \mathbb{R})d{\rho} +\frac{\upsilon}{AB(\upsilon)\Gamma{(\upsilon)}}\int_{t_{1}}^{t_{n+1}}(t-\rho)^{\upsilon-1}{\mho}_{5}(t, \mathbb{R})d{\rho}\ \ t_1 < t\leq T \end{cases} \nonumber\\ \mathbb{I}_r(t)& = &\begin{cases} \mathbb{I}_r(0)+\frac{1}{\Gamma{(\upsilon)}}\int_{0}^{t_{1}}(t-\rho)^{{\upsilon-1}{c}}{\mho}_{6}(t, \mathbb{I}_r)d{\rho}\ \ 0 < t\leq t_1, \\ \mathbb{I}_r(t_{1})+\frac{1-\upsilon}{AB(\upsilon)}{\mho}_{6}(t, \mathbb{I}_r)d{\rho} +\frac{\upsilon}{AB(\upsilon)\Gamma{(\upsilon)}}\int_{t_{1}}^{t_{n+1}}(t-\rho)^{\upsilon-1}{\mho}_{6}(t, \mathbb{I}_r)d{\rho}\ \ t_1 < t\leq T \end{cases} \nonumber\\ \mathbb{T}(t)& = &\begin{cases} \mathbb{T}(0)+\frac{1}{\Gamma{(\upsilon)}}\int_{0}^{t_{1}}(t-\rho)^{{\upsilon-1}{c}}{\mho}_{7}(t, \mathbb{T})d{\rho}\ \ 0 < t\leq t_1, \\ \mathbb{T}(t_{1})+\frac{1-\upsilon}{AB(\upsilon)}{\mho}_{7}(t, \mathbb{T})d{\rho} +\frac{\upsilon}{AB(\upsilon)\Gamma{(\upsilon)}}\int_{t_{1}}^{t_{n+1}}(t-\rho)^{\upsilon-1}{\mho}_{7}(t, \mathbb{T})d{\rho}\ \ t_1 < t\leq T \end{cases} \nonumber\\ \mathbb{H}_d(t)& = &\begin{cases} \mathbb{H}_d(0)+\frac{1}{\Gamma{(\upsilon)}}\int_{0}^{t_{1}}(t-\rho)^{{\upsilon-1}{c}}{\mho}_{8}(t, \mathbb{H}_d)d{\rho}\ \ 0 < t\leq t_1, \\ \mathbb{H}_d(t_{1})+\frac{1-\upsilon}{AB(\upsilon)}{\mho}_{8}(t, \mathbb{H}_d)d{\rho} +\frac{\upsilon}{AB(\upsilon)\Gamma{(\upsilon)}}\int_{t_{1}}^{t_{n+1}}(t-\rho)^{\upsilon-1}{\mho}_{8}(t, \mathbb{H}_d)d{\rho}\ \ t_1 < t\leq T \end{cases} \nonumber\\ \mathbb{H}(t)& = &\begin{cases} \mathbb{H}(0)+\frac{1}{\Gamma{(\upsilon)}}\int_{0}^{t_{1}}(t-\rho)^{{\upsilon-1}{c}}{\mho}_{9}(t, \mathbb{H})d{\rho}\ \ 0 < t\leq t_1, \\ \mathbb{H}(t_{1})+\frac{1-\upsilon}{AB(\upsilon)}{\mho}_{9}(t, \mathbb{H})d{\rho} +\frac{\upsilon}{AB(\upsilon)\Gamma{(\upsilon)}}\int_{t_{1}}^{t_{n+1}}(t-\rho)^{\upsilon-1}{\mho}_{9}(t, \mathbb{H})d{\rho}\ \ t_1 < t\leq T \end{cases} \nonumber\\ \mathbb{E}(t)& = &\begin{cases} \mathbb{E}(0)+\frac{1}{\Gamma{(\upsilon)}}\int_{0}^{t_{1}}(t-\rho)^{{\upsilon-1}{c}}{\mho}_{10}(t, \mathbb{E})d{\rho}\ \ 0 < t\leq t_1, \\ \mathbb{E}(t_{1})+\frac{1-\upsilon}{AB(\upsilon)}{\mho}_{10}(t, \mathbb{E})d{\rho} +\frac{\upsilon}{AB(\upsilon)\Gamma{(\upsilon)}}\int_{t_{1}}^{t_{n+1}}(t-\rho)^{\upsilon-1}{\mho}_{10}(t, \mathbb{E})d{\rho}\ \ t_1 < t\leq T \end{cases} \nonumber \end{eqnarray*}$

We put the Newton polynomials, so we obtain

$\begin{eqnarray} \mathbb{\mathbb{S}}(t_{n+1}) = \left\{ \begin{aligned}& \mathbb{\mathbb{S}}_0+\left\{\begin{aligned}& \frac{(\Delta{t})^{\upsilon-1}}{\Gamma{(\upsilon+1)}}\sum\limits_{{\bf k} = 2}^i\bigg[^C{\mho}_1(\mathbb{S}^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\Pi+\frac{(\Delta t)^{\upsilon-1}}{\Gamma{(\upsilon+2)}}\sum\limits_{{\bf k} = 2}^i\bigg[^C{\mho}_1(\mathbb{S}^{{\bf k}-1}, t_{{\bf k}-1})-^C{\mho}_1(\mathbb{S}^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\bigwedge\\& +\frac{\upsilon(\Delta t)^{\upsilon-1}}{2\Gamma{(\upsilon+3)}}\sum\limits_{{\bf k} = 2}^i\bigg[^C{\mho}_1( \mathbb{S}^{\bf k}, t_{\bf k})-2^C{\mho}_1(\mathbb{S}^{{\bf k}-1}, t_{{\bf k}-1})+^C{\mho}_1(\mathbb{S}^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\Delta \end{aligned}\right. \\ & {\mathbb{S}}(t_1)+\left\{\begin{aligned}& \frac{1-\upsilon}{ABC{(\upsilon)}}{^{ABC}{\mho}_1(\mathbb{S}^n, t_n)}+\frac{\upsilon}{ABC(\upsilon)}\frac{(\delta t)^{\upsilon-1}}{\Gamma{(\upsilon+1)}}\sum\limits_{{\bf k} = i+3}^n \bigg[^{ABC}{\mho}_1( \mathbb{S}^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\Pi\\& +\frac{\upsilon}{ABC{(\upsilon)}}\frac{(\upsilon t)^{\upsilon-1}}{\Gamma{(\upsilon+2)}}\sum\limits_{{\bf k} = i+3}^n\bigg[^{ABC}{\mho}_1(\mathbb{S}^{{\bf k}-1}, t_{{\bf k}-1}) +{ABC}{\mho}_1(\mathbb{S}^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\bigwedge\\& +\frac{\upsilon}{ABC{(\upsilon)}}\frac{\upsilon(\upsilon t)^{\upsilon-1}}{\Gamma{(\upsilon+3)}}\sum\limits_{{\bf k} = i+3}^n\bigg[^{ABC}{\mho}_1(\mathbb{S}^{{\bf k}}, t_{{\bf k}}) -2^{ABC}{\mho}_1(\mathbb{S}^{{\bf k}-1}, t_{{\bf k}-1}) + ^{ABC}{\mho}_1( \mathbb{S}^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\Delta \end{aligned}\right. \end{aligned}\right. \end{eqnarray}$

(5.3)

$\begin{eqnarray} \mathbb{I}(t_{n+1}) = \left\{\begin{aligned}& \mathbb{I}_0+\left\{\begin{aligned}& \frac{(\Delta{t})^{\upsilon-1}}{\Gamma{(\upsilon+1)}}\sum\limits_{{\bf k} = 2}^i\bigg[^C{\mho}_2(\mathbb{I}^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\Pi+\frac{(\Delta t)^{\upsilon-1}}{\Gamma{(\upsilon+2)}}\sum\limits_{{\bf k} = 2}^i\bigg[^C{\mho}_2(\mathbb{I}^{{\bf k}-1}, t_{{\bf k}-1})-^C{\mho}_2(\mathbb{I}^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\bigwedge\\& +\frac{\upsilon(\Delta t)^{\upsilon-1}}{2\Gamma{(\upsilon+3)}}\sum\limits_{{\bf k} = 2}^i\bigg[^C{\mho}_2( \mathbb{I}^{\bf k}, t_{\bf k})-2^C{\mho}_2(\mathbb{I}^{{\bf k}-1}, t_{{\bf k}-1}) +^C{\mho}_2(\mathbb{I}^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\Delta \end{aligned}\right. \\ & \mathbb{I}(t_1)+\left\{\begin{aligned}& \frac{1-\upsilon}{ABC{(\upsilon)}}{^{ABC}{\mho}_2(\mathbb{I}^n, t_n)}+\frac{\upsilon}{ABC(\upsilon)}\frac{(\delta t)^{\upsilon-1}}{\Gamma{(\upsilon+1)}}\sum\limits_{{\bf k} = i+3}^n \bigg[^{ABC}{\mho}_2( \mathbb{I}^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\Pi\\& +\frac{\upsilon}{ABC{(\upsilon)}}\frac{(\upsilon t)^{\upsilon-1}}{\Gamma{(\upsilon+2)}}\sum\limits_{{\bf k} = i+3}^n\bigg[^{ABC}{\mho}_2(\mathbb{I}^{{\bf k}-1}, t_{{\bf k}-1}) +{ABC}{\mho}_2(\mathbb{I}^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\bigwedge\\& +\frac{\upsilon}{ABC{(\upsilon)}}\frac{\upsilon(\upsilon t)^{\upsilon-1}}{\Gamma{(\upsilon+3)}}\sum\limits_{{\bf k} = i+3}^n\bigg[^{ABC}{\mho}_2(\mathbb{I}^{{\bf k}}, t_{{\bf k}}) -2^{ABC}{\mho}_2(\mathbb{I}^{{\bf k}-1}, t_{{\bf k}-1}) + ^{ABC}{\mho}_2( \mathbb{I}^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\Delta \end{aligned}\right. \end{aligned}\right. \end{eqnarray}$

(5.4)

$\begin{eqnarray} \mathbb{D}(t_{n+1}) = \left\{\begin{aligned}& \mathbb{D}_0+\left\{\begin{aligned}& \frac{(\Delta t)^{\upsilon-1}}{\Gamma{(\upsilon+1)}}\sum\limits_{{\bf k} = 2}^i\bigg[^C{\mho}_3(\mathbb{D}^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\Pi +\frac{(\Delta t)^{\upsilon-1}}{\Gamma{(\upsilon+2)}}\sum\limits_{{\bf k} = 2}^i\bigg[^C{\mho}_3(\mathbb{D}^{{\bf k}-1}, t_{{\bf k}-1})-^C{\mho}_3(\mathbb{D}^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\bigwedge\\& +\frac{\upsilon(\Delta t)^{\upsilon-1}}{2\Gamma{(\upsilon+3)}}\sum\limits_{{\bf k} = 2}^i\bigg[^C{\mho}_3( \mathbb{D}^{\bf k}, t_{\bf k})-2^C{\mho}_3(\mathbb{D}^{{\bf k}-1}, t_{{\bf k}-1}) +^C{\mho}_3(\mathbb{D}^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\Delta \end{aligned}\right. \\ & \mathbb{D}(t_1)+\left\{\begin{aligned}& \frac{1-\upsilon}{ABC{(\upsilon)}}{^{ABC}{\mho}_3(\mathbb{D}^n, t_n)}+\frac{\upsilon}{ABC(\upsilon)}\frac{(\delta t)^{\upsilon-1}}{\Gamma{(\upsilon+1)}}\sum\limits_{{\bf k} = i+3}^n \bigg[^{ABC}{\mho}_3( \mathbb{D}^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\Pi\\& +\frac{\upsilon}{ABC{(\upsilon)}}\frac{(\upsilon t)^{\upsilon-1}}{\Gamma{(\upsilon+2)}}\sum\limits_{{\bf k} = i+3}^n\bigg[^{ABC}{\mho}_3(\mathbb{D}^{{\bf k}-1}, t_{{\bf k}-1}) +{ABC}{\mho}_3(\mathbb{D}^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\bigwedge\\& +\frac{\upsilon}{ABC{(\upsilon)}}\frac{\upsilon(\upsilon t)^{\upsilon-1}}{\Gamma{(\upsilon+3)}}\sum\limits_{{\bf k} = i+3}^n\bigg[^{ABC}{\mho}_3(\mathbb{D}^{{\bf k}}, t_{{\bf k}}) -2^{ABC}{\mho}_3(\mathbb{D}^{{\bf k}-1}, t_{{\bf k}-1}) + ^{ABC}{\mho}_3( \mathbb{D}^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\Delta \end{aligned}\right. \end{aligned}\right. \end{eqnarray}$

(5.5)

$\begin{eqnarray} \mathbb{A}(t_{n+1}) = \left\{\begin{aligned}& \mathbb{A}_0+\left\{\begin{aligned}& \frac{(\Delta t)^{\upsilon-1}}{\Gamma{(\upsilon+1)}}\sum\limits_{{\bf k} = 2}^i\bigg[^C{\mho}_4(\mathbb{A}^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\Pi +\frac{(\Delta t)^{\upsilon-1}}{\Gamma{(\upsilon+2)}}\sum\limits_{{\bf k} = 2}^i\bigg[^C{\mho}_4(\mathbb{A}^{{\bf k}-1}, t_{{\bf k}-1})-^C{\mho}_4(\mathbb{A}^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\bigwedge\\& +\frac{\upsilon(\Delta t)^{\upsilon-1}}{2\Gamma{(\upsilon+3)}}\sum\limits_{{\bf k} = 2}^i\bigg[^C{\mho}_4( \mathbb{A}^{\bf k}, t_{\bf k})-2^C{\mho}_4(\mathbb{A}^{{\bf k}-1}, t_{{\bf k}-1}) +^C{\mho}_4(\mathbb{A}^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\Delta \end{aligned}\right.\\ & \mathbb{\mathbb{A}}(t_1)+\left\{\begin{aligned}& \frac{1-\upsilon}{ABC{(\upsilon)}}{^{ABC}{\mho}_4(\mathbb{A}^n, t_n)}+\frac{\upsilon}{ABC(\upsilon)}\frac{(\delta t)^{\upsilon-1}}{\Gamma{(\upsilon+1)}}\sum\limits_{{\bf k} = i+3}^n \bigg[^{ABC}{\mho}_4( \mathbb{A}^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\Pi\\& +\frac{\upsilon}{ABC{(\upsilon)}}\frac{(\upsilon t)^{\upsilon-1}}{\Gamma{(\upsilon+2)}}\sum\limits_{{\bf k} = i+3}^n\bigg[^{ABC}{\mho}_4(\mathbb{A}^{{\bf k}-1}, t_{{\bf k}-1}) +{ABC}{\mho}_4(\mathbb{A}^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\bigwedge\\& +\frac{\upsilon}{ABC{(\upsilon)}}\frac{\upsilon(\upsilon t)^{\upsilon-1}}{\Gamma{(\upsilon+3)}}\sum\limits_{{\bf k} = i+3}^n\bigg[^{ABC}{\mho}_4(\mathbb{A}^{{\bf k}}, t_{{\bf k}}) -2^{ABC}{\mho}_4(\mathbb{A}^{{\bf k}-1}, t_{{\bf k}-1}) + ^{ABC}{\mho}_4( \mathbb{A}^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\Delta. \end{aligned}\right. \end{aligned}\right. \end{eqnarray}$

(5.6)

$\begin{eqnarray} \mathbb{R}(t_{n+1}) = \left\{\begin{aligned}& \mathbb{R}_0+\left\{\begin{aligned}& \frac{(\Delta t)^{\upsilon-1}}{\Gamma{(\upsilon+1)}}\sum\limits_{{\bf k} = 2}^i\bigg[^C{\mho}_5(\mathbb{R}^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\Pi +\frac{(\Delta t)^{\upsilon-1}}{\Gamma{(\upsilon+2)}}\sum\limits_{{\bf k} = 2}^i\bigg[^C{\mho}_5(\mathbb{R}^{{\bf k}-1}, t_{{\bf k}-1})-^C{\mho}_5(\mathbb{R}^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\bigwedge\\& +\frac{\upsilon(\Delta t)^{\upsilon-1}}{2\Gamma{(\upsilon+3)}}\sum\limits_{{\bf k} = 2}^i\bigg[^C{\mho}_5( \mathbb{R}^{\bf k}, t_{\bf k})-2^C{\mho}_5(\mathbb{R}^{{\bf k}-1}, t_{{\bf k}-1}) +^C{\mho}_5(\mathbb{R}^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\Delta \end{aligned}\right. \\ & \mathbb{R}(t_1)+\left\{\begin{aligned}& \frac{1-\upsilon}{ABC{(\upsilon)}}{^{ABC}{\mho}_5(\mathbb{R}^n, t_n)}+\frac{\upsilon}{ABC(\upsilon)}\frac{(\delta t)^{\upsilon-1}}{\Gamma{(\upsilon+1)}}\sum\limits_{{\bf k} = i+3}^n \bigg[^{ABC}{\mho}_5( \mathbb{R}^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\Pi\\& +\frac{\upsilon}{ABC{(\upsilon)}}\frac{(\upsilon t)^{\upsilon-1}}{\Gamma{(\upsilon+2)}}\sum\limits_{{\bf k} = i+3}^n\bigg[^{ABC}{\mho}_5(\mathbb{R}^{{\bf k}-1}, t_{{\bf k}-1}) +{ABC}{\mho}_5(\mathbb{R}^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\bigwedge\\& +\frac{\upsilon}{ABC{(\upsilon)}}\frac{\upsilon(\upsilon t)^{\upsilon-1}}{\Gamma{(\upsilon+3)}}\sum\limits_{{\bf k} = i+3}^n\bigg[^{ABC}{\mho}_5(\mathbb{R}^{{\bf k}}, t_{{\bf k}}) -2^{ABC}{\mho}_5(\mathbb{R}^{{\bf k}-1}, t_{{\bf k}-1}) + ^{ABC}{\mho}_5( \mathbb{R}^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\Delta \end{aligned}\right. \end{aligned}\right. \end{eqnarray}$

(5.7)

$\begin{eqnarray} \mathbb{I}_r(t_{n+1}) = \left\{\begin{aligned}& \mathbb{I}_r(0)+\left\{\begin{aligned}& \frac{(\Delta t)^{\upsilon-1}}{\Gamma{(\upsilon+1)}}\sum\limits_{{\bf k} = 2}^i\bigg[^C{\mho}_6(\mathbb{I}_r^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\Pi +\frac{(\Delta t)^{\upsilon-1}}{\Gamma{(\upsilon+2)}}\sum\limits_{{\bf k} = 2}^i\bigg[^C{\mho}_6(\mathbb{I}_r^{{\bf k}-1}, t_{{\bf k}-1})-^C{\mho}_6(\mathbb{I}_r^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\bigwedge\\& +\frac{\upsilon(\Delta t)^{\upsilon-1}}{2\Gamma{(\upsilon+3)}}\sum\limits_{{\bf k} = 2}^i\bigg[^C{\mho}_6( \mathbb{I}_r^{\bf k}, t_{\bf k})-2^C{\mho}_6(\mathbb{I}_r^{{\bf k}-1}, t_{{\bf k}-1}) +^C{\mho}_6(\mathbb{I}_r^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\Delta \end{aligned}\right. \\ & \mathbb{I}_r(t_1)+\left\{\begin{aligned}& \frac{1-\upsilon}{ABC{(\upsilon)}}{^{ABC}{\mho}_6(\mathbb{I}_r^n, t_n)}+\frac{\upsilon}{ABC(\upsilon)}\frac{(\delta t)^{\upsilon-1}}{\Gamma{(\upsilon+1)}}\sum\limits_{{\bf k} = i+3}^n \bigg[^{ABC}{\mho}_6( \mathbb{I}_r^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\Pi\\& +\frac{\upsilon}{ABC{(\upsilon)}}\frac{(\upsilon t)^{\upsilon-1}}{\Gamma{(\upsilon+2)}}\sum\limits_{{\bf k} = i+3}^n\bigg[^{ABC}{\mho}_6(\mathbb{I}_r^{{\bf k}-1}, t_{{\bf k}-1}) +{ABC}{\mho}_6(\mathbb{I}_r^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\bigwedge\\& +\frac{\upsilon}{ABC{(\upsilon)}}\frac{\upsilon(\upsilon t)^{\upsilon-1}}{\Gamma{(\upsilon+3)}}\sum\limits_{{\bf k} = i+3}^n\bigg[^{ABC}{\mho}_6(\mathbb{I}_r^{{\bf k}}, t_{{\bf k}}) -2^{ABC}{\mho}_6(\mathbb{I}_r^{{\bf k}-1}, t_{{\bf k}-1}) + ^{ABC}{\mho}_6( \mathbb{I}_r^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\Delta \end{aligned}\right. \end{aligned}\right. \end{eqnarray}$

(5.8)

$\begin{eqnarray} \mathbb{T}(t_{n+1}) = \left\{\begin{aligned}& \mathbb{T}(0)+\left\{\begin{aligned}& \frac{(\Delta t)^{\upsilon-1}}{\Gamma{(\upsilon+1)}}\sum\limits_{{\bf k} = 2}^i\bigg[^C{\mho}_7(\mathbb{T}^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\Pi +\frac{(\Delta t)^{\upsilon-1}}{\Gamma{(\upsilon+2)}}\sum\limits_{{\bf k} = 2}^i\bigg[^C{\mho}_7(\mathbb{T}^{{\bf k}-1}, t_{{\bf k}-1})-^C{\mho}_7(\mathbb{T}^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\bigwedge\\& +\frac{\upsilon(\Delta t)^{\upsilon-1}}{2\Gamma{(\upsilon+3)}}\sum\limits_{{\bf k} = 2}^i\bigg[^C{\mho}_7( \mathbb{T}^{\bf k}, t_{\bf k})-2^C{\mho}_7(\mathbb{T}^{{\bf k}-1}, t_{{\bf k}-1}) +^C{\mho}_7(\mathbb{T}^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\Delta \end{aligned}\right.\\ & \mathbb{T}(t_1)+\left\{\begin{aligned}& \frac{1-\upsilon}{ABC{(\upsilon)}}{^{ABC}{\mho}_7(\mathbb{T}^n, t_n)}+\frac{\upsilon}{ABC(\upsilon)}\frac{(\delta t)^{\upsilon-1}}{\Gamma{(\upsilon+1)}}\sum\limits_{{\bf k} = i+3}^n \bigg[^{ABC}{\mho}_7( \mathbb{T}^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\Pi\\& +\frac{\upsilon}{ABC{(\upsilon)}}\frac{(\upsilon t)^{\upsilon-1}}{\Gamma{(\upsilon+2)}}\sum\limits_{{\bf k} = i+3}^n\bigg[^{ABC}{\mho}_7(\mathbb{T}^{{\bf k}-1}, t_{{\bf k}-1}) +{ABC}{\mho}_7(\mathbb{T}^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\bigwedge\\& +\frac{\upsilon}{ABC{(\upsilon)}}\frac{\upsilon(\upsilon t)^{\upsilon-1}}{\Gamma{(\upsilon+3)}}\sum\limits_{{\bf k} = i+3}^n\bigg[^{ABC}{\mho}_7(\mathbb{T}^{{\bf k}}, t_{{\bf k}}) -2^{ABC}{\mho}_7(\mathbb{T}^{{\bf k}-1}, t_{{\bf k}-1}) + ^{ABC}{\mho}_7( \mathbb{T}^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\Delta \end{aligned}\right. \end{aligned}\right. \end{eqnarray}$

(5.9)

$\begin{eqnarray} \mathbb{H}_d(t_{n+1}) = \left\{\begin{aligned}& \mathbb{H}_d(0)+\left\{\begin{aligned}& \frac{(\Delta t)^{\upsilon-1}}{\Gamma{(\upsilon+1)}}\sum\limits_{{\bf k} = 2}^i\bigg[^C{\mho}_8(\mathbb{H}_d^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\Pi +\frac{(\Delta t)^{\upsilon-1}}{\Gamma{(\upsilon+2)}}\sum\limits_{{\bf k} = 2}^i\bigg[^C{\mho}_8(\mathbb{H}_d^{{\bf k}-1}, t_{{\bf k}-1})-^C{\mho}_8(\mathbb{H}_d^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\bigwedge\\& +\frac{\upsilon(\Delta t)^{\upsilon-1}}{2\Gamma{(\upsilon+3)}}\sum\limits_{{\bf k} = 2}^i\bigg[^C{\mho}_8( \mathbb{H}_d^{\bf k}, t_{\bf k})-2^C{\mho}_8(\mathbb{H}_d^{{\bf k}-1}, t_{{\bf k}-1}) +^C{\mho}_8(\mathbb{H}_d^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\Delta \end{aligned}\right. \\ & \mathbb{H}_d(t_1)+\left\{\begin{aligned}& \frac{1-\upsilon}{ABC{(\upsilon)}}{^{ABC}{\mho}_8(\mathbb{H}_d^n, t_n)}+\frac{\upsilon}{ABC(\upsilon)}\frac{(\delta t)^{\upsilon-1}}{\Gamma{(\upsilon+1)}}\sum\limits_{{\bf k} = i+3}^n \bigg[^{ABC}{\mho}_8( \mathbb{H}_d^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\Pi\\& +\frac{\upsilon}{ABC{(\upsilon)}}\frac{(\upsilon t)^{\upsilon-1}}{\Gamma{(\upsilon+2)}}\sum\limits_{{\bf k} = i+3}^n\bigg[^{ABC}{\mho}_8(\mathbb{H}_d^{{\bf k}-1}, t_{{\bf k}-1}) +{ABC}{\mho}_8(\mathbb{H}_d^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\bigwedge\\& +\frac{\upsilon}{ABC{(\upsilon)}}\frac{\upsilon(\upsilon t)^{\upsilon-1}}{\Gamma{(\upsilon+3)}}\sum\limits_{{\bf k} = i+3}^n\bigg[^{ABC}{\mho}_8(\mathbb{H}_d^{{\bf k}}, t_{{\bf k}}) -2^{ABC}{\mho}_8(\mathbb{H}_d^{{\bf k}-1}, t_{{\bf k}-1}) + ^{ABC}{\mho}_8( \mathbb{H}_d^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\Delta \end{aligned}\right. \end{aligned}\right. \end{eqnarray}$

(5.10)

$\begin{eqnarray} \mathbb{H}(t_{n+1}) = \left\{\begin{aligned}& \mathbb{H}(0)+\left\{\begin{aligned}& \frac{(\Delta t)^{\upsilon-1}}{\Gamma{(\upsilon+1)}}\sum\limits_{{\bf k} = 2}^i\bigg[^C{\mho}_9(\mathbb{H}^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\Pi +\frac{(\Delta t)^{\upsilon-1}}{\Gamma{(\upsilon+2)}}\sum\limits_{{\bf k} = 2}^i\bigg[^C{\mho}_9(\mathbb{H}^{{\bf k}-1}, t_{{\bf k}-1})-^C{\mho}_9(\mathbb{H}^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\bigwedge\\& +\frac{\upsilon(\Delta t)^{\upsilon-1}}{2\Gamma{(\upsilon+3)}}\sum\limits_{{\bf k} = 2}^i\bigg[^C{\mho}_9( \mathbb{H}^{\bf k}, t_{\bf k})-2^C{\mho}_9(\mathbb{H}^{{\bf k}-1}, t_{{\bf k}-1}) +^C{\mho}_9(\mathbb{H}^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\Delta \end{aligned}\right. \\ & \mathbb{H}(t_1)+\left\{\begin{aligned}& \frac{1-\upsilon}{ABC{(\upsilon)}}{^{ABC}{\mho}_9(\mathbb{H}^n, t_n)}+\frac{\upsilon}{ABC(\upsilon)}\frac{(\delta t)^{\upsilon-1}}{\Gamma{(\upsilon+1)}}\sum\limits_{{\bf k} = i+3}^n \bigg[^{ABC}{\mho}_9( \mathbb{H}^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\Pi\\& +\frac{\upsilon}{ABC{(\upsilon)}}\frac{(\upsilon t)^{\upsilon-1}}{\Gamma{(\upsilon+2)}}\sum\limits_{{\bf k} = i+3}^n\bigg[^{ABC}{\mho}_9(\mathbb{H}^{{\bf k}-1}, t_{{\bf k}-1}) +{ABC}{\mho}_9(\mathbb{H}^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\bigwedge\\& +\frac{\upsilon}{ABC{(\upsilon)}}\frac{\upsilon(\upsilon t)^{\upsilon-1}}{\Gamma{(\upsilon+3)}}\sum\limits_{{\bf k} = i+3}^n\bigg[^{ABC}{\mho}_9(\mathbb{H}^{{\bf k}}, t_{{\bf k}}) -2^{ABC}{\mho}_9(\mathbb{H}^{{\bf k}-1}, t_{{\bf k}-1}) + ^{ABC}{\mho}_9( \mathbb{H}^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\Delta \end{aligned}\right. \end{aligned}\right. \end{eqnarray}$

(5.11)

$\begin{eqnarray} \mathbb{E}(t_{n+1}) = \left\{\begin{aligned}& \mathbb{E}(0)+\left\{\begin{aligned}& \frac{(\Delta t)^{\upsilon-1}}{\Gamma{(\upsilon+1)}}\sum\limits_{{\bf k} = 2}^i\bigg[^C{\mho}_{10}(\mathbb{E}^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\Pi +\frac{(\Delta t)^{\upsilon-1}}{\Gamma{(\upsilon+2)}}\sum\limits_{{\bf k} = 2}^i\bigg[^C{\mho}_{10}(\mathbb{E}^{{\bf k}-1}, t_{{\bf k}-1})-^C{\mho}_{10}(\mathbb{E}^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\bigwedge\\& +\frac{\upsilon(\Delta t)^{\upsilon-1}}{2\Gamma{(\upsilon+3)}}\sum\limits_{{\bf k} = 2}^i\bigg[^C{\mho}_{10}( \mathbb{E}^{\bf k}, t_{\bf k})-2^C{\mho}_{10}(\mathbb{E}^{{\bf k}-1}, t_{{\bf k}-1}) +^C{\mho}_{10}(\mathbb{E}^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\Delta \end{aligned}\right. \\ & \mathbb{E}(t_1)+\left\{\begin{aligned}& \frac{1-\upsilon}{ABC{(\upsilon)}}{^{ABC}{\mho}_{10}(\mathbb{E}^n, t_n)}+\frac{\upsilon}{ABC(\upsilon)}\frac{(\delta t)^{\upsilon-1}}{\Gamma{(\upsilon+1)}}\sum\limits_{{\bf k} = i+3}^n \bigg[^{ABC}{\mho}_{10}( \mathbb{E}^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\Pi\\& +\frac{\upsilon}{ABC{(\upsilon)}}\frac{(\upsilon t)^{\upsilon-1}}{\Gamma{(\upsilon+2)}}\sum\limits_{{\bf k} = i+3}^n\bigg[^{ABC}{\mho}_{10}(\mathbb{E}^{{\bf k}-1}, t_{{\bf k}-1}) +{ABC}{\mho}_{10}(\mathbb{E}^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\bigwedge\\& +\frac{\upsilon}{ABC{(\upsilon)}}\frac{\upsilon(\upsilon t)^{\upsilon-1}}{\Gamma{(\upsilon+3)}}\sum\limits_{{\bf k} = i+3}^n\bigg[^{ABC}{\mho}_{10}(\mathbb{E}^{{\bf k}}, t_{{\bf k}}) -2^{ABC}{\mho}_{10}(\mathbb{E}^{{\bf k}-1}, t_{{\bf k}-1}) + ^{ABC}{\mho}_{10}( \mathbb{E}^{{\bf k}-2}, t_{{\bf k}-2})\bigg]\Delta \end{aligned}\right. \end{aligned}\right. \end{eqnarray}$

(5.12)

Here

$\begin{eqnarray*} \Pi = \left[\begin{split}& (1-{\bf k}+n)^\upsilon\bigg(2(-{\bf k}+n)^2+(3\upsilon+10)(-{\bf k}+n)+2\upsilon^2+9\upsilon+12\bigg)\\& -(-{\bf k}+n)\bigg(2(-{\bf k}+n)^2+(5\upsilon+10)(n-{\bf k})+6\upsilon^2+18\upsilon+12\bigg) \end{split}\right], \end{eqnarray*}$

$\begin{eqnarray*} \bigwedge = \left[\begin{split}& (1-{\bf k}+n)^\upsilon\bigg(3+n+2\upsilon-{\bf k}\bigg)\\& -(-{\bf k}+n)\bigg(n+3\upsilon-{\bf k}+3\bigg) \end{split}\right], \end{eqnarray*}$

$\begin{eqnarray*} \Delta = \left[\begin{split}& (1-{\bf k}+n)^\upsilon-(-{\bf k}+n)^\upsilon \end{split}\right], \end{eqnarray*}$

and

$\begin{eqnarray*} \label{2} \begin{array}{l} ^C{\mho}_1(\mathbb{S}, t) = {^{ABC}{\mho}_1(\mathbb{S}, t)} = -(\alpha\mathbb{I}+\beta\mathbb{D}+\gamma\mathbb{A}+\delta\mathbb{R})\mathbb{S}, \\ ^C{\mho}_3(\mathbb{I}, t) = {^{ABC}{\mho}_3(\mathbb{I}, t)} = -(\epsilon+\zeta+\lambda)\mathbb{I}+(\alpha\mathbb{I}+\beta\mathbb{D}+\gamma\mathbb{A}+\delta\mathbb{R})\mathbb{S}, \\ ^C{\mho}_2(\mathbb{A}, t) = {^{ABC}{\mho}_2(\mathbb{A}, t)} = -(\eta+\rho)\mathbb{D}+\epsilon\mathbb{I}, \\ ^C{\mho}_4(\mathbb{D}, t) = {^{ABC}{\mho}_4(\mathbb{D}, t)} = -(\theta+\mu+\kappa)\mathbb{A}+\zeta\mathbb{I}, \\ ^C{\mho}_5(\mathbb{R}, t) = {^{ABC}{\mho}_5(\mathbb{R}, t)} = -(\nu+\xi)\mathbb{R}+\eta\mathbb{D}\theta\mathbb{A}, \\ ^C{\mho}_6(\mathbb{I}_r, t) = {^{ABC}{\mho}_5(\mathbb{I}_r, t)} = (\alpha\mathbb{I}+\beta\mathbb{D}+\gamma\mathbb{A}+\delta\mathbb{R})\mathbb{S}, \\ ^C{\mho}_7(\mathbb{T}, t) = {^{ABC}{\mho}_5(\mathbb{T}, t)} = -(\sigma+\tau)\mathbb{T}+\mu\mathbb{A}+\nu\mathbb{R}, \\ ^C{\mho}_8(\mathbb{H}_d, t) = {^{ABC}{\mho}_5(\mathbb{H}_d, t)} = \rho\mathbb{D}\xi\mathbb{R}+\sigma\mathbb{T}, \\ ^C{\mho}_9(\mathbb{H}, t) = {^{ABC}{\mho}_5(\mathbb{H}, t)} = \lambda\mathbb{I}+\rho\mathbb{D}+\kappa\mathbb{A}+\xi\mathbb{R}+\sigma\mathbb{A}, \\ ^C{\mho}_{10}(\mathbb{E}, t) = {^{ABC}{\mho}_5(\mathbb{E}, t)} = \tau\mathbb{T}. \end{array} \end{eqnarray*}$

The above Eqs (5.3)–(5.12) are the solution for the considered model.

6. Numerical simulations

In this section we provide the numerical simulation for all the five compartments of the proposed model using the initial data and parameters values taken from ^[19]. The initial populations are $\mathbb{S}(0) = 1, \ \mathbb{I}(0) = 0.001, \ \mathbb{D}(0) = 0.002, \ \mathbb{A}(0) = 0.0001, \ \mathbb{R}(0) = 0.0003,$ $\mathbb{I}_r(0) = 0.0009, \ \mathbb{T}(0) = 0.002, \mathbb{H}_d(0) = 0.003, \ \mathbb{H}(0) = 0.00012, \ \mathbb{E}(0) = 0.00014$ .

Table 2. Parameters values in model 1.1.

Parameter	Value	Parameter	Values
$\alpha$	$0.57$	$\beta$	$0.0114$
$\gamma$	$0.456$	$\delta$	$0.0114$
$\epsilon$	$0.171$	$\theta$	$0.3705$
$\zeta$	$0.1254$	$\eta_1$	$0.1254$
$\mu$	$0.0171$	$v$	$0.0274$
$\tau$	$0.01$	$\lambda$	$0.0342$
$\kappa$	$0.0342$	$\xi$	$0.0171$
$\sigma$	$0.0171$	$\rho$	$0.0171$

| Show Table

DownLoad: CSV

The graphical representation of all the ten compartments of the analyzed model has been shown on three different data of fractional orders and time durations in the sense of piecewise Caputo and ABC derivatives. The first compartment of susceptible population is shown in Figure 1a–c, respectively, on two sub intervals. The said class population decreases slowly in the first interval, while in the second interval it decreases very abruptly. On small fractional orders it is stable quickly, and piece wise behaviors are negligible in this case, as shown in Figure 1a, c.

Figure 1. Dynamical behaviors of susceptible individuals

$\mathbb{S}(t)$ on different arbitrary fractional orders

$\upsilon$ and time durations on sub interval

$[0, t_1]$ and

$[t_1, T]$ of

$[0, T]$ .

[1]	Kermack WO and McKendrick AG, (1927) A contribution to the mathematical theory of epidemics. Proc R Soc Lond 115: 700-721.
[2]	Lin Q, Zhao S, Gao D, et al. (2020) A conceptual model for the coronavirus disease 2019 (COVID-19) outbreak in Wuhan, China with individual reaction and governmental action. Int J Inf Dis 93: 211-216.
[3]	Anastassopoulou C, Russo L, Tsakris A, et al. (2020) Data-based analysis, modelling and forecasting of the COVID-19 outbreak. PloS One 15: e0230405.
[4]	Casella F, (2020) Can the COVID-19 epidemic be controlled on the basis of daily test reports?, Preprint, arXiv: 2003.06967.
[5]	Giordano G, Blanchini F, Bruno R, et al. (2020) Modelling the COVID-19 epidemic and implementation of population-wide interventions in Italy. Nat Med 26: 855-860.
[6]	Wu JT, Leung K, Bushman M, et al. (2020) Estimating clinical severity of COVID-19 from the transmission dynamics in Wuhan, China. Nat Med 26: 506-510.
[7]	Tam KM, Walker N and Moreno J, (2020) Projected development of COVID-19 in Louisiana. arXiv 2004.02859.
[8]	Hellewell J, Abbott S, Gimma A, et al. (2020) Feasibility of controlling COVID-19 outbreaks by isolation of cases and contacts. Lancet Global Health, 8: e488-e496.
[9]	Kucharski AJ, Russell TW, Diamond C, et al. (2020) Early dynamics of transmission and control of COVID-19: a mathematical modelling study, Lancet Infect Dis 20: 553-558.
[10]	Birbuet JC and López V R, (2020) Dinámica de expansión del COVID-19 en Bolivia durante las 6 primeras semanas. Working Paper. Available from: https://github.com/rafalopezv/modelo_seir_bolivia.
[11]	Tassier T, (2013) The Economics of Epidemiology, Springer-Verlag Berlin Heidelberg.
[12]	Munayco CV, Tariq A, Rothenberg R, et al. (2020) Early transmission dynamics of COVID-19 in a southern hemisphere setting: Lima-Peru: February 29^th-March 30^th, 2020. Infect Dis Model, 5: 338-345.

1.	Sara Salem Alzaid, Badr Saad T. Alkahtani, Real-world validation of fractional-order model for COVID-19 vaccination impact, 2024, 9, 2473-6988, 3685, 10.3934/math.2024181
2.	Badr Saad T. Alkahtani, Sara Salem Alzaid, Studying the Dynamics of the Rumor Spread Model with Fractional Piecewise Derivative, 2023, 15, 2073-8994, 1537, 10.3390/sym15081537
3.	Hardik Joshi, Mechanistic insights of COVID-19 dynamics by considering the influence of neurodegeneration and memory trace, 2024, 99, 0031-8949, 035254, 10.1088/1402-4896/ad2ad0
4.	Kottakkaran Sooppy Nisar, Muhammad Farman, Khadija Jamil, Ali Akgul, Saba Jamil, Onder Tutsoy, Computational and stability analysis of Ebola virus epidemic model with piecewise hybrid fractional operator, 2024, 19, 1932-6203, e0298620, 10.1371/journal.pone.0298620

Big Data and Information Analytics

Modeling the COVID-19 epidemic in Bolivia

Related Papers:

Abstract

1. Introduction

2. Preliminaries

3. Existence and uniqueness

4. Stability analysis

5. Numerical Scheme for the fractional piecewise COVID-19 model

6. Numerical simulations

7. Sensitivity of parameters

8. Conclusions

Acknowledgements

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog