Strength estimation of silicon nitride ceramics using a round-notched specimen subjected to shearing-tool indentation

1.   Introduction

Because of many advanced characteristics, for example, low density, good strength, high abrasion resistance, high seizure resistance, high corrosion resistance and flexibility of powder sintering, engineering fine ceramics are widely used in various applications, especially in automotive and aerospace industries ^[1,2]. However, due to their inherent brittle characteristic, cracks can occur in sintered ceramics tool during manufacturing process, such as a die surface for deep drawing ^[3]. Generally, to evaluate the mechanical properties of a raw material, a tensile test of a bar or ribbon specimen is the most common mechanical method. However, many sintered ceramics are brittle and hard at a room temperature and difficult to be machined for making arbitrary shaped specimen. There are a few of experimental difficulties that have to be solved to conduct a simple tensile test using a conventional tensile testing machine ^[4]. For an example, to avoid premature failures at a gripped surface is not easy when fastening a specimen on a tensile test apparatus ^[5,6,7]. Therefore, appropriate evaluation method of mechanical properties of sintered ceramics is desired for briefly grasping the difference of mechanical properties of target ceramics from other similar ceramics. From the aspects of easy measuring of the strength of brittle ceramics, a notched specimen seems to be convenient for making a stable breakage, and a shearing test using Iosipescu specimen ^[8,9] is easy to make a shearing state at the notched zone without any gripping failure. Since a shear state includes a principal tensile state and a principal compressive state, appropriate failure strength by the tensile state can be evaluated. In order to estimate the principal stresses and cracking resistance at the shearing state, a commercial based FEM code simulation is not so difficult recently for many researchers and engineers.

In this study, so far, the shear strength of two types of sintered silicon nitride (Si₃N₄) plate ^[10] was estimated using a round-notched specimen subjected to shearing-tool indentation. Although the Iosipescu specimen, which has a symmetric pair of round-edges on the top and bottom side, is more convenient for analyzing a pure shearing state, to make a pair of round-edges at the just same position on the upper and lower part in a specimen is empirically difficult, especially for machining brittle ceramics. Therefore, a shearing test of one side-notched specimen was proposed here to estimate the shear strength. In this case, a CO₂ laser-assisted diamond cutting wheel abrasion was used for making a round-edge on the upper side of a Si₃N₄ specimen. Also, a finite element method (FEM) analysis was conducted in order to further discuss about the resistance of crack propagation in a ceramics workpiece subjected to a shearing-tool indentation.

Many researchers have studied the shearing process of ductile sheet materials, and its breaking behavior ^[11,12,13]. However, the breaking behavior of ductile workpiece seems to be different from that of brittle workpieces. Crack initiation appeared to occur randomly on the surface and its propagation appeared to occur with a small plasticity due to the fragile property of the brittle materials ^[14]. Namely, the cutting profile of brittle materials is not smoother than that in ductile materials subjected to shearing process. Some researchers also have studied the cutting characteristics on the fragile material ^[15]. These researchers have just only investigated the deformation and stress distribution of the deformable body. There are almost not any research works which clarified a cracking behavior of a brittle workpiece. In order to promote the shearing technology for cutting the fragile materials, and also to briefly estimate the breaking strength of that materials, the cracking behavior of sintered Si₃N₄ workpiece must be understood. In the literature, some researchers demonstrated through experiments and simulations for modeling a crack propagation at the interfacial region in both brittle and ductile materials ^[16,17,18]. In this work, the VCCT model was applied to simulate a shearing process for investigating breaking behavior of Si₃N₄ workpiece subjected to a shearing-tool indentation.

By considering the appropriate resistance of crack propagation from the pre-cracked bending test, a propagation behavior of initial surface crack was numerically detected and compared with the shearing experiment of Si₃N₄ workpieces.

2.   Materials and experiments

2.1.   Materials

This study was performed by using two types of commercial silicon nitride (Si₃N₄), SNP02 and SNP03 (made by Japan Fine Ceramics Co., Ltd.). SNP02 was a sintered reaction bonded silicon nitride (SRBSN) while SNP03 was prepared via gas-pressure sintering of silicon nitride (SSN) method. Both of SNP02 and SNP03 had the same hardness at 15 GPa which was conducted by Vickers hardness test based on JIS R 1601 standard test method.

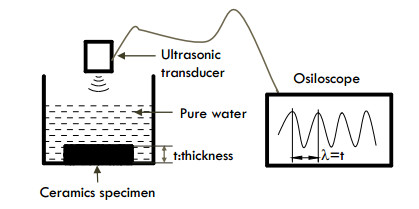
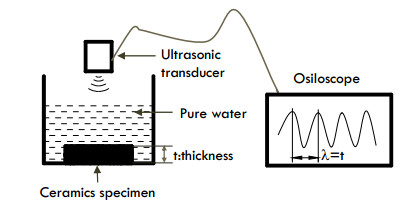
Silicon nitride (Si₃N₄) is a brittle material at the ambient temperature since the yielding is very small ^[19,20]. To detect the mechanical properties of Si₃N₄ workpiece, a non-destructive test method based on ASTM E 494-15, was investigated. In this test method, an ultrasonic pulse generator and sensors plus an oscilloscope was used to measure the sound velocity. Figure 1 indicates a schematic of the ultrasonic testing system. Young’s modulus E and Poisson’s ratio ν of a ceramics specimen were calculated from the longitudinal wave velocity v_l, transversal wave velocity v_s and density ρ using Eqs 1–2 ^[21,22]. and its mechanical properties were concluded into Table 1. It was found that SNP03 had slightly low stiffness compared with that of SNP02. The Young’s modulus of SNP03 was almost similar to that of Si₃N₄ which was estimated in ^[23].

There are many test methods to detect the fracture toughness of ceramics, including chevron-notched beam test, surface crack in flexure method and pre-cracked beam method. In this study, pre-cracked beam test (ASTM C 1421-10), which is easy to prepare the straight through pre-crack, was used. Crack intensive factor of two types of silicon nitride was calculated from the fracture force, the measured pre-crack length and the specimen size. The critical value of energy release rate G_C is calculated from Young’s modulus, Poison’s ratio and stress intensive factor K_I shown as Eq 3 ^[24]. The calculated stress intensive factor K and energy release rate G_C is shown in the last two rows of Table 1. These calculated stress intensive factors were nearly similar to that of Si₃N₄ reported in ^[23]. However, these values were quite larger than 5.3 MPa·m^1/2 of Kadin et al’s estimation ^[25]. Microstructure and manufacturing conditions seem to be reasons leading the difference between these kinds of ceramics.

2.2.   Experiment procedure of shearing

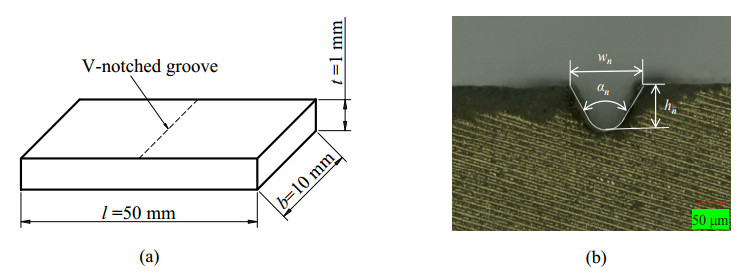
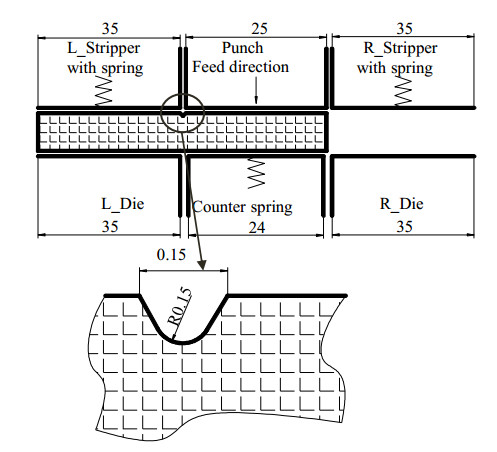
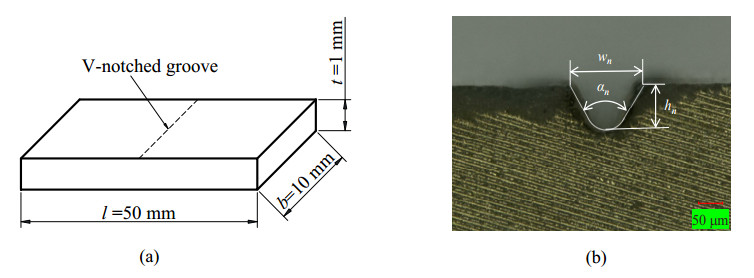
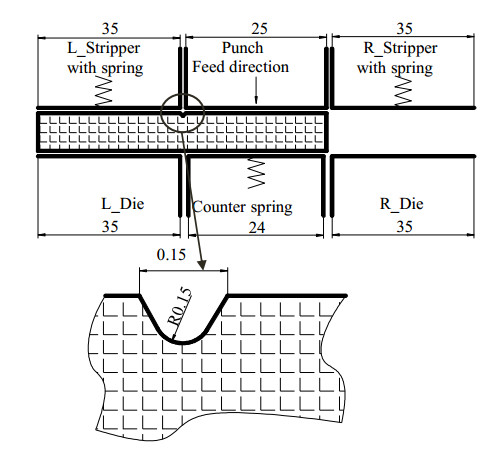
Specimens of SNP02, SNP03 were prepared as a rectangle shape which had a thickness of t = 1 ± 0.01 mm, a length l of 50 ± 0.05 mm and a width b of 10 ± 0.04 mm, using a diamond abrasive cutting wheel. A CO₂ laser machine (HAJIME CL1 PLUS) was used under a specific condition: 30 W power laser was scanned 7 times with a velocity of 1 mm·s⁻¹ to heat the surface of specimen and also the diamond abrasive machine was used for making a V-notched groove on the specimen. A single line V-sharp was generated as the following profile parameters: w_n = h_n = 0.15 ± 0.01 mm and α_n = 63^o. Machined notch has surface roughness Ra of 0.417–0.439 µm, which was observed by laser microscope. Various dimensions of a workpiece and round-notched groove are shown in Figure 2. All specimens were sufficiently washed with alcohol and naturally dried in a room with a temperature of 296 ± 1 K and a humidity of 50 ± 1%RH for approximately 24 h before the shear test.

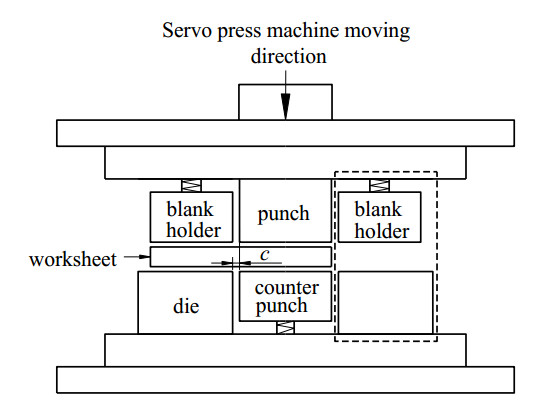
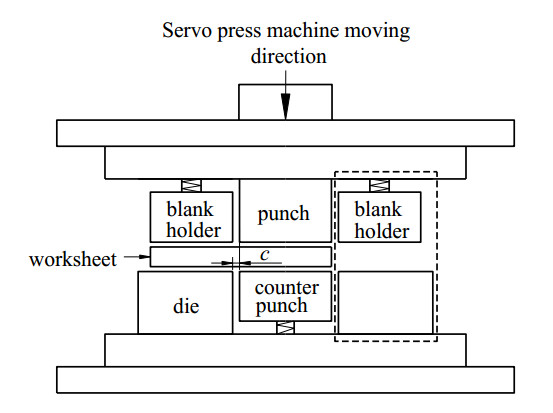
Figure 3 indicates a schematic of the experimental-press machine apparatus in configuration with a ceramics specimen. The shearing die set contains four main components: punch, dies, blank holders and counter punch. These parts were made of SKD11 steel (cold-work steel) which had a hardness of 58~60 HRC. In this shearing apparatus, the right blank holder and the right die, indicated by the dashed lines in Figure 3, were not used (the specimen was not put in this area). The clearance ratio between punch and die c/t was empirically chosen as 0.15, which was equal to a ratio of the width of the V-notch w_n by the thickness t. A force of blank holder (counter punch) and their displacement are controlled by the back-up springs with the stiffness of 5.0 and 4.5 N·mm⁻¹, respectively.

These shearing tests were performed on a digital servo-press machine (CYA-3-10, SINTOKOGIO) at the temperature of 296 K and humidity of 50%RH in a controlled room. Here, the downward speed of crosshead(punch) was chosen as 5 mm·min⁻¹. During the shearing test, the punching force F N and the displacement of the punch d mm were recorded. To observe the cracking propagation and the side-view of the specimen, a high-speed camera was installed. To evaluate the shear strength of brittle material, typically for ceramics, a significant number of specimens have to be prepared in order to obtain a reliable value. In this experiment, the shearing test was conducted with five specimens for each condition.

2.3.   Experimental results and discussions

In this experiment, a high-speed camera was used to record the cracking behavior during the punch indentation. Figure 4 shows the result of cracking behavior for SNP02 and SNP03 respectively. These cracking propagations were so fast and catch up by high-speed camera of 1000 frames per second. In two cases, crack initials start at the grooved notch and rapidly to separate into two parts. It was found that the initial crack did not locate at the middle of the notch but occurred at the side face of the notch.

The shear strength was defined and calculated by dividing the maximum load by the cross-sectional area of the specimen as shown in Eq 4.

Here, F_max is the maximum load, w = 1−0.15 = 0.85mm is the distance from notch to lower surface of the workpiece, and b = 10mm is the width of the workpiece.

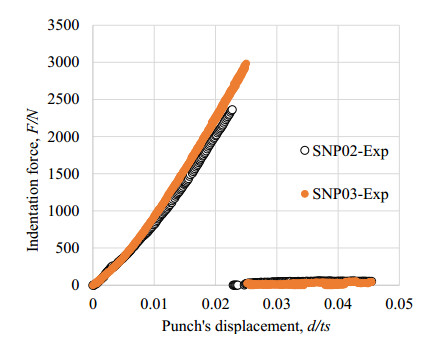
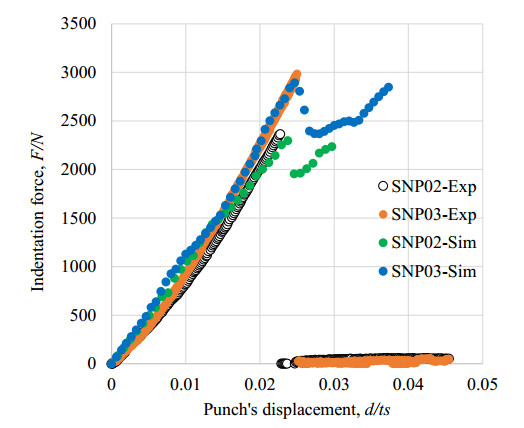
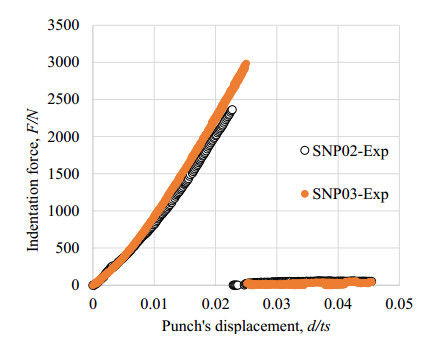
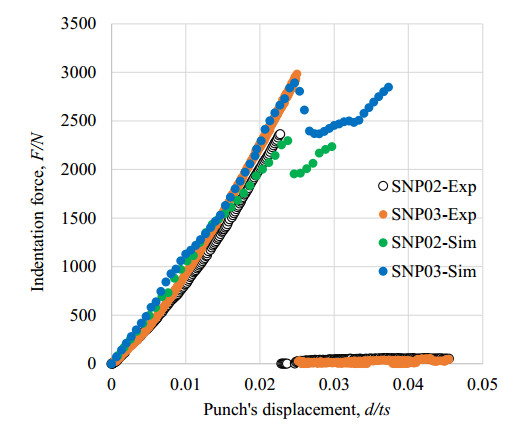
Figure 5 shows the comparison of load-displacement responses with two types SN02, SN03 of Si₃N₄ ceramics. From the load response curves, it was found that SNP02 and SNP03 were brittle elastic behavior up to the fracture point. The average ultimate failure load and shear strength outcome as Table 2. The shear strength of SNP02 was approximately 16% higher than that of SNP03, although they had the same chemical structure of Si₃N₄.

The surface grinding of two types of Si₃N₄ ceramics was performed using a ML-150P grinding machine in two processes. A coarse polishing was used a grinding wheel with diamond grains of 30 µm. After that, a fine polished surface was performed with diamond particles slurry of 2 µm. After grinding the surface of specimen of SNP02 and SNP03, a scanning electron microscopy SEM (Jeol JSM 6400) was used to observe the surface of these specimens.

In Figure 6, there were many imperfections including point defects and impurities in the SNP02 in comparison with the SNP03. Synthetically, it was found that a good microstructure (less point defects) contributed to perform the higher shear strength of Si₃N₄ ceramics.

3.   Simulation of cracked behavior

3.1.   Principle of VCCT cracking model

Many researchers succeeded to predict an initiated fracture of ductile material in a shearing process ^[11,12,13]. The initiation of fracture was predicted by an integral formulation of Eq 5 ^[12] which reached to a critical threshold value C during the shearing process:

Here, f(${\sigma }_{m}, \overline{\sigma }$) is a certain kind of functional form with arguments, and $\overline{\sigma, }{\sigma }_{m}, \overline{{\varepsilon }_{p}}$ are the Mises equivalent stress, the pressure (average of three normal stresses) and the equivalent plastic strain, respectively. This critical value C was empirically determined from an experimental tensile test. However, the failure behavior of brittle material is apparently different from that of ductile workpiece subjected to a shearing load. In a case of notched brittle material subjected to a shearing load, the critical release energy rate G_C is normally considered to discuss the crack propagation. In this work, the virtual cracking closer technique (VCCT) model based on the Griffith’s theory was used to predict the cracking resistance of brittle material ^{[26,27,28,29]}. In this theory, there are three modes of cracking propagation: the tensile (mode Ⅰ), the shearing (mode Ⅱ) and the tearing (mode Ⅲ). As for the crack opening and propagation, the total energy release rate of these modes must be equal to the required energy for creating a new surface.

A basic equilibrium of this process was expressed by Eq 6. Here, G_T was the total energy release rate and G_C was the critical release energy rate, which was evaluated from a 3-points bending test of pre-cracked beam.

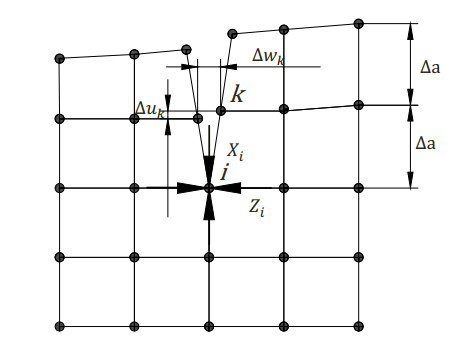
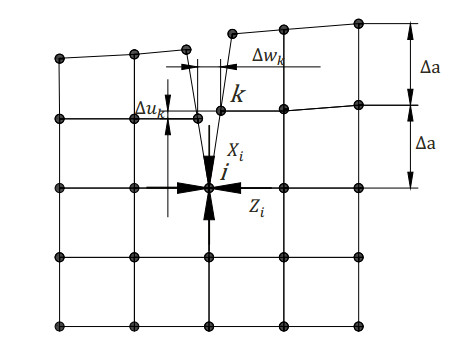
In a case of two-dimensional deformation as the plane strain, the mode Ⅲ is negligible, and then the total strain energy release rate as a sum of the mode Ⅰ and the mode Ⅱ, G_I, plus G_II, defined as Eq 7 is expressed with a crack length Δa, a shear displacement Δu_k and an opening displacement Δw_k, as shown in Eq 8 ^[16,17]. Here, Δa is measured from a node point l to a node point i; Z_i and X_i are an opening force and a shear force at the crack tip (node point i). Δu_k and Δw_k are calculated from the shear and opening displacement at the node l as shown in Figure 7.

In this work, the virtual cracking closer technique (VCCT) was used for investigating the initial cracking and its propagation in a round-notched ceramics specimen using the finite element code MSC. Marc 2015.0.0 (updated Lagrange procedure). Figure 8 shows a two-dimensional shearing FEM model and details of a notched profile. It was constructed as the similar shape with the experimental shearing specimen. The plane strain quadrilateral elements subdivided with 3500 meshes were initially prepared. To focus on the cracking of the workpiece and reduce the calculation time; the punch, dies, counterpunch and strippers were assumed to be rigid bodies, while the workpiece was assumed to be an elastic deformable body.

When discussing the simulation results, the mechanical properties of ceramics were assumed to be same as experimental values described in the section 2.1. The coulomb tan^-1 friction model with a relative velocity threshold of 0.01 was considered in this simulation. The friction coefficients of the blank holder and the ceramics: μ_b, the punch and the ceramics: μ_p and the die and the ceramics: μ_d were measured by the friction test based on JIS-K 7125. The results were approximated as μ_b = μ_p = μ_d = 0.21.

3.2.   Preliminary simulation for determining the initiation of crack

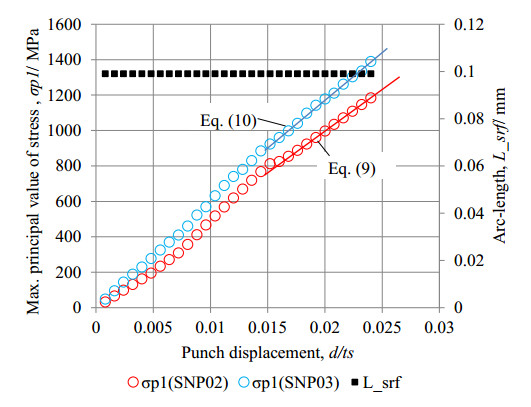
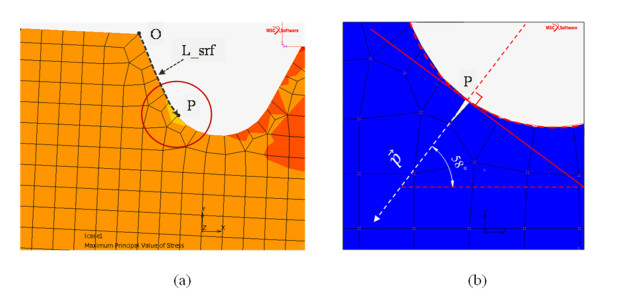
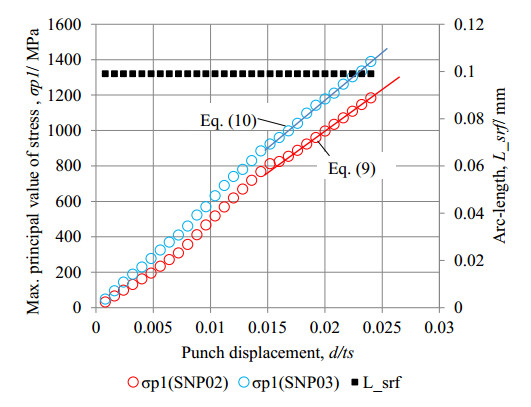
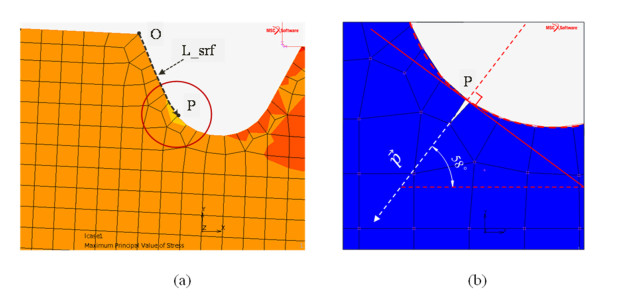
Figure 9 shows the flow schemes of numerical process to simulate the cracking behaviour during a shearing process. Firstly, an FEM model without cracking model was used for determining the stress distribution on the notched surface to detect the crack initiation. The mechanical condition of shearing process and the material properties of ceramics were considered to be same as the experiment described in the section 2.1. There was not any cracks on the surface in the first stage model. In Figure 10, the red-circled and blue-circled sequences show the peak value of maximum principal stress as a tensile state (σ_p1) in two cases of SNP02 and SNP03 with respect to the punch’s displacement, respectively. Linear approximations of simulated maximum principal stress σ_p1 by the least-squares method were derived as Eqs 9–10. The difference of Eqs 9–10 was caused from the difference of Young’s modulus of SNP02 and SNP03. The black-dotted sequence shows the tracking position of the peak value of σ_p1. Here, the arc-length, L_srf, was a distance from the left side of the rounded notch (O) to a peak position of σ_p1 (P) as shown in Figure 11a. It was found that the peak of σ_p1 occurred near a 0.1 mm off-set position (P) from the groove bottom during the shearing process in two cases of SNP02 and SNP03. This peak position was also corresponded to the position where the initial crack was observed in the shearing experiment. Therefore, a cracked position of the initiation in VCCT model was determined and a 0.012 mm depth initiation was defined across to the surface in a meshed model as shown in Figure 11b.

From the experiments, it was found that the cracking of groove zone of SNP02 and SNP03 started at the displacement d/t_s = 0.021 and d/t_s = 0.023, respectively. Then, the corresponded critical stress of SNP02 and SNP03 was estimated as 1035 and 1331 MPa respectively, using Eqs 9–10. This result was quite similar to the fracture strength which was estimated in ^[19]. Here, a maximum stress value is considered as the fracture strength to predict the cracking behavior in Si₃N₄ subjected to Vickers indentation.

After detecting the initiation position from the preliminary model, a cracking model based on the VCCT method, which was introduced in the section 3.1, was used to simulate the cracking propagation of ceramics workpiece during the shear process. In this cracking model, the critical release energy rate was assumed to be 0.019 N·mm⁻¹ and 0.021 N·mm⁻¹ for SNP02 and SNP03 respectively from the 3-points bending test of pre-cracked beam that was mentioned in the section 2. The crack grew and propagated whenever the calculated energy release rate was larger than the critical value in the process of punch indentation against the notched workpiece. From the experiment result, it was found that the cracking direction was approximately 58^o with the horizontal axis. Therefore, in this simulation, the crack propagation direction was specified by vector $\overrightarrow{p}$ as shown in Figure 11b. Here, the direction of crack propagation was approximately perpendicular to the tangent line of notch surface. The crack was propagated by the punch indentation until the workpiece was separated completely.

3.3.   Results of simulation and discussions

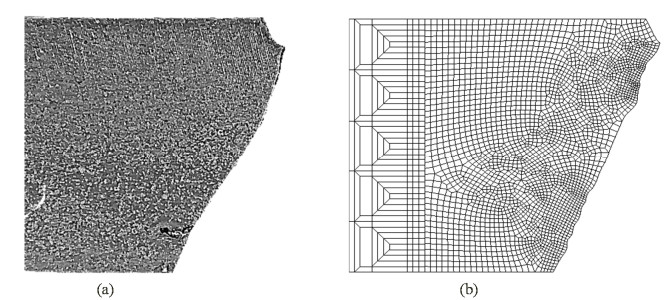
To discuss the VCCT based simulation, the initial crack position and the direction of its propagation were numerically measured and compared with the experimental shear results of notched workpiece. Figure 12 shows a simulated process of cracked behavior of SNP02. At the starting position d/t_s = 0, a 0.012 mm depth crack was defined on the groove surface as shown in Figure 12a.

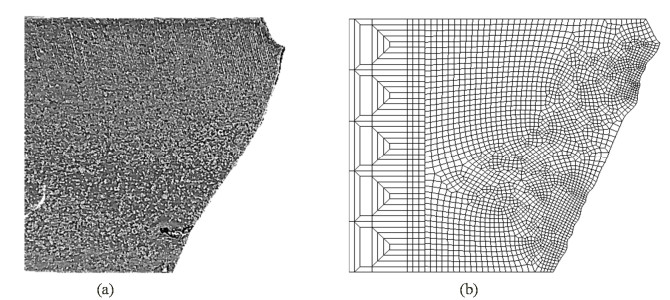
When the punch moved downward, the pushing load increased. Meanwhile, the strain energy increased at the cracked position until the value of G_T (expressed by Eq 8) exceeded the critical release energy rate G_C, and then the crack started to be enlarged at d/t_s = 0.021 (Figure 12b). In this Figure 12b, the crack tip was opened from the point P to the point Q in a small incremental step of convergence. Here, when the punch was indented with an incremental step dx = 8 × 10⁻⁴ mm, a crack length da = 0.01 mm was calculated. The maximum principal stress (σ_p1) at the crack tip was estimated as 1047 MPa in this state Figure 12b. After that, the crack was gradually propagated when the punch was continuously indented to the workpiece. In order to avoid unexpected stopping of crack growth, a global auto-remeshing function (2D solid: Advancing Front Quad was used in the FEM simulation. The initial coarse mesh pattern around the focused crack were automatically refined when the crack was propagated in every increment. The automatic-remeshing was performed when the strain change of each element was higher than 0.2 or the inner angle of element was greater than 175º or smaller than 5º. To ensure the mesh resolution which was large enough to generate the new crack tip, the minimum element size was defined as 0.012 mm in this simulation. Figure 12c shows a refined remeshing state which was allowed to make a small propagation of crack. Finally, the ceramics workpiece was completely broken at d/t_s  0.03 (Figure 12d). The crack was extended and progressed along the initial crack as shown in Figure 13. In case of simulation, the crack route relatively propagated in a straight line. However, seeing the direction of crack propagation in Figure 13, especially from the center part to the lower-side of the workpiece, the cracked route of the experiment deviated from the initial line. As the result, the experimental crack path had a slight curve. This mismatching tendency seems to be caused from the high geometry constraints, that was also reported in ^[30,31].

Comparing the cutting line force as shown in Figure 14, it was found that the breaking strength was almost similar to that of the experiment. In the simulation, it was easy to detect the initial crack position, although this transition point was not detected clearly in the experiment. Through this development of simulation model, any other loading models or different type of notched workpiece are possible to analyse. After passing the punch stroke d/t_s > 0.021 for SNP02 and d/t_s > 0.023 for SNP03, the cracking behaviour was different from the experimental results due to some reasons. One reason was a sort of unstable calculation of cracking, and another reason seemed to be caused from the mismatching of dynamic cracking behaviour. The real, experimental behaviour seemed to be affected by a dynamic resistance of cracking, while the G_T based VCCT model was assumed to be a static resistance model.

4.   Conclusion

In this study, the shear strength of two kinds of ceramics material was experimentally and numerically estimated by using a round-notched shear test method. The initial cracking and its propagation direction was analyzed using the VCCT method. The followings were concluded:

1.A good microstructure ceramics, which had a small number of impurities or point defects, had experimentally the higher shear strength than other ceramics which had many imperfections.

2.The Eq 8 based VCCT model plus the positioning of initiation by the maximum principal stress had a good agreement with the experiment to predict a crack initiation and the direction of crack propagation in a notched Si₃N₄ workpiece.

3.The developed simulation model using the Eq 8 based VCCT plus the initiation by the maximum principal stress has a possibility to predict the similar crack propagation in notched fragile materials subjected to a shearing tool indentation.

Acknowledgments

The authors thank for supporting a collaboration fund and advising a role and requirement on ceramics dies as a deep drawing tool from Shimizu Industrial Co. Ltd.

Conflict of interests

The authors declare that there is no conflict of interest regarding the publication of this manuscript.