1. Introduction

An option is a financial derivative which gives the option holder the right, but not the obligation, to buy or sell a specified amount of an underlying asset at a fixed price on or before the expiration date of the option. To price an option is to evaluate the integral of its expected payoff under a risk-neutral probability measure, if such a measure exists (which is assumed). In many practical applications, the underlying financial asset, which we shall assume throughout in this article, can be modelled by a diffusion process, or a pair of correlated diffusion processes (for instance stochastic volatility models). The value of the financial option is the expectation of the underlying along a (discrete) path under the risk neutral meausure associated to the process just described.

As the value of the option is seldom available, one often resorts to numerical methods to approximate it. Monte Carlo methods for pricing options dates back at least to ^[2]. These methods and their variants: quasi Monte Carlo (QMC), stratified sampling, control variate, antithetic variates and so on have been used extensively in the financial engineering literature; see for example ^[9] for a complete description of these techniques. The main advantage of MC methods for pricing options compared to other numerical methods is its ability to deal with high-dimensional integrals. It is this methodology that is focussed upon for the duration of the article.

In some recent works the standard MC method has been improved upon, especially when the diffusion process must be time-discretized. In this latter scenario, the method of MLMC has (for some pay-offs and diffusions) been shown to provide the same overall MSE as an MC method, but with less computational effort; see for instance ^[8] and the references therein. We briefly note that the MLMC method works by considering a hierarchy of time-discretizations and a simple collapsing sum representation of the expectation w.r.t. the most precise time-discretized diffusion process. For each summand, a difference of expectations under successively fine discretizations, the joint law of the discretized processes are coupled and sampled. This coupling, if sufficiently efficient can mean that the MLMC method achieves the afore-mentioned savings. In addition to this, several works beginning with ^[11] and more recently in ^[17,18] have shown that standard MC and importance sampling (IS) can be enhanced by using SMC or PF methodology. This is an algorithm that can approximate expectations w.r.t. a sequence of probability distributions by sampling a collection of $N$ particles (samples) in parallel, sequentially in time using sampling and resampling operations; see ^[6] for an introduction. The main improvement of SMC over IS for option pricing is that as the number of points of the path of the diffusion process grows, call it $n$ (and under several mathematical assumptions) the relative variance of the SMC estimate is $\mathcal{O}(n/N)$ whereas for IS it can be $\mathcal{O}(\kappa^n/N)$ for some $\kappa>1$ (see e.g. ^[3]). In this article, we show how using the works of ^[14,15], called the MLPF (see also ^[16]), MLMC and SMC can be combined to help to improve upon the estimation of options.

The main contribution of this article is two-fold:

1. To show how the MLPF technique can be used in pricing European type exotic options.

2. To illustrate by numerical examples the gains obtained when such methods are used to estimate option prices over vanilla particle filter.

In terms of $1$, we aim to demonstrate that the MLPF framework is applicable in estimating the price of an exotic options. We compare the computational benefits one obtained in using the MLPF compared with standard particle filter (introduced in ^[11]) in estimating both basic and path dependent options. With respect to $2$, detailed numerical examples on European call options, knock-out barrier options and TARNs are presented to verify the computational superiority of the MLPF over standard methods. We are not intended to show that these methods presented here are competitors to the existing ones but demonstrate that it enhances the existing methods in the literature.

The rest of the article is structured as follows. Section 2 introduces the option pricing problem and two path dependent options, barrier options and target accrual redemption notes (TARNs). It also reviews identities for approximation for evaluating the expected value of the function of the underyling process, and finally briefly reviews the multilevel particle filter technique relevant in this context. Section 3 numerically illustrates our methods. The article concludes in Section 4.

In what is to follow in the rest of the paper, the following notations will be adopted. For any vector $x_{1:n}$ will denote $\left(x_1, \dots, x_n\right)$. Expectations are written generically as ${\mathbb{E}}$ and subscript is added, if it is required to denote dependence upon a measure/point. ${\mathbb{R}}^d$ denote the $d$-dimensional Euclidean space. For $k\in {\mathbb{N}}$, ${\mathbb{T}}_k = \left\lbrace1, \dots, k\right\rbrace$.

---

2. The model, options and strategy

In this section, we briefly describe the option pricing problem of interest in this article. We focus on European options in this section, and describe the methods for pricing two kinds of exotic options, namely barrier options and TARNs, which we shall describe shortly.

---

2.1. The price process

Let $\left\lbrace S_t\right\rbrace_{t\in\left[0, T\right]}$ be the price process, $S_t\in{\mathbb{R}}^{+}$ and $T$ the terminal time of an underlying financial asset. We assume that it follows a diffusion:

$\begin{align}\label{op:eq1} \mathrm{d}S_t & = \alpha\left( S_t\right)\mathrm{d}t+\beta\left( S_t, V_t\right)\mathrm{d}W_t \nonumber \\ \mathrm{d}V_t & = \gamma\left( V_t\right)\mathrm{d}t+\nu\left( V_t\right)\mathrm{d}B_t \end{align}$

(2.1)

where $\alpha\thinspace\colon\thinspace{\mathbb{R}}^{+}\rightarrow {\mathbb{R}}$, $\beta\thinspace\colon\thinspace({\mathbb{R}}^{+})^2\rightarrow {\mathbb{R}}^{+}$ $\gamma\thinspace\colon\thinspace{\mathbb{R}}\rightarrow {\mathbb{R}}$, $\nu\thinspace\colon\thinspace{\mathbb{R}}\rightarrow {\mathbb{R}}^{+}$, with $\{V_t\}_{t\in\left[0, T\right]}$ is the volatility (or log-volatility) and $\left\lbrace W_t\right\rbrace_{t\in\left[0, T\right]}$, $\left\lbrace B_t\right\rbrace_{t\in\left[0, T\right]}$ are independent standard Brownian motion. Throughout $V_0, S_0$ is assumed known. In addition, the functions $\alpha, \beta, \gamma$ and $\nu$ are assumed known (see e.g. ^[1,11,18]). In some examples there will not be any volatility process.

We are interested in computing options of the form

${\mathbb{E}}\left[g\left(S_{t_1:t_k}\right)\right]$

for some $k\geq 1$ given and $g:({\mathbb{R}}^{+})^k\rightarrow{\mathbb{R}}^{+}$ and the expectation is typically w.r.t. the time discretized process (e.g. Euler discretization).

---

2.2. Barrier options

Barrier options are derivatives for which the payoff may be zero dependent on the path of the underlying asset $\left\lbrace S_t\right\rbrace_{t\in I}$, $I\subset\left[0, T\right]$, breaching a barrier. There are two broad types of barrier options:

1. Knock-in: the option pays zero unless a function of the underlying asset values breaches prespecified barriers (option springs into existence) and

2. Knock-out: the option pays zero if a function of the underlying asset values breaches prespecified barriers (option is extinguished).

Compared to basic options, barrier options are cheaper because it may expire worthless if knocked out (or knocked in) in the same condition in which the vanilla option would have paid off.

Barrier options are hard to price using standard MC methods due to most particles leading to a zero payoff and this gives inaccurate estimates of the option. As noted in ^[10] many paths may lead to zero Monte Carlo and a simple remedy suggested is to use conditional distribution gvien one-step survival.

---

2.2.1. Barrier options with constant volatility

In this paper, we will concentrate upon European style options

${\mathbb{E}}_{S_0}\left[g\left(\left\lbrace S_t\right\rbrace_{t\in I}\right)\right]$

with

$g\left(\left\lbrace S_t\right\rbrace_{t\in I}\right) = {\mathbb{I}}_{B}\left(\left\lbrace S_t\right\rbrace_{t\in I}\right)e^{-rT}\left(S_T-K\right)_{+}$

a barrier call option, with strike $K>0$, interest rate $r>0$ and $B$ the barrier set. Consider, for instance in a simpler case, a constant volatility and a discretely monitored knock-out barrier option, a series of monitoring dates $I = \left\lbrace t_1, \dots, t_k\colon 0 < t_1 < \dots < t_k = T\right\rbrace$, $t_0 = 0$, barrier set $B = \bigotimes_{i = 1}^{k}\left[L_{t_i}, U_{t_i}\right]$, where $L_{t_i}$ and $U_{t_i}$ denote a sequence of lower and upper barriers respectively. The option price is given by

$\int e^{-rT}\left(s_{t_k}-K\right)_{+}\prod\limits_{i = 1}^{k}\left\lbrace{\mathbb{I}}_{\left[L_{t_i}, U_{t_i}\right]}\left(s_{t_i}\right)p\left(s_{t_i}\mid s_{t_{i-1}}\right)\right\rbrace\mathrm{d}\left(s_{t_{1:k}}\right),$

(2.2)

where we assumed that the unknown transition densities can be written with respect to a dominating measure abusively denoted here as $\mathrm{d}\left(s_{t_{1:k}}\right)$. The estimation of the barrier option 2.2 is non-trivial in Monte Carlo integration. For instance, if we assume all the parameter functions and transition densities are known and the Euler discretization adopted, it is still the case that many paths may yield to a zero Monte Carlo estimate before the terminal time. We remark here that, a more complicated model of the volatility process can be adopted; for example, see ^[1,12]. We will consider in addition to the constant volatility model the case where the volatility process is a stochastic differential equation, in particular a Langevin SDE.

---

2.3. Target and accrual redemption options

These options are very popular in the FX trading market. It provides the holder a capped sum of payments over a period with the possibility of premature termination (knock-out) due to a target cap pre-specified on the accumulated payments. A specified amount of payment is made on coupon dates (referred to as fixing dates or cash flow dates) until the cap target is violated. One typical example is the target accrual redemption note. The note value on a coupon date depends on the spot value of the underlying asset and the accumulated payment amount up to the coupon date.

For simplicity, we consider in this article the typical TARNs introduced in ^[17]. Consider a sequence of cash flow dates $\left\lbrace T_n\right\rbrace_{n\in{\mathbb{T}}_k}$, where $T_k = T$ is the note's maturity date, and a real-valued function $f\thinspace\colon{\mathbb{R}}\rightarrow{\mathbb{R}}$. The gain and losses processes are given by

$G_p = \sum\limits_{i = 1}^{p}f^{+}\left(S_{T_i}\right), \quad L_p = \sum\limits_{i = 1}^{p}f^{-}\left(S_{T_i}\right),$

where $f^+, f^{-}$ are positive and negative parts of $f$ and $G_p, L_p$ are positive and negative cash flows respectively. Set

$\tau^{(L)} = \inf\{k\geq 1:L_k\geq \Gamma_L\}\quad \tau^{(G)} = \inf\{k\geq 1:G_k\geq \Gamma_G\}$

for two given constants $\Gamma_L, \Gamma_G$. Set

$\tau = \min\{\tau^{(L)}, \tau^{(G)}, k\}.$

The value of the TARN is the expected value of the overall cash flow

${\mathbb{E}}\left[\sum\limits_{i = 1}^{\tau}e^{-r\tau}f\left(S_{T_i}\right)\right],$

where $r$ is the interest rate. We have assumed that the interest rate is deterministic. A more practical version can be considered where the rate is underlying stochastic state variable. Additionally, the amount paid to the holder and the termination date is uncertain. Note that this can be written in the form of interest. Let

$A_i = \{S_{1:i}\in({\mathbb{R}}^+)^i:G_i<\Gamma_G\cap L_i<\Gamma_L\}$

then the value of the TARN is

${\mathbb{E}}\left[\sum\limits_{i = 1}^{k}e^{-r\tau}{\mathbb{I}}_{A_i}(S_{T_1:T_i})f\left(S_{T_i}\right)\right].$

Most TARNs price estimation are solved using standard MC techniques. In the situation where the function $f$ is discontinuous, the MC estimates are unreliable and thus SMC techniques offer the best alternative to the problem. In particular, we consider both the standard particle filter and multilevel particle filter when the volatility is a constant and modelled by a stochastic differential equation.

---

2.4. Identities for approximation

We will suppose that the process 2.1 is suitably exotic such that

1. One cannot compute ${\mathbb{E}}\left[g\left(S_{t_1:t_k}\right)\right]$

2. One cannot sample from the law of $S_{t_1:t_k}$ exactly, that is, without discretization error.

It is suppose that one will discretize (e.g. Euler or Milstein) and call the time discretization $h_L$, with the exact solution of (2.1) returned when $h_L = 0$. We then take expectations with respect to a law with the following finite dimensional law:

$\prod\limits_{i = 1}^{k} Q^L\left((v_{i-1}, s_{i-1}), (v_i, s_i)\right),$

(2.3)

where $Q^L$ is the transition kernel induced by the time discretization. Note that we are simply denoting $V_1, S_1, V_2, S_2, \dots$ as the random variables associated to the time discretization: the actual time in $\left[0, T\right]$ is suppressed from the notation. So we are reduced to computing

${\mathbb{E}}_{\pi_L}\left[g(S_{1:k})\right],$

where the expectation is with respect to the law associated to 2.3 i.e $\pi_L$ and denote by $m_L\in{\mathbb{N}}$, the number of points induced by the time discretization at a resolution level $L$ at time $k = m_L$. As noted in ^[13] even if one can sample from the law of $S_{1:k}$ exactly, using standard Monte Carlo can induce a substantial variance. This is also true when discretizing the time parameter.

---

2.4.1. Importance sampling

We suggest the following, close to optimal (in some sense), importance sampling procedure as used in ^[11,14]. Let $\tilde{g}\thinspace\colon\thinspace({\mathbb{R}}^{+})^k\rightarrow{\mathbb{R}}^{+}$ be a function 'related' to $g$ (which could be $g$ itself). Then consider the target density

$\pi_L\left(s_{1:k}, v_{1:k}\right)\propto\kappa_L\left(s_{1:k}, v_{1:k}\right) = \tilde{g}\left(s_{1:k}\right)\prod\limits_{i = 1}^{k} Q^L\left((v_{i-1}, s_{i-1}), (v_i, s_i)\right).$

(2.4)

We note that:

${\mathbb{E}}_{\pi_L}\left[g\left(S_{m_L}\right)\right] = Z_{L}{\mathbb{E}}_L\left[\frac{g\left(S_{1:k}\right)}{\tilde{g}\left(S_{1:k}\right)}\right]$

where $Z_L = \int_{\left({\mathbb{R}}^{+}\right)^{m_L}}\kappa_L\left(s_{1:m_L}\right)\mathrm{d}s_{1:m_L}$. It is this identity that we will try to approximate efficiently. In the ^[11,13], it is discussed why such an approach can be useful. For instance, as used in ^[10], in the context of barrier options a change of measure is useful to ensure that samples from the change of measure will stay in a region of importance, i.e. yield (relatively) low variance Monte Carlo estimates. Note that from a minimum variance perspective (i.e. for importance sampling), the optimal choice is $\tilde{g}\left(s_{1:k}\right) = g\left(s_{1:k}\right)$, but this may not always work well; see e.g. ^[11] for some discussion.

---

2.4.2. Multilevel identity

Consider a hierarchy of discretizations $0 < h_L < \dots < h_1 < +\infty$ with obvious extension of $\pi_L, \kappa_L, Z_L$. Then one has that

$\begin{align}\label{op:mlid} {\mathbb{E}}_{\pi_L}\left[g\left(S_{1:k}\right)\right]& = \sum\limits_{l = 1}^{L}\left({\mathbb{E}}_l\left[g\left(S_{1:k}\right)\right]-{\mathbb{E}}_{l-1}\left[g\left(S_{1:k}\right)\right]\right)\nonumber\\ & = \sum\limits_{l = 1}^{L}\Bigg\{ Z_{l}{\mathbb{E}}_l\left[\frac{g\left(S_{1:k}\right)}{\tilde{g}\left(S_{1:k}\right)}\right] - Z_{{l-1}}{\mathbb{E}}_{l-1}\left[\frac{g\left(S_{1:k}\right)}{\tilde{g}\left(S_{1:k}\right)}\right] \Bigg\}, \end{align}$

(2.5)

where we use the convention that $Z_{{0}}{\mathbb{E}}_{0}\left[\frac{g\left(S_{1:k}\right)}{\tilde{g}\left(S_{1:k}\right)}\right] = 0$. ^[15] show how the right hand side of the final line of 2.5 can be approximated using the multilevel particle filter ^[14]. They also show the theoretical benefits relative to using the procedure in the previous section. This is explicitly in the case of a pair of possibly correlated diffusion processes and under regularity conditions. It shown that for a specific choice of $L$ and number of samples at each level this MLPF has the same MSE as a PF but with less computational effort. We note that in the MLPF approach to be discussed in the next Section, these results also apply under the conditions in ^[14,15].

---

2.5. Pricing options using Multilevel Particle Filters

In this section, we briefly introduce the multilevel particle filter in particular context of estimating option prices. We begin by briefly explaining the standard particle filter and then its extension to the multilevel particle filter framework. We will suppose that for any $1\leq n \leq k$ one has a function $\tilde{g}_n:({\mathbb{R}}^+)^n\rightarrow{\mathbb{R}}^+$ associated to $\tilde{g}$. For instance, in the case of barrier options, we shall take

$\tilde{g}(s_{1:k}) = |s_k-K|^{\rho}\prod\limits_{i = 1}^k{\mathbb{I}}_{[L_i, U_i]}(s_i)$

for some fixed $\rho\in(0, 1)$ so there is a natural extension

$\tilde{g}_n(s_{1:n}) = |s_n-K|^{\rho}\prod\limits_{i = 1}^n{\mathbb{I}}_{[L_i, U_i]}(s_i).$

---

2.5.1. Estimating option prices using the PF

A standard PF is given in Algorithm 1 for a given $l\geq 1$; we use the notation $x_n = (v_n, s_n)$. The resampling step is described in detail in e.g. ^[6] and can be made adaptive, i.e. only resampling "when needed". The unbiased estimator ^[4] of ${\mathbb{E}}_l[g(S_{1:k})]$ is

$\Big(\prod\limits_{p = 1}^{k-1} \frac{1}{N_l}\sum\limits_{i = 1}^{N_{l}} W_p^{l, i}\Big) \frac{1}{N_l}\sum\limits_{i = 1}^{N_{l}}W_k^{l, i}g(\check{S}_{1:k-1}^{l, i}, S_k^{l, i}).$

Algorithm 1 A generic PF algorithm

● 0. Set $n=1$; for each $i\in{\mathbb{T}}_{N_{l}}$ sample $X_1^{(l, i)}\sim Q^l((v_0, s_0), \cdot)$ and set initial weights $W_{1}^{(l, i)}=\tilde{g}_1(s_1^{l, i})$.     ● 1. Resample $X_1^{(l, 1)}, \dots, X_1^{(l, N_l)}$ and write the resulting samples $\check{X}_1^{(l, 1)}, \dots, \check{X}_1^{(l, N_l)}$.     ● 2. Set $n = n+1$; for each $i\in{\mathbb{T}}_{N_{l}}$ sample $X_n^{(l, i)}\sim Q^{l}\left(\check{x}_{n-1}^{(l, i)}, \cdot\right)$ and compute weights $W_n^{(l, i)}=\tilde{g}_n(\check{s}_{1:n-1}^{l, i}, s_n^{l, i})/\tilde{g}_{n-1}(\check{s}_{1:n-1}^{l, i})$.     ● 3. Resample $(\check{X}_{1:n-1}^{(l, 1)}, X_{n}^{(l, 1)}), \dots, (\check{X}_{1:n-1}^{(l, N_l)}, X_{n}^{(l, N_l)})$ and write the resulting samples $\check{X}_{1:n}^{(l, 1)}, \dots, \check{X}_{1:n}^{(l, N_l)}$. If $n=k$ stop, otherwise return to 2.

Note that typically, this algorithm only works well if $\tilde{g}_n$ is of product form, or if $\tilde{g}_n$ depends only on $s_{n-u:n}$ for some small $u$ or $k$ is small; see ^[4] for the reasons why and a justification of the algorithm. One of these will be the case in all of our examples.

---

2.5.2. Estimating option prices using the MLPF

We now discuss how one may approximate the identity detailed in Section 2.4.2. In the case of the first summand, one can run the procedure detailed in the previous section. So we focus on the approximation of a term of the form, for $2\leq l \leq L$:

$Z_{l}{\mathbb{E}}_l\left[\frac{g\left(S_{1:k}\right)}{\tilde{g}\left(S_{1:k}\right)}\right] - Z_{{l-1}}{\mathbb{E}}_{l-1}\left[\frac{g\left(S_{1:k}\right)}{\tilde{g}\left(S_{1:k}\right)}\right].$

We will use $L-1$ independent algorithms to approximate the above expression. Critical to our approach will be the use of a coupling of the kernel $Q^l$. We will suppose that there is a $\check{Q}^{l, l-1}$ such that for any $(x^l, x^{l-1})\in({\mathbb{R}}_+\times{\mathbb{R}})^2$ one has for any set $A$

$\begin{align*} \int_{A\times({\mathbb{R}}_+\times{\mathbb{R}})}\check{Q}^{l, l-1}((x^l, x^{l-1}), (\tilde{x}^l, \tilde{x}^{l-1})) {d}(\tilde{x}^l, \tilde{x}^{l-1}) & = \int_{A} Q^{l}(x^l, \tilde{x}^l) {d}\tilde{x}^l \quad\textrm{and}\\ \int_{({\mathbb{R}}_+\times{\mathbb{R}})\times A}\check{Q}^{l, l-1}((x^l, x^{l-1}), (\tilde{x}^l, \tilde{x}^{l-1})) {d}(\tilde{x}^l, \tilde{x}^{l-1}) & = \int_{A} Q^{l-1}(x^{l-1}, \tilde{x}^{l-1}) {d}\tilde{x}^{l -1}. \end{align*}$

Such a coupling exists in our context, see the appendix. The algorithm is presented in Algorithm 2. Note that the coupled resampling procedure is described in detail in ^[14,15]. An unbiased estimate of ${\mathbb{E}}_l\left[g\left(S_{1:k}\right)\right]-{\mathbb{E}}_{l-1}\left[g\left(S_{1:k}\right)\right]$ is given by (see ^[15])

$\begin{equation*} \begin{split} \Big(\prod\limits_{p = 1}^{k-1} \frac{1}{N_l}\sum\limits_{i = 1}^{N_{l}} W_{p, l}^{l, i}\Big)\times& \frac{1}{N_l}\sum\limits_{i = 1}^{N_{l}}W_{k, l}^{l, i}g(\check{S}_{1:k-1}^{l, i}, S_k^{l, i})\\ & - \Big(\prod\limits_{p = 1}^{k-1} \frac{1}{N_l}\sum\limits_{i = 1}^{N_{l}} W_{p, l}^{l-1, i}\Big)\times \frac{1}{N_l}\sum\limits_{i = 1}^{N_{l}}W_{k, l}^{l-1, i}g(\check{S}_{1:k-1}^{l-1, i}, S_k^{l-1, i}). \end{split} \end{equation*}$

Algorithm 2 A generic MLPF algorithm

●0. Set $n=1$; for each $i\in{\mathbb{T}}_{N_{l}}$ sample $(X_1^{(l, i)}, X_1^{(l-1, i)})\sim \check{Q}^{l, l-1}((x_0, x_0), \cdot)$ and set initial weights $W_{1, l}^{(l, i)}=\tilde{g}_1(s_1^{l.i}), W_{1, l}^{(l-1, i)}=\tilde{g}_1(s_1^{l-1.i})$.     ● 1. Perform coupled resampling on $(X_1^{(l, 1)}, X_1^{(l-1, 1)}), \dots, (X_1^{(l, N_l)}, X_1^{(l-1, N_l)})$ and write the resulting samples $(\check{X}_1^{(l, 1)}, \check{X}_1^{(l-1, 1)}), \dots, (\check{X}_1^{(l, N_l)}, \check{X}_1^{(l-1, N_l)})$.     ● 2. Set $n = n+1$; for each $i\in{\mathbb{T}}_{N_{l}}$ sample $(X_n^{(l, i)}, X_n^{(l-1, i)})\sim \check{Q}^{l, l-1}\left((\check{x}_{n-1}^{(l, i)}, \check{x}_{n-1}^{(l-1, i)}), \cdot\right)$ and compute weights $W_{n, l}^{(l, i)}=\tilde{g}_n(\check{s}_{1:n-1}^{l, i}, s_n^{l, i})/\tilde{g}_{n-1}(\check{s}_{1:n-1}^{l, i})$, $W_{n, l}^{(l-1, i)}=\tilde{g}_n(\check{s}_{1:n-1}^{l-1, i}, s_n^{l-1, i})/\tilde{g}_{n-1}(\check{s}_{1:n-1}^{l-1, i})$.     ● 3. Perform coupled resampling on $((\check{X}_{1:n-1}^{(l, 1)}, X_n^{(l, 1)}), (\check{X}_{1:n-1}^{(l-1, 1)}, X_n^{(l-1, 1)})), \dots,$ $((\check{X}_{1:n-1}^{(l, N_l)}, X_n^{(l, N_l)}), (\check{X}_{1:n-1}^{(l-1, N_l)}, \check{X}_n^{(l-1, N_l)}))$ and write the resulting samples $(\check{X}_{1:n}^{(l, 1)}, \check{X}_{1:n}^{(l-1, 1)}), \dots,$ $(\check{X}_{1:n}^{(l, N_l)}, \check{X}_{1:n}^{(l-1, N_l)})$. If $n=k$ stop, otherwise return to 2.

---

3. Simulations

In this section we demonstrate, numerically, the computational savings obtained in using the MLPF over the standard PF for option pricing. In order to compare the $\mathcal{O}(\epsilon^2)$ mean square error estimate against the computational cost of Algorithms 1 and 2, we run each $50$ times. We then look at MSE of the $50$ estimates and report the MSE versus computational cost. In the sequel we consider the basic European call option, barrier options and target accrual redemption notes. The approach in ^[15] to choose $L$ and the $N_{1:L}$ is adopted for the MLPF. A time discretization $h_l = 2^{-l}$ is used. For both the PF and MLPF adaptive resampling is used.

---

3.1. Pricing basic European call option

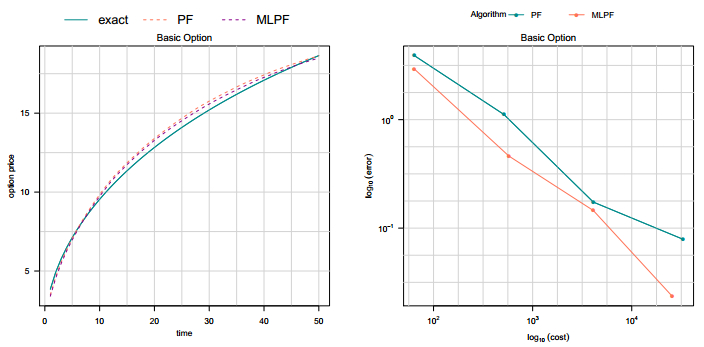
We consider a standard European call option and the underlying is geometric Brownian motion and there is only constant volatility. The functions $\tilde{g}_n$ are taken as $|S_n-K|^{\rho}$, where $K$ is the strike price; the choice of this potential function prevents the weights in the PF being zero (or infinite). We compare estimates from these two algorithms, PF and MLPF with exact option price from the Black-Scholes formula. Of course in this example, neither discretization nor MC are needed, but is just used as an example where the price is known. The PF and MLPF are run at time discretization $h_5$ and we consider time points ${\mathbb{T}}_{50}$ to demonstrate the performance of our proposed methods.

The results are shown in Figure 1. We can observe that both algorithms estimate the price with good precision. The error-versus-cost plots are shown in the computational savings plot. The fitted linear model of $\log$ cost against $\log$ MSE has a gradient of $-1.502$ and $-1.267$ for PF and MLPF respectively. We observe that the MLPF outperforms the standard PF in this basic option price estimate. In the subsequent sections, more exotic options difficult to price will be considered. A summary of these path dependent options results are given in Table 1.

---

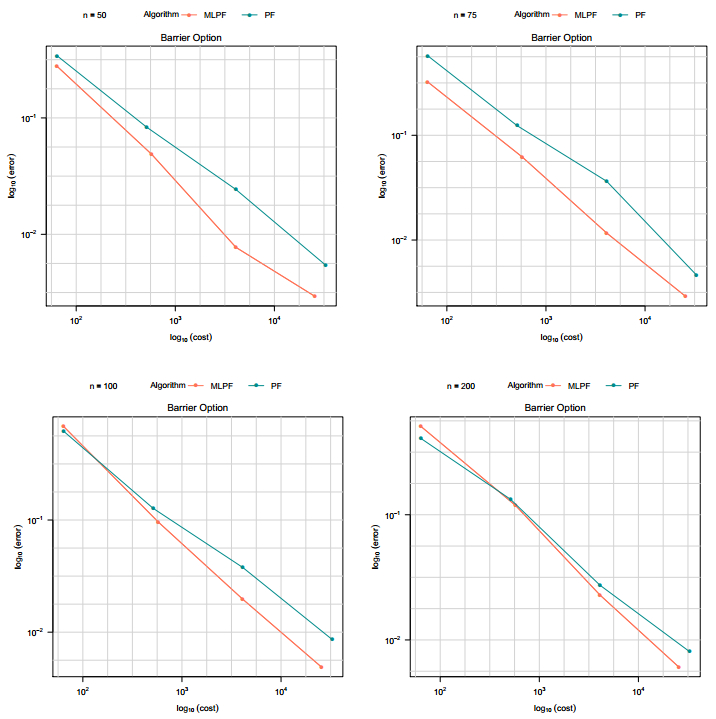
3.2. Barrier options

We consider a knock-out barrier option. As noted in the earlier sections of this article, this is a path dependent option which standard MC gives inaccurate estimates since most of the particles give zero MC estimate. The most common monitoring strategy adopted in the literature is to monitor the underlying assets after every $n$ units of time for a total of $k$ time periods. We consider four different $n$ units of time, that is $n\in\left\lbrace50, 75,100,200\right\rbrace$.

---

3.2.1. Constant volatility

The underlying process follows a geometric Brownian motion as above. The performance of both PF and MLPF can be seen in Figure 2 and Table 1. It can be observed that at all different time points considered, the MLPF achieves significant computational savings against the PF estimates. For example, at time point $n = 100$, a fitted linear model of $\log$ cost against $\log$ MSE has a gradient of $-1.478$ and $-1.212$ for PF and MLPF respectively. These computational rates are consistent with the expected asymptotic behavior Cost$\propto$MSE$^{-5/4}$ for MLPF and Cost$\propto$MSE$^{-3/2}$ for PF respectively. This agrees with the theoretical conlcusions contained in ^[14,15]. Note that these latter results do not consider the time parameter ($n$), but as seen here, the improvement seems to be uniform in time as conjectured in that work.

---

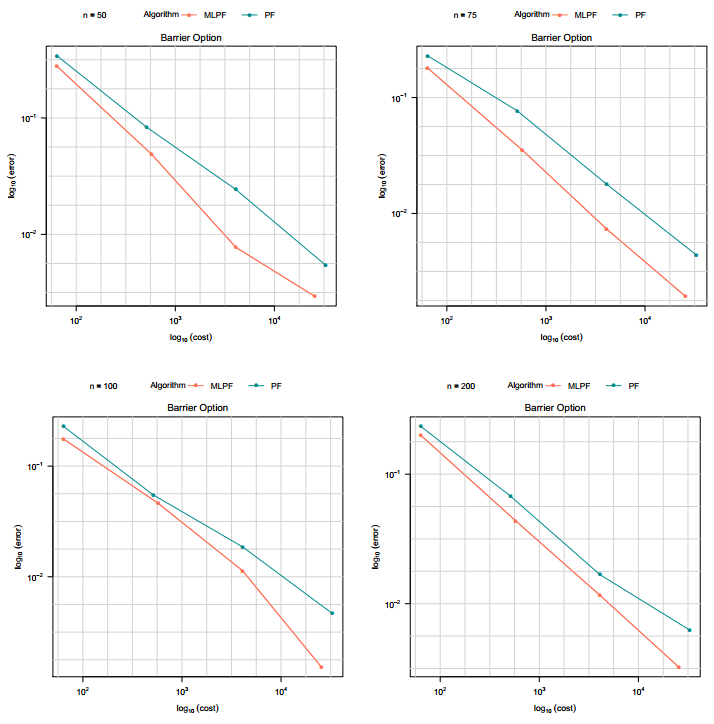
3.2.2. Stochastic volatility model

The underlying asset price follows a system

$\begin{align}\label{op:svmodel} \mathrm{d}S_t& = rS_t\mathrm{d}t+\sigma V_tS_t\mathrm{d}W_t\nonumber\\ \mathrm{d}V_t& = \frac{1}{2}{\bf{\nabla}}\log\pi\left(V_t\right)\mathrm{d}t+\beta\mathrm{d}B_t, \end{align}$

(3.1)

where $\sigma, \beta >0$ are scale parameters, $\pi\left(V_t\right)$ is the probability density chosen to be the Student t-distribution with degrees of freedom $\nu = 100$. $S_t$ is the price.

The following initial values were used in the simulation of Algorithms 1 and 2; $s_0 = 32, v_0 = 1.25$, the strike price $K = 30$ and the scale parameters $\sigma = 0.25, \beta = 0.75$.

The same settings for introducing the potential function in the case of constant volatility is adopted. It provides stable weights with minimal or no resampling at all time points considered. These weights guide particle into regions of interest and prevent the zero payoffs before the terminal time.

The cost-versus-error plots for PF and MLPF are shown in Figure 3 and the corresponding computational rates are given in Table 1. Again, the MLPF outperforms the PF at all different time units considered. For instance, at time point $n = 100$, a fitted linear model of $\log$ cost versus $\log$ MSE has a slope of $-1.628$ and $-1.257$ for the PF and MLPF respectively. It is observed that as the time parameter increases, the error increases slightly but in general, the error rates are consistent with the theoretical findings in the multilevel set-up literature.

---

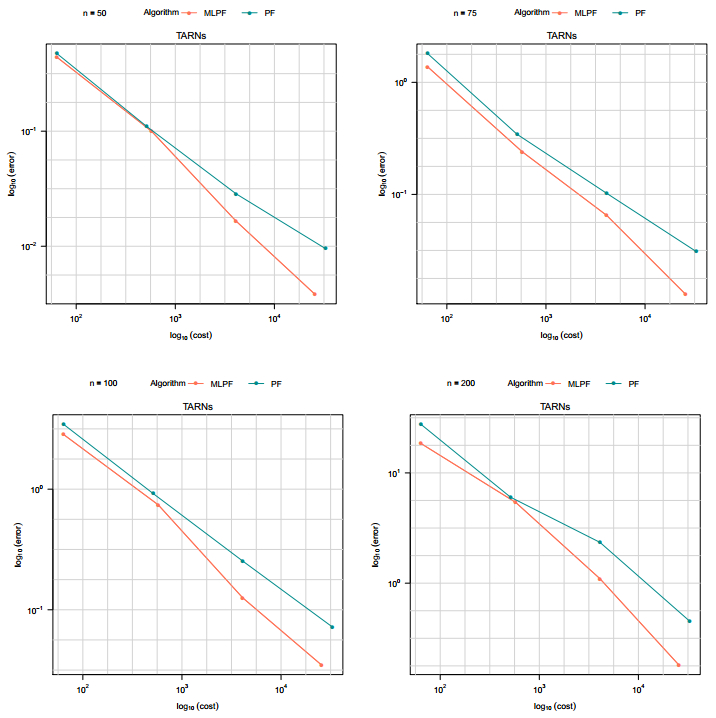
3.3. TARNs

We model the volatility as deterministic and stochastic differential equation. The possible discontinuity of the payoff function of the TARNs is the main challenge in using the standard MC methods. To illustrate our methods, we consider a discontinuous function $f$ of the form

$\begin{align*} f(s)& = \begin{cases} 2(s-60)+5 & \hbox{for} \;s>60, \\ 2(30-s)+5 & \hbox{for}\;s<40, \\ -5 & \hbox{for}\;40\leqslant s\leqslant 60. \end{cases} \end{align*}$

When standard MC is used in this case, most of the samples stay inside the interval $\left(40, 60\right)$, which could possibly lead to a zero payoff for the particle. For example, the contribution for the first ten fixing dates is $-50$. However, there is ocassional escapes of some of the particles within the first ten fixing dates and this contributes values significantly different from $-50$ due to discontinuity of the payoff function. This makes the variance of the MC estimates very high. We use $\tilde{g} = g$ and with an obvious truncation to $n$ variables.

---

3.3.1. Constant volatility

The underlying asset price process follows the same diffusion process with constant volatility as in the case of barrier options constant volatility model example above.

Several constant values of the volatility were used to check the performance of the estimated prices from the two algorithms. We notice that the TARNs favored lower values of volatility compared to the barrier options, we do not show these results here for the same conclusions has been made independently in ^[17]. We are interested in the computational savings gained while using the multilevel set-up over the standard particle filter.

In Figure 4, the error plotted against the computational cost for both multilevel particle filter and standard particle filter can be seen. The following initial values were used; $N_0 = 30, S_0 = 32$, where $N_0$ is the notional value and a constant volatility of $\sigma = 0.015625$. The corresponding computational rates for the four different time units are given in Table 1. For example, a fitted linear model of $\log$ cost against $\log$ MSE at time point $n = 100$ has a slope of $-1.614$ and $-1.326$ for PF and MLPF respectively. The error can be seen as slighlty increasing from left to right as fixing dates increases. It is clear from all the different time points considered that the MLPF has a significant advantage over PF in terms of computational savings.

---

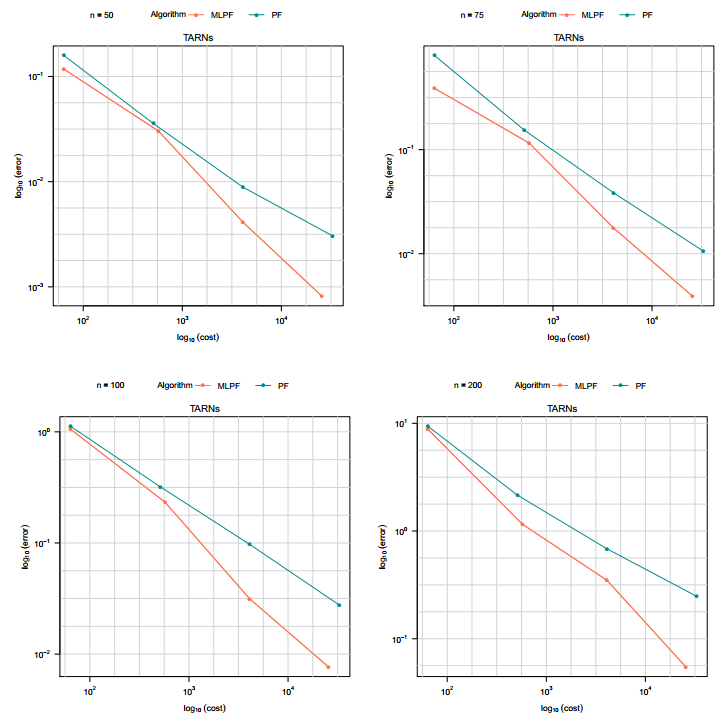
3.3.2. Stochastic Volatility Model

The underlying financial asset follows the same pair of correlated diffusion processes in 3.1 used in the barrier option case with stochastic volatility model. We use the Langevin SDE for the underlying volatility for the pricing of TARNs options.

The error-versus-cost plots on base $10$ logarithmic scales for PF and MLPF at four different time points are shown in the Figure 5. A fitted linear models of $\log$ cost against $\log$ MSE are given in the Table 1. Again the computational superiority of the MLPF over the PF can be seen. For instance, at time point $n = 100$, the fitted linear model of $\log$ cost versus $\log$ MSE has a slope of $-1.614$ and $-1.326$ for PF and MLPF respectively. These results again verify numerically the expected theoretical asymptotic behaviour of computational cost as a function of MSE in ^[14,15].

---

4. Conclusions

In this paper, we have shown how the PF and MLPF can be used to estimate the price of both vanilla and exotic European type options and TARNs. We considered some exotic options, namely knock-out barrier options and TARNs where standard Monte Carlo methods (see e.g. ^[9]) do not work well and particle filtering methods have previously been shown to be useful, see e.g. ^[11,17,18]. Multilevel particle filters are shown to further improve on these standard particle filters. The main idea is a slight algorithmic modifcation (based on importance sampling) which is necessary to devise an efficient simulation strategy for exotic options. The methods presented in this article can potentially be used in finance to price other kinds of path dependent options, e.g. the Asian options and the Greeks as in ^[11].

The methods considered in this article enhance the existing standard SMC methods (see e.g.^[11,17]) when one seek to leverage in an optimal way the nested problems arising from multilevel set-up. The option pricing formula involves essentially estimation of marginal likelihoods and this article have shown the application of these SMC-based methods as in ^[5,15]. It is observed that one underlying financial asset was considered in this article, and it will be of interest to apply the MLPF on basket of underlying financial assets.

---

Acknowledgments

We would like to thank the referee for his/her comments which have substantially improved the paper. AJ was supported by Singapore ministry of education AcRF tier 2 grant R-155-00-161-112 and he is affiliated with the Risk Management Institute, the Center for Quantitative Finance, and the OR & Analytics cluster at NUS. He was also supported by a King Abdullah University of Science and Technology Competitive Research Grant round 4, Ref:2584.

---

Conflict of interest

All authors declare no conflicts of interest in this paper.

---

Supplementary

---

A. Sampling the Coupling

Given the SDEs 2.1 we describe how to sample the Euler discretized coupling. We consider a pair of levels $(l, l-1)$, with $h_l = 2^{-l}$ for any $l\geq 2$. To sample the discretization at level $l$ up to some time $t$ we suppose this induces $k_l$ discretized points. Consider $W(m)\stackrel{i.i.d.}{\sim}\mathcal{N}(0, 1)$ ($\mathcal{N}(0, 1)$ is the standard normal distribution) and independently $B(m)\stackrel{i.i.d.}{\sim}\mathcal{N}(0, 1)$, $m\in\{0, \dots, k_{l}\}$. Then given the point $(v_0, s_0) = (v_0^l, s_0^l) = (v_0^{l-1}, s_0^{l-1})$ (note that one can easily have $(v_0^l, s_0^l)\neq(v_0^{l-1}, s_0^{l-1})$) for the finer discretization, we have the recursion, for $m\in\{0, \dots, k_l\}$

$\begin{align*} S_{m+1}^l & = S_m^l + \alpha(S_m^l)h_l + \beta(S_m^l, V_m^l)\sqrt{h_l} W(m) \\ V_{m+1}^l & = V_m^l + \gamma(V_m^l)h_l + \nu(V_m^l)\sqrt{h_l} B(m). \end{align*}$

For the more coarse trajectory, for $m\in\{0, \dots, k_{l-1}\}$

$\begin{align*} S_{m+1}^{l-1} & = S_m^{l-1} + \alpha(S_m^{l-1})h_{l-1} + \beta(S_m^{l-1}, V_m^{l-1})\sqrt{h_{l-1}}[W(2m)+W(2m+1)] \\ V_{m+1}^{l-1} & = V_m^{l-1} + \gamma(V_m^{l-1})h_{l-1} + \nu(V_m^{l-1})\sqrt{h_{l-1}}[B(2m)+B(2m+1)]. \end{align*}$

---