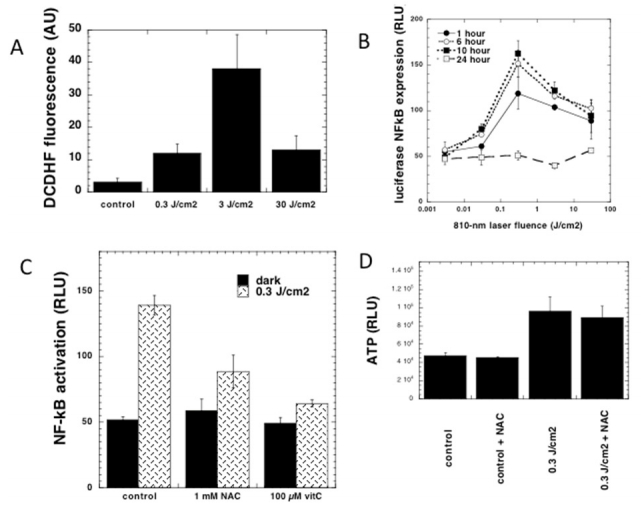
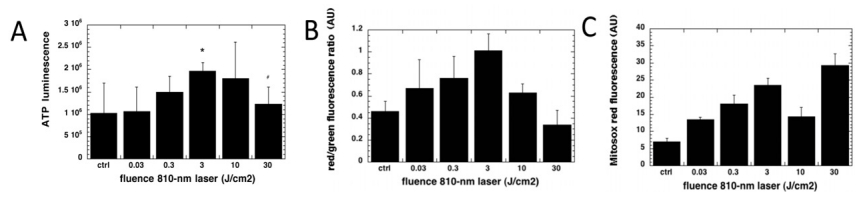
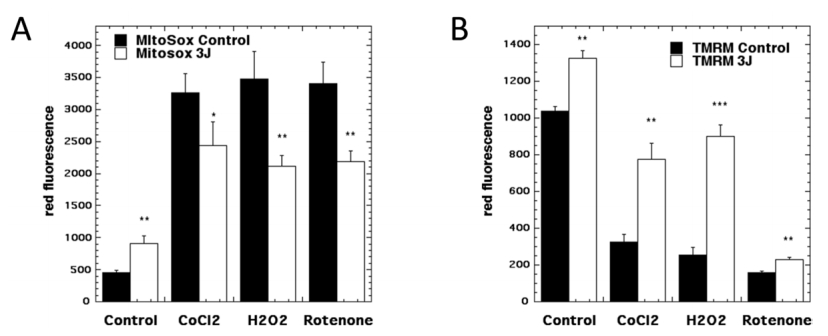
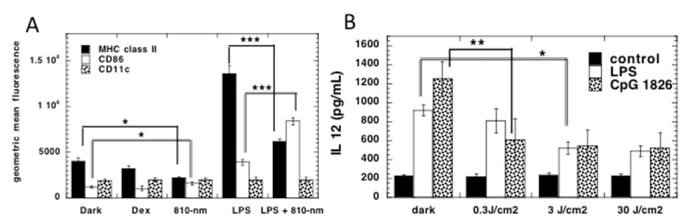
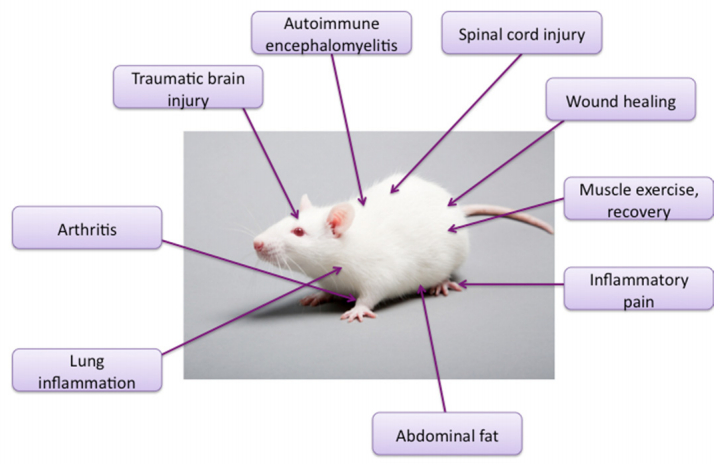
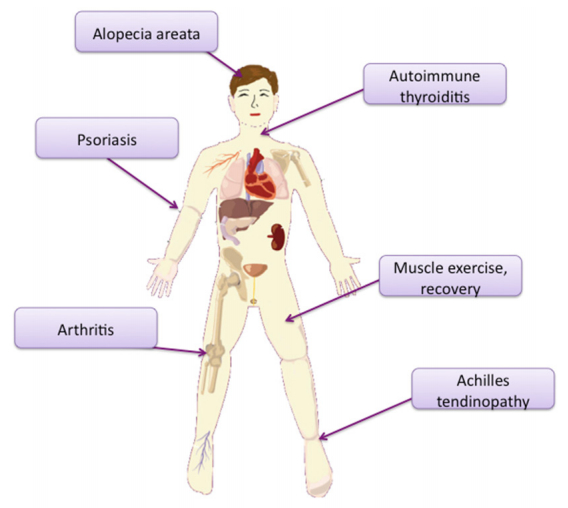
Photobiomodulation (PBM) also known as low-level level laser therapy is the use of red and near-infrared light to stimulate healing, relieve pain, and reduce inflammation. The primary chromophores have been identified as cytochrome c oxidase in mitochondria, and calcium ion channels (possibly mediated by light absorption by opsins). Secondary effects of photon absorption include increases in ATP, a brief burst of reactive oxygen species, an increase in nitric oxide, and modulation of calcium levels. Tertiary effects include activation of a wide range of transcription factors leading to improved cell survival, increased proliferation and migration, and new protein synthesis. There is a pronounced biphasic dose response whereby low levels of light have stimulating effects, while high levels of light have inhibitory effects. It has been found that PBM can produce ROS in normal cells, but when used in oxidatively stressed cells or in animal models of disease, ROS levels are lowered. PBM is able to up-regulate anti-oxidant defenses and reduce oxidative stress. It was shown that PBM can activate NF-kB in normal quiescent cells, however in activated inflammatory cells, inflammatory markers were decreased. One of the most reproducible effects of PBM is an overall reduction in inflammation, which is particularly important for disorders of the joints, traumatic injuries, lung disorders, and in the brain. PBM has been shown to reduce markers of M1 phenotype in activated macrophages. Many reports have shown reductions in reactive nitrogen species and prostaglandins in various animal models. PBM can reduce inflammation in the brain, abdominal fat, wounds, lungs, spinal cord.
1.
Introduction
Due to growing environmental concerns and economic interests, renewable energy continues to gain ground globally compared to fossil fuel-based energy resources [1,2,3,4,5,6,7]. The penetration of renewable resources on the grid has introduced significant changes to the structure, topologies, and architecture of power systems [8,9,10,11]. This is compounded by the growing energy demands in step with the increased ubiquity of electronic technology in the world [12], as well as the rapidly-increasing global population [13,14], and disruptive phenomena such as the COVID-19 pandemic [15,16,17,18]. The implication of this is that modern grids are highly-stressed and more complex to design and operate than ever before [19].
The stability of power systems is largely an electromechanical matter when power systems are dominated by large fossil-fuel-fired electrical generators [20]. These also tend to be easily dispatchable, and the fuel supply can easily be used to control the mechanical variables in these systems, thereby maintaining and changing the electrical variables as desired [21]. However, in power systems that are highly penetrated by renewable energy resources, dispatchability and governor-based control become less easily applied to maintaining the stability of the system [22]. The fact that many renewable sources of energy (such as wind, solar, and biomass) are intermittent and/or not easily predicted is yet another constraint to power system stability design [23,24].
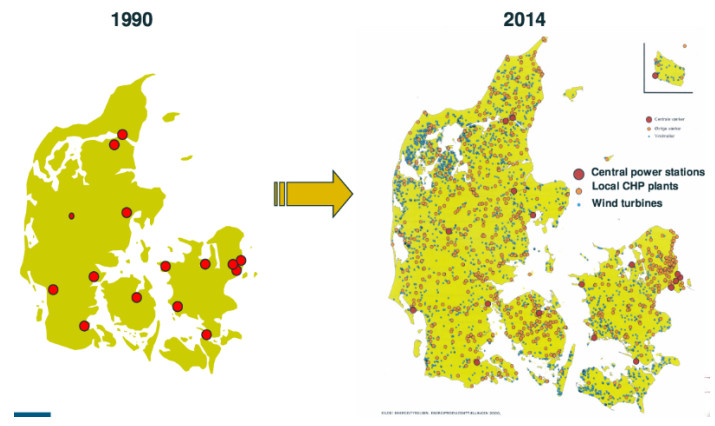
The grids of the modern age tend increasingly towards operating at unprecedented levels of interconnectednesss [25]. Generation installations have become more varied in technological construction and operating principles, which all introduce their implications for the functioning of the power systems [11]. Also, they are now found in larger numbers and smaller capacities than would be possible without the relatively-lower environmental impact of renewable energy infrastructures compared to traditional generation methods [26]. This emergent decentralized paradigm of power systems means that their analyses and operations have grown more complex in recent times [27]. Figure 1 shows the extent of generation decentralization in Denmark (a world leader in renewable energy) between 1990 and 2014, and it can be seen that there are many smaller power plants and wind turbines in the country now compared to a few large power stations in 1990.
With advances in semiconductor electronics and their consumer applications, the proportion of nonlinear loads on the world's electricity grids has increased to significant levels [28]. On the generation side, alternative energy sources, that are not based on the mechanical-to-electrical energy conversion, such as photovoltaic arrays and fuel cells, can be considered nonlinear generators, with the propensity for introducing undesired harmonics and distortion into the system [12]. This proliferation of nonlinearity in the grid is a major factor impacting the stability of power systems in the age of renewables [28].
Another important factor to consider in the stability of power systems with renewable penetration is that, in many cases, the existing transmission systems are designed to wheel power stably at lower levels of loading and to transmit power whose generation is centralized between a few large traditional power stations [30]. However, the nature of renewable energy sources, whose capacities usually make them more amenable to implementation in smaller units, usually favours a relatively-large number of relatively-small power plants on the grid [26]. The contrapuntal challenge of harmonizing the centralized, mostly unidirectional-power-flow nature of the existing grid with the decentralized, multidirectional-power-flow nature of distributed energy resources arises in places where the power grids have not been designed with substantial future modifications and expansions in mind [31].
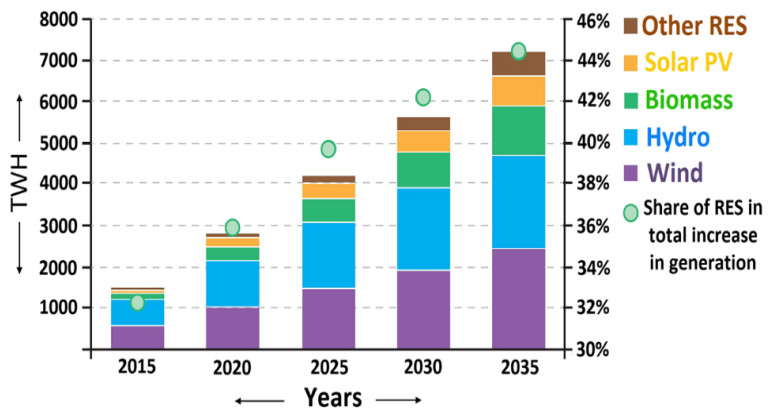
The design and operational challenges, as well as the constraints presented by the recent trends in power system development, are quite different from the well-known ones posed by traditional power systems that are mainly fed by massive impounded-hydropower and thermal power plants [32]. As a result of these factors and other localized reasons in various locations, traditional approaches to power system operation are becoming less suited to serve the complexities of modern evolving power systems with these increased quantitative and qualitative source, transmission, and load requirements being added to the grid over time [33,34]. Figure 2 shows the growth of renewable energy usage in electricity generation in the world in five-year periods from 2015 up to 2020 and gives projections up to 2035. It is evident from Figure 2 that solar photovoltaic (PV) and other power-electronics-based technologies for generating electricity are becoming more important over time.
In addition to Section 1, which is concluded in this paragraph, Section 2 of this paper discusses renewable energy, distributed generation, and establishes the concept of microgrids in the light of the attention it receives in recent energy research. Section 3 explores microgrid applications by classification. Section 4 examines recent developments, topological innovations, and evolution of physical (spatial) paradigms in the electricity generation technology used in DG systems, while Section 5 presents recommendations of the authors and concludes this article.
2.
Renewable energy and distributed generation
Renewable energy is the energy that is harnessed from resources that are perennial enough to be considered practically inexhaustible [35]. Solar, wind, hydropower, biomass, and tidal energy are examples of renewable energy because no matter how intensely they are used, they are replenished by the forces of nature [36]. Renewable energy is usually clean energy and green energy, and the definitions of those terms usually overlap significantly. In the light of global warming, there have been concerted efforts to reduce carbon footprints by stepping down the combustion of fossil fuels for electricity generation and transportation [37]. As a result of this, renewable energy has gained more research, investment and development priority over non-renewable energy in the past few decades.
Renewable technologies such as solar PV, solar thermal, and small hydropower have low pollution contributions in their deployment locations [38]. Due to this, they are frequently installed in close proximity to the electricity consumers. This creates a scenario that differs from the traditional setting in which power generation happens in separate locations from its consumption and features a mix of loads and sources in the distribution networks. This kind of grid structure is known as a Distributed Generation and the decentralized energy resources as Distributed Energy Resources [39].
2.1. Microgrid
A microgrid is a power system that contains its sources and loads within a small area, with the ability to operate in standalone mode, or while connected to the larger power system or macro-grid [40]. Microgrids usually integrate multiple alternative energy sources such as solar photovoltaic, wind turbines, and energy storage systems, sometimes with conventional sources such as diesel generators, to serve local loads [41,42]. They also sometimes exchange power with the macro-grid or other microgrids.
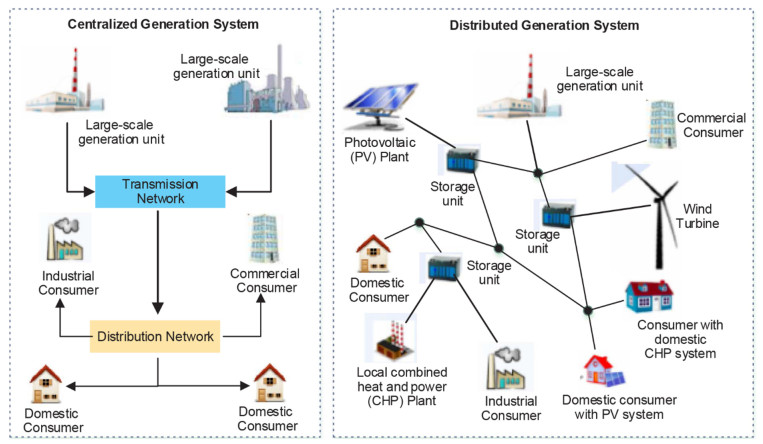
The sources that are connected to a microgrid are known as Distributed Generation Units (DGUs) [32]. Decentralization of electricity generation, when properly designed, can enhance system overall reliability because the power system has more generators, and the failure of a DGU is, in theory, not as catastrophic as the failure of a big generator in a traditional system. Figure 3 shows the differences between the traditional and distributed generation paradigms.
However, in practice, the interactions of the many various sources and loads in the system are more likely to lead to some destabilizing event in the microgrid, potentially hurting the quality of service [44]. Thus, the presence of many generation nodes (powered by intermittent resources) on a grid, with the potential for disconnection and reconnection to other power systems presents a complex grid structure in which special care must be taken to ensure stability of the system. This engineering problem has been widely identified in research as requiring the design of novel control strategies and power dispatch methods to allow for seamless integration and utilization of energy storage systems, especially when the renewable penetration level in the microgrid is very high [28,45,46,47,48,49,50].
In most microgrids, the primary source of energy is not one massive synchronous generator, but usually asynchronous machines and semiconductor-based electricity generation technologies. As such, traditional droop control used for machine-only power systems is mostly found to be inadequate [51,52,53]. The control strategies that are developed to operate these kinds of hybrid power systems frequently contribute to stability issues faced in microgrids, which has attracted significant research investigations into their effects on power system stability [54,55].
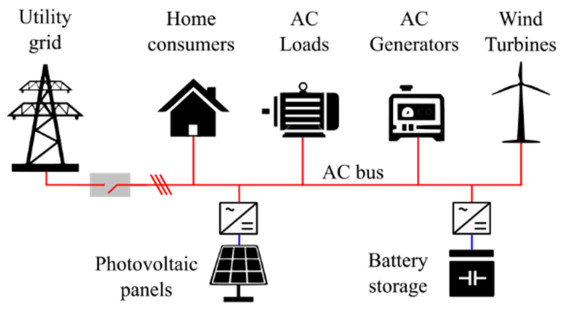
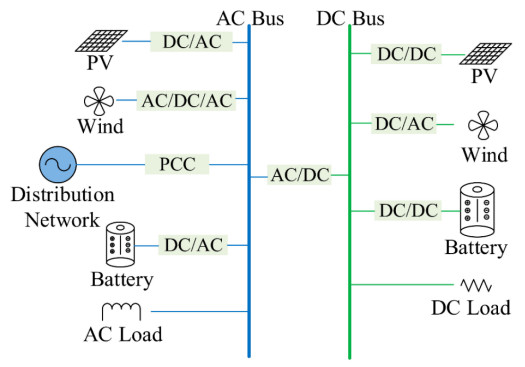
It is important to note that microgrids can be AC-based like traditional power systems [56], or they can be DC-based depending on the known nature of the loads to be used on them [57,58]. This is possible because long-distance transmission which usually calls for voltage level transformation (which is the main advantage of AC) is not always needed in microgrids. Also, where DC voltage transformation is needed, due to the smaller scale of the grid, power electronic converters of sufficient capacity are likely to be furnishable as opposed to when the volume of power to be handled is very large, such as a national grid. Figure 4 shows the typical structure of an AC microgrid.
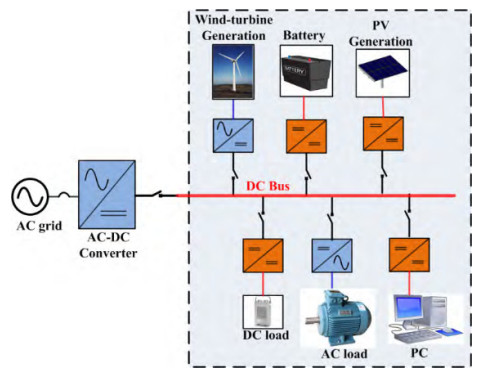
Furthermore, a single microgrid can have both AC and DC buses and sections [60,61]. The choice of any of these configurations tends to depend on local requirements, constraints, and existing infrastructure. However, it is worth noting that distributed generation is not always the optimal way of deploying renewable resources, as there are cases in which the abundance of the renewable resource to be harnessed is found at significantly long distances from the load centres [62]. For example, offshore renewable energy such as that captured by offshore wind turbines needs to be transmitted to the load centres, possibly over long distances. Figure 5 shows the typical structure of a DC microgrid while Figure 6 shows the typical components and load distribution on an AC-DC hybrid microgrid.
In addition to this, the variety of settings and locations in which microgrids may be found tend to present special performance requirements and special opportunities for enhanced operation [63]. For example, for commercial microgrids having only photovoltaic generation and chemical storage, the operation of the microgrid is likely to prominently feature a DC link, whereby much of the controls and power processing are implemented before the DC-AC conversion stage in the microgrid [64]. Furthermore, if the users of such a microgrid have a pool of electric vehicles and have a predictable schedule of both electric vehicle usage and building energy consumption, the energy usage patterns can be anticipated and microgrid operation can be optimized with a dispatch strategy that leverages the presence of the vehicles [65].
On the other hand, in a larger industrial microgrid that contains multiple rotating generators and heavy-duty motors, droop control and active-vs-reactive power allocation [56], and mechanical energy storage [66] may feature prominently in the operation of the system, and most of the important dynamics in the system will be found on its AC side [67]. Also, the role of big data in microgrid operation has gained research attention in tandem with demand-side management, both of which have emerged due to the development of wide-area monitoring and automation technology such as phasor measurement units (PMUs) [68,69,70]. Decentralized control methodologies for microgrids, as well as optimal energy management [71], including specialized digital architectures for intelligent "smart" microgrids [72], are also the subjects of research efforts.
3.
Microgrid applications
Microgrids emerged as autonomous integrated power systems with load, distributed generation, and the often-critical element of energy storage [73]. The presence of distributed generation units (generation close to the load) is what majorly sets microgrids apart from traditional grids. Energy storage is important for reducing the impact of the fact that renewable resources, on which many DGUs are usually based, are mostly intermittent [74]. For example, solar energy is only available in useful quantities during the daytime but not at night. Therefore, a microgrid which serves a community and is largely composed of photovoltaic generators is likely to experience power shortages at night unless the excess energy harnessed during the day can be stored for nocturnal utilization.
3.1. Evolution of microgrid classifications
The purposes for which microgrids are developed vary. Military microgrids are built to cater to the requirements of military bases, boost energy supply for power-intensive military operations and eliminate dependence on the grid [77]. Military microgrids are also made to be physically and digitally immune to attacks that may put down the civilian grids [78]. Renewable-based military microgrids eliminate the reliance on external fuel supply which could be a vulnerable link in the chain of operations. This is because transportation equipment could be attacked at any point on a long supply route, and fuel transport is always inherently risky [79].
Commercial microgrids, on the other hand, are developed to help in optimizing the financial profitability of an enterprise and usually operate in grid-connected mode [80]. The establishment of this kind of microgrid is to optimize demand and costs. For example, the microgrid may be designed to use external power when energy is cheap while optimally switching to low-cost internal generation as the price of energy rises [81]. Commercial microgrids also alleviate the risks that could be incurred due to power outages from the large-scale utilities. An advantage of commercial microgrids is that they can be constructed faster than new power plants in situations where grid access is not yet well-established or problematic [82].
Community microgrids are different from commercial microgrids in that they are established to shore up the quality of service and complement the functioning of electric utility companies in already-existing localities [40]. A community microgrid may be an aggregation of houses, some of which have solar photovoltaic arrays installed on their roofs, using the energy for individual purposes, and sending the excess to the grid to be used by other houses, or to the utility [36]. The excess energy could also be stored for the night. There may also be electric vehicle charging functions in the microgrid [83]. This kind of microgrid is a community enterprise and thus can be very complex to optimize in any particular way. Determination of the optimum mix of storage and generation infrastructure in community microgrids is highly location-specific [84,85].
Campus microgrids are developed in institutions such as universities, industries, medical establishments, and technology hubs [80]. They are usually established due to elevated requirements for uninterruptible power supply and special loads [40]. Unlike community microgrids, these can be designed with fewer uncertainties to consider and a centralized layer of control is also easier to implement on campus microgrids [86]. They help the institutions to optimize their energy costs [63]. Also, campus microgrids provide good study and test locations for novel designs and academic research on power systems to any educational institution that has them.
Remote microgrids are mostly operated off-grid (in standalone/islanded mode) in locations where utility access is unavailable or unprofitable for local reasons (such as a disproportionately high cost of building and maintaining the transmission lines) [87]. Usually, where remote microgrids are found, the alternatives are diesel and propane generators [88]. Establishing microgrids in these areas enables the incorporation of renewable resources as opposed to relying totally on fossil-fuel generators. This not only aims to reduce the carbon footprint of such power systems but also cut down on fuel-related running costs.
Usually, there is a choice of relying completely on renewable energy in an islanded microgrid, but this will require a considerable amount of energy storage capacity for there to be any dispatchability of power on the microgrid. However, this kind of system would have no running costs associated with fueling. It would also be lacking in rotational inertia (except for hydropower) and its stability could be more complex to design for, especially given a high proportion of inverter-sourced power [89].
On the other hand, a system with a high proportion of dispatchable fossil-fuel generators running on diesel or propane would need less or no energy storage but would have significant fuel costs and emissions. Such a system is also likely to be more robust than a purely renewable-based system without needing complex arrangements for its stability [90]. This presents a common optimization problem that project financiers and engineers face in standalone microgrid development. The optimal solution to this kind of problem depends on factors such as renewable energy resources, environmental impact, local regulations, financial constraints, project scale, and government policies. Also, it is usually more costly to develop and operate a self-sufficient standalone system than a grid-reliant system [91].
3.2. Management of load uncertainty in microgrids
Due to the desired independence of microgrids from the grid, which is partial in grid-connected microgrids and total in standalone microgrids, a microgrid needs to be able to supply its own energy needs. Hence, load uncertainties must be accounted for in the design and operation of the microgrid, especially in systems that are not grid-tied, as such systems have no external reserves to draw on in case of a local shortage [92]. The most direct way of managing load uncertainty is by the addition of energy storage facilities such as Battery Energy Storage Systems (BESS) and Flywheel Energy Storage Systems (FESS) to the microgrid [93,94]. These have the purpose of storing excess energy when there is a surplus of generation and ideally supplying the deficit when there is a power shortage in the system [81]. Energy Storage Systems (ESSs) are very important for the continuity of power supply in microgrids that rely solely on intermittent resources, especially solar energy, for generation.
In AC microgrids, a number of techniques have been investigated in managing the load uncertainty of microgrid networks. Optimal control algorithms have been investigated such as a combination of Fractional Order Proportional-Integral-Derivative (FOPID) control with the Sine-Cosine Algorithm (SCA) [95]. In this technique, thermal loads such as heat pumps, as well as electric vehicles, are selected for their relative ease of control and for their contribution to load frequency control. Load tends to impact frequency in sensitive networks such as microgrids [35], and sometimes, this is also regulated using a strategy based on virtual frequency control that emulates the dynamic behaviour of large synchronous generators [96]. Online distributed algorithms that use the on-load tap changers to pre-empt voltage violations based on renewable resource prediction have also been developed [97].
Load coordination involves cooperative management of the system participants, in which participants seek to optimize microgrid dynamics to favour all parties in certain respects [98], while negotiation involves the resolution of conflicting situations in which system participants may not have the same objectives (such as a situation in which the utility wants to maximize generation and the consumers want to minimize consumption) [99]. Both demand negotiation coordination and demand negotiation are techniques for achieving demand-side flexibility.
In DC microgrids, numerous techniques for load and generation coordination have been investigated [100]. Because solar PV naturally generates power in DC form, it is particularly amenable to use in DC microgrids. However, the reliance on ESSs to maintain smooth operation can involve exceeding the charge and limits of the storage especially when more than one ESS is used. To mitigate this, fuzzy-logic-based control has been used [101]. This, however, did not solve the issue of sudden charging and discharging degrading the system components more rapidly than expected, and so, ultracapacitors have been incorporated into such fuzzy-logic controlled systems with promising levels of success, especially in battery-ultracapacitor DC microgrids [102]. Another method which is used in DC microgrids is the bus signalling method in which the states of charge of the ESSs and their high and low thresholds are communicated across the DC bus utilizing each converter's threshold voltage [103,104]. This method reduces transient disturbances in multi-mode microgrids during the transitions from one mode to another [105]. Droop control is also adapted to islanded DC microgrids combined with maximum power point tracking (MPPT) that is regulated by DC bus voltage to achieve generator-storage coordination which helps in meeting load requirements under uncertainty [105].
In hybrid (AC-DC) microgrids, many of the techniques from the other microgrid topologies are adapted. Furthermore, separate strategies are used in the AC and DC sub-microgrids that make up the hybrid microgrid. Sometimes, in a master-slave control setting, a source whose power can be adjusted is selected as the master control power supply while real and reactive power control is used together with voltage-frequency control to maintain stable operation of the microgrid under varying load conditions [106]. In other cases, a peer-to-peer control is implemented, such that the system participants have the same status and plug-and-play functioning is achieved. Sometimes, the two approaches are implemented in different parts or on different levels in a microgrid [107]. Price-based demand response has been used on microgrids of different topologies [108].
4.
Recent developments in generation in microgrids
Microgrids are small-scale, localized power systems. As such, they are not physically constrained to have only renewable generation connected. Rather, purely fossil-fuel-based microgrids also exist. Coal-based generation is largely unacceptable for development in populated areas due to its high and visible impact on its immediate environment, as well as the fact that it is less resource-efficient on the scales likely to be found in a microgrid [109]. However, diesel and natural gas are less obtrusive in their application, and microgrids based on them exist [110]. However, the microgrid concept is to localize not only power distribution but also its generation and transmission [81].
For the most part, fuels such as diesel and natural gas have to be transported from locations far away from the microgrid [77]. In many cases, these fuels need to be imported from other countries. In examples like this, even if generation is done within a defined area, there are long distances in the energy supply chain that transcend the area serviced by the power system. This can be said to defeat one of the main purposes of microgrids: shortening the energy supply chain. However, when renewable sources are used on a microgrid system, such a system relies on local natural energy resources which are self-replenishing (i.e., free of cost and transportation) and also mostly nonpolluting [77]. This is why the benefits of the microgrid are most effectively expressed in a system that integrates renewable generation, and why research on microgrids has mostly explored this kind of system.
The installed capacity of a microgrid can be a few kilowatts, up to a few megawatts [111]. Apart from providing dispatchability of power, the combustion-based generators provide mechanical inertia in concert with any hydropower generators in the system which boosts its stability [42]. For the reason of the complexity of control and stability concerns, it is not always desired to have a system completely composed of inverter-based sources [112]. As a result of this, it is quite common to find diesel and natural gas generators incorporated as DGUs in otherwise renewable-based microgrids. However, solar PV and wind energy conversion systems (WECS) are the predominant renewable technologies used for generation in microgrids [74].
4.1. Evolution of chemical manufacturing processes in solar cells
Solar PV arrays harness the energy of the sun during the day and work best in clear skies and cool temperatures [36]. Preliminary research into moonlight utilization for photovoltaics has shown the moon does not have enough luminous intensity to produce practical amounts of solar power using existing technologies [113]. Since the development of monocrystalline and polycrystalline silicon crystals for PV cells, other technologies have been developed and some are still in the research and development pipeline [114]. Thus, PV cell technology has become more diverse and manufacturers have furnished a variety of options over time.
Hybrid photovoltaic cells are formed by combining crystalline and non-crystalline silicon and are quite complex to manufacture as a result [115]. However, they have high performance-to-cost ratios and are competitively efficient at high temperatures and with reduced light incidence. Carbon nanotube cells are formed using hexagonal lattice carbon in conjunction with silicon to create transparent conductors that can source high currents [115]. Competitive efficiencies have been reported, and it has been suggested that their efficiency has the potential to eventually surpass that of the state-of-the-art silicon PV modules, which would increase the output of PV arrays and DGUs.
Dye-sensitised solar cells and multi-junction solar cells have been explored [116]. These technologies use the band gaps of different semiconductor materials in different composite topologies to increase the amount of energy that can be extracted by a single module [116]. The use of organic dyes and stacking of multiple solar cells is being researched. In addition to this, organic solar cells that are made out of organic polymers have been demonstrated [114]. However, their efficiencies have not been competitive and alternative research directions such as the use of liquid crystal semiconductors in these organic cells. Also, it has been found that the cells are degraded by prolonged exposure to sunlight [114].
4.2. Evolution of optimal deployment strategies
By their nature, PV arrays depend on covering areas of the earth's surface to capture incident light. This sometimes leads to land-use issues especially in microgrid applications because land is very valuable and finite [114]. For this reason, many approaches have been developed to optimize land use in solar PV schemes.
4.2.1. Bifacial solar cells
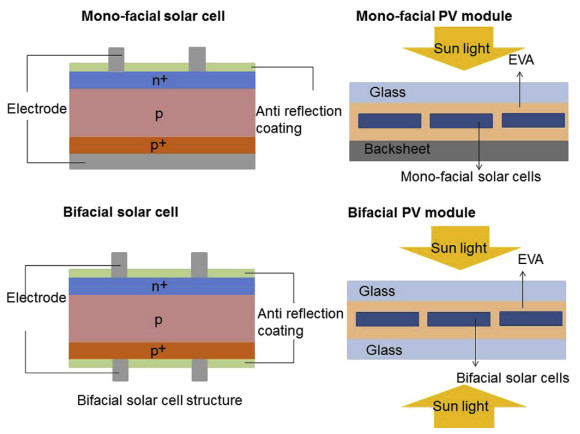
Bifacial solar cells have been the subject of research and development due to their ability to absorb photonic energy from both sides [117]. The performance of bifacial PV arrays depends on factors such as orientation, spacing, elevation, soiling, and shading. Also, the efficiency depends on the reflectiveness of the ground [118]. The use of bifacial panels, as opposed to monofacial ones, can increase PV array output [119]. However, outside the laboratories and academia, the pricing of true bifacial modules and the misleading trademarking of back-to-back monofacial modules as true bifacial modules has occasionally proved to be detrimental to massive adoption in developing countries. Figure 7 shows the difference in construction between monofacial and bifacial PV modules, with glass and anti-reflective coating being applied on both sides of the module.
4.2.2. Floating photovoltaic
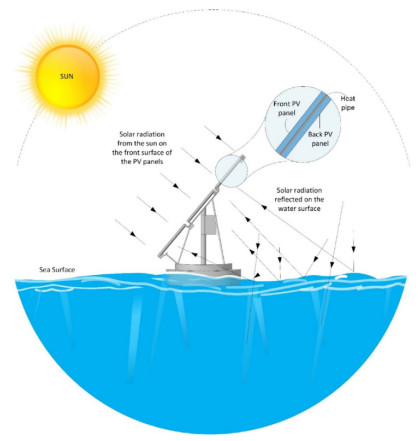
Floating/off-shore photovoltaic applications use the area over water bodies as opposed to the area over land. This can be on rivers, lakes, or the seas [121]. Offshore PV is considered inherently risky compared to land-based PV systems, and fuzzy logic and analytic network process methods have been used by researchers for the risk analysis of such projects [122,123]. A model-based simulation of floating PV systems showed that, at sea, the relative output can be significantly higher than that of equivalent land-based systems, providing an additional incentive for siting PV systems offshore [124]. Other researchers have found that bifacial PV modules employed in floating applications can harness reflected energy regardless of the presence of waves on the water and that the orientation of the PV modules matters [118]. The prospect of improvement by the inclusion of axis tracking on the efficiency of such systems looks promising. However, cost analysis has not been conducted for such an arrangement. Figure 8 shows how a floating photovoltaic system can use bifacial modules to harvest both direct incident and reflected light for electricity generation while floating on water.
4.2.3. Cable pooling
Cable pooling is the combination of offshore wind and solar resources for optimal cable utilization. The cables that are used to transmit power onshore from the generation points are frequently underutilized when the generation from one source is low [125]. For example, solar energy is unavailable at night, meaning that the duty cycle of a PV-only offshore transmission cable will be limited to daylight hours. On the other hand, wind power varies throughout the day and can be low at times. Thus, solar PV can be deployed alongside wind in offshore installations so that more value can be gotten out of a single cable system. This makes the installations more profitable per unit capital, provided that the optimization is properly done.
The higher efficiencies associated with offshore photovoltaics are largely due to the cooling environment of the ocean, the reduced presence of dust for soiling, and the virtual absence of obstacles for panel shading [126]. Considering that many population centres are situated close to the world's coasts, it is promising to consider a microgrid paradigm in which floating generation resources supply densely-populated coastal cities with electricity. However, many factors will have to be considered, such as the impact on the marine ecosystems and other purposes of use of the water bodies.
4.2.4. Solar trees
Solar PV trees also provide a way of improving the use of land for PV by taking advantage of the third dimension, height [127]. The panels are mounted on an erect structure on branches analogous to the leaves on plants. The optimal spacing of the PV modules and panels is derived by mimicking phyllotaxy, which is the biological process by which plants optimize their leaf placement for efficient light-harvesting and photosynthesis [127,128]. It has also been demonstrated that this kind of arrangement is useful for harvesting wind power by the provision of mobility to allow parts of it to function as a wind turbine [129]. Due to its customizable aesthetics, the solar PV tree is promising as an unobtrusive way of deploying photovoltaic panels to also serve decorative purposes [130]. Figure 9 shows an example of a solar tree deployed in an urban space, showing how the generation of electricity may be achieved using unobtrusively designed solar arrays in form of trees.
4.2.5. Agrophotovoltaics
Agrophotovoltaic is the use of the same area of land for agriculture and solar PV generation purposes. This directly mitigates the conflict between solar PV and the most critical application of land, which is agriculture [131]. Some plants are known to benefit from having shelter from direct sunlight or reduced exposure to sunlight [132]. On farms with these kinds of shade-resistant plants, crop yields can be increased by the strategic mounting of photovoltaic arrays such that the temperature and lighting conditions favourable for crop yield are achieved in addition to generating electricity [133].
The choice to go with agrophotovoltaic arrangements is largely dependent on financial factors, as it is usually used to retrofit existing farms and must be considered profitable to the farmer [134]. Agrophotovoltaics are found to be promising in desert agriculture where the water lost by plants is reduced due to shelter provided by solar panels so that irrigation becomes more efficient [133]. In agrophotovoltaic sites, there is the need to optimize the balance between the amount of light that is used for crop growth and the amount that is used for the generation of electricity. Applications of solar tracking in such systems have shown that it improves both the PV yield and the light available to crops as compared to fixed-module arrangements [133]. It has also been found that the density (spacing) of the panels plays a major role in controlling the light-sharing on the site even with solar-axis tracking implemented [132]. Figure 10 shows the agrophotovoltaic paradigm.
4.3. Hydrogen in microgrids
Hydrogen is traditionally used in industries for the production of important materials such as steel, ammonia, and methanol [135]. In addition to this, it has gained prominence as a major material used in the operation of fuel cells, and hydrogen-based fuels are emerging as a promising low-carbon alternative to fossil fuels in the long-distance transportation industry [41]. In power generation, in particular, hydrogen is an important energy carrier as it can store renewable-generated electricity, especially from solar PV, which has made it gain an increasing presence in microgrids [136].
Hydrogen is generated mainly by thermal processes (for natural gas), or by electrolysis (from water). Traditionally, the thermal process is preferred and responsible for almost all of the global hydrogen production [135]. However, in recent times, with the production of surplus electricity by some renewable energy installations, the electrolytic production of hydrogen as an energy carrier is increasingly promising. In this use case, water is hydrolyzed by using the energy from, say, photovoltaic arrays, and then the hydrogen can be consumed in a fuel cell to produce electrical energy at a later time. This use case is referred to as "green hydrogen" and research is ongoing on ways to optimize hydrogen utilization in microgrids [137].
5.
Conclusions
Apart from power flow optimization and control algorithms, which are usually completely dependent on grid structure and heavily involved in terms of mathematics for the engineer, several novel applications and concepts are emerging in DG which are important for the engineer to know about. It is beneficial to have a solid grounding in the trends that concern the physical implementation of DG hardware/infrastructure to inform the directions of research with a perspective that seeks to improve the real-life microgrid. A selection of these recent design paradigms in multiple levels of the microgrid (from device to system level) provides insight into promising future trends in the qualitative aspects of the physical implementation of microgrids, especially concerning the use of spatial resources. Also, this article has seemingly focused more on photovoltaics, not by design, but because there is less variety in the implementation of wind energy in DG systems beyond the stereotypical wind farms and standalone turbines, because wind energy infrastructure is not as easily fitted near humans and livestock compared to solar energy, and requires more dedicated mechanical supports than solar panels which can be mounted on existing structures. This presents a wide research opportunity for the future. The use of distributed algorithms allowing for plug-and-play operation of the microgrid in more scenarios should also be investigated for further refinement. In addition, the protection of components in hybrid microgrids is an area of research which could prove critical going forward.
Acknowledgement
The authors want to thank the management of Landmark University Omu-Aran in Kwara state for the provision of enabling environment to carry out the work and for the provision of funds.
Conflict of interest
There is no conflict of interest from all the authors.









 DownLoad:
DownLoad: