Nomenclature

---

1. Introduction

Nowadays, renewable energy sources (RESs) are catching a lot of attention toward a low-carbon society without using fossil fuels. Moreover, distributed generators (DGs) using RESs are installed for self-sufficiency of electric power energy in distribution systems ^[1]. Huge amount of photovoltaic (PV) generator mainly has been introduced because of simple structure and easy maintenance. Wind turbine generator (WG) can generate power both in the day and night ^[2]. However, the output power of RES includes uncertainty ^[3,4]. As results, voltage deviation and reverse power flow have occurred by high penetration of DGs using RES ^[5,6,7,8]. A large blackout is caused by voltage deviation and reverse power flow. The voltage deviation problem has solved by using the method of reactive power control by static var compensator (SVC) ^[6,9,10]. On the other hand, problem of reverse power flow has been solved by absorbing power using large capacity battery energy storage system (BESS) at the interconnection point of power system ^{[11,12,13,14]}.

Technically, the above solution methods have been found to be adequate for the described problems. However, the huge capital cost for the introduction of these control devices cannot be overlooked. Therefore, a method of reactive power control from PV inverter installed on the customer side is proposed to reduce the cost of additional SVC device ^[15]. Also, a reactive power incentive method was proposed to promote cooperative support from the customers ^[12]. DisCo provides reactive power incentive for their clients in order to reduce the need for introduction of additional control devices ^[16].

While it is becoming a common practice to provide incentive to customer based on reactive power control for voltage quality improvement. A little attention has been given to active power control incentive approach. Active power is easily affected by sale or market contract of electricity ^[17], so to adapt incentive system based on active power consumption has not attracted much attention. Recently, methods of load-shedding and demand response (DR), using real-time pricing (RTP) for peak cut of demand and load leveling, respectively, have been proposed ^[18,19,20]. Load shedding method is an important concept; but, the customers suffer severe hardship when the needed electricity supply is suppressed during the peak hour or busy season. In addition, it becomes a problem because the effect of DR to these short term measures are small, since the short term elasticity price index by RTP has very little value ^[21]. Electricity is a necessary form of energy for daily activities, so it is called an inelastic good. As a result of this, the DR of electricity consumption cannot be adequately controlled by RTP.

Therefore, in this paper an incentive system of DR instead of RTP system has been proposed. This method reveals how utility company can coordinate efficient electric energy trading that will enhance the stability of the power system. In this approach, the incentive is offered separately from the electricity consumption tariff. In other words, it is not necessary for all customers to obey this incentive system, since the conventional pricing system will not be changed. The consumers who want to receive incentive may shift part of their load consumptions off the normal peak periods, and this will possibly help to achieve a better power quality, reduction of the power losses within the system, and the cost of introducing more control devices could be reduced ^[22].

In the liberalized electricity market, both the DisCos and the consumers are concerned with how to maximize their individual profit, with little consideration for the other players. While the consumers' main concern is how to enjoy maximum satisfaction at a reduced cost of service, the DisCos are concerned about providing high quality power supply, achieving few distribution losses sometimes by limiting the load demand from the consumer end. This is often achieved through load shedding and whenever this is done, the satisfaction levels of the customers reduce. Generally, it can be seen that there is a conflict of interest between the DisCos and the consumers, especially during the peak period of load demand; and it is difficult to satisfy all goals of the players at the same time, because those goals sometimes contradict each other in the trade-off relationship ^[23,24]. Thus, a two-level hierarchical optimization approach is applied to the system being considered in this paper as explained below:

First level: DisCo use daily load and weather forecasting to determine some optimal scheduling strategies that will bring about cost reduction and improved power quality. Using these scheduling strategies, DisCos make offer to the customers for cooperative operation of the power system. In order to ensure participation from the customer, DisCo provides incentive options using suitable DR menus.

Second level: Willing customers consider the offer, and their preferred schedule strategies are determined by evaluating their demand priority, the provided incentive from the DisCos and their level of tolerable dissatisfaction. Then, the system returns the preferred schedule of each customer to the DisCos for planning the system operation.

Finally, the schedule strategy that produces optimal profits for both sides, as created by the two-level optimization approach, is implemented by the DisCo for individual customer based on the customer's preference.

---

1.1. Contribution of this paper

The DisCo and its customers can gain profits by using the proposed active and reactive power incentive method rather than the conventional method. This method provides a cooperative control of the distribution system instead of the marginalize control provided by the conventional method. The proposed method is different compared to the pricing-based menu of the conventional DR, and can also be distinguished from the incentive-based menu of interruptible loads (ILs) or some other incentive-based menus ^[25]. Customers can buy or sell active power for use in a management approach which is different from common unilateral contracts prevalent in DR. It means that these customers can receive as many incentive profits as possible without being forced to make load consumption changes that can significantly affect their life style. In order to ensure mutual benefits, two-level optimization approach that has been earlier discussed is applied and the effectiveness is verified by simulation results. At their end, the DisCos can achieve reduction in the required capacity of BESSs, required numbers of SVC installations and the amount of distribution losses ^[12], while the customers also make profits by participating in energy management through the active and reactive power control incentives that are made available by the DisCos.

The remaining sections of this paper are organized as follow; Section 2 explained the problems associated with the high penetration of DGs in the smart distribution system, section 3 provided an overview of energy management strategies in electricity market, section 4 described the problem formulation and the adopted two-level optimization solution approach. Simulation results and conclusion were given in section 5 and 6 respectively.

---

2. Problem of the Smart Grid System

---

2.1. Voltage deviation

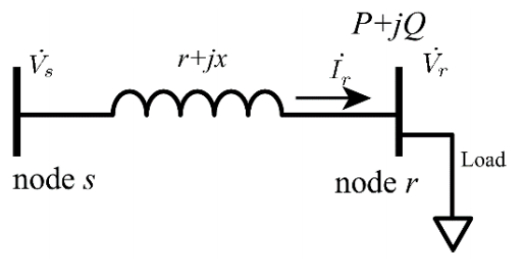
It is expected that an amount of 10% to 50% of RESs capacity are connected to distribution network that has high penetration of DGs. As a result, the problems associated with voltage fluctuation such as voltage drops or voltage deviation from upper limit are inevitable in such a network. Generally, the following equations of Figure 1 explained the effectiveness of using reactive power for controlling the terminal voltage.

$P + jQ = {{\dot V}_r} \times {{\dot I}_{{r^*}}} = {{\dot V}_r} \times {\left( {\frac{{{{\dot V}_s} - {{\dot V}_r}}}{{r + jx}}} \right)^*}$

(1)

$\left( {P + jQ} \right){\left( {r + jx} \right)^*} = \left| {{V_r}} \right|\left( {cos{\theta _r} + jcos{\theta _r}} \right){\left\{ {\left| {{V_s}} \right|\left( {cos{\theta _s} + jcos{\theta _s}} \right) - \left| {{V_r}} \right|\left( {cos{\theta _r} + jcos{\theta _r}} \right)} \right\}^*}$

(2)

$\left( {rP + xQ} \right) + j\left( {rQ - xP} \right) = \left( {VsVrcos\left( {\theta s - \theta r} \right) - V_r^2} \right) - j\left( {VsVrsin\left( {\theta s - \theta r} \right)} \right)$

(3)

$\left( {rP + xQ} \right) + j\left( {rQ - xP} \right) = \left( {VsVrcos\theta - V_r^2} \right)--jVsVrsin\theta$

(4)

where, θ is the phase difference of θ_s and θ_r. Eq. (4) can be divided into real and imaginary parts as follows:

$Re\left( {Eq\left( 4 \right)} \right):\left( {rP + xQ} \right) = VsVrcos\theta - V_r^2$

(5)

$Im\left( {Eq\left( 4 \right)} \right):\left( {rQ - xP} \right) = - VsVrsin\theta$

(6)

Since sin²θ + cos²θ = 1, Eq. (4) can be written as follows:

$\left( {rP + xQ + V_r^2} \right)2 + \left( {rQ - xP} \right)2 = \left( {VsVr} \right)2$

(7)

In order to find sensitivity of the receiving-end voltage to active power and reactive power, the relationship is assumed as follows:

$Vr = f\left( {P,Q} \right)$

(8)

Partial differential values of receiving-end voltage $\frac{{\partial {V_r}}}{{\partial P}}, \frac{{\partial {V_r}}}{{\partial Q}}$ are provided from Eq. (7) and Eq. (8).

$\left\{ {2\left( {rP + xQ + V_r^2} \right) \times \left( {r + 2{V_r}\frac{{\partial {V_r}}}{{\partial P}}} \right)} \right\} + \left\{ {2\left( {rQ - xP} \right) \times \left( { - x} \right)} \right\} = V_s^2 \times 2{V_r}\frac{{\partial {V_r}}}{{\partial P}}$

(9)

$\frac{{\partial {V_r}}}{{\partial P}} = \frac{{\left( {{r^2} + {x^2}} \right)P + r \cdot V_r^2}}{{{V_r}\left\{ {V_s^2 - 2\left( {rP + xQ + V_r^2} \right)} \right\}}}$

(10)

where, Z = (r + x²) is the line impedance between node s and r; then Eq. (10) can be expressed as:

$\frac{{\partial {V_r}}}{{\partial P}} = \frac{{{Z^2} \cdot P + r \cdot V_r^2}}{{{V_r}\left\{ {V_s^2 - 2\left( {rP + xQ + V_r^2} \right)} \right\}}}$

(11)

Similarly, the $\frac{{\partial {V_r}}}{{\partial Q}}$ is calculated as well as the $\frac{{\partial {V_r}}}{{\partial P}}$:

$\frac{{\partial {V_r}}}{{\partial Q}} = \frac{{{Z^2} \cdot Q + x \cdot V_r^2}}{{{V_r}\left\{ {V_s^2 - 2\left( {rP + xQ + V_r^2} \right)} \right\}}}$

(12)

The voltage regulation rate of receiving-end by active power or reactive power are compared as follows:

$\rho = \frac{{\frac{{\partial {V_r}}}{{\partial P}}}}{{\frac{{\partial {V_r}}}{{\partial Q}}}} = \frac{{Z \cdot P + r \cdot {P_s}}}{{Z \cdot Q + x \cdot {P_s}}}$

(13)

where, $Ps = V_r^2/Z$ is the short circuit capacity at the receiving-end. Obviously, ${P_s} \gg Q$ and $Z \simeq x$ are realized on any distribution line, therefore, Eq. (14) is established:

$\rho = \frac{{ZP + r{P_s}}}{{x{P_s}}} \simeq \frac{P}{{{P_s}}} + \frac{r}{x} \ll 1 \Rightarrow \frac{{\partial {V_r}}}{{\partial Q}} \gg \frac{{\partial {V_r}}}{{\partial P}}$

(14)

The effectiveness of reactive power control for maintaining the terminal voltage is recognized from Eq. (14).

---

2.2. Reverse power flow

At the time when there is a huge flow of surplus power from the DGs in the network, reverse power flow may occur; even after the distribution voltage profile has been controlled by reactive power control devices. Therefore, it is necessary to introduce BESS to absorb surplus energy and prevent reverse power flow towards the generators ^[12].

---

3. Energy Management in Electricity Market

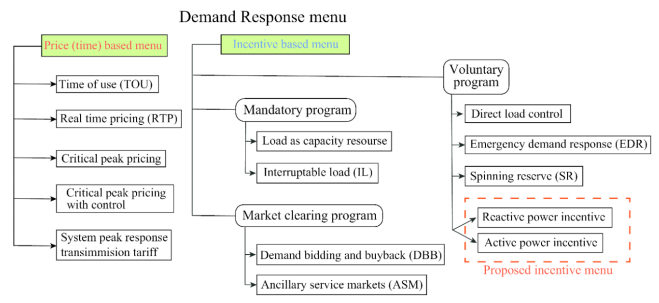
Worldwide liberalization of electricity market has promoted research on the deployment of DR in solving some of the problems associated with power system congestion management. So far, various DR models have been proposed ^[26,27], and some DR menus have been demonstrated by simulation ^[28,29]. DR provides a good opportunity for customer to play important part in the operation of power system. System manager can maintain power system safely by adopting customer side management of DR. The recent development in smart grid technology has made it more possible for carrying out system management from consumer side. However, a management approach is required that can yield profit for both the consumer and the distribution company. Therefore, system operators provide DR menu that can be divided into two categories namely price (or time) based and incentive based DR approach, as shown in Figure 2. In this paper, DR menus that involve incentive, based on the control of both the reactive power and active power, are proposed. Previous works that involve traditional DR menus have focused on DR menus that involve only the active power consumptions; reactive power control incentive is not usually included. However, providing incentive to consumers based on the reactive power consumption is capable of improving the voltage profile along the power system. The traditional DR menu provide compensation for system's frequency and real power consumption with little consideration for maintaining the voltage profile ^[25,27]. Also, in real time pricing (RTP) strategy, the cost of electricity depends on the amount of active power consumed; and in most cases, the cost per kWh which varies from time to time, is exclusively determine by the DisCos based on the density of the active power consumption at a particular time. Hence, consumers are expected to schedule their load demand to period of less density, if they want to pay low bill. But customers who cannot change their load demand pattern, due to the sensitive nature of their loads, will not be able to benefits from this kind of approach and they are at a loss, most times. Therefore, the incentive-based menu, which provides some price flexibility based on individual customer situation and preference, is being proposed in this research instead of the price-based DR menu.

---

3.1. Load flexibility

Traditionally, electric loads are treated as inelastic goods. However, load side management using EVs and house BESS can change these existing conventions. Also, it is possible to develop load models that have huge flexibility by incorporating some price elasticity models in economics. In this research, load flexibility depends on SOC of EV and house battery; and an hour ahead calculation for load flexibility modeling is employed in this study. Therefore, load flexibility equations are determined by the following equations.

---

3.2. Price elasticity

Price elasticity of load is defined as follows ^[25]:

$PED\left( {i,i} \right) = PE{D_{ii}} = \frac{{{p_l}\left( i \right)\partial D\left( i \right)}}{{D\left( i \right)\partial {P_l}\left( i \right)}}$

(15)

According to Eq. (15) the price elasticity at term $i, j$ can be defined as ^[25]:

$PED\left( {i,j} \right) = PE{D_{ii}} = \frac{{{p_l}\left( j \right)\partial D\left( i \right)}}{{D\left( i \right)\partial {P_l}\left( j \right)}}$

(16)

Some of the load such as the interruptible loads in Figure 2, can easily be turn on or off, such is called "self-elasticity" and the self-elasticity has ordinary negative value. On the other hand, for the alternative goods such as shiftable loads in Figure 2, it is possible to shift the usage of the loads to off-peak time from peak-time, that is called "cross elasticity". Generally the cross elasticity is a positive value.

$\left[ {\begin{array}{*{20}{c}} {\Delta D\left( 1 \right)}\\ {\Delta D\left( 2 \right)}\\ {\begin{array}{*{20}{c}} {\Delta D\left( i \right)}\\ {\begin{array}{*{20}{c}} \vdots \\ {\Delta D\left( {24} \right)} \end{array}} \end{array}} \end{array}} \right] \\ = \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {PED\left( {1,1} \right)}\\ {PED\left( {2,1} \right)}\\ {\begin{array}{*{20}{c}} \vdots \\ {\begin{array}{*{20}{c}} \vdots \\ {PED\left( {i,24} \right)} \end{array}} \end{array}} \end{array}}&{\begin{array}{*{20}{c}} {PED\left( {1,2} \right)}\\ {PED\left( {2,2} \right)}\\ {\begin{array}{*{20}{c}} \vdots \\ {\begin{array}{*{20}{c}} \vdots \\ \ldots \end{array}} \end{array}} \end{array}}&{\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} \ldots \\ \ldots \\ {\begin{array}{*{20}{c}} {PED\left( {i,i} \right)}\\ {\begin{array}{*{20}{c}} {PED\left( {j,i} \right)}\\ \ldots \end{array}} \end{array}} \end{array}}&{\begin{array}{*{20}{c}} \ldots \\ \ldots \\ {\begin{array}{*{20}{c}} {PED\left( {i,j} \right)}\\ {\begin{array}{*{20}{c}} \ddots \\ \ldots \end{array}} \end{array}} \end{array}}&{\begin{array}{*{20}{c}} {PED\left( {1,j} \right)}\\ \vdots \\ {\begin{array}{*{20}{c}} \vdots \\ {\begin{array}{*{20}{c}} \vdots \\ {PED\left( {24,24} \right)} \end{array}} \end{array}} \end{array}} \end{array}} \end{array}} \right] \times \left[ {\begin{array}{*{20}{c}} {\Delta {p_l}\left( 1 \right)}\\ {\Delta {p_l}\left( 2 \right)}\\ {\begin{array}{*{20}{c}} {\Delta {p_l}\left( i \right)}\\ {\begin{array}{*{20}{c}} \vdots \\ {\Delta {p_l}\left( {24} \right)} \end{array}} \end{array}} \end{array}} \right]$

(17)

In this research, load flexibility is determined by Eq. (17); simulation period is considered as 24 hours. The diagonal elements represent self elasticity and non-diagonal elements correspond to cross elasticity.

$PE{D_i} = \mathop \sum\nolimits_{j = 1}^n PED\left( {i,j} \right)$

(18)

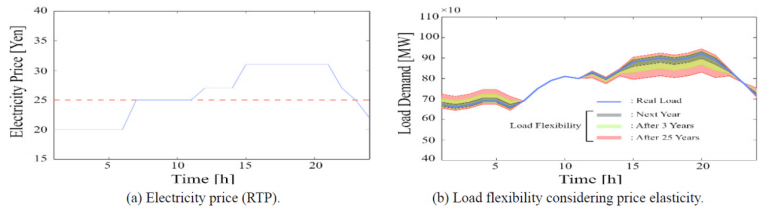
Total price elasticity during one day at node i is obtained from Eq. (18). In Figure 3b the elasticity balance for LF is assigned –0.12, –0.24, and –0.40 ^[21]. An example of LF is illustrated in Figure 3. Figure 3a shows the RTP approach and 3b shows the price elasticity approach using Eq. (17) and Eq. (18).

---

3.3. EV management

EV management can compensate power ramp of PV output and it is effective for leveling load demand. This is possible without changing the actual load pattern of human life style by using the EV connected to the distribution network. However, load flexibility by EV management depends on the number of connection rates of EVs and EV SOC. The management strategies for each customer can be generalized as Eq. (19).

${\boldsymbol{x}_{i,\boldsymbol{d}}} = \left[ {x_{i,\boldsymbol{d}}^1\;\;x_{i,\boldsymbol{d}}^2 \ldots \;\;x_{i,\boldsymbol{d}}^n} \right]$

(19)

Each of these strategies are constrained by the capacity of the attached inverter D as shown in Eq. (20).

${\boldsymbol{d}_{inv,min}} \le x_{i,\boldsymbol{d}}^n \le {\boldsymbol{d}_{inv,max}}$

(20)

Hence, EV charging or discharging strategy is determine as ${x_{i, EV}}$ and each strategy can be limited within the output constraints of the EV inverter as shown in Eq. (21).

$E{V_{inv,min}} \le x_{i,EV}^n \le E{V_{inv,max}}$

(21)

From Eq. (21), the load flexibility and the upper and lower bounds of the EV schedule are estimated by Eqs. (22) and (23), respectively:

$L{F_{EV}}\left( {t + 1} \right) = \sum\nolimits_{i = 1}^{{N_{node}}} {\left[ {Re\left( {{\boldsymbol{x}_{i,EV}}\left( {t + 1} \right)} \right) \times {{\left( {{\boldsymbol{\varphi }_{i,EV}}\left( {t + 1} \right)} \right)}^T}} \right]}$

(22)

$\left\{ \begin{array}{l} L{F_{EV,ub}}\left( {t + 1} \right) = \mathop \sum\nolimits_{i = 1}^{{N_{node}}} \left[ {Re\left( {{x_{i,EV}}\left( {t + 1} \right)} \right) \times {{\left( {{\varphi _{i,EV}}\left( {t + 1} \right)} \right)}^T}} \right]\;\;\;\;\left( {\mathop \sum\nolimits_{n = 1}^{{N_{EV}}} x_{i,EV}^n\left( {t + 1} \right) \ge 0} \right)\\ L{F_{EV,lb}}\left( {t + 1} \right) = \mathop \sum\nolimits_{i = 1}^{{N_{node}}} \left[ {Re\left( {{x_{i,EV}}\left( {t + 1} \right)} \right) \times {{\left( {{\varphi _{i,EV}}\left( {t + 1} \right)} \right)}^T}} \right]\;\;\;\;\left( {\mathop \sum\nolimits_{n = 1}^{{N_{EV}}} x_{i,EV}^n\left( {t + 1} \right) < 0} \right) \end{array} \right.$

(23)

The upper and lower bounds depend on the constraints of the EV strategy ${x_{i, EV}}$. And a strategy group is determined as (24).

${\boldsymbol{\psi }_{i,EV}} = \left[ {\psi _{i,EV}^1,\psi _{i,EV}^2, \ldots ,\psi _{i,EV}^{{N_{EV}}}} \right],\;\;\;\;\psi _{i,EV}^n \in \left\{ {1,0} \right\}$

(24)

where, ${x_{i, EV}}$ is a EVs strategy group of the EVs connected at node i. ${\psi _{i, EV}}$ is a factor that represents the connection state of EVs into the distribution network. This factor is represented as binary code; here, a "1" shows that the EV is connected, a "0" means that the EV is used as vehicle away from the system.

EVs SOC are represented by Eq. (25), and these determine the three status of the EV battery.

${\zeta _{i,EV}}\left( {t + 1} \right) = \left\{ \begin{array}{l} {\zeta _{i,EV}}\left( t \right) - \frac{{{x_{i,EV}}\left( t \right) \times {\psi _{i,EV}}}}{{{C_{EV}}}} \times \frac{1}{\eta } \ge {\zeta _{i,EV,{\rm{min}}}}\left( t \right)\;\;\;\;\left( {{x_{i,EV}}\left( t \right) \ge 0 \wedge {\psi _{i,EV}}\left( t \right) = 1} \right)\\ {\zeta _{i,EV}}\left( t \right) - \frac{{{x_{i,EV}}\left( t \right) \times {\psi _{i,EV}}}}{{{C_{EV}}}} \times \eta \le {\zeta _{i,EV,{\rm{max}}}}\left( t \right)\;\;\;\;({x_{i,EV}}\left( t \right) < 0 \wedge {\psi _{i,EV}}\left( t \right) = 1)\\ {\zeta _{i,EV}}\left( t \right) - \frac{{\left| {{x_{i,EV}}\left( t \right)} \right| \times \left( {1 - {\psi _{i,EV}}} \right)}}{{{C_{EV}}}} \times \frac{1}{\eta } \le {\zeta _{i,EV,{\rm{max}}}}\left( t \right)\;\;\;\;\left( {{\psi _{i,EV}}\left( t \right) = 0} \right) \end{array} \right.$

(25)

The first line represents discharging, second line is charging state and the third line represents when the EV is disconnected from the power system. Figure 4 shows the comparison between load flexibility using RTP and EVs management strategies.

---

3.4. Home energy management using house BESS

The house battery storage system is introduced for effective usage of PV output surplus. Instead of abandoning the surplus power from the PV system by technical saturation, this surplus from the PV output is used for charging the battery. The available energy from the charged battery is used at peak load time to meet the excess load demand. Therefore, it is possible to manage the battery from the consumer side. Similar to EV management in section 3.3, strategy constraint, load flexibility, flexibility limits, and SOC of house batteries are formulated as shown in Eqs. (26)–(29), respectively. House BESS strategy may have assigned values similar to that of Eq. (19), hence, the strategies are limited as:

$s{B_{inv,min}} \le x_{i,sB}^n \le s{B_{inv,max}}$

(26)

Where, $sB$ represent house BESS. From Eq. (26), load flexibility is estimated as follows:

$L{F_{sB}}\left( {t + 1} \right) = \mathop \sum\nolimits_{i = 1}^{{N_{node}}} \left[ {Re\left( {{x_{i,sB}}\left( {t + 1} \right)} \right)} \right]$

(27)

and the upper and lower bounds depend on constraints of house BESSs strategies ${x_{i, sB}}$.

$\left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {L{F_{sB,ub}}\left( {t + 1} \right) = \mathop \sum\nolimits_{i = 1}^{{N_{node}}} \left[ {Re\left( {{\boldsymbol{x}_{i,sB}}\left( {t + 1} \right)} \right)} \right]}&{\left( {\mathop \sum\nolimits_{i = 1}^{{N_{sB}}} {\boldsymbol{x}_{i,sB}}\left( {t + 1} \right) \ge 0} \right)} \end{array}}\\ {\begin{array}{*{20}{c}} {L{F_{sB,lb}}\left( {t + 1} \right) = \mathop \sum\nolimits_{i = 1}^{{N_{node}}} \left[ {Re\left( {{\boldsymbol{x}_{i,sB}}\left( {t + 1} \right)} \right)} \right]}&{\left( {\mathop \sum\nolimits_{i = 1}^{{N_{sB}}} {\boldsymbol{x}_{i,sB}}\left( {t + 1} \right) < 0} \right)} \end{array}} \end{array}} \right.$

(28)

Where, ${\boldsymbol{x}_{i, sB}} = \left[ {x_{i, sB}^1, x_{i, sB}^2, \ldots, x_{i, sB}^{{N_{sB}}}} \right]$ is a house battery strategy group of smart house at i node.

${\zeta _{i,sB}}\left( {t + 1} \right) = \left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{\zeta _{i,sB}}\left( t \right) - \frac{{{x_{i,sB}}\left( t \right)}}{{{C_{sB}}}} \times \frac{1}{\eta } \ge {\zeta _{i,sB,{\rm{min}}}}\left( t \right)}&{\left( {{x_{i,sB}}\left( t \right) \ge 0} \right)} \end{array}}\\ {\begin{array}{*{20}{c}} {{\zeta _{i,EV}}\left( t \right) - \frac{{{x_{i,EV}}\left( t \right)}}{{{C_{EV}}}} \times \eta \le {\zeta _{i,sB,{\rm{max}}}}\left( t \right)}&{({x_{i,sB}}\left( t \right) < 0)} \end{array}} \end{array}} \right.$

(29)

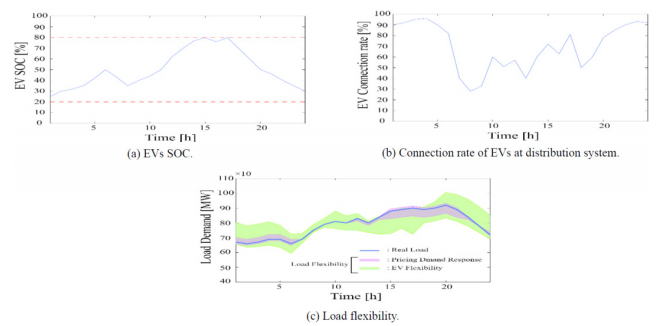
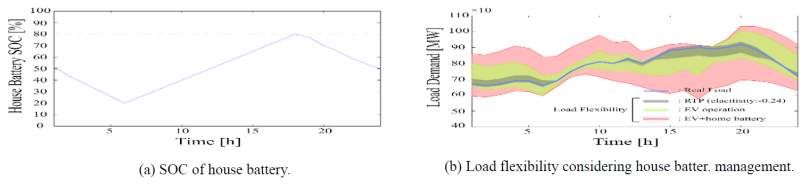
House battery is different from EV's battery because house battery is fixed at a house. Hence, it is unnecessary to consider connection rate in house battery management as it is in EVs management. Figure 5 shows load flexibility by considering both EV and home battery management.

---

3.5. Incentive menu and method

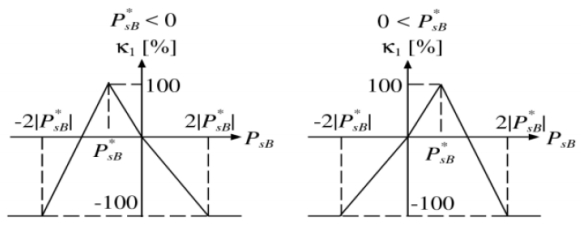
In the Previous section, management of active power consumption by battery and EV charging and discharging actions had been discussed. However, customers can also participate in the electricity market by using cooperative reactive power control for maintaining the voltage. DisCo can reduce the cost of introducing and maintaining power control devices by providing incentive to customers that are willing to enter into the cooperative operation of the power system instead. The amount of incentive profit obtainable depends on each customer's contributions to the reactive power control of the power system. The contribution factor is shown in Figure 6 and the incentive is calculated by Eqs. (30)–(33). The investment cost for some of the real power control devices without and with reactive power control coordination is shown on Table 1 and Table 2.

---

3.6. Unit price of active power incentive

Reduced investment cost of 33% is distributed for cooperating customers, and the incentive unit price per kWh rate of active power is calculated by Eq. (30):

${v_p} = \frac{{{C_{LB}}}}{{20 \times 365 \times 24 \times {S_{LB}}}}.$

(30)

The depreciation term of large BESS and inverter is estimated as 20 years. The incentive price is applied to both the house battery and EVs managements.

---

3.7. Unit price of reactive power incentive

The unit price of reactive power incentive per kVarh ${v_q}$ depends on the amount of reduced control devices by cooperative operation from customer side. The unit price is described by Eq. (31);

${v_p} = \frac{{{C_Q}}}{{20 \times 365 \times 24 \times {S_{SVC}} \times {N_{node}}}}$

(31)

And, ${C_Q}$ can be described as:

${C_Q} = {C_{SVC}} \times {N_{node}} + {C_{SVR}} \times 3$

(32)

Where, N is total number of nodes in the distribution system, depreciation term is determined as 20 years.${C_{SVC}}$, ${C_{SVR}}$ are devices and installation cost of SVC and SVR, respectively. It is necessary to install SVCs at each node and three SVRs between nodes 3–4, 2–7 and 4–11 without cooperative operation. However, with cooperative operation, the reduced total cost ${C_Q}$ will be distributed as reactive power incentive.

---

3.8. Profit of customer side by incentive options

The customer who participates in cooperative operation market can gain profit from active and reactive power incentive. The profit of customers are calculated as follows:

${v_{pro}} = \left\{ {\left( {{P_{PV}} + {v_{PV}}} \right) + \left( {{{P'}_{inv,sB}} + {{P'}_{inv,EV}}} \right) \times \left( {{{Q'}_{inv,sB}} + {{Q'}_{inv,EV}}} \right) \times {v_q}} \right\} \times {P_{base}}$

(33)

${{P'}_{sB}} = \left| {{P_{sB}}} \right| \times {k_1}$

(34)

${{P'}_{EV}} = \left| {{P_{EV}}} \right| \times {k_2}$

(35)

${{Q'}_{inv}} = \left| {{Q_{inv}}} \right| \times {k_3}$

(36)

${{Q'}_{EV}} = \left| {{Q_{EV}}} \right| \times {k_4}$

(37)

Where, ${P_{PV}}$ is PV output power and ${v_{PV}}$ is selling price of PV output. ${{P'}_{inv, sB}}$, ${{P'}_{inv, EV}}$ are active power contribution from house BESS and EV system. Similarly, ${{P'}_{inv, sB}}$, ${{P'}_{inv, EV}}$ are also contribution from reactive power of house BESS and EV. The ${\kappa _{1-4}}$ represent contribution factors, those values take positive and negative values. The images of the contribution factors are shown in Figure 6. When the order value for cooperative operation is negative, it means negawatt trading.

---

4. Two-Level Optimization in the Smart Grid System

In previous research, multi-objective optimization has provided an evaluation criterion for trade-off relationship. However, in order to achieve more realistic trading process, two-level optimization is applied in this paper. Moreover, this approach was able to find a solution with less computational requirement than the multi-objective optimization method. the procedure is described as follows:

A provisional optimal schedule is made by DisCo from day-ahead forecasting data of DG output and load profile.

Step 1: The factor of incentive and desirable values for cooperative operation are provided by using provisional optimal schedule in Step 1.

Step 2: Second level optimization schedule is customer side management. This schedule is made for all customer in each node, with respect to priority factor of each nodes and incentive, as preferred by each customer.

DisCo decide an optimal control schedule considering each customer's preferred strategies.

---

4.1. DisCo side optimization

In this study, optimal scheduling is used to minimize distribution losses as follow:

$min:{F_1}\left( {{P_{LB}},{Q_{LB}},{P_{sB}},{Q_{inv}},{P_{EV}},{Q_{EV}},{T_k}} \right) = \mathop \sum\nolimits_{t = 1}^{24} \mathop \sum\nolimits_{i = 1}^{{N_{node}}} {P_{Loss,i}}\left( t \right)$

(38)

The DisCo decides the contribution factor shown in Figure 6, as results, maximum contribution from the customer is archived when losses are minimized. Active and reactive power incentive profits are maximized when first objective function is satisfied. To avoid the problems of voltage deviation and reverse power flow, constraints are provided as shown in Eqs. (39)–(41):

${V_{min}} \le {V_i}\left( t \right) \le {V_{max}}$

(39)

$P_f^{min} \le {P_f}\left( t \right) \le P_f^{max}$

(40)

$Q_f^{min} \le {Q_f}\left( t \right) \le Q_f^{max}$

(41)

Voltage constraint used at all nodes, and also power flow constraints are given as shown in Eq. (39), (41) and (40) in order to avoid reverse power flow. Maximum and minimum reactive power flow constraints are determined from high power quality point of view. Therefore, those values are given as follows:

$Q_f^{min} = - {P_f}\left( t \right){\rm{tan}}\left( {{{\cos }^{ - 1}}\left( {0.85} \right)} \right)$

(42)

$Q_f^{min} = - {P_f}\left( t \right){\rm{tan}}\left( {{{\cos }^{ - 1}}\left( {0.85} \right)} \right)$

(43)

Power factor is maintained at least as 0.85 at the interconnection point. DisCo and customers have battery as control devices and management facilities, inverters are attached to all batteries and the battery outputs depend on inverter capacity. Each inverter capacity constraints are determined as follows:

$\begin{array}{*{20}{c}} {\sqrt {P_d^2\left( t \right) + Q_d^2\left( t \right)} \le {S_d},}&{\boldsymbol{d} \ni \left\{ {LB,EV,sB} \right\}} \end{array}$

(44)

${\zeta _{d,{\rm{min}}}} \le {\zeta _\boldsymbol{d}}\left( t \right) \le {\zeta _{\boldsymbol{d},{\rm{max}}}}\;\;\;\;\left[ \% \right]$

(45)

${\zeta _\boldsymbol{d}}\left( {t + 1} \right) = \left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{\zeta _\boldsymbol{d}}\left( t \right) - \frac{{{p_d}\left( t \right)/\eta }}{{{C_d}}}}&{\left( {{p_d}\left( t \right) \ge 0} \right)} \end{array}}\\ {\begin{array}{*{20}{c}} {{\zeta _\boldsymbol{d}}\left( t \right) - \frac{{{p_d}\left( t \right).\eta }}{{{C_d}}}}&{({p_d}\left( t \right) < 0)} \end{array}} \end{array}} \right.$

(46)

The set of control devises d includes inverters. The capacity and SOC constraints are represented by Eq. (44) and Eq. (45), respectively. The inverter efficiency is considered, therefore, charging and discharging losses are included at Eq. (46). All SOC minimum values are set as 20%, and maximum values are set as 80% except EV's battery. EV battery can charge up to 100%. House BESS inverter is also connected to PV, thus the inverter capacity constraint is represented as follows:

$\sqrt {{{\left( {{P_{PV}}\left( t \right) + {P_{sB}}\left( t \right)} \right)}^2} + Q_{sB}^2\left( t \right)} \le {S_{sB}}$

(47)

Finally, tap changing transformer LRT constraint is described by Eq. (48):

$T_k^{min} \le {T_\boldsymbol{k}}\left( t \right) \le T_k^{max}.$

(48)

---

4.2. Customer side strategy

Each customer group requires different satisfaction option such as lower electricity price or high power quality, etc. The customer objective function is shown in Eq. (49), as the difference between incentive profit and dissatisfaction factor.

$max:{F_2}\left( {{\boldsymbol{x}_{i,\boldsymbol{d}}}} \right) = \mathop \sum\nolimits_{i = 1}^{24} \mathop \sum\nolimits_{i = 1}^{{N_{node}}} \left\{ {{v_{pro,i}}\left( t \right) - \mathop \sum\nolimits_{k = 1}^{{N_{cus,d}}} \left( {{\varphi _{i,{d_k}}}\left( t \right)} \right)} \right\},\;\;\;\;\boldsymbol{d} \ni \left\{ {EV,sB} \right\}$

(49)

The dissatisfaction factor is expressed as follows:

${\varphi _{i,\boldsymbol{d}}} = {e^{{\beta _{i,\boldsymbol{d}}}\left( {1 - \left( {{U_{i,d}}/{{U'}_{i,\boldsymbol{d}}}} \right)} \right)}} - 1,\;\;{\beta _{i,\boldsymbol{d}}} > 0$

(50)

In Eq. (50), ${\beta _{i, \boldsymbol{d}}}$ is defined as priority factor for each of devices. The part of ${\left ({{U_{i, d}}/{{U'}_{i, \boldsymbol{d}}}} \right)}$ represents response of power usage as a result of cooperative operation. Each devices strategy is decided in the second level optimization based on Section 3.3, 3.4, and Eq. (45).

---

4.3. Adaptive inertia weight particle swarm optimization

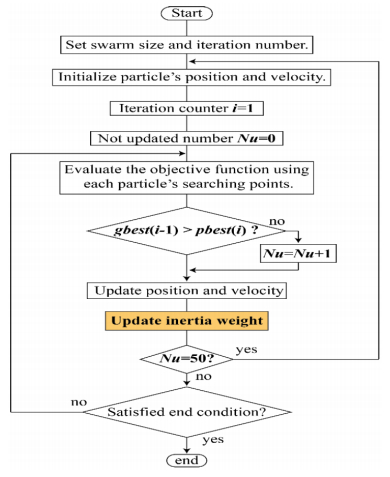
There are many methods to solve optimization problem. In this paper, PSO method was selected to solve the above optimization problem ^[30,31]. This method modeled an action of swarm such as fish, the swarm find the path to food through cooperation. In this paper, modified method of PSO referred to as AIWPSO ^[32,33] is verified. The flowchart is shown in Figure 7.

The AIWPSO searching algorithm communicates information about the best positions to all swarms, and each continues updating their own positions and velocities until searching is finished. The updating of velocity and search position is decided by the following equations:

${v_i}\left( {i + 1} \right) = {\omega _i} \cdot {v_i}\left( k \right) + {c_1} \cdot rand \cdot \left( {pbest\left( k \right) - {S_i}\left( k \right)} \right) + {C_2} \cdot rand \cdot \left( {gbest - {S_i}\left( k \right)} \right)$

(51)

${S_{k + 1}}\left( i \right) = {S_k}\left( i \right) + {v_{k + 1}}\left( i \right)$

(52)

where, ${V_{k + 1}}\left (i \right)$: i-th Particle velocity in $k + 1$-th search, rand1: uniform random numbers from 0 to 1, ${S_{k + 1}}$: search position of i-th particle in k-th search, ${\omega _i}$ is adaptive inertia weight, ${c_1}$ and ${c_2}$ express weight for position of current best particle and for best position of particle swarm, respectively. $pbest$ is the position of current best particle and $gbest$ is best position of particle swarm.

The inertia weight ^[34] is updated by

${\omega _i}\left( {k + 1} \right) = \omega \left( 0 \right) + \left( {\omega \left( {{n_k}} \right) - \omega \left( 0 \right)} \right) \times \frac{{{e^{{m_i}\left( k \right)}} - 1}}{{{e^{{m_i}\left( k \right)}} + 1}}$

(53)

${m_i}\left( k \right) = \frac{{gbest - current}}{{gbest + current}}$

(54)

Where, ${\omega _i}$ is updated inertia weight value, nh represents particle number n_h at generation h, m_i is adjustment value of inertia weight at generation h. Swarm acceleration is adjusted by the adaptive inertia function. As the objective function value improves, the AIW value becomes smaller. This way, the AIW function helps to find a more accurate solution than the conventional PSO method.

---

5. Simulation Results on Case Studies

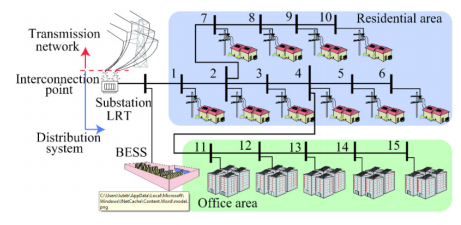
This section describes the simulation results of the proposed methodology. Based on the situation before application of the proposed cooperative operation from customers and DisCo, as shown in Figure 8, 9 and 10, it can be noticed that:

(1) The simulation model shown in Figure 8 distinguishes office and residential area so that EV activities can be separately analyzed for each.

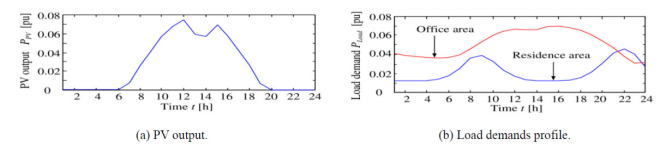
(2) The PV output and the load demand curves, according to illustrations in Figures 9a and 9b, do not match due to fluctuating nature of RESs (no PV output in some hours).

The Table 3 shows contents of case studies such as operation type, optimization approach and method.

---

5.1. Case 1

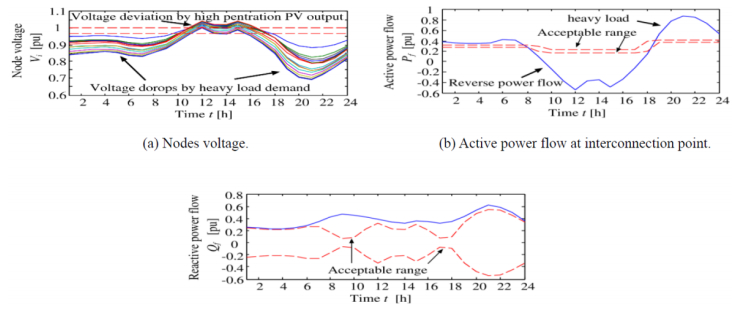
The case 1 operation is without coordination, there is a huge node voltage deviations, beyond and below the admissible range, according to illustration in Figure 10a. Figure 10b, shows reverse power flow at the interconnection point in some hours of the day, with huge deviations from the acceptable range. Also, at the interconnection point the reactive power flow goes beyond the acceptable range, as depicted in Figure 10c. These conditions show that the recommended power factor of 0.85 cannot be achieved at this point and this adversely affects the active power flow.

---

5.2. Case 2

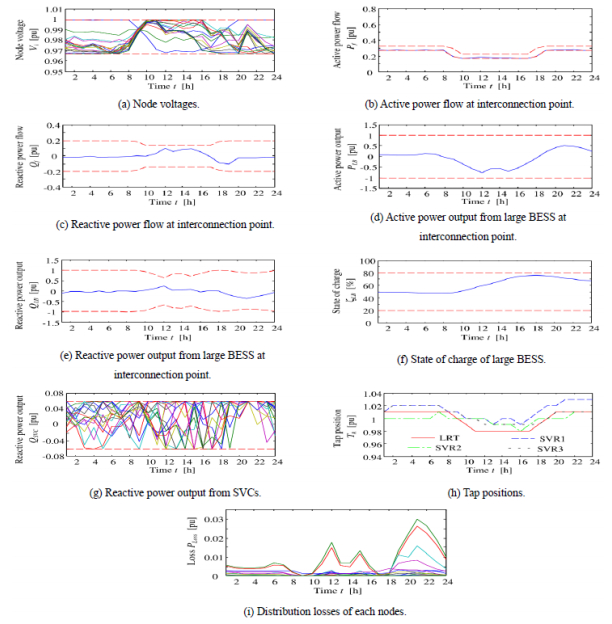
In the previous work done by the authors ^[35], the use of the conventional methodologies to solve the above mentioned problems, showed that there is a need for large values of BESS, SVCs, LTR and SVRs. These equipment help in solving the node voltages, bringing them to the acceptable range, as illustrated in Figure 11a. They also allow acceptable active and reactive power flow at the interconnection point, as depicted in Figure 11b and 11c. The BESS installed in the interconnection point gives outputs according to representation in Figure 11d and 11e, which depends upon the SOC represented in Figure 11f. The SOC of the BESS is limited within the range of 20% to 80% in order to avoid deep charging and discharging. On the other hand, the SVC guarantees the compensation of reactive power by outputting in each node reactive power as depicted in Figure 11g. The regulation of voltage is guaranteed by setting the tap changer position according to the representation in Figure 11h, bounded in the range of 0.98 to 1.03. The combination of this devices reduces the node active power losses as depicted in Figure 11i. The only problem of applying all these equipment is the capital cost involved, which sometimes affect the feasibility of its implementation.

---

5.3. Case 3

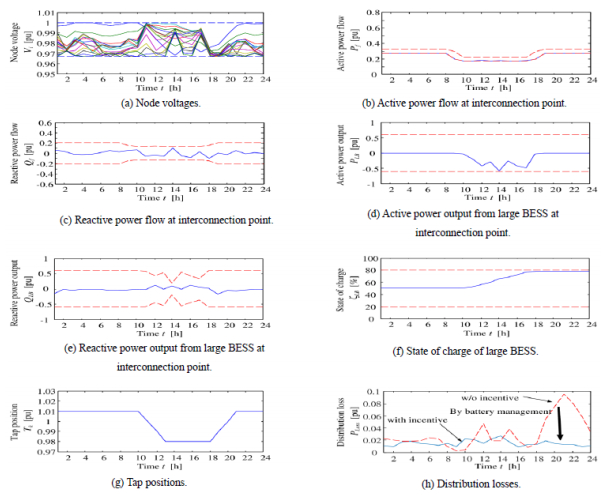
The proposed methodology reduced the number of BESS and LRT that needs to be installed by DisCos, as the customer participates by managing EV, PV and house BESS inverter. This makes the capital cost less than that of the conventional methodology. As the DisCo controls the BESS and LRT, the behaviors of the system in terms of node voltages, active and reactive power flow at the interconnection point, active and reactive power output of the BESS at the interconnection point, the SOC of the BESS, tap position of LRT and distribution losses are depicted by Figures 12a to 12h, respectively. Comparing the proposed method (Figure 12) to conventional method (Figure 11), it was observed, from the simulation result, that it is not necessary to install SVCs at every node for achieving voltage security in the proposed method. Also, from the simulation results of case 3 shown in Figure 12h, it can be seen that there is a reduction in the distribution losses when compared to the conventional methodology (case 2).

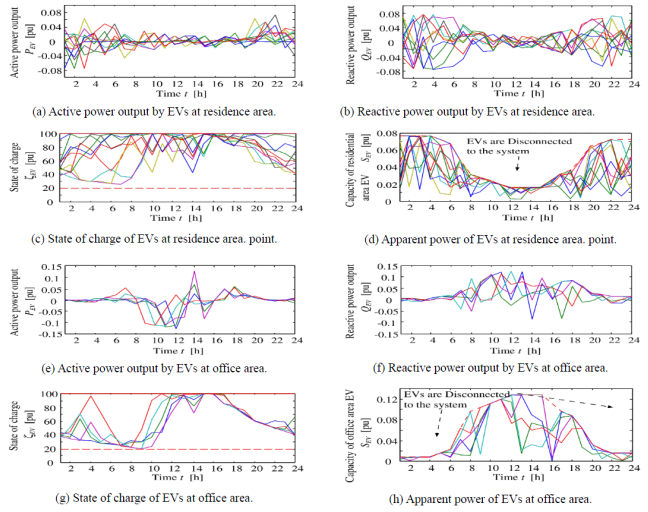
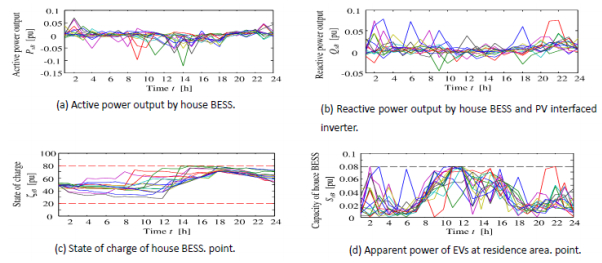
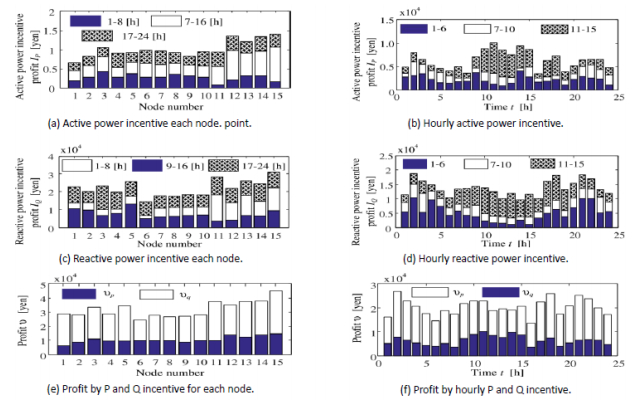
Figures 13a to 13h show the effect of including EV management. Figures 13d and 13h depict the apparent power of the EVs at residential and office area, respectively; with the dashed lines showing the boundary of the connection rates. From Figure 13a and 13b, it can be seen that there is active and reactive power output from the EV at the residential area. This power outputs depend on the SOC of the EVs, as seen in Figure 13c. Similarly, in the office areas the EV produced active and reactive power output as shown in Figures 13e and 13f. Here also, both power outputs depend on the SOC of the EVs for the office area, as shown in Figure 13g. For the house BESS management, the house BESS when interfaced with the PV system and inverter produced active, reactive and apparent power output that are shown in Figures 14a, 14b and 14d, respectively. The profile of the SOC of the BESS during simulation is shown in Figure 14c. The results of profit gained from the cooperative control of the active and reactive power consumption or supply based on the incentive strategy are shown in Figure 15. It can be deduced from Figure 15 that there is a reduction in the total consumption cost below the ordinary purchase cost. In both the active and reactive power incentive results, it can be seen from Figure 15a and 15c, that office area (11–15 nodes) relatively gain profit. This is because, these nodes absorb the surplus energy from the PV at daytime (7:00–18:00) from Figure 15b and 15d, thereby preventing reverse power flow. This is necessary in order to preserve power quality and to safely compensate for the fluctuation of PV output. By comparing the incentive profits, as shown in Figure 15e and 15f, it is observed that customers can gain more profit by reactive power contribution than by active power. The profit gained by each customer depends on the incentive unit price. In this research, the reactive power incentive unit price is considered to be greater than the active power incentive price as shown in Table 2. Consequently, DisCo can achieve and maintain a high power quality and reliability without compulsorily changing the consumption on the customer side. This brings about mutual profits and satisfactions to the DisCo and the participating customers.

Table 4 provides the comparison between the proposed PSO optimization method (AIWPSO) and the conventional PSO method. The time of decision-making to optimize the DisCo and customer strategy is one day (24 hours). From the table, it is clearly shown that the ordinary PSO algorithm took more time to achieve the optimal scheduling. Moreover, AIWPSO provided better results in comparison to the conventional PSO method in all the cases considered.

---

6. Conclusion

In this work, the technical impacts of customer-side real and reactive power flow management using DR incentive strategy in the smart grid system has been verified and a two-level optimization approaches applied for mutual profits between both sides. Also, the superiority of a modified particle swarm optimization technique over the conventional PSO was shown for implementing the DR strategy. It can be concluded that by using cooperative DR management of distribution system, the DisCo was able to achieve a significant reduction in the capacity of BESS and EV needed to be integrated into the distribution system; and the necessity for the integration of SVRs and SVCs was reduced as well. In this work, AIWPSO was presented as a suitable algorithm for implementing a variable DR incentive strategy for achieving real and reactive power management in smart-grids, in terms of technical effectiveness and time-efficiency.

---

Acknowledgments

This work was supported by JSPS KAKENHI Grant-in-Aid for JSPS Fellows, Grant Number JP17J08955.

---

Conflict of Interest

All authors declare no conflicts of interest in this paper.

---