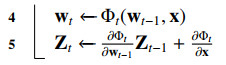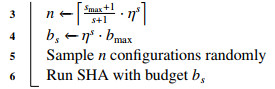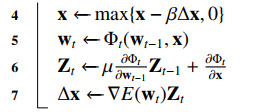Social Networking of Quasi-Species Consortia drive Virolution via Persistence

1.   Introduction

Machine learning (ML) is a discipline of artificial intelligence (AI) that uses the theory of statistics in building mathematical models to program computers to "learn" or "discover" algorithms, where an algorithm is a sequence of instructions for solving a problem or performing a computation, to optimize the performance criteria for given tasks using example data or past experiences ^[1]. ML has found applications across various domains, such as image recognition ^[2], healthcare ^[3], natural language processing ^[4], games and strategy ^[5], etc. In ML models, parameters fall into two categories: model parameters (e.g., weights and biases of the connections between neurons of a neural network, centroids in k-means clustering) and hyperparameters (e.g., learning rate, number of hidden layers of a neural network, number of clusters in k-means clustering). While model parameters can be learned and adapted during the training process based on the training dataset, hyperparameters serve as external configuration variables that are to be determined before the training commences. The tuning of hyperparameters has played an essential role both from the methodological perspective, e.g., deep neural networks and shallow models, as well as from the application aspect, with models derived from computer vision, natural language models, speech, etc. Though it seems trivial at first glance that hyperparameters can be tuned by humans, in modern systems, manual tuning can be ineffective and is nearly impossible when dealing with large-scale hyperparameters.

Differing from the human tuning process, which can be tedious and heavily dependent on human expertise and experience, hyperparameter optimization (HPO) aims to automatically tune the relevant hyperparameters for the system, where the performance is measured by certain metrics, e.g., classification accuracy for a classifier model could be tuned to a better point. Apart from saving human labor and boosting model performance to its fullest potential, another advantage lies in enhancing the evaluation of different models. This can be achieved by diligently fine-tuning their respective hyperparameters, even when the models differ from one another. In contrast, the traditional trial-and-error procedure by humans can be ad-hoc and less reproducible, posing challenges in the evaluation process.

In recent years, deep learning (DL) techniques have reached remarkable achievements on various AI tasks, including image classification ^[6], language modeling ^[4], and speech recognition ^[7]. However, these models are sensitive to diverse task-specific configurations, costing substantial expert efforts to redesign them through a trial-and-error process. Automated machine learning (AutoML) ^[8] has been proposed to tackle this problem in areas such as data preparation, feature engineering, model generation, and model evaluation.

Given the search space, optimization methods in model generation can be classified into two categories: HPO and architecture optimization. In this paper, we mainly focus on HPO algorithms. A generic HPO algorithm for an unknown objective function $f \colon \mathcal{X}\xrightarrow{}\mathbb{R}$, where $\mathcal{X}\in\mathbb{R}^d$ and $d$ is the size of design space of interest, is to find the $\mathbf{x}$, a hyperparameter configuration, e.g., learning rate and batch size that globally minimizes $f$:

Although gradient descent ^[9] is popular in DL, which is capable of tuning the learning rate, the cases where it is possible to obtain the training gradient of hyperparameters are rare. Therefore, traditional HPO frameworks treat $f$ as a non-convex black-box function and search for optimum without leveraging derivatives. As shown in Figure 1, classical HPO algorithms cover grid search and random search ^[10], metaheuristic search ^[11,12], Bayesian optimization ^[13], etc.

Unfortunately, despite the success of liberating humans from the loop ^[14], most conventional HPO algorithms follow a sequential querying approach and therefore suffer delays of the convergence of neural network training, which is always computationally resource-intensive. For instance, the whole training process for the once-for-all (OFA) network ^[15] took 1200 GPU hours with V100 GPUs. The community has thus proposed many acceleration methods to shorten the optimization process and avoid unnecessary repetition. Another drawback of classical HPOs is that they often yield fixed configurations throughout the entire run of AI models, even though the optimum may change at different phases. To tackle this, some dynamic algorithm configuration (DAC) methods ^{[16,17,18,19]} emerge to optimize on-the-fly, i.e., dynamically tune both parameters and hyperparameter schedules during the training procedure. In practical settings, there can be more than one metric to optimize beyond the conventional prediction accuracy (cf. Eqs (1.1) and (5.1)). Additional considerations such as space/time overheads and adherence to specific business constraints can play pivotal roles. The field has thus recently witnessed a growing interest in multi-objective HPO (MOHPO), the HPO counterpart to multi-objective optimization (MOO) ^[20,21].

As a well-established field, HPO has attracted wide and growing attention over the decades from both academia and industry. There exist numerous surveys covering a range of related topics, including the specific topic of HPO itself ^{[22,23,24,25,26,27]}, some closely related topics, e.g., Bayesian optimization ^{[14,28,29,30]}, as well as topics of broader scopes such as AutoML ^[8,31,32].

Existing surveys on general HPO ^{[22,23,24,26,27]} introduce HPO algorithms by categorizing them into several major classes: grid search (GS), random search (RS), Bayesian optimization (BO) and variants, multi-fidelity or Hyperband, population- or evolutionary-based, and gradient-based. This work takes a distinctive approach (Figure 1) and considers these algorithms as (ⅰ) classical methods for HPO, i.e., simple searches, BOs, and metaheuristics, (ⅱ) techniques for acceleration, i.e., multi-fidelity, bandit-based, and early stopping, (ⅲ) DAC optimizers that are either gradient-, population-, or reinforcement learning-based, and (ⅳ) strategies for MOHPO. Notably, DAC and MOHPO algorithms in particular have been either minimally explored or entirely overlooked in ^{[22,23,24,26,27]}. A list of popular frameworks and tools for HPO is compiled and tabulated, serving as an accessible guide for individuals new to the field, students, researchers, or practitioners in search of diverse options or alternatives for their HPO tasks or workflow integration.

This survey is structured as follows. In Section 2, we provide the basics of the primary classical algorithms in HPO. Section 3 then delves into strategies for accelerating these conventional algorithms from different perspectives. This is followed by Sections 4 and 5, where we explore the increasingly recognized DAC and MOHPO algorithms, respectively. After presenting popular tools and frameworks for HPO in Section 6.1, exploring applications in Section 6.2, and providing further discussions in Section 6.3, the paper is concluded in Section 7.

2.   Classical optimization methods

In this section, we introduce three kinds of optimization methods that are commonly applied in HPO. These methods have to handle two key considerations: (ⅰ) the exploration vs. exploitation trade-off, which refers to the budget spent on exploring unknown search space or on exploiting known search space, and (ⅱ) the inference vs. search trade-off, referring to the overhead used to analyze existing information to guide the search process versus the budget allocated for the search itself. Table 1 summarizes the classical optimization methods.

2.1.   Simple search scheme

2.1.1.   Gradient-based search (GradS)

Gradient descent-based methods are extensively used for optimization problems including the HPO task, which often involves non-convex optimization, and a local optimum is acceptable. Hypergradients (HGs) refer to the gradients of the model selection criterion such as cross-validation performance and validation error with respect to hyperparameters. With hypergradients, gradient descent can be employed to handle a large number of hyperparameters efficiently.

Reverse-mode differentiation (RMD) ^[33], known as backpropagation in DL, has been the standard method for computing gradients with respect to parameters in ML models. It was introduced to HPO problems to compute hypergradients ^[34]. While algorithms for computing hypergradients for optimization methods, including gradient descent, were derived in Domke ^[35], their impracticality for DL models due to high memory consumption for storing all intermediate variables has been recognized. In Maclaurin et al. ^[36], reverse-mode differentiation of stochastic gradient descent (SGD) with momentum has been proposed, overcoming the problem by computing intermediate variables during the reverse pass. It is further improved in Pedregosa ^[37] with the adoption of approximate gradients. In Franceschi et al. ^[38], reverse-mode algorithms for hypergradients are explained from the perspective of Lagrangian formulation, and a forward-mode algorithm is introduced for situations involving a small number of hyperparameters. Later, Lorraine et al. ^[39] devised a scalable gradient-based HPO technique capable of handling millions of hyperparameters. Reverse-mode and forward-mode hypergradient algorithms are summarized in Algorithms 1 and 2, respectively, based on the derivations in Franceschi et al. ^[38]. In these two algorithms, $\Phi$ represents parameter optimization methods such as gradient descent, $\mathbf{w}$ denotes parameters or weights of DL models, $\mathbf{x}$ signifies hyperparameters, and $E$ is the validation objective.

2.1.2.   Grid search (GS)

GS is the most basic HPO method. It requires the user to select a finite subset for each hyperparameter and then exhaustively evaluate every possible combination point to find the optimum. GS inherently supports parallel implementation but fails in efficiency once the search space is large or objective dimensions get high, as the number of combinations to evaluate grows exponentially. To tackle these challenges, a multi-scale grid approach is used in Hsu et al. ^[40], where a coarse grid is first applied to identify a good region, and then a finer grid is conducted on that region. Alternatively, direct search ^[41] queries only the neighbors around current points to update the optimum. When neither improvement nor degradation is observed in any parameter, the search step is reduced until convergence.

2.1.3.   Random search (RS)

Contrary to GS, RS randomly and independently samples candidates from the search space until the defined budget is exhausted. While GS is inefficient in high dimensions, RS is less affected, benefiting from lower effective dimensionality where only a few hyperparameters have an influence on the performance ^[10]. Given the same budget, RS can explore a larger area of the effective dimensions compared to GS, leading to better performance. As shown in Figure 2, RS tends to explore a broader space than GS with a limited budget, avoiding lingering in less promising areas. Bergstra and Bengio ^[10] have proved empirically and theoretically that RS is more practical than GS while in some cases sophisticated methods may bring little advantage over RS. Additionally, RS is readily resource-allocated since it can be extended by further samples, and the probability of sampling in different regions can be adjusted manually so exploration of valuable regions can be prioritized. While RS may lead to suboptimal solutions, its performance can be arbitrarily close to the optimum in expectation when provided with enough budgets.

2.2.   Bayesian optimization (BO) with surrogates and acquisitions

BO ^[13] is an efficient global black-box optimization framework for expensive functions. Recently, it has gained widespread application in HPO problems and achieved state of the art results across various ML domains like image classification ^[13] and speech recognition ^[42].

BO is the most popular sequential model-based optimization (SMBO) algorithm, which has proven its superiority in optimizing expensive black-box functions ^[14] and exhibits impressive performance on even hard-to-tune hyperparameters ^[43]. Figure 3 illustrates a general sequential optimization framework that utilizes a model learned from observations to recommend promising candidates, which then gets queried to generate feedback for updating the model.

A classic BO framework comprises a probabilistic surrogate model and an acquisition function. The surrogate model approximates the unknown objective function $f$ based on the observation dataset $\mathcal{D} = \{(\mathbf{x}_t, y_t)\}_{t = 1}^N$, where $\mathbf{x}_t \in \mathcal{X}$ and $y_t \in \mathbb{R}$ are the input and the observation value of $f$, respectively. The prior distribution of the surrogate model captures our knowledge about $f$ and is updated with $\mathcal{D}$ to generate a posterior distribution, which provides predictions and uncertainties over the search space $\mathcal{X}$. The acquisition function $\alpha$ utilizes the posterior distribution to guide the sequential search. Instead of observing the expensive objective function, BO optimizes the cheap acquisition function globally to generate candidates. The main property of the acquisition function is the trade-off between the exploration of areas with high uncertainty and the exploitation of areas with low predictions (for minimization task).

One common choice for the surrogate model is Gaussian process (GP) ^[44], and for the acquisition function, it is the expected improvement (EI) ^[45]. We summarize the BO algorithm with GP and EI in Algorithm 3, where $\phi$ and $\Phi$ denote the standard normal probability density function (p.d.f.) and cumulative distribution function (c.d.f.), respectively, and $f^*$ is the best-known value.

2.2.1.   Surrogate models

The performance of BO significantly hinges on the choice of surrogate model. GP, random forest (RF), tree-structured Parzen estimator (TPE), and Bayesian neural network (BNN) are the commonly employed surrogate models for BO. A concise comparison of surrogates is presented in Table 2. A detailed discussion of these surrogate models follows.

• GP is a nonparametric model that is fully specified by a prior mean function $\mu_0 \colon \mathcal{X}\xrightarrow{}\mathbb{R}$, which is usually set to a constant, and a covariance function $k \colon \mathcal{X}\times \mathcal{X}\xrightarrow{}\mathbb{R}$. Any finite collection of GP induces a multivariate normal distribution. The marginalization properties of GP enable them to compute marginals and conditionals in closed form simply and flexibly. Given the observation dataset $\mathcal{D}_t$ at step $t$, the posterior mean and variance functions are:

where $\mathbf{k}_*$ denotes a vector of covariances between $\mathbf{x}$ and all points in $\mathcal{D}_t$, $k_{**} = k(\mathbf{x}, \mathbf{x})$ denotes the variance of $\mathbf{x}$, and $\mathbf{K}$ is the covariance matrix of all points in $\mathcal{D}_t$. The property of GP is determined by the covariance function $k$, with Mátern $5/2$ kernel being the most commonly used.

While BO with GP performs well on real-valued hyperparameters, it has difficulty with discrete, non-numeric, or conditional hyperparameters. Special kernels are required to address these situations ^[46]. In addition, GP scales poorly (cubically) with increasing data due to the necessity of the inversion of a dense covariance matrix. To mitigate this, some sparsification techniques have been proposed. Among them are sparse pseudo-input GPs (SPGPs) ^[47], which select a subset of the original dataset as inducing pseudoinputs to reduce the rank of the covariance matrix and compute the approximate posterior quickly. Another drawback of the standard GP is its poor scalability with dimensions, limiting the number of hyperparameters it can tune. The properties of hyperparameter space have been leveraged to design new kernels, such as cylindrical kernels ^[48] and additive kernels ^[49].

• RF, which is used in sequential model-based algorithm configuration (SMAC), models the objective function using an ensemble of regression trees ^[50]. The algorithm works as follows: $B$ regression trees are constructed with $n$ data points randomly sampled with replacement from the dataset of size $n$. For each split point of a tree, the split criterion is chosen from a subset of size $pd$ that is randomly selected from $d$ hyperparameters, where $p$ is a split ratio that defaults to $5/6$. When the number of data points on a node falls below a threshold $n_{min}$, the node is set to a leaf and the leaf's prediction is set to the mean or median of the data points on it. Given a new hyperparameter configuration, these trees can produce $B$ predictions for which the mean and variance can be computed.

SMAC can handle continuous, discrete, categorical, and conditional hyperparameters naturally. The time complexities for fitting and predicting are $\mathcal{O}(n\log n)$ and $\mathcal{O}(\log n)$, respectively. The limitation of data points on leaves and parallel training of trees can further reduce budgets, making RF suitable for larger datasets compared to GP. The subsampling of hyperparameters also helps it work on high-dimensional search spaces. However, despite RF's good predictive performance in the vicinity of training data, it exhibits poor performance far from the data. In areas with missing data, the variance can be highly erratic, ranging from very large to very small.

• TPE ^[51] uses kernel density estimation and classifies observations instead of regression. In contrast to most approaches modeling $P(y\mid\mathbf{x})$ directly, TPE considers Bayes' rule $P(y\mid\mathbf{x}) = \frac{P(\mathbf{x}\mid y)P(y)}{P(\mathbf{x})}$ and models $P(\mathbf{x}\mid y)$ and $P(y)$. Two densities, $l(\mathbf{x})$ and $g(\mathbf{x})$, are built over the search space $\mathcal{X}$ as follows:

where $y^*$ is a predefined percentile determined by a threshold $\gamma$ such that $P(y < y^*) = \gamma$. The time complexity is $\mathcal{O}(n\log n)$. The EI acquisition function is then optimized. By construction and simplification, we have the result:

Based on this expression, when optimizing $EI_{y^*}(\mathbf{x})$, finding the optimum point of $\frac{g(\mathbf{x})}{l(\mathbf{x})}$ suffices and it is not necessary to model $P(y)$. Since the Parzen estimators are organized in a tree structure, TPE can handle conditional hyperparameters naturally and outperform GP in structured HPO tasks ^[52,53].

• BNN places a distribution over neural network parameters, amalgamating the strengths of neural networks and probabilistic models ^[54]. Neural networks have strong capabilities of approximating continuous functions, extending the applicability of BO to more complex tasks. Probabilistic models can generate a complete posterior distribution on the predictions, suitable for Bayesian analysis. In Deep Networks for Global Optimization (DNGO) ^[55], the prior distribution is put on the weights of the output layer, while other parameters are learned via point estimation (typically stochastic training). BOHAMIANN ^[56] also adopts a BNN to construct the response surface, with weights sampled using a stochastic gradient Hamiltonian Monte-Carlo (SGHMC) method ^[57] to evaluate the posterior. BNN is more scalable than GP and is faster when the dataset is large ^[55].

2.2.2.   Acquisition functions

Leveraging the predictive posterior, acquisition functions recommend the most promising candidate in the trade-off between the exploitation of known optima and the exploration of uncertainty.

EI is an improvement-based function ^[14]. It measures both the amount and the probability of improvement:

When $f(\mathbf{x})$ is normally distributed with mean $\mu(\mathbf{x})$ and variance $\sigma(\mathbf{x})$, the expectation can be computed analytically as:

where $\phi$ and $\Phi$ denote the standard normal p.d.f. and c.d.f., respectively, and $f^*$ is the best-known value.

Lower confidence bound (LCB), or upper confidence bound (UCB) for maximization problems ^[58], treats uncertainty as an additive incentive. It uses the optimum point of a fixed probability surface according to the model. In the GP case, LCB is computed as:

where $\beta$ is a control parameter and this function is to be minimized. Some guidelines for choosing $\beta$ have been proposed to achieve optimal regret ^[58].

Information-based policies aim to deduce the position of optimum point $\mathbf{x}^*$ by considering the posterior distribution $P(\mathbf{x^*}\mid\mathcal{D})$. Entropy search (ES) ^[59] selects the point that maximally reduces the entropy of $P(\mathbf{x^*}\mid\mathcal{D})$. It measures the expected information gain about the position of $\mathbf{x^*}$:

where $H(\mathbf{x^*}\mid\mathcal{D})$ is the differential entropy of $P(\mathbf{x^*}\mid\mathcal{D})$, and the expectation is over the predictive distribution of $y = f(\mathbf{x})+\delta_n$, where $\delta_n$ is the observation noise. However, this function is intractable and is usually approximated by expensive methods such as Monte Carlo (MC) sampling, whose computation cost is quartic.

Predictive entropy search (PES) ^[60] reformulates the function of ES with the symmetric property of mutual information as:

where the expectation is over distribution $P(\mathbf{x^*}\mid\mathcal{D})$. This function is approximated by expectation propagation and Thompson sampling. The computation cost is cubic, and the performance is not worse than ES empirically.

Max-value entropy search (MES) ^[61] uses the information about the optimum value $y^* = f(\mathbf{x^*})$ instead of $\mathbf{x^*}$. The expected information gain about $y^*$ is expressed as:

Here, $y^*$ is sampled via Gumbel distribution or from the posterior distribution, and the expectation is approximated using MC estimation. The computation cost of MES is much lower since the distribution $P(\mathbf{x^*}\mid\mathcal{D})$ is $d$-dimensional, while $P(y^*\mid\mathcal{D})$ is one-dimensional. Empirically, MES performs at least as well as ES and PES.

2.2.3.   Recent BOs

Although optimizers are epoch efficient with little overheads and some parallel versions of algorithms are now available ^[13], two common drawbacks still exist ^[62]: First, the intrinsic observation process can be time-consuming; second, SMBO provides only fixed hyperparameters. Many methods emerge to accelerate the vanilla BO as will be discussed in Section 3. Notably, BFO (Bayesian Functional Optimization) ^[63] has been proposed to optimize hyperparameters on function spaces. 2-OPT (Two-step optimal) ^[64] enables the acquisition functions to look ahead for two steps to alleviate the shortsightedness of BO. In an attempt to scale BO to high-dimensional domains, while LineBO ^[65] decomposes iteratively the global problem into a sequence of one-dimensional sub-problems, TuRBO (trust region BO) ^[66] maintains a collection of local BO models and performs search across trust regions centered around the best solutions. Nguyen and Osborne ^[67] transform the GP to incorporate more foregone information (e.g., cases where classification accuracy is less than 100%). Meanwhile, MiVaBo (mixed-variable BO) ^[68] extends BO to optimize variables of mixed types. Several methods, including BOPrO (BO with a Prior for the Optimum) ^[69], $\pi$BO ^[70], and PriorBand ^[71], have been proposed to incorporate expert insights on promising configurations into BO, using this prior information to guide the search.

2.3.   Metaheuristic search

A metaheuristic is a generic or high-level optimization strategy or algorithmic framework designed to efficiently explore and exploit solution spaces to find approximate solutions to optimization problems ^[11]. Metaheuristic search often draws inspiration from natural phenomena, such as evolution and annealing. In general, metaheuristics make no assumptions about the objective function, and they do not rely on gradient information, enabling them to tackle non-convex, noncontinuous, and non-smooth optimization problems. According to the number of solutions they hold, metaheuristics can be categorized into single-solution-based methods and population-based methods. Population-based methods run a population of solutions in parallel and evaluate their quality using a fitness function, demanding significant computing power. Advances in computer technology and parallel architectures have facilitated the realization of many algorithms. The distinctions among population-based methods lie in how they initialize and update populations, with performance being greatly influenced by parameter settings. This section introduces two types of population-based methods: evolutionary algorithms and swarm intelligence.

2.3.1.   Evolutionary algorithms (EA)

Evolutionary algorithms (EAs) ^[73] are inspired by Darwin's evolutionary theory. Generally, EAs update populations through the crossover of two ancestral individuals and mutation. Genetic algorithm (GA) ^[74] is the most commonly used method. As shown in Figure 4, GA typically represents solutions as chromosomes, often in the form of a fixed-length binary string, and implements crossover and mutation by simple bit manipulation operations. Two critical parameters in GA are the probabilities of crossover and mutation. The procedures of GA are as follows: A population with $N$ individuals is initially generated by randomly initializing chromosomes. Subsequently, a fitness function, whose outcome often reflects the performance of a configuration, is applied to each individual. Based on the results, selection, crossover, and mutation are performed on the population to yield a new generation with $N$ individuals. These two steps are repeated until convergence or some conditions are met. A majority of innovations of GAs are the selection schemes for producing offspring, including roulette-wheel, tournament, and ranking selection ^[75].

In a certain context, evolution strategy (ES) ^[76] slightly differs from GA by extending the values of GA's chromosomes to the real number domain and introducing the heritable step to guide mutation. Mutation for real numbers is realized by adding noise sampled from a zero-mean normal distribution. The standard deviations for different genes significantly impact the performance of ES. They can be kept constant or adjusted dynamically based on the number of generations and performance ^[77,78]. Selection in ES involves eliminating the worst individuals to maintain a constant population size. While ES was originally designed for real numbers, it can be easily extended to other data types, such as integers ^[79]. ES prefers exploration to exploitation, so it is less prone to getting stuck in local optima.

CMA-ES (Covariance matrix adaptation evolution strategy) ^[80] is the most representative and effective ES algorithm. It dynamically adapts distribution parameters and the step by modifying the covariance matrix. Differential evolution (DE) ^[81] inherits from GA but drives the evolution through mutation based on a differential vector rather than relying on crossover. In the recent decade, EAs have enlightened optimization methods for neural architecture search (NAS) ^[8].

2.3.2.   Swarm intelligence (SI)

SI algorithms are inspired by the collective behavior of biological groups, including ants, grey wolves, grasshoppers, etc. ^[82] Within these groups, each individual has limited capability, but they can jointly accomplish complex tasks through local interactions without any centralized control.

The particle swarm optimization (PSO) algorithm is arguably the most popular SI paradigm ^[83]. The vanilla PSO imitates the flocking behavior observed in bird communities to address optimization problems ^[84]. In PSO, each particle represents a potential solution to the problem and is defined by a position and a velocity. The position is initialized randomly, and the velocity starts at zero. A topology is assigned to the swarm to describe the interconnections among particles, where particles connected to a specific particle are considered its neighbors. At each step, a particle's velocity is updated based on the best positions it and its neighbors have found thus far, and the position is updated accordingly. This enables particles to search for the optimum in parallel, sharing the current best position and fitness value with one or more particles to determine their next movements. To prevent the swarm from being trapped in local optima, mutations are introduced by incorporating slight randomness into the update process.

Additionally, inertia PSO ($\omega$-PSO) ^[85] introduced the inertia weight $\omega$, a positive constant or function, to balance the trade-off between exploration and exploitation. The process of standard $\omega$-PSO is summarized in Algorithm 4 for minimization problems. $x_i$ and $v_i$ are $d$-dimensional vectors representing the position and velocity of particle $p_i$, respectively. $r_1$ and $r_2$ are random variables sampled from the uniform distribution in the range $[0, 1]$. In the algorithm, each particle is the neighbor of all other particles, and thus the topology is a fully connected graph. For alternative topologies, $x_g^*$ in the update formula of $v_i$ should be replaced with the best position of $p_i$'s neighbors.

2.4.   Summary

Table 1 at the beginning of this section provides a concise overview of classical HPO methods just discussed. GradS methods are suitable only in situations where the objective functions are differentiable and obtaining the gradients of hyperparameters is feasible (e.g., learning rate in neural networks). Since gradient provides only local information, these approaches might converge quickly to a local optimum instead of a global optimum ^[16,27]. GS and RS are conceptually simple and are the most basic HPO methods. They can both be readily implemented, and since each hyperparameter configuration evaluation is independent of each other, GS and RS possess the advantage of easier parallelization. In practice, RS is more efficient than GS for large search space and when some hyperparameters have higher importance over others in high-dimensional hyperparameter configuration space ^[10].

In contrast to the simple search schemes above that are either only exploitative (GradS) or explorative (GS and RS), BO allows the exploration of unknown search space and the exploitation of promising regions. While BO is an efficient strategy for the global optimization of expensive black-box functions, its performance fundamentally hinges on the surrogate model and the acquisition function chosen ^[13,86]. Specifically, the quality of BO using GP as the surrogate model, BO-GP, also depends on the choice of the kernel function. Compared to BOs using other surrogates, e.g., RF, TPE, and BNN, BO-GP struggles with large dataset and high dimensions and is only applicable to continuous hyperparameters. Due to the inherently sequential nature of BO algorithms, where the acquisition function guides the selection of subsequent hyperparameter sets based on the current model ^[14], it is challenging to efficiently parallelize the entire optimization process.

Evolutionary algorithms (EAs, includes GA and ES) and swarm intelligence (SI, includes PSO), owning to their population-based nature and the independence of evaluation for different individuals, support parallelization. Similar to BO, they are capable of both exploration (diversification) and exploitation (intensification). The exploration of GA and ES is primarily driven by crossover (recombination for ES ^[87]) and mutation, and the exploitation by the selection mechanism; PSO explores by the stochasticity embedded in its update rules and exploits by the convergence of individuals toward the best-known positions. These advantages come with the cost of additional considerations. In the case of GA and ES, this entails managing supplementary hyperparameters like the fitness function and crossover and mutation rates. For PSO, the challenge lies in careful parameter and topology selection, along with proper population initialization to mitigate the risk of premature convergence ^[83].

3.   Acceleration techniques

Approaches addressing HPO can be distilled into two main methodological families: model-free metaheuristic methods and model-based BO methods. Despite the small overheads of meta-guiders, both conventional metaheuristics and BO methods remain computationally resource-intensive. Specifically, metaheuristic methods need to maintain a considerably large population to prevent the collapse of the solution space. On the other hand, BO algorithms suffer from an iterative waiting period due to the time-consuming observation process throughout the sequential search. To overcome these challenges, numerous methods have been proposed to accelerate the search process and optimize the allocation of computational resources.

This section aims to categorize these methods into the following groups: multi-fidelity optimization, bandit-based algorithm, and early stop. These represent prominent lines of research in the ongoing efforts to enhance the efficiency of HPO.

3.1.   Multi-fidelity optimization

Multi-fidelity (MF) optimization leverages auxiliary information from various sources to reduce the total evaluation cost. In practice, conventional techniques discard intermediate information and overlook the iterative nature of modern DL algorithms. Strategies that combine information from related tasks to speed up the search efficiency also work. Both approaches revolve around finding a balance between the actual objectives, which are expensive and of high-fidelity, and the auxiliary observations, which are cheap and of low-fidelity.

3.1.1.   Multi-fidelity / multi-source

MF-GP-UCB ^[88] pioneered the formalization of a multi-fidelity bandit algorithm by taking GP to establish the relations between low-fidelity approximations and final performance. Impressively, FABOLAS (fast BO on large datasets) ^[89] presents to take the subset size of training data as an auxiliary variable, accelerating the search process 10 to 100 times faster than vanilla BOs for large datasets. FABOLAS has also proposed a classical method for modeling the relation via GP using a product kernel. Simultaneously, misoKG (multi-information source optimization with a Knowledge Gradient) ^[90] describes another generative model that estimates the $i$-th output by summing up two GPs representing the high-fidelity result and the corresponding discrepancy separately.

Furthermore, methods have emerged to improve multi-fidelity approaches by reinforcing acquisition functions. taKG ^[91] suggests a trace-aware knowledge-gradient algorithm that is provably convergent. MF-MES ^[92] incorporates MES ^[61] to enable a better exploit-explore trade-off for multi-fidelity BO without introducing extra parameters, providing an information-theoretic guarantee.

3.1.2.   Multitask / warm start

MTBO (Multitask BO) ^[93] recommends applying a multitask GP via a Kronecker product kernel for a warm start, avoiding unnecessary re-exploration in familiar search space. MI-SMBO (Meta-learning-based initialization SMBO) ^[94] proposed a meta-learning-based initialization to warm start BO. Specifically, BO is initialized by well-performing configurations in similar datasets, with a set of meta-features defining the distances between datasets. ABLR (Adaptive Bayesian linear regression) ^[95] scales MTBO with BNN with a sharing neural network to learn basis features and a Bayesian layer to model the posterior for each output. Recently, WS-CMA-ES (warm starting CMA-ES) ^[96] has also proposed warm-starting the initialization of CMA-ES to address the conflict between the costly adaptation phase and limited evaluation budget.

3.2.   Bandit-based algorithm

Bandit-based algorithms derived from RS have been proven to be compelling in the allocation of limited resources. The successive halving (SHA) algorithm ^[97] dynamically allocates budgets to top-performing configurations by regularly discarding the least promising half.

A notable extension of SHA is the Hyperband algorithm ^[98], a multi-armed bandit algorithm designed to terminate poorly performing configurations. Algorithm 5 summarizes the Hyperband process. Compared to SHA, which refrains from allocating resources to underperforming configurations, Hyperband takes a step further by dividing the budget into iterations. This strategy aims to strike a balance between exploration and exploitation, enhancing the algorithm's ability to navigate the search space effectively. Benefiting from the elegant simplicity and flexibility, Hyperband typically outperforms RS and vanilla BO in practice. Another adaptation made to SHA is asynchronous SHA (ASHA) ^[99], leveraging asynchrony for parallelization. The main idea is to promptly promote configurations to the next rung level, foregoing the necessity to wait for rung completion. While this decision rule may lead to unfavorable configurations being promoted, by the law of large number the impact is expected to diminish as the total number of configurations grows ^[99].

However, the convergence of Hyperband is constrained by its randomly drawn strategy, leading to underutilization of known observations. To address this, BOHB (BO and Hyperband) ^[53] proposed a Hyperband and BO hybrid, replacing the random selection of each Hyperband iteration with a modified TPE surrogate to guide the search. Notably, BOHB employs a multi-dimensional kernel density estimation (KDE) instead of the hierarchy of one-dimensional KDEs in TPE. BOHB is often regarded as the best previous off-the-shelf optimizer.

Recent developments have seen the emergence of methods building upon Hyperband and BOHB. HyperSTAR ^[100] adapts the surrogate model to specific tasks and ranks the hyperparameters by estimation in a joint dataset-hyperparameter space. DEHB (DE and Hyperband) ^[101] combines DE and Hyperband, achieving more robust performance for high-dimensional and combinatorial data than BOHB. The overheads of model-free DE operations remain constant and precede BOHB by up to one order of magnitude. In addition to Hyperband's random sampling, PriorBand ^[71] includes also prior-based and incumbent-based sampling strategies.

3.3.   Early stop

Besides model-free Hyperband, many other stopping criteria are exploited to early terminate poor configurations.

3.3.1.   Curve estimation

Modeling the learning curve to allocate resources and stop running individuals dynamically is in vogue. Freeze-thaw BO ^[102] extends the BO framework with a strong assumption that the training loss curve follows an exponential decay toward some value. A well-designed time kernel gets developed to support this nonstationary prior. However, Freeze-thaw BO has been proven ineffective in describing learning curves of deep networks in practice ^[103].

To enhance representational capacity, learning curve extrapolation (LCE) ^[103] suggests modeling the curves with a set of parametric model families. Various increasing and saturating functions, each of which may capture certain aspects of curves, are ensembled to describe the entire learning process. To further get rid of manually designed functions, which may introduce undue strong assumptions, Klein et al. ^[104] recommends using BNN with basis function layers for prediction. Baker et al. ^[105] incorporates sequential regression models to estimate curves, achieving notable advancements in both NAS and HPO.

3.3.2.   Other criteria

Lately, BO-BOS ^[106] has been proposed to unify the BO and Bayesian optimal stop (BOS) mechanism to eliminate unnecessary queries. A significant difference between BO-BOS and multi-fidelity methods is that BO-BOS determines whether to stop in the training process. BOIL (BO for iterative learning) ^[107] inherits the advantages of both multi-fidelity BOs and curve estimation techniques by optimizing the numeric score of curves compression instead of averaged final performance. Makarova et al. ^[108] suggests an automatic termination criterion based on the discrepancy between the actual HPO objective and the BO-optimized target function.

3.4.   Summary

This section has introduced three main strategies for speeding up the hyperparameter optimizing process: Multi-fidelity, bandit-based algorithms, and early stopping. Multi-fidelity optimization methods operate by leveraging auxiliary information and exploiting more cost-effective approximations of the expensive objective function. In navigating the trade-off between optimization performance and runtime, practical implementations often witness the speed improvements outweighing the errors introduced by the approximations ^[27]. These methods can either actively or adaptively determine the appropriate fidelity (or fidelities), or transfer knowledge from previous experiments or similar tasks. Some literature, e.g., Yang and Shami ^[24] and Shawi et al. ^[31], consider also bandit-based algorithms such as SHA ^[97] and Hyperband ^[98] introduced in Section 3.2 as a subset of multi-fidelity approaches. While most methods that enhance the efficiency of HPO have been predominantly proposed within the context of BO frameworks, learning curve-based prediction for early termination proposed by Domhan et al. ^[103] and Baker et al. ^[105] work on deep neural networks and are agnostic to the hyperparameter optimizer used.

4.   Dynamic algorithm configuration

The above strategies have demonstrated their superiority through various acceleration tricks. However, most HPO algorithms only search for fixed configurations, while dynamic or scheduling hyperparameters can be more welcomed in practice. In this section, we broadly convey recent trends of the emerging DAC algorithms covering the following aspects: gradient-based optimizers, population-based algorithms, and reinforcement learning methods. We also explore a few miscellaneous approaches. A succinct summary of these algorithms is presented in Table 3. They are compared from several aspects, including the types of hyperparameters they can handle and their approach to managing hyperparameters and parameters during the training process.

4.1.   Gradient-based optimizers

In Section 2, we have discussed gradient-based search and introduced both reverse-mode and forward-mode algorithms. While reverse-mode is less computationally demanding with a large number of hyperparameters, forward-mode exhibits greater memory efficiency and is suitable for real-time hyperparameter updates.

Baydin et al. ^[109] derived the hypergradient with respect to the learning rate and updated the learning rate at each iteration. The hypergradient is based on the partial derivative of one-step parameter training, and parameters from the previous time step are irrelevant to the current learning rate. SGD, SGD with Nesterov, and Adam are generalized to online update forms, termed hypergradient descent (HD) variants. HD is considered shortsighted ^[110]. RTHO (Real-time hyperparameter optimization) ^[38] modifies the forward-mode hypergradient algorithm in Algorithm 1 to a real-time update form, which is longsighted but too slow to adapt to abrupt changes in the loss surface. MARTHE (Moving Average Real-Time Hyperparameter Estimation) ^[17] (Algorithm 6) tries to find the balance between HD and RTHO by introducing a discount factor $\mu$, providing globally useful update directions while formal methods fail to cope with loss surface that varies too fast or too slow. Both RTHO and HD can be interpreted as special cases of MARTHE when $\mu = 1$ and $\mu = 0$, respectively. Li et al. ^[111] unified hypergradient approximation methods including back propagation through time, Neumann series, and conjugate gradient descent under the same framework, and has proposed a fully single loop algorithm (FSLA) ^[111] for bi-level optimization based on this framework.

4.2.   Population-based algorithms

Population-based training (PBT) ^[62] derives from evolution search but updates both weights and hyperparameters of the population of agents in a single training process instead. Proportional agents with poor performances get eliminated regularly to generate new individuals exploited from the best-performing ones. Typically, neural network weights are copied from one of the tops while hyperparameters are randomly resampled from the whole space or slightly mutated from best values.

However, the reliance on metaheuristics for exploration leads to space collapse when the population is small. PB2 ^[18] proposed to guide the exploration by a time-varying GP with sublinear regret guarantees, which enable it to search with a small computational budget. A novel trick of batch sampling for the acquisition function helps maintain the diversification of the population. HPM (Hyperparameter mutation) ^[112] regards the agents as students that update their hyperparameters with hypergradient. Meanwhile, an attention-based teacher model is leveraged to learn a mutation schedule. While PB2-Mix ^[113] uses a hierarchical approach to allow PB2 to tackle hyperparameters of continuous and categorical types, BG-PBT (Bayesian generational PBT) ^[114] extends PBT-style methods to consider also ordinal (in addition to continuous and categorical) variables by employing trust-region (TR), GP-based BO.

4.3.   Reinforcement learning methods

Reinforcement learning (RL) ^[115] has gained widespread application in optimizing algorithm configurations ^[116]. Typically, a controller is used to sample new candidates to get a return from the environment, where an evaluator scores the return to generate a reward. The controller then gets updated based on the received reward and current network states.

HOOF (Hyperparameter Optimization on the Fly) ^[117] proposed an off-policy method to adapt sensitive RL hyperparameters to changing environments. In HOOF, candidates are regularly generated and estimated by trajectories sampled from the current policy. The policy then gets updated greedily using the values of candidates. A novel generation strategy with importance sampling and a Kullback-Leibler (KL) constraint reduces the computation cost further.

While HOOF is tailored for RL tasks, Biedenkapp et al. ^[19] formalized learning DAC as a contextual Markov decision process (MDP) where multiple agents sample sequences of parameters across different stages. A global policy is generated according to the distribution of stages, and self-paced learning (SPL) is adopted to evaluate this policy to maximize its reward.

4.4.   Remarks

DAC facilitates the real-time application of HPO while training of the model parameters makes progress. The capability of automatically determining algorithm configuration (or schedule) adaptively in an online fashion is particularly advantageous in scenarios where learning dynamics exhibit high non-stationarity, and a fixed configuration (or schedule) for the entire training duration could potentially be suboptimal ^[62,118]. Successful DAC, however, may require more computational resources compared to static methods ^[16].

Given the iterative nature of many AI algorithms ^[19], especially in the context of RL recognized as a universal modeling framework for sequential decision problems ^[119], dynamically learning optimal hyperparameter configurations that may vary over time during the training process becomes a natural proposition. AutoRL (Automated RL) ^[120,121], a recent area of research, has arisen to address RL algorithms' sensitivity to design choices ^{[122,123,124]} that often leads to laborious and costly manual tuning. AutoRL aims to automate different components of the RL framework, including (PO)MDP modeling, algorithm selection, HPO, and, when DL is used, the architecture search. Considering the nonstationary nature of RL, which adds to the vulnerability of RL algorithms ^[125], integrating dynamic HPO in the AutoRL pipeline can be beneficial ^[120,124].

As DAC is an emerging field, there are approaches optimizing hyperparameter schedules beyond the major classes discussed earlier. AutoLRS (Automatic learning rate scheduler) ^[126] trains a time-series forecasting model to estimate performance based on observations from the initial steps at each training stage and utilize a GP to explore the search spaces further. Multistage QHM (quasi-hyperbolic momentum) ^[127] provides a quasi-hyperbolic momentum modification for almost all momentum variants to dynamically tune hyperparameters, including SGD parameters and batch size.

5.   Multi-objective hyperparameter optimization

Methods presented in earlier sections consider HPO problems with a single objective, e.g., prediction accuracy or error-based measure. Many real-world challenges, however, demand the simultaneous optimization of multiple, sometimes conflicting, objectives (or criteria). These objectives or criteria may encompass, for instance, training accuracy/error, generalization capability, model complexity, sensitivity, specificity, energy consumption, and inference time ^[128].

Karl et al. ^[20] gave the definition of the general MOHPO problem, representing the generalized HPO problem taking into account $m\in\mathbb{N}$ objectives or criteria,

where $f_1\colon\mathcal{X}\xrightarrow{}\mathbb{R}, \ldots, f_m\colon\mathcal{X}\xrightarrow{}\mathbb{R}$ and $f\colon\mathcal{X}\xrightarrow{}\mathbb{R}^m$. A hyperparameter configuration $\mathbf{x}\in\mathcal{X}$ (Pareto) dominates another configuration $\mathbf{x}'\in\mathcal{X}$, if and only if $f(\mathbf{x})\prec f(\mathbf{x}')$, i.e.,

A configuration $\mathbf{x}^*$ is non-dominated, Pareto optimal, or Pareto efficient if and only if there exists no other configuration $\mathbf{x}\in\mathcal{X}$ that dominates $\mathbf{x}^*$. From Figure 5 illustrating a simple MOO example with two minimizing objectives, it can be seen that in contrast to single-objective optimization, MOO problems lack a single universally optimal solution that satisfies all objectives simultaneously. The set of Pareto optimal solutions is referred to as the Pareto set $\mathcal{P}$ ^[20],

and $f(\mathcal{P})$ is the Pareto front. The Pareto set represents solutions that achieve the best trade-off between objectives, where no objective can be made better without making another worse off. The ideal goals of MOO, and thus MOHPO, algorithms are to ^[129]: (ⅰ) find a set of solutions that lies on the Pareto front, and (ⅱ) ensure the solution set found in (ⅰ) is diverse enough to represent the entire range of the Pareto front.

Perhaps the simplest approaches to MOHPO are GS (Section 2.1.2) and RS (Section 2.1.3). To adapt single-objective GS and RS to MOHPO problems, given that each point represents a combination of hyperparameters in the hyperparameter space, one can simply evaluate the performance based on multiple objectives at each chosen point and return all non-dominated solutions as the Pareto set. When dealing with high- or large-dimensional search space, GS and RS can be computationally inefficient and lack the ability to exploit the structure of the search space efficiently. They can, however, serve as simple baselines for specialized MOHPO algorithms, e.g., ^[130,131].

Below we introduce the canonical approaches tailored for MO(HP)O problems, distinguishing them into three main categories: scalarization, metaheuristic-based, and model-based. For detailed discussions on MOHPO, interested readers are referred to Karl et al. ^[20] and Morales-Hernández et al. ^[21].

5.1.   Scalarization

Scalarization is a straightforward technique to MOHPO. This approach works by transforming multiple objectives into a single objective function, which then single-objective optimizers can be used ^{[132,133,134]}. Two of the most popular scalarization methods are the (i) weighted sum, which combines the objectives linearly with each objective $f_i(\mathbf{x})$ multiplied by a user-specified weight $\lambda_i$,

and the (ⅱ) $\epsilon$-constraint ^[135], which retains only one objective $f_i$ and turns the rest of the objectives $f_j, \forall j = 1, \ldots, m, \, j\neq i$, into constraints, i.e., restrict them to be within user-specified values $\epsilon_j$,

Another scalarization function or its variants that has been used in other MOO approaches (such as those introduced in the following sections) is the (weighted) Chebyshev or Tchebycheff function (TCH) ^[132],

where $(z_{i}^{*})$ is usually set to the ideal reference point, i.e. $z_{i}^{*} = \min_{\mathbf{x}\in\mathcal{X}}f_i(\mathbf{x})$ for $i = 1, \ldots, m$.

5.2.   Multi-objective metaheuristics

NSGA-Ⅱ (Non-dominated sorting GA Ⅱ) ^[136], building on the primitive NSGA algorithm ^[137], is a widely adopted algorithm for MOO problems. It employs a GA framework and introduces non-dominated sorting to categorize solutions based on their dominance relationships, and crowding distance to sustain a diverse set of solutions on the Pareto front. NSGA-Ⅲ ^[138,139] extends NSGA-Ⅱ to MOO problems with a larger number of objectives by involving predefined reference points to aid in diversity preservation.

SPEA2 (Strength Pareto EA 2) ^[140] employs a strength-based approach within its EA framework, using Pareto dominance to guide the selection, favoring individuals that dominate more other individuals. Diversity is achieved through an external, fully-filled archive. SPEA2 and NSGA-Ⅱ both incorporate elitism in which the best individuals are preserved in each generation.

MOEA/D (Multi-objective EA based on decomposition) ^[141] takes a decomposition approach, explicitly using scalarization to transform the multi-objective problem into a set of single-objective subproblems. These subproblems are simultaneously optimized, achieving diverse and evenly distributed solutions along the Pareto front through properly selected decomposition methods and weight vectors ^[141].

To maximize the hypervolume indicator, where the hypervolume (or the $\mathcal{S}$-metric) can be considered as the size covered in the objective space by a set of non-dominated solutions with respect to a user-defined reference point ^[142], SMS-EMOA ($\mathcal{S}$-metric selection evolutionary MOO algorithm) ^[143] proposes a steady-state EA with constant population size. SMS-EMOA applies non-dominated sorting from NSGA-Ⅱ ^[136] as first ranking criterion and discards individuals with low marginal hypervolume contribution.

Analogous to EAs, PSO has also been used for MOO. NSPSO (Non-dominated sorting PSO) ^[144] extends single-objective PSO to MOO through information sharing, motivating the entire swarm population progress toward the Pareto front. Non-dominated sorting and crowding distance from NSGA-Ⅱ ^[136] are used in NSPSO. Inspired by multi-objective EAs, Coello et al. ^[145] incorporated the concept of Pareto dominance and a secondary (external) population in its MOO approach via PSO. An adaptive mutation operator facilitates throughout exploration, while a historical record of previously non-dominated solutions promotes convergence toward the Pareto front.

5.3.   Multi-objective model-based optimization

Approaches for multi-objective BO can broadly be categorized into scalarization, leveraging Pareto hypervolume (PHV) indicator ^[142], and information-theoretic methods.

ParEGO (Pareto efficient global optimization) ^[146] using GP as the surrogate based on the EGO approach ^[45], approximates the Pareto front with a single objective scalarized via the augmented Tchebycheff function ^[146], where the parameterization of the weight vector is sampled uniformly per iteration.

SMS-EGO ^[147] is another approach based on EGO ^[45]. Instead of using scalarization, SMS-EGO models each objective with a separate surrogate model, with the optimization and selection based on the hypervolume indicator ^[142]. SMS-EGO enhances the expected hypervolume improvement (EHI/EHVI) ^[148] acquisition function, initially proposed for surrogate-assisted evolutionary multi-objective search ^[149], by introducing adaptive search space reduction for improved scalability. As EHVI demands high computational complexity, Daulton et al. ^[150] proposed qEHVI, a differentiable hypervolume improvement acquisition function. qEHVI allows gradient-based parallel and sequential greedy optimization via the inclusion-exclusion principle.

PESMO (Predictive entropy search) ^[151] and MESMO (multi-objective maximum entropy search) ^[152] are information-theoretic methods rooted in information theory. Both PESMO and MESMO build an individual surrogate model for each objective. PESMO's acquisition function utilizes input space entropy, selecting the next evaluation that maximizes information gain about the optimal Pareto set. In contrast, MESMO proposes an output-space-entropy-based acquisition function for candidate selection, evaluating the input that maximizes information gain about the optimal Pareto front.

5.4.   Remarks

Evolutionary-based methods, particularly exemplified by tools like NSGA-Ⅱ ^[136] (refer to Table 4), have been predominant in MOO, owing to their derivative information-free nature, simplicity for implementation, and flexibility with widespread applicability ^[129]. As we have seen in Section 5, MOO aims to find a set of solutions, the Pareto set, making EAs a natural choice as they inherently rely on population for optimization.

Apart from the prominent approaches introduced earlier, recently there has been growing interest in encompassing additional considerations when working with MOO problems. For instance, observing that observations are often subject to noise while optimization formulations assume noiseless observations, Daulton et al. ^[153] proposed NEHVI (noisy expected hypervolume improvement) for noisy multi-objective BOs. Lin et al. ^[154] and Misitano et al. ^[155] advocated incorporating decision-maker preferences. Instead of searching for the Pareto front, Malkomes et al. ^[156] proposed the constraint active search (CAS) formulation to search for diverse solutions satisfying objectives-turned-constraints.

In MOHPO, efforts have also been put toward adapting advanced single-objective HPO techniques to the multi-objective counterpart. For instance, a multi-fidelity method for MOHPO building upon the Hyperband algorithm ^[98] and scalarization was proposed by Schmucker et al. ^[131]. Similarly, Chen et al. ^[157] adapted BOHB ^[53] to MOHPO, leveraging the integrated information from a multi-fidelity ensemble model effectively in an online fashion. Dushatskiy et al. ^[158] introduced MO-PBT, the multi-objective version of PBT ^[62], demonstrating superior performance over MO-ASHA ^[159], the multi-objective version of ASHA ^[99].

6.   Tools, applications, and further discussion

6.1.   Public frameworks and tools

In the past, hyperparameters were usually tuned manually, which is time-consuming. To reduce the bar of using HPO algorithms and enhance their widespread applicability, various libraries and frameworks have been developed. We tabulate the popular frameworks used for HPO, referencing notable works such as ^{[22,23,24,31,32,160]}.

Existing HPO frameworks can be categorized in several ways. Based on the distribution of computing resources, they fall into three main categories: centralized, distributed, and cloud-based ^[31]. When considering optimization methods, they can be distinguished as RS-based, BO-based, metaheuristic-based, and so on. They can also be classified based on the type of problems they address, including HPO, NAS, and AutoML. HPO tools are primarily designed for tuning given hyperparameters; NAS tools are used to automatically discover the optimal architecture or structure of a neural network for a given task; AutoML considers all or most tasks in building ML models, including feature engineering, model construction, and HPO. Overview of existing HPO frameworks and tools is provided in Table 4.

6.2.   HPO applications

HPO has emerged as a pivotal component of AutoML, finding extensive applications across diverse domains and tasks. For instance, it is applied for software sensor design ^[196], electroencephalography (EEG) data decoding ^[197], smart grid ^[198], P systems optimization ^[199], and healthcare ^[200].

Data-driven models have become integral in the realm of software sensor design for vehicles, where the performance is notably influenced by hyperparameters. A specific study ^[196] focused on designing a roll angle estimator based on an artificial neural network (ANN), employing techniques including GS, Hyperband, BO, and GA. The results emphasized the significant impact of search space size on performance, with knowledge-based methods outperforming their counterparts.

In the domain of EEG data decoding for brain-computer interfaces (BCIs), HPO methods play a crucial role in optimizing DL models for the classification of EEG recordings. In Stober et al. ^[201], hyperparameters associated with the convolutional neural networks (CNN) used to classify EEG recordings of rhythm perception were optimized with BO. In another work by Drouin-Picaro and Falk ^[202], GS for HPO was used in the classification of EEG signals corresponding to natural saccade with CNN and multilayer perceptron (MLP). Coonet et al. ^[197] suggested that more experiments should be conducted to investigate whether the generalization of HPOs across subjects is feasible.

In a smart grid, the consumption of electricity varies from time to time, which burdens the electricity systems. Prediction with the ML models can help achieve the balance between demand and supply, and manage the energy efficiently ^[198]. ML models such as support vector machine (SVM), ANN, and BNN are commonly used for this problem. To achieve a good predictive performance, tuning the hyperparameters is of vital importance. For example, Zhou et al. ^[203] proposed a system based on autoencoders and tuned the hyperparameters using GA. Additionally, AutoML frameworks are likely to be applied to this field in the future search.

In recent attempts to create bridges between adaptive P systems and ML paradigms, the optimization of one of the hyperparameters, which is the type of the spiking neuron used in spiking neural (SN) P systems, prior to the training of P systems, can potentially benefit from HPO ^[199].

Biomedical applications, encompassing healthcare, biomedical research, and big biomedical data, have also witnessed the advantages of integrating HPO methods in the ML pipelines^[200]. Hospitals can deploy ML models for health outcome improvement, healthcare cost reduction, and clinical research advancement ^[204]. In fact, certain frameworks are developed exclusively for healthcare. One example is AutoPrognosis ^[205], which uses BO to optimize models and hyperparameters for clinical prognosis. HPO also has non-negligible impact when working with medical images using AI techniques ^[206]. For instance, BO was used to optimize the network architecture of Nishio et al. ^[207] for lung segmentation using chest X-ray (CXR) images with severe abnormalities. BO with TPE as the surrogate was also used in Abdellatif et al. ^[208] on the Improved Weighted RF for predicting the presence of cardiovascular disease and patient survival. Experiments by Belete and Huchaiah ^[209] employing GS-based HPO on eight ML models have shown improvement over statistical way of optimization in predicting HIV/AIDS test results. Similarly, Nematzadeh et al. ^[210] demonstrated that by employing dedicated HPO algorithms for ML models in the classification and regression of biomedical datasets, training process and model performance improved when compared to using blindly chosen hyperparameters. Despite these advancements, challenges persist. This includes the limited interpretability of ML models contributing to user skepticism regarding predictions, efficiency concerns as current methods struggle to swiftly identify a near-optimal hyperparameter configuration, and the protracted trial-and-error processes presenting an impracticality given the demand for approaching thousands of predictive modeling problems in personalized medicine. In light of these challenges, DAC algorithms emerge as a promising avenue.

6.3.   Further discussion

In this paper, we have discussed four kinds of HPO methods that are closely connected. Classical techniques, with their foundational concepts proposed over a decade ago, have evolved alongside advancements in ML models. On one hand, these techniques are employed to tune hyperparameters, enhancing the performance of ML models. On the other hand, ML models contribute to the expansion and evolution of these techniques. ML models such as RF and BNNs can serve as surrogate models of BO. As ML models experience longer training times, there is a growing demand for more efficient HPO techniques. Researchers have responded by designing various frameworks to carefully manage computing resources, while retaining the core ideas. DAC algorithms, for instance, aim to utilize resources efficiently within a single training cycle to achieve near-optimal performance. These algorithms often involve structural modifications to classical techniques, such as gradient-based and population-based methods, allowing for on-the-fly updates to hyperparameters. However, a common challenge faced by these methods is the inherent trade-off between performance and efficiency. Driven by real-world situations where practical considerations involve additional metrics or criteria, framing the HPO problem as an MOHPO problem is a more pragmatic approach. MOHPO, being an extension of the broader MOO, leverages existing MOO methodologies, with recent endeavors adapting single-objective HPO algorithms for multi-objective cases.

HPO algorithms encounter several challenges and issues. First, the diversity of hyperparameter types and complex search spaces can impact the usability of algorithms, often requiring disharmonious extensions that may affect performance and theoretical properties. Second, the high-dimensionality of hyperparameters makes convergence challenging due to the vast number of samples required to explore the search space. Identifying the few influential hyperparameters is a daunting task. Third, handling the intricate relationships among hyperparameters poses difficulty, as the value of one hyperparameter may significantly affect another, while others remain independent. Capturing these relations can reduce the complexity of the search space. Additionally, scalability is a concern, with standard BO-GP having a complexity of $\mathcal{O}(n^3)$, which becomes impractical with a large number of samples. Furthermore, the issue of transferring hyperparameters from task to task or leveraging knowledge from previous search results remains a challenge. Most algorithms treat different tasks independently, even when sharing the same datasets or models, leading to inefficiencies. Lastly, the optimal hyperparameters may change as datasets grow in size. Many existing algorithms require a search from scratch, which is not conducive to the dynamic nature of big data.

In this paper, we have only reviewed approaches to general HPO, acceleration techniques, and algorithms for the emerging DAC and MOHPO. It is noteworthy that various efforts explore HPO from distinct perspectives, warranting attention. For instance, work looking at constrained HPO ^{[211,212,213,214]} or constrained BO ^{[215,216,217]} and investigations on robustness ^{[53,180,218,219,220]}. Explorations of HPO with meta-learning and AutoML ^{[221,222,223,224]} also offer valuable insights into related areas.

7.   Conclusion and outlook

Complex computing systems, exemplified by modern ML pipelines, have found diverse applications across various domains. In the pursuit of more effective and efficient deployment of these pipelines, researchers have increasingly focused on the performance and efficiency of HPO algorithms – a focal point of this paper. We begin by providing a broad overview of HPO, delving notably into strategies tailored for DL algorithms. Subsequently, we explore methods to accelerate optimization procedures. This is followed by comprehensive and systematic reviews of the emerging DAC and MOHPO, offering insights for future research. We also present a comparative analysis of existing HPO tools and their applications across different domains, laying the groundwork for potential future research endeavors.

The potential applications of HPO span diverse areas, presenting a promising landscape for exploration and advancement. From the ML application perspective, here we discuss important areas that underscore the impact of HPO. One key domain is NAS, wherein HPO manifests as a task within a discrete search space. First, NAS can be regarded as an HPO task on discrete search space, and recent works have explored various search methods, including RL ^[225], EA ^[226], BO ^[227], and gradient-based methods ^{[228,229,230]}. Noteworthy applications of NAS extend to complex vision tasks such as object detection ^[231,232] and segmentation ^[233,234]. Recent work by Wang et al. ^[235] introduces a NAS framework based on the “mergeNAS” technique ^[229], allowing for searches within any custom search spaces across a spectrum of vision tasks.

In addition to ML, the fusion of combinatorial optimization ^[236,237] with HPO within the realm of applied mathematics offers a platform for further exploration. This includes but is not limited to, tackling challenges like the traveling salesman problem ^[238], vehicle routing problem ^[239], mix-integer programming ^[240], boolean satisfiability ^[241], portfolio optimization ^[242], graph matching, either through ML approaches ^[2434] or conventional methods ^[244], graph clustering ^[245], and graph edit distance computing ^[246].

Despite HPO's long history spanning over half a century, numerous promising areas warrant continued efforts. We envision that this comprehensive survey will not only equip researchers with diverse backgrounds to understand the current state and evolution of HPO, facilitating its seamless integration into future work, but also provide practical insights for practitioners in ML and HPO-related domains.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgment

This work was partly supported by National Natural Science Foundation of China (623B1009, 62073333), and Shanghai Municipal Science and Technology Major Project (2021SHZDZX0102). The authors are also thankful for the anonymous reviewers for their valuable suggestions and comments to help improve this survey in all aspects.

Conflict of interest

Junchi Yan is an editorial board member for Mathematical Biosciences and Engineering and was not involved in the editorial review or the decision to publish this article. All authors declare that there are no competing interests.