Figure 1.
EBSD-0.4 µm showing OM for as-received sample.
The restoration mechanism (RM) and subgrain characteristics of 0.05C-1.52Cu-1.51Mn steel in single-hit plane strain compression (PSC) were investigated using a thermomechanical simulator (Gleeble). It was observed that at diminished deformation temperature (DT) and larger strain rate, the austenitic phase (during deformation) showed some thermal/dynamic softening (TH/DRS), but it did not reach the condition where the "work hardening rate" (WH rate)became constant with the stress, i.e., dynamic recovery (DRV) softening balances work hardening (WH). However, it was observed that at higher DT and lower strain rate, the "WH rate" for samples deformed at 850 ℃ (at a strain rate of 0.01 s−1), 950 ℃ (at strain rates of 0.1 and 0.01 s−1) and 1000 ℃ (at strain rates of 0.1 and 0.01 s−1) increased to negative peak, and then decreased to almost zero (for samples deformed at 950 and 1000 ℃ at a strain rate of 0.01 s−1), which is the onset of steady-state flow. When the sample deformed at 750 ℃ followed by quenching, the microstructure was indicative of a deformed microstructure rather than a transformed microstructure. It was observed that there was an increase in the extent of substructure formation and a decrease in mean subgrain size with increasing strain rate. When samples deformed at 850,950 and 1000 ℃, these temperature ranges were above Ar3 temperature. Hence quenching would lead to a phase transformation and hence the deformed microstructure would be eliminated. The room temperature microstructures when the sample deformed at a strain rate of 1 s−1, were nicely equiaxed and clean with no dislocations present. However, at lower strain rates of 0.1 and 0.01 s−1, microstructure showed substructures.
Citation: Pawan Kumar. Subgrain characterization of low carbon copper bearing steel under plane strain compression using electron backscattered diffraction[J]. AIMS Materials Science, 2023, 10(6): 1121-1143. doi: 10.3934/matersci.2023060
| [1] | ME Makhatha . Effect of titanium addition on sub-structural characteristics of low carbon copper bearing steel in hot rolling. AIMS Materials Science, 2022, 9(4): 604-616. doi: 10.3934/matersci.2022036 |
| [2] | Marcílio M. A. Filho, Paulo A. G. Piloto, Carlos Balsa . The load-bearing of composite slabs with steel deck under natural fires. AIMS Materials Science, 2022, 9(1): 150-171. doi: 10.3934/matersci.2022010 |
| [3] | Marcin Kargul, Marek Konieczny . Copper matrix composites reinforced with steel particles. AIMS Materials Science, 2021, 8(3): 321-342. doi: 10.3934/matersci.2021021 |
| [4] | Yustina M Pusparizkita, Vivi A. Fardilah, Christian Aslan, J. Jamari, Athanasius P Bayuseno . Understanding of low-carbon steel marine corrosion through simulation in artificial seawater. AIMS Materials Science, 2023, 10(3): 499-516. doi: 10.3934/matersci.2023028 |
| [5] | Andrea Di Schino . Corrosion behavior of new generation super-ferritic stainless steels. AIMS Materials Science, 2019, 6(5): 646-656. doi: 10.3934/matersci.2019.5.646 |
| [6] | Ivan Jandrlić, Stoja Rešković, Dušan Ćurčija, Ladislav Lazić, Tin Brlić . Modeling of stress distribution on the basis of the measured values of strain and temperature changes. AIMS Materials Science, 2019, 6(4): 601-609. doi: 10.3934/matersci.2019.4.601 |
| [7] | Yerbolat Koyanbayev . Applying the Hollomon-Jaffe parameter to predict changes in mechanical properties of irradiated austenitic chromium-nickel steels during isothermal exposure. AIMS Materials Science, 2024, 11(2): 216-230. doi: 10.3934/matersci.2024012 |
| [8] | Falko Böttger-Hiller, Klaus Nestler, Henning Zeidler, Gunther Glowa, Thomas Lampke . Plasma electrolytic polishing of metalized carbon fibers. AIMS Materials Science, 2016, 3(1): 260-269. doi: 10.3934/matersci.2016.1.260 |
| [9] | Krzysztof Gargul . Ammonia leaching of slag from direct-to-blister copper smelting technology. AIMS Materials Science, 2020, 7(5): 565-580. doi: 10.3934/matersci.2020.5.565 |
| [10] | Songtam Laosuwan, Shigeru Nagasawa . Development of compressive testing device for glass fiber based single face corrugated structure sheet, and estimation of buckling strength of straight panel of that structure sheet. AIMS Materials Science, 2021, 8(6): 881-898. doi: 10.3934/matersci.2021054 |
The restoration mechanism (RM) and subgrain characteristics of 0.05C-1.52Cu-1.51Mn steel in single-hit plane strain compression (PSC) were investigated using a thermomechanical simulator (Gleeble). It was observed that at diminished deformation temperature (DT) and larger strain rate, the austenitic phase (during deformation) showed some thermal/dynamic softening (TH/DRS), but it did not reach the condition where the "work hardening rate" (WH rate)became constant with the stress, i.e., dynamic recovery (DRV) softening balances work hardening (WH). However, it was observed that at higher DT and lower strain rate, the "WH rate" for samples deformed at 850 ℃ (at a strain rate of 0.01 s−1), 950 ℃ (at strain rates of 0.1 and 0.01 s−1) and 1000 ℃ (at strain rates of 0.1 and 0.01 s−1) increased to negative peak, and then decreased to almost zero (for samples deformed at 950 and 1000 ℃ at a strain rate of 0.01 s−1), which is the onset of steady-state flow. When the sample deformed at 750 ℃ followed by quenching, the microstructure was indicative of a deformed microstructure rather than a transformed microstructure. It was observed that there was an increase in the extent of substructure formation and a decrease in mean subgrain size with increasing strain rate. When samples deformed at 850,950 and 1000 ℃, these temperature ranges were above Ar3 temperature. Hence quenching would lead to a phase transformation and hence the deformed microstructure would be eliminated. The room temperature microstructures when the sample deformed at a strain rate of 1 s−1, were nicely equiaxed and clean with no dislocations present. However, at lower strain rates of 0.1 and 0.01 s−1, microstructure showed substructures.
Abbreviations: BC: Band contrast; BCGB: Band contrast with grain boundaries; DT: Deformation temperature; DRS: Dynamic softening; DRV: Dynamic recovery; DRX: Dynamic recrystallization; EBSD: Electron backscattered diffraction; EBSD-0.4 µm: EBSD image at a step size of 0.4 µm; LAMs: Low angle misorientation; MAD: Misorientation angle distribution; HAMs: High angle misorientation; OM: Orientation map; PSC: Plane strain compression; RM: Restoration mechanism; WH: Work hardening
Low carbon copper bearing steel becomes one of the most common types of steel that is used for construction purposes. The diminution in carbon weight % advances toughness and weldability at the cost of strength. However, the low amount of carbon imparts malleability and additional copper content provides necessary strengthening by precipitation hardening [1]. Therefore it is neither extremely brittle nor ductile; therefore it is widely used in sheet metal industries due to its significant malleability. It is also endowed with softer properties as compared to the steel that contains higher carbon content, therefore it is easier to weld and forge, hence low carbon copper-bearing steel is most widely used in automotive plates, rivets, wire tubes, structural and steel plates, low-temperature pressure vessels. In the context of the above description of low carbon copper bearing steel, it can be said that such steel possesses a better combination of weldability and strength. Hence it has significant applications in automobile industries and sheet metal work.
The microstructure of such materials can be improved by controlling their restoration process/mechanism. Depending upon process parameters and composition, the microstructure changes associated with hot deformations are the creation of dislocations, WH, annihilation and re-arrangement of dislocations (recovery) and dynamic recrystallization (DRX). Therefore knowledge of the flow curve (at different process parameters) and microstructure is vital to determine the RM of such steel in hot deformation [2]. Various simulation tests like the hot tensile test, uniaxial compression test and the strain-induced crack opening test have been used to optimize process parameters and study the restoration process in steel. However, PSC tests are widely used because the deformation force, strain (ε) and thermal flow are in the same direction as those found in hot rolling. Link et al. reported WH in steel [3]; the WH phenomenon in steel is associated with the rate of storage of dislocations, which depends upon carbon content and initial grain size. It is favoured at a higher ε̇ (strain rate) at smaller strains. Low stacking-fault energy steels generally have discontinuous dynamic recrystallization (DDRX) [4,5,6]. However, steel with a high degree of stacking fault usually has a continuous dynamic recrystallization (CDRX) [7,8,9,10]. Junior et al. proposed that steel having highly mobile dislocations tends to show a higher degree of DRV [11]. DRV is reported at larger ε̇ and diminished DT, while DRX is favoured at lower ε̇ [12]. It seems that the sub-structure characteristics and RM of such low carbon copper bearing steel in PSC were not reported to date, therefore the knowledge of flow curve, WH rate and microstructure evolution is very important to study the RM of such steel. Therefore, in the present work, the "study of RM and subgrain characteristics of low carbon copper bearing steel deformed under single-hit PSC" has been done.
The alloy under investigation was 0.05C-1.52Cu-1.51Mn (in wt%) steel. The single-hit PSC tests were done on brick-shaped samples with a width of 20 mm, a length of 15 mm and a thickness of 10 mm using a thermomechanical simulator (Gleeble 3800). The specimens were preheated at 1100 ℃ and carried out for 120 s to standardize the temperature. They were cooled down at a cooling rate of 5 ℃ s−1 to different temperatures of 750,850,950 and 1000 ℃. It was then subjected to PSC at 750 ℃ (at a ε of 0.95 and ε̇ of 1, 2 and 5 s−1), 850 ℃ (at a ε of 0.7 and ε̇ of 1, 0.1 and 0.01 s−1), 950 ℃ (at a ε of 0.7 and ε̇ of 1, 0.1 and 0.01 s−1) and 1000 ℃ (at a ε of 0.7 and ε̇ of 0.1 and 0.01 s−1) trailed by water quenching to study the microstructure at different thermomechanical conditions. The microstructure was carried out using electron backscatter diffraction (EBSD) operated at 20 kV. The working distance was 25 mm from the gun with an aperture of 60 μm. Samples were prepared by standard mechanical polishing. The EBSD characterization was done using FEG LEO 1530 scanning electron microscope. The step size for EBSD maps was 0.4 µm.
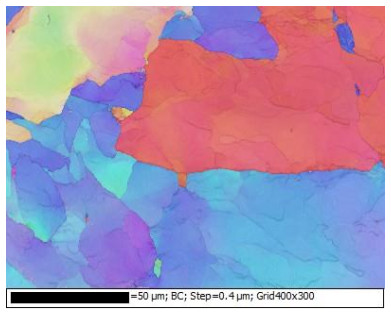
The EBSD image at a step size of 0.4 µm (EBSD-0.4 µm) for orientation map (OM), band contrast (BC), band contrast with grain boundaries (BCGB) and misorientation angle distribution (MAD) of of the as-received sample is shown in Figures 1–4, respectively. The OM (Figure 1) defined the crystallographical orientation of the as-received sample. Similar crystallographical orientation is exhibited by similar colours. It was observed with a continuous variation in the Euler angle considering the scanned area of EBSD mapping. The BC image (Figure 2) exhibited the single phase of the microstructure; however, the BCGB image (Figure 3) showed BC with grain boundaries. It was observed that the microstructure was not free from substructures. It was also confirmed by MAD (Figure 4), considering the fractions of misorientation from 0 to 60°. The fraction of LAMs was higher as compared to HAMs.
The true stress-true strain (σ-ε) flow curve for samples deformed under single-hit PSC is shown in Figures 5 and 6. The contraindication of the steady-state flow was observed for samples deformed at lower DT of 850 and 750 ℃ at all employed ε̇ and higher DT of 950 and 1000 ℃ at ε̇ of 1 and 0.1 s−1. However, the sample showed steady-state flow at DT of 950 and 1000 ℃ and ε̇ of 0.01 s−1. The ε at peak σ, and ε for steady state initiation for samples deformed under various thermomechanical conditions is shown in Table 1.
| Deformation condition | ε at peak σ | ε for steady state initiation |
| 1000 ℃-ԑ̇ 0.1 s−1 | 0.28 | No indication of a steady state |
| 1000 ℃-ԑ̇ 0.01 s−1 | 0.21 | 0.32 |
| 950 ℃-ԑ̇ 1 s−1 | 0.49 | No indication of a steady state |
| 950 ℃-ԑ̇ 0.1 s−1 | 0.26 | No indication of a steady state |
| 950 ℃-ԑ̇ 0.01 s−1 | 0.22 | 0.35 |
| 850 ℃-ԑ̇ 1 s−1 | 0.55 | No indication of a steady state |
| 850 ℃-ԑ̇ 0.1 s−1 | 0.41 | No indication of a steady state |
| 850 ℃-ԑ̇ 0.01 s−1 | 0.28 | No indication of a steady state |
| 750 ℃-ԑ̇ 5 s−1 | 0.82 | No indication of a steady state |
| 750 ℃-ԑ̇ 2 s−1 | 0.83 | No indication of a steady state |
| 750 ℃-ԑ̇ 1 s−1 | 0.89 | No indication of a steady state |
DownLoad:
CSV
The ε at peak σ decreased for samples deformed at 1000,950 and 850 ℃ with a decrease in the ε̇ from 1 to 0.01 s−1. This is due to a diminution in the degree of work-hardening at elevated DT and lower ε̇ (i.e., thermal/strain softening was favoured) [13]. However, there was a very marginal change in the ε at peak σ when the sample was deformed at a temperature of 750 ℃.
It is known that the WH effect is prominent at lower DT and higher ε̇, while strain softening is preferred at higher DT and lower ε̇ [13]. To apprehend the flow behaviour, the exploration of the "WH rate" is vital. The variation of the WH rate with σ diagram is shown in Figures 7 and 8. There were two distinct regions (positive and negative) of "WH rate".
The initial stage is the region where the "WH rate" was positive (before peak σ) and a swift increase in the flow stress was observed (for all samples), it envisages WH phenomena. This was the region where the dislocation density surges as the strain enriches, endorsing the subgrain creation [14]. It was also described that DRX initiates before attaining the σ peak [15,16,17]. As an outcome, there is a change in the slope of the WH rate vs σ diagram (Figures 7 and 8) just before the peak σ. This resembles the region where "stored energy" reaches the activation energy for recrystallization. At the commencement of this stage, a slightly positive "WH rate" delivers the critical driving force for recrystallization and neutering the WH rate behaviour. However, the recrystallization is yet to be confirmed by the microstructural advancement.
The subsequent stage of the WH rate was negative (after the peak σ), designating the predomination of thermal softening over WH. The values of "WH rate" showed three types of variation propensity with the σ such as positive increasing variables with σ (a decrease in the value of "WH rate" with a decrease in the σ), almost positive constants (value of "WH rate" became constant) and negative variables with σ (an increase in value of "WH rate" with a decrease in σ). In context to the variation of the value of WH rate with the σ, Quan et al. reported that the positive increasing variables represent the predominance of WH, positive constants represent the balance between dominant DRV softening and WH, and negative variables represent the predominance of DRX softening [14]. Therefore, the type of flow stress evolution was distinguished by the following three characteristics at different thermomechanical conditions: WH followed by DRX, WH followed by DRV, and WH followed by minimal dynamic softening (DRS). When the sample deformed at 750 ℃ (at ε̇ of 1, 2 and 5 s−1), this temperature might be below the Ar3. Therefore it is most likely that it was ferrite/austenite-ferrite which was deformed during straining. Therefore the quenched microstructure might be a deformed microstructure rather than a transformed microstructure. When samples deformed at 750 ℃ at a strain rate of 1 s−1, it was a ferritic/austenite-ferrite region that showed mostly WH. However, some TH/DRS was observed when the sample deformed at 750 ℃ (at ε̇ of 2 and 5 s−1). When samples deformed at higher temperatures of 850 (at a ε of 0.7 and ε̇ of 1, 0.1 and 0.01 s−1), 950 (at a ε of 0.7 and ε̇ of 1, 0.1 and 0.01 s−1) and 1000 ℃ (at a ε of 0.7 and ε̇ of 0.1 and 0.01 s−1), these temperatures might be above the Ar3 and hence the samples deformed in the austenitic phase. The microstructure during deformation was most likely austenite and the quenching would lead to a phase transformation (rather than a deformed microstructure), hence the deformed microstructure would be eliminated. However, it is once again to be confirmed by microstructural evolution. It is important to note that the deformed austenite may be fine-grained or large-grained depending upon process parameters used during deformation. Some TH/DRS of austenite at 850 (at ε̇ of 1 and 0.1 s−1) and 950 (at a ε̇ of 1 s−1) was also observed but it did not reach the condition where the "WH rate" value became constant with the σ. However, when the DT increases and the rate of deformation decreases, the "WH rate" values for the austenitic phase deformed at 850 (at ε̇ of 0.01 s−1), 950 (at ε̇ of 0.1 and 0.01 s−1) and 1000 ℃ (at ε̇ of 0.1 and 0.01 s−1) increased up to the negative peak, which corresponds to the valley point of WH rate vs σ curve and then decreased to almost zero (for samples deformed at 950 and 1000 ℃ at ε̇ of 0.01 s−1), which corresponds to the onset of steady-state flow [14]. The samples deformed at elevated temperatures (950 and 1000 ℃) and lower ε̇ (0.01 s−1) showed some regions where austenitic WH rate was steady (after a ε of 0.35 and 0.32, respectively); it indicated the possible balance between DRV and WH (in austenitic phase).
It is important to note that the quenched microstructure was dependent upon the initial microstructure during deformation. It may be in a transformed or deformed state (after quenching), which again depends on DT. When samples deformed at 750 ℃, the ferritic/austenite-ferrite region underwent WH/softening during straining. However, the extent of WH/softening depended upon ε̇. Therefore, after quenching the microstructure was a deformed microstructure (in ferrite) rather than a transformed microstructure. The ε̇ during deformation were 1, 2 and 5 s−1, hence the quenched microstructure contained deformed ferrite with substructures and marginally recrystallized ferrite grains. As reported in earlier section 3.2, when the sample deformed at 750 ℃ at a ε of 0.95 and strain rate of 1 s−1, the ferrite/austenite-ferrite underwent WH during deformation; therefore the quenched microstructure showed deformed ferrite rather than transformed ferrite (Figure 9). When ε̇ increased to 2 s−1, the quenched microstructure appeared to have ferrite subgrains and some fine grains were also locally observed (Figure 10). The formation of the substructure is related to the initial microstructure during straining. At higher ε̇ (of 2 s−1), the mobility of grain boundaries was lower [15,18,19]. Therefore, the deformed matrixes were transformed into substructures/subgrains; hence the quenched microstructure was the deformed microstructure with subgrains (Figure 10). Some TH/DRS of the ferritic/austenite-ferrite region (during straining) might be possible when the ε̇ was further increased to 5 s−1, but it did not reach to the condition where "WH rate" values become constant with the σ (DRV softening balances WH) as reported in the earlier section 2. Therefore the quenched microstructure having slightly larger ferrite subgrains (due to dynamic/thermal softening) along with some fine grains was observed (Figure 11).
MAD and BCGB for the sample deformed at a temperature of 750 ℃ at a ε of 0.95 and strain rate of 1, 2 and 5 s−1 are shown in Figures 12–14, respectively. The fractions of LAMs and HAMs are complementary to each other considering the total fraction as 1. It was observed that a higher fraction of HAMs was present at a ε̇ of 1 s−1 (Figure 12). Considering the LAMs as less than 10°, the total fraction of LAMs was 0.207 while it's complementary (total fraction of the HAMs) was 0.793.
When the ε̇ was increased to 2 and 5 s−1, the MAD mostly showed LAMs (i.e., reducing the population of HAMs, Figures 13 and 14). The total fraction of LAMs was 0.778 and 0.765 at the strain rate of 2 and 5, respectively. However, the total fractions of HAMs were 0.222 and 0.235 at the strain rate of 2 and 5, respectively. The formation of LAMs substructure at elevated ε̇ and diminished DT (of 750 ℃) was also observed through the BCGB images.
Figure 15 shows the variation in mean subgrain size and mean LAMs of ferrite for the samples deformed at 750 ℃ at a ε of 0.95 and strain rates of 1, 2 and 5 s−1 followed by quenching. The stress accumulation and the concentration of dislocation in the ferritic/austenite-ferrite region were more prominent at higher ε̇ (during deformation) [15,19]. Therefore, the ferritic/austenite-ferrite region became more and more strained. Hence the room temperature microstructure is indicative of a deformed microstructure with mean subgrain size decreased from 3.31 to 1.36 µm when the ε̇ increased from 1 to 5 s−1. The room temperature microstructure (after quenching) showed an increase in the mean LAMs from 1.35 to 2.46° when the ε̇ increased from 1 to 5 s−1 (Figure 15). An increase in the mean LAMs with the ε̇ was related to the mobility of substructures [18] during deformation in the ferritic/austenite-ferrite region. When the ε̇ was increased from 1 to 5 s−1, the mobility of LAMs substructure decreased during deformation. Therefore, the rearrangements of the LAMs substructure were inhibited at higher ε̇. Hence the room temperature microstructure which is a deformed state rather than a transformed state showed a further increase in the LAMs.
When samples deformed at 850 ℃ (at a ε of 0.7 and ε̇ of 1, 0.1 and 0.01 s−1), 950 ℃ (at a ε of 0.7 and ε̇ of 1, 0.1 and 0.01 s−1) and 1000 ℃ (at a ε of 0.7 and ε̇ of 0.1 and 0.01 s−1), it might be possible that at this DT range (850–1000 ℃) it was austenite that deformed during straining and quenching would lead to a phase transformation and hence the deformed microstructure would be eliminated. Hence it was most likely that microstructures after quenching were a transformed phase rather than a deformed phase. It is also important to note that the transformed microstructure after quenching was dependent upon the initial microstructure during deformation. The RM during deformation had a major effect on the transformed microstructure [20]. It was observed in section 3.2. that when the sample deformed at 850 ℃ at a ε of 0.7 and strain rate of 1 s−1, it showed mostly DRV of austenite during straining. The DRV (of austenite) was favoured at lower DT and higher ε̇ [11]. Therefore the transformed ferrite (after quenching) mostly free from LAMs was observed as shown in Figure 16. This would also suggest that it was transformed ferrite from fine-grain austenite. However, when the ε̇ decreased to 0.1 and 0.01 s−1, it was observed that the transformed microstructures after quenching were not equiaxed and contained substructures as shown in Figures 17 and 18. The transformed microstructures (Figures 17 and 18) were related to the initial austenitic microstructure during straining. The DRV and complete DRX (of austenite) was not prominent at lower ε̇ (0.1 and 0.01 s−1) and lower DT of 850 ℃, there is the accumulation of dislocations and formation of LAMs austenitic substructure. Hence the quenched microstructures were transformed phases with substructures observed. This would also suggest the phase transformation from large-grain austenite leading to bainite, acicular ferrite or martensite.
The microstructure after quenching, which is mostly free from LAMs was observed when DT increased to 950 ℃ at a ε̇ of 1 s−1 (Figure 19). It is once again suggested that the quenching would lead to a phase transformation (austenite to ferrite) from fine-grain austenite. It is also suggested that the higher ε̇ of 1 s−1, favoured DRV of deforming austenite during straining. Therefore, annihilation of dislocations occurred through DRV at higher ε̇ (of 1 s−1) [20]. Hence, deformed austenite might be free from substructures and hence the transformed ferrite (after quenching) with no dislocations was observed (Figure 19). When the ε̇ was decreased to 0.1 and 0.01 s−1, the extent of DRV of austenite (during deformation) decreased and recrystallization phenomena took place. However, it is proposed that the ε of 0.7 was not sufficient for the complete DRX of austenite during deformation. Therefore, the quenched microstructure consisted of acicular ferrite/bainite/martensite or a combination, as shown in Figures 20 and 21. When the sample was deformed at elevated DT (of 1000 ℃) at a ε of 0.7 and ε̇ of 0.1 and 0.01 s−1, it might be possible that it was austenite that underwent DRV with some extent of CDRX (during deformation). Therefore, quenching leads to the formation of ferritic substructures (after transformation) due to incomplete DRX of austenite (during deformation), as shown in Figures 22 and 23.
MAD of samples deformed at 850 and 950 ℃ at a ε̇ of 1 s−1 followed by quenching showed mostly HAMs with a few LAMs (Figures 24 and 25). It is important to note that the quenched microstructure was a transformed phase (of ferrite), therefore the deformed microstructure would be eliminated. The microstructural characteristics of the transformed phase (room temperature microstructure) were related to characteristics of the austenitic phase during deformation. It is proposed that the annihilation of dislocations/substructures took place through DRV (in austenitic phase) at higher ε̇ (of 1 s−1) during straining. The same is also described by Junior et al. [11]. Hence it is advised that quenching leads to the formation of clean microstructure with HAMs (with almost no dislocations) as shown in Figures 24 and 25. When the ε̇ was decreased to 0.1 s−1, the extent of DRV of austenite during deformation was decreased and the generation of three-dimensional arrays of deformation LAMs might take place during straining. The quenching transformed deformed austenite (during deformation) into ferrite. Therefore, it is suggested that quenching leads to the formation of non-equiaxed microstructure with LAMs. Hence MAD showed mostly LAMs, as shown in Figures 26–28. However, when the ε̇ was further decreased to 0.01 s−1, the room temperature microstructure (transformed phase) showed LAMs with some fractions of HAMs, as shown in Figures 29–31. The above characteristic of microstructure at room temperature (after quenching) was related to initial austenitic microstructure during deformation. It is proposed that austenitic HAMs developed during deformation at lower ε̇ of 0.01 s−1; however, it is also possible that some of the austenitic LAMs were converted into HAMs [7,8,9,10]. It might be possible that deformed austenite (having lower stacking fault energy) envisages some extent of DRX. However, Prasad et al. also reported DRX at higher DT for lower stacking fault materials [21]. Therefore it is proposed that the room temperature microstructure (after quenching) is bainite, acicular ferrite or martensite or a combination, and it transformed from large grain austenite.
The characteristics of the WH rate concerning σ at different deformation conditions and corresponding mean subgrain sizes is shown in Table 2. It was observed that the finer subgrain was observed when the samples were deformed at the lowest strain rate (0.01 s−1). The nature of the WH rate at this strain rate envisages an increase up to the negative peak, becomes constant and then decreases to nearly zero. Therefore, the austenite envisages predominance of work hardening (WH rate increases up to negative peak), followed by DRV softening at a constant rate (WH rate becomes constant) and then reaching the condition of steady-state flow (WH rate becomes nearly zero). The work-hardened substructures disintegrated by the combination of DRV softening followed by steady-state flow produced a finer subgrain of size of 0.6 µm (at a DT of 1000 ℃ and a ε̇ of 0.01 s−1) and 1.04 µm (at a DT of 950 ℃ and a ε̇ of 0.01 s−1). It is suggested that a higher deformation temperature (1000 ℃) provided activation energy for nearly complete DRX as compared to when the sample deformed at a lower temperature of 950 ℃. Hence, a finer subgrain was observed. When the DT was decreased to 850 ℃, the WH rate increased up to the negative peak and then decreased. The absence of steady-state flow limited the softening mechanism and hence a relatively coarser subgrain of size 1.21 µm was observed. The lower DT (850 ℃) did not allow the steady state to reach as compared to the higher DT (1000 and 950 ℃); in other words, the thermal energy required for the steady state was not achieved.
| Deformation condition | Characteristics of WH rate concerning σ | Mean subgrain size (µm) |
| 1000 ℃-ԑ̇ 0.1 s−1 | increases up to the negative peak and then decreases | 1.3 |
| 1000 ℃-ԑ̇ 0.01 s−1 | increases up to the negative peak, becomes constant and then decreases to zero | 0.6 |
| 950 ℃-ԑ̇ 1 s−1 | increases up to the negative peak and then decreases to zero | 3.38 |
| 950 ℃-ԑ̇ 0.1 s−1 | increases up to the negative peak and then decreases | 1.24 |
| 950 ℃-ԑ̇ 0.01 s−1 | increases up to the negative peak, becomes constant and then decreases to zero | 1.04 |
| 850 ℃-ԑ̇ 1 s−1 | positive variables with σ | 3.32 |
| 850 ℃-ԑ̇ 0.1 s−1 | positive variables with σ | 1.85 |
| 850 ℃-ԑ̇ 0.01 s−1 | increases up to the negative peak and then decreases | 1.21 |
| 750 ℃-ԑ̇ 5 s−1 | positive variables with σ | 1.36 |
| 750 ℃-ԑ̇ 2 s−1 | positive variables with σ | 1.07 |
| 750 ℃-ԑ̇ 1 s−1 | positive variables with σ | 3.31 |
DownLoad:
CSV
When the strain rate was increased to 0.1 s−1 at a DT of 1000 and 950 ℃, the nature of the WH rate at this strain rate envisages an increase up to the negative peak and then decreases. Hence a relatively coarser subgrain was observed (Table 2 and Figure 32). Austenite envisages predominance of work hardening (WH rate increases up to negative peak) followed by a dominant DRV softening (WH rate decreased). In this case, the austenite did not reach the condition of steady-state flow, therefore a coarser subgrain size of 1.3 µm (at a DT of 1000 ℃ and a ε̇ of 0.1 s−1) and 1.24 µm (at a DT of 950 ℃ and a ε̇ of 0.1 s−1) were observed. When the sample was deformed at the same strain rate (0.1 s−1) and a lower DT (850 ℃) the WH rate envisages positive variables with σ, which facilitates the dominance of work hardening over DRV softening and hence a coarser subgrain of size 1.85 µm was observed. It is suggested that at lower ε̇ (0.01 and 0.1 s−1), the extent of recovery decreased and recrystallization phenomena were initiated in austenite during deformation [15,22]. Although DRX of austenite was not fully completed at a ε of 0.7 as well, it led to the accumulation of LAMs substructure as only a few of austenitic LAMs were converted into HAMs (due to incomplete DRX). Hence the room temperature microstructure (transformed microstructure) showed finer subgrains as shown in Figure 32.
When the strain rate was further increased to 1 s−1 at a DT of 950 ℃ and 850 ℃, the nature of WH rate envisages an increase up to a negative peak and then decreases to zero at a DT of 950 ℃. Here, a higher DT and strain rate limited the span of the WH rate curve and hence the time required for DRV softening was not sufficient. Hence, a coarser subgrain size of 3.38 µm was observed. However, when the DT was decreased to 850 ℃, the WH rate showed positive variables with σ. Hence, work hardening dominated over DRV softening and a coarser subgrain of size 3.32 µm was observed. It is suggested that the DRV of austenite at higher ε̇ (1 s−1) annihilated most of the LAMs substructures. Therefore, the room temperature microstructure (after quenching) showed a lower fraction of ferritic LAMs substructures leading to the formation of coarsening subgrains.
The WH rate neither becomes constant nor reaches the condition of steady-state flow (WH rate becomes zero) for all the strain rates (1, 2 and 5 s−1) at a DT of 750 ℃. However, at this lower DT, the quenched microstructure was a deformed microstructure (as discussed in section 3.2.1.2). The WH rate envisages positive variables with σ. However, at a strain rate of 5 s−1, the WH rate envisages a larger area in the negative region (Figure 7), hence DRV softening was also highest; therefore a subgrain of size 1.36 µm was observed. However, the negative region of WH rate was lowest at a strain rate of 1 s−1, hence DRV softening was limited; therefore a subgrain of size 3.31 µm was observed. The moderate strain rate of 2 s−1 envisages a finer subgrain of size 1.07 µm.
The principle premise of the current research is concluded as:
1. It is proposed that the microstructure during deformation was most likely austenite at 850–1000 ℃. At lower DT and higher ε̇, the austenitic phase showed some TH/DRS, but it did not reach the condition where the "WH rate" value became constant with the σ (i.e., DRV softening balances WH). However, it was observed that when the temperature increased and ε̇ decreased, the "WH rate" values for samples deformed at 850 (at ε̇ of 0.01 s−1), 950 (at ε̇ of 0.1 and 0.01 s−1) and 1000 ℃ (at ε̇ of 0.1 and 0.01 s−1) increased up to the negative peak, and then decreased to almost zero (for samples deformed at 950 and 1000 ℃ at ε̇ of 0.01 s−1), corresponding to the beginning of the steady-state flow. The samples deformed at elevated temperatures (950 and 1000 ℃) and lower ε̇ (0.01 s−1) showed some regions where the WH rate was steady; it indicated the possible balance between DRV and WH.
2. It is proposed that microstructure during deformation was most likely ferritic or in the austenite-ferrite region at DT of 750 ℃. Therefore, when the sample deformed at a ε of 0.95 and strain rate of 1, 2 and 5 s−1 followed by quenching, the room temperature microstructure was indicative of deformed microstructure rather than transformed microstructure. The extent of deformation and formation of the substructure was a function of ε̇ because it was deformed in the ferritic or austenite-ferrite region followed by quenching. It was observed that there was an increase in the extent of substructure formation and a decrease in mean subgrain size with increasing ε̇.
3. Samples deformed at 850 (at a ε of 0.7 and ε̇ of 1, 0.1 and 0.01 s−1), 950 (at a ε of 0.7 and ε̇ of 1, 0.1 and 0.01 s−1) and 1000 ℃ (at a ε of 0.7 and ε̇ of 0.1 and 0.01 s−1). It might be possible that at this DT range (850–1000 ℃), it was austenite which deformed during straining and quenching would lead to a phase transformation and hence the deformed microstructure would be eliminated. The room temperature microstructures when the sample deformed at a ε̇ of 1 s−1 was nicely equiaxed and clean with no dislocations present. This would suggest that it was transformed ferrite from fine-grain austenite. However, when the ε̇ decreased to 0.1 and 0.01 s−1 followed by quenching, it was observed that the transformed microstructures contained substructures.
The author declares that no Artificial Intelligence (AI) tools were used in the creation of this article.
The author declares no conflict of interest.
| [1] |
Makhatha ME (2022) Effect of titanium addition on sub-structural characteristics of low carbon copper bearing steel in hot rolling. AIMS Mater Sci 9: 604–616. https://www.aimspress.com/article/doi/10.3934/matersci.2022036 doi: 10.3934/matersci.2022036
|
| [2] |
Sakai T, Belyakov A, Kaibyshev R, et al. (2014) Dynamic and post-dynamic recrystallization under hot, cold and severe plastic deformation conditions. Prog Mater Sci 60: 130–207. https://doi.org/10.1016/j.pmatsci.2013.09.002 doi: 10.1016/j.pmatsci.2013.09.002
|
| [3] | Link TM, Hance BM (2003) Effects of strain rate and temperature on the work hardening behavior of high strength sheet steels. SAE Trans 112: 211–219. http://www.jstor.org/stable/44699575 |
| [4] |
Sakai T, Jonas JJ (1984) Overview no. 35 Dynamic recrystallization: Mechanical and microstructural considerations. Acta Metall 32: 189–209. https://doi.org/10.1016/0001-6160(84)90049-X doi: 10.1016/0001-6160(84)90049-X
|
| [5] |
Gourdet S, Montheillet F (2000) An experimental study of the recrystallization mechanism during hot deformation of aluminium. Mater Sci Eng A 283: 274–288. https://doi.org/10.1016/S0921-5093(00)00733-4 doi: 10.1016/S0921-5093(00)00733-4
|
| [6] |
Belyakov A, Tsuzaki K, Miura H, et al. (2003) Effect of initial microstructures on grain refinement in a stainless steel by large strain deformation. Acta Mater 51: 847–861. https://doi.org/10.1016/S1359-6454(02)00476-7 doi: 10.1016/S1359-6454(02)00476-7
|
| [7] |
Solberg JK, McQueen HJ, Ryum N, et al. (1989) Influence of ultra-high strains at elevated temperatures on the microstructure of aluminium. Philos Mag A 60: 447–471. https://doi.org/10.1080/01418618908213872 doi: 10.1080/01418618908213872
|
| [8] |
Hales SJ, McNelley TR, McQueen HJ (1991) Recrystallization and superplasticity at 300 ℃ in an aluminum-magnesium alloy. Metall Trans A 22: 1037–1047. https://doi.org/10.1007/BF02661097 doi: 10.1007/BF02661097
|
| [9] |
Tsuji N, Matsubara Y, Saito Y (1997) Dynamic recrystallization of ferrite in interstitial free steel. Scripta Mater 37: 477–484. https://doi.org/10.1016/S1359-6462(97)00123-1 doi: 10.1016/S1359-6462(97)00123-1
|
| [10] |
McNelley TR, McMahon ME (1997) Microtexture and grain boundary evolution during microstructural refinement processes in SUPRAL 2004. Metall Mater Trans A 28: 1879–1887. https://doi.org/10.1007/s11661-997-0118-2 doi: 10.1007/s11661-997-0118-2
|
| [11] |
Jorge AM, Balancin O (2005) Prediction of steel flow stresses under hot working conditions. Mat Res 8: 309–315. https://doi.org/10.1590/S1516-14392005000300015 doi: 10.1590/S1516-14392005000300015
|
| [12] |
Kingkam W, Li N, Zhang HX, et al. (2017) Hot deformation behavior of high strength low alloy steel by thermo mechanical simulator and finite element method. IOP Conf Ser Mater Sci Eng 205: 012001. https://dx.doi.org/10.1088/1757-899X/205/1/012001 doi: 10.1088/1757-899X/205/1/012001
|
| [13] |
Doherty RD, Hughes DA, Humphreys FJ, et al. (1997) Current issues in recrystallization: A review. Mater Sci Eng A 238: 219–274. https://doi.org/10.1016/S0921-5093(97)00424-3 doi: 10.1016/S0921-5093(97)00424-3
|
| [14] |
Quan GZ, Wang Y, Liu YY, et al. (2013) Effect of temperatures and strain rates on the average size of grains refined by dynamic recrystallization for as-extruded 42CrMo steel. Mat Res 16: 1092–1105. https://doi.org/10.1590/S1516-14392013005000091 doi: 10.1590/S1516-14392013005000091
|
| [15] |
Kumar P, Hodgson P, Beladi H, et al. (2020) EBSD investigation to study the restoration mechanism and substructural characteristics of 23Cr-6Ni-3Mo duplex stainless steel during post-deformation annealing. Trans Indian Inst Met 73: 1421–1431. https://doi.org/10.1007/s12666-020-01884-1 doi: 10.1007/s12666-020-01884-1
|
| [16] |
Montheillet F, Jonas JJ (1996) Temperature dependence of the rate sensitivity and its effect on the activation energy for high-temperature flow. Metall Mater Trans A 27: 3346–3348. https://doi.org/10.1007/BF02663887 doi: 10.1007/BF02663887
|
| [17] |
Davenport SB, Silk NJ, Sparks CN, et al. (2000) Development of constitutive equations for modelling of hot rolling. Mater Sci Technol 16: 539–546. https://doi.org/10.1179/026708300101508045 doi: 10.1179/026708300101508045
|
| [18] |
Sarkar A, Chakravartty JK (2013) Investigation of progress in dynamic recrystallization in two austenitic stainless steels exhibiting flow softening. J Metall Eng 2: 130–136. https://doi.org/10.5923/j.ijmee.20130202.03 doi: 10.5923/j.ijmee.20130202.03
|
| [19] |
Sarkar A, Kapoor R, Verma A, et al. (2012) Hot deformation behavior of Nb-1Zr-0.1C alloy in the temperature range 700–1700 ℃. J Nucl Mater 422: 1–7. https://doi.org/10.1016/j.jnucmat.2011.11.064 doi: 10.1016/j.jnucmat.2011.11.064
|
| [20] |
De Oliveira TS, Silva ES, Rodrigues SF, et al. (2017) Softening mechanisms of the AISI 410 martensitic stainless steel under hot torsion simulation. Mat Res 20: 395–406. https://doi.org/10.1590/1980-5373-MR-2016-0795 doi: 10.1590/1980-5373-mr-2016-0795
|
| [21] |
Prasad YVRK, Ravichandran N (1991) Effect of stacking fault energy on the dynamic recrystallization during hot working of FCC metals: A study using processing maps. Bull Mater Sci 14: 1241–1248. https://doi.org/10.1007/BF02744618 doi: 10.1007/BF02744618
|
| [22] |
Kumar P, Hodgson P, Beladi H, et al. (2021) Restoration mechanism and sub-structural characteristics of duplex stainless steel with an initial equiaxed austenite morphology during post-deformation annealing. Key Eng Mater 882: 64–73. https://doi.org/10.4028/www.scientific.net/KEM.882.64 doi: 10.4028/www.scientific.net/KEM.882.64
|
Pawan Kumar. Subgrain characterization of low carbon copper bearing steel under plane strain compression using electron backscattered diffraction[J]. AIMS Materials Science, 2023, 10(6): 1121-1143. doi: 10.3934/matersci.2023060
| Deformation condition | ε at peak σ | ε for steady state initiation |
| 1000 ℃-ԑ̇ 0.1 s−1 | 0.28 | No indication of a steady state |
| 1000 ℃-ԑ̇ 0.01 s−1 | 0.21 | 0.32 |
| 950 ℃-ԑ̇ 1 s−1 | 0.49 | No indication of a steady state |
| 950 ℃-ԑ̇ 0.1 s−1 | 0.26 | No indication of a steady state |
| 950 ℃-ԑ̇ 0.01 s−1 | 0.22 | 0.35 |
| 850 ℃-ԑ̇ 1 s−1 | 0.55 | No indication of a steady state |
| 850 ℃-ԑ̇ 0.1 s−1 | 0.41 | No indication of a steady state |
| 850 ℃-ԑ̇ 0.01 s−1 | 0.28 | No indication of a steady state |
| 750 ℃-ԑ̇ 5 s−1 | 0.82 | No indication of a steady state |
| 750 ℃-ԑ̇ 2 s−1 | 0.83 | No indication of a steady state |
| 750 ℃-ԑ̇ 1 s−1 | 0.89 | No indication of a steady state |
DownLoad:
CSV
| Deformation condition | Characteristics of WH rate concerning σ | Mean subgrain size (µm) |
| 1000 ℃-ԑ̇ 0.1 s−1 | increases up to the negative peak and then decreases | 1.3 |
| 1000 ℃-ԑ̇ 0.01 s−1 | increases up to the negative peak, becomes constant and then decreases to zero | 0.6 |
| 950 ℃-ԑ̇ 1 s−1 | increases up to the negative peak and then decreases to zero | 3.38 |
| 950 ℃-ԑ̇ 0.1 s−1 | increases up to the negative peak and then decreases | 1.24 |
| 950 ℃-ԑ̇ 0.01 s−1 | increases up to the negative peak, becomes constant and then decreases to zero | 1.04 |
| 850 ℃-ԑ̇ 1 s−1 | positive variables with σ | 3.32 |
| 850 ℃-ԑ̇ 0.1 s−1 | positive variables with σ | 1.85 |
| 850 ℃-ԑ̇ 0.01 s−1 | increases up to the negative peak and then decreases | 1.21 |
| 750 ℃-ԑ̇ 5 s−1 | positive variables with σ | 1.36 |
| 750 ℃-ԑ̇ 2 s−1 | positive variables with σ | 1.07 |
| 750 ℃-ԑ̇ 1 s−1 | positive variables with σ | 3.31 |
DownLoad:
CSV
| Deformation condition | ε at peak σ | ε for steady state initiation |
| 1000 ℃-ԑ̇ 0.1 s−1 | 0.28 | No indication of a steady state |
| 1000 ℃-ԑ̇ 0.01 s−1 | 0.21 | 0.32 |
| 950 ℃-ԑ̇ 1 s−1 | 0.49 | No indication of a steady state |
| 950 ℃-ԑ̇ 0.1 s−1 | 0.26 | No indication of a steady state |
| 950 ℃-ԑ̇ 0.01 s−1 | 0.22 | 0.35 |
| 850 ℃-ԑ̇ 1 s−1 | 0.55 | No indication of a steady state |
| 850 ℃-ԑ̇ 0.1 s−1 | 0.41 | No indication of a steady state |
| 850 ℃-ԑ̇ 0.01 s−1 | 0.28 | No indication of a steady state |
| 750 ℃-ԑ̇ 5 s−1 | 0.82 | No indication of a steady state |
| 750 ℃-ԑ̇ 2 s−1 | 0.83 | No indication of a steady state |
| 750 ℃-ԑ̇ 1 s−1 | 0.89 | No indication of a steady state |
| Deformation condition | Characteristics of WH rate concerning σ | Mean subgrain size (µm) |
| 1000 ℃-ԑ̇ 0.1 s−1 | increases up to the negative peak and then decreases | 1.3 |
| 1000 ℃-ԑ̇ 0.01 s−1 | increases up to the negative peak, becomes constant and then decreases to zero | 0.6 |
| 950 ℃-ԑ̇ 1 s−1 | increases up to the negative peak and then decreases to zero | 3.38 |
| 950 ℃-ԑ̇ 0.1 s−1 | increases up to the negative peak and then decreases | 1.24 |
| 950 ℃-ԑ̇ 0.01 s−1 | increases up to the negative peak, becomes constant and then decreases to zero | 1.04 |
| 850 ℃-ԑ̇ 1 s−1 | positive variables with σ | 3.32 |
| 850 ℃-ԑ̇ 0.1 s−1 | positive variables with σ | 1.85 |
| 850 ℃-ԑ̇ 0.01 s−1 | increases up to the negative peak and then decreases | 1.21 |
| 750 ℃-ԑ̇ 5 s−1 | positive variables with σ | 1.36 |
| 750 ℃-ԑ̇ 2 s−1 | positive variables with σ | 1.07 |
| 750 ℃-ԑ̇ 1 s−1 | positive variables with σ | 3.31 |
