Preparation of gold-containing binary metal clusters by co-deposition-precipitation method and for hydrogenation of chloronitrobenzene

Ya-Ting Tsu; Yu-Wen Chen; Ya-Ting Tsu; Yu-Wen Chen

doi:10.3934/matersci.2017.3.738

AIMS Materials Science

2017, Volume 4, Issue 3: 738-754. doi: 10.3934/matersci.2017.3.738

Previous Article Next Article

Research article Topical Sections

Preparation of gold-containing binary metal clusters by co-deposition-precipitation method and for hydrogenation of chloronitrobenzene

Ya-Ting Tsu ¹,
Yu-Wen Chen ^{1,2
,
,}

1.
Department of Chemical and Materials Engineering, National Central University, Jhong-Li 32001, Taiwan
2.
Department of Chemistry, Tomsk State University, Tomsk, Siberia, Russia

Received: 25 April 2017 Accepted: 07 June 2017 Published: 13 June 2017

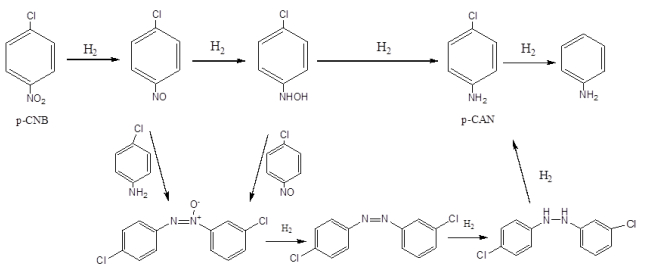
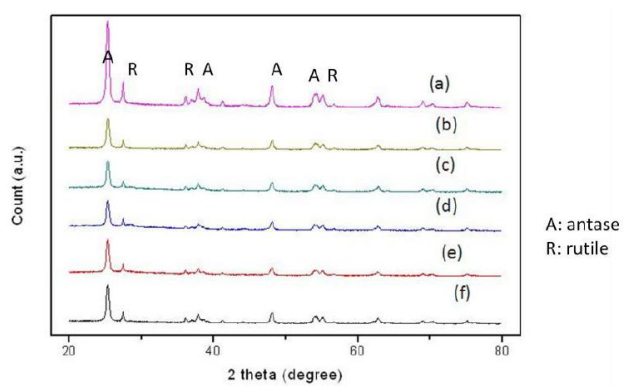
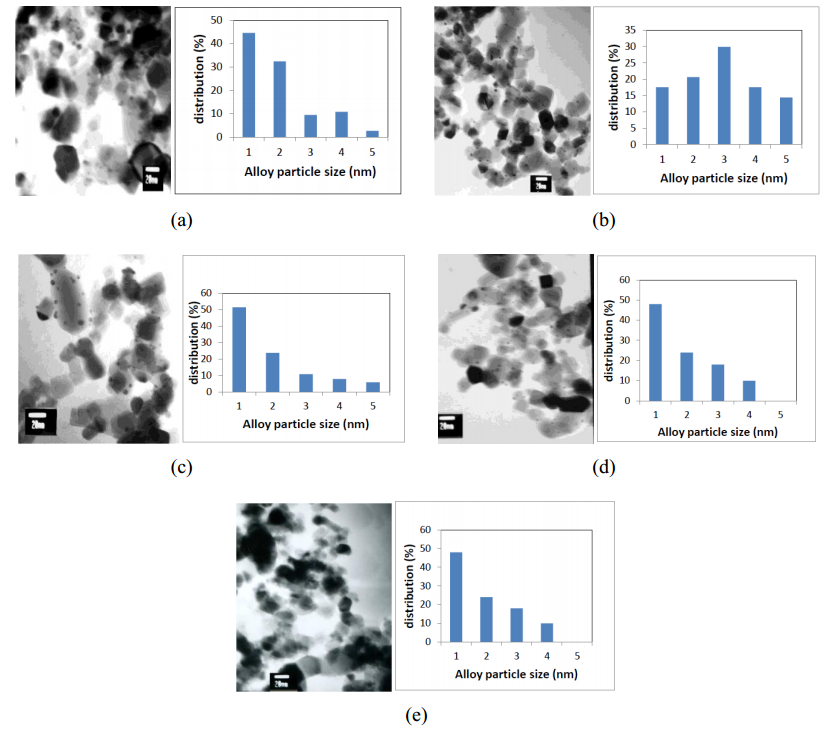
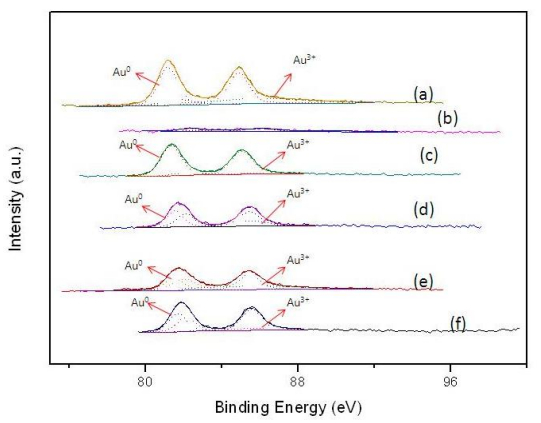
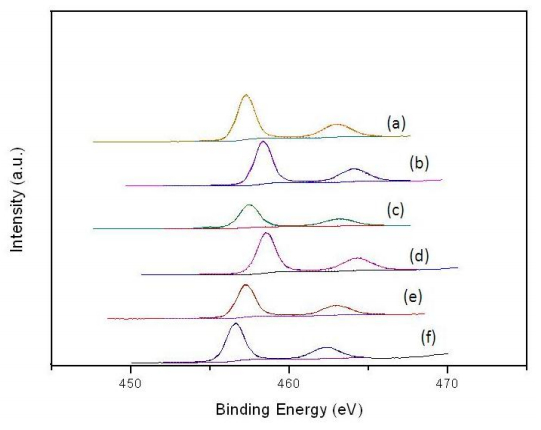
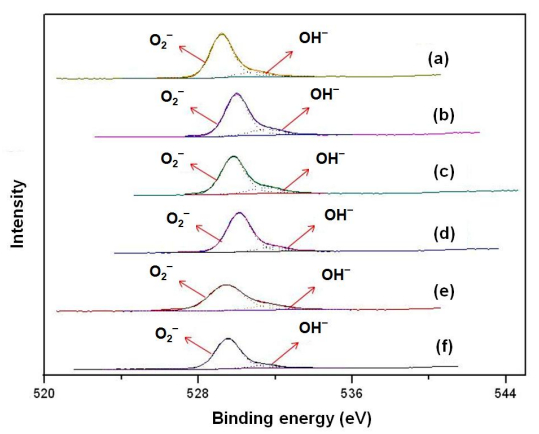
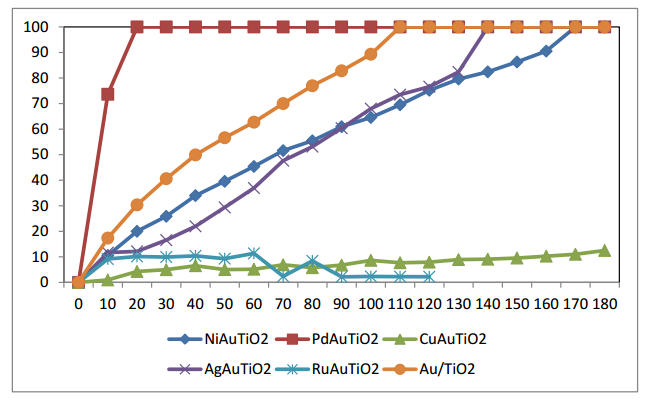
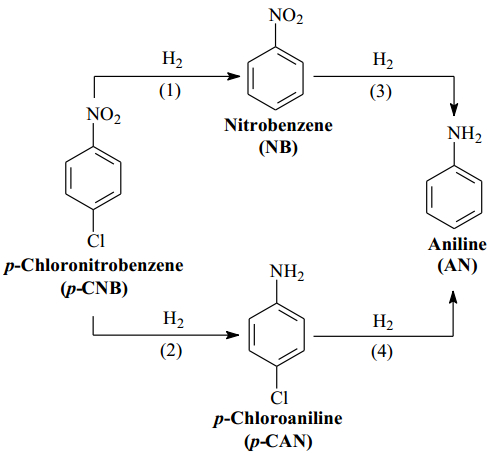
Nano-gold catalyst has been reported to have high activity and selectivity for liquid phase hydrogenation reaction. In this study, gold-containing bimetals were loaded on TiO₂. For bimetallic catalysts, gold and different metals were prepared by the deposition-precipitation method, and then used NaBH₄ to reduce metal cations. The catalysts were characterized by X-ray diffraction, transmission electron microscopy, high resolution transmission electron microscopy, and X-ray photoelectron spectroscopy. The catalytic properties of these catalysts were tested by hydrogenation of p-chloronitrobenzene (p-CNB) in a batch reactor at 1.1 MPa H₂ pressure, 373 K and 500 rpm. Cu, Ag, Ru, and Pd formed nano-alloy with Au. In addition, Cu–Au, Ag–Au, and Ru–Au alloy had Cu-, Ag-, and Ru-enriched surface, respectively. Instead, Pd–Au alloy had Pd-enriched surface. There are two kinds of alloy effects: (1) geometric effects, i.e., the surface-enriched metal would change the distance of Au–Au atoms that is required for facilitating the hydrogenation of chloronitrobenzene; and (2) electronic effects, which involve charge transfer between the metals. The activity decreased in the following order: PdAu/TiO₂ > Au/TiO₂ > NiAu/TiO₂ > AgAu/TiO₂ > RuAu/TiO₂ > CuAu/TiO₂. Comparing with other metals, adding Pd in Au showed a higher activity. Adding palladium could reduce gold-valence state, and increased active sites for reaction.

Keywords:

Citation: Ya-Ting Tsu, Yu-Wen Chen. Preparation of gold-containing binary metal clusters by co-deposition-precipitation method and for hydrogenation of chloronitrobenzene[J]. AIMS Materials Science, 2017, 4(3): 738-754. doi: 10.3934/matersci.2017.3.738

Related Papers:

[1]	Moh. Alakhrass . A note on positive partial transpose blocks. AIMS Mathematics, 2023, 8(10): 23747-23755. doi: 10.3934/math.20231208
[2]	Mohammad Al-Khlyleh, Mohammad Abdel Aal, Mohammad F. M. Naser . Interpolation unitarily invariant norms inequalities for matrices with applications. AIMS Mathematics, 2024, 9(7): 19812-19821. doi: 10.3934/math.2024967
[3]	Sourav Shil, Hemant Kumar Nashine . Positive definite solution of non-linear matrix equations through fixed point technique. AIMS Mathematics, 2022, 7(4): 6259-6281. doi: 10.3934/math.2022348
[4]	Kanjanaporn Tansri, Sarawanee Choomklang, Pattrawut Chansangiam . Conjugate gradient algorithm for consistent generalized Sylvester-transpose matrix equations. AIMS Mathematics, 2022, 7(4): 5386-5407. doi: 10.3934/math.2022299
[5]	Junyuan Huang, Xueqing Chen, Zhiqi Chen, Ming Ding . On a conjecture on transposed Poisson $n$ -Lie algebras. AIMS Mathematics, 2024, 9(3): 6709-6733. doi: 10.3934/math.2024327
[6]	Arnon Ploymukda, Kanjanaporn Tansri, Pattrawut Chansangiam . Weighted spectral geometric means and matrix equations of positive definite matrices involving semi-tensor products. AIMS Mathematics, 2024, 9(5): 11452-11467. doi: 10.3934/math.2024562
[7]	Pattrawut Chansangiam, Arnon Ploymukda . Riccati equation and metric geometric means of positive semidefinite matrices involving semi-tensor products. AIMS Mathematics, 2023, 8(10): 23519-23533. doi: 10.3934/math.20231195
[8]	Nunthakarn Boonruangkan, Pattrawut Chansangiam . Convergence analysis of a gradient iterative algorithm with optimal convergence factor for a generalized Sylvester-transpose matrix equation. AIMS Mathematics, 2021, 6(8): 8477-8496. doi: 10.3934/math.2021492
[9]	Arnon Ploymukda, Pattrawut Chansangiam . Metric geometric means with arbitrary weights of positive definite matrices involving semi-tensor products. AIMS Mathematics, 2023, 8(11): 26153-26167. doi: 10.3934/math.20231333
[10]	Ahmad Y. Al-Dweik, Ryad Ghanam, Gerard Thompson, M. T. Mustafa . Algorithms for simultaneous block triangularization and block diagonalization of sets of matrices. AIMS Mathematics, 2023, 8(8): 19757-19772. doi: 10.3934/math.20231007

Abstract

1. Introduction

Let $\mathbb{M}_n$ be the set of $n\times n$ complex matrices. $\mathbb{M}_n(\mathbb{M}_k)$ is the set of $n\times n$ block matrices with each block in $\mathbb{M}_k$ . For $A \in \mathbb{M}_n$ , the conjugate transpose of $A$ is denoted by $A^*.$ When $A$ is Hermitian, we denote the eigenvalues of $A$ in nonincreasing order $\lambda_1(A) \geq \lambda_2(A) \geq... \geq \lambda_n(A)$ ; see ^[2,7,8,9]. The singular values of $A$ , denoted by $s_1(A), s_2(A), ..., s_n(A),$ are the eigenvalues of the positive semi-definite matrix $|A| = (A^*A)^{1/2}$ , arranged in nonincreasing order and repeated according to multiplicity as $s_1(A) \geq s_2(A) \geq... \geq s_n(A).$ If $A\in \mathbb{M}_n$ is positive semi-definite (definite), then we write $A \geq 0\; (A > 0)$ . Every $A\in \mathbb{M}_n$ admits what is called the cartesian decomposition $A = {{{\rm{Re\, }}}} A+i{{{\rm{Im\, }}}} A,$ where ${{{\rm{Re\, }}}} A = \frac{A+A^*}{2}, \ {{{\rm{Im\, }}}} A = \frac{A-A^*}{2}.$ A matrix $A\in \mathbb{M}_n$ is called accretive if ${{{\rm{Re\, }}}} A$ is positive definite. Recall that a norm $||\cdot||$ on $\mathbb{M}_n$ is unitarily invariant if $||UAV|| = ||A||$ for any $A\in \mathbb{M}_n$ and unitary matrices $U, V\in \mathbb{M}_n$ . The Hilbert-Schmidt norm is defined as $||A||_2^2 = {{{\rm{tr}}}}(A^*A)$ .

For $A, B > 0$ and $t\in [0, 1]$ , the weighted geometric mean of $A$ and $B$ is defined as follows

$\begin{eqnarray*} A\sharp_{t} B\ = A^{1/2}(A^{-1/2}BA^{-1/2})^{t}A^{1/2}. \end{eqnarray*}$

When $t = \frac{1}{2}$ , $A\sharp_{\frac{1}{2}} B$ is called the geometric mean of $A$ and $B$ , which is often denoted by $A\sharp B$ . It is known that the notion of the (weighted) geometric mean could be extended to cover all positive semi-definite matrices; see [3, Chapter 4].

Let $A, B, X\in \mathbb{M}_n$ . For $2\times 2$ block matrix $M$ in the form

$\begin{eqnarray*} M = \left( \begin{array}{cc} A & X \\ X^* & B\\ \end{array} \right)\in \mathbb{M}_{2n} \end{eqnarray*}$

with each block in $\mathbb{M}_{n},$ its partial transpose of $M$ is defined by

$\begin{eqnarray*} M^\tau = \left( \begin{array}{cc} A & X^* \\ X & B\\ \end{array} \right). \end{eqnarray*}$

If $M$ and $M^\tau \geq0$ , then we say it is positive partial transpose (PPT). We extend the notion to accretive matrices. If

$\begin{eqnarray*} M = \left( \begin{array}{cc} A & X \\ Y^* & B\\ \end{array} \right)\in \mathbb{M}_{2n}, \end{eqnarray*}$

and

$\begin{eqnarray*} M^{\tau} = \left( \begin{array}{cc} A & Y^* \\ X & C\\ \end{array} \right)\in \mathbb{M}_{2n} \end{eqnarray*}$

are both accretive, then we say that $M$ is APT (i.e., accretive partial transpose). It is easy to see that the class of APT matrices includes the class of PPT matrices; see ^[6,10,13].

Recently, many results involving the off-diagonal block of a PPT matrix and its diagonal blocks were presented; see ^[5,11,12]. In 2023, Alakhrass ^[1] presented the following two results on $2\times2$ block PPT matrices.

Theorem 1.1 (^[1], Theorem 3.1). Let $\left(\begin{array}{cc} A & X \\ X^{*} & B\\ \end{array} \right)$ be PPT and let $X = U|X|$ be the polar decomposition of $X$ , then

$\begin{eqnarray*} |X| \leq ( A\sharp_t B)\sharp (U^*( A \sharp_{1-t} B)U), \quad t \in [0, 1]. \end{eqnarray*}$

Theorem 1.2 (^[1], Theorem 3.2). Let $\left(\begin{array}{cc} A & X \\ X^{*} & B\\ \end{array} \right)$ be PPT, then for $t\in [0, 1],$

$\begin{eqnarray*} {{{\rm{Re\, }}}} X\leq ( A\sharp_t B)\sharp ( A \sharp_{1-t} B)\leq \frac{(A\sharp_t B)+(A\sharp _{1-t} B)}{2}, \end{eqnarray*}$

and

$\begin{eqnarray*} {{{\rm{Im\, }}}} X \leq ( A\sharp_t B)\sharp ( A \sharp_{1-t} B)\leq \frac{(A\sharp_t B)+(A\sharp _{1-t}B)}{2}. \end{eqnarray*}$

By Theorem 1.1 and the fact $s_{i+j-1}(XY)\leq s_i(X)s_j(Y)\; (i+j\leq n+1)$ , the author obtained the following corollary.

Corollary 1.3 (^[1], Corollary 3.5). Let $\left(\begin{array}{cc} A & X \\ X^{*} & B\\ \end{array} \right)$ be PPT, then for $t\in [0, 1],$

$\begin{eqnarray*} s_{i+j-1}(X)\leq s_i(A\sharp_t B)s_j(A\sharp_{1-t} B). \end{eqnarray*}$

Consequently,

$\begin{eqnarray*} s_{2j-1}(X)\leq s_j( A\sharp_t B)s_j(A\sharp_{1-t} B). \end{eqnarray*}$

A careful examination of Alakhrass' proof in Corollary 1.3 actually revealed an error. The right results are $s_{i+j-1}(X)\leq s_i(A\sharp_t B)^{\frac{1}{2}}s_j((A\sharp_{1-t} B)^{\frac{1}{2}})$ and $s_{2j-1}(X)\leq s_j((A\sharp_t B)^{\frac{1}{2}})$ $s_j((A\sharp_{1-t} B)^{\frac{1}{2}}).$ Thus, in this note, we will give a correct proof of Corollary 1.3 and extend the above inequalities to the class of $2\times2$ block APT matrices. At the same time, some relevant results will be obtained.

2. Main results

Before presenting and proving our results, we need the following several lemmas of the weighted geometric mean of two positive matrices.

Lemma 2.1. [, Chapter 4] Let $X, Y\in \mathbb{M}_{n}$ be positive definite, then

$1)$ $X\sharp Y = \max\left\{Z:Z = Z^*, \left(\begin{array}{cc} X & Z \\ Z & Y\\ \end{array} \right)\geq 0\right\}.$

$2)$ $X\sharp Y = X^{\frac{1}{2}}UY^{\frac{1}{2}}$ for some unitary matrix $U$ .

Lemma 2.2. [, Theorem 3] Let $X, Y\in \mathbb{M}_{n}$ be positive definite, then for every unitarily invariant norm,

$\begin{eqnarray*} \begin{aligned} \label{f2} ||X\sharp_tY||&\leq||X^{1-t}Y^t||\\ &\leq||(1-t)X+tY||. \end{aligned} \end{eqnarray*}$

Now, we give a lemma that will play an important role in the later proofs.

Lemma 2.3. Let $M = \left(\begin{array}{cc} A & X \\ Y^{*} & B\\ \end{array} \right)\in \mathbb{M}_{2n}$ be APT, then for $t\in [0, 1]$ ,

$\left( \begin{array}{cc} {{{\rm{Re\, }}}} A\sharp_t {{{\rm{Re\, }}}} B & \frac{X+Y}{2} \\ \frac{X^*+Y^*}{2} & {{{\rm{Re\, }}}} A\sharp_{1-t} {{{\rm{Re\, }}}} B\\ \end{array} \right)$

is PPT.

Proof: Since $M$ is APT, we have that

${{{\rm{Re\, }}}} M = \left( \begin{array}{cc} {{{\rm{Re\, }}}} A & \frac{X+Y}{2}\\ \frac{X^*+Y^*}{2} & {{{\rm{Re\, }}}} B\\ \end{array} \right)$

is PPT.

Therefore, ${{{\rm{Re\, }}}} M \geq 0$ and ${{{\rm{Re\, }}}} M^{\tau} \geq 0$ .

By the Schur complement theorem, we have

$\begin{eqnarray*} {{{\rm{Re\, }}}} B- \frac{X^*+Y^*}{2}({{{\rm{Re\, }}}} A)^{-1}\frac{X+Y}{2}\geq 0, \end{eqnarray*}$

and

$\begin{eqnarray*} {{{\rm{Re\, }}}} A-\frac{X^*+Y^*}{2}({{{\rm{Re\, }}}} B)^{-1}\frac{X+Y}{2} \geq 0. \end{eqnarray*}$

Compute

$\begin{eqnarray*} \begin{aligned} &\frac{X^*+Y^*}{2}({{{\rm{Re\, }}}} A\sharp_t {{{\rm{Re\, }}}} B)^{-1}\frac{X+Y}{2}\\ & = \frac{X^*+Y^*}{2}(({{{\rm{Re\, }}}} A)^{-1}\sharp_t ({{{\rm{Re\, }}}} B)^{-1})\frac{X+Y}{2}\\ & = \left(\frac{X^*+Y^*}{2}({{{\rm{Re\, }}}} A)^{-1}\frac{X+Y}{2}\right)\sharp_t \left(\frac{X^*+Y^*}{2}({{{\rm{Re\, }}}} B)^{-1}\frac{X+Y}{2}\right)\\ &\leq {{{\rm{Re\, }}}} B\sharp_t {{{\rm{Re\, }}}} A. \end{aligned} \end{eqnarray*}$

Thus,

$\begin{eqnarray*} ({{{\rm{Re\, }}}} B \sharp_t {{{\rm{Re\, }}}} A)-\frac{X^*+Y^*}{2}({{{\rm{Re\, }}}} A\sharp_t {{{\rm{Re\, }}}} B)^{-1}\frac{X+Y}{2} \geq0. \end{eqnarray*}$

By utilizing $({{{\rm{Re\, }}}} B\sharp_t {{{\rm{Re\, }}}} A) = {{{\rm{Re\, }}}} A\sharp_{1-t} {{{\rm{Re\, }}}} B$ , we have

$\begin{eqnarray*} \left(\begin{array}{cc} {{{\rm{Re\, }}}} A\sharp_t {{{\rm{Re\, }}}} B & \frac{X+Y}{2}\\ \frac{X^*+Y^*}{2} & {{{\rm{Re\, }}}} A\sharp_{1-t} {{{\rm{Re\, }}}} B\\ \end{array} \right)\geq0. \end{eqnarray*}$

Similarly, we have

$\begin{eqnarray*} \left(\begin{array}{cc} {{{\rm{Re\, }}}} A\sharp_t {{{\rm{Re\, }}}} B & \frac{X^*+Y^*}{2}\\ \frac{X+Y}{2} & {{{\rm{Re\, }}}} A\sharp_{1-t} {{{\rm{Re\, }}}} B\\ \end{array} \right)\geq 0. \end{eqnarray*}$

This completes the proof.

First, we give the correct proof of Corollary 1.3.

Proof: By Theorem 1.1, there exists a unitary matrix $U\in \mathbb{M}_{n}$ such that $|X|\leq (A\sharp_t B)\sharp (U^*$ $(A\sharp_{1-t} B)U).$ Moreover, by Lemma 2.1, we have $(A\sharp_t B)\sharp (U^*(A\sharp_{1-t} B)U) = (A\sharp_t B)^{\frac{1}{2}}V(U^*$ $(A\sharp_{1-t} B)^{\frac{1}{2}}U).$ Now, by $s_{i+j-1}(AB)\leq s_i(A)s_j(B)$ , we have

$\begin{eqnarray*} s_{i+j-1}(X) &\leq& s_{i+j-1}((A\sharp_t B)\sharp(U^*(A\sharp_{1-t}B)U)) \\ & = & s_{i+j-1}((A\sharp_t B)^{\frac{1}{2}}VU^*(A\sharp_{1-t} B)^{\frac{1}{2}}U) \\ &\leq& s_{i}((A\sharp_t B)^{\frac{1}{2}})s_j((A\sharp_{1-t} B)^{\frac{1}{2}}), \end{eqnarray*}$

which completes the proof.

Next, we generalize Theorem 1.1 to the class of APT matrices.

Theorem 2.4. Let $M = \left(\begin{array}{cc} A & X \\ Y^{*} & B\\ \end{array} \right)$ be APT, then

$\begin{eqnarray*} \left|\frac{X+Y}{2}\right| \leq ({{{\rm{Re\, }}}} A\sharp_t{{{\rm{Re\, }}}} B)\sharp (U^*({{{\rm{Re\, }}}} A \sharp_{1-t}{{{\rm{Re\, }}}} B)U), \end{eqnarray*}$

where $U\in \mathbb{M}_{n}$ is any unitary matrix such that $\frac{X+Y}{2} = U\left|\frac{X+Y}{2}\right|$ .

Proof: Since $M$ is an APT matrix, we know that

$\left( \begin{array}{cc} {{{\rm{Re\, }}}} A\sharp_t {{{\rm{Re\, }}}} B & \frac{X+Y}{2}\\ \frac{X^*+Y^*}{2} & {{{\rm{Re\, }}}} B\sharp_{1-t} {{{\rm{Re\, }}}} A\\ \end{array} \right)$

is PPT.

Let $W$ be a unitary matrix defined as $W = \left(\begin{array}{cc} I & 0\\ 0 & U\\ \end{array} \right)$ . Thus,

$\begin{eqnarray*} W^*\left(\begin{array}{cc} {{{\rm{Re\, }}}} A\sharp_t {{{\rm{Re\, }}}} B & \frac{X^*+Y^*}{2}\\ \frac{X+Y}{2} & {{{\rm{Re\, }}}} A\sharp_{1-t} {{{\rm{Re\, }}}} B\\ \end{array} \right)W = \left(\begin{array}{cc} {{{\rm{Re\, }}}} A\sharp_t {{{\rm{Re\, }}}} B & |\frac{X+Y}{2}|\\ |\frac{X+Y}{2}| & U^*({{{\rm{Re\, }}}} A\sharp_{1-t} {{{\rm{Re\, }}}} B)U\\ \end{array} \right)\geq0. \end{eqnarray*}$

By Lemma 2.1, we have

$\begin{eqnarray*} \left|\frac{X+Y}{2}\right|\leq({{{\rm{Re\, }}}} A\sharp_t {{{\rm{Re\, }}}} B)\sharp (U^*({{{\rm{Re\, }}}} A\sharp_{1-t} {{{\rm{Re\, }}}} B)U). \end{eqnarray*}$

Remark 1. When $M = \left(\begin{array}{cc} A & X \\ Y^{*} & B\\ \end{array} \right)$ is PPT in Theorem 2.4, our result is Theorem 1.1. Thus, our result is a generalization of Theorem 1.1.

Using Theorem 2.4 and Lemma 2.2, we have the following.

Corollary 2.5. Let $M = \left(\begin{array}{cc} A & X \\ Y^{*} & B\\ \end{array} \right)$ be APT and let $t\in[0, 1]$ , then for every unitarily invariant norm $|| \cdot ||$ and some unitary matrix $U\in \mathbb{M}_n,$

$\begin{eqnarray*} \begin{aligned} \left|\left|\frac{X+Y}{2}\right|\right|&\leq ||({{{\rm{Re\, }}}} A\sharp_t {{{\rm{Re\, }}}} B)\sharp (U^*({{{\rm{Re\, }}}} A\sharp_{1-t} {{{\rm{Re\, }}}} B)U)||\\ &\leq \left|\left|\frac{({{{\rm{Re\, }}}} A\sharp_t {{{\rm{Re\, }}}} B) + U^*({{{\rm{Re\, }}}} A\sharp_{1-t} {{{\rm{Re\, }}}} B)U}{2}\right|\right|\\ &\leq \frac{||{{{\rm{Re\, }}}} A\sharp_t {{{\rm{Re\, }}}} B|| + ||{{{\rm{Re\, }}}} A\sharp_{1-t} {{{\rm{Re\, }}}} B||}{2}\\ &\leq \frac{||({{{\rm{Re\, }}}} A)^{1-t} ({{{\rm{Re\, }}}} B)^t|| + ||({{{\rm{Re\, }}}} A)^t ({{{\rm{Re\, }}}} B)^{1-t}||}{2}\\ &\leq \frac{||(1-t){{{\rm{Re\, }}}} A+t{{{\rm{Re\, }}}} B|| + ||t{{{\rm{Re\, }}}} A+(1-t) {{{\rm{Re\, }}}} B||}{2}. \end{aligned} \end{eqnarray*}$

Proof: The first inequality follows from Theorem 2.4. The third one is by the triangle inequality. The other conclusions hold by Lemma 2.2.

In particular, when $t = \frac{1}{2},$ we have the following result.

Corollary 2.6. Let $M = \left(\begin{array}{cc} A & X \\ Y^{*} & B\\ \end{array} \right)$ be APT, then for every unitarily invariant norm $|| \cdot ||$ and some unitary matrix $U\in \mathbb{M}_n,$

$\begin{eqnarray*} \begin{aligned} \left|\left|\frac{X+Y}{2}\right|\right|&\leq ||({{{\rm{Re\, }}}} A\sharp {{{\rm{Re\, }}}} B)\sharp (U^*({{{\rm{Re\, }}}} A\sharp {{{\rm{Re\, }}}} B)U)||\\ &\leq \left|\left|\frac{({{{\rm{Re\, }}}} A\sharp {{{\rm{Re\, }}}} B) + U^*({{{\rm{Re\, }}}} A\sharp {{{\rm{Re\, }}}} B)U}{2}\right|\right|\\ &\leq ||{{{\rm{Re\, }}}} A\sharp {{{\rm{Re\, }}}} B||\\ &\leq ||({{{\rm{Re\, }}}} A)^{\frac{1}{2}}({{{\rm{Re\, }}}} B)^{\frac{1}{2}}||\\ &\leq \left|\left|\frac{{{{\rm{Re\, }}}} A+{{{\rm{Re\, }}}} B}{2}\right|\right|. \end{aligned} \end{eqnarray*}$

Squaring the inequalities in Corollary 2.6, we get a quick consequence.

Corollary 2.7. If $M = \left(\begin{array}{cc} A & X \\ Y^{*} & B\\ \end{array} \right)$ is APT, then

$\begin{eqnarray*} \begin{aligned} {{{\rm{tr}}}}\left(\left(\frac{X^*+Y^*}{2}\right)\left(\frac{X+Y}{2}\right)\right)&\leq {{{\rm{tr}}}}(({{{\rm{Re\, }}}} A\sharp {{{\rm{Re\, }}}} B)^2)\\ &\leq {{{\rm{tr}}}}({{{\rm{Re\, }}}} A {{{\rm{Re\, }}}} B)\\ &\leq {{{\rm{tr}}}}\left(\left(\frac{{{{\rm{Re\, }}}} A+{{{\rm{Re\, }}}} B}{2}\right)^2\right). \end{aligned} \end{eqnarray*}$

Proof: Compute

$\begin{eqnarray*} \begin{aligned} {{{\rm{tr}}}}\left(\left(\frac{X^*+Y^*}{2}\right)\left(\frac{X+Y}{2}\right)\right)&\leq {{{\rm{tr}}}}(({{{\rm{Re\, }}}} A\sharp {{{\rm{Re\, }}}} B)^*({{{\rm{Re\, }}}} A\sharp {{{\rm{Re\, }}}} B))\\ & = {{{\rm{tr}}}}(({{{\rm{Re\, }}}} A\sharp {{{\rm{Re\, }}}} B)^2)\\ &\leq {{{\rm{tr}}}}(({{{\rm{Re\, }}}} A)({{{\rm{Re\, }}}} B))\\ &\leq {{{\rm{tr}}}}\left(\left(\frac{{{{\rm{Re\, }}}} A+{{{\rm{Re\, }}}} B}{2}\right)^2\right). \end{aligned} \end{eqnarray*}$

It is known that for any $X, Y\in \mathbb{M}_n$ and any indices $i, j$ such that $i+j\leq n+1$ , we have $s_{i+j-1}(XY)\leq s_i(X)s_j(Y)$ (see [2, Page 75]). By utilizing this fact and Theorem 2.4, we can obtain the following result.

Corollary 2.8. Let $M = \left(\begin{array}{cc} A & X \\ Y^{*} & B\\ \end{array} \right)$ be APT, then for any $t\in [0, 1]$ , we have

$\begin{eqnarray*} s_{i+j-1}\left(\frac{X+Y}{2}\right)\leq s_i(({{{\rm{Re\, }}}} A\sharp_t {{{\rm{Re\, }}}} B)^{\frac{1}{2}})s_j(({{{\rm{Re\, }}}} A\sharp_{1-t} {{{\rm{Re\, }}}} B)^{\frac{1}{2}}). \end{eqnarray*}$

Consequently,

$\begin{eqnarray*} s_{2j-1}\left(\frac{X+Y}{2}\right)\leq s_j(({{{\rm{Re\, }}}} A\sharp_t {{{\rm{Re\, }}}} B)^{\frac{1}{2}})s_j(({{{\rm{Re\, }}}} A\sharp_{1-t} {{{\rm{Re\, }}}} B)^{\frac{1}{2}}). \end{eqnarray*}$

Proof: By Lemma 2.1 and Theorem 2.4, observe that

$\begin{eqnarray*} \begin{aligned} s_{i+j-1}\left(\frac{X+Y}{2}\right)& = s_{i+j-1}\left(\left|\frac{X+Y}{2}\right|\right)\\ &\leq s_{i+j-1}(({{{\rm{Re\, }}}} A\sharp_t {{{\rm{Re\, }}}} B)\sharp (U^*({{{\rm{Re\, }}}} A\sharp_{1-t} {{{\rm{Re\, }}}} B)U))\\ & = s_{i+j-1}(({{{\rm{Re\, }}}} A\sharp_t {{{\rm{Re\, }}}} B)^{\frac{1}{2}}V(U^*({{{\rm{Re\, }}}} A\sharp_{1-t} {{{\rm{Re\, }}}} B)U)^{\frac{1}{2}})\\ &\leq s_i(({{{\rm{Re\, }}}} A\sharp_t {{{\rm{Re\, }}}} B)^{\frac{1}{2}}V)s_j((U^*({{{\rm{Re\, }}}} A\sharp_{1-t} {{{\rm{Re\, }}}} B)U)^{\frac{1}{2}})\\ & = s_i(({{{\rm{Re\, }}}} A\sharp_t {{{\rm{Re\, }}}} B)^{\frac{1}{2}})s_j(({{{\rm{Re\, }}}} A\sharp_{1-t} {{{\rm{Re\, }}}} B)^{\frac{1}{2}}). \end{aligned} \end{eqnarray*}$

Finally, we study the relationship between the diagonal blocks and the real part of the off-diagonal blocks of the APT matrix $M$ .

Theorem 2.9. Let $M = \left(\begin{array}{cc} A & X \\ Y^{*} & B\\ \end{array} \right)$ be APT, then for all $t\in [0, 1]$ ,

$\begin{eqnarray*} \begin{aligned} {{{\rm{Re\, }}}}\left(\frac{X+Y}{2}\right)&\leq ({{{\rm{Re\, }}}} A\sharp_t {{{\rm{Re\, }}}} B)\sharp({{{\rm{Re\, }}}} A\sharp_{1-t} {{{\rm{Re\, }}}} B)\\ &\leq \frac{({{{\rm{Re\, }}}} A\sharp_t {{{\rm{Re\, }}}} B)+({{{\rm{Re\, }}}} A\sharp_{1-t} {{{\rm{Re\, }}}} B)}{2}, \end{aligned} \end{eqnarray*}$

and

$\begin{eqnarray*} \begin{aligned} {{{\rm{Im\, }}}}\left(\frac{X+Y}{2}\right)&\leq ({{{\rm{Re\, }}}} A\sharp_t {{{\rm{Re\, }}}} B)\sharp({{{\rm{Re\, }}}} A\sharp_{1-t} {{{\rm{Re\, }}}} B)\\ &\leq \frac{({{{\rm{Re\, }}}} A\sharp_t {{{\rm{Re\, }}}} B)+({{{\rm{Re\, }}}} A\sharp_{1-t} {{{\rm{Re\, }}}} B)}{2}. \end{aligned} \end{eqnarray*}$

Proof: Since $M$ is APT, we have that

${{{\rm{Re\, }}}} M = \left( \begin{array}{cc} {{{\rm{Re\, }}}} A & \frac{X+Y}{2} \\ \frac{X^{*}+Y^{*}}{2} & {{{\rm{Re\, }}}} B\\ \end{array} \right)$

is PPT.

Therefore,

$\begin{eqnarray*} \begin{aligned} \left( \begin{array}{cc} {{{\rm{Re\, }}}} A\sharp_t {{{\rm{Re\, }}}} B & {{{\rm{Re\, }}}} \left(\frac{X+Y}{2}\right) \\ {{{\rm{Re\, }}}}\left(\frac{X^{*}+Y^{*}}{2}\right) & {{{\rm{Re\, }}}} A\sharp_{1-t} {{{\rm{Re\, }}}} B\\ \end{array} \right)& = \frac{1}{2} \left( \begin{array}{cc} {{{\rm{Re\, }}}} A\sharp_t {{{\rm{Re\, }}}} B & \frac{X+Y}{2} \\ \frac{X^{*}+Y^{*}}{2} & {{{\rm{Re\, }}}} A\sharp_{1-t} {{{\rm{Re\, }}}} B\\ \end{array} \right)\\ &+\frac{1}{2} \left( \begin{array}{cc} {{{\rm{Re\, }}}} A\sharp_t {{{\rm{Re\, }}}} B & \frac{X^{*}+Y^{*}}{2} \\ \frac{X+Y}{2} & {{{\rm{Re\, }}}} A\sharp_{1-t} {{{\rm{Re\, }}}} B\\ \end{array} \right)\geq0. \end{aligned} \end{eqnarray*}$

So, by Lemma 2.1, we have

$\begin{eqnarray*} {{{\rm{Re\, }}}} \left(\frac{X+Y}{2}\right)\leq({{{\rm{Re\, }}}} A\sharp_t {{{\rm{Re\, }}}} B)\sharp({{{\rm{Re\, }}}} A\sharp_{1-t} {{{\rm{Re\, }}}} B). \end{eqnarray*}$

This implies the first inequality.

Since ${{{\rm{Re\, }}}} M$ is PPT, we have

$\begin{eqnarray*} \left( \begin{array}{cc} {{{\rm{Re\, }}}} A & -i\frac{X+Y}{2} \\ i\frac{X^{*}+Y^{*}}{2} & {{{\rm{Re\, }}}} B\\ \end{array} \right) = \left( \begin{array}{cc} I & 0 \\ 0 & iI\\ \end{array} \right) ({{{\rm{Re\, }}}} M) \left( \begin{array}{cc} I & 0 \\ 0 & -iI\\ \end{array} \right)\geq0, \\ \left( \begin{array}{cc} {{{\rm{Re\, }}}} A & i\frac{X^{*}+Y^{*}}{2} \\ -i\frac{X+Y}{2} & {{{\rm{Re\, }}}} B\\ \end{array} \right) = \left( \begin{array}{cc} I & 0 \\ 0 & -iI\\ \end{array} \right) (({{{\rm{Re\, }}}} M)^\tau) \left( \begin{array}{cc} I & 0 \\ 0 & iI\\ \end{array} \right)\geq0. \end{eqnarray*}$

Thus,

$\left( \begin{array}{cc} {{{\rm{Re\, }}}} A & -i\frac{X+Y}{2} \\ i\frac{X^{*}+Y^{*}}{2} & {{{\rm{Re\, }}}} B\\ \end{array} \right)$

is PPT.

By Lemma 2.3,

$\left( \begin{array}{cc} {{{\rm{Re\, }}}} A\sharp_t {{{\rm{Re\, }}}} B & -i\frac{X+Y}{2} \\ i\frac{X^{*}+Y^{*}}{2} & {{{\rm{Re\, }}}} A\sharp_{1-t} {{{\rm{Re\, }}}} B\\ \end{array} \right)$

is also PPT.

So,

$\begin{eqnarray*} \frac{1}{2}\left( \begin{array}{cc} {{{\rm{Re\, }}}} A\sharp_t {{{\rm{Re\, }}}} B & -i\frac{X+Y}{2} \\ i\frac{X^{*}+Y^{*}}{2} & {{{\rm{Re\, }}}} A\sharp_{1-t} {{{\rm{Re\, }}}} B\\ \end{array} \right) +\frac{1}{2}\left( \begin{array}{cc} {{{\rm{Re\, }}}} A\sharp_t {{{\rm{Re\, }}}} B & i\frac{X^{*}+Y^{*}}{2} \\ -i\frac{X+Y}{2} & {{{\rm{Re\, }}}} A\sharp_{1-t} {{{\rm{Re\, }}}} B\\ \end{array} \right)\geq0, \end{eqnarray*}$

which means that

$\left( \begin{array}{cc} {{{\rm{Re\, }}}} A\sharp_t {{{\rm{Re\, }}}} B & {{{\rm{Im\, }}}}\left(\frac{X+Y}{2}\right) \\ {{{\rm{Im\, }}}}\left(\frac{X+Y}{2}\right) & {{{\rm{Re\, }}}} A\sharp_{1-t} {{{\rm{Re\, }}}} B\\ \end{array} \right)\geq 0.$

By Lemma 2.1, we have

$\begin{eqnarray*} {{{\rm{Im\, }}}}\left(\frac{X+Y}{2}\right)\leq({{{\rm{Re\, }}}} A\sharp_t {{{\rm{Re\, }}}} B)\sharp({{{\rm{Re\, }}}} A\sharp_{1-t} {{{\rm{Re\, }}}} B). \end{eqnarray*}$

This completes the proof.

Corollary 2.10. Let $\left(\begin{array}{cc} {{{\rm{Re\, }}}} A & \frac{X+Y}{2} \\ \frac{X+Y}{2} & {{{\rm{Re\, }}}} B\\ \end{array} \right)\geq0.$ If $\frac{X+Y}{2}$ is Hermitian and $t\in[0, 1]$ , then,

$\begin{eqnarray*} \begin{aligned} \frac{X+Y}{2}&\leq ({{{\rm{Re\, }}}} A\sharp_t {{{\rm{Re\, }}}} B)\sharp({{{\rm{Re\, }}}} A\sharp_{1-t} {{{\rm{Re\, }}}} B)\\ &\leq \frac{({{{\rm{Re\, }}}} A\sharp_t {{{\rm{Re\, }}}} B)+({{{\rm{Re\, }}}} A\sharp_{1-t} {{{\rm{Re\, }}}} B)}{2}. \end{aligned} \end{eqnarray*}$

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The work is supported by National Natural Science Foundation (grant No. 12261030), Hainan Provincial Natural Science Foundation for High-level Talents (grant No. 123RC474), Hainan Provincial Natural Science Foundation of China (grant No. 124RC503), the Hainan Provincial Graduate Innovation Research Program (grant No. Qhys2023-383 and Qhys2023-385), and the Key Laboratory of Computational Science and Application of Hainan Province.

Conflict of interest

The authors declare that they have no conflict of interest.

References

[1]	Bond GC, Sermon PA, Webb G, et al. (1973) Hydrogenation over supported gold catalysts. J Chem Soc Chem Commun 444–445.
[2]	Bond GC, Thompson DT (1999) Catalysis by gold. Catal Rev 41: 319–388. doi: 10.1081/CR-100101171
[3]	Haruta M, Kobayashi T, Sano H, et al. (1987) Novel gold catalysts for the oxidation of carbon monoxide at a temperature far below 0 °C. Chem Lett 16: 405–408.
[4]	Bailie JE, Hutching GJ (1999) Promotion by sulfur of gold catalysts for crotyl alcohol formation from crotonaldehyde hydrogenation. Chem Commun 2151–2152.
[5]	Pawelec B, Cano-Serrano E, Campos-Martin JM, et al. (2004) Deep aromatics hydrogenation in the presence of DBT over Au–Pd/γ-alumina catalysts. Appl Catal A-Gen 275: 127–139. doi: 10.1016/j.apcata.2004.07.028
[6]	Boronat M, Illas F, Corma A (2009) Active sites for H₂ adsorption and activation in Au/TiO₂ and the role of the support. J Phys Chem A 113: 3750–3757.
[7]	Bus E, Miller JT, van Bokhoven JA (2005) Hydrogen chemisorption on Al₂O₃-supported gold catalysts. J Phys Chem B 109: 14581–14587. doi: 10.1021/jp051660z
[8]	Caballero C, Valencia J, Barrera M, et al. (2010) Selective hydrogenation of citral over gold nanoparticles on alumina. Powder Technol 203: 412–414.
[9]	Campo B, Ivanova S, Gigola C, et al. (2008) Crotonaldehyde hydrogenation on supported gold catalysts. Catal Today 133: 661–666.
[10]	Cárdenas-Lizana F, Gomez-Quero S, Baddeley CJ, et al. (2010) Tunable gas phase hydrogenation of m-dinitrobenzene over alumina supported Au and Au–Ni. Appl Catal A-Gen 387: 155–165. doi: 10.1016/j.apcata.2010.08.019
[11]	Cárdenas-Lizana F, Gomez-Quero S, Keane MA (2008) Ultra-selective gas phase catalytic hydrogenation of aromatic nitro compounds over Au/Al₂O₃. Catal Commun 9: 475–481. doi: 10.1016/j.catcom.2007.07.032
[12]	Cárdenas-Lizana F, Gomez-Quero S, Keane MA (2009) Gas phase hydrogenation of m-dinitrobenzene over alumina supported Au and Au–Ni alloy. Catal Lett 127: 25–32. doi: 10.1007/s10562-008-9660-9
[13]	Cárdenas-Lizana F, Gomez-Quero S, Keane MA (2008) Exclusive production of chloroaniline from chloronitrobenzene over Au/TiO₂ and Au/Al₂O₃. ChemSusChem 1: 215–221. doi: 10.1002/cssc.200700105
[14]	Cárdenas-Lizana F, Keane MA (2013) The development of gold catalysts for use in hydrogenation reactions. J Mater Sci 48: 543–564.
[15]	Claus P (2005) Heterogeneously catalysed hydrogenation using gold catalysts. Appl Catal A-Gen 291: 222–229. doi: 10.1016/j.apcata.2004.12.048
[16]	Claus P, Brückner A, Mohr C, et al. (2000) Supported gold nanoparticles from quantum dot to mesoscopic size scale: effect of electronic and structural properties on catalytic hydrogenation of conjugated functional groups. J Am Chem Soc 122: 11430–11439. doi: 10.1021/ja0012974
[17]	Chambers RP, Boudart M (1966) Selectivity of gold for hydrogenation and dehydrogenation of cyclohexene. J Catal 5: 517–528. doi: 10.1016/S0021-9517(66)80070-2
[18]	Chen YW, Lee DS (2013) Liquid phase hydrogenation of p-chloronitrobenzene on Au–Pd/TiO₂ catalysts: effects of reduction method. Mod Res Catal 2: 25–34. doi: 10.4236/mrc.2013.22004
[19]	Choudhary TV, Sivadinarayana C, Datye AK, et al. (2003) Acetylene hydrogenation on Au-based catalysts. Catal Lett 86: 1−8.
[20]	Corma A, Boronat M, González S, et al. (2007) On the activation of molecular hydrogen by gold: a theoretical approximation to the nature of potential active sites. Chem Commun 3371–3373.
[21]	Díaz G, Antonio GC, Orlando HC, et al. (2011) Hydrogenation of citral over IrAu/TiO₂ catalysts. effect of the preparation method. Top Catal 54: 467–473.
[22]	Fujitani T, Nakamura I, Akita T, et al. (2009) Hydrogen dissociation by gold clusters. Angew Chem Int Ed 48: 9515–9518. doi: 10.1002/anie.200905380
[23]	Gomez S, Torres C, Luis JGF, et al. (2012) Hydrogenation of nitrobenzene on Au/ZrO₂ catalysts. J Chil Chem Soc 57: 1194–1198. doi: 10.4067/S0717-97072012000200029
[24]	Guan Y, Hensen EJM (2009) Cyanide leaching of Au/CeO₂: highly active gold clusters for 1,3-butadiene hydrogenation. Phys Chem Chem Phys 11: 9578–9582.
[25]	Hartfelder U, Kartusch C, Makosch M, et al. (2013) Particle size and support effects in hydrogenation over supported gold catalysts. Catal Sci Technol 3: 454–461. doi: 10.1039/C2CY20485A
[26]	Hashmi ASK (2007) Gold-catalyzed organic reactions. Chem Rev 107: 3180–3211. doi: 10.1021/cr000436x
[27]	Hugon A, Delannoy L, Louis C (2008) Supported gold catalysts for selective hydrogenation of 1,3-butadiene in the presence of an excess of alkenes. Gold Bull 41: 127–138. doi: 10.1007/BF03216590
[28]	Jia J, Haraki K, Kondo JN, et al. (2000) Selective hydrogenation of acetylene over Au/Al₂O₃ catalyst. J Phys Chem B 104: 11153–11156. doi: 10.1021/jp001213d
[29]	Milone C, Crisafulli C, Ingoglia R, et al. (2007) A comparative study on the selective hydrogenation of α,β-unsaturated aldehyde and ketone to unsaturated alcohols on Au supported catalysts. Catal Today 122: 341–351. doi: 10.1016/j.cattod.2007.01.011
[30]	Milone C, Ingoglia R, Schipilliti L, et al. (2005) Selective hydrogenation of α,β-unsaturated ketone to α,β-unsaturated alcohol on gold-supported iron oxide catalysts: role of the support. J Catal 236: 80–90. doi: 10.1016/j.jcat.2005.09.023
[31]	Cárdenas-Lizana F, Gomez-Quero S, Hugon A, et al. (2009) Pd-promoted selective gas phase hydrogenation of p-chloronitrobenzene over alumina supported Au. J Catal 262: 235–243. doi: 10.1016/j.jcat.2008.12.019
[32]	Zhang X, Shi H, Xu BQ (2005) Catalysis by gold: isolated surface Au³⁺ ions are active sites for selective hydrogenation of 1,3-butadiene over Au/ZrO₂ catalysts. Angew Chem Int Ed 44: 7132–7135. doi: 10.1002/anie.200502101
[33]	Corma A, Garcia H (2008) Supported gold nanoparticles as catalysts for organic reactions. Chem Soc Rev 37: 2096–2126. doi: 10.1039/b707314n
[34]	Mohr C, Hofmeister H, Claus P (2003) The inﬂuence of real structure of gold catalysts in the partial hydrogenation of acrolein. J Catal 213: 86–94. doi: 10.1016/S0021-9517(02)00043-X
[35]	Mohr C, Hofmeister H, Radnik J, et al. (2003) Identification of active sites in gold-catalyzed hydrogenation of acrolein. J Am Chem Soc 125: 1905–1911. doi: 10.1021/ja027321q
[36]	Stobinski L, Zommer L, Dus R (1999) Molecular hydrogen interactions with discontinuous and continuous thin gold films. Appl Surf Sci 141: 319–325. doi: 10.1016/S0169-4332(98)00517-0
[37]	Boronat M, Concepcion P, Corma A (2009) Unravelling the nature of gold surface sites by combining IR spectroscopy and DFT calculations. Implications in catalysis. J Phys Chem C 113: 16772–16784.
[38]	Nikolaev SA, Smirnov VV (2009) Synergistic and size effects in selective hydrogenation of alkynes on gold nanocomposites. Catal Today 147: S336–S341. doi: 10.1016/j.cattod.2009.07.032
[39]	Nikolaev SA, Permyakov NA, Smirnov VV, et al. (2010) Selective hydrogenation of phenylacetylene into styrene on gold nanoparticles. Kinet Catal 51: 288–292. doi: 10.1134/S0023158410020187
[40]	Guo X, Liu Q, Wang L, et al. (2012) Synthesis, morphology and optical properties of multi-pods Au/FeO(OH) and Au/Fe₂O₃ nanostructures. Mater Sci Eng B-Adv 177: 321–326. doi: 10.1016/j.mseb.2011.12.036
[41]	Radnik J, Mohr C, Claus P (2003) On the origin of binding energy shifts of core levels of supported gold nanoparticles and dependence of pretreatment and material synthesis. Phys Chem Chem Phys 5: 172–177. doi: 10.1039/b207290d
[42]	Crook R, Deering J, Fussell SJ, et al. (2010) Enhance reactivity of silver- and gold-catalysted hydrogenations using silver(I) salts. Tetrahedron Lett 51: 5181–5184. doi: 10.1016/j.tetlet.2010.07.143
[43]	Edwards JK, Solsona BE, Landon P, et al. (2005) Direct synthesis of hydrogen peroxide from H₂ and O₂ using TiO₂-supported Au–Pd catalysts. J Catal 236: 69–79. doi: 10.1016/j.jcat.2005.09.015
[44]	Liao S, Yu Z, Xu Y, et al. (1995) A remarkable synergic effect of polymer-anchored bimetallic palladium-ruthenium catalysts in the selective hydrogenation of p-chloronitrobenzene. J Chem Soc Chem Commun 1155–1156.
[45]	Hosseini M, Siffert S, Tidahy HL, et al. (2007) Promotional effect of gold added to palladium supported on a new mesoporous TiO₂ for total oxidation of volatile organic compounds. Catal Today 122: 391–396. doi: 10.1016/j.cattod.2007.03.012
[46]	Nutt MO, Heck KN, Alvarez P, et al. (2006) Improved Pd-on-Au bimetallic nanoparticle catalysts for aqueous-phase trichloroethene hydrodechlorination. Appl Catal B-Environ 69: 115–125. doi: 10.1016/j.apcatb.2006.06.005
[47]	Nutt MO, Hughes JB, Wong MS (2005) Designing Pd-on-Au bimetallic nanoparticle catalysts for trichloroethene hydrodechlorination. Environ Sci Technol 39: 1346–1353. doi: 10.1021/es048560b
[48]	Vasil'kov AY, Nikolaev SA, Smirnov VV, et al. (2007) An XPS study of the synergetic effect of gold and nickel supported on SiO₂ in the catalytic isomerization of allylbenzene. Mendeleev Commun 17: 268–270. doi: 10.1016/j.mencom.2007.09.006
[49]	Venezia AM, La Parola V, Deganello G, et al. (2003) Synergetic effect of gold in Au/Pd catalysts during hydrodesulfurization reactions of model compounds. J Catal 215: 317–325. doi: 10.1016/S0021-9517(03)00005-8
[50]	Piccinini M, Edwin NN, Edwards JK, et al. (2010) Effect of reaction conditions on the performance of Au–Pd/TiO₂ catalyst for the direct synthesis of hydrogen peroxide. Phys Chem Chem Phys 12: 2488–2492. doi: 10.1039/b921815g
[51]	Rousset JL, Cadete-Santos-Aires FJ, Sekhar BR, et al. (2000) Comparative X-ray photoemission spectroscopy study of Au, Ni, and AuNi clusters produced by laser vaporization of bulk metals. J Phys Chem B 104: 5430–5435.
[52]	Yuan G, Louis C, Delannoy L, et al. (2007) Silica- and titania-supported Ni–Au: application in catalytic hydrodechlorination. J Catal 247: 256–268. doi: 10.1016/j.jcat.2007.02.008
[53]	Wu Z, Zhao Z, Zhang M (2010) Synthesis by replacement reaction and application of TiO₂-supported Au–Ni bimetallic catalyst. ChemCatChem 2: 1606–1614. doi: 10.1002/cctc.201000165
[54]	Liu YC, Huang CY, Chen YW (2006) Hydrogenation of p-chloronitrobenzene on Ni–B nanometal catalysts. J Nanopart Res 8: 223–230. doi: 10.1007/s11051-005-5944-9
[55]	Liu YC, Huang CY, Chen YW (2006) Liquid-phase selective hydrogenation of p-chloronitrobenzene on Ni–P–B nanocatalysts. Ind Eng Chem Res 45: 62−69.
[56]	Wang X, Perret N, Delgado JJ, et al. (2013) Reducible support effects in the gas phase hydrogenation of p-chloronitrobenzene over gold. J Phys Chem C 117: 994–1005. doi: 10.1021/jp3093836
[57]	Yan X, Liu M, Liu H, et al. (2001) Role of boron species in the hydrogenation of o-chloronitrobenzene over polymer-stabilized ruthenium colloidal catalysts. J Mol Catal A-Chem 169: 225–233. doi: 10.1016/S1381-1169(00)00565-3
[58]	Chen YW, Lee DS, Chen HJ (2012) Preferential oxidation of CO in H₂ stream on Au/ZnO–TiO₂cataalysts. Int J Hydrogen Energ 37: 15140–15155. doi: 10.1016/j.ijhydene.2012.08.003
[59]	Sandoval A, Aguilar A, Louis C, et al. (2011) Bimetallic Au–Ag/TiO₂ catalyst prepared by deposition-precipitation: high activity and stability in CO oxidation. J Catal 281: 40–49. doi: 10.1016/j.jcat.2011.04.003
[60]	Sarkany A, Geszti O, Safran G (2008) Preparation of Pd shell–Au core/SiO₂ catalyst and catalytic activity for acetylene hydrogenation. Appl Catal A-Gen 350: 157–163. doi: 10.1016/j.apcata.2008.08.012
[61]	Sarkany A, Horvath A, Beck A (2002) Hydrogenation of acetylene over low Loaded Pd and Pd–Au/SiO₂ catalysts. Appl Catal A-Gen 229: 117–125. doi: 10.1016/S0926-860X(02)00020-0
[62]	Serna P, Concepción P, Corma A (2009) Design of highly active and chemoselective bimetallic gold–platinum hydrogenation catalysts through kinetic and isotopic studies. J Catal 265: 19–25. doi: 10.1016/j.jcat.2009.04.004
[63]	Stakheev AY, Kustov LM (1999) Effects of the support on the morphology and electronic properties of supported metal clusters: modern concepts and progress in 1990s. Appl Catal A-Gen 188: 3–35. doi: 10.1016/S0926-860X(99)00232-X
[64]	Steiner P, Hüfner S (1981) Core level binding energy shifts in Ni on Au and Au on Ni overlayers. Solid State Commun 37: 279–283.
[65]	Zafeiratos S, Kennou S (2001) Photoelectron spectroscopy study of surface alloying in the Au/Ni (s) 5(0 0 1) × (1 1 1) system. Appl Surf Sci 173: 69–75. doi: 10.1016/S0169-4332(00)00885-0

Reader Comments

Your name:*

Email:*
© 2017 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)