1. Introduction
An acrylic sheet is a kind of resin which shows several advantages such as excellent transparency to the visible light, high shattered resistance, good resistance to many chemicals and so on. Due to these advantages, the acrylic sheet is proposed to be an ideal material for making advertising boards, control panels, etc [1]. Moreover, this resin becomes an important raw material for dental applications [2,3].
To cut a raw acrylic sheet into net and/or near net shape products, a punch/die shearing is one of attractive cutting methods. Many researchers have paid a lot of attention on the shearing of ductile metallic sheet materials. Klocke et al., numerically analyzed the effect of mechanical conditions of the shearing process on the breaking pattern of a 42CrMo4 steel sheet subjected to a punch/die tool. They revealed that a too large punch/die clearance caused the formation of an excessive incline sheared edge of the worksheet [4]. Chen et al., investigated the tearing failure on a sheared edge of a SS400 structural steel sheet subjected to the punch/die shearing. Such failure was found to be strongly affected by the tensile stress in the sheared zone and the friction between the cutting tool and the worksheet interfaces [5]. Thipprakmas studied the application of a V-ring indenter for the shear cutting of a JIS-S45C cold-rolled steel sheet. The use of this indenter resulted in the increase of the compressive stress in a sheared zone and the suppression of the material flow during cutting. These conditions contributed to suppress the formation of unexpected cracks. As the result, a smooth sheared edge of the worksheet was generated [6].
From the above literature survey, sheared edge features of ductile metallic sheets cut by the punch/die shearing process appear to be remarkably influenced and varied by a state of stresses at the sheared zone and mechanical conditions of the shearing process.
In the case of fragile resin sheet shearing, there are almost not any research works aiming to investigate the change of cracking/deformation pattern when a state of stress at the sheared zone is varied by varying shearing tool geometry. Therefore, in this work, a couple of side-wedge punch/die tools were prepared and employed to experimentally cut off a fragile acrylic worksheet. Moreover, a two-dimensional FEM analysis of the side-wedge punch/die shearing was conducted.
2. Materials and Method
2.1. Material, Tool Condition and Method
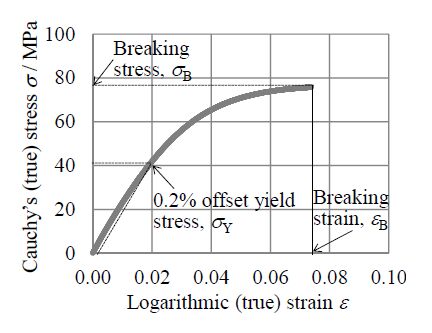
In the experiment, a fragile resin, acrylic worksheet (AC) which had a thickness tS = 1.0 mm was chosen as the worksheet. The in-plane mechanical properties of the AC worksheet were evaluated by the uni-axial tensile test.
Figure 1 and Table 1 show the true stress-true strain curve and the fundamental mechanical properties of the AC worksheet. Shearing specimens were cut from a raw acrylic sheet to have a width (wS) and a length (lS) of 20 and 70 mm, respectively. Protective films attached on the surfaces of the AC specimens were removed, and then the specimens were sufficiently washed water and naturally dried. After that, they were kept in a room with a temperature of 296 ± 1 K and a humidity of 50 ± 1 %RH for approximately 24 hours before the shearing test.
Table 1. In-plane mechanical properties of acrylic worksheet.
| tS = 1.0 mm, strain rate = 0.002 s-1 |
| Young’s modulus | Yield strength | Breaking strength | Breaking strain |
| E/MPa | σY/MPa | σB/MPa | εB |
| 2216 | 41 | 75 | 0.07 |
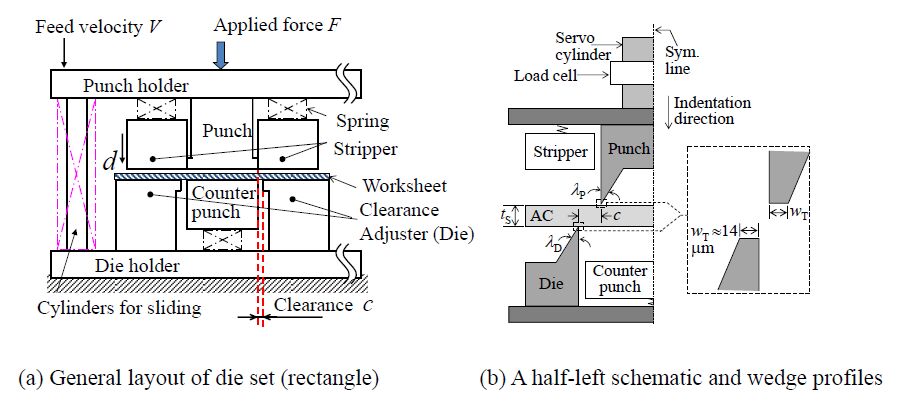
To cut off the worksheet, a straight shearing tool with a central punch and right and left dies shown in Figure 2 was used. In this experiment, two-line cutting was considered as a symmetric structure. The punch was pushed downward to indent to the worksheet by a servo press machine. The wedge tools were made of a JIS-SKD11 cold work tool steel which had a hardness of 58~60 HRC. A load cell was used to measure the cutting load resistance F. To investigate the side-view deformation of the worksheet, a CCD camera was installed. The cutting/feed velocity V was fixed as 0.05 mm·s -1. The clearance ratio c/tS was basically chosen as 0.025 in the cases of symmetric wedge profile of punch/die, as shown in Figure 2(b). The shearing test of the worksheet was carried out in the temperature and humidity controlled room. The shearing test was carried out 10 times for each condition.
As the experimental condition of tool geometry, the side-wedge angles of the punch (λP) and die (λD) were chosen as 30 and/or 60° in this work. The square punch/die tool of λP = λD = 90° was referred from the previous report [7] and compared here. The tip thickness of these tools (wT) was 14 µm in average (13.30~14.25 µm). The cutting load resistance, the side-view deformation behavior and the final sheared edge of the worksheet were compared and discussed with our previous shearing results of an acrylic worksheet subjected to a square punch/die tool (λP = λD = 90°) [7]. The square angle of punch/die condition was named here as Case 1: λP = λD = 90°, while other side-wedge angles were named as Case 2: λP = λD = 60° and Case 3: λP = λD = 30° for the sake of convenience.
Furthermore, an asymmetric wedge combination (Case 4: λP = 90° and λD = 60°) was investigated in order to observe the effect of asymmetric wedge indentation on a cracking pattern. Here, the clearance c/tS was 0.03 in the case of asymmetric condition.
2.2. Cutting Load Resistance and Side-View Deformation of Worksheet
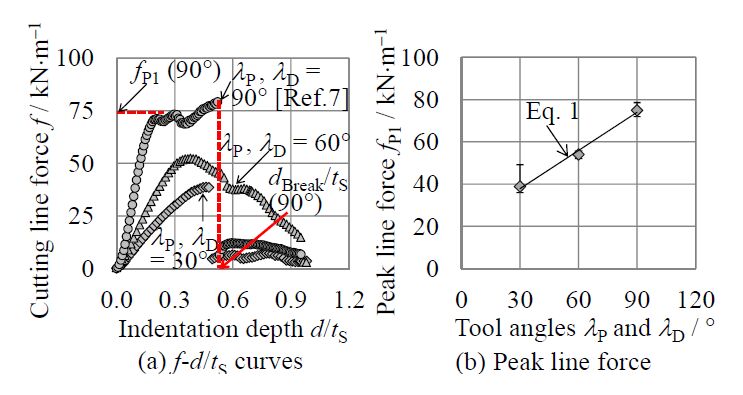
Figure 3(a) illustrates the relationship between the cutting line force f (f = F/2wS) and the normalized indentation depth of punch d/tS for the angles λP and λD. The f-d/tS curve of the square punch/die (Case 1: λP = λD = 90°, referred from [7]) was also plotted in Figure 3(a). The depth d/tS was defined to be zero when the punch touched the upper surface of the worksheet. From Figure 3(a), the following features of f were revealed: (i) the gradient of f(∂f/∂(d/tS)) in the shallow indentation depth 0 < d/tS ≤ 0.1 increased when increasing the side-wedge angles. (ii) The first peak point of f(fP1) increased with the side-wedge angles, as show in Figure 3(b). This relationship was linearly approximated by Eq. (1). (iii) After passing through fP1, wavy residual force was observed in Cases 2, 1 of λP = λD = 60°, 90°. But, this wavy residual response did not occur in Case 3 of λP = λD = 30°. (iv) The breaking position of the worksheet (dBreak/tS) in Cases 3, 1 of λP = λD = 30°, 90° was detected at d/tS ≈ 0.45~0.5, while the separation of the worksheet was delayed up to d/tS ≈ 0.79 in Case 2 of λP = λD = 60°.
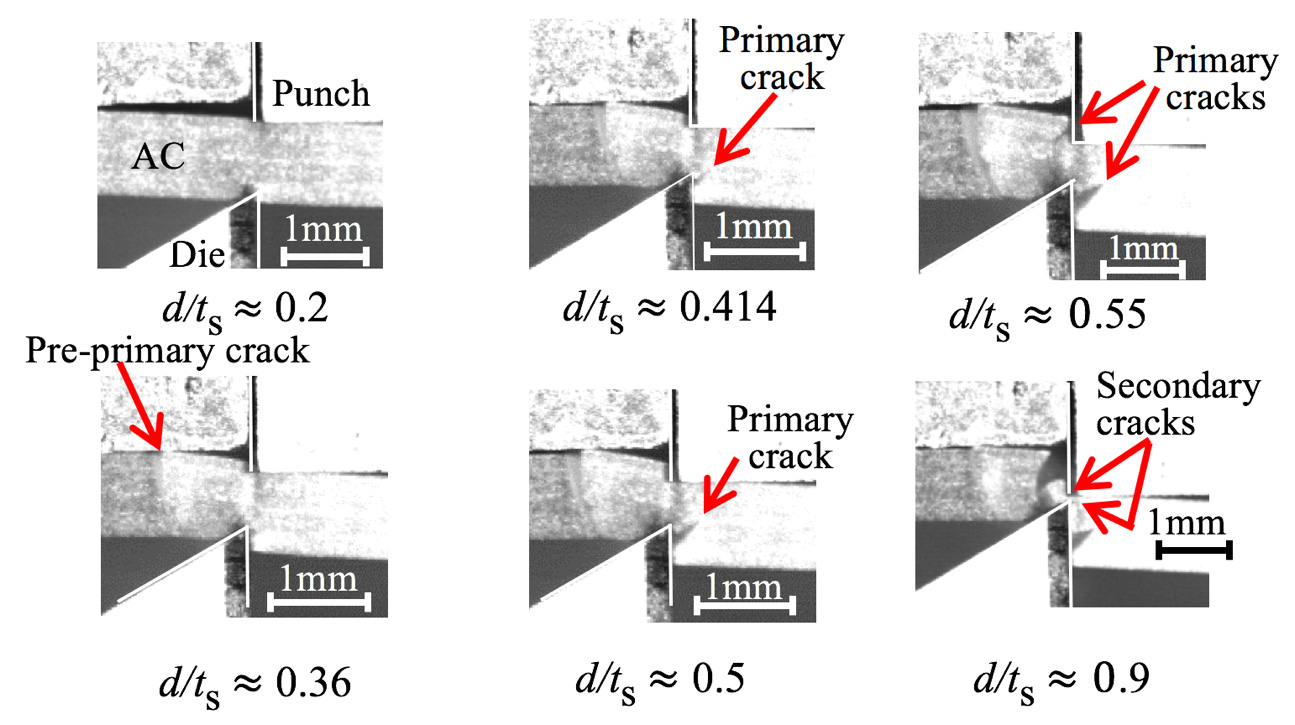
Figure 4 shows the side-view deformation photographs of the worksheet for the side-wedge angles λP and λD at some representative indentation depths. When the square punch and die (Case 1: λP and λD = 90°) were considered, at d/tS ≈ 0.25, two primary cracks were apparently observed on the upper and lower surfaces of the worksheet. The upper crack tended to be initiated close to the cutting tool corner, while the lower crack occurred on the lower free surface where is a little far from the cutting tool corner. These two primary cracks were propagated and appear to be similar patterns when d/tS ≈ 0.35 as seen in Figure 5(c). At the final shearing stage, the propagation of the primary cracks stopped, and then the worksheet was completely cut off by the propagation of the secondary crack, as illustrated in Figure 5(c) at d/tS ≈ 0.52.
For both cases of the side-wedge tools (Case 3, 2: λP = λD = 30°, 60°), as shown in Figure 4(a) and (b) at d/tS ≈ 0.4, the initiation of the primary cracks were always detected in the vicinity of the tool tips. After the primary crack occurrences at the early stage, the crack pattern was quite different when varying the angles of the side-wedge tools. In Case 2 of λP =λD = 60°, the crack pattern was fairly similar to that of the square punch/die tool case. Namely, the secondary cracks were largely propagated into the inner and outer portions of the worksheet. But, when using the smallest-angle wedge tool (Case 3: λP = λD = 30°), the primary crack initiated at the tip of the die and propagated parallel to the indentation direction of the wedge punch. This propagation seems to contribute the generation of a straight sheared edge, as seen in Figure 4(a) at d/tS ≈ 0.94. From Figure 4, the small-angle side-wedge tool (Case 3: λP = λD = 30°) seems to be superior for generating the straight sheared edge of the fragile acrylic worksheet.
2.3. Initiation of First Surface Crack
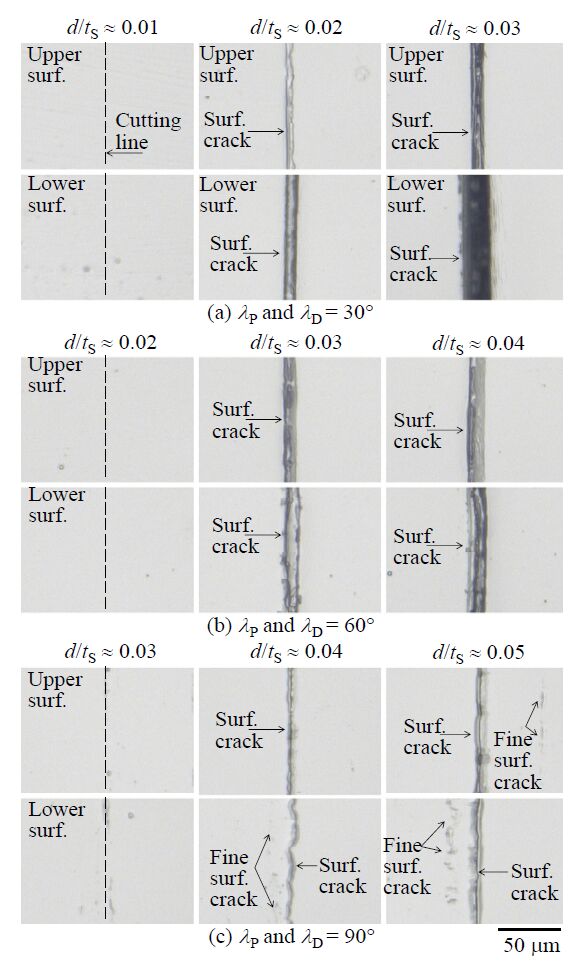
In the AC resin cutting, when the punch and die corners indented to the surface of the worksheet, the first surface crack occurrence (initiation) seems to strongly affect a subsequent cracking pattern and a final feature of the sheared edge. Thus, in order to furthermore discuss about the first surface crack with respect to the side-wedge angles of the punch and die, an intermediate cutting experiment of the worksheet was carried out. Here, all the side-wedge and square punch/die tools were considered. The punch was indented to the worksheet with the indentation depth d/tS ≈ 0.01, 0.02, 0.03, 0.05 and 0.1. When the indentation reached the specified depth, the punch was quickly withdrawn. Then, the scored specimens were observed by an optical microscope for investigating the first surface cracks initiated on the upper and lower surfaces of the worksheet.
Figure 5 illustrates representative optical micrographs for the upper and lower surfaces of the scored worksheets using the three cases λP = λD = 30°, 60° and 90°.
From Figure 5, it was found that the first surface crack initiation on the worksheet surfaces occurred at the shallow indentation depth d/tS ≈ 0.02 in Case 3 of λP = λD = 30°, while this initiation was slightly postponed up to d/tS ≈ 0.03 and 0.04 in Cases 2, 1 of λP = λD = 60°, 90°, respectively.
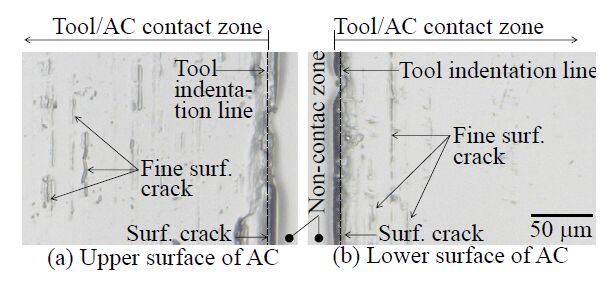
In addition, from this first surface crack investigation, in Case 1 of the square punch/die tool (λP = λD = 90°), many fine surface cracks shown in Figure 6 were detected on the upper and lower surfaces of worksheet which contacted with the lower surface of the punch and the upper surface of the die during the intermediate indentation. From Figure 5(c) and Figure 6, the cracking zones on the upper and lower contact surfaces of the worksheet were detected at approximately 50 µm far from the tool indentation lines or the cutting tool corners. In section 3.3, the initiation of the surface cracks is furthermore discussed.
When the 30 and 60° angle tools were applied to the specimens, there were not any fine surface cracks except for the ones that were generated by the deep indentation of the punch and die tips.
2.4. Profile Feature of Sheared Worksheet with Symmetric Wedge Combination
Figure 7 shows the representative side-view photographs of sheared edges and sheared surfaces with respect to the angles λP and λD. By using the smallest-angle side-wedge punch and die (Case 3: λP = λD = 30°), a straight sheared edge and a quite smooth sheared surface of the worksheet were generated, as shown in Figure 7(a). However, seeing Figure 7(b), for the worksheet sheared by the 60° angle punch/die tool, a concave sheared edge which was caused by the deviated propagation of the primary crack was formed. Also, there was a small core portion adhered at the sheared edge. Since this portion seems to be easily separated from the sheared edge, here, it is recognized to be dust and called “rod-like dust”.
In the case of square punch/die tool (Case 1: λP = λD = 90° [7]), as shown in Figure 7(c), although the rod-like dust was not observed, an inferior final sheared edge due to the large propagation of the primary crack was generated.
Through this sheared edge investigation, it was confirmed that the smallest-angle wedge punch and die (Case 3: λP = λD = 30°) was superior for the smart cut of the fragile acrylic worksheet, compared to the cases 2 and 1: λP = λD = 60° and 90° angle punch/die tool.
2.5. Sheared Profile and Load Response in Asymmetric Wedge Combination
Figure 8 shows the relationship between the cutting line force f and the normalized indentation depth of punch d/tS for the asymmetric angles λP = 90° and λD = 60°.
Seeing the gradient κ = (∂f/∂(d/tS)) in the indentation depth 0 < d/tS ≤ 0.3, it was estimated as κ ≈ 207 N·mm-1. This gradient seems to be intermediate state between Case 1 [7] of λP = λD = 90° and Case 2 of λP = λD = 60°. The gradients κ1, κ2 = (∂f/∂(d/tS)) in Cases 1 and 2 are estimated for 0 < d/tS ≤ 0.3 from Figure 3(a). They were κ1 ≈ 250 N·mm-1 and κ2 ≈ 166.7 N·mm-1, respectively. According to a combination model of asymmetric wedges indentation [8], the gradient κ is equivalently derived by using Eq. (2) with respect to κ1 and κ2. This relation is generally known as the inverse rule of mixture.
Putting κ1 = 250 N·mm-1 and κ2 = 166.7 N·mm-1 in Eq. (2), the calculation of κ outcomes 200.0 N·mm-1. Therefore, it is found that the gradient of cutting resistance is fairly estimated using the combination model [8].
After passing through the peak point fP1, a wavy residual force was observed in this case. This wavy residual response was similar to that of Case 2 (λP = λD = 60°). The breaking position of the worksheet (dBreak/tS) was detected at d/tS ≈ 0.6. This breaking position was almost same as that of Cases 1, 2 and 3.
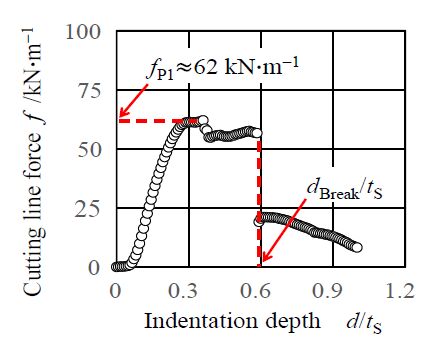
Figure 9 shows the side-view CCD photographs of the worksheet for the case of λP = 90° and λD = 60° at some representative indentation depths (d/tS ≈ 0.2, 0.36, 0.414, 0.5, 0.55 and 0.9). When the punch was indented at d/tS ≈ 0.36, a pre-primary crack was apparently observed on the upper of the worksheet, while the upper/lower primary cracks were apparently observed at d/tS ≈ 0.55 and a small rod-like dust was generated. The upper primary crack tended to be initiated close to the corner of square punch, while the pre-primary crack occurred on the upper contact surface where is a little far (about 1 mm distance) from the cutting tool corner. Seeing the pictures of d/tS ≈ 0.414, 0.5, 0.55, the initiation of lower primary crack was earlier than that of upper primary crack. Considering the initiation of those cracks, the peak point fP1 at d/tS ≈ 0.3 seems to be caused by the occurrence of pre-primary crack. The cutting force for d/tS ≈ 0.4-0.6 was kept in a stationary resistance without any large growth of upper primary crack. The breaking point of d/tS ≈ 0.6 seems to be caused by the growth of upper primary crack. In the next stage for d/tS ≈ 0.6-0.9, the secondary cracks on the rod-like dust were processed by the cutters.
Figure 10 shows the side-view microscope photograph of the completely sheared worksheet. Seeing the occurrence of pre-primary crack, it was revealed that the asymmetric wedges indentation made the outside body rotate strongly. Here, since the indentation depth of lower edge (λD = 60°) was relatively larger than that of upper edge (λP = 90°) due to the difference of wedge indentation resistance, this inclination of outside body seemed to be caused. Synthetically, it is revealed that this combination of asymmetric wedges generates the smaller rod-like dust, compared to Case 2, although the asymmetric wedge profile makes the unbalance indentation depth between the upper and lower cutter. If the occurrence of pre-primary crack can be restricted using appropriate fixture, the sheared profile is almost similar to Case 2. Therefore, a fixing condition of worksheet is important for making smart edge profile.
3. Numerical Analysis
3.1. Model Conditions
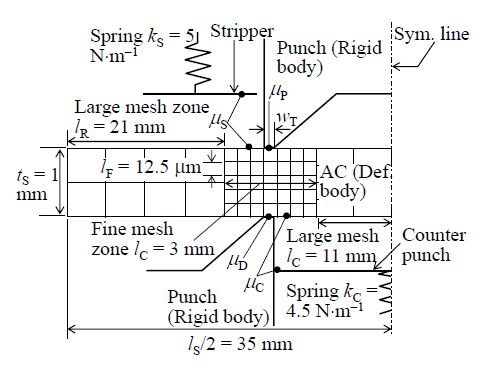
In this work, an FEM analysis of the worksheet which was subjected to the side-wedge punch/die shearing was conducted in Cases 1, 2 and 3. The general propose FEM code MSC.MARC software ver. 2012.1.0 was used. Figure 11 shows the schematic of the two-dimensional FEM model for the side-wedge punch/die shearing. A pair of two-line cutting was considered as a half symmetric model. The worksheet was assumed to be deformable body. Fine elements which had a side length lF = 12.5 µm was used for modeling the worksheet at the sheared zones, while the other far zones of the worksheet were modeled using the larger elements which had a side length of about 300 µm. The material properties of the worksheet were assumed to be isotropic elasto-plastic with work-hardening. The constitutive equation of the worksheet proposed by Mitsomwang and Nagasawa [7] was used in this FEM analysis. The glue contact function of the MARC [9] was used to connect the fine mesh zones with the large mesh zones. The punch, dies, counter punch and strippers were assumed to be rigid bodies. During indentation of the punch, the vertical displacement of the strippers and the counter punch were controlled by their attached backing springs. The spring stiffness kS = 5 N·m-1 and kC = 4.5 N·m-1 were assumed. These stiffness values were experimentally evaluated from the load-displacement curves of the springs.
When the cutting tool indented into the deformable worksheet, few elements around the cutting tool corners tended to be severely crushed. This caused an unstable calculation and its stop. To avoid this problem, a re-meshing function was considered on the fine mesh zone using the advancing front quad method [10,11]. The re-meshing was performed when the following criteria were satisfied: (i) when distortion of elements exceeded a certain level, an inner angle of elements was greater than 175° or less than 15°, and (ii) a penetration of the side-wedge into the deformed body was larger than 10 µm. The side length of re-meshing elements was controlled to be approximately 20 µm.
The coulomb tan-1 friction model with a relative slipping velocity threshold of 0.01 was considered. The friction coefficients at all the contact interfaces, µP, µD, µS and µS, were assumed to be 0.25. This value was referred from the friction coefficients used in a prior simulation work of the AC shearing [7].
The first surface crack initiation is mainly discussed using the proposed FEM model when the punch and die just touched the worksheet surface. Since there were not any apparent cracks in this early stage, no damage model was considered. The angles λP and λD were chosen as 30, 60 and 90°, while the clearance was fixed as c/tS = 0.025.
Regarding the asymmetric combination of Case 4, λP = 90°, λD = 60°, the similar cutting model was carried out, using the upper stripper which has the spring stiffness kS = 5 N·m-1. The clearance was chosen as c/tS = 0.03 and the indentation of punch was considered up to d/tS = 0.3~0.5. Here, since the tip angles λP of punch and the tip angle λD of die were different with each other, the punch indentation depth dP is not equal to the die indentation depth dD in general, while the total indentation depth is evaluated as the sum of them: d = dP + dD. The square punch/die model of Case 1 [7] was renewed as Case 1’ using c/tS = 0.03 and the upper stripper and the central counter punch.
3.2. Verification of Assumed Parameters
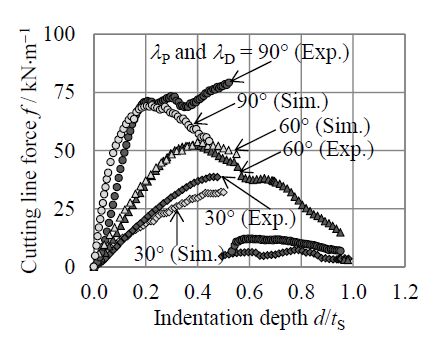
For the square punch/die shearing FEM simulation, assumed FEM parameters were already confirmed in a previous work [7]. However, for this side-wedge punch/die shearing problem, a couple of modified conditions were required for successful running, e.g., an incremental balance between the side length of divided elements and the contact length of a sharp wedge as a rigid body; the re-meshing criteria for avoiding any insufficient convergence state of cross contact between a sharp rigid edge and a deformable body. In order to verify the applicability of the modified conditions, a new developed FEM model was numerically simulated and its cutting line force was compared with the experiment.
Figure 12 shows the simulated and experimental cutting load response f-d/tS for λP and λD = 30, 60, 90°. For all the tool angles, the simulated cutting line forces showed a good agreement with the experiment until the first local maximum point (e.g., d/tS ≈ 0.2 for the square punch/die). Therefore, it was confirmed that the modified FEM conditions were applicable for simulating the side-wedge punch/die shearing in the shallow indentation state.
When the indentation depth exceeded the first local maximum point (e.g., d/tS > 0.2 for the squared punch/die, and/or d/tS > 0.5 for Case 3, the smallest angles λP = λD = 30°), the simulated load response f-d/tS tended to be deviated from the experiment. In Case 2 of λP = λD = 60°, the simulated load response almost matched to the experiment for a wide range (0 < d/tS < 0.7). The mismatch in Cases 3 and 1 of 30, 90° suggests that an appropriate damage model is necessary for estimating the deformation behavior when any apparent cracks are generated.
3.3. Stress Distribution at Sheared Zone
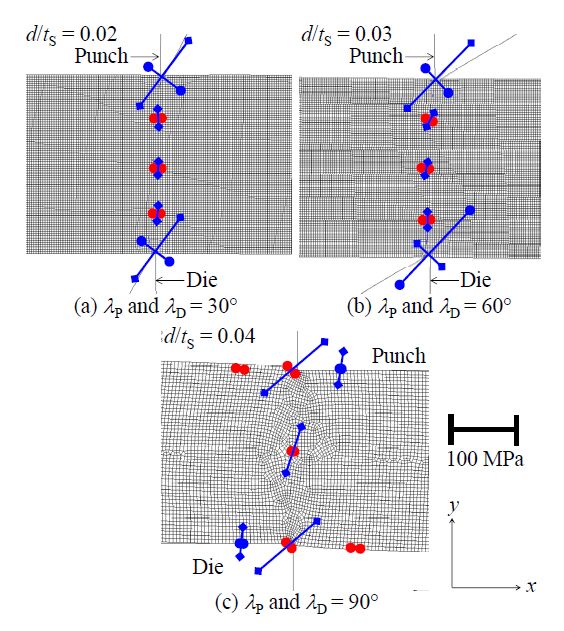
To discuss about the first crack initiation, a vector diagram of stress components in the sheared zone at the first crack initiation for each case of the tool angle was plotted, as illustrated in Figure 13. The vectors with circle-end and diamond-end represent the maximum and minimum principal stresses σP1 and σP2, respectively. The red line indicates the norm of tensile stress while the blue line represents the norm of compressive stress.
At the position of the first surface crack initiation in the cases of the side-wedge punch/die tools (for λP and λD = 30, 60°), the max. (σP1) and min. (σP2) principal stresses near the tool tips were estimated as ≈ -61.9~-67.3 MPa and -127.7~-148.9 MPa. Hence, the two principal stresses generated the maximum shear stress as τMax. ≈ (σP1 - σP2)/2 ≈ 32.9~40.8 MPa (≈ 0.5σB). Figure 13(a) and (b) indicated that the initiation of the first surface crack was mainly caused by the high compressive pressure at the contact surface between the cutting tool tips and the worksheet surfaces, in the two cases of side-wedge punch/die tools (for λP and λD = 30, 60°).
In the case of the square punch/die tool, as shown in Figure 13(c), the stress components at the first surface crack initiation appeared to be fairly different from that of the side-wedge punch/die case. Namely, at the punch and die corners, the maximum principal stress σP1 was detected as the tensile state (positive). Here, since the principal stresses σP1, σP2 at the cutting tool corners were 3.5~4.4 MPa and -127.6~-128.5 MPa, respectively, the maximum shear stress was calculated as τMax. ≈ 62.1~65.6 MPa (≈ 0.85σB). Due to the positive (tensile) state of σP1, the initiation of surface crack appeared to be enlarged across to the direction of σP1, namely in parallel to the direction of σP2 (minimum compressive). In the cases of side-wedge angles of 30, 60°, since the both components of σP1, σP2 were compressive state, as shown in Figure 13(a) and (b), any initiation of small cracks appeared to be suppressed at the early stage d/tS = 0.02~0.03.
So far, from the stress vector diagrams shown in Figure 13, it was indicated that the stress distribution at the first surface crack initiation in the sheared worksheet was fairly different when varying the cutting tool angle.
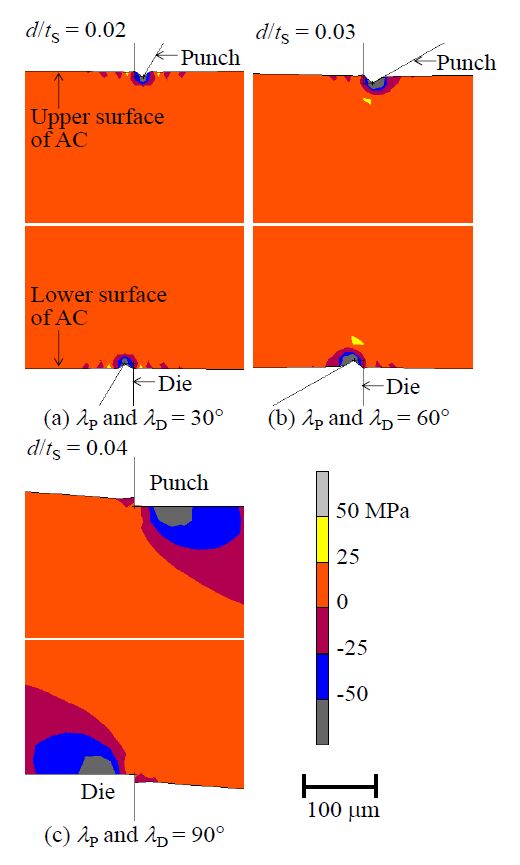
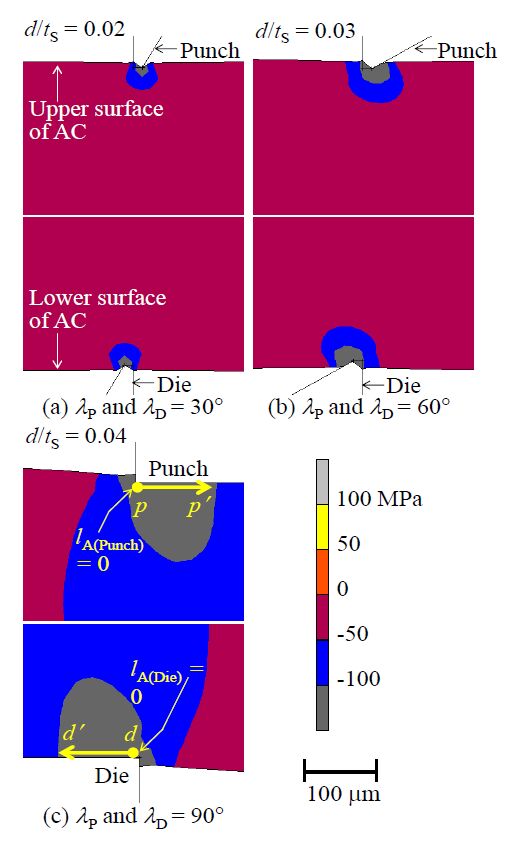
Figure 14 shows the contour band diagram of the maximum principal stress σP1 near the cutting tool tips at the first surface crack initiation, while Figure 15 shows the contour band diagram of minimum principal stress σP2. From Figure 14 and Figure 15, the high compressive maximum (σP1 > -50 MPa) and minimum (σP2 > -200 MPa) principal stresses which were represented by the dark-gray band was detected in the vicinity of the tool tips in the cases of the side-wedge punch/die shearing. But, in the case of the square punch/die shearing, such high compressive stresses was also generated at the tool contacted zone which were slightly far from the punch and die corners, as shown in Figure 14(c) and Figure 15(c).
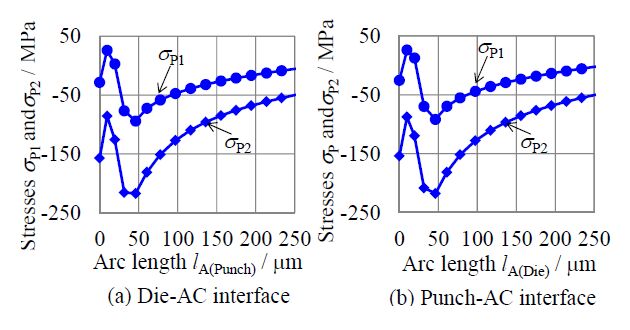
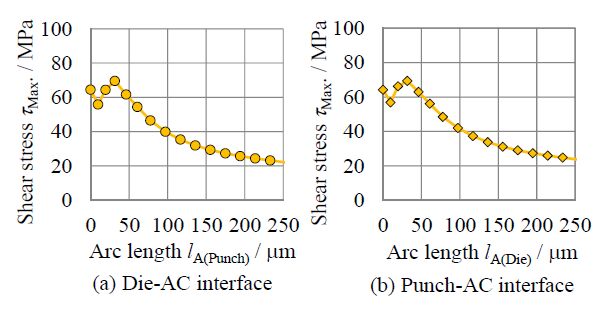
Next, in order to investigate the correlation between the high compressive stress zone and the initiation of the fine surface cracks, the magnitude of σP1, σP2 and τMax. along the path p-p' and d-d' lines, as shown in Figure 15(c), was plotted. Figure 16 shows the relationship between the principal stresses σP1, σP2 and the arc lengths lA(Punch), lA(Die), while Figure 17 illustrates the maximum shear stress τMax. with respect to the arc lengths lA(Punch), lA(Die). From these figures, it was found that the peaks of σP1, σP2, τMax. which were simulated at lA(Punch), lA(Die) ≈ 46.3 µm were fairly similar to the fine surface cracking zone observed in the experiment. This indicated that the compressive stresses (σP1 and σP2) and/or the maximum shear stress were primary factors of the fine surface crack initiation, as shown in Figure 5(c) at d/tS≥0.04 and Figure 6.
3.4. Comparison of Asymmetric with Square Symmetric
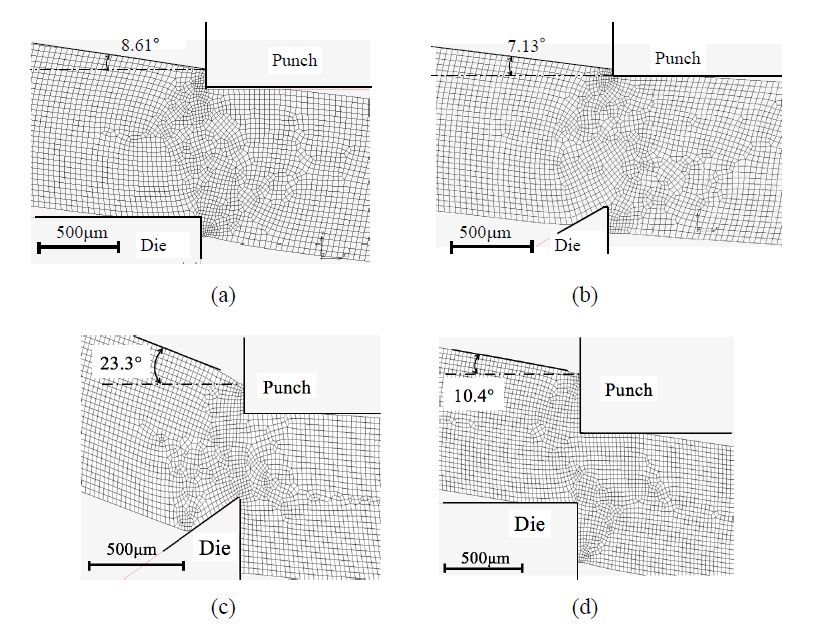
Figure 18(a) and (b) show the deformation of worksheet when the total indentation depth was d/tS = 0.2, and Figure 18(c) and (d) show that of d/tS = 0.5 in two cases: Case 1’ and Case 4, respectively. The punch indentation dP was almost equal to the die indentation dD in Case 1’ for d/tS = 0.2, 0.5, while the ratio of indentation depth was almost dD/dP ≈ 3.8, 2.8 in Case 4 when d/tS = 0.2, 0.5, respectively. The right side (punch side) of worksheet of Case 1’ and Case 4 were bent with almost same order when d/tS = 0.2. However, the latter Case 4 was remarkably bent compared to the former Case 1’ when d/tS = 0.5. This inclination tendency seems to cause the pre-primary crack in Case 4. When the right side of worksheet is a product part and the left side is a waste part, this inclination of attitude is preferable for cutting off, because the right is not so much rotated.
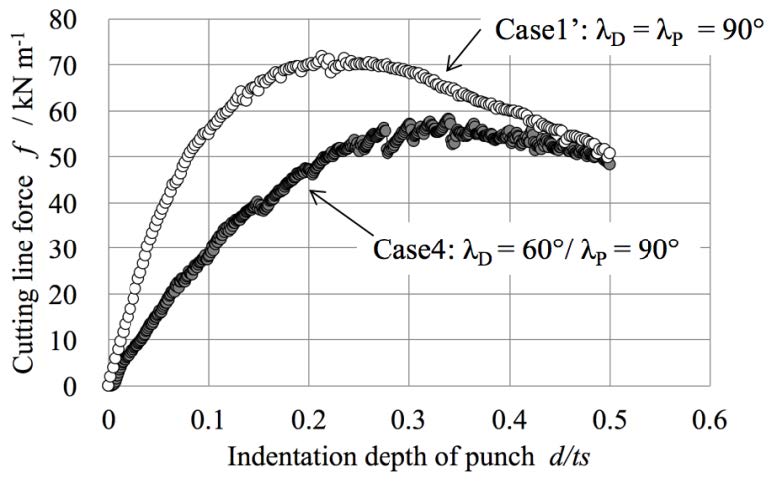
Figure 19 shows the simulated cutting line force for Case 1’ and Case 4. The loading response of Case 1’ was almost same as that of Case 1 described in Figure 12, while the loading response of Case 4 was close to that of Case 2. This seems to be caused by asymmetric indentation of dD/dP > 1. Seeing the experimental result of Figure 8 and Figure 9, the ratio of indentation was dD/dP ≈ 1 when d/tS < 0.3. Seeing the condition of d/tS ≈ 0.3, the experimental drop of force seems to be caused by the pre-primary cracking, while the simulated force response was smoothly peaked owing that none cracks. In order to discuss a range of deep indentation d/tS> 0.3, to predict the primary crack is required.
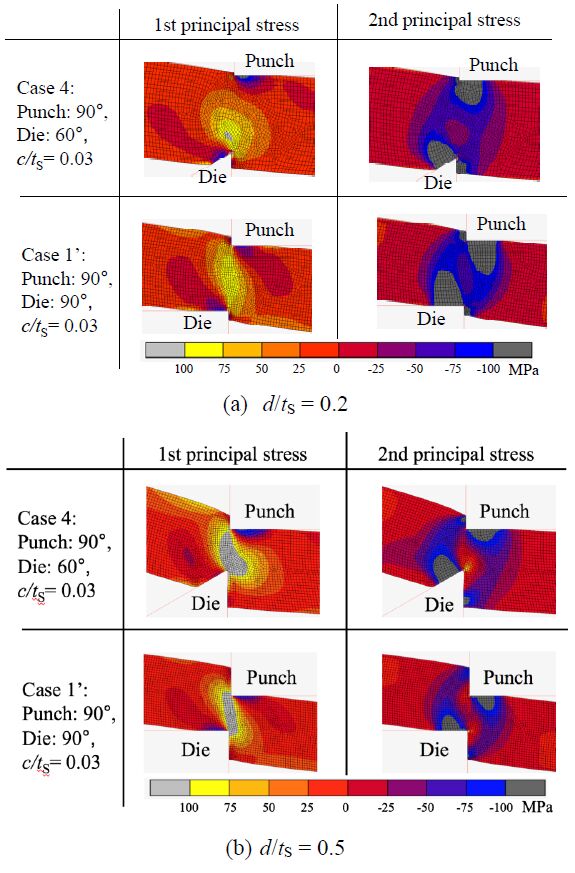
Figure 20 shows the magnitude of 1st and 2nd principal stresses σP1, σP2 as contour band diagrams for c/tS = 0.03 at d/tS = 0.2, 0.5. From this figure, the followings were revealed: (1) A quite-high tensile state was detected nearby the 60° wedge die, while there was not such a high tensile state beneath the 90° square punch in Case 4. This appears to cause the eccentric indentation ratio dD/dP ≈ 3.8. (2) There is a high tensile state behind of the blade back side (on the right side) of 60° wedge in Case 4. This tensile distribution seems to be related to the occurrence of primary crack in the experimental result shown in Figure 9 (d/tS = 0.414). (3) The pre-primary crack was experimentally detected on the upper surface of worksheet as seen in Figure 9. This seems to be contributed by the restriction of rotation by the upper stripper and lower wedge surface when d/tS > 0.3. Seeing the contour band of σP1 in Case 4 of Figure 20(b) when d/tS = 0.5, a certain level of tensile stress on the upper surface of worksheet was detected. It shows a determinate features in the contour band diagram.
4. Conclusions
In this work, a 1.0 mm thickness fragile acrylic worksheet was subjected to a couple of side-wedge punch/die shearing tool. The cutting velocity and the punch/die clearance were fixed as V = 0.05 mm·s-1 and c/tS = 0.025. Under these mechanical conditions, the experimental and numerical investigation results were revealed as follows:
(i) The punch/die angles significantly affected the cutting load resistance, the cracking pattern and the final sheared profile of the acrylic worksheet.
(ii) A straight sheared edge and a smooth sheared surface were successfully generated when applying the 30° angle wedge punch/die tool.
(iii) The initiation of the first surface crack in the side-wedge punch/die tool shearing was revealed to be mainly caused by a high compressive state of stresses at the tool tip-worksheet interfaces, while a slight tensile stress was detected when increasing the cutting tool angles to 90°.
(iv) In the case of the square (rectangle) punch/die shearing, the high compressive stresses and/or the maximum shear stress at the cutting tool-worksheet contacted interface seemed to cause the initiation of the fine surface cracks.
Furthermore, in order to reveal the effect of asymmetric combination of wedge angles, the square (rectangle) punch and the side-wedge die of angle 60° were examined for cutting the worksheet. Through this experiment, it was found that the initial gradient of cutting resistance was estimated using an inverse rule of mixture, and the unbalance of indentation depth of the upper/lower cutters tended to cause an additional shear rotation when considering the upper stripper. An FEM simulation of asymmetric combination was examined up to 50% indentation depth. Through this simulation, the upper surface tensile on the left side well corresponded to the occurrence position of pre-primary crack, and the eccentric indentation of square punch and wedge die was revealed.
Acknowledgement
This work was supported by a fund for developing a core of excellence as innovation and branding project with a sustainable package sheet processing, from the GIGAKU Innovation Promotion Center, NUT, 2012-2015.
Conflict of Interest
The authors declare that there is no conflict of interest regarding the publication of this manuscript.









 DownLoad:
DownLoad: