Nowadays, piano key (PK) weir with an expanded crest length are often used to deal with surplus discharge in dams due to unexpected climate change effects, increasing safety. The present study deals with the numerical modelling of a group of PK weirs with auxiliary geometrical parameters to predict the flow over a PK weir using different FLOW-3D turbulence models. The numerical outcomes were compared with the experimental results to check the accuracy of the underlying FLOW-3D models. It was found that the k-𝜀 turbulence model of FLOW-3D estimated the flow over a piano key weir more closely to the experimental results than the RNG (renormalized group) and LES (large eddy simulation) models. Statistical parameters were used to evaluate the simulated results. It was observed that the coefficient of correlation (CC) was close to one and the root mean square error (RMSE) close to zero when numerical outcomes were compared with experimental datasets. The results show that the FLOW-3D software is quite effective in estimating the flow. Therefore, the present study will help to understand the best combination of mesh, models, adaption and convergence processes in simulation and provide an insight into the numerical analysis of flow configuration over PKW by considering one of the best numerical models.
Citation: Binit Kumar, Rahil Ahmad, Manish Pandey, Anil Kumar Gupta. Numerical and statistical analysis of auxiliary geometrical parameter effects on piano key weir discharge capacity[J]. AIMS Environmental Science, 2024, 11(5): 723-740. doi: 10.3934/environsci.2024036
| [1] | Maryem EL FAHEM, Abdellah BENZAOUAK, Habiba ZOUITEN, Amal SERGHINI, Mohamed FEKHAOUI . Hydrogeochemical assessment of mine water discharges from mining activity. Case of the Haut Beht mine (central Morocco). AIMS Environmental Science, 2021, 8(1): 60-85. doi: 10.3934/environsci.2021005 |
| [2] | Huixuan Li, Cuizhen Wang, Yuqin Jiang, Andrew Hug, Yingru Li . Spatial assessment of sewage discharge with urbanization in 2004–2014, Beijing, China. AIMS Environmental Science, 2016, 3(4): 842-857. doi: 10.3934/environsci.2016.4.842 |
| [3] | María Sancho, José Miguel Arnal, Gumersindo Verdú-Martín, Cristina Trull-Hernandis, Beatriz García-Fayos . Management of hospital radioactive liquid waste: treatment proposal for radioimmunoassay wastes. AIMS Environmental Science, 2021, 8(5): 449-464. doi: 10.3934/environsci.2021029 |
| [4] | Djordje Vilimanovic, Gangadhar Andaluri, Robert Hannah, Rominder Suri, A. Ronald MacGillivray . Occurrence and aquatic toxicity of contaminants of emerging concern (CECs) in tributaries of an urbanized section of the Delaware River Watershed. AIMS Environmental Science, 2020, 7(4): 302-319. doi: 10.3934/environsci.2020019 |
| [5] | Marta Rodrigues, André B. Fortunato . Assessment of a three-dimensional baroclinic circulation model of the Tagus estuary (Portugal). AIMS Environmental Science, 2017, 4(6): 763-787. doi: 10.3934/environsci.2017.6.763 |
| [6] | M.A. Rahim, M.G. Mostafa . Impact of sugar mills effluent on environment around mills area. AIMS Environmental Science, 2021, 8(1): 86-99. doi: 10.3934/environsci.2021006 |
| [7] | Maryam Navi, Shahram Nasiri, Chris Skelly . Basin-wide groundwater vulnerability assessment: a GIS based DRASTIC approach to the problem of coal seam gas extracted water. AIMS Environmental Science, 2017, 4(1): 168-186. doi: 10.3934/environsci.2017.1.168 |
| [8] | Liron Shoshani, Asher Brenner, Chaim Sheindorf . Use of an integrated biophysical process for the treatment of halo- and nitro- organic wastes. AIMS Environmental Science, 2017, 4(4): 523-539. doi: 10.3934/environsci.2017.4.523 |
| [9] | Joyanto Karmoker, Sazal Kumar, Biplob Kumer Pal, Md. Sajal Sorowar, Md. Aminur Rahman, Md Hafijur Rahaman Khan, Rafiquel Islam . Characterization of wastewater from Jhenaidah municipality area, Bangladesh: A combined physico-chemical and statistical approach. AIMS Environmental Science, 2018, 5(6): 389-401. doi: 10.3934/environsci.2018.6.389 |
| [10] | Muhammad Shahid Iqbal, Muhammad Nauman Ahmad, Nynke Hofstra . The Relationship between Hydro-Climatic Variables and E. coli Concentrations in Surface and Drinking Water of the Kabul River Basin in Pakistan. AIMS Environmental Science, 2017, 4(5): 690-708. doi: 10.3934/environsci.2017.5.690 |
Nowadays, piano key (PK) weir with an expanded crest length are often used to deal with surplus discharge in dams due to unexpected climate change effects, increasing safety. The present study deals with the numerical modelling of a group of PK weirs with auxiliary geometrical parameters to predict the flow over a PK weir using different FLOW-3D turbulence models. The numerical outcomes were compared with the experimental results to check the accuracy of the underlying FLOW-3D models. It was found that the k-𝜀 turbulence model of FLOW-3D estimated the flow over a piano key weir more closely to the experimental results than the RNG (renormalized group) and LES (large eddy simulation) models. Statistical parameters were used to evaluate the simulated results. It was observed that the coefficient of correlation (CC) was close to one and the root mean square error (RMSE) close to zero when numerical outcomes were compared with experimental datasets. The results show that the FLOW-3D software is quite effective in estimating the flow. Therefore, the present study will help to understand the best combination of mesh, models, adaption and convergence processes in simulation and provide an insight into the numerical analysis of flow configuration over PKW by considering one of the best numerical models.
A weir is generally used to raise the water level in a river to recharge groundwater and control water flow of lakes and reservoirs. When floods occur, the inflow to hydraulic structures exceeds the designed flow. Therefore, to protect these hydraulic structures, there is a need to release more water. PK weirs are an effective solution to increase outlet flows compared to linear weirs as their crest length is extended due to downstream and upstream overhangs. In addition, PK weirs provide more discharge, and are easier to replace on existing dams due to their smaller base area than labyrinth weirs, making them an improved version of labyrinth weirs. For the last two decades, engineers and researchers have worked with PK weirs because of their discharge capacity [1]. PK weir constructed on the Goulours dam in France as an improvement over the labyrinth weir [2], which was developed by Hydro-cooperation (France) in collaboration with the laboratories of the University of Briska (Algeria), Électricité de France (EDF), and IIT Roorkee (India). The initial PK weir model tests showed that discharge is 4 to 5 times higher than the traditional frontal weirs [3].
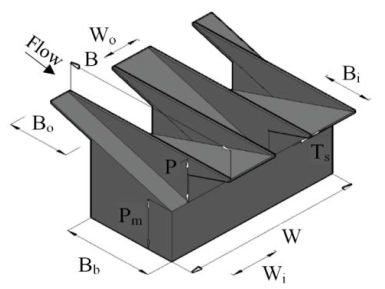
The PK weir is an advanced structure that involves more geometric parameters than a labyrinth weir. Li et al. [4] conducted experiments on the effect of an auxiliary geometric parapet wall on the discharge coefficient of the PK weir. They concluded that a weir with a curved nose and parapet wall increases the discharge coefficient by 11.6%–16.8% compared to weirs without any auxiliary geometric parameter. The parameters of the PK weir studied by Li et al. are shown in Figure 1 [4], in which weir height is P, incoming and outgoing key widths are Wi and Wo, the width of the channel is W, the wall thickness is Ts, the crest length is L, and overhanging spans for inlet and outlet keys are Bi and Bo, respectively. Li et al. [4] performed a numerical study using Ansys-Fluent software to analyse the PK weir's flow behaviour and discharge capacity. They concluded that discharge decreases as the head over the crest increases, and the gradual submergence of the weir reduces its discharge capacity. Simulation results showed that the software could accurately estimate laboratory experiment results and is suitable to simulate the flow over a PK weir. Machiels et al. [5] experimentally investigated the parapet wall effect on the PK weir discharge capacity using various laboratory-based models. They observed that by increasing the parapet wall height, the discharge capacity of the weir increases, and the parapet wall on the inlet key yields better results by decreasing axial velocity and increasing lateral flow velocity. The increased flow along the sidewall of the PK weir, further increases the discharge capacity of the weir. Mehboudi et al. [6] investigated the discharge capacity of PK weirs by changing the plan view from rectangular to trapezoidal. They concluded that CD (the discharge coefficient of the PK weir) is more significantly influenced by the L/W ratio than by the Wi/Wo ratio. A trapezoidal PK weir predicted a larger discharge than a rectangular PK weir, with a 22% higher CD.
The FLOW-3D software has been used to simulate complex flow in and over hydraulic structures like weirs and spillways [7,8,9,10]. Hu et al. [11] simulated an experimental study with a numerical technique using FLOW-3D software and concluded that the side crest effect has a lower effect on the weir discharge capacity. Wi/Wo and weir heights are the primary factors that affect weir efficiency. Guo et al. [9] suggested a relationship for the discharge coefficient by using a numerical study for existing experimental data. Khassaf and Al-Baghdadi [12] investigated the effect of discharge capacity of the non-rectangular PK weir by altering the sidewall and sidewall leaning angle. Changing the sidewall angle to 5˚ led to a 4% increase in discharge; increasing the sidewall angle to 10.25˚ decreased discharge by 8%, and changing the sidewall inclination to 5˚ led to no change in the discharge. When the sidewall inclination angle was 10˚, the discharge capacity was reduced by 18%.
Kumar et al. [13] conducted laboratory tests on trapezoidal and rectangular PK weirs and found that the discharge coefficient of the former is 2–15% larger. They used machine learning methods (random forest and M5 tree models) to estimate the CD (discharge coefficient); the random forest method performed better. Singhal et al. [14] experimentally investigated PK weirs with different L/W and Wi/Wo ratios at different H/P ratios and concluded that the enhancement ratio (r), which is the ratio of discharge on a PK weir to that on a linear weir, is greater than 1 for PK weirs and increases when L/W ratio increases.
The presence of a ramp (sloped floor) also increases the discharge capacity of PK weirs. Ribeiro et al. [15] conducted experiments with type-A PK weirs and provided discharge equations in terms of H and Q categorized the geometrical parameters into primary and secondary based on their effect on the discharge capacity of PK weirs. The primary geometrical parameters are L and H (head over the crest), which impact the discharge capacity of the PK weirs with slight modifications. The secondary geometrical parameters are Wi/Wo (inlet key width to outlet key width) ratio, Pi/Po (inlet key height to outlet key height) ratio, overhang length, and parapet wall. Anderson and Tullis [16] examined PK weirs with and without slopes and concluded that sloped-floor weirs are more effective than rectangular labyrinth weirs which have no sloped floors at all heads. In a laboratory study, Cicero and Delisle [17] investigated PK weirs type A, B, C, and D, which have upstream and downstream projections on both sides, only upstream projection, only downstream projection, and no upstream and downstream projections respectively, for free flow and submerged flow. They concluded that type-B PK weirs were 10% more efficient than type-A; on the other hand, type-C PK weirs were 15% less efficient than type C. Type-D weirs were less efficient than type-A but more efficient than type-C. The percentage loss in discharge for an ogee crest weir, sharp-crested weir, and broad-crested weir compared to a PK weir is 40%, 50–70%, and 50–60%, respectively. Crookston et al. [18] suggested an equation to compute the discharge coefficient based on the Anderson and Tullis [16] experimental data.
Al-Baghdadi and Khassaf [19] conducted an experimental study on the effect of crest length on type-A PK weirs and proposed a discharge coefficient equation. They concluded that crest length is directly proportional to discharge; by increasing the L/W ratio by ±1%, discharge increases by ±20% for a constant water head-on weir crest. Al-Shukur and Al-Khafaji [20] examined the effect of PK weir type-B geometry on its discharge capacity under free-flow conditions. They concluded that by reducing the ratio of inlet key height to outlet key height to 0.7 and increasing the L/W ratio to 1.0, the discharge coefficient increased by 42%. A PK weir predicts maximum discharge when the ratio of inlet key width to outlet key length equals one. By increasing the B/P ratio from 2.5 to 3, 4, and 5, there is decrease in the discharge coefficient by 3%, 18%, and 32%, respectively, by decreasing it from 2.5 to 2 and 1.5, there is increase in the discharge coefficient of 13% and 27%, respectively. Kabiri-Samani and Javaheri [21] experimentally investigated the effect of weir length, height, key width, and overhang length on the discharge capacity of PK weirs. They determined that discharge increases when the inlet key width is higher than the outlet key width. However, as the outlet key width decreases, local submergence increases, and after submergence, the discharge capacity of the PK weir decreases. They also proposed the discharge coefficient equation for both free flow and submerged flow, which is useful for all types of PK weir. Abhash and Pandey [22] investigated rectangular and trapezoidal PK weirs to check which one allows more discharge and has the better self-cleaning ability for sedimentation. They conducted their research using the Ansys-Fluent software and decided that a rectangular PK weir has additional discharge and more self-cleaning capacity than a trapezoidal PK weir.
Kumar et al. [23] investigated sediment transport over a type-A PK weir. They found that 17– 43% of shear stress was required to transport sediment on the upstream side and suggested an equation to compute the upstream shear stress as a function of particle size and the ratio of length to width of the weir. Senarath et al. [24] reviewed the environmental and social impact of mini hydropower plants. The impact of climate change on water resources in Northern Thailand was studied by Gunathilake et al. [25]. Tuan et al. [26] explored the hydraulic behavior of PK weirs and concluded that they show more discharge at low heads. Ghanbari et al. [27] conducted an experimental study of PK weirs with and without a triangular notch (triangular nose) below the upstream key. They concluded that the triangular notch resulted in a 36% higher CD than the PK weir without a triangular notch. Khassaf et al. [28] conducted an experimental study on the submergence of PK weirs due to geometric parameters. They concluded that, by suddenly increasing the ratio of inlet key width to outlet key width from 1 to 2.5, the CD decreases by 12%. By decreasing the ratio from 1 to 0.4, the CD decreases by 5%. When the B/P ratio decreased from 3 to 2, the CD decreased by 5%. Mahabadi and Sanayei [29] compared the numerical model outcomes with the experimental study results of Mehboudi et al. [6] and concluded that the FLOW-3D software can properly simulate the flow of a PK weir. They investigated five new models of PK weirs with bilateral slopes of 5˚, 10˚, 15˚, 20˚, and 25˚ and concluded that the 25˚ slope provided a high discharge rate at a constant water head. Pralong et al. [30] presented regular geometrical parameters of PK weirs. Seyedjavad et al. [31] experimentally investigated the trapezoidal PK weir discharge coefficient and concluded that it is 1.5 times higher than a triangular labyrinth weir. Eslinger et al. [32] studied energy dissipation of type-A PK weirs by altering the ratio of Wi/Wo at various H/P ratios and established that energy dissipation is high in low flows and low in high flows. They also concluded that energy dissipation, irrespective of Wi/Wo, is in the range of 0.07≤ H/P≤ 0.2 and 0.8≤ H/P≤ 0.95.
Only a few numerical studies have considered different FLOW-3D turbulence models. Although many studies were conducted on PK weirs to know which geometric parameter was more effective in increasing discharge capacity only a few have analysed PK weirs numerically with auxiliary geometric parameters. The flow behaviour of a PK weir with auxiliary geometric parameters has not been studied yet using FLOW-3D software. The present study deals with the numerical modelling of a group of piano key weirs with auxiliary geometrical parameters to predict their flow using different FLOW-3D turbulence models. A total of six PK weir models are studied numerically. To check the accuracy of the FLOW-3D turbulence models, numerical results are compared with experimental results of Li et al. [4]. The present study will provide insights for using the suitable FLOW-3D turbulence model for obtaining flow configurations and will be helpful in hydraulic design and application of PK weirs.
The discharge of a weir is proportional to the crest length and head over the weir crest. Lemperiere and Ouamane [2] assumed the PK weir as a linear weir, and the discharge capacity of a linear weir is given as equation (1):
| Q=(2/3)CDLL√2gH3 | (1) |
Where Q is the discharge over the weir, L is crest length, H is head over the weir crest, g is the acceleration due to gravity, and CDL is the discharge coefficient of a linear weir.
The total hydraulic head of the fluid is the sum of the datum head, pressure head, and velocity head, as shown in Figure 2 and equation (2):
| hydraulichead=z+(h+H)+(V2/2g)(2) | (2) |
Where z is datum head, h+H is pressure head (H is the head over the weir crest and h is the head on the upstream side of weir up to weir crest), V is the velocity of a fluid on the upstream side, and V2/2g is velocity head, HT is the total head-on upstream side, and HTD is the total head-on downstream side.
The numerical simulation steps are as follows: a) create geometry, b) create meshing, c) define boundary condition, d) run the simulation, and e) validate the numerical results with the experimental results of Li et al. [4]. Numerical modelling was used to study the flow over a PK weir with auxiliary geometries: a rounded nose, triangular nose, parapet wall, and a combination of rounded nose and parapet wall. The simulation is conducted for six different PK weir models. The six models of Li et al. [4] are MA, MAT, MAR, MAP16, MAP25, and MARP25 (the same models and their names are used in this numerical study). All models are type-A PK weirs with the following details: MA is the weir without any auxiliary geometry, MAT is the weir with the triangular nose, MAR is the weir with a rounded nose, MAP16 is the weir with a parapet wall height of 16 (mm), MAP25 is the weir with parapet wall height of 25 (mm), and MARP25 is the weir with rounded nose and parapet wall height of 25 (mm). The input discharge variation is in the range of 0.015 – 0.110 (m3s-1). In the experimental study of Li et al. [4], the head-on upstream side for each input discharge was 1.2 (m) from the weir after 20 minutes of each flow adjustment when the flow was in a steady condition. The total number of models is 78.
The models are observed and collected from Li et al. [4]. Li et al. [4] conducted laboratory experiments in a flume with a length of 16 (m), width of 0.5 (m), and depth of 0.75 (m). The experimental data were collected by using advanced instruments so the experimental uncertainties were negligible. The geometric parameters dimensions of model MA are shown in Table 1. The Pm is dam height, P is the PK weir height, Wi is inlet key width, Wo is the outlet key width, W is the transverse width, L is the developed length of crest, Bi is the inlet key length of the downstream side, Bo is outlet key length of the upstream side, and Bb is footprint length given in Table 1.
The weir heights of the six models are shown in Table 2. Li et al. [4] proposed the discharge coefficient (CD) equation for the MA model as given in equation (3):
| CD=2.4−4.31(H/P)+4.64(H/P)2−2.46(H/P)3+0.54(H/P)4 | (3) |
Where H is head over weir crest (m), P is the height of the weir (m).
FLOW-3D is a computational fluid dynamics (CFD) software that has shown enough accuracy and capability in simulating different hydro morphology problems [33,34]. Total six models are used for simulation, drawn with the exact specifications from Li et al. [4] with a discharge range of 0.015 –0.110 (m3s-1). The models drawn using AutoCAD software are shown in Figure 3. The input for the simulation is discharge, and the required output is head over weir crest (by removing the weir height from the total head-on upstream side). The FLOW-3D turbulence models estimate the flow over a PK weir similarly to laboratory experiment results. However, the simulation results significantly underestimated the flow over a PK weir compared to experimental results for all six models. These disparities are due to the meshing method used in the FLOW-3D model setup [35,36,37,38].
In FLOW-3D, Volume of Fluid (VOF) is the technique to locate and track the free surface flow. In this method, the modelling region is shared into a net of elements. Another technique is Fractional Area-Volume Obstacle Representation (FAVOR), used to simulate the solid geometries defined in the rectangular grid to predict the flow around the solid obstacle [8]. This method is very useful because it provides simple and economical way to observe free boundaries in two- or three-dimensional grids than the finite- difference method. The accuracy in geometry depends upon the cell size or cell numbers. The equations used by the FLOW-3D solver are the Navier Stokes equation (equation 4) and the mass momentum equation (equation 5). The Navier-Stokes equations is basically a time-dependent continuity equation for mass conservation, three time-dependent conservation of momentum equations, and a time-dependent conservation of energy equation. These equations are presented below:
| ∂∂x(uAx)+∂∂y(vAy)+∂∂z(wAz)=0 | (4) |
| ∂ui∂t+1VF(ujAj∂ui∂xj)=1ρ∂p∂xi+Gi+fi | (5) |
where xi is the direction in the coordinate, u, v, and w are the velocities, and Ax, Ay, and Az are fractional areas open to flow in x, y, and z-direction, respectively. ui is the velocity in the subscript direction, Aj and VF are the fractional areas. Fractional volume becomes unity when the mesh cells are full with fluid, and equation (5) becomes one-fluid incompressible Reynolds-averaged Navier-Stokes (RANS) form. t is time, p is pressure, 𝜌 is the fluid density, and Gi and fi are body and viscous acceleration, respectively.
Input and output boundary conditions are discharge and outlet, respectively. Bottom and sidewall boundary conditions are the rigid walls, as observed in the laboratory experiment [4]. Other boundary conditions, mesh cell numbers, and equations in the model are shown in Table 3 and Figure 4. Proper boundary conditions are required to get accurate results by the simulation [39,40]. A finer mesh is given near the PK weir model to get accurate flow results, and for numerical simulation, water is considered an incompressible fluid [41]. The flume length in the simulation is considered 5 (m) (the portion of the 4 to 9 m used in the experimental study). From primary simulations, the length of the computational domain (flume) is selected by considering fully developed stream in the flume. The inlet and outlet of the flume are given at 3.175 (m) upstream and 1.575 (m) downstream of the weir, as shown in Figure 5. y+ is an analytical profile considering the two layers' viscous sub layer and the buffer layer. In fact, the boundary layer thickness comprises mainly three regions as moving away from the wall, starting with the viscous sub layer, the buffer layer, and the turbulent layer. y+ is supposed to cover only the first two sections and it is expected to be started from the very beginning of the turbulent layer. In the current study, y+ value is taken as around 1(which is less than 5) for fairly good results.
Meshing sensitivity analysis is performed to choose the suitable grid size. The nested block feature improves the resolution of a simulation by providing the finer grid sizes near the PK model. When cell numbers increase, the simulated results of the head over the weir crest are similar to the laboratory experiment results [39,42]. Meshing with cell size for simulation is presented in Figure 5. The sensitivity analysis of meshing is done by changing the grid size and comparing the simulated result with the experimental result of Li et al. [4] at 0.09 (m3s-1) on model MAR, which is shown in Table 4. At 950,000 cells, simulated results have enough accuracy as laboratory experiment results. Meshing sensitivity analysis was conducted for a grid size of 0.09 m3/s and the MAR model. The refinement ratios (1.38 and 2) are above the minimum recommended value of 1.3 [43]. It indicates a very satisfactory grid convergence. Readers and researchers may choose a grid size for a different input discharge range.
A total of three FLOW-3D models were used in this study, namely RNG (renormalized group of k-𝜀 model), k-𝜀, and large eddy simulation (LES). The performance of turbulence models like k-ε, RNG k-ε, and LES can differ significantly depending on the flow condition, computational resources, and modelling assumptions. In our simulations, the k-ε model's performance probably benefited from its suitability for high Reynolds number flows, desirable computational cost, appropriate grid resolution requirements, and accurate representation of near-wall turbulence effects. To know which turbulence model is the best, simulations are performed for input discharges of 0.03, 0.035, 0.04, 0.05, 0.06, 0.07, 0.08, 0.09, 0.10, and 0.11 (m3s-1) on the MA model by using turbulence models k-𝜀, RNG, and LES [input discharges are given same as in Li et al. [4]. It is found that the LES model underestimates the head over the weir crest for low discharges. By increasing the input discharge, estimation of head over the weir crest approximated the experimental results [4]. The RNG model estimated head over the weir crest values close to the experimental results for low discharges; increasing the input discharge underestimated the experimental outcomes of Li et al. [4]. After comparing the numerical results of turbulence models with the results of Li et al. [4], it is found that the k-𝜀 turbulence model outcomes are near to the experimental results, as presented in Table 5. The k-𝜀 turbulence model results are in good agreement with the experiment results of Li et al. [4], as shown in Figure 6; the same was observed in the study of Mahabadi and Sanayei [29].
A total of 78 simulations were done across the six models, namely MA, MAT, MAR, MAP16, MAP25, and MARP25, with 13 input discharges (0.015, 0.02, 0.025, 0.03, 0.035, 0.04, 0.05, 0.06, 0.07, 0.08, 0.09, 0.1, 0.11 (m3s-1)). The results of all six models were compared with the experimental outcomes of Li et al. [4]. The uncertainty in both the experimental and numerical studies is minimal because the upstream head over the weir crest was used for the input discharge in steady flow conditions in both the experimental study [4] and the current study. The upstream head over the weir crest (m) of PK weir versus input discharge (m3s-1) for the six models is shown in Figure 7.
There was a good agreement between the simulated results and the laboratory results of Li et al. [4], as shown in Figure 7. The commercially available FLOW-3D software can estimate the flow over a PK weir with a reasonable accuracy, agreeing with previous study results [36,39]. In the past, similar numerical simulation studies and machine learning techniques have been used to study the scour depth around hydraulic structures [44,45]. Furthermore, it observed that the numerical simulations result for higher discharges on the PK weir model showed fewer disparities compared to laboratory experiment results. Six statistical indices were applied to quantify the accuracy of the FLOW-3D simulation results. These statistical tests were used to evaluate whether an estimated variable has a statistically significant relationship with the outcome variable [46,47]. The statistical indices were the coefficient of correlation (CC), the error efficiency (EE), the mean absolute error (MAE), the mean square error (MSE), the root mean square error (RMSE), and the mean absolute percentage error (MAPE), which are presented in equations (6-11):
| CC=∑ni=1(Oi−−O)∗(Si−−S)√∑ni=1(Oi−−O)2∗∑ni=1(Si−−S)2 | (6) |
| EE=∑ni=1(Oi−−O)2−∑ni=1(Oi−Si)2∑ni=1(Oi−−O)2 | (7) |
| MAE=∑ni=1|Oi−Si|n | (8) |
| MSE=∑ni=1(Oi−Si)2n | (9) |
| RMSE=√∑ni=1(Oi−Si)2n | (10) |
| MAPE=∑ni=1|Oi−SiOi|n∗100 | (11) |
Where Oi is the experimental results of Li et al. [4], Si is the results from the numerical simulation study, and n is the number of observations.
The comparison of the statistical indices between the results of the experimental study [4] and the numerical study is shown in Table 6. CC and EE are close to one, and MAE, MSE, RMSE, and MAPE are close to zero. Furthermore, the significance level at a 95% confidence interval is less than 5%, as shown in Table 6. Therefore, the FLOW-3D numerical study is acceptable for estimating flow over a PK weir.
From the numerical study, it is observed that the discharge capacity of model MAT is 7.9% higher than model MA but 8.5% in Li et al. [4]. The model MAP16 discharge capacity is 5%–22% higher than model MA but 5%–15.5% in the experimental study. The model MAP25 discharge capacity is 4%–21% higher than model MA but 8%–14.5% in the experimental study. The model MARP25 discharge capacity is 11.3%–30% higher than model MA, but 11.6%–16.8% in Li et al. [4]. It was observed that the flow over the PK weir models MAT and MAR is identical. The maximum percentage of error between numerical results and experimental results of Li et al. [4] in the estimation of head over the weir crest is 8.64%. This overestimation is due to the underestimation of the head over the weir crest. Significant errors are due to the limitation of the applied mesh method, which also influenced the results. The nose (auxiliary geometric parameter) below the upstream weir key divides the flow. It diverges the flow smoothly into the inlet key, decreasing entering velocity, and increasing the discharge over a weir [4].
The numerical results of six models were compared using different input discharges to obtain the most efficient auxiliary geometric parameter, as shown in Figure 8. For all simulated models at constant discharges, it was observed that the MARP25 model provides a lower head on the upstream side of the PK weir compared to the remaining models shown in Figure 8. Head over weir crest is inversely proportional to the discharge coefficient, presented in equation (3). This means that if the head over the weir crest decreases, the discharge coefficient of the model will increase. Therefore, model MARP25 gives a higher discharge than the remaining models, as observed by Li et al. [4] in their experimental investigation. The discharge capacity does not increase when a parapet wall is positioned on a PK weir that already has an ideal weir height, as mentioned by Machiels et al. [5]. The CD (discharge coefficient) is calculated using equation (1) at different H/P ratios. Additionally, CD is calculated using equation (3) proposed by Li et al. [4] to know the relation between CD and H/P. It is seen that CD decreases the H/P ratio increases, which means the PK weir is more effective in releasing the discharge at a low H/P ratio, as shown in Figure 9.
The present study investigated flow behaviour over a PK weir with and without auxiliary geometric parameters with a constant weir crest length and transverse width by using the FLOW-3D software, improving previous knowledge to know which underlying model of FLOW-3D better predicts the flow over a PK weir.
Interestingly, few numerical studies have explored the flow over a PK weir with auxiliary geometric parameters. It was observed that k-𝜀 turbulence model was more accurate than the RNG and LES turbulence models. The RNG turbulence model estimated a flow close to the experimental results of Li et al. [4] for low input discharge (≤0.06 m3s-1), and the LES turbulence model estimated a flow close to the experimental results of Li et al. (2020) for high input discharge (≥ 0.1 m3s-1).
By decreasing the cell size (increasing the total of mesh cells), the agreement between the numerical and experimental results improved. Additionally, the discharge coefficient of the PK weir model MARP25 (rounded nose and parapet wall 25 mm) is 11.3% to 30% higher than the model without any auxiliary geometric parameter.
PK weir provides a high discharge coefficient at low head over weir crest. However, by increasing the head over the weir crest, the discharge coefficient decreases, which means that PK weirs are more efficient in releasing the flow at a low head over the weir crest.
Moreover, statistical analysis showed that CC and EE were close to one, and MAE, MSE, RMSE, MAPE were close to zero. Furthermore, the significance level at the 95% confidence interval was less than 5%. Therefore, the FLOW-3D numerical study is acceptable for estimating flow over a PK weir.
The present study provides insights into using the suitable FLOW-3D turbulence model for obtaining flow configurations and will be helpful in hydraulic design and applications of PK weirs. The numerical investigation of rectangular, triangular, and trapezoidal PK weirs may be considered for future studies. In the future, a large number of experimental datasets of different researchers will be checked using simulations and statistical analysis relating to aeration, interference of falling jets with varying cycles, etc.
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
The authors declare no conflict of interest.
| [1] | Laugier F (2007) Design and construction of the first piano key weir spillway at Goulours dam. Int J Hydropower Dams 14: 94–101. |
| [2] | Lemperier F, Ouamane A (2003) The Piano Keys Weir: a new cost-effective solution for spillways. Int J Hydropower Dams.10: 144–149. |
| [3] |
Li S, Li G, Jiang D (2020) Physical and Numerical Modelling of the Hydraulic Characteristics of Type-A Piano Key Weirs. J Hydraul Eng 146: 06020004. https://doi.org/10.1061/(ASCE)HY.1943-7900.0001716 doi: 10.1061/(ASCE)HY.1943-7900.0001716
|
| [4] |
Li S, Li G, Jiang D, et al. (2020) Influence of auxiliary geometric parameters on the discharge capacity of piano key weirs. Flow Meas Instrum 72: 101719. https://doi.org/10.1016/j.flowmeasinst.2020.101719 doi: 10.1016/j.flowmeasinst.2020.101719
|
| [5] |
Machiels O, Erpicum S, Archambeau P, et al. (2013) Parapet Wall Effect on Piano Key Weir Efficiency. J Irrig Drain Eng 139: 506–511. https://doi.org/10.1061/(ASCE)IR.1943-4774.0000566 doi: 10.1061/(ASCE)IR.1943-4774.0000566
|
| [6] |
Mehboudi A, Attari J, Hosseini S A (2016) Experimental study of discharge coefficient for trapezoidal piano key weirs. Flow Meas Instrum 50: 65–72. https://doi.org/10.1016/j.flowmeasinst.2016.06.005 doi: 10.1016/j.flowmeasinst.2016.06.005
|
| [7] |
Abbasi S, Fatemi S, Ghaderi A, et al. (2021) The effect of geometric parameters of the anti-vortex on a triangular labyrinth side weir. Water 13:13010014. https://doi.org/10.3390/w13010014 doi: 10.3390/w13010014
|
| [8] |
Ghaderi A, Abbasi S, Di Francesco S (2021) Numerical study on the hydraulic properties of flow over different pooled stepped spillways. Water 13: 710. https://doi.org/10.3390/w13050710 doi: 10.3390/w13050710
|
| [9] |
Guo X, Liu Z, Wang T, et al. (2019) Discharge capacity evaluation and hydraulic design of a piano key weir. Water Sci Technol Water Supply 19: 871–878. https://doi.org/10.2166/ws.2018.134 doi: 10.2166/ws.2018.134
|
| [10] |
Gupta L K, Pandey M, Anand R P (2023) Numerical simulation of local scour around the pier with and without air foil collar (AFC) using FLOW-3D. Environ Fluid Mech 1-19. https://doi.org/10.1007/s10652-023-09932-2. doi: 10.1007/s10652-023-09932-2
|
| [11] |
Hu H, Qian Z, Yang W, et al. (2018) Numerical study of characteristics and discharge capacity of piano key weirs. Flow Meas Instrum 62: 27–32. https://doi.org/10.1016/j.flowmeasinst.2018.05.004 doi: 10.1016/j.flowmeasinst.2018.05.004
|
| [12] | Khassaf S I, Al-Baghdadi M B (2015) Experimental study of non-rectangular piano key weir discharge coefficient. J Energy 6: 425–436. |
| [13] |
Kumar M, Sihag P, Tiwari N, et al. (2020) Experimental study and modelling discharge coefficient of trapezoidal and rectangular piano key weirs. Appl Water Sci 10: 1–9. https://doi.org/10.1007/s13201-019-1104-8 doi: 10.1007/s13201-019-1104-8
|
| [14] |
Singhal G D, Sharma N, Ojha C S P (2011) Experimental study of hydraulically efficient piano key weir configuration. ISH J Hydraulic Eng 17: 18–33. https://doi.org/10.1080/09715010.2011.10515029 doi: 10.1080/09715010.2011.10515029
|
| [15] |
Ribeiro M L, Pfister M, Schleiss A J, et al. (2012) Hydraulic design of a-type piano key weirs. J Hydraul Res 50: 400–408. https://doi.org/10.1080/00221686.2012.695041 doi: 10.1080/00221686.2012.695041
|
| [16] |
Anderson R M, Tullis B P (2012) Comparison of piano key and rectangular labyrinth weir hydraulics. J Hydraul Eng 138: 358–361. https://doi.org/10.1061/(ASCE)HY.1943-7900.0000509 doi: 10.1061/(ASCE)HY.1943-7900.0000509
|
| [17] |
Cicero G M, Delisle J R (2011) Discharge characteristics of piano key weirs under submerged flow. Labyrinth Piano Key Weirs Ⅱ. 101–109. https://doi.org/10.1201/b15985-15 doi: 10.1201/b15985-15
|
| [18] |
Crookston B M, Anderson R M, Tullis B P (2018) Free-flow discharge estimation method for Piano Key weir geometries. J Hydro-Environment Res 19: 160–167. https://doi.org/10.1016/j.jher.2017.10.003 doi: 10.1016/j.jher.2017.10.003
|
| [19] | Al-Baghdadi M B N, Khassaf S I (2018) Evaluation of crest length effect on piano key weir discharge capacity. Int J Energy Environ 9: 473–480. |
| [20] | Al-Shukur A H K, Al-Khafaji G H (2018) Experimental study of the hydraulic performance of piano key weir. Int J Energy Environ 9: 63–70. |
| [21] |
Kabiri-Samani A, Javaheri A (2012) Discharge coefficients for free and submerged flow over Piano Key weirs. J Hydraul Res 50: 114–120. https://doi.org/10.1080/00221686.2011.647888 doi: 10.1080/00221686.2011.647888
|
| [22] |
Abhash A, Pandey K K (2021) Experimental and numerical study of discharge capacity and sediment profile upstream of Piano Key Weirs with different plan geometries. Water Resour Manag 35: 1529–1546. https://doi.org/10.1007/s11269-021-02800-y doi: 10.1007/s11269-021-02800-y
|
| [23] |
Kumar B, Kadia S, Ahmad Z (2021) Sediment movement over type A Piano Key Weirs. J Irrig Drain Eng147: 04021018. https://doi.org/10.1061/(ASCE)IR.1943-4774.0001561 doi: 10.1061/(ASCE)IR.1943-4774.0001561
|
| [24] |
Senarth G P, Khaniya B, Baduge N, et al. (2017) Environmental and social impacts of mini-hydropower plants–A case study from Sri Lanka. J Civil Eng Archit 11: 1130-1139. https://doi.org/10.17265/1934-7359/2017.12.008 doi: 10.17265/1934-7359/2017.12.008
|
| [25] |
Gunathilake M B, Amaratunga Y, Perera A, et al. (2020) Evaluation of future climate and potential impact on streamflow in the upper nan river basin of northern Thailand. Adv Meteorol https://doi.org/10.1155/2020/8881118 doi: 10.1155/2020/8881118
|
| [26] |
Tuan L A, Hiramatsu K (2020) Hydraulic investigation of piano key weir. Environ life Sci 310–322. https://doi.org/10.7831/ras.8.0_310 doi: 10.7831/ras.8.0_310
|
| [27] |
Ghanbari R, Heidarnejad M (2020) Experimental and numerical analysis of flow hydraulics in triangular and rectangular piano key weirs. Water Sci 34: 32–38. https://doi.org/10.1080/11104929.2020.1724649 doi: 10.1080/11104929.2020.1724649
|
| [28] | Khassaf S I, Al-Baghdadi M B N (2018) Experimental investigation of submerged flow over piano key weir. Int J Energy Environ 9: 249-260. |
| [29] |
Mahabadi N A, Sanayei H R Z (2020) Performance evaluation of bilateral side slopes in piano key weirs by numerical simulation. Model Earth Syst Environ 6: 1477–1486. https://doi.org/10.1007/s40808-020-00764-3 doi: 10.1007/s40808-020-00764-3
|
| [30] |
Pralong J, Montarros F, Blancher B, et al. (2011) A Sensitivity analysis of Piano key weirs geometrical parameters based on 3D numerical modelling. Labyrinth and piano key weirs-PKW 2011. 133-139. https://doi.org/10.1201/b12349-21 doi: 10.1201/b12349-21
|
| [31] |
Seyedjavad M, Naeeni S T O, Saneie M (2019) Laboratory investigation on the discharge coefficient of trapezoidal piano key side weir. Civ Eng J 5: 1327-1340. https://doi.org/10.28991/cej-2019-03091335 doi: 10.28991/cej-2019-03091335
|
| [32] |
R Eslinger K, Crookston B M (2020) Energy dissipation of type a piano key weir. Water 12: 1253. https://doi.org/10.3390/w12051253 doi: 10.3390/w12051253
|
| [33] |
Pourshahbaz H, Abbasi S, Pandey M, et al. (2020) Morphology and hydrodynamics numerical simulation around groynes. ISH J Hydraul Eng 1-9. https://doi.org/10.1080/09715010.2020.1830000 doi: 10.1080/09715010.2020.1830000
|
| [34] | Bayón-Barrachina A, Valero D, Vallès-Morán F, et al. (2014) Comparison of CFD models for multiphase flow evolution in bridge scour processes. 5th International Junior Researcher and Engineer Workshop on Hydraulic Structures, Spain. 28–30. |
| [35] | Vasquez J A, Walsh B W (2009) CFD simulation of local scour in complex piers under tidal flow. 3rd IAHR Congress: Water Engineering for a Sustainable Environment (IAHR) 913-920. |
| [36] |
Ghaderi A, Daneshfaraz R, Abbasi S, et al. (2020) Numerical analysis of the hydraulic characteristics of modified labyrinth weirs. Int J Energy Water Res 4: 425-436. https://doi.org/10.1007/s42108-020-00082-5 doi: 10.1007/s42108-020-00082-5
|
| [37] |
Ghaderi A, Abbasi S, Abraham J, et al. (2020) Efficiency of trapezoidal labyrinth shaped stepped spillways. Flow Meas Instrum 72: 101711. https://doi.org/10.1016/j.flowmeasinst.2020.101711 doi: 10.1016/j.flowmeasinst.2020.101711
|
| [38] | Flow Science I. Flow-3d User manual: V11.2. (2016). |
| [39] |
Daneshfaraz R, Ghaderi A, Akhtari A, et al. (2020) On the effect of block roughness in Ogee spillways with flip buckets. Fluids 5: 1–17. https://doi.org/10.3390/fluids5040182 doi: 10.3390/fluids5040182
|
| [40] |
Singh U K, Ahmad Z, Kumar A, Pandey M (2019) Incipient motion for gravel particles in cohesion less sediment mixtures. Iran J Sci Technol Trans Civ Eng 43: 253-262. https://doi.org/10.1007/s40996-018-0136-x doi: 10.1007/s40996-018-0136-x
|
| [41] | Gualtieri C, Chanson H (2021) Physical and numerical modelling of air-water flows: an introductory overview". Environ Model Softw105109. https://doi.org/10.1016/j.envsoft.2021.105109 |
| [42] |
Pu J H, Wallwork J T, Khan M, et al. (2021) Flood suspended sediment transport: combined modelling from dilute to hyper-concentrated flow. Water 13: 379. https://doi.org/10.3390/w13030379 doi: 10.3390/w13030379
|
| [43] |
Celik I B (2008) Procedure for estimation and reporting of uncertainty due to discretization in CFD applications. J Fluid Eng 130: 1-4. https://doi.org/10.1115/1.2960953 doi: 10.1115/1.2960953
|
| [44] |
Guguloth S, Pandey M, Pal, M (2024) Application of hybrid AI models for accurate prediction of scour depths under submerged circular vertical jet. J Hydrol Eng 29: 04024010. https://doi.org/10.1061/JHYEFF.HEENG-6149 doi: 10.1061/JHYEFF.HEENG-6149
|
| [45] |
Nou M, Moghaddam A, Mehdi B, et al. (2019) Estimation of scour depth around submerged weirs using self-adaptive extreme learning machine. J Hydro Inform 21. https://doi.org/10.2166/hydro.2019.070 doi: 10.2166/hydro.2019.070
|
| [46] |
Pandey M, Sharma P K, Ahmad Z, et al. (2018) Maximum scour depth around bridge pier in gravel bed streams. Nat Hazards 91: 819–836 (2018). https://doi.org/10.1007/s11069-017-3157-z doi: 10.1007/s11069-017-3157-z
|
| [47] |
Kumar B, Kadia S, Ahmad Z (2019) Evaluation of discharge equations of the piano key weirs. Flow Meas Instrum 68: 101577. https://doi.org/10.1016/j.flowmeasinst.2019.101577. doi: 10.1016/j.flowmeasinst.2019.101577
|
Binit Kumar, Rahil Ahmad, Manish Pandey, Anil Kumar Gupta. Numerical and statistical analysis of auxiliary geometrical parameter effects on piano key weir discharge capacity[J]. AIMS Environmental Science, 2024, 11(5): 723-740. doi: 10.3934/environsci.2024036
DownLoad:
