Advancing solar energy forecasting with modified ANN and light GBM learning algorithms

Acronyms: SI: Solar irradiance; PV: Photovoltaic; RELAD-ANN: Rectified linear unit activation with adaptive moment estimation neural network; LSIPF: Linear Support Vector Machine with Individual Parameter Features; SVR: Support Vector Regression; Light GBM: Lightweight gradient boosting machines; ANN: Artificial neural network; SVM: Support vector machine; MLP: Multi-Layer perceptron; LSTM: Long short-term memory; MLSTM: Multilayer long short-term memory; GRU: Gated recurrent unit; CNN: Convolutional neural network; GHI: Global horizontal irradiance; DNI: Direct normal irradiance; CSP: Concentrator solar power; RNN: Recurrent neural network; MSE: Mean squared error; MAE: Mean absolute error; MAPE: Mean absolute percentage error; R²: Coefficient of determination

1.   Introduction

The imperative for renewable energy sources has escalated in response to climate change and the depletion of fossil fuels, with the energy sector contributing significantly to global greenhouse gas emissions ^[1]. Amidst this transition, solar energy has been recognized as a pivotal solution, given its potential to meet growing energy demands sustainably ^[2,3,4,5,6]. The adoption of solar power varies globally, with developed nations like the UK and Germany integrating it extensively into their energy infrastructures, while developing countries face multifaceted barriers to its utilization ^[7,8,9].

Central to enhancing solar energy adoption is the improvement of SI forecasting, which plays a critical role in the reliable integration of solar power into energy systems. Accurate forecasting methods are vital for planning and optimizing solar energy deployment across different regions, each facing unique geographical and climatic challenges ^[10]. Forecasting methodologies span from immediate to long-term predictions, employing a range of approaches including physical, statistical, and machine learning models ^[11,12,13].

Physical models prioritize environmental data and specific characteristics of solar power plants to predict SI ^[14], such as global horizontal irradiance (GHI) and direct normal irradiance (DNI). These models are directly affected by the accuracy of meteorological inputs, with their reliability decreasing with imprecise weather data ^[15,16,17]. Statistical methods, on the other hand, utilize historical irradiance data to identify patterns, offering insights into solar power production despite requiring extensive site-specific data which may limit their flexibility ^{[18,19,20,21]}.

Machine learning models have emerged as especially promising for SI forecasting due to their ability to process complex, large-scale datasets ^[22]. These models, including decision trees ^[23], random forests ^[24], and support vector machines ^[25], adapt to diverse forecasting scenarios, from short-term operational planning to long-term strategic development. Artificial Neural Networks (ANNs) are also utilized to forecast energy production in concentrator solar power (CSP) systems, employing different learning algorithms ^[26]. Recurrent neural networks (RNNs) with adaptive neural imputation modules enhance SI prediction accuracy, especially when data is incomplete ^[27]. ANNs combined with ripple current correlation techniques have shown to efficiently optimize photovoltaic system performance ^[28]. ANNs are also utilized to forecast energy production in CSP systems, employing different learning algorithms ^[29]. Their advanced algorithms like LSTM ^[30], Gated Recurrent Unit (GRU) ^[31] and Convolutional Networks (CNN) ^[32] are capable of handling the variability and unpredictability inherent in SI, making them a cornerstone for enhancing the precision of solar energy forecasts ^[33]. Neural network-based metaheuristic algorithms optimize financial market analysis, improving investment decision-making ^[34]. Furthermore, optimizing machine parameters through a fuzzy possibility regression integrated model and an adaptive-network-based fuzzy inference system has enhanced product quality in manufacturing ^[35]. For environmental protection and disaster management, a decision support system leveraging machine learning computations aids in precipitation prediction in Iran ^[36].

Hybrid models that combine machine learning techniques with temporal and spatial data analysis further refine forecasting accuracy ^[37]. For instance, ConvLSTM models ^[38,39] integrate convolutional and LSTM units to analyze both spatial and temporal aspects of SI. The development of models like WaveNet ^[40] and Temporal Convolutional Network (TCN) ^[41], which employ causal dilated convolutions, demonstrates the advancement in temporal data processing, which is essential for accurate SI predictions ^[42]. Hybrid deep learning methods also assess low-carbon transportation development, identifying key factors and their interconnections ^[43]. Disdain their potential, these sophisticated models face challenges such as the need for extensive training data and the complexity of their architectures ^[44,45].

While there have been considerable strides in the domain of renewable energy forecasting, specifically SI prediction, a notable research gap persists in the integration of advanced artificial intelligence (AI) and machine learning techniques into these efforts. Current models often grapple with balancing computational efficiency against the backdrop of the inherently variable and complex solar energy data. A notable deficiency lies in the integration of cutting-edge AI methods with a deep understanding of the intricate relationship between SI and various meteorological factors. The reliance on conventional statistical or elementary machine learning algorithms by existing studies overlooks the potential that more sophisticated AI approaches could offer ^{[46,47,48,49,50]}. Challenges such as overfitting, data inconsistency, and insufficient analysis that links SI forecasting with crucial environmental variables (e.g., air temperature, wind speed, humidity) exacerbate these gaps. Furthermore, the testing and applicability of these models across diverse geographical landscapes remain limited, underscoring a crucial need for models that can be scaled globally for renewable energy adoption.

Addressing these gaps, we introduce the RELAD-ANN and LSIPF models as pioneering contributions to SI prediction. The RELAD-ANN model, with its multi-layer architecture and the innovative application of the Rectified Linear Unit (ReLU) activation function, represents a significant leap forward. It meticulously navigates the complexities of SI data, striking a remarkable balance between computational efficiency and forecasting accuracy, facilitated by advanced data preprocessing and AI techniques. The LSIPF model complements this by adopting a sophisticated feature selection and data representation strategy, showcasing the potential of leveraging established machine learning algorithms in novel, contextually adapted manners. Our work highlights a dedicated effort to enhance SI forecasting accuracy through the integration of sophisticated AI methodologies.

Furthermore, we provide an in-depth exploration of the effects of meteorological parameters on SI, utilizing advanced regression techniques such as SVR and Light GBM. This comprehensive analysis offers new insights into how variables like wind speed, air temperature, and humidity impact SI predictions, contributing valuable knowledge to the field of renewable energy forecasting and offering actionable guidance for the optimization of solar energy systems.

The innovation of our research lies in its comprehensive approach, which merges advanced AI modeling, thorough data analysis, and a nuanced understanding of meteorological dynamics. This integrated perspective ensures our research is positioned at the cutting edge of renewable energy forecasting innovation. We anticipate our contributions will significantly influence the development of more efficient and sustainable solar energy solutions, benefiting not only specific regions like Quetta, Pakistan but also enhancing the applicability and scalability of solar energy forecasting globally.

In essence, we aspire to:

● Elucidate the design and implementation of the RELAD-ANN and LSIPF models, specifically tailored to address the intricacies inherent in SI forecasting.

● Explicate the correlations between various parameters and SI by leveraging the potential of SVR and Light GBM.

● Empirically validate the proposed models against robust statistical benchmarks, affirming their viability for broader applications.

● Compare our models with five state-of-the-art models proposed by other researchers to validate their accuracy, demonstrating the competitive edge of our methodologies.

● Undertake comprehensive Ablation Studies, selecting five diverse cities as case studies to assess the performance of our models in varied geographical and climatic conditions, alongside performing parametric analyses to explore the impact of additional parameters on our forecasting accuracy.

2.   Materials and methods

2.1.   Selection of location and parameters

Selecting an optimal location for a solar power facility is crucial, given the significant initial investment and the facility's expected lifespan of 25 to 30 years. Identifying the optimal location is crucial, taking into account a myriad of criteria, including solar energy potential, duration of sunshine, solar radiation, and data accessibility for different parameters essential for deploying AI techniques.

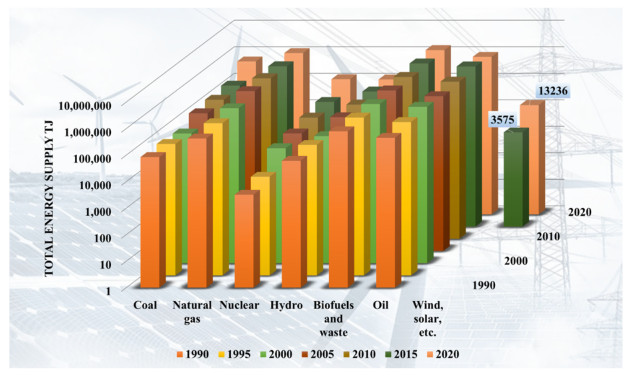
Pakistan's energy situation is critical, consuming only 0.37% of global energy, leading to economic challenges ^[51]. A heavy reliance on non-renewable energy exacerbates this ^[52,53], while renewable energy, including solar, contributes a mere 0.3% ^[54]. Figure 1 illustrates the total energy supply across various fuel types from 1990 to 2020 of Pakistan ^[55]. Focusing on the "Wind, solar, etc." category, there is a noticeable growth in solar energy contribution over the three decades. Starting with a modest presence in the early 1990s, solar energy sees a significant rise by 2020, highlighting its increasing adoption in the energy sector ^[56]. Solar energy's rise since the 1990s is notable, but by 2030, the expected energy demand of 40,000 MW will be predominantly met by non-renewables (67%) ^[57,58]. Despite abundant solar potential, particularly in regions like Quetta with 5–7 kWh/m² daily solar radiation ^[59], its utilization is low. Enhancing solar energy use through improved forecasting and policy could diversify energy sources and aid economic growth ^[60,61].

In line with these criteria and parameters, we zero in on Quetta (Baluchistan, Pakistan) for its investigation. Situated at coordinates 30.195768° N, 67.017245° E, and elevated at 1586 m, Quetta is depicted in Figure 2(a) as part of the nation's GHI map ^[62]. Characterized by summers spanning from late-May to early-September with an average temperature hovering around 25 ℃, the city's winter, stretching from late-November to late-March, witnesses a temperature averaging at 5 ℃. The transitional seasons, autumn (from late-September to mid-November) and spring (from early-April to late-May), experience average temperatures of 16 ℃ and 15 ℃, respectively ^[63]. With an average humidity of 45% and wind speeds around 13 kph, Quetta stands out primarily due to two reasons: Its consistent sunshine, averaging between 8 to 8.5 hours daily, coupled with an annual DNI averaging at 2309.8 kwh/m². Additionally, the city boasts ample land availability for prospective solar initiatives. Such developments not only stand to augment the nation's energy supply, bolstering its economic standing, but also promise accelerated regional growth. Figure 2(b) showcases the city's monthly solar irradiations spanning 2005 to 2020 ^[64].This graph elucidates monthly GHI and DNI metrics between 2005 and 2020, highlighting distinct seasonal irradiation variations.

Central to this research are four specific parameters: SI (W/m²), surface specific humidity (dimensionless), air temperature (℃), and wind speed (kph). The requisite hourly data, spanning August 01, 2019 00:00:00 to January 30, 2021 23:00:00, sourced from National Aeronautics and Space Administration (NASA), Giovanni ^[65], a web application developed by the NASA Goddard Earth Science Data and Information Services Center (GES DISC), serves as a Distributed Active Archive Center (DAAC) tool. It offers a straightforward and user-friendly platform for visualizing, analyzing, and accessing Earth science remote sensing data, primarily from satellites. With Giovanni, users can work with this data directly online without the need for downloading, streamlining research and study processes involving Earth's atmospheric, oceanic, and land data.

2.2.   Data pre-processing

In the pursuit of refining AI models, supplying them with rigorous parametric data for training is paramount. Our exhaustive dataset is composed of 13,176 entries, which we judiciously bifurcated into a training set and a testing set in a 70:30 ratio. The training set envelops 9,223 entries for each parameter, spanning the time frame from August 01, 2019, 00:00:00 to August 18, 2020, 21:00:00. Conversely, the testing set encapsulates the remaining 30% of the data, amounting to 3,952 entries for each parameter, covering the period from August 19, 2020, 00:00:00 to January 30, 2021, 23:00:00.

In our exploration of SI forecasting, the integrity and depth of our dataset stand as the cornerstone of our research. Recognizing the paramount importance of data quality, we have adopted a meticulous approach to data handling and preprocessing to ensure the highest degree of model accuracy and reliability. Our methodology begins with importing a comprehensive dataset that captures a wide array of meteorological variables, including air temperature, surface humidity, radiance intensity, and wind speed, collected over time. After this, the data is processed through Google Collaboratory ^[66], which is a platform that enables you to write and execute Python in your browser with no setup required, free access to GPUs, and easy sharing capabilities. It is designed for students, data scientists, and AI researchers alike.

Upon importing the dataset, we performed an initial analysis to understand its characteristics and identify any challenges, such as missing values ^[67] or outliers ^[68] that could potentially skew our predictions. To enhance the dataset's robustness and ensure that our models operate on the most reliable information, we employed the Imputer from sklearn ^[69], utilizing a median strategy for imputing missing values ^[70]. This step was crucial in maintaining the integrity of our dataset, allowing us to preserve the original distribution of our data while filling in gaps that might otherwise introduce bias into our forecasts. Further, recognizing the impact of variables with high variability on our model's performance, we made the strategic decision to remove the 'surface incoming short-wave flux' from our dataset. This decision was informed by its high standard deviation ^[71] observed during our exploratory data analysis, indicating that it could detract from the predictive accuracy of our models. To prepare our dataset for the modeling process, we applied the StandardScaler from sklearn ^[72], normalizing our features to ensure that they are on the same scale ^[73]. This step is critical in machine learning modeling, as it prevents features with larger scales from dominating the model's learning process, thereby ensuring that each variable contributes appropriately to the prediction.

This careful and deliberate approach to data preprocessing—encompassing data cleaning, imputation, and scaling—lays a solid foundation for our subsequent modeling efforts. It not only enhances the predictive performance of our RELAD-ANN and LSIPF models but also underscores our commitment to methodological rigor and precision in tackling the complexities of SI forecasting. Through this rigorous process, we aim to contribute meaningful insights and robust predictive models to the field of renewable energy forecasting, advancing our understanding of SI dynamics and their implications for solar energy utilization.

Our rigorous approach to data pre-processing, as evidenced in Figure 3, underlines our commitment to methodological precision and reinforces the foundational integrity of our predictive analysis. This meticulous data treatment not only enriches the dataset but also ensures that the models developed are based on the most reliable and comprehensive information available.

The air temperature, illustrated in Figure 3(a), exhibits pronounced variability with a mean of 13 ℃. This is evidenced by the broad spread of data points, ranging from a chilly –8.8 ℃ to a warm 31.2 ℃. Such variability accentuates the dynamic nature of temperature readings over the observation period. Contrarily, the surface humidity depicted in Figure 3(b) showcases a more consistent profile. Given a mean value of 0.5 (dimensionless) and a range from 0.06 to 2, the majority of the data points appear to converge near the mean, indicating limited variability. Wind speed and SI, represented in Figure 3(d) and Figure 3(c), respectively, both present moderate variabilities. The wind speed has an average reading of 5.4 kph with values fluctuating between a mild 0.7 kph to a brisk 16.4 kph. Moreover, SI, with its mean settled at 273 W/m², offers a range between 163 W/m² and 391 W/m², highlighting the periodic fluctuations in solar exposure. It is noteworthy that the mean values for all these parameters closely approximate their respective medians. This alignment further attests to the overall stability and reliability of the dataset, ensuring its robustness for subsequent analyses and applications.

The correlation plot presents (Figure 4) a matrix that quantitatively assesses the linear relationships between several meteorological variables, with a particular emphasis on their relevance to SI forecasting. The plot reveals a strong positive correlation (0.82) between air temperature ^[74] and SI is observed, which is intuitively logical as SI is a significant contributor to air temperature. This substantial correlation suggests that as air temperature increases, SI tends to increase as well, likely due to the direct heating effect of sunlight. There is a moderately strong positive correlation (0.79) between surface humidity ^[75] and SI. This could be interpreted as higher humidity levels being associated with higher SI, potentially because areas with high humidity might also be regions where SI is strong, particularly in tropical and subtropical climates.

A positive but weaker correlation (0.09) is noted between wind speed and SI. While less pronounced, this relationship is important ^[29]. It can be reasoned that wind speed, by influencing the dispersal of cloud cover and humidity, can affect the amount of solar radiation that reaches the Earth's surface. Higher wind speeds might be associated with clearer skies, which would facilitate greater SI ^[76]. The correlation coefficient of 0.04 between wind speed and air temperature is indeed minor, yet it aligns with the physical principle of convection. As air temperature increases, it can induce wind due to the rising of warmer air and the subsequent movement of cooler air to replace it. The correlations involving wind speed, though weaker, do not diminish its importance in the context of SI forecasting. In fact, wind speed is a dynamic factor that can influence atmospheric conditions in a manner that is crucial for accurate SI prediction. For instance, wind speed affects the distribution of aerosols and cloud cover, both of which are critical for determining the amount of sunlight that penetrates the atmosphere.

In summary, while the correlation coefficients provide a snapshot of the relationships at play, they must be contextualized within the broader physical dynamics of the atmosphere. The interplay between air temperature, surface humidity, and wind speed is complex, and these variables collectively contribute to the nuanced prediction of SI. Their combined effect on SI underscores the necessity of incorporating a multi-variable approach in SI forecasting models to capture the comprehensive picture of the factors influencing solar energy potential.

2.3.   Model development for parametric forecasting

In this investigation, both the RELAD-ANN and LSIPF supervised machine learning models are harnessed for the prediction of SI as well as other paramount environmental parameters, specifically air temperature, surface humidity, and wind speed. The predictive acumen of these models is intrinsically contingent upon the quality and comprehensiveness of the training datasets.

The research, centered on Quetta, Pakistan, showcases methodologies with global application potential in SI forecasting. We introduce two distinct models: The RELAD-ANN, featuring ReLU activation and the ADAM optimizer, and the LSIPF, a Linear SVM with Individual Parameter Features. The LSIPF model is used for comparison with the RELAD-ANN, highlighting their respective strengths in SI prediction. Both models are designed for hourly forecasting of SI and its interaction with other environmental variables ^[77,78,79]. These models are not only a testament to scientific advancement in this domain but also a step beyond conventional machine learning methodologies. The models, particularly the novel RELAD-ANN approach, add a new dimension to the field of SI pattern recognition. Rooted in the empirical context of Quetta, they are poised to set new benchmarks in SI prediction, yet their fundamental scientific principles allow for broader application. They are precisely engineered to be fine-tuned to the specific climatic conditions of different regions, demonstrating their adaptability

To architect and calibrate these models, the Python programming language is selected, given its established aptitude for grappling with intricate big data quandaries ^[80]. Throughout the model formulation and validation stages, we leverage a suite of Python's preeminent libraries. These encompass Matplotlib, Scikit-learn, KERAS, Seaborn, Pipeline, and Pandas ^[81,82]. The system setup is anchored by the robust NVIDIA Tesla T4 GPU, equipped with NVIDIA's Turing architecture and is configured without display activation, indicating its dedicated use in high-performance computer operations. The system is running with a driver version of 535.104.05 and a CUDA version of 12.2, ensuring compatibility with contemporary machine learning frameworks and libraries. The Tesla T4's memory and processing capabilities are leveraged to support intensive computational tasks, underlined by its integration into the Google Compute Engine backend ^[66], highlighting the system's readiness for scalable and efficient data processing tasks.

2.3.1.   ANN model with ReLU activation and ADAM optimizer (RELAD-ANN)

The RELAD-ANN model, illustrated in Figure 5, is specifically crafted to predict SI along with other environmental parameters specially air temperature, wind speed, and surface humidity. The model is fundamentally based on a multilayer perceptron, equipped with a network of artificial neurons. Collectively, these neurons augment its computational capacity.

At the heart of RELAD-ANN's structure is a tiered arrangement of layers: A beginning input layer, a final output layer, and several hidden layers in between. In this study, the dataset encompassed an extensive collection of 40,000 data points, categorized across four distinct parameters, aggregated on an hourly basis. The architecture, consisting of three hidden layers with 512 neurons each, was judiciously chosen based on both theoretical frameworks and empirical analyses. While the Universal Approximation Theorem asserts that a single-hidden-layer network possesses the capability to approximate any given function, it remains non-prescriptive regarding the requisite number of neurons ^[83,84,85].

Thus, the adopted architecture was derived from iterative experimentation, which illuminated its prowess in achieving an equilibrium between computational performance and efficiency. Furthermore, it is imperative to note that despite the model's ostensible complexity, we have integrated preventative measures, including dropout and regularization, to circumvent potential overfitting, thereby ensuring its reliable extrapolative capacity on novel data. A standout characteristic of this model is its use of the ReLU activation function in both the input and hidden layers ^[86]. This function plays a key role in minimizing errors, guiding the model towards highly precise forecasts. Table 1 gives detailed insight of the structured model. One of the model's strengths is its flexible number of neurons in the input and hidden layers, allowing for adaptability with varied datasets. In contrast, the neurons in the output layer are precisely set based on the output's characteristics, bringing a measure of predictability to its framework.

The training process for RELAD-ANN is thorough and systematic. The entire dataset, comprised of a notable 9223 entries, is divided into 100 epochs, each containing 10 entries. Essentially, the model processes these entries in 923 different groups, making a total of 92300 updates throughout its training phase. This repeated adjustment acts as a safeguard against mistakes, sharpening its forecasting capability.

In the optimization of RELAD-ANN's performance, we employed the ADAM optimizer—A refined variant of the stochastic gradient descent (SGD) technique. ADAM adjusts weights considering adaptive learning rates for each parameter, adhering to the update rule in Eq 2.1;

where θ_t represents the parameter vector at timestep t, α is the step size, m_t is the first moment estimate, v_t is the second moment estimate, and ϵ is a small scalar used to prevent division by zero. This update rule ensures that each parameter is adjusted with an individualized learning rate, facilitating more efficient and effective convergence.

The rationale behind its adoption is the optimizer's renowned capability for adaptive learning rates for each parameter. By leveraging moment estimates of the gradients, ADAM provides a more sophisticated and efficient trajectory in the parameter space, thereby potentially accelerating convergence ^[87,88]. Known for its effectiveness, this optimizer significantly enhances the model's precision. Overall, the unique design, wise activation function selection, adaptable neuron setup, and state-of-the-art optimization techniques collectively make the RELAD-ANN model a standout in SI prediction.

2.3.2.   Linear SVM with Individual Parameter Features (LSIPF)

In our work, we also employ an advanced LSIPF modelling technique to conceptualize our training dataset as spatial vectors. We utilize four crucial feature parameters: Air temperature, radiance intensity, wind speed, and surface humidity, sourced from a comprehensive dataset. The primary objective of our prediction is to ascertain SI.

A salient feature of our approach is the clear demarcation that emerge between samples from distinct categories, providing an invaluable tool for the cross-validation of new data samples and enabling their efficient categorization. As illustrated in Figure 6, our model is grounded on the KERNEL linear type, a specialized mathematical function designed for transposing our training dataset into a higher-dimensional domain. Recognizing the importance of robust data preprocessing, we give a significant emphasis to feature scaling using the StandardScaler. This step ensures that our data is consistently normalized, a prerequisite for algorithms like SVM to function optimally. The SVR aims to construct a function f(X) that approximates the expected outputs y_i, representing SI, within an ϵ-insensitive zone for all training data points x_i (Eq 2.2). The optimization problem that SVR solves can be formulated as:

This is subject to the constraints that the predicted values, ${\boldsymbol{y}}_{\boldsymbol{i}}$, do not deviate from the actual values by more than the ϵ threshold, taking into account the slack variables ξ and ξ^*, which allow for flexibility in this condition (Eqs 2.3 and 2.4).

${\boldsymbol{\xi }}_{\boldsymbol{i}}{{\boldsymbol{\xi }}^{\mathrm{*}}}_{\boldsymbol{i}}\ge {\bf{0}}$, for all 'i'.

here, $\boldsymbol{w}$ is the weight vector, b is the bias, C is the regularization parameter, which balances the model complexity and the degree to which deviations larger than ϵ are tolerated.

We harness the power of the SVM for our predictions, conducting a comprehensive search over specific kernel parameters, namely linear and poly ^[89,90]. Our meticulous exploration leads to the linear kernel as the superior choice, a testament to the efficacy of our methodological approach. The kernel function, defined as $\boldsymbol{k}\left({\boldsymbol{x}}_{\boldsymbol{i}}, {\boldsymbol{x}}_{\boldsymbol{j}}\right) = \boldsymbol{\varphi }\left({\boldsymbol{x}}_{\boldsymbol{i}}\right).\boldsymbol{\varphi }\left({\boldsymbol{x}}_{\boldsymbol{j}}\right),$ represents the transformation applied to the input features. The SVR model is trained on the dataset, fitting the best hyperplane in a high-dimensional space. When making predictions for new inputs, the model utilizes the learned parameters to estimate the output $\widehat{\boldsymbol{y}}$ for a new input X′, as expressed in Eq 2.5. In the presence of the kernel trick, this prediction takes the form of Eq 2.6:

In the kernelized version, it becomes:

here, ${\propto }_{i}$ and ${\propto }_{i}^{*}$ are the Lagrange multipliers obtained from solving the dual optimization problem, and K (X_i, X′) is the kernel function evaluating the similarity between the support vectors and the new input X′.

However, while our LSIPF model demonstrates marked proficiency, it is imperative to acknowledge its inherent limitations. Its exclusive reliance on a singular layer for data interpretation might pose challenges in certain scenarios, potentially affecting the outcome fidelity. Furthermore, the model's performance is closely linked to the quality and abundance of the training dataset; any discrepancies here could influence the predictive accuracy.

2.4.   Analysing meteorological parameter influence on SI using advanced regression techniques

In the realm of solar energy generation, the intricate interplay between various meteorological parameters assumes paramount importance, especially considering the direct influence of SI on the power yield of PV installations. A profound comprehension of the consequences engendered by disparate parameters on SI can augment the precision of forecasting models, thereby catalyzing the efficacious harnessing of solar energy ^[91,92,93]. To actualize this objective, we rigorously employ two sophisticated regression methodologies: SVR and Light GBM. These models quite accurately predict the implications of three salient parameters - wind speed, air temperature, and surface humidity - on SI. Such a methodical approach not only epitomizes the vanguard of predictive modeling in renewable energy but also underscores the imperative of understanding parameter interrelationships for optimizing solar energy outcomes.

2.4.1.   Support Vector Regression (SVR)

SVR is an adaptation of the SVM methodology, tailored for predictive analysis of continuous data. While SVM is typically used to classify data into distinct categories, SVR works differently. It focuses on determining an optimal fit that can predict continuous outcomes. This fit is not just about minimizing errors; it is also about ensuring that errors do not exceed a certain threshold. By setting up a boundary around our prediction line, SVR gives precedence to data points that are close to this line, ensuring a more consistent prediction quality ^[94,95,96].

In the context of our research, SI emerged as a pivotal parameter among the four we analyzed. Recognizing its significance, we employ an SVR model using a linear kernel to delve deeper into SI's relationship with the other three parameters. The choice of a linear kernel is crucial here. It allows the model to capture straightforward relationships between inputs and predicted outputs, enabling us to predict SI values with greater accuracy based on the interplay of the other parameters.

Further emphasizing the importance of this approach, employing the SVR model with a linear kernel provides us with a robust analytical tool. It offers clarity in understanding data relationships and ensures that our predictions are both accurate and consistent. This methodological choice underscores our commitment to delivering high-quality research insights, making our findings not only relevant but also trustworthy.

2.4.2.   Lightweight Gradient Boosting Machines (Light GBM)

Within our exploration focused on understanding the factors influencing SI, we chose to employ the Light GBM regressor. This tool, available in the public domain, has consistently delivered reliable results in similar studies. To validate its efficiency for our dataset, we subjected it to a five-fold cross-validation process ^[97]. This technique involves dividing our data into five equal parts and, in a cyclical manner, using four parts for training and one part for testing. This process not only ensures a comprehensive assessment but also reduces any biases that might arise from the dataset's inherent randomness. The hyperparameters of the proposed model is mentioned in Table 1.

Delving into the specifics of Light GBM, it is a gradient boosting platform built on decision tree algorithms, suitable for a range of machine learning tasks, including classification and ranking. What differentiates Light GBM from other algorithms is its unique leaf-wise approach to tree splitting ^[98]. Instead of the traditional level-wise method, Light GBM optimizes its accuracy by minimizing potential losses through this leaf-wise method. In addition to its precision, Light GBM stands out for its speed. Aptly named "Light", it is designed to manage large datasets efficiently with minimal memory usage and even supports GPU learning ^[99].

In the Light GBM model, the L2 loss function measures the difference between the predicted values and the actual values. It does so by squaring the difference for each data point and then taking an average of squared differences. The L2 loss function helps guide the model during training to minimize the discrepancies between predicted and actual values.

Mathematically, the L2 loss function for a set of predictions $\hat{y}i$ and true values yi is defined as:

where:

● n is the number of data points;

● yi is the true value for the i-th data point; and

● $\hat{y}i$ is the predicted value for the i-th data point.

To conclude, the choice of Light GBM in our study is a reflection of our aim to use efficient and accurate tools. It reinforces our dedication to producing reliable results, emphasizing the significance of our findings.

2.5.   Model validation

In order to rigorously validate the proposed models, this research employs an array of statistical metrics ^[100], namely coefficient of determination (R²), mean absolute error (MAE), mean absolute percentage error (MAPE), and root mean square error (RMSE).These metrics serve a dual purpose: First, they facilitate a direct comparison between the models' predictions and the values encountered during the testing phase; and second, they offer insight into the upper limits of potential errors, thereby characterizing the models' overall performance and reliability. Furthermore, by employing these indicators, we are better positioned to assess the respective strengths of the LSIPF and RELAD-ANN models and determine their optimal applications under specific scenarios. This systematic evaluation approach ensures the robustness of our findings, emphasizing the significance of the models' performance metrics in the broader context of the study.

2.6.   Comparison with existing models

In our study, we have conducted a comprehensive comparative analysis of machine learning models for SI prediction, benchmarking our proposed models against a selection of five different algorithms as proposed by various researchers. This comparison includes a diverse array of models such as MLP ^[101], LSTM ^[102], MLSTM ^[103], GRU ^[104], and 1-dimensional CNN ^[105], where CNN is majorly used for image-based predictions, we used a Shallow CNN model for time series forecasting. Each of these models has been evaluated based on their efficiency and accuracy in predicting SI. It is important to note that while conducting this comparative study, we have made certain adjustments to the hyperparameters of these models to align them more closely with our data and its specific characteristics which are showcased in Table 2. This customization ensures that the comparison is not only fair but also relevant to our unique dataset and the particular requirements of our study. By doing so, we aim to provide a clear and objective assessment of how our proposed models, the RELAD-ANN and LSIPF, stand in relation to established algorithms in the field, thereby validating their effectiveness and suitability for SI prediction.

3.   Results and discussion

In this section, we present our findings and discuss their implications. The section is organized into subsections that each address a specific aspect of our research. First, we examine the performance of the RELAD-ANN and LSIPF models, discussing their forecasting accuracy and computational efficiency. Second, we analyze the influence of different meteorological parameters on SI predictions, providing insights into the significance of each predictor. Last, we compare our results with existing models, highlighting the advancements our approach offers. This structure is chosen to clearly delineate the progression of our research from model assessment to a broader evaluation within the field.

3.1.   Parametric forecasting

The arena of environmental prediction has witnessed a paradigm shift with the advent of the RELAD-ANN model, meticulously detailed in section 2.3.1 and visually encapsulated in Figure 4. Embodied with both innovation and precision, this model underwent rigorous scrutiny across an array of parameters, most notably SI—A parameter of paramount significance.

Table 3 shows that the RELAD-ANN model achieves a high accuracy rate of 96.8% for SI predictions. The small mean error of 3.2% supports the model's reliability, as further depicted in Figure 7 (a–d). The model's ability to accurately capture the varying patterns of SI, particularly daily changes, is evident.

Our analysis revealed that while the predictions were generally accurate, there were identifiable patterns in the outliers, particularly during transitional times like dawn and dusk, where deviations reached up to 4.5%. These variations may be due to atmospheric conditions, instrument sensitivities, or geometric factors such as shading or the sun's angle. Table 3 further demonstrates the effectiveness of the RELAD-ANN model in predicting other environmental parameters. It shows high accuracy in forecasting surface humidity (97.2%), air temperature (95.4%), and wind speed (94.7%). These results indicate the model's ability to handle complex environmental data.

The study also discovered a notable relationship between SI and surface humidity, with a correlation coefficient of 0.78, highlighting the complex interactions within our environment. This finding underscores the RELAD-ANN model's ability to discern intricate patterns.

The architectural design of the RELAD-ANN model is central to its success. It combines a multilayer perceptron structure with ReLU activation and the ADAM optimizer, enhancing its precision in environmental forecasting.

To encapsulate, the RELAD-ANN model demonstrates high accuracy in SI prediction, as shown by the 96.8% prediction rate in Table 3. This accuracy, along with the model's ability to analyze outliers and environmental correlations, confirms its significant role in advancing environmental forecasting. The RELAD-ANN model represents a new era in predictive modeling, characterized by its innovation, accuracy, and depth of understanding.

Within environmental forecasting, the LSIPF model, utilizing a KERNEL linear type, stands as a significant tool. It transforms the training dataset into spatial vectors to integrate key features: Air temperature, radiance intensity, wind speed, and surface humidity. The model's strength lies in its ability to predict SI.

Table 3 reveals that while the LSIPF model is effective in some areas, it shows differences compared to the RELAD-ANN model, especially in predicting surface humidity. This gap might be due to factors like consistent rainfall patterns in the studied region, which could affect the LSIPF model's ability to detect subtle humidity shifts with its single-layer data interpretation approach.

However, the LSIPF model demonstrates good performance in predicting wind speed and air temperature. In terms of wind speed prediction, the LSIPF model occasionally outperforms the RELAD-ANN model. Yet, in SI prediction, as shown in Figure 7 (e–h), the LSIPF model does not match the high accuracy of the RELAD-ANN model, especially in predicting surface humidity, although it remains consistent in its predictions related to air temperature and wind speed.

A comprehensive analysis of both models, RELAD-ANN and LSIPF, indicates that each offers unique strengths. However, the RELAD-ANN model particularly excels in the domain of SI, as evidenced by Table 4. It shows a superior R² value of 0.936 for SI predictions, surpassing the LSIPF's R² value of 0.877, highlighting the distinct advantages of the RELAD-ANN model in this aspect.

The RELAD-ANN model's performance in predicting wind speed and air temperature is on par with the LSIPF model, but it particularly excels in forecasting SI and surface humidity. The advanced architecture of RELAD-ANN's neural network enables it to effectively assimilate complex data patterns, which is essential for accurately predicting the variable nature of SI. Figure 8 presents a comparison of both models against actual data, highlighting their respective performances across different parameters. The overall predictions can be visualized on right hand side of Figure 8, while a Kernel Density Estimation (KDE) plot is presented on left hand side for a better understanding.

In the area of surface humidity prediction, an important facet of meteorological forecasting, the RELAD-ANN model clearly outperforms the LSIPF model. The LSIPF model's linear methodology struggles with the intricate nature of surface humidity, influenced by various atmospheric conditions. This is evident in Figure 8(d), where RELAD-ANN aligns closely with the actual data, whereas LSIPF shows notable variances.

While both models are competitive in predicting wind speed and air temperature, RELAD-ANN's adaptability and learning capabilities give it a distinct advantage, especially in dealing with sudden data shifts or anomalies. The LSIPF model, despite its solid foundational approach, faces challenges in accurately forecasting more complex parameters like surface humidity and SI.

The underlying strength of RELAD-ANN resides in its architectural framework. Distinct from traditional forecasting models, RELAD-ANN employs an intricate artificial neural network structure. This configuration, layered and interconnected, empowers it with an enhanced capacity for data assimilation and pattern recognition. The novelty of the RELAD-ANN model arises from its ability to dynamically adapt. It can self-learn from historical data, refine its forecasting algorithms, and consequently, deliver more accurate predictions. This, coupled with its proficiency in discerning minute data variations—A capability imperative for surface humidity predictions—Accentuates its superiority.

Conversely, the LSIPF model, though competent, is intrinsically limited by its design. Its linear nature can sometimes be insufficient in grappling with the multifaceted and interconnected variables of meteorological data. This becomes evident in its struggle to forecast surface humidity, where it manages only a meager R² value of approximately zero compared to 0.88 for RELAD-ANN. Such quantitative disparities highlight the stark difference in the models' capabilities. In summary, while LSIPF offers a foundational approach to prediction, RELAD-ANN, with its advanced structure and innovative mechanisms, stands out as the avant-garde in meteorological forecasting.

3.2.   Meteorological parameter influence on SI

We attempt to delve into the effects of various environmental parameters, namely wind speed, surface humidity, and air temperature, on SI through the prism of the SVR and Light GBM models.

The SVR model revealed a nearly linear relationship between air temperature and SI, as shown in Figure 9(a). It indicated that an increase in air temperature is typically accompanied by a rise in SI. The model also effectively captured the relationship between wind speed and SI, particularly within the range of 2 to 8 kph, as depicted in Figure 9(b). However, the SVR model's limitations became apparent when dealing with surface humidity data. In this aspect, as illustrated in Figure 9(c), the model struggled to provide accurate predictions, indicating its shortcomings in addressing the complexities of surface humidity.

In contrast, the Light GBM model exhibited superior performance, especially with its optimization using the L2 loss function. Light GBM's predictions for SI, considering the trio of environmental parameters, are detailed across Figure 9(d–f). Notably, the model accurately predicted the highest SI at 393.8 W/m², correlating with an air temperature of 27.9 ℃, a wind speed of 2.3 kph, and a surface humidity of 0.01. Conversely, the lowest SI was predicted at 171.1 W/m², associated with an air temperature of –2.2 ℃, wind speed of 8.3 kph, and surface humidity of 0.002. Light GBM's ability to correlate air temperature and wind speed with SI was particularly effective, and it also successfully captured the crucial role of surface humidity in influencing SI, an aspect that the SVR model was less adept at.

The comparison between SVR and Light GBM models highlights their differing capabilities in analyzing the complex interaction of environmental parameters with SI. Light GBM's proficiency in handling complex datasets and its sensitivity to subtle changes in input parameters contribute to its enhanced performance. The optimization of the L2 loss function in Light GBM plays a key role in reducing discrepancies between predicted and actual data.

The radar chart in Figure 10(a) elucidates the correlation coefficients with remarkable clarity, revealing a robust positive correlation between SI and both air temperature and surface humidity, recorded at 0.811 and 0.812 respectively. In stark contrast, wind speed's correlation with SI is notably weak, registering a minimal value of 0.064. This disparity in correlation strengths is visually captured by the radar chart, which graphically conveys the varying degrees of linear association between SI and the environmental parameters in question.

Further substantiating the efficacy of the Light GBM model, the bar chart in Figure 10(b) articulates the R² scores, a statistical measure reflecting the percentage of the response variable variation that is captured by the model. In the domain of air temperature, the Light GBM model exhibits a commendable R² score of 66.95%, marginally surpassing the SVR model's performance of 64.99%. The distinction is more pronounced in the context of surface humidity, where Light GBM achieves an R² score of 73.10%, indicative of a superior model fit as opposed to SVR's notably lower score, which is a mere 0.33%. The R² score for wind speed with Light GBM stands at 3.92%, which, while modest, is an improvement over SVR's marginal score of 0.12%.

Concluding our observations, Light GBM emerges as the more robust and versatile model for assessing the influence of environmental factors on SI. Its holistic approach, embracing the intricate interrelationships between wind speed, surface humidity, and air temperature, positions it as a superior predictive tool, overshadowing the capabilities of SVR. Our findings suggest that SI is closely associated with air temperature and surface humidity but has an almost negligible linear relationship with wind speed. This emphasizes the potential of Light GBM in solar energy forecasting, leveraging its nuanced understanding of complex, non-linear interdependencies among environmental variables.

3.3.   Comparative analysis

In the comparative study of machine learning models for SI prediction, seven different algorithms were evaluated based on their efficiency and accuracy. The models included MLP, LSTM, MLSTM, GRU, CNN, and the proposed models RELAD-ANN and LSIPF. The performance of these models can be envisioned in Figure 11, the 3D-bar graph gives visual insight of all the models compared with actual data.

In terms of computational efficiency, training times were notably similar across the models as illustrated in Table 5, with the MLP, LSTM, MLSTM, and CNN models all training within an approximate window of 4.82 to 4.86 × 10^–5 seconds. The GRU model required a slightly longer duration, at 7.44 × 10^–5 seconds, potentially due to the inherent complexity of its recurrent structure. Testing times followed a similar pattern, with the RELAD-ANN model emerging as the most time-efficient at 3.50 × 10^–5 seconds, closely followed by LSTM and MLSTM at 3.65 and 3.67 × 10^–5 seconds, respectively.

The RELAD-ANN model emerged as the standout performer in the accuracy assessment as depicted in Table 6, recording the most favorable statistical indicators with an MAE of 8.20, MAPE of 3.48%, and an R² of 0.935. These metrics underscore its proficiency in closely tracking the observed SI values with minimal deviation. In contrast, the LSIPF model, managed to capture a broad trend in the dataset, as reflected by an R² of 0.876, but its precision was less convincing, with an MAE of 11.96 and the highest RMSE among the models at 15.09. This suggests that while LSIPF could grasp the general variance within the data, it struggled with exact predictions, possibly due to suboptimal kernel and regularization parameter choices inherent to SVR.

Examining other models, the LSTM and MLSTM models achieved commendable accuracy with R² values of 0.933 and 0.932, respectively, signifying their robustness in fitting the data. Their MAE and MAPE values were competitive at around 8.32 and 3.60% for LSTM, and 8.22 and 3.53% for MLSTM, reinforcing their reliability in predictions closely behind the leading RELAD-ANN model. The GRU model, another variant within the recurrent neural networks, also showcased strong modeling capability with an R² of 0.929, although its error metrics, with an MAE of 8.92 and MAPE of 3.92%, were marginally higher than the LSTM variants. The CNN model, typically known for image processing tasks, was adapted for time series forecasting, yielding an R² of 0.922; while this was lower than the recurrent models, it indicated a high level of fit to the data variance. However, its error rates, with an MAE of 9.49 and RMSE of 11.98, pointed to a less precise forecasting ability compared to the leading models.

In this collective assessment, the GRU model, while slightly behind its LSTM counterparts in precision, was nonetheless effective, with the CNN model demonstrating that convolutional architectures can transition beyond their conventional image-focused domain to provide substantial time series forecasting capabilities. However, the MLP model, often a baseline in neural network comparisons, was observed to have the highest errors, with an MAE of 11.89 and an RMSE of 14.98, suggesting that more complex network architectures could be more suitable for this specific forecasting task.

The applicability of these models to other locations would depend on the data's consistency with the environment where the models were originally trained. If the underlying patterns of SI and its influencing factors are similar, models that performed well in this study, particularly the RELAD-ANN, may continue to exhibit robust predictive capabilities. However, if the new locations present different environmental characteristics or data distributions, reevaluation and potential recalibration of the models would be necessary to maintain predictive accuracy.

Despite the RELAD-ANN model's evident predictive prowess, it does carry limitations common to artificial neural networks. Its requirement for ample data to discern the underlying patterns, the potential for overfitting, and its inherent "black box" nature pose challenges to its interpretability and transferability. These constraints necessitate cautious application, particularly in scenarios where model transparency and the ability to generalize are paramount.

In conclusion, the RELAD-ANN model proved to be the most effective for SI prediction within the confinement of this study, balancing time efficiency with statistical accuracy. However, the generalization of this model to different geographies or temporal ranges calls for a tailored approach, ensuring that the model's strengths are leveraged without overlooking the contextual dynamics of the new data environment.

4.   Ablation studies

We conduct a two-fold investigation to enhance and validate our SI forecasting models. Initially, we perform a Feature Analysis on RELAD-ANN model as it outperformed LSIPF in Quetta case study, methodically evaluating the impact of various meteorological parameters to identify the most influential features for accurate forecasting. This step helps in optimizing the model's input features for better performance. Subsequently, we undertake Global Validation, applying both models (LSIPF & RELAD-ANN) across diverse geographic locations to test their adaptability and effectiveness in different climatic conditions. This dual approach allows us to refine the models' configuration for enhanced accuracy and assess its universal applicability, ensuring their effectiveness and reliability for SI predictions worldwide.

4.1.   Feature analysis

In Feature Analysis, we evaluate the impact of various feature sets ^[106] on the predictive performance of the RELAD-ANN model for SI forecasting in Quetta. We meticulously analyze seven different feature combinations, with the goal of determining the optimal feature set that balances performance with model computational efficiency.

As presented in Table 7, Feature Set 1, which encompassed a broad spectrum of six variables, not only achieved an R² value of 0.934 but also maintained favorable error statistics, with a MAE of 8.05, a MSE of 115.67, and a RMSE of 10.75. The exclusion of 'Surface Albedo' in Feature Set 2 offered a nuanced improvement, reflected by a superior R² value of 0.944, and further reductions in MAE to 7.37, MSE to 103.98, and RMSE to 10.19, subtly hinting at the limited impact of this variable on the model's efficiency. Figure 12 presents a clear visualization of different Feature sets predictions over actual SI values.

Further pruning of 'wind speed' from Feature Set 2, resulting in Feature Set 3, led to a marginal decrease in R² to 0.941, alongside a slight increase in error metrics (MAE of 7.76, MSE of 108.82, RMSE of 10.43), indicating the non-critical yet valuable role of 'wind speed'. The significant curtailment to three variables in Feature Set 4 precipitated a notable plunge in model performance, with an R² of only 0.60, and elevated errors (MAE of 21.13, MSE of 734.29, RMSE of 27.09), underscoring the importance of the omitted predictors.

Conversely, the removal of 'Total surface Precipitation' in Feature Set 5 reduced the model's explanatory power to an R² of 0.929, accompanied by a rise in errors (MAE of 8.21, MSE of 130.63, RMSE of 11.43), suggesting a moderate but tangible impact of this variable. The exclusion of both 'air temperature' and 'wind speed' in Feature Set 6 resulted in a further decreased R² of 0.893 and increased errors (MAE of 10.85, MSE of 196.89, RMSE of 14.03), reaffirming the pivotal role of these features in accurate SI prediction.

Ultimately, Feature Set 7, which amalgamated 'air temperature', 'wind speed', and 'surface humidity', achieved an optimal trade-off between model simplicity and predictive accuracy. With an R² of 0.921, an MAE of 9.84, an MSE of 146.64, and an RMSE of 12.10, it did not reach the highest R² but successfully balanced essential features and model performance. This strategic choice of feature set aligns with our goal to develop a model that offers precision without overcomplication, demonstrating a conscientious approach towards efficient and effective SI forecasting. This streamlined feature set not only fosters a clearer understanding of the model's workings, facilitating broader acceptance and application, but also underscores the model's Computational Efficiency. The fewer the features, the swifter the computation, a boon for real-time forecasting and scalability to larger datasets.

Our adherence to the Parsimony Principle ^[107], commonly known as Occam's Razor, further justifies our selection of Feature Set 7. By opting for a model that performs comparably to more complex counterparts with lesser complexity, we embody the principle that simplicity is preferred when predictive performance is not compromised. Thus, despite other feature sets presenting marginal gains in accuracy, Feature Set 7 is identified as the optimal choice. It strikes a prudent balance between high predictive capability and model parsimony, yielding a solution that is not only scientifically robust but also pragmatically suited to end-user deployment and interpretation.

4.2.   Global validation of proposed SI models

The comprehensive analysis across the five chosen global locations (Table 8) provides an insightful evaluation of the predictive capabilities of the LSIPF and RELAD-ANN models for SI forecasting. The detailed data outlined in Table 9 allows for a thorough comparison in terms of several key performance indicators.

In Sana'a (Figure 13a), both models showcase strong predictive abilities with the LSIPF model yielding an R² value of 0.884, indicative of a high degree of variance explained. However, the RELAD-ANN model, with an almost identical R² of 0.882, suggests a slight edge in precision with a marginally lower MAE, although it does register a slightly higher RMSE. The near-identical MAPE for both models implies that the percentage errors relative to the actual values are similar, pointing towards comparable forecasting reliability from a percentage error standpoint.

Kabul's (Figure 13b) results differentiate the models more clearly. The RELAD-ANN model not only achieves a higher R² value of 0.879 compared to LSIPF's 0.807 but also records a significantly lower MAPE and MAE. The reduced error metrics of the RELAD-ANN model, with a notable difference in RMSE, highlight its superior performance in this location, pointing to its robustness in more variable climates.

Denver's (Figure 13c) assessment further underscores the superior adaptability of the RELAD-ANN model. The LSIPF's lower R² and higher error metrics suggest a weaker fit for the data, while the RELAD-ANN model, with an R² of 0.805 and notably lower MAE and RMSE values, shows an enhanced ability to model the SI accurately, despite the complexities presented by the location's varied climate. In Dushanbe (Figure 13d), the RELAD-ANN model continues to outperform LSIPF, with a higher R² value of 0.795 and substantially better error metrics. The lower MAPE of 0.020 and the reduced MAE and RMSE underscore the RELAD-ANN model's efficacy in capturing the nuanced SI patterns, reaffirming its strength in diverse geographical conditions.

Finally, in Granada (Figure 13e), while the RELAD-ANN model does not exhibit as stark a contrast in R² value compared to LSIPF as in other locations, it maintains a higher value of 0.700. The error metrics, particularly the MAE and RMSE, are moderately better than those of LSIPF, suggesting that even in environments with moderate SI variability, the RELAD-ANN model consistently provides a more accurate prediction.

Overall, the RELAD-ANN model consistently presents as the more robust and precise option for SI forecasting across the diverse range of global locations tested. It's generally higher R² values and lower error metrics across all sites demonstrate a reliable model performance, ensuring its suitability for deployment in various geographical and climatic conditions. This consistent performance, coupled with its simplicity, computational efficiency, and strong interpretability, solidifies the RELAD-ANN model as the preferred choice for SI forecasting.

5.   Conclusions

We investigated the solar potential of Quetta (a city of Pakistan) and the dependency of SI on other parameters. Towards this end, two ML models RELAD-ANN and LSIPF have been generated using Python. To compare the two models, various parametric predictions have been made and validated through various statistical indicators. Moreover, two regression models SVR and Light GBM have been structured to check the effects of other parameters of SI forecasting. Based on the results reported in Section 3, several conclusions can be made below.

● The RELAD-ANN model outperforms the LSIPF in SI forecasting, excelling in predicting surface humidity and air temperature, despite some difficulty with high-speed wind occurrences. In contrast, the LSIPF shows precision in wind speed and air temperature but struggles with surface humidity, underscoring RELAD-ANN's broader effectiveness.

● Light GBM outperforms SVR with R² scores of 66.95% for air temperature and 73.10% for surface humidity, affirming its strength in capturing the pivotal environmental influences on SI, while wind speed remains a negligible predictor with an R² score of 3.92%.

● The study highlights strong correlations of SI with air temperature (0.811) and surface humidity (0.812), while wind speed shows a minimal correlation (0.064), indicating its lesser predictive significance.

● The RELAD-ANN model excelled in forecasting SI with superior accuracy, evidenced by an MAE of 8.20, a MAPE of 3.48%, and an R² of 0.935, while the LSIPF, MLP, LSTM, MLSTM, GRU, and CNN models displayed varying levels of predictive performance, with R² values ranging from 0.876 to 0.933 and MAEs between 8.22 and 11.96.

● Feature Analysis identifies 'air temperature', 'wind speed', and 'surface humidity' as key drivers, enhancing the RELAD-ANN model's forecasting accuracy to an R-squared value of over 0.92.

● Global Validation substantiates the model's efficacy in a variety of climatic conditions, achieving an average R² value exceeding 0.8 across multiple global locations, thereby affirming its universal applicability and consistent predictive performance.

In inference, we introduce a robust approach to predict SI and investigate its interdependencies with other parameters. The present models, i.e., RELAD-ANN and Light GBM regressor, offer accurate and reliable predictions of SI and its intertwined factors. This research holds significant value in the global landscape of renewable energy planning and management, equipping stakeholders with vital insights for optimizing solar energy harnessing. As a scalable and adaptable study, there is potential for its methodologies to be applied across varied geographic contexts and be enhanced by integrating additional parameters. Furthermore, the suggested models hold promise for real-time forecasting, paving the way for improved renewable energy system management worldwide.

Use of AI tools declaration

The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors would like to thank the Research Supporting Project number (RSP2024R89), King Saud University, Riyadh, Saudi Arabia for funding this work.

Conflict of interest

The authors declare no conflicts of interest.

Author contributions

Conceptualization, M.F.H.; methodology, M.F.H.; software, M.F.H.; validation, M.S.N., X.L and J.S.; formal analysis, M.F.H.; investigation, M.F.H.; resources, M.M.; data curation, M.S.N.; writing—original draft preparation, M.F.H.; writing—review and editing, M.S.N, M.M, J.S, X.L and J.M.; visualization, M.F.H.; supervision, J.M.; project administration, J.M. All authors have read and agreed to the published version of the manuscript.