A novel experimental procedure for lock-in thermography on solar cells

1.   Introduction

Photovoltaic solar generation has assumed a prominent role in the area of energy generation. The investments made in more efficient and robust new photovoltaic technologies aim, among other goals, to develop techniques capable of monitoring the performance of these systems. Therefore, it would be possible to identify and diagnose defects, such as the photovoltaic cell degradation as a result of the fabrication process, transport and installation, which is often not identifiable through visual inspection alone. These imperfections directly impact the electrical energy generated by these devices ^[1]. Among the main photovoltaic systems monitoring techniques currently available, infrared thermography (IRT) stands out as one of the leading tools for the non-destructive monitoring of photovoltaic devices ^[2].

IRT makes it possible to obtain images of a sample from a certain distance without establishing direct contact, combining high thermal sensitivity with high image acquisition rates ^[3]. These characteristics enable the IRT to be powered by an active external source, reducing its dependency on environmental conditions ^[4], as in the application to characterize defects in solar cells ^{[5,6,7,8,9,10,11,12]}. Furthermore, powered by a modulated source, it upgrades the method to a time-frequency domain, increasing significantly the available signal processing techniques. The most common and widely used techniques are fast Fourier transform (FFT) application, the four-step phase-shifting method (4 SPSM) and principal component analysis (PCA).

In the present work, it is proposed to apply active thermography by using a true sinusoidal wave in the place of the conventional pulse width modulation (PWM). The use of PWM forces the cell to always operate at the same operational point. Some good results of this approach can be found in the literature ^{[13,14,15,16,17]}. From a heat transfer perspective, it could be the same. However, a sinusoidal power source makes the solar cell operate at a wide range of I-V points on its characteristic curve. It is expected that this small change in the experimental procedure could highlight some defects better.

This novel experimental procedure will be compared to PWM and evaluated using the most widely used signal processing techniques. The methodology comprised the following steps: create a structured database with thermal images from two solar cells (one is defective and the other is non-defective) through the use of radiometric videos that use both sinusoidal electric current and PWM excitation modes; resize the original database into a set of principal components by using PCA; obtain a set of phase images through the application of both 4 SPSM and FFT; characterize the defects using the set of images obtained from the application of those methods; and, finally, establish a comparison between the proposed method and the conventional PWM.

The other sections of this work are organized as follows. In Section 2 the theoretical foundations for the experiment and algorithms are presented; Section 3 presents the adopted methodology with the description of the experimental parameters; Section 4 contains the results achieved; and, lastly, final comments and conclusions are presented in Section 5.

2.   Theory

In this section, a theoretical basis for the experimental procedure adopted is presented in Section 2.1. Additionally, it is worth noting that, despite the experimental procedure selected, the image processing technique adopted can also be a decisive factor to determine the success in the detection of defects. With that in mind, three well-known and suitable algorithms were used to process the radiometric videos. The theoretical background for each technique employed for the data analysis of the thermal imaging sequence and reasoning for their selection are provided in Subsections 2.2 (PCA), 2.3 (4 SPSM) and 2.4 (FFT).

2.1.   Lock-in thermography

In lock-in thermography (LIT) procedures, temperature values resulting from the propagation of thermal waves on the material's surface are measured by an infrared (IR) camera, producing thermal images with high resolution and low noise. The thermal waves induce changes in phase angle and amplitude at each pixel with respect to the input signal. For a flat sample, the temperature across the sample varies according to Eq (1) ^[18].

where ${T}_{0}$ is the initial change in temperature [℃]; $z$ is the defect depth [m]; $\omega$ is the angular frequency [rad/s]; $\lambda$ is the thermal wavelength [m]; $A\left(z\right)$ is the thermal amplitude [℃]; $\phi \left(z\right)$ is the thermal wave's phase shift [rad]; and $\mu$ is the thermal diffusion length [m], which is defined by Eq (2).

where $f$ is the frequency [Hz]; $\alpha = \frac{k}{\rho {C}_{p}}$ is the material's thermal diffusivity [m²s^-1], where $k$ is the thermal conductivity [W/m℃], ρ is the density [kg/m³] and ${C}_{p}$ is the specific heat [J/kg℃].

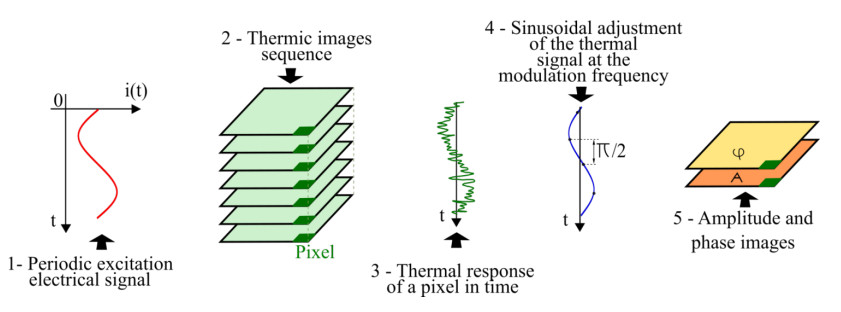
Figure 1 presents the steps taken in order to process the thermal images produced by LIT tests in which the resulting amplitude and phase images (obtained by techniques such as 4 SPSM and FFT) are highlighted.

Figure 1.  LIT image processing steps to derive the amplitude and phase images from the thermal images.

DownLoad: Full-Size Img PowerPoint

2.2.   PCA

PCA is a statistical technique of multivariate analysis that linearly transforms an original set of variables, initially correlated among each other, into a smaller set of uncorrelated variables that contains most of the information of the original set ^[16,19]. PCA algorithms are of special interest for the detection of defects in solar cells because they are able to reduce large amounts of data from the thermographic sequences to a set of matrices dubbed principal components. The principal components are defined as linear combinations of random variables that have special properties in terms of variance ^[20]. The difference in variability of the pixels can be used to highlight regions of interest in the solar cell, which might aid in the detection of defects. Several works have applied PCA algorithms to process radiometric videos ^[4,19,20,21].

Given a matrix $A\left(n\times m\right)$ related to a certain image, let ${X}_{1}, {X}_{2}, \dots, {X}_{p}$ be the variables associated with every pixel of the image. To compute the principal components, it is necessary, in first place, to calculate their average values ${\mu }_{1}, {\mu }_{2}, \dots, {\mu }_{p}$ and variances ${\sigma }_{1}^{2}, {\sigma }_{2}^{2}, \dots, {\sigma }_{p}^{2},$ respectively. These variables are not independent and, therefore, have covariance between the i-th and k-th variable defined by ${\sigma }_{ik}$ for $i\ne k = \mathrm{1, 2}, \dots, p$, forming the covariance matrix $\sigma$.

Afterward, the pairs of eigenvalues ($\lambda$) and eigenvectors ($e$) of the covariance matrix $\left({\lambda }_{1}, {e}_{1}\right)$, $\left({\lambda }_{2}, {e}_{2}\right)$, ..., $\left({\lambda }_{p}, {e}_{p}\right)$ can be ascertained, where ${\lambda }_{1}\ge {\lambda }_{2}\ge$...${\lambda }_{p}$ are also associated with the covariance matrix. As such, the i-th principal component can be computed by Eq (3):

The percentage of the total variance (${C}_{k}$) from each principal component (${Z}_{i}$) can be computed through the use of Eq (4) ^[19]:

The first principal component is usually the most relevant one since it presents the higher variance value and, therefore, also presents more data variability. The second principal component has the second highest relevance, and so on. In this paper, each pixel can be considered a different variable (${X}_{1}, {X}_{2}, \dots, {X}_{p}$), meaning that each frame of the thermographic sequence constitutes a different observation for every single variable, resulting in a temporal PCA instead of a spatial one. As such, the matrix $A\left(n\times m\right)$ contains in its columns the arrays of temperature values over time for every single pixel, where $m$ is the number of pixels and $n$ is the number of frames.

2.3.   4 SPSM

This method extracts the amplitudes and phases from the measurement results by considering a sinusoidal pattern of the solar cell thermal temporal response. The phase images are especially important because they improve the detection sensitivity and minimize the number of defect detection errors due to the discrepancies of surface emissivity. In fact, Eqs (9) and (10) result in an approximation of the value of the Fourier transform when it is considered that four equidistant points per modulation cycle of the stationary thermal temporal response (of each pixel) are known with exact phases and in amplitudes given by the sine wave signs. Therefore, it is possible to visualize amplitude and phase images of the solar cell with satisfactory contrast and defect delimitation.

The specific aim of the 4 SPSM is to determine the phase distribution from the choice of four thermographic images, i.e., ${I}_{1}\left(x, y\right)$ to ${I}_{4}\left(x, y\right)$, that are equidistant $\frac{\pi }{2}$ from each other, where ${I}_{i}\left(x, y\right)$ is the intensity of the i-th pattern ($i = \mathrm{1, 2}, \mathrm{3, 4}$). ${I}_{a}\left(x, y\right)$ and ${I}_{m}\left(x, y\right)$ represent the average intensity and the intensity modulation, respectively. The four sets of intensities can be mathematically described by Eqs (5), (6), (7) and (8).

Using the trigonometric relations between the sine and cosine functions, Eqs (5) to (8) can be rewritten with some additional algebraic manipulations in order to find the equation for the phase angle $\varphi \left(x, y\right)$, and it can be expressed through the use of Eq (9) ^[22].

The 4 SPSM also provides the modulation amplitude $A\left(x, y\right)$ values mathematically described by Eq (10) ^[22].

The details of each step of the 4 SPSM application, as shown in Figure 1, are explained as follows: initially, the temperature matrices of the thermal images are obtained from the radiometric video by considering a temporal thermal cycle of the cell's steady-state operation; then, the thermal images are segmented by applying Otsu thresholding using the temperature matrices as input and generating new smaller-sized matrices containing only the area of interest; then, a sinusoidal curve is obtained by fitting in the temporal thermal response pattern from each pixel, and this curve is used to make the selection of four images that are 90° out of phase; the phase is calculated for each pixel by using Eq (9); finally, it is possible to plot the resulting phase image.

2.4.   FFT

The study of signals and systems using sinusoidal representations is called Fourier analysis. The Fourier transform converts a signal from the time domain to the frequency domain, resulting in two spectra, i.e., magnitude and phase ones, making it easier to verify the contribution of each harmonic component with respect to the periodic signal. More complex problems in which a direct solution is not so easily obtainable can have their solution facilitated by taking the problem to another domain by using the Fourier transform, solving it, and then applying the inverse transform to find the solution in the original domain ^[17].

For a non-periodic continuous signal $f\left(t\right)$, the one-dimensional Fourier transform, denoted by $F\left\{f\left(t\right)\right\}$, can be mathematically expressed as Eq (11) ^[23].

where $j = \sqrt{-1}$; $t$ is the continuous variable of the integration (representing time in most cases), and $\mu$ is the variable related to frequency, given in cycles per second.

An implementation of one of Fourier's methods, the FFT, can be said to be the most important numerical algorithm of the current era, as well as the most important discrete transform ^[24]. The FFT is an optimized algorithm for implementing the discrete Fourier Transform (DFT), which is used to represent a discrete and non-periodic signal as a superposition of complex sinusoids. This algorithm has been applied to lock-in thermography in many previous and related works; the amplitude and phase images have shown to be useful in surface heat distribution analysis ^[16]. In essence, the FFT is a sampled form of the Fourier transform which takes a continuous function in time as input. The DFT transforms a set of numbers {${f}_{n}$}, consisting of $M$ samples of a continuous signal $f\left(t\right)$, into another set, {${F}_{m}$}, of M discrete complex values according to Eq (12) ^[25].

Thus, the application of an FFT fits well with the sinusoidal characteristic of the excitation signal, as well as with the thermal temporal response of the solar cells in the proposed method, as it is possible to decompose the latter (input to the FFT algorithm) in a series of sines and cosines while knowing the contribution of each harmonic. In particular, the Fourier transform is used to transform the thermal temporal response of the solar cells into the frequency domain in order to extract the amplitude and phase of the response at each modulation frequency. That leads to a remarkable improvement in the contrast, which is observable in the amplitude and phase images and, consequently, the identification of defective and non-defective areas.

Figure 1 can also be referenced to explain the application of the FFT since it first needs the temperature matrices of the temporal sequence of the segmented thermal images regarding the cell's steady-state operation, as it was described for 4 SPSM; then, the sequence of temperature matrices is reshaped into a two-dimensional format; the average of the temperature values is calculated and subtracted from the temperature values of each pixel; afterward, the one-dimensional FFT is applied to each pixel by considering their temporal thermal response within an adequate time lapse during steady-state operation; finally, the phase spectrum inherent to the FFT, as well as the plots of the phase images for the fundamental frequency and second harmonic, are obtained.

3.   Materials and methods

In this section, the methods used in this work are presented, along with the description of the experimental setup highlighting the technical information of the chosen specimen and the other components of the experiment.

3.1.   Experimental setup

Thermal image data were obtained by using defective and non-defective SunPower™ C60 monocrystalline silicon cells of 3.4 Wp as samples with dimensions of 12.5 × 12.5 cm² each. The defective solar cell has some defects that cannot be identified by simple visual inspection. The specific defects of the defective solar cell will be expanded upon in Section 4, where the electroluminescent images are presented. In Figure 2(a), the provided schematic illustrates the experimental process of the application of LIT.

Figure 2.  (a) Schematic of the application of DLIT using a solar cell as a sample, and (b) photo from inside the dark room used in the experiment showing the IR camera and solar cell positioning.

DownLoad: Full-Size Img PowerPoint

As it can be seen in the diagram of Figure 2(a), a function generator (model: Agilent 33250A) is the element that generates the sinusoidal electrical voltage signal that is first applied to a push-pull power amplifier circuit (to supply the required power to heat the sample) and then connected, by the circuit output, to the terminals of the solar cell. The function generator parameters had to be configured with respect to the forward bias operation mode of the device, which means that the signal offset and amplitude were adjusted to 1.35 V and 800 mV, respectively. The signal frequency was set to fixed values of 6 mHz, 11 mHz, 50 mHz and 100 mHz in each experiment.

To better evaluate the potential of the proposed method in this research, an additional analysis is made by performing tests using a classic methodology, which is the application of periodic heat pulses on the surface of the solar cell by means of a PWM electrical signal to be injected into the terminals of the cell. The objective is to generate the effect of a discrete sine wave signal through the variation of the duty cycle of the pulses to provide higher or lower voltage sine values. Regarding the PWM tests, the function generator is replaced by an ATmega2560 microcontroller that has been properly configured to generate pulses with a variable duty cycle aiming to result in sinusoidal waveform behavior with a frequency of 100 mHz. The microcontroller from ATmega2560 was used to develop the algorithm for the PWM electrical signal generation. A voltage divider circuit was adopted to decrease the value of the voltage applied to the solar cell to keep the maximum values of voltage and current in the same range of the previous tests: 1.3 V and 2.8 A.

Both setup configurations cause a sinusoidal current signal to appear in the solar cell whose peak value is not above 3 A, equivalent to approximately 50% of its short-circuit current, and an amplitude around 1.5 A; the solar cell operation region is also demonstrated in Figure 2(a) in the blue curve. Voltage and current levels were visualized and monitored using a Keysight oscilloscope (model: EDUX1002G).

In order to execute the tests, the solar cell must be positioned inside a closed dark room to perform dark lock-in thermography (DLIT), as shown in Figure 2(b), because it allows one to see more clearly where the dark current flows and reduce measurement noise from ambient light. The solar cell surface temperature is captured by an IR camera (model: FLIR T420), properly positioned with an angle of 45° with respect to the normal plane to avoid reflectivity on the cell, and also connected to a processing unit in which the radiometric videos are recorded and processed.

The tests were performed in accordance with ^{[26,27,28,29,30]}. It is advisable in ^[28,29,30] that, in any case, the performance of all photovoltaic modules that show significant hotspots should be investigated. These hotspots may indicate an electrical problem, such as series resistance or shunt resistance, such as in ^[28]. The defective solar cell showed some unusual hotspots while heated, as expected, so it must be monitored.

To carry out the LIT tests, it was necessary to first know the emissivity of the solar cells to set its value in the IR camera. Their emissivity was experimentally determined according to the procedure indicated by the IR camera manufacturer. The first step to determine the emissivity refers to the determination of the reflected apparent temperature, and it was done according to the reflector method standardized in ^[26]. Then, the reflected apparent temperature value was set in the camera in order to be able to proceed with the experimental determination of the emissivity, which was carried out by using the heated solar cell. It was placed in contact with part of the solar cell surface, a material of known emissivity (black tape). Therefore, the emissivity of this material was set in the IR camera and its temperature measured. Finally, by centering the camera's measurement spot on the cell surface immediately next to the tape, the emissivity was manually adjusted in the camera until the temperature measured on the tape was obtained. The solar cell emissivity was found to be about 0.74.

In order to validate the interpretation of the images obtained by using the proposed method, electroluminescent images of the same solar cells were used. The purpose of choosing electroluminescence tests at this point is to provide, as a highly reliable and accurate technique, a reference image that can be used to be compared with the results obtained from the application of LIT.

4.   Results and discussion

4.1.   Results of the proposed method

In Figure 3(a), the photography of a non-defective solar cell is presented, and its electroluminescent image is shown in Figure 3(b). In the electroluminescent image, it is illuminated where there is electric current flowing through the PN junctions present in the solar cell. In this case, a solar cell that does not contain significant failures was tested.

Figure 3.  (a) Photograph of the non-defective SunPower™ C60 solar cell and (b) its electroluminescent image.

DownLoad: Full-Size Img PowerPoint

In Figure 4(a), a photograph of the tested defective solar cell can be seen. It is possible to detect, by visual inspection, some regions of wear on the semiconductor surface and two diagonal cracks (one of them is the largest and more centralized and the other one is smaller and near the bottom right corner), but not all of the most significant defects. In Figure 4(b), the solar cell electroluminescent image is shown. The dark regions in Figure 4(b) marked with indicative arrows (within the borders of the cell) represent defects that become clearer the more they conduct electric current.

Figure 4.  (a) Photograph of the defective SunPower™ C60 solar cell and (b) its electroluminescent image.

DownLoad: Full-Size Img PowerPoint

The darkened small regions in the upper and lower portions of the device belong to the zone that was affected by the heat of the welding process of the terminals. Other darkened regions of even smaller proportions distributed throughout the extension of the solar cell may also be related to inadequate device packaging. Since the solar cell used in this research does not have encapsulation, it becomes susceptible to the influence of environmental conditions. In addition, it is noticed that there are also several diagonal cracks, in particular a larger main crack whose ends coincide with the upper-right and lower-left corners. The most compromised regions of the cell, in terms of proportion and inactivity, are the darkened portions identified by 1, 2 and 3 in the image of Figure 4(b). It is important to note that the secondary diagonal cracks do not cause current interruptions, although they may reflect a reduction in the electricity generation and, possibly, reduction of the electrons' recombination rates.

It is noticeable that, although the solar cell shown in Figure 3(a) and (b) is classified as non-defective, it cannot be considered as completely exempt from failures. It means that it is not possible to eliminate, as it was seen in the electroluminescent image, the non-uniformity originating from the device manufacturing process and the welding points of the metallic terminals. Despite that, the other failures in the solar cell that is classified as defective are those that have the greatest impact on the solar cell performance, and they are not observable in the non-defective one.

Table 1 shows the contributions of the first seven principal components after applying PCA to the processed thermal image sequence, and it is clear that the first two components contain the greatest contributions as compared to the others. As mentioned in Section 2.2, each pixel in the thermal sequence is considered an input variable for the PCA.

Table 1.  Percentage contributions of principal components.

Component	Modulation frequency (${\mathit{f}}_{\mathit{l}\mathit{o}\mathit{c}\mathit{k}-}$)
	6 mHz	11 mHz	50 mHz	100 mHz
	Contribution (%)
1 PC	98.4846	97.9574	89.9684	72.2808
2 PC	1.1968	1.6144	5.0112	4.7008
3 PC	0.0276	0.1198	0.2671	1.3798
4 PC	0.0151	0.0116	0.0583	0.3342
5 PC	0.0071	0.0047	0.0526	0.3305
6 PC	0.0044	0.0038	0.0520	0.2805
7 PC	0.0037	0.0030	0.0454	0.2665

---

 | Show Table

DownLoad: CSV

Figure 5 shows the images of the first, second and third principal components, i.e., (a) to (c), respectively, for the test carried out with the non-defective solar cell at a frequency of 50 mHz. The patterns observed in these images (concentric circular pattern and vertical stripes) are related only to imperfections of its manufacturing process, as previously mentioned.

Figure 5.  Images of the (a) first, (b) second and (c) third principal components for a lock-in frequency of 50 mHz (${f}_{lock-}$) in the test using the non-defective solar cell.

DownLoad: Full-Size Img PowerPoint

Figure 6 shows images of the first principal component for the defective solar cell excited at different modulation frequencies (lock-in frequencies): 6, 11, 50 and 100 mHz, i.e., (a) to (d), respectively. The first component contains the greatest amount of information regarding the original thermal images. In terms of characterizing the real dimensions of the solar cell's most important defects (portions 1, 2 and 3), the images for the frequencies of 50 mHz and 100 mHz (see Figure 6) are the most expressive ones. However, it can be observed that there is, in the central part of the solar cell, an overlapping of less intense heat sources by the more intense ones at their surroundings, reducing the certainty with respect to the real extent of the defects. Regarding the solar cell's most critical diagonal crack, this is highlighted in all images. It should also be noted that the other diagonal cracks, as they do not result in current interruption, are not characterized in the images of the main components because they allow a more uniform surface temperature distribution.

Figure 6.  Images of the first principal component from the tests carried out with (a) 6 mHz, (b) 11 mHz, (c) 50 mHz and (d) 100 mHz using the defective solar cell.

DownLoad: Full-Size Img PowerPoint

Figure 7 shows images of the second principal component of the solar cell when it is excited by the modulated signal with frequencies of 6, 11, 50 and 100 mHz, i.e., (a) to (d), respectively. In this case, it is possible to realize from the images a tendency toward better detailing and characterization of the main defect compared to the images of the first component, but they are all still not substantially conclusive.

Figure 7.  Images of the second principal component from the tests carried out with (a) 6 mHz, (b) 11 mHz, (c) 50 mHz and (d) 100 mHz using the defective solar cell.

DownLoad: Full-Size Img PowerPoint

For the third principal component, the results showed a pattern of prominent vertical stripes that had not been noticeable in the images of the previous components. Two possible causes are attributed to this new standard: the heating effect of the metallization completely located at the back of the solar cell, or even another consequence of the manufacturing process. Regarding the other main components, the results did not show any pattern, and, for this reason, the images related to these components were omitted.

Figure 8.  Images of the third principal component from the tests carried out with (a) 6 mHz, (b) 11 mHz, (c) 50 mHz and (d) 100 mHz using the defective solar cell.

DownLoad: Full-Size Img PowerPoint

Another image processing technique applied to the thermal images sequence was 4 SPSM, which resulted in two images being obtained for each test performed: amplitude and phase images. From the phase image, the phase contrast was measured based on the phase angle difference between the defective and non-defective regions so that all points that were "in phase" with each other, presenting the same brightness. The amplitude image, on the other hand, demonstrates the maximum absolute temperature range at each pixel.

Regarding the phase images obtained from the test with the non-defective solar cell at a frequency of 50 mHz, it is possible to observe, in Figure 9, that imperfections related to the manufacturing process do not critically affect the phase distribution on its surface, yielding a phase difference between pixels significantly smaller than that observed in the phase images of the defective solar cell (see Figure 10). In this case, it can be inferred that the heating of the surface due to the excitation from the electric current occurs more uniformly, as expected for its condition.

Figure 9.  Phase image obtained from the 4 SPSM for the test carried out with 50 mHz using the non-defective solar cell.

DownLoad: Full-Size Img PowerPoint

Figure 10.  Phase images obtained from the 4 SPSM for the tests carried out with (a) 6 mHz, (b) 11 mHz, (c) 50 mHz and (d) 100 mHz using the defective solar cell.

DownLoad: Full-Size Img PowerPoint

The defect characterization in the phase images of the defective solar cell proved to be better and have a greater degree of reliability in terms of the actual dimensions and location of the main defects, as shown in Figure 10. The phase contrast, especially of the images related to the frequencies of 50 mHz and 100 mHz, provides a clearer picture of the extension of regions 1, 2 and 3, and it allows one to better infer the delimitation of the defective portions. There were no sudden visual changes at the points where there is the presence of weaker heat sources at the surroundings of the defective regions. The phase image of 6 mHz was the one that contributed less to the characterization of the main defect after the application of the 4 SPSM.

In the case of the amplitude image, which consists of the maximum amplitude variations observable in the temporal thermal response of each pixel in steady state, the results were very close to those obtained in the images of the first principal component (PCA method) showing the overlapping of the less intense heat sources by those that are more intense in the neighborhood. For this reason, the amplitude images were suppressed in this work.

Very similar results were obtained by applying an FFT to the same sequence of thermal images, both for non-defective and defective solar cells, as it can be seen in Figure 11 (4 SPSM) and Figures 12 and 13 (FFT). It is possible to notice the similarity of the phase images derived from the Fourier phase spectrum, which considers the fundamental frequency component, and via the 4 SPSM. This similarity was expected because the two methods resulting in a phase distribution of the solar cell surface and the phase differences between the pixels, for both cases, are very close since the techniques consider the same radiometric video. Therefore, the thermal imaging sequence was evaluated at the same instants. Concerning the defective solar cell, in the phase images, it is also possible to observe that, at regions with more intense heat sources (regions where the defect is concentrated and its surroundings), the phase tends to assume the lowest values compared to other areas.

Figure 11.  Phase images obtained from the FFT for the tests carried out with (a) the fundamental frequency and (b) the second and (c) third harmonics for a lock-in frequency of 50 mHz using the non-defective solar cell.

DownLoad: Full-Size Img PowerPoint

Figure 12.  Phase images obtained from the FFT for the tests carried out with the fundamental frequency and a lock-in frequency of (a) 6 mHz, (b) 11 mHz, (c) 50 mHz or (d) 100 mHz using the defective solar cell.

DownLoad: Full-Size Img PowerPoint

Figure 13.  Phase images obtained from the FFT for the tests carried out with the second harmonic for a lock-in frequency of (a) 6 mHz, (b) 11 mHz, (c) 50 mHz or (d) 100 mHz using the defective solar cell.

DownLoad: Full-Size Img PowerPoint

The two sets of phase images obtained for the defective solar cell demonstrate that the image for the frequency of 50 mHz yielded more details about the actual extension of the main defects, indicating an optimized frequency value, unlike the others that were used. In terms of the spatial resolution of the images, it was also found that there is a relationship between the length of the heat diffusion.

For the second harmonic, the resulting phase images did not exhibit any improvement, as with the other higher-order harmonics, regarding the visualization of the main defects (see Figure 13). However, the sharpness of the pattern of vertical stripes, which was also observed in the images of the third principal component of the PCA method, was noticed as well.

4.2.   Comparison between the proposed method using a true sinusoidal electric current and the technique using PWM

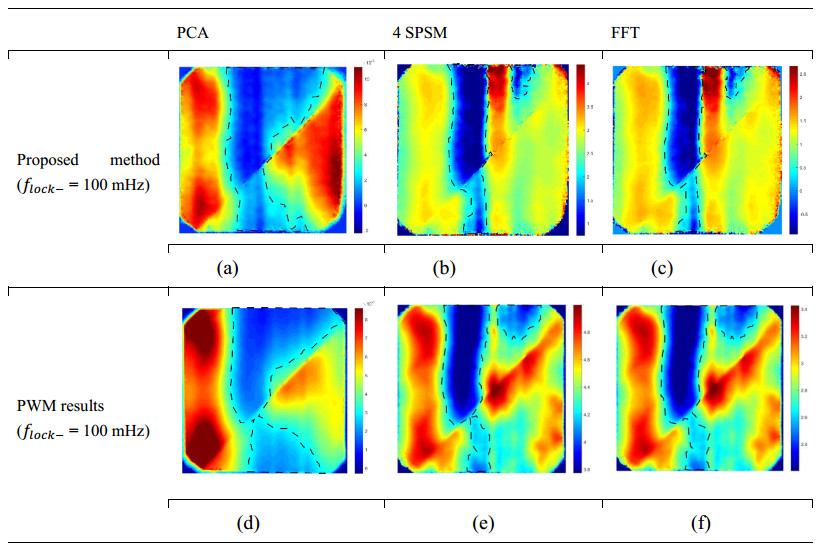
Table 2(b)–(c) shows the phase images obtained by applying the algorithms of PCA, the 4 SPSM and the FFT to the thermal imaging sequence of the defective solar cell submitted for the PWM test described in Section 3. By analyzing the images, it is possible to identify the defective region (main defects), although there are some subtle differences worth noting when comparing them to Table 2(e)–(f). Comparing those four figures, the 4 SPSM phase images and FFT phase images, for the same modulation frequency (100 mHz), reveal that it is possible to verify a better resolution with smoother, clearer and more continuous operation in terms of the delimitation of the defects revealed using the proposed method (Table 2(b)–(c)). This verification does not discard the potential of the PWM technique, but it reinforces the effectiveness and advantages of the proposed method of this research through a qualitative image analysis.

Table 2.  Comparison between phase images obtained via the proposed method and PWM test with an excitation frequency of 100 mHz; the used techniques were (a) and (d) PCA —the first principal component; (b) and (e) 4 SPSM; and (c) and (f) FFT.

---

 | Show Table

DownLoad: CSV

In general, the results indicate that, although the electroluminescence images visually explain almost all of the existing solar cell nonconformities, the images obtained from the LIT tests highlight only those defects that cause current interruption; therefore, they are found to be the most critical defects.

5.   Conclusions

In the present paper, a methodology based on non-destructive testing performed by applying lock-in thermography to solar cells is proposed. Some traditional image processing techniques (principal thermographic component analysis, 4 SPSM and FFT) were used as tools to evaluate the thermal images recorded in radiometric videos. From the images of the principal components and phase images of the solar cell with multiple failures used in this study, it was possible to distinguish defective regions from non-defective ones with a satisfactory characterization of the main defects. Defective regions were previously characterized by electroluminescence tests, which assisted the validation of the other results.

It is possible to conclude that the new methodology proposed in this research work presents very promising and effective results, even if compared with the results from other consolidated conventional methodologies in the literature, such as the one that uses PWM. Then, it can be inferred that the use of a true sinusoidal electric current as an excitation source for solar cells has given some promising evidence that it might be able to be used to improve the evaluation of the state of the solar cell's operating capacity. Both techniques (electroluminescence and LIT) should be used in parallel to obtain more detailed results.

Future work can be carried out as a continuation of this approach by considering the use of other image processing techniques that may prove to be potentially better for the visualization of the defects and comparable to the images obtained so far. Some research is already in progress to establish a quantifiable analysis of the images and eliminate the subjectivity inherent to it. In addition, the replication of the proposed method using solar cells made from other materials (polycrystalline or amorphous silicon, for instance), with or without encapsulation and presenting defects of different natures, may also indicate a possible application of LIT in the quality control process of solar cell fabrication. Furthermore, it is intended that, in the future, tests will be carried out without the use of a dark room, which would expand the possibilities of its application, mainly in installed photovoltaic systems.

Acknowledgments

We would like to thank the institutions Coordenação de Aperfeiçoamento de Pessoal de Nível Superior—Brasil (CAPES), Fundação de Apoio à Pesquisa e à Inovação Tecnológica do Estado de Sergipe (FAPITEC), Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) and the Universidade Federal de Sergipe (UFS) for their support while we were conducting the research.

Author contributions

Conception and design of study: Thiago Vieira, Tarso Ferreira and Douglas Riffel. Execution of the tests/experiments: Thiago Vieira and Renan Silva. Drafting the manuscript: Thiago Vieira, Ézio Santana, Luiz Souza and Renan Silva. Analysis and/or interpretation of data: Thiago Vieira, Luiz Souza, Ézio Santana, Tarso Ferreira and Douglas Riffel.

Conflict of interest

The authors declare no conflict of interest.