Estimation of state of charge for lithium-ion batteries - A Review

1.   Introduction

The SOC of a battery is defined as the ratio of its current capacity Q(t) to the nominal capacity Q_n which demonstrates the maximum amount of charge that can be stored in the battery ^[1].

Precise SOC estimation reflects some significant information such as battery performance, remaining life of battery ^[2] that ultimately lead to an effective management and utilization of the battery power and energy ^[3,4]. Furthermore SOC estimation can be used to regulate over-discharging and over-charging of the battery, which lead to a reduction in battery life, explosion or flame, accelerating aging and permanent damage to the cell structure of batteries ^[5]. Accurate SOC indication is thus important for the user convenience and to ensure the battery's efficiency, safety, and longevity. An accurate estimation of SOC is a fundamental consideration to eliminate failures due to thermal runaways and to regulate cell balancing ^[6].

Most of the SOC estimation techniques require very accurate measurements of either the battery chemical content (type of electrolyte), its operating conditions or cell variables (voltage, current) and thus are only suitable for laboratory rather than real world applications. Also a given method of SOC estimation will be more suitable or applicable for a particular application than another ^[7]. Furthermore the SOC of a battery is not a state that can be measured directly but estimated from available parameters such as voltage, applied current or surface temperature.

As the most improved and flexible battery technology, lithium ion batteries exhibits high power capabilities, high energy density, low self-discharge, long life cycle and high number of charge discharge cycles, low operational and maintenance requirements, satisfactory operating temperature ranges, high reliability, technological diversity as compared to other standard battery types such as lead-acid and nickel cadmium ^[8,9,10,11]. However, over charging or over discharging of Lithium-Ion batteries can cause permanent damage to the battery cells which may cause fire or even exploding batteries ^[12]. So an accurate estimation of SOC can conserve the lifetime of batteries by preventing frequent charge and discharge.

Estimating and controlling the SOC is vitally important in various power system applications such as Battery Energy Storage Systems (BESSs) and Electric Vehicles (EVs). When it comes to the high penetration of renewable energy in the distribution network, BESS is a potential solution to address the issues caused by the intermittent nature of renewable energy ^[13]. But the operation of the BESS is affected by dynamic disturbances such as unbalance load dynamics, the application of Electric Vehicle charging and single phase distributed generations (Solar PV). Therefore to develop a BESS incorporating such dynamic aspects and involving aspects such as modelling, simulation, development of control schemes and standard test procedures require an adequate battery model to imitate the true battery characteristics.

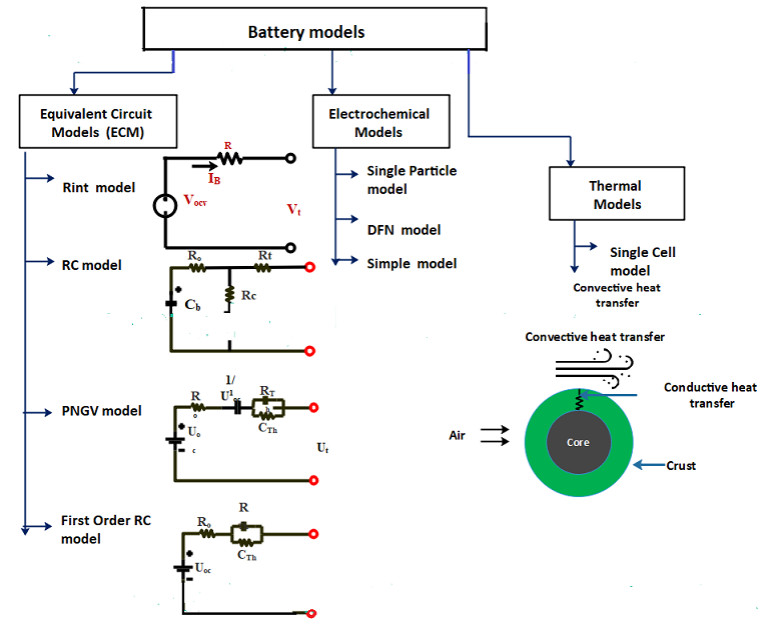
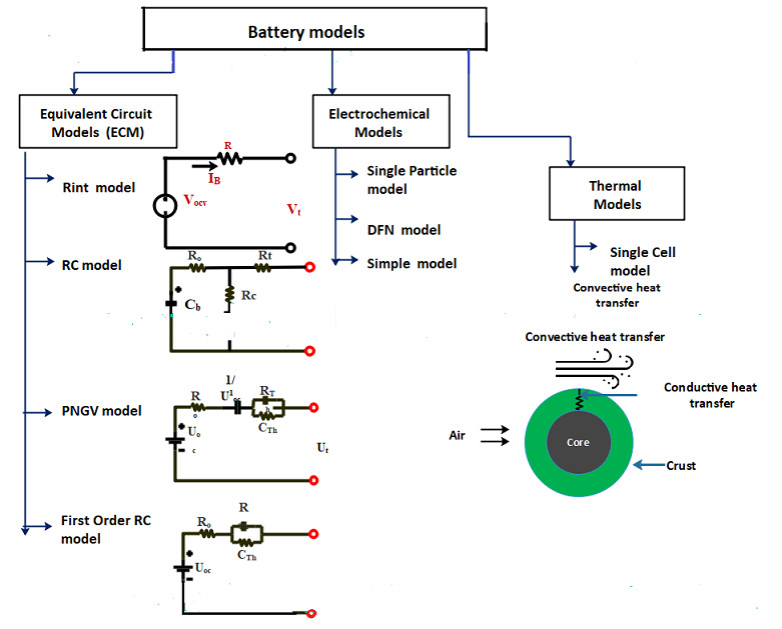
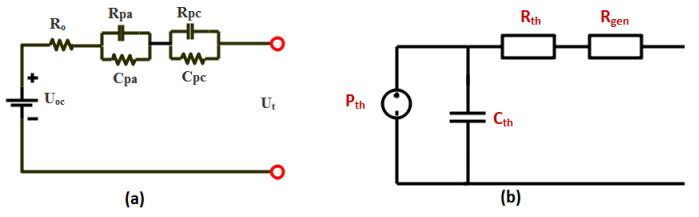
The most frequently employed battery models are Equivalent Circuit Battery models and Electrochemical battery models ^[14,15,16]. Equivalent Circuit Models (ECMs) are flexible and easy to compute compared to Electrochemical models which are complex as they consider chemical process and degradation processes in the battery employing mathematical equations (time-variant spatial partial differential equations) ^{[15,17,18,19,20]}. One of the most frequently employed Electrochemical model is Single Particle model (SPM) for which a backstepping PDE state estimator is designed. Since the SPM model captures less cell dynamics and this method requires high computational cost and time, in this paper only the ECM models are considered. Equivalent Circuit Models consists of voltage sources, resistors and capacitors to describe the electrochemical processes and dynamics of a battery ^[21]. Generally selected ECMs which include the Rint model, the Thevenin model (first order RC ECM), the RC model, the PNGV model and the improved Thevenin model (second order RC ECM)(see Figure. 1). Among these ECMs, the second order RC ECM consists polarization capacitors to represent the response of transient behavior (see Figure 1a).

In order to accurately estimate the SOC, battery model must be able to precisely represent the both statistic and dynamic responses. When the accuracy of the battery model increases, the computational cost and time will also increase. Therefore in regards to the compromise between the model accuracy and computational efficiency, second order RC ECM presents considerably better outcomes. Other model which are mentioned here have high computational efficiency but less accuracy. In second order Rc ECM, a voltage source represents the battery Open Circuit Voltage (OCV). Therefore to obtain an accurate battery model, it is necessary to adopt a definite SOC estimation method. There should be a compromise between the accuracy and the complexity of the SOC estimation method.

The SOC estimation algorithm is generally programmed in the Battery Management System (BMS) that regulates the energy flow in a battery pack with respect to voltages of individual cells, temperature, state of charge and state of health. The main function of BMS is to maintain a safe operating environment for the battery system, and to protect it from damages ^[19,23,24]. Even though the estimation of battery SOC is key function of BMS, its accuracy and online estimation is challengeable due to non-linear complex electrochemical process in the battery ^[25].

In this paper both traditional methods and improved methods of estimating of SOC are presented. Each method is described with its strengths and drawbacks in relation to the accuracy of the Equivalent Circuit Battery Models in imitating battery dynamic behavior.

2.   Estimation methods of SOC

Various experimental methods, models and algorithms, of estimating the SOC of a battery have been proposed and developed each having its own advantages and disadvantages ^[12]. Table 1 summarizes the various estimation methods in view point of the methodology ^[3,26].

Apart from these methods there are some other methods such as particle filter algorithms, non-linear observer method and reference governor method. The comparison between the methods is given by the Table 2.

2.1.   Direct measurement

In direct measurement methods, to estimate SOC value physical measurements such as the voltage and impedance of the battery [3] are used. Frequently used direct measurement methods are Open Circuit Voltage (OCV) method, terminal voltage method, impedance method and impedance spectroscopy method.

2.1.1.   Open circuit oltage method

Open circuit voltage(OCV) is the battery thermodynamic potential under no load condition that has a non linear relationship with SOC for a lithium ion battery ^[3,27]. The OCV is usually obtained through offline OCV test at definite ambient temperatures and aging stages ^[28]. Even though the open-circuit voltage (OCV) method is very accurate, it requires a rest time to estimate the SOC and hence difficulty to be utilized in real world applications.

OCV is present in Electrical Equivalent Circuit models (ECM) as an ideal but variable voltage source to which over-potential is added by the remaining resistor and capacitor elements of the ECM ^[27].

Furthermore the relationship of the OCV–SOC differs among batteries and therefore an unacceptable error can be occurred due to the usage of this varying OCV–SOC data for the SOC estimation algorithms ^[29]. The conventional relationship of the OCV–SOC is developed by measuring the OCV at each SOC state. The relationship differs with the variation in capacity among batteries and shows different results even if the batteries are composed with the same structures and materials. But estimating the OCV of each battery at each SOC for the validity of estimation process is a considerably time-consuming process ^[29].

SOC estimation can be significantly influenced by OCV hysteresis ^[32]. Hysteresis can be defined as the dissimilarity between the OCV of charging process and the OCV of discharging process ^[32]. Therefore it can be stated that the information of OCV alone is not sufficient to determine the SOC and the history of charge-discharge should also be taken into account ^[27].

Furthermore the hysteresis characteristics differ with type of the electrode in li-ion batteries (electrodes with lithium iron phosphate as the active material exhibit hysteresis phenomenon). In order to analyze the effect of hysteresis on battery SOC estimation or ECM parameters, hysteresis effect should be measured against battery SOC value or capacity. The OCV-SOC function is implemented either as an analytical expression or look-up table where there are a number of advantages in analytical method including data processing efficiency ^[33].

2.1.2.   Terminal Voltage method

It can be stated that only a few researches have been carried out to determine SOC using terminal voltage method of Lithium ion batteries. The method is based on the fact that when the battery is discharged because of the internal resistance, terminal voltage falls and Electromotive Force (EMF) is equivalent to the terminal voltage ^[3].

2.1.3.   Impedance method

In order to calculate the SOC using the impedance method, both voltage and current measurement are recorded at different excitation frequencies since the battery impedance depends on the frequency. The principle consists of injecting current in a certain range of frequencies to find impedance. The change of impedance is negligible for higher values of the SOC but when the SOC reaches a certain low SOC level, the impedance increases swiftly ^[3].

Among many methods, Electrochemical Impedance Spectroscopy (EIS) which brings significant information about the complex electrochemical processes occuring inside the battery is considered. Even though there are many methods of estimating SOC based on EIS, the complexity of using EIS directly is considerable high ^[35]. As one approach, an impedance Model is constructed on account of EIS data which is presented as a Nyquist plot where the measured impedance is plotted as the real part against the imaginary part ^[23]. The Nyquist plot impedance spectra is parted into three section: low frequency section, mid frequency section and high frequency section. The parameter identification is simplified due to this partition process and the SOC can be estimated using ECM model-based methods which are discussed in this paper ^[23].

2.2.   Book-keeping method

The coulomb counting method and modified coulomb counting method are categorized as two kinds of book-keeping methods. The battery charging/discharging current is taken as the input to this method. It allows to add several battery internal effect; such as capacity-loss and self-discharge, for the SOC estimation, and also battery data such as nominal capacity. ^[3].

2.2.1.   Coulomb counting method

In the coulomb counting method (also known as Ampere-hour method), the SOC of a battery is calculated by cumulating the charge flowed in or out of the battery ^[36].The accuracy of the coulomb counting method is affected by the accuracy of initial SOC estimation and measurement of the battery current (accuracy of current sensors) ^[37]. The coulomb counting method is convenient for SOC estimation of lithium-ion batteries with high charging and discharging efficiencies ^[36] and required long time monitoring. Even though the method is not suitable for real-time SOC estimation, it can be used to verify the accuracy of the results obtained by other estimation methods.

Where SOC₀ is the initial SOC value and i(t) is the current of the battery with a negative value at charge, C_rated is the rated capacity. The initial SOC value (SOC₀) can be obtained by OCV method. Even though the method is simple and inexpensive, the drawbacks of the method can be listed as follows ^[38].

Since the coulomb counter is an open loop estimator, errors in the current sensor is added by the estimator. The cumulative error becomes larger, when the SOC estimator operates through a longer time period. Also, an incorrect result can be generated faster, when the current sensor has massive errors.

When the battery ages in real time, the battery capacity varies, but the coulomb counter cannot detect or take measures for the issue. As a result, SOC estimation will not be accurate, if the real pattern of the battery estimation deviates from the expected pattern.

The initial SOC should be measured by the terminal voltage of the battery pack. So any error contained in the initial estimation method will be carried throughout the process and this method cannot detect or repair the initial error.

The Coulomb Counting method can be improved by considering the Coulombic efficiency ($\eta_{Ah}$) at different temperature and charge rates. It is defined as the ratio between the number of charges extracted during the discharging process and the number of charges enter during the charging process or the ratio of the discharging capacity to the charging capacity ^[39,40] (given by the below equation).

Since $\eta_{Ah}$ depends on the current rate (discharge or charge) as mentioned above, an Equivalent Coulombic Efficiency (ECE) ($\eta_{eq}$) is developed including the discharge and charge Coulombic Efficiency. In general According to that the modified Coulomb Counting equation can be depicted as below with $\eta_{eq}$ and C_a representing the ECE and the present available capacity which differs from the rated capacity C_rated due to temperature and age effect ^[41].

Among the different battery chemistries, li-ion batteries offer the highest Coulombic efficiency in the normal SOC region (exceeds 99%) ^[39,40]. But the estimation of Coulomb efficiency is difficult task as it requires highly accurate equipment.

2.3.   Indirect measurement method

The adaptive systems are consistent, because of their ability to deal with the nonlinearities of battery systems and show considerably excellent accuracy. Yet, in order to obtain good results from the adaptive systems, the specific information of battery characteristics or an accurate Equivalent Circuit Model (ECM) are required ^[42].

2.3.1.   Neural network method

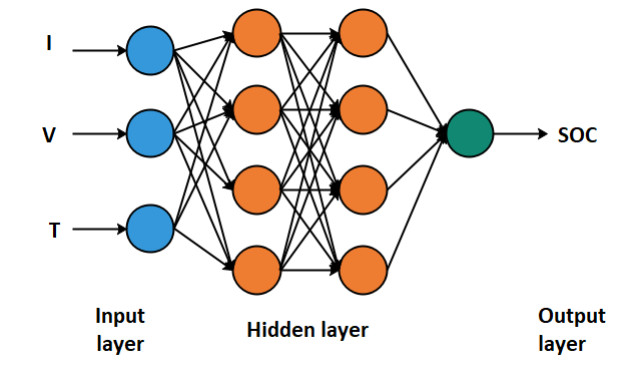
Neural Network is a mathematical model (subfield of artificial intelligence) that consists of interconnected artificial neurons stimulated by biological neural networks and to predict the output of a nonlinear system past data of that system is used ^[26]. Neural Network methods do not rely on any, physical, electrical, chemical or thermal model and take less time period to generate results compared to Extended Kalman Filter (EKF) ^[26,43]. Neural Network consists of inputs and outputs and is made of a number of processing units called neurons interconnected with each other. The accuracy of Neural Network method depends on how far the network is trained and the training process is the most important phase.

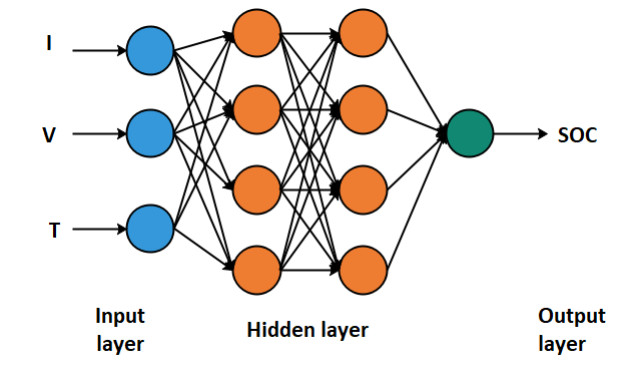
The most two common network architectures to estimate the SOC are the nonlinear input-output (NIO) feed-forward network and nonlinear autoregressive with exogenous input (NARX) feed-back network ^[26]. Figure 3 shows the structure of a feed-forward neural network ^[44]. In order to represent the input variables and output variables, the neural network consists of an input layer with nodes and output layer respectively. Additionally there are one or more hidden layers to simulate the nonlinearity between the input variables and output variable. The nodes between two adjacent layers are interconnected ^[45]. Only in the output layer and the hidden layers are the processing layers with activation functions at each nodes. There are several types of activation functions such as logistic tanh-hyperbolic tangent and ReLu-rectified linear units. In most scenarios hyperbolic tangent sigmoid function and the linear transfer function are used as functions of activation the hidden layer and the output layer respectively. As there are no theoretical criteria when it comes to selecting the number of hidden layers and the neurons, it will be done using the expertise knowledge. In regarding to the SOC estimation, the neural network method determines the SOC direct from the voltage and current without OCV-SOC look-up tables following steps can be considered as the constructive approach to the neural network SOC estimation.

1.Initialization (determination of the dimensions of the input layer and the number of neurons in the hidden layer)

2.Train the neural network with input variables (current, voltage, temperature) and output variable (SOC)

3.Error calculation between the estimated output and the actual inputs

4.If the error is within the expected level searching is ended; otherwise repeat the step 2

There are many factors that influence the SOC of the power battery ^[44,47,48]. Since the current, terminal voltage and temperature have the greatest influence on the SOC of the battery, these three parameters are chosen as the input of the network, the battery SOC value is chosen as the output, and the number of nodes in the hidden layer is set according to the experience ^[44].

2.3.2.   Kalman filter

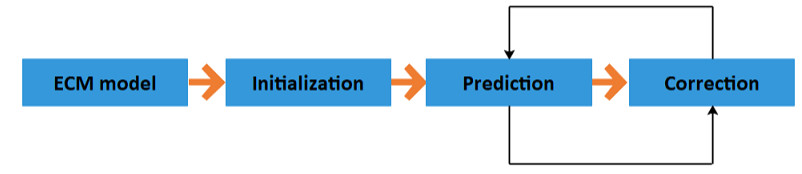
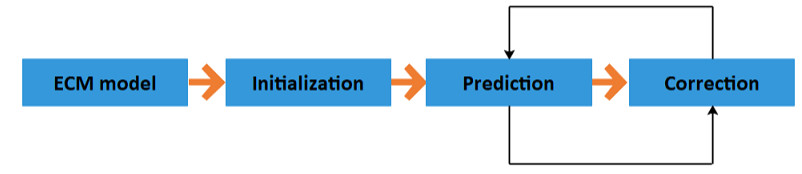
Kalman filter (KF) is a recognized technique that is used as an optimal estimator to estimate the inner state of dynamic linear system. Basically, KF is a recursive set of equations that consists of two steps: prediction step which predicts the system output, system state and error ^[49] and correction step which corrects the current state estimate value based on system output value ^[26,49]. The block diagram of Kalman filtering process is shown in figure 4.

In order to design estimate SOC using Kalman filter, a battery state-space model is constructed using the equivalent circuit model. Considering the system noise and observation noise, the discrete state-space model is constructed ^[46]. Since the battery OCV (which is shown by a voltage source in a second order RC ECM) and SOC has a non-linear relationship and KF algorithm is only suitable for linear systems, a linearization method should be followed with an acceptable accuracy as a supplementary part. As a result of the linearization process, the discrete space-state model equation (output equation) is reduced to a less complex condition. The generalized error between the measurable value and system state variable (ex: SOC) is calculated the KF using the output equation. Then the Kalman gain is adapted to update the system variables (SOC)

Because of highly nonlinear characteristics of battery system and unsuitable battery model inaccurate outputs can be generated in KF method.

Basically, where the input is applied current, the terminal voltage is used as output, and the battery SOC is placed as the hidden state ^[50]. Then the hidden state is estimated by KF, EKF, Unscented Kalman Filter (UKF) or Particle Filter (PF).

But, in the EKF method, the Jacobian matrix must be constructed and if the system is highly nonlinear with non-Gaussian noise, the results may be generated with large errors ^[51]. But as an advantage, if there is an incorrect initial SOC value, the KF system can conquer it and could detect and represent cell aging.

2.3.3.   Extended kalman filter

Extended Kalman Filter (EKF) is the improved version KF and is used to estimate the inner state of a nonlinear dynamic system using a state-space mode ^[26]. Simply it predicts the future state of system based on the previous data ^[52]. when it comes to the estimation of SOC, it employs advanced battery cell models and requires a relatively high computation capability.

The EKF consists of two equations. One equation consists of matrices constructed using the parameters of ECM along with the system state matrices (SOC) measurable input matrices and non-measurable process noise ^[53,54]. The parameters will be identified performing standard test procedures. The second equation is the measurement equation which shows the output voltage in terms of system state vectors, measurable input matrices and measurement noise. Employing appropriate software tool (MATLAB simulink) SOC can be estimated.

In some EKF methods, an inner filter is established to adjust the SOC and the battery model is adjusted by an outer filter ^[55].

According to the SOC and the cell model, the inner filter proposes a corresponding voltage using the measured current. The SOC is adjusted by comparing the measure voltage and proposed voltage. Thus, the system feedback is voltage and its output is SOC. After monitoring the applied current and voltage over a long period of time, the outer filter gradually adjusts the parameters of the system model. In this method, the cell aging and other lifetime effects are detected and modeled in real time.

An accurate battery model must be established in order to obtain better results from the EKF method and the battery system must be treated as a nonlinear time-variant dynamic system ^[26]. Most common models are shepherd model, Unnewehr Model, Nernst Model, Linear Model, Thevenin model and RC Model ^[56].

The EKF algorithm not only can be used for online SOC estimation and track the battery state of charge parameter, but also can be employed to identify the parameter of the battery model ^[56].

2.3.4.   Unscented kalman filter

Since SOC estimation of lithium-ion battery system inherits highly non linear characteristics ^[57], it can produce large errors for EKF method, because it is a first or second order Taylor series expansion to approximate the nonlinear functions ^[56]. Apart from the above disadvantage, EKF must compute the Jacobian matrix and if the system consists of non-Gaussian noise, the produced results may not be at an acceptable level. So Unscented Kalman Filter (UKF) has been established to improve the accuracy of KF and EKF methods. Since the UKF deals with non Gaussian noises as well and Jacobian matrix is not calculated, it more suitable for SOC estimation ^[51].

In this method the battery's SOC is chosen as an element of the state vector. The two sub-models in the proposed UKF methods are the process model and measurement model, which describe the relationship between the SOC and cell states such as, current, the terminal voltage and temperature.

2.3.5.   Fuzzy logic method

Fuzzy logic method can be used to model, non-linear and time-varying systems without the need for mathematical models or ECMs of a battery ^[58]. For the estimation of SOC using Fuzzy logic method, environmental temperature, applied current and battery terminal voltage are considered as the input variable balancing the complexity and accuracy well. The higher the number of input variables (dimensions of fuzzy controller), more accurate are the results. But when the dimension is higher, the rules of fuzzy control will be much complex to implement ^[59,60]. As the first step, Fuzzification is the mapping from the above input with fuzzy variables using membership functions. Membership functions can be triangular-shaped or trapezoidal-shaped functions considering the memory storage and efficiency. In the second step, the relationship between the input and output is described using rule based representation of expert knowledge ^[61]. The third step is the reasoning mechanism that performs inference procedure. Defuzzification is the third step that converts the modified control outputs into real valued outputs. The membership functions and rule sets are defined by generating as a result of neural network algorithm or an expert. In order that the Fuzzy logic model to accurately predict the SOC of the battery without considering the initial capacity, a "training" data set are constructed ^[62].

In most fuzzy logic methods, the SOC value of the battery is predicted without the rated capacity or previous knowledge of the discharge history of the cell and only by measuring the imaginary component of the impedance at a few specific frequencies ^[63].

In most scenarios, clustering algorithms are used to construct input membership functions and rules. The output membership parameters are optimized using least square fit.

2.3.6.   Support vector machines

Support Vector Machines (SVM) are a set of related supervised learning methods used for regression and classification that can be generally appropriate for any multi-variable function to a higher accuracy level ^[56] and have been effectively applied especially in highly nonlinear systems.

In order to estimate SOC using SVM regression model temperature, current measurement and voltage are considered nonlinear input variables ^[64]. Using a kernel function in the SOC estimation process, a training data set of the above input variable which covers the expected range of operation should be selected ^[38,65]. Then the proposed SVM model is validated using the new data not used for training ^[66].

2.3.7.   Particle filter Algorithm

Particle filter (PF) is an effective nonlinear filter technique that can obtain the particles and corresponding weight values through random sampling ^[68]. The principle is to represent the probability densities with a set of weighted particles ^[69]. The accuracy of the PF algorithm depends on the experimental data and the structure of the PF. In order to estimate SOC of the battery using PF algorithm method, it is necessary to establish a discrete state-state model which consists of state equation and observation equation ^[70]. The state equation is derived by the SOC definition which is expressed in the coulomb-counting method. The observation equation is obtained considering the terminal voltage of the second order RC equivalent circuit as the observed valued. The parameters of the second order RC ECM is acquired through standard test procedures ^[71].

The collected data from charging process or discharging process data are stored as experimental data. Then to establish the state equation of the state-space model, the SOC estimation equation is discretized and considering the characteristics of collected data.

The particle filter algorithm has high accuracy for SOC estimation and the estimation error is comparatively small ^[72]. Using PF algorithm as an individual SOC estimation method, combination of PF and KF, PF and EKF, PF and EKF will improve the robustness of the KF algorithm while solving probability distribution function selection of PF algorithm ^[73].

3.   Analyze of the SOC estimation methods

3.1.   Qualitative analysis

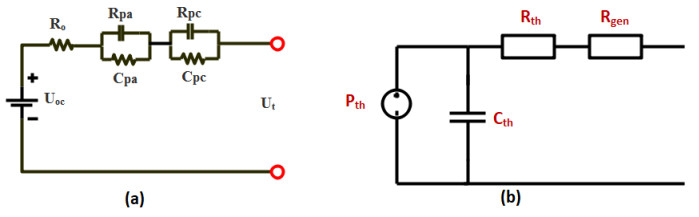
When it comes to the BESS in microgrids with Distributed Generations (DGs), dynamic behavior (Ex: unbalance loads, unequal line impedances, phase asymmetry in branch configurations at the common coupling point of the microgrid at grid connection) of the power system has a negative impact on the battery performance ^[96]. So to optimize the Battery management System, the requirement of an accurate battery model for the BESS is inevitable. Due to the flexible nature and ability to represent the above mentioned dynamic situations, Equivalent Circuit Models (ECM) have been adapted by many researchers ^[67,96,97]. Since the battery model is the foundation for the BESS operation, the representation of ECM with appropriate model parameters will enhance the modelling of BESS. As many ECMs are established, considering the ability to represent dynamic response and less complexity of the model, the second order RC Equivalent Circuit Model can be considered as the most suitable model. Figure 1a showed the schematic diagram of second order RC ECM which consists of controllable voltage source denoting the Open Circuit Voltage (OCV) which normally varies nonlinear with SOC, RC parallel networks representing the polarization response and R₀ ohmic resistance denoting the electrolyte resistance ^{[17,21,50,98,99]}. The addition of the RC network improve the representation of the dynamic behavior of the battery, but it is much complex to simulate.

Since the OCV in the second order ECM varies nonlinear with SOC, when identifying the above mentioned parameters, it is necessary to consider the battery SOC value as an input to the simulation process ^[22,100]. So appropriate SOC estimation method should be included for the modelling of BESS. The objective of this paper is to identify the SOC estimation approach that can be used to update the OCV (controllable voltage source) of the ECM. Also when selecting a method, the dynamic modelling of the battery must be preserved. The objective can be achieved by either adopting model-based SOC approach which calculate SOC and update OCV in the same procedure or adopting non-model based method then considering the estimated SOC as an input to the ECM. The most frequently used ECM model-based SOC techniques are Kalman Filter methods including EKF, UKF, CKF (Cubature Kalman Filter) and PF algorithm which consist of both estimator and battery model ^[101,102]. All other methods mentioned in this paper are non ECM-based methods which usually use physical parameters, mathematical or artificial intelligence algorithms.

The most important factor to be considered is the thermal behavior of li-ion battery and how it effects the performance of the BESS. The battery internal resistance and battery capacity are influenced by temperature distribution in terms of battery lifetime degradation or battery performance ^[103]. Furthermore round-trip efficiency, operation of electrochemical reactions and charge acceptance are influenced by the temperature ^[104]. Also higher temperature will be a cause to hazardous situations of lithium ^[31]. Therefore in order to maintain the battery temperature within the appropriate range, suitable cooling and heating systems whose operation depends on the battery cell surface temperature and internal temperature are required ^[22,105]. Since the battery SOC and ECM parameters are varied according to the temperature, those variations should be taken into account. As one approach, temperature can be considered as an input to the SOC estimation method, but the ambient temperature is not sufficient enough because it is necessary to model the heat generation and heat transfer (conductive, convective and radiation) ^[31] to accurately represent thermal behavior.

The most widely used thermal model is the lumped capacitor model which is shown in the Figure 1b ^[22,105,106]. In this model P_gen represents the heat generation inside the battery. The R_th, R_con and R_th describe the internal resistance, the convection heat transfer and the thermal capacitance respectively. Since the thermal behaviour is represented using electrical elements, these three parameters also depends on the battery current, SOC and battery internal temperature.

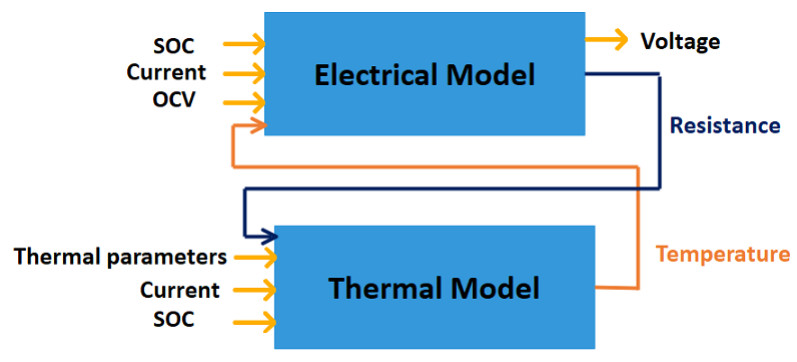
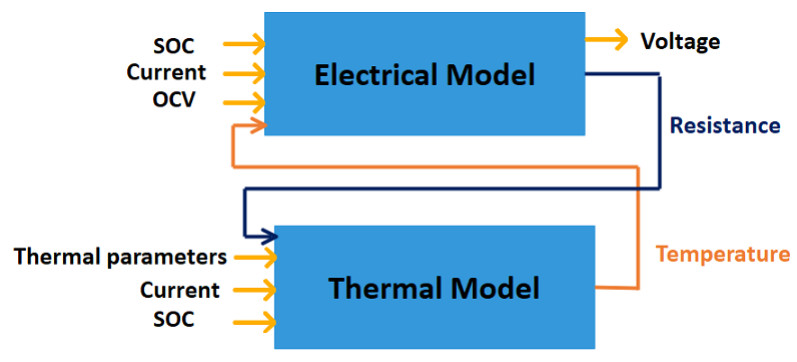
Therefore coupling the thermal model that represent the above mentioned thermal phenomena with the second order RC equivalent circuit is convenient (see Figure 6).

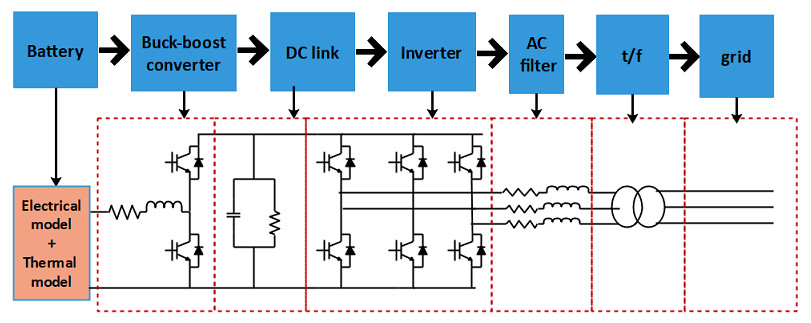
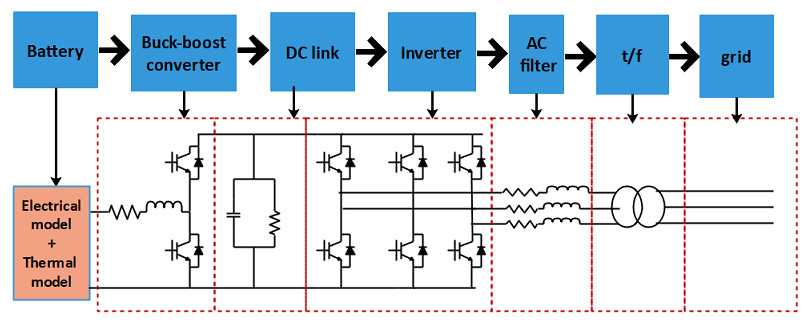
Since the complexity of the battery model increases when coupling the ECM model and thermal model, it is insightful to acquire a less complex SOC calculation method for this objective. More importantly, typical BESS consist of buck/boost converter, DC link, inverter, AC filter and the grid ^[96] which are shown by the Figure 5. The analysis of different operation conditions (grid-connected or isolated) with balanced loads or unbalanced loads may be affected by the complexity of those models. Therefore a suitable SOC method must be adopted considering the simulation time, because even adopting the rint model may increase the time of computation considerably ^[96]. Preserving those factors, the above mentioned SOC estimation methods will be accessed.

As KF is suitable for linear system, EKF, UKF and CKF can be considered as an optimum state estimator for nonlinear systems such as li-ion battery systems ^[107]. The advantages of KF based method is that it is not sensitive to the initial SOC error ^[108], but there are disadvantages such high computational cost and complexity. Since these methods involves complex matrix operations, it is difficult to implement the algorithms in ordinary micro-controllers. Also they exhibits limitations such as linearization inaccuracy and uncertainties due to measurement noise. Even though the temperature is taken as an input while considering the ECM for the estimation, KF methods do not consider the above mentioned heat generation and heat transfer. So applying KF methods with coupled electro-thermal battery model to calculate SOC and update OCV (of ECM) will require considerable time and computational cost.

The neural network method exhibits limitations such as errors due to the over-training, effects of the previous sample data set on the present data set and the presence of too many neurons. The risk of over-fitting increases due to the presence of excessive neurons while limited neurons will under-fit the data ^[45]. Neural network method requires high computation as well as a large number of data set to trained. Fuzzy logic method requires high computational cost, expertise knowledge as well as clearly defined fuzzy rules. The support vector machines method demonstrates the superiority over the neural network method including no requirement to select the number of neurons, no requirement to identify the network topology and less problems regarding overfitting ^[109]. Additionally both neural network method and Support vector method present better results only for constant current situations and for dynamic situation the error is not in an acceptable level.

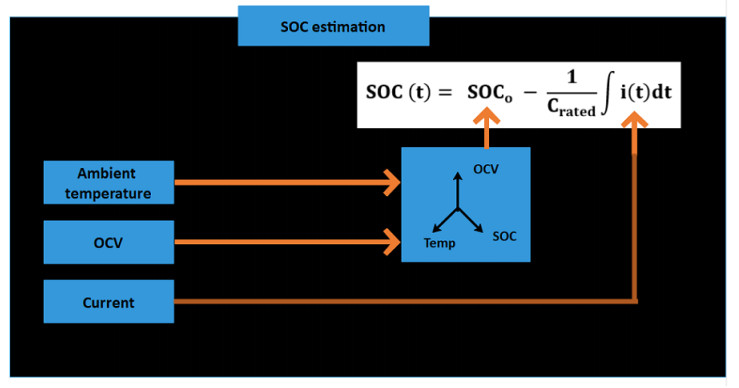
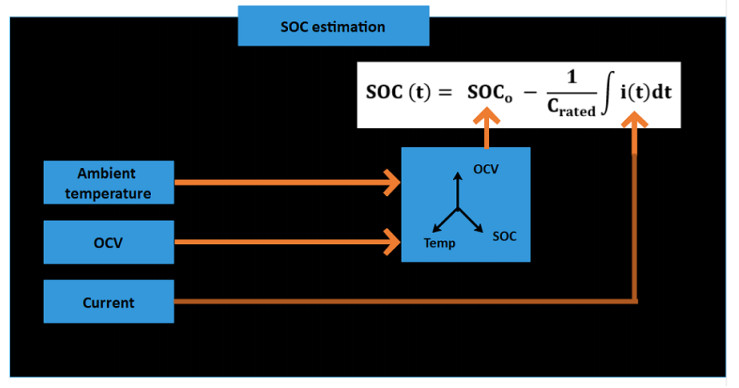
Hence non model based (direct measurement) are more suitable and among them OCV method and coulomb counting method are widely used. But adopting one of these methods alone may generate inaccuracy results. Therefore combination of the OCV method and coulomb counting method is suggested as the SOC estimation method for this purpose. The limitation of coulomb counting method can be overcome by adopting high accuracy current sensor and calculating the initial SOC value using the OCV-SOC method. The Figure 7 show the block diagram for the proposed SOC estimation method. The inputs are ambient temperature, current and OCV. The initial SOC is estimated using OCV-SOC method where the SOC values are stored using three dimensional table.The calculated SOC values is an input to the electro-thermal model.

In the electro-thermal model in Figure 6 the current, SOC, OCV and internal temperature are taken as inputs to the second order RC ECM and internal resistance, current, thermal parameters and entropy coefficients are considered as thermal model inputs.

3.2.   Quantitative analysis

The results from the previous research work were investigated for the quantitative analysis where the error of the estimated SOC value using indirect methods was calculated taking coulomb counting method as the reference. When calculating the SOC value using the coulomb counting method, in order to eliminate the integration error a high sensitive calibrated current sensor was used. In order to perform the quantitative analysis, in previous research work LiFePO₄ batteries were tested under different temperature (0 ℃–60 ℃) and current profiles.

In neural network method it emphasizes that the RMS errors are within 4%, but the maximum error at some temperature (10 ℃–50 ℃) are larger than 10%. The errors are presented in the middle range of SOC (30%–80%). The most important fact is the inability of solving this problem by increasing the number of neurons or hidden layers because of over-fitting of neural network ^[45]. As a different approach, the estimated SOC curve using neural network method is compared with the reference SOC curve estimated using coulomb counting method in terms of current disturbance response ^[110]. In the normal situation without a current disturbance, the RMS error is less than 0.006% which is acceptable, but for a dynamic situation with a current disturbance, even though the estimated SOC converges to the reference value after some time, the deviation at the moment of the disturbance is at a considerable level.

In support vector method, for a normal condition the RMS error is over 5% where the maximum error is about 15%. For a dynamic situation error is about 2.5% where the maximum error is recorded as 13% ^[38]. For the fuzzy logic method the RMS error is roughly about 5% ^[63].

As for extended Kalman filter, the RMS error varies according to the adopted battery model ^[55]. As for an example for Thevenin model, the error is less than 0.6% which is acceptable ^[94]. for the second order RC ECM the RMS value is close to 0.75% where the maximum error is close to 2% ^[111].

4.   Conclusion

This paper presented a review of methods of estimating of SOC of lithium-ion batteries. The estimation methods have been reviewed and evaluated in both qualitative and quantitative manner to encounter the suitability for Battery Energy Storage Systems dynamic modelling. In order to represent the dynamic behavior, the second order RC ECM is proposed and to encounter thermal effect thermal model is suggested to couple with the proposed ECM model. Since the OCV source of the second order RC ECM is nonlinear function of SOC, appropriate SOC estimation method should be adopted to achieve the objective of dynamic modelling of battery. Due to the fact of the additional complexity with the electro-thermal model, indirect measurement SOC estimation methods (model based methods) exhibits high computational cost and time. Furthermore those methods give better results only for the constant current situations. Therefore combination of two direct measurement SOC methods namely Coulomb counting method and OCV method is suggested. The primary part of the SOC estimation method consists of coulomb counting method where the initial SOC value is taken from the OCV method. As the BESS compromise of complex control schemes to regulate power, voltage and current, adopting this combination of SOC estimation method will give appreciable balance to the whole process.

Acknowledgments

The authors gratefully acknowledge the support provided by the Senate Research Council, University of Moratuwa (SRC/LT/2018/15).

Conflict of interest

The author declares that there is no conflict of interests in this paper.