Reliability enhancement of distribution networks with remote-controlled switches considering load growth under the effects of hidden failures and component aging

1.   Introduction

By 2030, the Population Division of the Department of Economic and Social Affairs at the United Nations forecasts that around 66% of the global population will live in urban areas. As a consequence of this fast urbanization, the notion of a smart city has become critical for improving city life by encouraging and promoting sustainability and healthier urban areas. Smart technology is already reshaping vital urban infrastructures, lifestyles and functions including education, transit and community security, while residents have recently realized its capability to advance health and environmental concerns ^[1,2,3,4]. The necessity to manage healthcare expenses and maintain healthy lifestyles is also a significant motivator for governments to engage in intelligent cities ^[5,6].

Wearable devices provide service delivery to end customers at any time and from any location, using various static and mobile instruments such as actuators, sensors and controllers ^[7]. The intensive connection between these appliances, some of which are intelligent (i.e., equipped with cognitive capabilities), has enabled wearable devices to reach every sector, from home automation to the revolution of Industry 4.0. Inspiring findings from other portable devices support their adoption in health studies. Most notably, wearable accelerometers present robust associations between physical movement and various health consequences, including obesity, diabetes, various cardiovascular diseases, mental health, and mortality ^[8]. However, there are some significant disadvantages to embracing wearables for the investigation of people's health: 1) the ownership of wearables is much lower than that of smartphones; 2) the majority of people discontinue utilizing wearables after six months ^[9]; and 3) raw data from wearable instruments are often unavailable. This final argument often leads researchers to depend on proprietary appliance measures, which further reduces the already poor rate of repeatability in biomedical research in general ^[10], and makes quantifying measurement uncertainty rather difficult in practice.

Human activity recognition (HAR) has attracted considerable interest in both educational research and industry implementation. HAR supports the discovery of more profound knowledge in various situations including healthcare monitoring, human-computer interaction and the kinematics of physical activities ^[11]. Numerous industrial applications centered on HAR have been developed including rehabilitative activities ^[12], human activity-based recommendation systems ^[13], aberrant motion analysis ^[14] and kinematics interpretation ^[15]. HAR can be broadly classified into two types as video-based HAR and sensor-based HAR. For video-based HAR, human movement is captured using a video camera and then assessed for activity categorization. Sensor-based HAR collects and analyzes human movement utilizing sophisticated motion sensors (e.g., accelerometers, gyroscopes and magnetometers) to identify human activities. Recent advancements in the Internet of Things (IoT) and wearable sensors, such as inertial measurement unit (IMU) sensors included in smartwatches, enable the collection and analysis of a vast quantity of customized data for HAR ^[16].

HAR sensors are vital to satisfy the demands of an urbanized population in terms of healthcare-related solutions ^[17]. Healthcare professionals (i.e., doctors, physicians, nurses and gym instructors) can analyze a person's health status by assessing their daily living activities ^[18] to preserve economic development while establishing sustainable cities and communities ^[19,20]. Many studies used sensing frameworks as benchmarks to collect and assess everyday living patterns and behaviors ^[21]. Urban residents are now more health-conscious and concerned about healthy lifestyles ^[22]. Various disorders can be identified by monitoring physical activity, such as Parkinson's disease ^[23] and dementia ^[24].

HAR using motion sensors is usually addressed as a multivariate time series classification issue ^[25], involving the extraction of vital raw signal statistical properties in time and frequency domains such as variance, mean, entropy and correlation coefficients ^[26]. Traditional machine learning (ML) techniques such as decision trees, support vector machines, naïve Bayes and random forest have proven effective in recognizing many human activities ^[27,28,29]. These ML methods produced excellent results but feature engineering remains a significant constraint for those lacking domain knowledge or experience in the subject. As a result, most classic ML techniques showed limited success in detecting and categorizing basic activities or movements.

Recent advances during the last decade in the field of deep learning have ushered in a new age of supervised, unsupervised and semi-supervised ML. Numerous applications have proved successful in areas including object identification ^[30], natural language processing ^[31] and logic reasoning ^[32] demonstrating the strength of deep learning techniques. Integrating a deep learning model with a powerful computing platform as a neural network enhanced end-to-end accuracy in the high-level learning processes and features contained in raw sensor data.

Recently, major advancements in deep learning have included the invention of two fundamental deep learning techniques termed convolutional neural networks (CNNs) and recurrent neural networks (RNNs). The CNN model is often used when ML approaches require human feature extraction. In particular, CNNs extract incorporate convolutional processes inside themselves that are domain-independent with generalization characteristics ^[33]. Constructing deeper CNNs improved performance for a variety of HAR operations but consumed more resources (e.g., memory and computing power ^[34]). CNNs collect the spatial dimensions of sensor data as signals that can be indicated by a point, line or polygon, and perform reasonably well for simple human activities ^[35,36]. Simple activities such as walking, jogging and clapping are defined by repeated movements ^[37,38]; they do not accurately represent everyday activities. By contrast, complex activities take longer to perform and include many specific activities ^[39], frequently with high-level interpretations such as cooking, cleaning and dining. Most recent research has concentrated on identifying simple activities but knowledge of simple tasks is insufficient for many real-world applications. Complex activities serve as an adequate and more accurate representation of everyday living ^[40]. Conventional CNNs are incapable of capturing complex actions involving evaluating temporal properties that change throughout time as time series data from a wearable sensor. As a consequence, RNNs were used to recognize wearable sensor activity ^[41]. Unfortunately, RNNs were impacted by the vanishing or growing gradient issue, which impacted training to a sufficient level. This issue was solved by inventing long short-term memory neural networks (LSTMs), with additional gates for information flow between distinct periods. LSTMs are widely used in natural language processing for word prediction, language understanding and various other tasks including those in the HAR domain ^[42,43].

Additionally, the Temporal Convolutional Network (TCN) attained state-of-the-art performance in a wide variety of timing issues, including natural language processing and audio synthesizing. The TCN has been provided to support the advancement of HAR studies ^[44]. TCN provides a more accurate expected output and has a more straightforward structure than traditional recurrent networks such as the LSTM and Gated Recurrent Unit (GRU). LSTM and GRU, on the other hand, have their benefits. TCN can extract both high- and low-frequency data from a sequence, while LSTM and GRU excel at identifying long-term dependency in a series ^[45]. The state-of-the-art deep learning algorithms for sensor-based HAR are generally based on RNNs, CNNs and hybrid models constructed from CNNs or RNNs to increase identification performance and effectiveness. DeepConvLSTM ^[46] was employed to continuously extract spatial-temporal features from raw sensor data and demonstrated significant improvement on HAR datasets. LSTM-CNN ^[47] was developed as a deep neural network that includes convolutional layers and LSTM to recognize human activities. The CNN's weight parameters are primarily concerned with the fully linked layer. iSPLInception ^[48] was recently offered as a reason to advance the boundaries of model performance in human activity identification. The model promotes higher by being based on the Inception-ResNet model.

Nowadays, most sensor-based HAR techniques primarily focus on simple human activities of everyday living like walking, jogging, sitting and standing. However, real-world practical applications for business and industry can benefit from HAR research integrating complex human activities ^[49]. To fill this research gap, this study proposed a deep learning model called Att-BiGRU to efficiently classify complex human activities. Our proposed model was designed to extract sequence information in both forward and backward directions and pay more attention to the important temporal contexts of complex sensor data.

The Att-BiGRU model was evaluated using the publicly available HAR dataset WISDM-HARB. Findings indicated that our model outperformed the existing baseline deep learning models CNN, LSTM, BiLSTM, GRU and BiGRU using the same dataset. The main contributions of this paper are as follows:

● The proposal of a new RNN-based DL (deep learning) architecture sought to assess the recognition of human actions through the use of a BiGRU (bidirectional gated recurrent unit) alongside an attention mechanism. This proposed model exhibited superior performance when compared to alternative baseline models for deep learning.

● An examination of Att-BiGRU performance was carried out, noting that it was possible to enhance the recognition performance through the leverage of an advanced BiGRU network which carried out both forward and backward processing of sequential sensor data to automate the process of feature learning and the encoding of sequential data. The present state of the gate recurrent units is hidden, and is determined via two-directional operation which makes use of both past and future information. This enhances the process of feature learning. The significance of both feature learning and time step learning through the BiGRU network is emphasized by the use of the attention mechanism. Those time steps or features of greater importance were allocated greater weightings when recognizing complex human actions, thus improving the overall accuracy.

● Experimentation showed the performance advantages of the Att-BiGRU model in the recognition of complex human actions when utilizing data from a smartwatch sensor. Comparisons were then drawn between the results of the proposed model and the outcomes from earlier models which made use of different benchmark HAR datasets.

The remainder of the paper is divided as follows. Section 2 discusses several sophisticated techniques for recognizing human activity from wearable sensor data, with the proposed HAR methodology for automated feature learning and selection introduced in Section 3, followed by the Att-BiGRU model. Section 4 presents the experimental dataset and environment in a variety of contexts, with the results discussed in Section 5. Finally, Section 6 summarizes the findings of this study and discusses possible future endeavors.

2.   Literature review

This section discusses related research in sensor-based HAR that employ deep learning techniques for inferring complex human activities utilizing RNN-based models and their enhancement via an attention mechanism.

2.1.   Recurrent neural networks (RNNs)

CNNs are optimized for interpreting a grid of values to extract spatial characteristics, while RNNs are optimized for processing sequences. Unlike conventional feed-forward neural networks (FNNs), RNNs maintain a state that can reflect temporal input from any length of context window. Thus, while an FNN can only map between input and output vectors, an RNN can theoretically map between all previous inputs and outputs. RNNs have been utilized in a variety of deep learning applications involving variable-length inputs and outputs, such as speech recognition and natural language processing ^{[50,51,52,53,54]}. The RNN is distinctive because its hidden states are related to both current and previous inputs, making this algorithm appropriate for sequence or time series-based models. Standard RNNs are inefficient for predicting long-term reliance due to the vanishing gradient issue that demands extensive changes to the underlying RNN architecture. To address these problems, gated mechanisms were included in RNNs, leading to the development of long short term memory (LSTM) ^[42,55] and gated recurrent units (GRUs) ^[56].

2.1.1.   Long short term memory (LSTM)

To alleviate the issue of vanishing gradients, Hochreiter and Schmidhuber ^[42] proposed the long short term memory (LSTM) network in 1997. This network is similar to a conventional RNN, except that the unit cell of the RNN is substituted by a memory cell. Technically, the LSTM contains memory units for handling the vanishing gradient issue, which enables the network to learn when to forget and when to update previous hidden states in the presence of new data ^[55,56]. Recent HAR research studies have proposed a variety of LSTM networks to tackle the problem of time-series classification in HAR.

Singh et al. ^[57] used LSTMs to evaluate information on human movement collected by smart-home sensors to compare LSTMs to CNNs and conventional ML methods. LSTMs and CNNs surpassed other ML algorithms, with CNNs being significantly quicker but less accurate than LSTMs during training.

In 1997, the BiLSTM was presented by Schuster and Paliwal as a means of increasing accessible information quantities within an LSTM network ^[58]. Two hidden layers were used, linked to the BiLSTM to allow information to be drawn simultaneously from past and future sequences. It is not necessary to reconfigure the input data for the BiLSTM, as inputs are acceptable in their present state. Comparisons of unidirectional and bidirectional LSTM models were carried out by Alawneh et al. ^[59] involving human action obtained using sensors in a study based on HAR. The results suggested superior performance from the BiLSTM method when compared to the unidirectional approach in terms of accuracy of recognition.

Recently, LSTM-based deep learning strategies have been applied to HAR applications. For example, Mekruksavanich et al. ^[60] investigated the efficacy of LSTM-based models for Smart Home applications using smartphone data. The researchers showed the effectiveness of LSTMs for extracting temporal features from sensor data. Nafea et al. ^[34] used the BiLSTM to study simple and complex human movements. The objective was to develop time-dependent expressions for short-term forecasting and long-term human movement synthesis challenges. The LSTM network was integrated with CNNs in the health assistance area to improve temporal and spatial data extraction to identify fall occurrences ^[61].

2.1.2.   Gated recurrent unit (GRU)

One advantage of the LSTM lies in its ability to mitigate the problem of the exploding/vanishing gradient, since its cell architecture offers enhanced memory capacity. The gate recurrent unit (GRU) network was proposed by Cho et al. ^[62] in 2014 in the form of a novel RNN-based model. It is a simplified version of the LSTM, and the design lacks specific memory cells ^[63]. The GRU network also contains update and reset gates which control the extent of the update of any hidden state through specifying which data can be transmitted to the next state and which data cannot be transmitted ^[64,65].

An excellent robust model for deep learning model utilizing the GRU network was created by Okai et al. ^[66] in order to manage sensor-based HAR problems through augmentation of the data. This approach proved superior to the LSTM models, but had the slight problem of being unidirectional. In this case, the output for any given time step could be governed solely by the data which made up the input sequence used in the preceding time step. However, in some scenarios this could be beneficial in facilitating forecasts taking the past and future into consideration ^[67]. Alsarhan et al. ^[68] proposed the use of HAR models which had their basis in BiGRUs (bidirectional gated recurrent units), reporting that this approach was quite effective in the detection of human actions using sensor data.

Additionally, it has been said that GRU-based networks can correct for near data points in time series sequences - for example, sensor data ^[69]. Numerous HAR studies benefited from GRU's ability to maintain stability between prior and fresh memory contents by disclosing its memory scopes at each time interval. For example, Xu et al. ^[70] offer a HAR model that employs a GRU layer to extract high-level characteristics from low-level information assembled through a CNN-based network. The recommended approach revealed efficiency gains across a variety of publicly available datasets. Alsarhan et al. ^[68] created a BiGRU model for recognizing movements in daily living as well as fall states with high efficiency. The produced BiGRU model could be used to track older patients' health levels.

2.1.3.   Attention mechanism

Attention models were created originally in order to recognize images ^[31], and were based on the workings of human vision, which would normally focus upon a certain component of an image when performing the recognition process, changing the focus over time where necessary. When the attention model is used, the machine is able to maintain focus on one specific area to carry out the recognition process, with no distraction from other areas, leading to successful and effective image recognition. The attention model has also been demonstrated to work well in the context of natural language processing. In the case of employing an encoder-decoder model in the absence of machine translation, the process involved an input sentence being encoded within a fixed hidden vector for the purpose of translation during the translation procedure, so that every one of the words comprising the input sentence could play an equal part in the translation for every time step. This procedure performed poorly. However, when the encoder-decoder model was applied with the attention mechanism, the translation at various time phases paid greater attention to words more closely connected to the present translation material.

Attention mechanisms have attracted attention in HAR as a result of their achievement in other fields involving temporal sequences, such as natural language processing ^[71] and speech recognition ^[72]. Recently, deep learning architectures have integrated attention mechanisms to emphasize both visible and hidden important information. For feed-forward networks, a simplified version of attention mechanism ^[73] was presented that captured certain long term dependencies. Another solution described by ^[71] employed an attention mechanism on top of a complicated DeepConvLSTM structure to determine the appropriate temporal context for behavior identification. Combining a hierarchical attention mechanism with a gated recurrent unit neural network improved complex HAR ^[74].

3.   Proposed methodology

This section introduces a sensor-based HAR for recognizing complex activities. Wristwatch sensor data were used to explain our proposed attention-based deep learning model, Att-BiGRU, for complex human activity recognition.

3.1.   Complex human activity recognition

To develop an activity recognition model, activity taxonomies were investigated ^[75,76] using a representative model termed $\mathrm{SC^2}$ ^[77]. This classified human behavior into two broad categories based on their temporal interactions as simple human activity and complex human activity.

● A simple activity cannot be further divided into additional atomic-level activities. For example, walking, jogging and sitting are all basic activities due to their inability to be combined into others.

● A complex activity is a high-level activity constructed by ordering or overlapping atomic-level activities. For example, "drinking a cup of coffee" combines the two atomic activities "sitting" and "lifting a cup of coffee to sip".

3.1.1.   Overview of the proposed HAR methodology

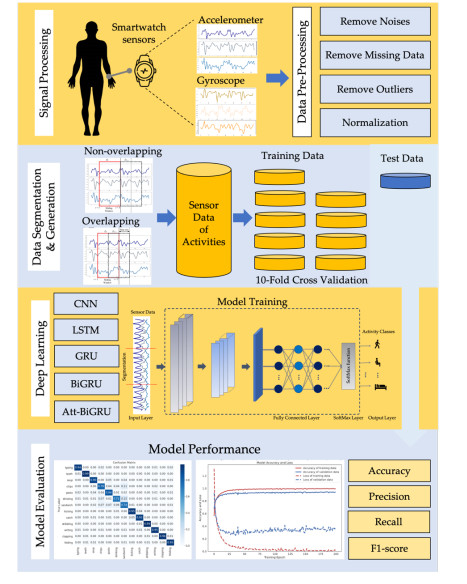
This section summarizes the entire process of the proposed HAR methodology. The process began with signal processing, which comprised data gathering from smartwatch sensors, data loading, noise removal, data normalization and outlier elimination. The following stage of data segmentation and generation ensured that the data was in a suitable state for model training. This involved establishing temporal windows, their overlap, class assignment and labeling, and the separation of training and test data. The nested cross-validation approach was used to train deep learning techniques, using variants of deep learning models including CNN, LSTM, GRU, BiGRU and our proposed Att-BiGRU. Finally, effective assessment indicators such as accuracy, precision, recall and F1 score were used to validate the model. Confusion matrices were then constructed to compare the performances of the various deep learning models. Our proposed HAR methodology is depicted in Figure 1.

3.2.   Data pre-processing

Sensor data obtained from wearable devices must be pre-processed to eliminate the noise, handle incomplete data, remove outliers and fragment the data to increase sequence quality. The following subsection describes these strategies in detail.

3.2.1.   Noise reduction

In general, employing some noise reduction approach is required when dealing with time series. The measured values of a sensor are susceptible to uncertainties, such as noise introduced in the signal. Complicated activities include a range of successive motions, and the uninterrupted streaming of inertial sensor data over time increases the quantity of noise present in the recordings. The noise was decreased in this study utilizing a median filter and a 3rd order low-pass Butterworth filter with a cutoff frequency of 20 Hz. This rate was sufficient to record physical movements since 99% of its energy occurred below 15 Hz ^[78].

This technique delivered a softer version of the original signal by removing noise from sequences that impaired the model's capacity to learn well throughout training.

3.2.2.   Missing data handling

During the sampling period, missing values for contact activities implied that there were no recordings, while missing values for other sensors were caused by a cold start, reading stability or sensor failure. Contact sensor missing data were given a value of zero, while elevation values missing from the elevation data were adjusted to the most recently observed value.

The missing values from additional sensors were interpolated using the mean of previously identified data points within a five-point frame. This data interpolation method is widely used to handle missing values based on the statistics (e.g., minimum, maximum, mean or median) of adjacent data points to generate sufficient approximations of missing data points ^[79].

3.2.3.   Data normalization

We normalize the data acquired during the data gathering step to reduce the influence of noise. Additionally, since most of the dimensions of an input data $X^{(t)} = x_1, x_2, x_3, ..., x_D \in \mathbb{R}^{D}$ adjust the values of readings from various sensors to a range between 0 and 1, that would support the learning algorithm in balancing the impacts of distinct dimensions. The normalization procedure is conducted to data collected over a specified period (e.g., one or five seconds), in which normalized data points are determined ${\hat X}^{(t)} = {\hat x}_1, {\hat x}_2, {\hat x}_3, ..., {\hat x}_D$, where ${\hat x}_i = \frac{x_i - x^{min}_{i}}{x^{max}_i - x^{min}_{i}} \in \mathbb{R}\; |\; \forall x_i \in [0, 1]$ denotes the total number of normalized data points and $x^{min}_{i}$ and $x^{max}_i$ denote the minimum and maximum values of the dimension i over the specified period, respectively.

3.2.4.   Data segmentation

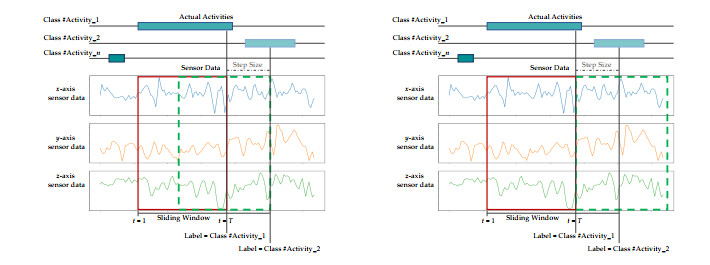
For the data segmentation step, all normalized sensor data were aligned to the exact size of a sliding window. Several techniques for obtaining data segments in HAR studies involve the utilization of temporal windows. The most often utilized window in sensor-based HAR investigations is the overlapping temporal window (OW) ^[25]. This technique applies a fixed-size window to the input data sequence to deliver training and test samples using a specific validation technique. However, this approach is significantly biased since succeeding sliding windows overlap by 50%. This bias can be avoided using another technique called the non-overlapping temporal window (NOW) ^[25]. Compared to the OW approach, the NOW technique has the drawback of providing a restricted number of samples because the temporal windows no longer overlap. Figure 2 illustrates two sample generation strategies for segmenting sensor data, where X, Y and Z denote the three components of a tri-axial IMU sensor.

In this study, normalized time series data from wearable sensors were split into temporal segments before training the deep learning network. This process utilized two segmentation techniques, namely the OW scheme with a 50% overlap and the NOW scheme. Sensory data sequences of 200 length were generated using a sliding window of ten seconds.

3.3.   Proposed Att-BiGRU model for complex human activity recognition

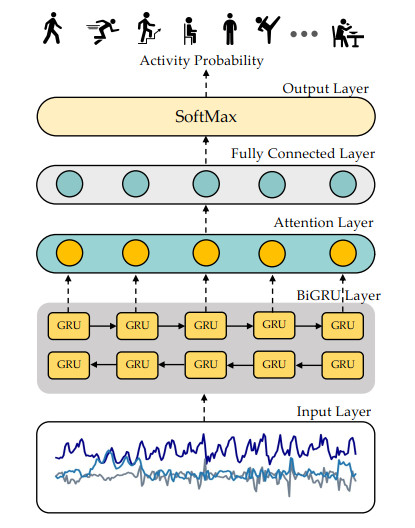
This section introduces Att-BiGRU, an attention-based neural network for identifying complex human activities using a wristwatch sensor. Our proposed Att-BiGRU architecture was composed of five layers as an input layer, a BiGRU layer, an attention layer, a fully linked layer and an output layer that are discussed in detail below.

3.3.1.   Input layer

Given the raw sensor data $X = (X^{(1)}, X^{(2)}, X^{(3)}, …, X^{(T)}) \in \mathbb{R}^{T \times D}$, the learning algorithm for human activity recognition attempt to estimate $y \in \mathbb{R}^{m}$, i.e., a type of activity from a predefined set of activities $A = \{a_1, a_2, a_3, …, a_m\}$. Here, $X^{(t)} \in \mathbb{R}^{D}$, represents the i-th measurement, T and D represent the length of the signal and the dimension of the sensor data, respectively. For example D = 6 when using the two sensors readings, given tri-axial accelerometer reading $X_{acc}^{(t)} \in \mathbb{R}^3$ and tri-axial gyroscope reading $X_{gyro}^{(t)} \in \mathbb{R}^3$. There is a time-series sequence $s = (X_1, X_2, …, X_j, …, X_n)$ of sensor reading that captures the activity information, where $X_j \in \mathbb{R}^{T \times D}$ denotes the sensor j-th reading and n denoted length of sequence and $n \geq m$.

3.3.2.   BiGRU layer

The GRU neural network is a subtype of the recurrent neural network (RNN). A GRU is a simple LSTM neural network that allows for more straightforward computations, while retaining the function of an LSTM neural network. A GRU unit comprises an update and reset gate that controls the updated degree of each hidden state and decides which data must be conveyed to the next state and data that does not need to be transferred ^[55,56]. At time $t$, GRU determines the hidden state $h_t$ utilizing the update gate's output $z_t$ the reset gate's output $r_t$ and the current input $x_t$. The preceding hidden state $h_{t-1}$ can be represented as:

where $\sigma$ is a sigmoid function and ${ \bigoplus}$ is a fundamental addition operation, and ${ \bigotimes}$ is a fundamental multiplication operation.

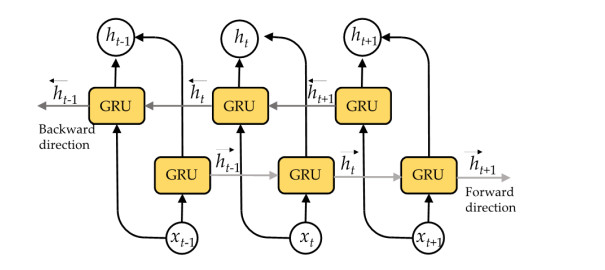
A GRU with a bidirectional technique named BiGRU was employed in our proposed deep learning network for complex human activity recognition. Each unit cell in the illustration could be an RNN, an LSTM or a GRU. One significant drawback of this network was its unidirectional character. Apart from the current input, the output at any given time step was entirely controlled by the information stored in the input sequence. In certain instances, it would be beneficial to consider both the past and future while forecasting. This scenario was resolved by using a bidirectional network, as illustrated in Figure 4.

To fully utilize the contextual information included in complex activity data, this study employed the BiGRU structure that contained both forward and backward hidden layers. As illustrated in Figure 4, each input sequence was fed into forwarding and backward GRU networks, resulting in two symmetrical hidden layer state vectors. By symmetrically combining these two state vectors, the final output representation of the input series was obtained, as described in the following section.

3.3.3.   Attention layer

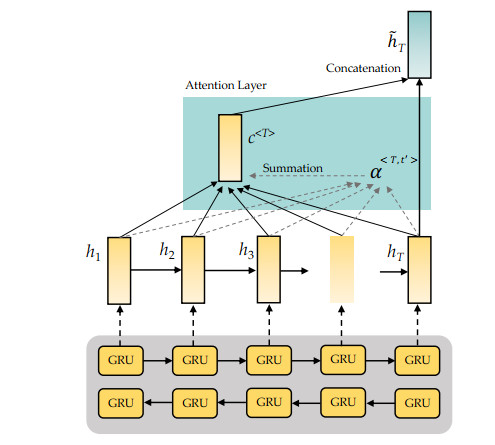
Following the acquisition of context characteristics by the BiGRU network, this study proposed a self-attention technique to capture more meaningful information by precisely assigning weight to critical data to better comprehend sequence semantics. Figure 5 illustrates the computation of the self-attention mechanism.

After computing the pre-processed information $X = (x_1, x_2, ...., x_t)$ from the BiGRU layer, we could retrieve the vector $H = [h_1, h_2, ...., h_t, ..., h_T]$. While $T$ is the length of the vector data $X$ and $h_t$ is the hidden state of the BiGRU at timestep $t$. We can design the BiGRU's self-attention technique as follows:

Additionally, $w_2$ is a time-level context vector, $b_t$ is a normalized weight calculated using a softmax function, and $d$ is the uniform representation of the entire sequence obtained by adding the weights of all hidden states.

3.3.4.   Fully connected layer and output layer

An output layer is linked to the output of the attention-based BiGRU subnet.

We convert $\delta$ to the likelihood of each action using a fully connected layer and a softmax function. We then derive the predicted label by exploring the action with the highest probability.

4.   Experimental results

We evaluated our proposed Att-BiGRU model by employing three experiments based on distinguishable categories of activity data from the WISDM-HARB dataset. Each investigation experimented with the proposed model against five baseline deep learning models (CNN, LSTM, BiLSTM, GRU, and BiGRU) utilizing a variety of activity sensor combinations. We demonstrated the accuracy of deep learning models using a binomial confidence interval with a confidence level of 95%.

4.1.   Setting for experiment

The platform employed in this research to conduct the experiments was Google Colab Pro, while training of the deep learning model made use of the Tesla V100-SXM2 with 16 GB graphics processor. Deep learning models were implemented by using Python (version 3.9.1) and CUDA (version 8.0.6), so the Python libraries described below supported the experiments:

● Data manipulation can be carried out using Numpy (version 1.19.5) and Pandas (version 1.1.5) following the receipt, modification, and interpretation of the sensor data.

● Matplotlib (version 3.3.2) and Seaborn (version 0.11.2) were used to display and visualize the data investigation results along with the assessment of the model.

● The sampling and data generation library employed for the experiments was Scikit-learn (Sklearn version 8.0.6).

● The implementation and training of deep learning models can be performed through the use of TensorBoard, TensorFlow (version 2.6.0), and Keras (version 2.6.0).

4.2.   Dataset description

The UCI Repository "WISDM Human Activity Recognition and Biometric Dataset" (WISDM-HARB dataset) served as the source for sensor data from watches. These data were made available in 2019 from Fordham University (New York, USA). The datasets to be analyzed comprised information from a tri-axial accelerometer and tri-axial gyroscope obtained at 20 Hz using Android 6.0 (Google Nexus 5/5X and Samsung Galaxy S5) smartphones or Android Wear 1.5 (LG G Watch) watches. The watches were worn on the dominant hands of a sample group comprising 51 subjects, and data from the sensor were recorded to evaluate a total of 18 human actions, including 7 which focused on the hands, 6 which did not focus on the hands, and 5 which were associated with the process of eating. These actions were performed in isolation for a duration of 3 minutes while data collection was conducted at a rate of 20 Hz. Two protocols were used to categorize the data from the sensors in order to address the HAR issue with time series data. Firstly, a 10-second sliding window of fixed dimensions was employed with an overlap rate of 50%, and secondly, a 10-second sliding window with no overlap was used.

According to Table 1, activities in WIDSM-HARB could be classified into SHA and CHA based on graphical plots of selected representative activities. Simple activities are usually periodic, while complex activities are asynchronous, making them harder to track with just an accelerometer.

4.3.   Data splitting for model performance

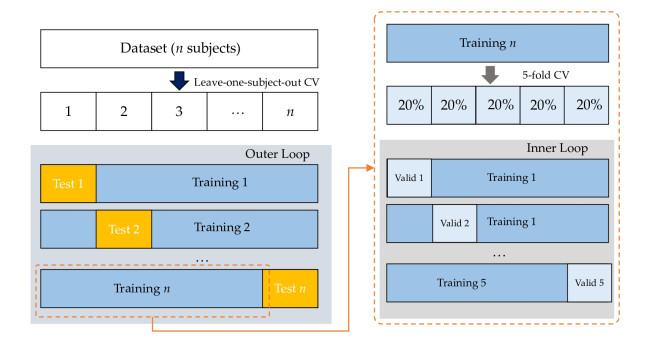
The highest performing classifier and window length were determined in this study using a layered cross-validation strategy ^[80]. Nested cross-validation is a powerful technique for determining a model's generalizability. It is frequently used to build a classification model that requires the tuning of hyperparameters ^[81]. Varma and Simon ^[82] proved that stacked cross-validation could provide a nearly-unbiased estimate of the actual error. The schematic of the layered cross-validation is shown in Figure 6. It incorporates both internal and external cross-validation. The inner loop employed a 5-fold cross-validation technique to find optimal hyperparameters against the training set. The training set was partitioned into five equal parts, which operated as validation data. At the same time, the other four were utilized for training the classifier hyperparameters. This method was conducted five times to ensure that all samples were subjected to the forecast step. The hyperparameters chosen contribute to the effectiveness of the validation set explicitly. The outer loop is where the model's interpretation is evaluated. To ensure a user-independent assessment in this investigation, we initially split the dataset into n groups according to the subjects. One unit was operated as a test set and the remaining units as an outer training set. The 5-fold cross-validation approach was employed to determine the ideal hyperparameters of the inner loop.

4.4.   Experimental results

4.4.1.   Experiment I : simple human activity (SHA) recognition

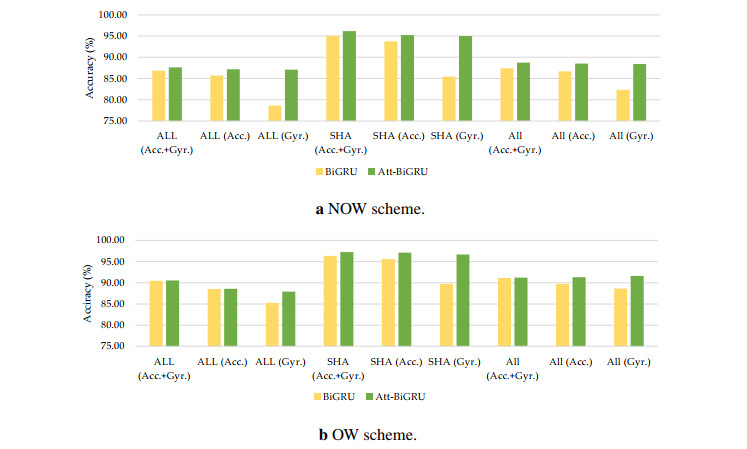
Experimental results of the non-overlapping sliding window of 10 seconds are shown in Table 2. Using only accelerometer data for SHA recognition gave high accuracy, except for the CNN model with only 86.05%. Activity recognition accuracy was found to be more effective when using both accelerometer and gyroscope data than using only accelerometer data or gyroscope data. Our proposed Att-BiGRU model obtained the highest accuracy of 96.14% using both datasets.

Experimental results with SHA recognition showed increased accuracy of 2–3% when using the fixed-size sliding window of 10 seconds with a 50% overlap rate, as shown in Table 3. Our proposed Att-BiGRU model also gave the highest accuracy of 97.22% when using both sensor datasets.

4.4.2.   Experiment II : complex human activity (CHA) recognition

The CHA dataset was evaluated using a non-overlapping sliding window for feature extraction. An entire activity acted as a combination instance. CHAs gave greatly reduced recognition performance accuracy of 10–15% less than SHA recognition. Our proposed Att-BiGRU model still obtained the highest accuracy at 88.76% for both datasets.

This experiment examined the impact of various window sizes on the ability of classifiers to identify activities using a fixed-size sliding window with a 50% overlap of 10 seconds, as summarized in Table 3. The overall classification accuracy for CHAs remained over 80% for each sliding window with 50% overlap, except for the CNN model. Our suggested Att-BiGRU model gave the highest recognition at 91.22% accuracy. This experiment indicated that shorter window frames outperformed larger ones by a considerable margin. This finding was unexpected because a shorter window is less likely to include more than a single movement in a complex human activity.

4.4.3.   Experiment III : all human activity recognition

Performance recognition using non-overlapping sliding windows gave the lowest accuracy with both sensor types. The CNN model still produced low accuracy with non-overlapping data. By contrast, the BiGRU model yielded promising results but returned an accuracy of less than 80%, while our Att-BiGRU model derived the highest accuracy at 87.63%.

The BiGRU model showed good accuracy level at over 90% for a fixed-size sliding window with a 50% overlap of 10 seconds, while our proposed Att-BiGRU model gained the highest accuracy at 90.54%.

4.5.   Comparison with previous studies

Our Att-BiGRU model addressed complex human activity recognition compared with previous studies using the same activity dataset (WISDM-HARB dataset). ^[47] presented an LSTM-CNN architecture to recognize complex human activities with promising performance, while ^[46] proposed a hybrid deep learning model called DeepConvLSTM to extract spatial and temporal features of complex movements from wearable sensors. The achievement of this hybrid model outperformed other baseline deep learning models with high accuracies. ^[48] introduced the iSPLInception model based on the Inception and ResNet models that expanded the limits of model performance to improve recognition in various HAR datasets. These three studies were selected as representatives of state-of-the-art models for complex human activity recognition and compared with our proposed Att-BiGRU model. The three models in this section were developed following their descriptions in the related articles. To deliver consistency and more relevant comparability, all models were trained on the same training, validation, and test sets. Architectures were implemented with Tensorflow and Keras libraries and evaluated using the WISDM-HARB dataset, with comparative results summarized in Table 4.

4.6.   Comparison with other benchmark HAR datasets

Further experiments were performed to assess the recognition performance and effectiveness of our proposed model against UCI-HAR, PAMAP2 and Opportunity as three publicly available HAR datasets that included both simple and complex human activities.

4.6.1.   UCI-HAR dataset

Anguita et al. ^[83] introduced the UCI-HAR dataset containing personal movement collected from 30 people of varied ages (18–48), nationalities, heights and body weights. The subjects performed daily tasks while carrying a Samsung Galaxy S-II smartphone at waist level. Each engaged in six physical exercises as walking, walking upstairs and downstairs, sitting, standing and lying down. Sensor data were collected using the integrated tri-axial measurements of the smartphone accelerometer and gyroscope while each participant completed the six predefined activities. Tri-axial values of linear acceleration and angular velocity data were acquired at a constant rate of 50 Hz. The data were sampled using fixed-width sliding windows with a 50% overlap of 2.56 seconds. Table 5 summarizes the comparative findings for this dataset.

Table 5 shows the results obtained from the UCI-HAR dataset using different state-of-the-art models. Our Att-BiGRU model attained the highest accuracy of 99.00% and F1 score of 99.00% compared to other models, closely followed by the DeepConvLSTM that attained lower accuracy of 1.42%. However, our proposed model size was only 140, 679 parameters, which was significantly low compared with the other models.

4.6.2.   PAMAP2 dataset

For the recording of physical actions, the PAMAP2 dataset was introduced by Reiss and Stricker ^[84] using a sample group of 9 people (8 males) aged 27.2 $\pm$ 3.3 years, with BMI 25.1 $\pm$ 2.6 $\mathrm{kg/m^2}$. The 9 subjects wore three wireless IMUs positioned on the chest, ankle, and wrist before carrying out 13 exercises, 9 of which were simple while 3 were considered complex. The IMUs were composed of a tri-axial magnetometer sensor, a tri-axial acceleration sensor, a tri-axial gyroscope sensor, and sensors to record orientation and temperature, while sampling was performed at a rate of 100 Hz. In the case of the wrist sensors, the data underwent evaluation on the basis of a 10-second sliding window, as indicated in Table 6.

Results in Table 6 showed that our Att-BiGRU model achieved the highest accuracy of 95.82% and F1 score of 95.83% on the PAMAP2 dataset, and significantly outperformed all the other models.

4.6.3.   Opportunity dataset

Roggen et al. ^[85] introduced the Opportunity human action recognition dataset, consisting of realistic behaviors recorded using 72 ambient and body sensors in a sensor-rich setting. Their dataset contained observations of 12 participants made with 15 networked sensor systems equipped with 72 sensors covering ten different modalities that were incorporated into surrounding objects and the body. These properties provided an excellent candidate for benchmarking other techniques of human action recognition. This study analyzed data from the triaxial accelerometer, gyroscope, magnetometer and other sensors classified as columns 38–134 but not from the quaternion measures. A total of 77 channels were received as input. The data were sampled at 30 Hz and extracted using a three-second window with 90 samples per window. Table 7 summarizes the findings for the Opportunity dataset.

Our Att-BiGRU model performed on a par with the other state-of-the-art models as shown in Table 7. However, our proposed model had only 194, 322 parameters, which was significantly low when compared with the other models.

5.   Discussion of experimental results

5.1.   Impact of data segmentation

Two unique data segmentation schemes were investigated as overlapping and non-overlapping windows. Results in Tables 2 and 3 showed that deep learning algorithms which used the non-overlapping window approach outperformed those using overlapping windows. Section 4 compared the two segmentation strategies based on the results of three experiments. As illustrated in Figure 7, findings indicated that deep learning classifiers functioned better in all experiments when the overlapping window method was used. Specifically, when only gyroscope data were used, overlapping window classifiers performed much better.

5.2.   Impact of attention mechanism

The ability to learn an interpretable representation is critical for most ML applications. Deep learning methods have the benefit of extracting characteristics from raw data but it is often hard to comprehend the relative contributions of the input data. To address this concern, previous research ^[86] proposed the idea of attention. In this study, an attention mechanism developed for neural network machine translation tasks ^[86] was implemented into our classification algorithm. This task supported the development of an interpretable representation that described the focus of individual input data sections of the model. Findings demonstrated that the attention mechanism enhanced recognition performance in all scenarios, as shown in Figure 8. Notably, our Att-BiGRU model gave a considerably superior performance in cases that only used gyroscope data.

5.3.   Impact of bidirectional computation of RNN-based models

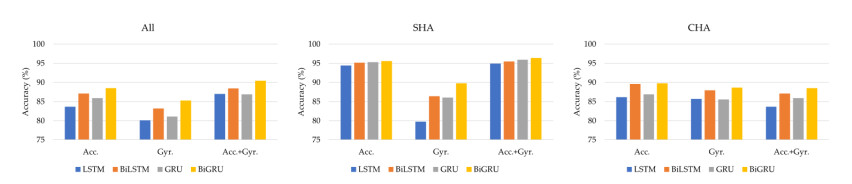
This study introduced various deep learning techniques to address the complex problem of HAR. Five models as CNN, LSTM, BiLSTM, GRU and BiGRU were chosen as standard deep learning models. These models were employed to evaluate the performance of our proposed Att-BiGRU model, which integrated an attention mechanism in the BiGRU layers. To determine the effect of the bidirectional technique, the predicted outcomes of a model incorporating both bidirectional and unidirectional RNNs were compared, as represented in Figure 9. Results revealed that our proposed model obtained superior accuracy than standard deep learning models such as CNNs and RNNs.

Findings in Figure 9 demonstrate that bidirectional RNNs outperformed those utilizing unidirectional RNNs. This result was satisfactory since the data were analyzed bidirectionally from the past to the future and from the future to the past. Nevertheless, this advantage was gained at the expense of additional computation time.

5.4.   Limitations

This article's study has several limitations. At first, there was an imbalance in the number of physical activities provided in each group. Positive reviews outnumber negative reviews by a large margin, which could also influence findings to deviate. Another issue of this work is that the deep learning algorithms were developed and evaluated using laboratory results. Previous research has shown that the performance of learning algorithms under laboratory circumstances does not accurately address performance in real life ^[87]. The second restriction is that this research does not tackle the issues of transitional behaviours (Sit-to-Standing, Sit-to-Lay, etc.) in real-world scenarios, which is a challenging priority. Nevertheless, the recommended HAR architecture can be applied to various practical applications in pervasive computing using high-performance deep learning networks, such as optimizing human mobility in sports, tracking healthcare, and monitoring older adults' safety.

6.   Conclusions and future works

A sensor-based HAR paradigm was proposed to efficiently identify complex human activities. Our methodology Att-BiGRU model incorporated an RNN-based deep learning model with an attention mechanism into a bidirectional gate recurrent unit model. Several significant discoveries were achieved by comparing the performance of our proposed methodology to baseline deep learning models.

First, compared to two classic deep learning techniques such as convolutional neural networks and long short-term memory neural networks, our attention-based BiGRU was significantly more appropriate for discriminating complex human features. Experimental findings demonstrated that the attention mechanism accurately extracted critical temporal characteristics from complex human activities. Second, our proposed architecture revealed that sensor integration impacted the effectiveness of deep learning models in terms of recognition. The experimental outcomes suggested that accelerometer and gyroscope sensors achieved high accuracy performance for complex HAR processes.

As a result of the above, we inferred that our proposed methods effectively recognized multiclass complex human behavior and surpassed the existing methods. When reliable, repeatable, and portable techniques for detecting various appropriate movement patterns become unrestricted, smartphone-based HAR strategies will correspondingly become vital for public health researchers and practitioners. We expect this study to shed some light on how smartphones might be employed to quantify human behavior in health research, and upon the intrinsic sophistication in gathering and processing such data in this challenging but critical sector. In the future, we intend to analyze more complex activities in daily living and apply our proposed methodology to data gathered from a more significant number of participants belonging to different age groups.

Acknowledgments

This research project was supported by Thailand Science Research and Innovation fund, University of Phayao (Grant No. FF65-RIM041), National Science, Research and Innovation Fund (NSRF), King Mongkut's University of Technology North Bangkok with Contract no. KMUTNB-FF-65-27.

Conflict of interest

The authors declare there is no conflict of interest.