An investment strategy based on the first derivative of the moving averages difference with parameters adapted by machine learning

Abbreviations: MA: moving averages; dMA: moving averages difference; OHLC: the vector open high, low, close; SL: Stop loss

1.   Introduction

Each investment strategy basically boils down to defining a way for a trader (or an automated system acting on his behalf) to open and close positions in a time sequence. This sequence of decisions should ensure profit, measured by the cumulative sum of many consecutive profits and losses, and minimize the investor's risk, measured e.g. by the variance of consecutive returns from investment decisions made. The aim of this article is to present such investment strategy derived from the idea of observing the mutual crossing of two moving averages.

For decades investors, both theoreticians and practitioners, are interested in the use of moving averages (MAs) as prediction method in time series. During several decades of the second half of the last century, there were many pieces of research performed in that area MA (Johnston and DiNardo; 1972; Yamane, 1973; Schwager, 1984; Brock et al., 1992; LeBaron, 1992; Hamilton, 1994; Gencay, 1996; Gencay, 1998; Murphy, 1999). This interest has not ceased in recent years, (Ellis and Parbery, 2005; Wei, 2006; Moon and Kim, 2007; Zhu and Zhou, 2009; Metghalchi et al. 2012; Babu, 2014; Wilinski and Zablocki, 2015).

There are several popular usages for MAs:

● Single MA: one individual used as a filter to determine the trend;

● Double Mas: when two MAs are considered, short and long-term, their crossing are sought as signals suggesting opening or closing of the position

● Three Mas: e.g. the Bill Williams indicator called Alligator

● More Mas: searching for places where a bunch of curves intersects, looking for patterns from mutual relations, e.g. in multiple regression models

In addition to the Simple Moving Averages (SMA), also their modifications Weighted Moving Averages (WMA) and Exponential Moving Averages (EMA) are used. In the further part of the article, if it is not marked, the authors will use Simple Moving Average. Moving averages can be built on various elements of OHLC bars (Japanese candlestick). The bar closing price is most commonly used, but also there are strategies which are using MAs based on highest and lowest price in time-series.

Additionally, regardless of the number of MAs used, some traders are creating buffers around them, the most popular ones are Bollinger Bands and MAs Envelopes. The creators of popular indicators such as George Lane (Oscillator Stochastic) and Larry Williams [Investopedia.com/dictionary] also sought inspiration in moving averages.

In most of these historical achievements, the creators of these strategies recommended fixed parameters for moving averages on specific markets as the best solution, often uncritically suggesting the use of them. Of course, it should be assumed that they had knowledge and awareness of the volatility of markets, and such an average approach (recommending constant parameters) was then due to the limited calculation capabilities.

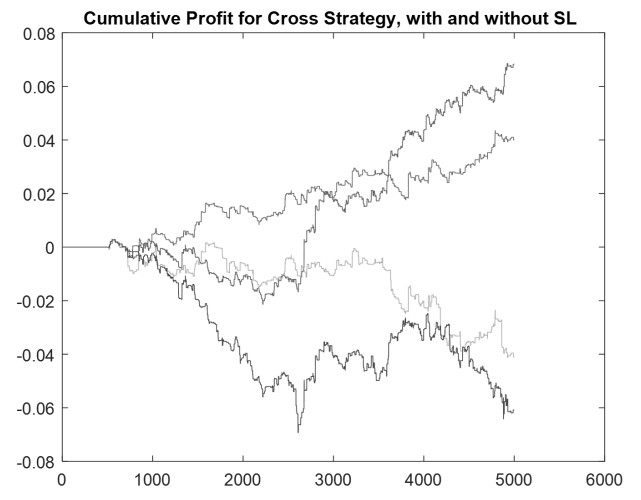
Example results of strategy based on the crossing of two SMAs are shown in Figure 1. Currency pair EUR/USD (most popular currency pair) sampled every hour was used in the experiment. Long positions were opened when the short-term MA broke through from the bottom of long-term MA and short positions were opened when the opposite happened. All positions were closed after one cycle, one hour as time series was sampled by an hour. The chart presents examples of cumulative profit for randomly selected MAs pairs with the parameters {10, 15} where parameter f = 6 concerns the so-called a short-term MA and s = 10 long-term MA. The second considered MA pair in the chart was the pair with parameters {6, 9}. The parameter f of MA is the number of periods from the current time taken into account when calculating the average. Additionally, the impact of the Stop Loss parameter of 10 pips was checked. The tests were carried out on several thousand samples.

Two worse results, concluding loss, were obtained for tests without SL, two better for SL = 0.0010 (10 pips). The best result for the MA6 and MA9 was around 700 pips on several thousand candles, but due to the large capital drop, it also gives no reason to be satisfied.

This brief introduction to one of the most popular strategies warns against using fixed parameters-moving averages as a very unreliable approach can lead to large losses.

The solution used in this paper is inspired by these historical achievements. However, in addition to the classic idea of the strategy, nowadays it is usually enriched with the eagerly used continuous adaptation of parameters to changing market circumstances, implemented using machine learning.

The paper will present the author's concept of a strategy based on the use of Simple Moving Averages and in particular attention will focus on the first derivative of the difference of these averages. Additional parameters will be added to the strategy and optimised through the decision-making process in subsequent periods in the time-series. Research on strategy in the Matlab computing environment will be presented next. The paper will be concluded with the analysis of the results in terms of their possible improvement and on the effectiveness of the strategy. As well as possible future opportunities and threats. To sum up, the most important contribution of the authors to the consideration of the effectiveness of short-term investments in time series is the enrichment of the traditional strategies based on moving averages with additional parameters. These parameters are related to the first derivative of the difference of averages and constant adaptations of their values resulting from machine learning are considered.

2.   The Method—the conception of the investment strategy

As mentioned in the introduction, the inspiration for building new investment strategy was the idea of using the intersection of two moving averages.

The idea of using intersecting moving average charts is well known and has been presented in many publications listed above in the Introduction. Its effectiveness has also been repeatedly studied e.g. Metghalchi M. et. Al. (2012), Moon Y.S. and Kim J., (2007). In the most general outline the concept of this simple method comes down to the observation of graphs of two moving averages determined for two rather significantly different parameters. These two parameters are the number of candles (periods) taken into account to determine these two averages. They were usually called fast moving averages with the parameter f, e.g. 5–10 (the number of periods for which the average MAf was determined) and the second slow moving average MAs with the parameter s of the order 2–3 times larger than the first parameter f. The values of these parameters have been the subject of many optimizations also in the machine learning mode. The basis of this concept is the statistical assumption that the fast moving average (with parameter f), if it is above the slow moving average (with parameter s), then the probability of its return under the graph of the slow moving average will be high, higher than the probability of staying above the graph of the slow moving MA. Similarly for the situation on the other side of the graph. If the fast moving average MAf is below MAs, then the probability of it returning above MAs will be higher than the probability of it staying below MAs.

Such a strategy does not ensure high efficiency, as it requires constant corrections of the values of parameters s and f. The concept of the investment strategy presented here is based on the idea of observing the intersections of the graphs of two moving averages, but it also goes much further: to the observation of the first derivative of the distance between the moving averages MAf and MAs, and using these changes to optimize the decision-making process.

Let there be two simple moving averages: so-called short-term MA with parameter f and long-term MA with parameter s > f. The parameter indicates the number of period (candlestick) closing events values in the time series taken into account for the calculation of the average. Candlestick i is a period of the time series defined by length of time-series sampling. Described by a vector of four variables OHLC (Open, High, Low and Close) or in other words a row of data matrix at the time t_i.

So, the simple moving average with the parameter f is calculated as:

Similarly, for the long-term MA:

where:

C_i: closing price (value) of current bar;

N_c: index of available bar in sample data;

Both MA series begin with (s+1) place in the time series as this is the first point where both MAf and MAs can be calculated if s > f. In Equations (1) and (2) C_i was the closing price (value) of each candlestick. In some cases another way of indexing is used, for example on the broker platform Metatrader [book.mql4.com] data is indexed from the current (index 0) value backwards.

The main prediction indicator of the strategy will be the difference between both MAs:

To clarify the above definitions, on Figure 2 the upper part shows examples of moving average waveforms for f = 4 and s = 8 for a fragment of the EURUSD 1h time series. In this article, authors use graphic examples based on EURUSD 1h currency pair and a contract for the WIG20 index. The graph below shows the difference in these dMA averages for EURUSD according to Equation (3). The MA4 notation means SMA with the parameter n = 4 (the number of candles taken backwards when calculating the average).

The difference of both MAs (dMA) takes positive and negative values behaving similar to many technical analysis indicators, called oscillators (Moon Y.J. and Kim J., 2007; Murphy J.J, 1999; Schwager D.J., 1984). These dMA fluctuations will be crucial in the strategy discussed here, which is why it is worth recognizing dMA changes in a broader context. For a larger range of data, the dMA difference behaves as shown in Figure 2. This graph allows an initial estimate of the magnitude of the oscillation. Figure 3 presents changes in dMA for about one thousand samples of the WIG20 contract sampled once a day (at the end of the trading session). In this chart, the largest maximum deviation of the mean dMA difference is on the range of 140 index points and the largest negative on the range of 115 points. Many investment strategies are containing at least as a component a condition for the mutual crossing of moving averages. In the diagram Figure 3 these are represented as zero points of the dMA function.

For example a popular strategy [https://www.investopedia.com/university/movingaverage/movingaverages4.asp] is recommending to open the short position when the short-term average MAf breaks through the long-term MAs from above. Figure 1 shows an attempt to assess the effectiveness of such a strategy. In the dMA chart in Figure 3, this is the case when dMA changes from positive to negative values. This condition can be written as:

Also the other way round: a buy signal will be generated when MAf breaks from the bottom of MAs, so open a long position condition is:

To validate this case, the following simulation experiment was carried out.

On the dMA curve (fragment such as in Figure 3), the endpoints of the candlesticks are marked with white circles (tokens) when the next candlestick is "white", i.e. when the course value increases in the period (i + 1) - candlestick: Close(i+1) > Open(i+1) or more precisely Ci+1 – Ci > 0. Black circles will declare "black" candlesticks, i.e. those for which Ci + 1 – Ci < 0 occurs. A brief observation of this fragment of the time-series does not confirm the effectiveness of the generally appreciated rule for opening positions (4)–(5). The white or black token appears after the dMA sign changes fairly randomly. It should be noted that for a time-series such as the stock index sampled daily, closing values of the previous day are not equal to the values of the opening of the current day. These values are separated by so-called night gap when the stock market is closed.

A fragment of the time-series marked with tokens is shown in Figure 4.

There is a pattern in this sample that can be an inspiration to improve the strategy. Well, most of the ascending parts of the dMA curve (for the positive first derivative of dMA) are dominated by white circles, the descending one has mostly black circles. This observation allows some modification of the previous strategy definition Equations (4)–(5). The arrangement of white and black circles shows that the intersection of moving averages (zero value points) is less significant than the first derivative of the MA difference. Thus, at this stage the strategy can be defined as follows:

The correctness of this formula is confirmed by the location of most black and white tokens in Figure 5. For such simple rules, these strategies have been implemented in the Matlab environment and tested on the WIG20 stock index sampled daily. However, the results were not satisfactory. Analyzing the distribution of tokens on a larger piece of data, it can be concluded that the use of all tokens located on the increasing or decreasing parts of the dMA oscillator leads to equalization of the probability of success and failure of the strategy Equations (6)–(7). Therefore, it was decided to introduce additional attributes in the pattern classifier of the investment strategy. Horizontal bu and bd thresholds have been introduced on the dMA curve, separately for white and black tokens, after exceeding which and passing Equation (6) or (7) conditions the appropriate position would be opened. Then the modified strategy will be defined as:

where:

bd: threshold placed on the increasing part of the dMA curve, when it's exceeded from the bottom it ends a series of opened long positions;

bu: threshold placed on the decreasing part of dMA, beyond which short positions are not opened.

The arrangement of bu and bd thresholds is illustrated in Figure 6. The slices of the dMA curve evaluating the opening zones of the respective positions are marked on it. According to Equation (8), long positions are opened below the lower threshold, and short positions according to Equation (9) above the upper one.

The strategy assumes that each position will be closed after one candlestick period. For the WIG20 contract, this means closing at the end of the trading session on a given day. Then, taking into account the already defined OHLC candlestick markings, the profit after opening a long position will be calculated as:

and after opening the short position

The last parameter of the strategy considered here will be Stop Loss (SL). The value of this parameter determines the amount of loss acceptable to the investor. Most broker platforms have a built-in SL mechanism for manual setting that facilitates semi-automatic play.

Any long or short position open according to Equation (8) or (9) will be checked to ensure that the acceptable level of loss is not exceeded:

For long positions:

For short positions:

where

H_i: the highest value of the observed variable in the i-th candlestick;

L_i: the lowest value of the observed variable in the i-th candlestick;

So the strategy defined by (8)–(13) has 5 parameters:

The selection of the values of these parameters or the selection of the boundaries of their variability ranges and increments in these ranges is a separate complex optimization problem most often formulated as a decision tree. The obvious quality measure of the solution (a strategy with optimal parameters) is the sum of profits achieved in individual test periods, each of which consists of several single day periods:

where:

P_ik: profit achieved in the i-step of the k-th testing cycle;

k: learning and testing cycle number;

Z: final profit is a function of the parameters considered Equation (14): Z = f (F);

N_s: the number of learning and testing periods planned in the simulation;

T_p: number of steps (candlesticks, here—one-day periods) in one test period;

The testing cycle is periodically repeated investment period with the fixed set of parameters, set during the learning cycle. Therefore, each testing cycle will be preceded by a learning period L_p to determine optimal parameters at a given point in the time series. The L_p/T_p cycle is a typical machine learning mechanism. The relationship between the number of L_p candlesticks used in the learning cycle, to find the best parameters, and the number of T_p candlesticks during the testing cycle of these parameters, will be selected through the experiment.

During the learning cycle the criterion of maximizing local profit will be used:

Optimal parameters in a given learning cycle are those that maximize profit (16).

Then the best parameters in the learning cycles:

where:

CR: Calmar Ratio, discussed below.

The ${F}_{opt}$ parameters will then be applied by the T_p steps in the test cycle directly after the learning cycle. As it is usually assumed that the learning period is greater than the testing period L_p > T_p, the cycle learning period (k + 1) will partially overlap the k-th testing cycle.

The profit maximization rule is often criticized in the investment aspect as not providing an adequate level of risk and thus allowing a large variance in the partial results that make up the local profit.

Taking into account investment risk, the above-defined rule is no longer so obvious. For example, the final result may be preceded by large unacceptable losses in accumulated profit. Therefore, it is safer for the investor to test rule Equation (15) while taking into account another measure of strategy quality, e.g. Calmar ratio (CR). Calmar ratio is calculated as the ratio of the final profit to the largest capital drawdown (Young W.T., 1991).

where

Z_Ns: the final value of the cumulative profit of the strategy;

MDD: maximum drawdown on the cumulative profit curve;

Measure Equation (19) was applied the entire final capital increase curve Equation (15) assessment and omit in the partial profit assessment Equation (16). Partial profits are obtained because of short periods of testing, usually consisting of only a few candlesticks. Introduction of an additional assessment using CR would lead to significant and random differences in subsequent learning/testing cycles. By building a strategy based on fairly frequent and short learning periods and even shorter testing periods in the time series under consideration, the authors here deliberately avoid introducing a validation period after the learning period. This is because the "memory" of the time series with learned parameters is so short that introducing validation would mean losing some of the profitable openings in the first testing period.

Matlab script was implemented to carry out the simulation using the algorithm described above and verify the effectiveness of the strategy.

3.   Results-strategy simulations analysis

The strategy described by Equations (8)–(13) after implementation in Matlab was checked on the FW20WS data from the last few years (from 20/01/2015 to 28/04/2018). The FW20WS series was downloaded from the Bossa brokerage house resources, keeping the original name [http://bossa.pl/notowania/pliki/eod/omega/] as futures contracts based on the most important Polish WIG20 stock index.

Matlab simulations were carried out for different learning to testing cycles ratio to find the best result. Both criteria-final profit and Calmar risk indicator were used to assess the quality of the simulation.

The first trial used a learning cycle of L_p = 15 candlesticks and a testing cycle of T_p = 8 candlesticks. The result in the form of the cumulative profit curve is shown in Figure 7. The final result after 300 cycles (each with 8 candles in the testing phase, and thus 2400 candlesticks in total), was Z_Ns = 504 index points. The Calmar factor for this curve is CR = 2.02. The profit per one day candle was Z_pd = 0.21 index point. This chart does not make a good impression. Even if you accept the risk expressed by the Calmar ratio, the average profit per candle is very low. The chart shows clear 2 periods, the first one with large fluctuations in accumulated profit and the second more promising one, where are probably better L_p/T_p relationships.

In the described experiment, each learning period was focused on searching for the best result (profit) in a particular decision tree built on 5 attributes defined in (18), in which branches were properly selected values for individual attributes—method parameters.

Thus, for the example above, the values of the parameter f for the short-term average were selected from the set f ∈ {2, 3, 4, 5}; values for the mean s ∈ {7, 12, 17, …}; bu and bd barrier values from the set {−42, −38, −34 …} and SL from the set {80,160,240, …}. During the simulation for the listed sets of values, one value from each set was selected and used in the strategy decision rules for opening positions. Learning cycle results for each set were compared in the terms of the profit. Set with the best profit was used in the testing period. And this sequence was repeated until the final result was obtained as showed in Figure 7.

In the search for these better L_p/T_p relationships and better cumulative profit curve, many learning to test cycles ratios were checked, finally stopping at very short learning and even shorter testing cycles. It turned out that very good results were obtained for L_p/T_p = (5/1) as well as (3/1) or even (2/1).

The simulation result for L_p/T_p = (5/1) is shown in Figure 8. The final profit was Z_Ns = 2059 points and Calmar ratio achieved a spectacular result of 10.54. This result was obtained on 600 candlesticks, i.e. after 600 days. The result can already be considered excellent. Maine recognizes values CR > 5 as outstanding (Main R., 2015).

Gain per candlestick of Z_pd = 3.43 points is several times better than in the first attempt with a long period of learning and testing cycles. This is an important tip in which area of learning/testing relationships you should look for the best solutions.

It was noted that the final results are very sensitive to changes in SL values. Therefore, the above simulations were carried out for relatively small SL values. The set of values for the SL attribute was a multiple of 10; SL belongs to the set {10, 20, 30, …}. It turned out that this minimum value of the SL parameter was key for the simulation result.

For example, Figure 9 shows the results of testing using SL twice as large, SL belongs to the set {20, 40, 60, …}.

In this case, the results are worse, although still acceptable. The final profit was 1273 index points and Calmar was 3.60. Another increase in the SL set resulted in a worsening of the results. SL reduction is limited either by broker regulations that do not allow very low SL values or through the market. The use of small SLs can cause almost immediate closing of most positions and therefore rather does not allow to make a profit.

Given the very good results obtained for the Polish WIG20, it was decided to check the strategy on the German DAX stock index. The latest data (until September 29, 2019) was downloaded from the resources of the MetaTrader 4 brokerage platform., it is called DE3 there. Tests were carried out, similarly to WIG20, on daily data. After several attempts, relatively good results were obtained for the ratio of a learning to testing cycle (5/3) - Figure 10.

These results are not as spectacular as for WIG20 from Figure 8, however, there were 2965 index points in 600 candles with a Calmar of 4.34. The profit achieved for one candlestick is Zpd = 4.94 index point.

At the time of this research, the DAX index reached the value of 12300 points and WIG20 index approx. 2200 points. This means that the decision tree drawn up at each learning step for DAX should have values of individual attributes greater than for WIG20. Of course, this ratio does not apply to moving average parameters f and s. The other parameters bu, bd and SL used here were much larger.

Further experiments were conducted on the EUR / USD currency pair, maintaining the current sampling frequency, i.e. examining daily candles.

It was necessary to use completely different ranges of values in the decision tree of each learning cycle. Parameters of moving averages f and s were used in approximately the same range of variations as in previous simulations, while barriers bu and bd were selected from the range of several dozen to several hundred pips. SL was changed per 20 pips steps.

For such defined ranges of attribute variability in the simulation on 500 daily candles, a profit curve was obtained as in Figure 11.

A profit of 1014 pips was achieved here, which is on average 2.0 pips per candlestick, with Calmar = 2.73.

Compared with previous results of the profit curve, this profit is riskier.

There were attempts made to improve the results for all considered financial instruments.

4.   Discussion and conclusions

The results of the simulations of the considered strategy which is based on the idea of observing the first derivative of the moving average difference were presented in the form of two criteria - one representing profit and the other representing risk. Of course, the higher the profit and the lower the risk, the better for the investor and the authors propose to settle at this statement. Sometimes an attempt is made to create a bi-criterion from both of these components with certain weights, often other measures of strategy quality are also used, e.g. Sharpe index (Murphy J.J., 1999; Schwager D., 1996). The Calmar coefficient Equation (19) has the disadvantage of misrepresenting the risk (understatement) when used for very long time series (Young T., 1991). However, for this work, it seems very suitable, because similar numbers of candlesticks are compared: usually several hundred.

Since the important distinguishing feature of the work is the use of machine learning for the current adaptation of strategy parameters, it is worth discussing the problem of optimization of these parameters. As stated in Equation (14), the strategy has 5 parameters interchangeably called attributes, whose values are selected as a result of consideration in each learning cycle of a certain decision tree. These attributes are the nodes of this tree. On each node - attribute, several values of this attribute are tested and for each of these values an edge emerging from this node leading to the next node - attribute. Of course, each decision on optimal values throughout the entire learning period must contain 5 values, one for each parameter. The optimization consists of looking for conjunction of 5 values for which the local criterion reaches its maximum.

To check if these values change in subsequent learning cycles, Figure 12 presents 3 selected parameters and their values for several subsequent learning cycles.

These waveforms are highly mutable, which means, that the parameters are quite well extracted and have an impact on local criteria. Secondly, they indicate the threat of overfitting, i.e. over-matching their values to local changes in the time series. Periods with constant values of a given parameter (horizontal sections) rarely appear on the charts. However, the results in the form of cumulative profit curves, show that with this set of features, achieved results are worth presenting. Additional researches have found that both increasing and decreasing the number of edges in the decision tree (the number of values of individual parameters) results in a deterioration of results, most often at the same time the final profit and the Calmar indicator (Wilinski A., 2011).

Further experiments were carried out to slightly improve the results obtained. An attempt was made to do this by introducing additional filters: conditions which, if met, would allow the final opening of the position (which would have been open without this filter). One of the filters considered was an additional barrier to the value of the local profit criterion. It was checked if a positive return was achieved as a result of learning, if not, the position was not opened in the next test period. This filter gave some improvement in final profit over some time series.

Another well-considered filter was the well-known indicator RSI (Relative Strength Index) – (Wilder J., 1978). For example, it was considered to improve the profit achieved on the DAX index shown in Figure 10. The RSI index was set to 10 periods (candlesticks) backwards, and thresholds (barriers) beyond which it was possible to open positions were set completely unconventional. The upper barrier is usually set at 70% (lower barrier 30%) and its reversal suggests opening the short position. Here, as a result of many attempts, the upper barrier set at 33% determined the area in which it was allowed to open short positions. Below this barrier, the opening of short was blocked. Opening long positions was similarly blocked when the RSI was greater than 67%.

For these RSI parameters obtained results are presented in the table 1. A fairly significant improvement in results was obtained compared to the simulation without this filter.

Noteworthy is a completely different way RSI is behaving in this case, it is excluding itself. The effect is then a slight reduction in the number of opened positions with an increasing probability of excluding losing positions.

It might also be interesting to compare the effectiveness of the strategy proposed here with any other strategy with a completely different theoretical basis and different assumptions. There are thousands of such strategies. One of the many commonly known strategies is the strategy based on observation of so-called pivot points, i.e. specifically determined levels of expected price changes. In principle it is somewhat similar to this strategy, as it is assumed that in case of a significant deviation (upward or downward) from the previously observed price, there will be a tendency to return (to a horizontal trend), but also to maintain the observed upward or downward trend.

The study was conducted on the same data in the same time range.

After running in the Matlab environment the author's script based on this strategy, it is possible to obtain, among others, the cumulative profit result presented in Figure 14. Replication of these calculations is possible because the authors put the bayesWIG1b script and FW20WS data in the GitHub repository in the public directory awilin/dMA.

The results presented in Figure14 are far from being an essential part of the publication. The cumulative gain of 478 index points achieved by this strategy is several times lower than the results presented in Figure 9 (1273 points) or Figure 8 (2059 points).

To sum up the paper, the most important conclusions can be noted:

● It's pretty easy to refute the myth that the strategy, the often described one, based on two simple moving averages will be effective. Crossing the long-term MA from the short-term MA suggests opening the short position, crossing the long-term from the bottom MA suggests opening the long position. This can be accidentally effective on selected fragments of a selected time series.

● The presented trading results can be improved by using additional filters. They can be commonly used indicators used individually or perhaps in combination. Without additional research, it is difficult to see what their effectiveness may be. Here, the RSI for the DAX index was successfully used.

● The presented simulations did not use a time-varying ratio of a learning cycle to test cycle. When observing the test results presented in the form of cumulative profit curves, better and worse parts of this curve can be seen. Maybe it is worth, especially if you have a lot of computing power, check the poor segment of the curve looking for a better L_p/T_p ratio.

● Searching for other time series, both in the field of Forex and in the field of indexes or commodities, for other periodicities of candlesticks is highly recommended.

The paper was developed without any financial support.

Conflict of interest

All authors declare no conflicts of interest in this paper.