1 Introduction

The therapeutic use of protons, suggested by R.R. Wilson in 1946 ^[1], permits to distribute dose radiation in a completely different way and with higher ballistic precision with respect to photons. The reason for this is in the completely different dose profile in depth that permits to deposit low dose in the entrance channel of the beam while increasing it in depth, that is in the region corresponding to the Bragg peak (BP), sparing completely the tissue beyond it. Moreover, charged particles are an effective alternative for the treatment of resistant tumors because they have an higher relative biological effectiveness in comparison with photons ^{[2,3,4,5,6,7,8]}.

Nowadays, proton therapy represents the state of the art of radiotherapy in terms of dose delivery techniques ^{[9,10,11,12,13,14,15,16,17]} but its uses are limited by the high cost of construction and maintenance of the equipment.

During treatment planning for Intensity Modulated Proton Therapy (IMPT) the intensity, energy and position of “spots” (Gaussian-shaped beams with a 3-5mm size (one sigma)), is optimized via mathematical criteria and specific algorithms for obtaining the best compromise between the higher dose achievable on the target tumor and the sparing of critical organs ^{[3,9,17,18,19,20,21,22,23,24,25]}. The two most commonly used treatment planning approaches are the single-field uniform dose method and full IMPT ^[5]. In the former method, each beam is optimized independently of the other proton beams with the aim to produce a uniform dose distribution inside the target tumor and to release a minimum dose outside. The latter method performs a simultaneous optimisation of all beams taking into account the objective of reducing, as low as reasonably achievable, the dose to normal tissues and to release the dose to the target regions ^{[26,27,28,29,30]}.

The main challenges in proton therapy planning are related to basic physics about radiation-matter interaction and the non-homogeneous patient body composition. The intrinsic physics uncertainty in particle range makes the argument of “sub-millimetre precision” an issue, which deserves careful consideration. In fact, the major advantage in the use of protons, that is the steep fall-off in dose deposition after the Bragg peak, has to be balanced with the disadvantage that it is not possible to determine with high accuracy where proton stops in matter. The range uncertainty is due also to CT calibration and is generally about 3.5%, but also related to patient motion during treatment and physical calculation of the deposited dose ^{[31,32,33,34,35,36]}. However, it can be minimized with better calibration techniques. The mentioned limitation could induce a non-correct calculation of the dose released in the patient that is affected anyway from errors due to complex inhomogeneities composition along the proton beam. The difficulty on the definition of safe planning and robust dose distribution on target sites where geometrical uncertainty is an important issue, requires the optimisation of the inverse treatment planning system ^{[37,38,39,40,41,42]}.

2 Materials and methods

2.1 Aims and Objective Functions in Treatment Plans

Inverse planning is the procedure used to define a treatment plan in the case of Intensity Modulated Proton Therapy (IMPT). The computation of the treatment plan is commonly achieved by using classical optimisation algorithms on some objective functions ^{[43,44,45,46,47]}.

A therapeutic treatment plan has the purpose of giving the best care to the individual patient. Since there is no formal definition of “best care” and each case is to some extent unique, the medical doctors in charge have some degrees of freedom in choosing the objectives of the treatment, also in agreement with the patients. These aims can then be translated in a multiobjective treatment plan that, in turn, can be expressed by objective function(s) and constrains ^[48,49]. There are in literature several objective functions and the research for objective functions that well formalise specific situations is a very active field but it is not the concern of this paper. Usually the objective function quantifies, in a proportional way, the dose of energy supported by healthy tissues/organs with a cost that is tissue/organs dependent. The constrains usually limit the amount of energy that an healthy tissue/organ must receive for not being compromised. There exist several protocols on this subject that can vary depending on age, gender, nations, medical doctors organizations and other variables. There is not an uniform consensus and, again, medical doctors have several freedom degrees on setting such constrains ^{[22,36,50,51,52,53,54,55,56]}.

Choosing the appropriate objective functions and constrains is a complex task. The first attempt is to find a treatment plan which leads to a low risk of exposition for healthy tissues while delivering the prescribed dose in the target zone. In some cases not all the constrains can be fulfilled, and, in such cases, a trade-off is required between the effectiveness of the plan and the constrains that cannot be fulfilled. As an example that is particularly relevant in this paper, let consider that in some plan it could be necessary to sacrifice part of healthy tissues in order to reach the prescribed coverage in the target region. The decision on what to sacrifice is left to the medical doctors, but, inside a plan optimisation problem, among several possibilities, it is possible to allow to go behind the safe dose on healthy tissues by assigning a function cost to every sacrifice option and include this in a new objective function ^{[8,42,57,58,59,60,61,62]}.

2.2 Complexity Theory approach in proves of hardness

Depending on the objective function and the constrains, which can formalise multiple requests (multiobjective) and even formalise uncertainty in order to have robust plans, the problem of finding an optimal therapeutic plan can became an hard task from the computational point of view and, indeed, it is commonly considered “hard”, even if a precise definition of “hardness” is not always clear.

From an extensive survey on scientific papers concerning the complexity of the plan optimisation problem (scientific articles, official reports, Ph.D. thesis etc.)*, it is common practice to embed an “instance” of plan optimisation in an “instance” of another problem, say Mixed Integer Programming or Sphere Packing, to claim correctly that Mixed Integer Programming or Sphere Packing is known to be computationally “hard” and then seek for some approximation of the second problem. This is a correct procedure from a practical point of view, and, also, the claims of hardness are correct, but these claims do not imply (i.e., there are not sufficient conditions to imply) the hardness of the plan optimisation problem. In order to prove the hardness, the most known technique in the Theory of Computation is to make the embedding in the reverse direction, i.e. to embed any “instance” of a chosen problem known to be hard into an “instance” of plan optimisation such that a fast solution of plan optimisation would give a fast solution of the chosen hard problem. These kind of embeddings are called reductions in the Theory of Computation and there are many kinds of reductions such as “polynomial reductions” for decisional problems or L-reductions, PTAS-reduction, APX-reductions and so on, for optimisation problems. Indeed very few scientific results claim hardness of plan optimisation, and all of them, in the considered set of scientific results, refer to IMRT and not to IMPT. Among them we cite Baatar et al. ^[63] that has as a consequence that the Beam On Problem, i.e. the problem of optimizing the time of a whole treatment plan considering the time needed to light-on the beams, is computationally hard. This result extends immediately also to IMPT if one wants to optimise the time of positioning the medical apparatus for the sequence of beams, and, also, it is not surprising in complexity theory since it is related to the tsp problem.

In this paper we prove an hardness result in the IMPT case but this result can be extended to the IMRT case with few changes, as discussed in Subsection 4.

2.3 A Combinatorial Definition of treatment planning optimization

Concerning the Complexity Theory and the Combinatorial Optimisation Theory, we consider the reader to be aware of the basic definitions and notations. In any case, we refer to ^[64,65,66] for any notations and definitions not given in this paper. We just notice a very small discrepancy among above papers: A (Fully) Polynomial Approximation Scheme is sometimes shortened as (F)PAS and sometimes referred as (F)PTAS for (Fully) Polynomial Time Approximation Scheme, where the added T stands for “Time”. In this paper we will use the latter form, i.e. (F)PTAS, that is an acronym that is more common in the literature than PAS.

In what follows when we say that a problem is computationally hard we mean that the problem does not belong to the class of the Polynomial-Optimization problems (PO), e.g. the class of problems for which exists an algorithm that finds optimal solutions in polynomial time. In particular, we will show in next section that the plan optimisation problem does not belong to PO under the usual assumption that ℙ ≠ ℕℙ. More precisely we will prove, under the same assumption, that plan optimisation does not belong to the class PTAS, that is the class of problems that admit a Polynomial Time Approximation Scheme, which includes class PO.

We consider the body to be treated as a subset V of ℤ³, or, equivalently, a cubic matrix. We consider a discretisation of the volume. Each unitary volume to be treated is usually called “voxel”. The idea is that a discrete grid is set through the body. More precise scales (for instance unit grid size of 1 millimetre instead of 3 millimetres) will lead to larger (artificially) volumes and, in turn, to more computationally demanding plans.

Each voxel in the body belongs to exactly one tissue class. Tissue classes can be defined through image segmentation, clustering, and labelling ^[67] and are used to recognize organs and tissues composing the target volume and, then, to describe the desired dose, or the admitting range of dose, to be delivered class by class. In fact, to each class C there are also associated two real constants c_min and c_max greater than or equal to zero representing respectively the minimum and the maximum dose value that each voxel containing a tissue of class C should receive. By means of c_min and c_max and, hence, the tissue classes, we can differentiate between Organs at Risk, Target Volume, and normal tissues of any kind with their own target dose.

We are going to define the treatment planning problem as an optimization (minimization) problem by means of penalty function that increases as the dose delivered to a voxel is out of the admissible range for the tissue in the voxel.

Moreover, to each tissue class C it is associated, formally by a function f_C, a numerical value that semantically represents, in the planning, the penalty cost for that tissue of having received a certain dose. In normal tissue f_C is usually assumed to increase linearly since it represents the risk of a radiation-induced illness whilst in neoplastic or target tissues it represents several weighted kinds of risks, first of all the possibility of non reaching the prescribed dose quantity that is given by c_min.

Notice that, for the combinatorial complexity purposes, function f_C is arbitrary at the moment, polynomial time computable, and it can be, for instance, linear for normal tissues and quadratic for some specific tissues, up to a certain dose and then increases drastically after c_max.

With abuse of notation we can say that a voxel contains a specific tissue. Also with abuse of notation we can consider the function f_C to depend on voxels since the tissue in the voxel is uniquely determined. Since each voxel in the body belongs to exactly one tissue class it is well defined a global function penalty (or cost) f whose restriction to a voxel belonging to class C coincides with the function f_C.

Function f depends on voxels, and, more precisely, on the class of the voxels and on the dose received by the voxels. In what follows we will explain how voxels can receive a dose, usually measured in Gray (Gy).

As part of the instance of the problem there is a set of beams B and the associated spacial distributions. More precisely each beam has a geometric 3-D “shape”, i.e. each beam b can give a non-zero dose to a finite subset S_b of voxels called the shape of b. The distribution of dose is a real function of the elements of the shape S_b that is explicitly described. For instance, a fixed beam b can be described by saying that b delivers a dose of 0.8 Gy to voxel indexed by coordinates (x, y, z), of 0.7 Gy to voxel indexed by coordinates (x, y − 1, z − 1) and so on for any voxel in the shape of b. Notice that the shapes can depend on the volume V to be treated. In this description, the voxels receiving zero dose are not considered even if, formally, any shape is defined on the entire volume. Whit abuse of notation, when it is clear from the context, we say that those voxels not receiving any dose from a beam b are not in the shape of b.

The shapes can be also described in some succinct way and often, in practical cases, the voxels of each shape represent a figure that is close to a discretized segment of a 3D-straight digital line and that has thickness equal to the size of voxels.

The dose delivered to a single voxel by a set B of beams is the sum of the doses that each beam of the set gives to that voxel, i.e. given a voxel v, the total dose received by v is

where b(v) is the dose delivered to voxel v by the beam b, according to the shape of b. In other words, doses adds-up linearly. The overall dose received by a volume V by a set B of beams is

Analogously, fixed a volume V and the shapes of the beams, we can define the overall dose D(b) given by a beam b such as

and the overall dose given by a set of beams B to be

Obviously we have that D(B) = d_B(V), i.e. the overall dose delivered to a volume V by a set of beams can be computed by adding-up the doses given by all beams or by adding-up the doses received by each voxel.

Given a beam b, for any non negative real number α it is possible to define the beam αb that is the new beam such that to each voxel of the shape S_b of b it delivers the dose of b times the real number α and it delivers no dose to all other voxels. Notice that αb is a new beam that is different from the original beam b, unless α = 1.

If a beam b is multiplied by a coefficient α = 0 this means that the beam αb does not deliver any dose, i.e. the beam b is absent and it will be not used in the computed plan.

A solution of the plan optimisation problem is a function A that to each beam b assigns a non negative real coefficient α_b for the set of beams given in the instance. As usual in combinatorial complexity, real numbers such as α_b have a description of fixed size, such as the request of a finite approximation description.

Through the solution A, the set of beams B is modified and changed into a new set of beams B_A, where each beam b in B has been modified into α_bb.

A solution A is feasible if the target(s) volume(s), i.e. all the voxels having a tissue with c_min > 0, has (have) received the prescribed dose of energy by the set of beams B_A following the dose-volume constraints.

Examples of dose-volume constraints can be the requirements that:

i no voxel in the target classes has received less than 90 per cent of the prescribed dose, where c_min can represent this 90 per cent, that

ii at least 95 per cent of the voxels in each target class C have received the prescribed dose, and that

iii at most a given percentage of voxels having tissue of some specific class must receive a dose greater than a given bound.

Other kinds of constrains are also used in practice but in this simplified model we consider only the constrains of the kind i and we do not consider any other kind of constrains but we will still obtain an hardness result.

If we admit the value +∞ as penalty value for a volume receiving a dose smaller than c_min, then any solution A is feasible from the combinatorial complexity point of view. Hence from now on we admit that the function f can assume the value +∞ and that any solution A is feasible. We stress the fact that solutions where f assumes value +∞ are usually considered non-valid solutions in practical cases.

Among all the possible solutions A one look for minimizing the the sum of the penalty function f over all voxels of the volume. The function f is calculated on the dose that the set of beams B_A = {α_bb | b ∈ B, α_b = A(b)} gives to each voxel. More precisely the sum to be optimized, that we call the penalty of the treatment is

where, we recall that, according to Equation 1, dBA(v)=∑b∈BAb(v), with b(v) the dose delivered to voxel v by the beam b ∈ B_A^†

It must be clear that it is not possible to give a dose to a single voxel without affecting other voxels next to it or lying on the trajectory of the beams; this should be taken into account when we describe the shapes of the beams in the instances.

It is easy to prove that the plan optimisation belongs to the complexity class NPO. Indeed after choosing in linear non-deterministic time a solution A, all the other computations can be performed in polynomial deterministic time.

In what follows we state the plan optimisation problem in the style of the hundreds of problems stated in ^[68]. We give here the name minimum penalty treatment problem in order to empathize the penalty function f, but in this paper, often in the discussions, we will maintain the name “plan optimisation” problem as a synonymous.

MINIMUM PENALTY TREATMENT

•   INSTANCE: i. A body V ∈ ℤ³. ii. A disjoint partition of V = C₁ ∪ C₂ ∪ … C_n into n tissue classes. iii. A penalty function f that to each voxel associates a non-negative value or +∞. iv. A set B of beams.

The value f(v) depends only on the class to which v belongs and on the dose that v will receive by the set of beams given as solution. Any beam b in general is a non-negative real function whose domain is V and b(v) is called the dose delivered by b to voxel v.

•   SOLUTION: A function A that associate to each beam b ∈ B a non-negative value α_b, and the associated set of beams B_A = {α_bb | b ∈ B, α_b = A(b)}.

•   MEASURE: The overall penalty, i.e. ∑v∈Vf(dBA(v)), where dBA(v)=∑b∈BAb(v).

In previous formalisation we did not stated the constants c_min and c_max since they can be implicitly considered in the function penalty. As already noticed, real numbers here have a finite description such as, for instance, 8 bytes.

Above simple formalisation of the plan optimisation problem is sufficient to have computationally hard instances. Consequently, any more complex formulation of the plan optimisation problem that include our model will contain hard instances too. Hence, those complex formulations will be at least as computationally hard as our simplified model.

Before giving in Section 3 the proof that plan optimisation is computationally hard (id est, that it belongs to NPO\PO under the standard assumption that ℙ ≠ ℕℙ), we list the following observations.

1. The function f represents the cost, for a given voxel containing a specific tissue, of having received a dose. Since it is often assumed that radiation side effects are proportional to the dose, function f often increases linearly up to a threshold c_max which represents the point where the cells starts dying. The threshold can be a strict constrain or a flexible constrain as described in what follows.

1. Medical doctors can ask to not irradiate some tissue either by setting a constrain or simply by setting the function f extremely high (or even infinite) for low radiation dose in that tissue class. Here tissue class may differ from actual tissue and we can have more than one tissue class referring to a tissue. For instance, if a particular region of the body has to receive a lower dose than another, we can assign all voxels in that region to a “virtual” tissue class having specific values of the penalty function f.

1. The dramatic increasing of the function f, even a discontinuous step, after a certain threshold represents the fact that the tissue in the considered voxel is close to or have received a dose causing a complete destruction. After this threshold, the function f can be constant in order to represent the fact that, once the tissue in a voxel is destroyed, there is nothing left to loose.

Our purpose here is to give an acceptable simplified formalisation that allows us to prove our main result that will be described in the next section by allowing to embed, via an L-reduction, all the instances of 3-vertex cover (see ^[68]), which will be defined in the following paragraphs.

L-Reduction definition. Given two NP optimization problems F and G and a polynomial time transformation f from instances of F to instances of G, we say that f is an L-reduction if there are positive constants α and β such that for every instance x of F^‡

1. opt_G(f(x)) ≤ α · opt_F(x),

1. for every feasible solution y of f(x) with objective value m_G(f(x), y) = c₂ we can in polynomial time find a solution y' of x with m_F(x, y') = c₁ such that |opt_F(x) − c₁| ≤ β|opt_G(f(x)) − c₂|.

Using L-reductions one can show that a problem F is APX-complete, i.e., F is approximable within c for some c and every approximable problem can be L-reduced to F.

3-Vertex Cover definition. Given a graph G = (V, E) with out-degree of each node ≤ 3, A 3-Vertex Cover for G is a subset V' ⊆ V such that, for each edge (u, v) ∈ E, at least one of u and v belongs to V'. The measure of the solution is the cardinality of the vertex cover, i.e. |V'|.

3 Results

3.1 The minimum penalty treatment problem is computationally hard

In some cases the target volume has a complex shape, such as non-convex polytope or, may even have non connected parts, such as in the case of multiple focal lesions. It is possible that in any planning some voxel of healthy tissue next to the target will receive an amount of energy that will destroy the underlying tissue. The doctor in charge can decide, and this usually happens, that an optimal planning has to minimize the volume of such kind of healthy tissue to be destroyed whilst respecting the remaining constrains and objectives. As noticed in above subsection, this request of saving as much tissue as possible can be formalised through the function f that will be set to be very high and eventually constant once the above threshold on the dose has been attained.

Next proof is technical. In particular to any instance of 3-vertex cover it will be associated a formal instance of plan optimisation in a constructive way. This association will be therefore algorithmic (and feasible in polynomial time) and any optimal solution of the corresponding instance of plan optimisation will be an optimal solution for the 3-vertex cover instance. In technical words the association will be an L-reduction.

It must be clear that the instances of the plan optimisation problem that we are going to build are totally artificial/formal. To build realistic instances corresponding to strange shapes/graphs is not required for our purposes. Our result, even with artificial instances, tell us that, under the assumption that ℙ ≠ ℕℙ, any automatic solver for the general plan optimisation problem must face also hard instances that cannot be optimized in polynomial deterministic time.

Despite above disclaimer, we want here to add that situations where the target tissues are almost surrounded by Organ At Risk (OAR) like the instances that we are going to build, can be found in practical cases, such as in prostate cancer and in cases where, unfortunately, the target tissue (focal lesions) is itself a part of an OAR.

The problem vertex cover is the very first problem among the hundreds reported in ^[68]. The 3-vertex cover problem restricts the instances to graphs with vertex out-degree smaller than or equal to 3, and it is formally defined at the end of Section 2. In Figure 1 there is an instance of 3-vertex cover and in Figure 2 its solution.

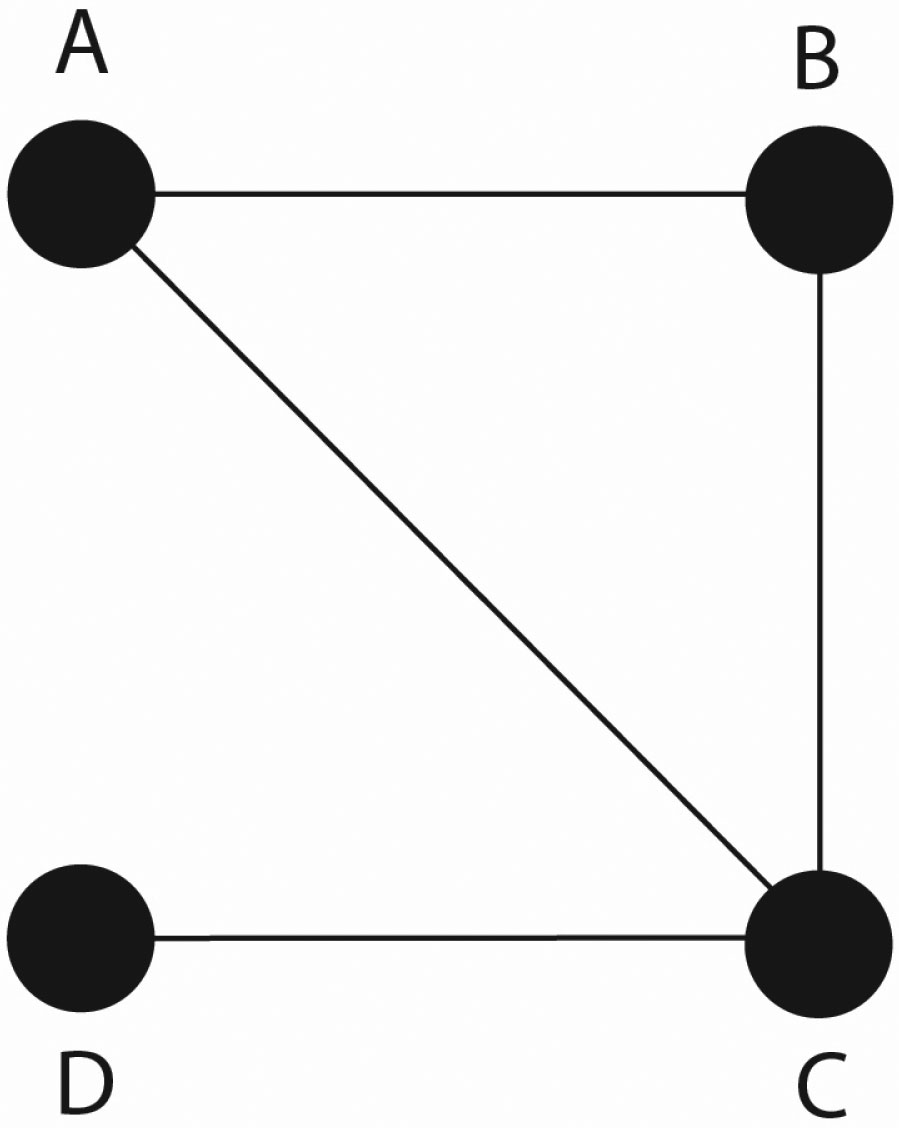Figure 1. An example of instance of 3-vertex cover.

DownLoad: Full-Size ImgPowerPoint

Figure 2. A solution for the 3-vertex cover in Figure 1, i.e. a solution is the set {B, C}.

DownLoad: Full-Size ImgPowerPoint

We associate to a generic instance of 3-vertex cover an instance of plan optimisation in the following way: to any edge (u, v) ∈ E we associate a voxel containing target tissue that has as name uv. Semantically they can be considered as focal lesions. We consider them evenly spaced in an horizontal stripe inside a cube of healthy tissue that is surrounded by six square voxel surfaces of a tissue that we call “Organ At Risk tissue” (OAR tissue) having the constrain that the irradiation dose tolerated per voxel must be close to zero (or, analogously, that the function f assume values close to +∞ even for very small amounts of energy). One of this square voxel surface has |V| “entrances”, small voxels squares where there is healthy tissue and not OAR tissue. Also this cube is contained inside a larger volume of healthy tissue. The “entrances” are in a bijective correspondence with vertices in V, through a polynomial computable function g. The entrances are holes of the smallest size that allows beams to enter in the main area giving negligible dose to OAR tissue. We assume that the grid resolution is large enough to neglect the issues about the discretisation of continuous variables.

In the general case, we require that all the “entrances” are in an horizontal stripe. They are equally spaced of at least 4s(|V| + |E|) voxels, where s is the average linear geometrical size of our beams when in the chosen resolution they intersect the entrances. More details for the specific instance corresponding to the instance of Figure 1 are given in Figure 3 and in Figure 5.

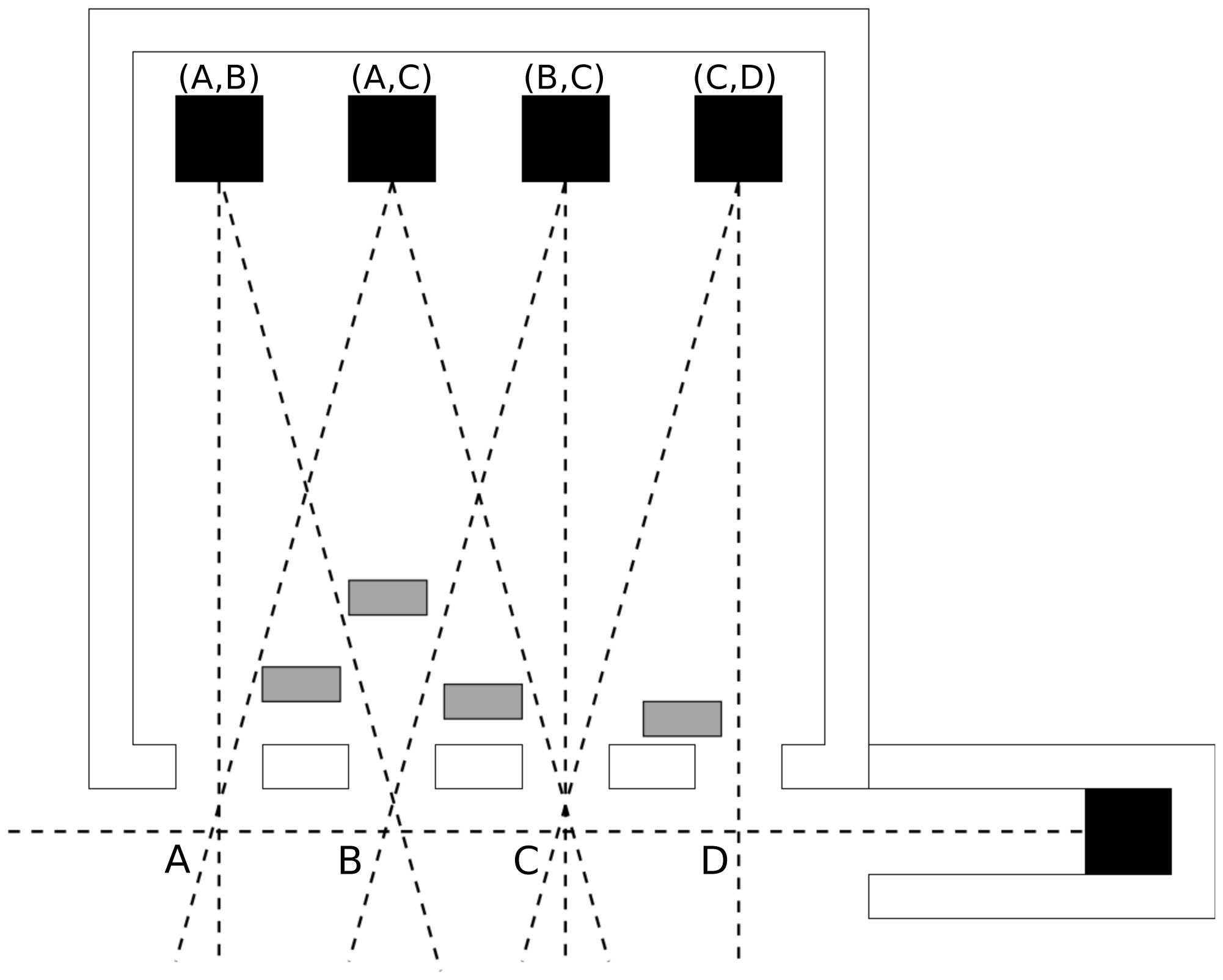Figure 3. A 2D projection of the corresponding instance of plan optimisation in Figure 1. White boxes are obstacles/forbidden regions of voxels. Dark boxes represent target volume. Points A, B, C, and D are entrances for the main area. Lines represent viable trajectories from an entrance to a target in the main area. Any beam targeting the external target volume (in the lower-right corner) has to pass over points A, B, C, and D.

DownLoad: Full-Size ImgPowerPoint

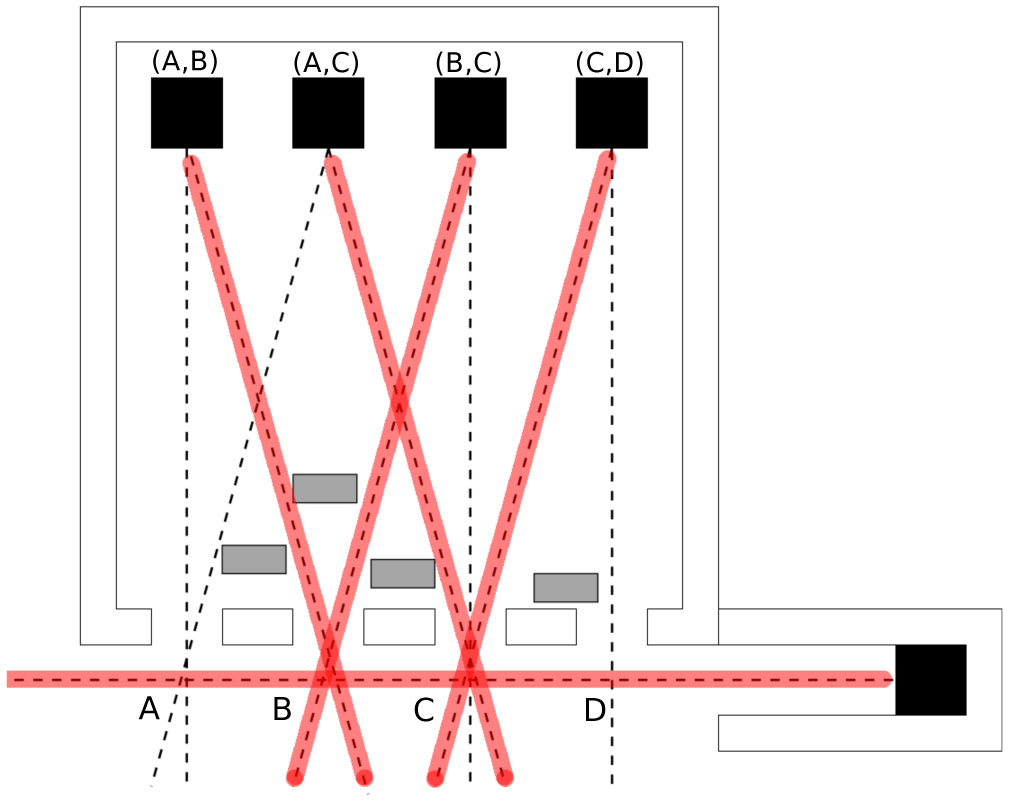Figure 4. A solution for the instance of the plan optimization problem in Figure 3. It corresponds to the solution of Figure 2. When f is a 0 - 1 step function, the overall penalty is 2 where penalty equal to 1 comes from entrance B and 1 from entrance C. These are the only places where normal tissue has been destroyed

DownLoad: Full-Size ImgPowerPoint

In the construction of the corresponding instance of plan optimisation we add a target volume that is external to the cube that can be irradiated only by using a beam that covers all the entrances. This is feasible by using a geometric box of OAR tissue surrounding a target volume that have an entrance strip on one side. The energy per voxels that is released by these beams must be on the entrances very close to the threshold (that we set) of normal tissue. Notice that in real cases this can be done by the mean of a technique known as “spread-out Bragg peaks”. The external target volume in Fig. 3 is on in the lower-right corner because it force the solution to have a beam entering on the lower-left corner, traverse the points A, B, C, D and reach the target volume on the lower-right corner of the figure. It is carefully placed in order to release a dose also to points A, B, C, D and make them almost hot spots, i.e. points that will take a dose almost equal to what a normal tissue can tolerate. Any further energy would destroy the tissue that they contain, and this gives a big penalty (or penalty 1 in the case when f is a 0 - 1 step function). After that the intersection/entrance has the tissue destroyed, any other beam passing there would not give further penalty. This stress the importance to carefully choose, and in turn minimize, the use of beams through those points.

In the new associated instance we have to define the set of beams B. The shapes of the beams are discretized segments of 3D-straight digital lines with uniform distribution. Moreover we allow proton beams to pass from an entrance g(v) (in Figure 3 we called the entrances with the same labelling of the corresponding vertex) to a target volume xy if and only if x = v or y = v. We can do it by setting the set of beams of the instance to be composed by exactly these beams, or, in order to be more realistic, we can use “obstacles” of OAR tissue to forbid the non allowed directions, whilst the set of beams is composed by all beams that can reach any focal lesion from any entrance, plus the “external” beam that has to hit the “external” target. Notice that in this way the cardinality of the set of beams is polynomial in the size of original instance since its cardinality is O(|V| × |E|) and also the cardinality of the “obstacles” has the same bound.

We left enough space between entrances and between target volumes in order to have the possibility of putting such obstacles and we put the target volumes in diagonal in order to maintains non-overlapping or crossing beams. Figure 3 reports a 2D projection of the instance of the plan optimization and Figure 4 one of its solutions. Notice that beams that have to hit one internal target tissue must have the direction uniquely determined by the target volume and the entrance.

Last, but not least, we can suppose that all the beam have the cost C_B. This can be done by playing on the external boundaries of the instances (that are not represented in the figures) or by using voxel of other defined tissue with different cost-values. Here, with cost of a beam C_B we mean the sum of the function cost over all the voxels affected by the beam except where they can intersect, i.e. in S_b\(g(V) ∪ g(E)), where g(V) is the set of entrances and g(E) is the set of targets.

We can also have equal-cost beams by setting the cost function f to be 0 up to the threshold c_max of normal tissue and 1 at the threshold and over, i.e. the cost can be formally set to be a classical 0 - 1 step function.

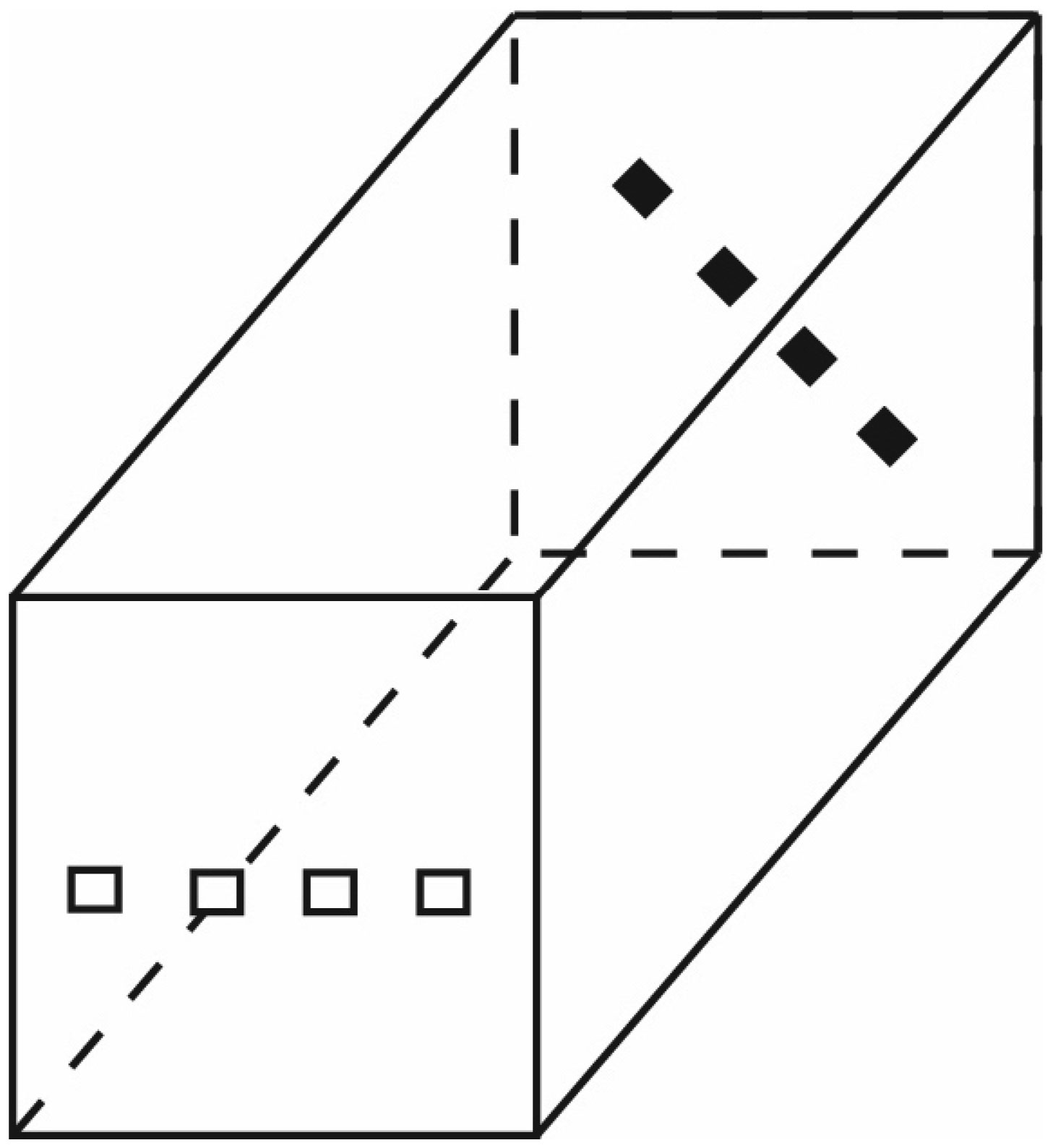Figure 5. Partial 3D representation of the corresponding instance of Plan Optimisation. Black cubes represent target volume. White cubes represent the entrances lying on an horizontal stripe. Due to the spatial distribution, no beam can intersect any other except in the target volumes and in the entrances.

DownLoad: Full-Size ImgPowerPoint

In Figure 5 there is represented a part of the corresponding instance of plan optimisation where it is emphasized the spatial distribution of entrances and target volumes. It is not difficult to prove that no beam intersect any other except in the target volumes and in the entrances.

Now we have transformed any instance of 3-vertex cover into an instance of plan optimisation. This transformation can be done in polynomial time. Let us now try to find an optimal solution of the newly defined instance of plan optimisation.

Moreover, without loss of generality, we can set the function f on normal tissue to be linearly non-decreasing up to the threshold value and, after, f to have a larger constant value. The threshold value is the unique point of discontinuity with gap value (that is the difference between the value of the right and left limit of f in the threshold point) equal to G_f. Therefore the cost of any plan is equal to the costs of beams used to cover the external target volume plus C_B × |E| plus G_f times the number of voxels of normal tissue where the threshold has been attained.

An optimal plan minimize above value. Since the costs of beams for the external target volume plus C_B × |E| represent a constant in any plan, an optimal plan must minimize the number of voxels of normal tissue where the threshold has been attained.

Any generic uv inner target (to the cube) voxel can be reached only by the two beams passing through either entrance g(u) or entrance g(v) or both. Since we suppose that entrances have already received a dose very close to the threshold, the voxels at the entrance g(u) or the voxel at the entrance g(v) or both will eventually receive a dose that exceeds the threshold. Therefore, an optimal plan which aims to minimize the (normal) tissue on which the threshold will be attained, will choose only one of the two entrances per target, and, then, it will minimise the number of entrances used to reach all the target volumes. This, in turn, corresponds to find a minimal vertex cover in the original 3-vertex cover instance.

Let us now prove that there exists a polynomial reduction between the two languages associated to the above optimisation problems.

An instance of the language associated to 3-vertex cover is equal to an instance of the general problem together a number k. It has solution yes if there exists a vertex cover of size smaller than or equal to k and no otherwise.

An instance of the language associated to minimum penalty treatment is equal to an instance of the general problem together a number H. It has solution yes if there exists a plan that costs less than H (i.e. the overall penalty ∑v∈Vf(dBA(v)) is smaller than H) and no otherwise.

We have to define a reduction from the language associated to 3-vertex cover and the language associated to minimum penalty treatment.

Above construction, with a specific value H, is the reduction that we are looking for. The value H is equal to the sum of the costs of beams used to cover the external target volume plus C_B × |E| plus G_f times the number of voxels constituting each entrance times k, where k is the value of the original instance.

It can be proved that above construction can be done by a polynomial time computable function. Moreover this construction brings instances with answer yes in instances with answer yes and instances with answer no in instances with answer no. This means that it is a polynomial reduction between languages. Since the language associated to 3-vertex cover is ℕℙ complete, the same holds for the language associated to minimum penalty treatment. The theory tell us also that in this case, under the hypothesis that ℙ ≠ ℕℙ, the corresponding optimisation problem is in NPO and not in PO, i.e. we have proved that plan optimisation is computationally hard.

We improve previous result as in the following.

Let us define now the function f to be the 0 - 1 step function described above over the healthy tissue and define the f to have also value equal to zero over the target volume if the desired dose has been attained. It is easy to prove that above transformation between instances of the two original optimisation problems is an L-reduction.

Indeed an L-reduction can be obtained also by using a function f built in a way such that there exists an ε > 0 having the property that the gap value G_f is greater than ε × C_B (and also greater than a percentage of the cost of the beam for the external target if this cost is not considered constant). In this last case, that is more realistic than the previous that uses the 0 - 1 step function, it is essential the use of 3-vertex cover instead of vertex cover in order to have an L-reduction.

Since there exists an L-reduction between 3-vertex cover and minimum penalty treatment, and 3-vertex cover is APX complete and there exist no Polynomial Approximation Schemes for it, if ℙ ≠ ℕℙ (see ^[69]), the Theory of Calculability tell us that the same hold for minimum penalty treatment. Therefore we have proved the following theorem.

Theorem 1 If ℙ ≠ ℕℙ, the minimum penalty treatment Problem belongs to NPO\PO. More precisely it belongs to NPO\PTAS and it is APX complete.

4 Discussion

Theorem 1 can be extended to the IMRT case. The construction of an instance of minimum penalty treatment can be modified by adding some “exit” holes in correspondence of the exits of photon beams after that they have reached the targets volumes. In particular, there must be an “exit” in the OAR behind every target volume. Indeed, corresponding to each trajectory from one entrance g(v) to one target vx, we add a beam-size “exit” that allows the photon beam to pass through without delivering energy to OAR tissues.

We want here to recall that even if a problem is computationally hard it is still possible that for a sub-problem (i.e. for a set of instances that represent a proper subset of the instances of the original problem) there exists a PTAS or, better, a FPTAS or, even better, a linear algorithm that would mean that the instances of our interest can be settled efficiently in practice. The Combinatorial Optimisation Theory offers plenty of practical solutions for other problems that could be used, via reductions, for the instance of interest of the plan optimisation problem. Some of these techniques have already been used in practice for finding effective solutions to instances of the plan optimisation problem. Indeed computing a treatment plan for radio and proton therapy is nowadays commonly achieved by means of optimisation algorithms according to an approximation approach.

The Theory of complexity offers many possibilities of modelling some huge subsets of instances of minimum penalty treatment into an hard problem or sub-problem that admit a PTAS or a FPTAS. For example, it is possible, to simulate a treatment plan with a weighted graph, where the voxels of target volumes are the target nodes, the voxels that represent the possible beam-entrance points into the body are non targeted nodes that are all linked to a single outer node, called root, with arcs having a common low weight that can represent the average time cost of lighting a single beam, whilst the cost of arcs between the beam-entrance points and target nodes correspond to the assigned a weight to be defined by the doctor. With this model, under the hypothesis that no voxels have to be sacrificed (i.e. all of them can receive a dose below the threshold in an optimal plan), finding an optimal Steiner tree in this graph would be a “close to optimum” treatment plan and there exists Polynomial Approximation Schemes if every element of the target set S is adjacent to Θ(|V − S|) elements from V − S (see ^[68]).

We conclude this discussion with several open questions.

What is the degree of approximation that standard solutions achieve? Are there other approximation techniques suitable for this problem? Are all the practical instances of this problem all belonging to the same class of complexity? Are there fully polynomial approximation schemes or even linear time algorithms that can allow in practice a dynamic/real time update of the planning in the majority of the real cases? Are there classes of instances of plan optimisation problem that can be easily recognised, by the geometry of the instance or other characteristic, as belonging to a sub-problem that allows fast solutions and dynamic/real-time update?

5 Conclusion

We investigate on the plan optimisation problem under the point of view of the Theory of Complexity in general and, in particular, of the Combinatorial Optimisation Theory where precise notions of hardness and of approximability are given. In this setting we prove the hardness of the general plan optimisation problem; moreover, we show that variations of some algorithms used for other hard problems can be fruitfully used in the plan optimisation problem and we leave open several natural questions. The proposed results suggest that the Theory of Complexity can give valuable conceptual and practical tools for new deterministic algorithms of treatment planning with bounded time complexity. Time saving in planning, by exploiting near real-time procedures, could be effectively employed for improving spatial resolution of planning strategies. Part of the time saved could be used for considering diagnostic images with higher resolution and/or for applying planning procedures interleaved to radiotherapy sessions in order to verify the effectiveness of the therapy itself and for correcting potential errors. Moreover, time reduction would increase the frequency of treatment sessions (the number of patients treated for time unit).

Acknowledgements

The authors thank Professor Guido Proietti for valuable discussions and the anonymous referee for her/his comments that helped to improve the presentation of this article.

*According to Google Scholar database, there are more than 400 documents containing the words “plan optimization” and one of “NP”, “hard”, “beam”. About 200 of those documents are related to plan optimisation in radiotherapy. It is worth noticing that Google Scholar in this search recalled and highlighted also documents containing the word “difficult” as synonymous of “hard” and also the word “complete” associated to “NP”.

^†Nowadays, for IMPT robust planning, the average number of beams in feasible solutions ranges between 10³ to 10⁴. In literature, what we call here beam is often called sub-beam and a beam is often referred to a small set of spatially-close beams.

^‡This definition of L-reduction is reported from ^[69].

Conflict of interest

All authors declare no conflicts of interest in this paper.