Citation: Hassam Nasarullah Chaudhry, John Kaiser Calautit, Ben Richard Hughes. The Influence of Structural Morphology on the Efficiency of Building Integrated Wind Turbines (BIWT)[J]. AIMS Energy, 2014, 2(3): 219-236. doi: 10.3934/energy.2014.3.219
| [1] | Nour Khlaifat, Ali Altaee, John Zhou, Yuhan Huang . A review of the key sensitive parameters on the aerodynamic performance of a horizontal wind turbine using Computational Fluid Dynamics modelling. AIMS Energy, 2020, 8(3): 493-524. doi: 10.3934/energy.2020.3.493 |
| [2] | Ammar E. Ali, Nicholas C. Libardi, Sohel Anwar, Afshin Izadian . Design of a compressed air energy storage system for hydrostatic wind turbines. AIMS Energy, 2018, 6(2): 229-244. doi: 10.3934/energy.2018.2.229 |
| [3] | Navid Majdi Nasab, Jeff Kilby, Leila Bakhtiaryfard . Integration of wind and tidal turbines using spar buoy floating foundations. AIMS Energy, 2022, 10(6): 1165-1189. doi: 10.3934/energy.2022055 |
| [4] | Nathnael Bekele, Wondwossen Bogale . Parametric study of a diffuser for horizontal axis wind turbine power augmentation. AIMS Energy, 2019, 7(6): 841-856. doi: 10.3934/energy.2019.6.841 |
| [5] | Rashid Al Badwawi, Mohammad Abusara, Tapas Mallick . Speed control of synchronous machine by changing duty cycle of DC/DC buck converter. AIMS Energy, 2015, 3(4): 728-739. doi: 10.3934/energy.2015.4.728 |
| [6] | Nadwan Majeed Ali, Handri Ammari . Design of a hybrid wind-solar street lighting system to power LED lights on highway poles. AIMS Energy, 2022, 10(2): 177-190. doi: 10.3934/energy.2022010 |
| [7] | Azevedo Joaquim, Mendonça Fábio . Small scale wind energy harvesting with maximum power tracking. AIMS Energy, 2015, 2(3): 297-315. doi: 10.3934/energy.2015.3.297 |
| [8] | Ayman B. Attya, T. Hartkopf . Wind Turbines Support Techniques during Frequency Drops — Energy Utilization Comparison. AIMS Energy, 2014, 2(3): 260-275. doi: 10.3934/energy.2014.3.260 |
| [9] | Saiyad S. Kutty, M. G. M. Khan, M. Rafiuddin Ahmed . Estimation of different wind characteristics parameters and accurate wind resource assessment for Kadavu, Fiji. AIMS Energy, 2019, 7(6): 760-791. doi: 10.3934/energy.2019.6.760 |
| [10] | Sri Kurniati, Sudirman Syam, Arifin Sanusi . Numerical investigation and improvement of the aerodynamic performance of a modified elliptical-bladed Savonius-style wind turbine. AIMS Energy, 2023, 11(6): 1211-1230. doi: 10.3934/energy.2023055 |
The wind power industry has gone through a steady development over the years, focusing on an increasing interest in generating electricity from the wind. With the global energy concerns about the greenhouse gas emissions, considerable investment has been made into using wind as a renewable source of energy for the purpose of generating electricity. In 2007, the Bahrain World Trade Centre introduced the world’s first building integrated wind turbines. This was the first instance that a commercial development integrated large-scale wind turbines within its design to harness the power of the wind. The three turbines, measuring 29 meters in rotor diameter were supported by bridges spanning between the complex's two towers. Through its positioning and the unique aerodynamic design of the towers, the prevailing on-shore Gulf breeze is intended to be funneled into the path of the turbines, helping to create power generation efficiency. The anticipated benefits determined that once the system was operational, the wind turbines delivered approximately 11-15 % of the energy needs of the building, or 1, 100 to 1, 300 megawatt-hours per year [1].
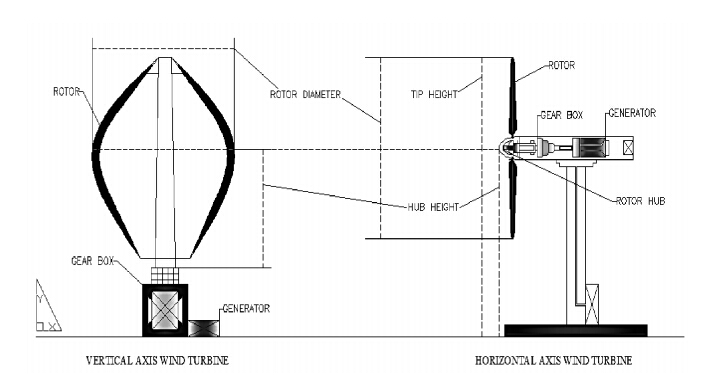
There are currently two major types of operational wind turbine technologies which can be used for building integration. These are classified as the Horizontal Axis Wind Turbines (HAWT) and the Vertical Axis Wind Turbines (VAWT). Horizontal axis wind turbines are the more common type of wind turbines in demand. In these turbines, the focus rotor shaft is pointed parallel to the direction of wind while the blades move perpendicular to that direction, thus providing high overall efficiency. On the other hand, the vertical axis wind turbines orientate on vertical axis where the focus rotor shaft is aligned vertically. A two-dimensional ‘not-to-scale’ design modeling based on the two wind turbine technologies is shown in Figure 1. The schematic provides the essential information on the individual situation of the major components in the wind turbine structure [2].
Figure 1. Structural comparison between the horizontal axis wind turbines and vertical axis wind turbines [2].
The potential of integrating wind turbines into buildings is vast since the wind speed is intensified at high altitudes resulting in an increase in electricity generation. Several wind turbine manufacturers have conducted extensive research on this technology since it aligns well with a strong appeal to shift from fossil fuels to renewables. Theoretically, the air velocity incrimination is directly proportional to increasing elevation, as it is unaffected by the urban environment and surrounding topography. Thus, installing wind turbines on top of buildings allows for taking advantage of this height efficiently. However, in many cases, the building geometry and its aerodynamic features can further assist in enhancing wind turbine performance by inducing a higher volume of air than the macro-climate [3,4].
Numerical analyses involving Computational Fluid Dynamics (CFD) are often carried out for evaluating building design and energy performances. In the past few years, CFD has been playing an increasingly important role in the design of buildings. The information provided by CFD assists in investigating the impact of building technologies, quantifying indoor environment quality, and in integrating renewable energy systems. In this paper, the CFD modeling approach is used out in order to determine the influence of building morphology on the efficiency of building-integrated wind turbines.
Work related to implementation of renewable energy as power sources in buildings, in particular wind energy is rapidly increasing. Following is a concise assessment of previous work related to this investigation.
Chong et al. [5] conducted a study on the design of a wind turbine generator for the purpose of energy consumption in buildings. Two VAWTs in cross-wind orientation were integrated with an enclosure were installed above a cooling tower in order to harness the discharged wind for electricity generation. The enclosure in this case acts as a wind-power augmentation device to improve the performance of the wind turbine. The effect of installing the energy recovery turbine generator at the outlet of an exhaust air system was investigated via laboratory test on a scaled model of a cooling tower.
The tests were conducted with and without the VAWTs on the performance of the system. From the laboratory testing, it was observed that installing VAWTs at a correct position above the exhaust air system did not indicate any significant negative impacts on the performance of the cooling tower model. The performance of the cooling tower model was improved by the increment of intake air speed and the reduction off the motor power consumption. The rotational speed of the VAWTs were very high (> 400 rpm) while the tip speed ratios were in the range of 1.28-1.29, making it preferable for electricity generation. The exercise of using VAWTs in building was further studied by Muller et al. [6]. The study established graphical models to determine the theoretical efficiency of the Sistan type windmill. The work supports the initiative of integrating wind energy converters into buildings by employing geometry changes to the model under study in order to indicate the maximum expected convertor efficiency of 61 %.
Sharpe and Proven [7] carried out detailed work on the concept and early development of a building integrated wind turbine in Scotland. The Crossflex proposal used in this investigation is based on the Darrieus turbines approach, consisting of two or more flexible aero foil blades attached to both the top and bottom of a vertical rotating shaft. The blade design incorporated low solidity and low mass materials for its construction. Although the development of this technology is still in its early stage, the study has outlined the remaining tasks of its work. The subsequent stages will involve supplementary computer modeling using CFD analysis to model airflow over the cowling to establish the nature of augmentation and flow stability that may occur, and to optimise the design in respect of these.
Lu and Sun [8] presented an integrated method of both macro (weather data and domain topography) and micro aspect (CFD) analysis in order to design wind turbines around numerous high-rise buildings with predominant wind in Hong Kong. Long-term wind data were compared at dense urban island and small island stations. The mean wind speeds for the urban locations were estimated at 2.93 m/s at 25 m above ground level. The study’s findings determined that the wind power density at 4 m above the building roof was enhanced numerously by 1.3-5.4 times with 5-7 m/s inlet velocity.
Mithraratne [9] investigated the performance of wind turbines mounted on roof-tops, used for micro-generation in municipal houses in New Zealand. The research focused on energy consumption over a lifetime of the wind turbine with respect to the energy generation and Green House Gas (GHG) emissions at various circumstances in the life cycle. The work concluded that the feasibility level of roof-top wind turbines is generally poor as compared to large scale wind turbines for micro-generation.
Bahaj et al. [10] studied the significance of micro-wind turbines in generating energy in buildings. The work was based on various cities in the UK in accordance with accurate wind speed data, to evaluate the financial feasibility and appropriateness for domestic houses. The research concluded that areas of high wind speeds are most likely to benefit from micro-wind turbines as the payback period is notably less than the design lifetime and a significant reduction in carbon footprint is likely.
Lu and Ip [11] carried out work on the viability of implementing wind energy as a major power source for buildings in Hong Kong. The study comprised of CFD modeling based on the energy and turbulence models for analysis of various building structures. The research concluded that the height of high-rise buildings could be exploited to its optimum capability to improve the efficiency of wind turbines for power generation.
Li et al. [12] investigated the wind loads on the Pearl River Tower building in China to determine the power generation potential of wind turbines using wind tunnel testing. The Pearl River Tower, located in Guangzhou has 71 stories and rises about 310 m from the ground, which features four open holes (tunnels) equipped with four wind turbines at mechanical floors on two height levels. The objective of this study was to evaluate the wind speed amplifications in the tunnels for wind-power generation through the installation of wind turbines and to gain a better understanding of the wind effects on such a high-rise building with open holes. The findings from the analyses indicated that the bell-mouthed shape of the wind tunnels with contracted inner sections were useful in increasing the wind velocities at the location of the turbines. In addition, the work revealed that the presence of surrounding buildings influences wind speed amplifications and wind loads on the building structure.
Building upon the previous work carried out in literature, the focus of this study was to investigate the power generation potential of building-integrated wind turbines by analysing the effect of the structural morphology on its efficiency. The physical geometry of the Bahrain Trade Centre was taken as the benchmark model and the performance of wind turbines in response to the extracted wind using the building envelope was investigated using advanced numerical and theoretical analysis.
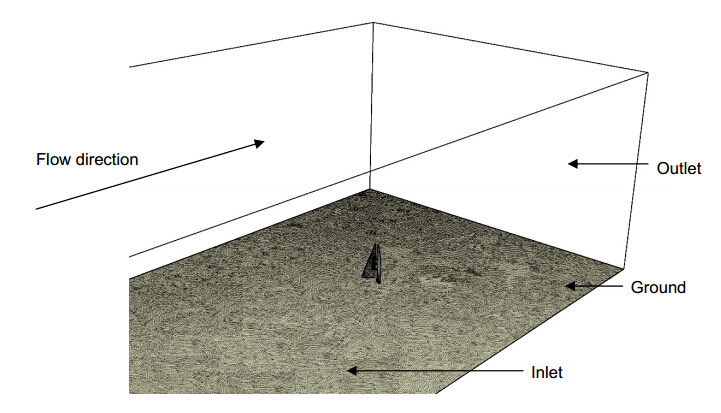
The computational domain comprised of the building geometry, which was designed according to the actual specifications of the high-rise tower and the specific wind turbines. The two 50 storey sail shaped towers are reported to measure to a height of 240 m and support three horizontal-axis wind turbines incorporating a rotor diameter of 29 m [1].
The three-dimensional Reynolds-Averaged Navier-Stokes (RANS) equations along with the momentum and continuity equations were solved using the commercial CFD code for the velocity and pressure field simulations. The model employs the control-volume technique and the Semi-Implicit Method for Pressure-Linked Equations (SIMPLE) velocity-pressure coupling algorithm with the second order upwind discretisation. The standard k-e transport model which is frequently used for incompressible flows was used to define the turbulence kinetic energy and flow dissipation rate within the model [13,14]. The use of the standard k-e transport model on building configurations has been found in previous works of [2,15,16,17]. The turbulence kinetic energy, k, and its rate of dissipation, e, are obtained from the following transport equations formulated in equation 1 and equation 2.
| ∂∂t(ρk)+∂∂xi(ρkui)=∂∂xj[(μ+μtσk)∂k∂xj]+Gk+Gb−ρε−YM+Sk |
(1) |
| ∂∂t(ρe)+∂∂xi(ρeui)=∂∂xj[(μ+μtσe)∂e∂xj]+C1eek(Gk+C3eGb)−C2ερe2k+Se |
(2) |
Where: Gk represents the generation of turbulence kinetic energy due to the mean velocity gradients, Gbrepresents the generation of turbulence kinetic energy due to buoyancy. YMrepresents the contribution of fluctuating dilatation in compressible turbulence to the overall dissipation rate. C1e, C2e and C3e are constants; σk andσe are the turbulent Prandtl numbers for k and e.
Mesh generation is one of the most important processes in CFD simulation. The quality of the mesh plays an important role on the accuracy of results and the stability of the solution. For the investigated computational domain, patch independent CFD tetrahedron meshing technique was applied on the geometry wherein the boundary conditions were applied on the edges and faces. The patch independent mesh algorithm for tetrahedron elements is based on the subsequent spatial subdivision algorithm which ensures refinement of the mesh where essential, but retains larger elements where feasible, therefore allowing faster computing times. The meshed model comprised of 2, 013, 428 nodes and 10, 849, 999 elements as displayed in Figure 2. The minimum face angle was 5.67° while the maximum edge length and element volume ratios were 9.9 and 44.6. Figure 2 and Figure 3 display the schematic of the benchmark geometry along with the meshed model.
Figure 2. (a) Actual building configuration (b) meshed model.
Figure 3. Representation of the flow domain.
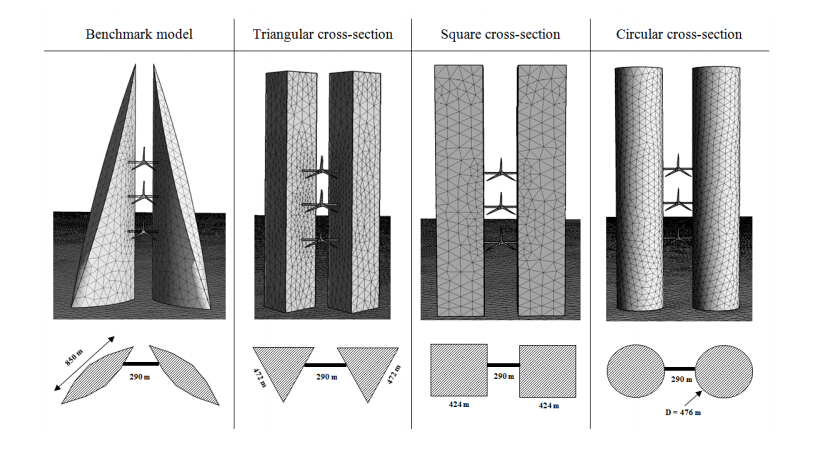
For the current investigation, four individual shapes of the building envelope were evaluated in order to identify the optimum morphology for integrating wind turbines. Using the design of the Bahrain Trade Centre as the benchmark model, the analyses were conducted on buildings having a triangular, square and circular cross-section in order to determine the optimum configuration for mounting wind turbines. The design specifications of the investigated building models are displayed in Figure 4.
Figure 4. Design specifications of the investigated building models.
In order to verify the accuracy of the numerical models, a grid independency test was carried out to determine the variation in results over increasing mesh sizes. Basic concepts associated with mesh refinement deals with the refinement and evaluation of elements where the posterior error indicator is larger than the preset criterion, while mesh enrichment considers running higher order polynomials till the solution is expected to improve with a fixed mesh [14]. Grid verification was carried out using mesh refinements (h-method) in order to optimise the distribution of mesh size h over a finite element.
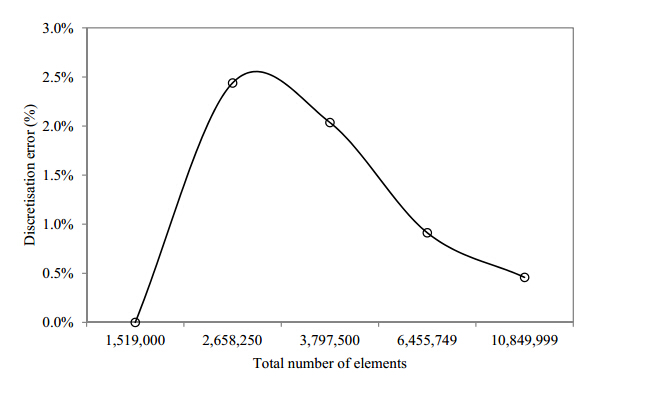
The area-weighted average value of the static pressure on the three wind turbines located on the building façade was taken as the error indicator, as the grid was refined from 1, 519, 000 to 10, 849, 999 elements with the average pressure value being 4.36 Pa. The grid was evaluated and refined until the posterior estimate error became insignificant between the number of elements and the posterior error indicator. The discretisation error was found to be the lowest at over ten million elements for both indicated variables and the mesh was thus selected to achieve a balance between accuracy and computational time. Figure 5 displays the variation in discretisation error at increasing number of meshed elements.
Figure 5. Variation in discretisation error at increasing number of elements. The applied boundary conditions (Table 1) comprised of a reference velocity (uref) of 6 m/s at a height of 300 m (zref) approaching directly perpendicular to the building façade [18]. The geometry was modeled as a solid zone while the enclosure was modeled as a fluid zone for the analyses. The boundary conditions were kept identical throughout the numerical investigation for all analysed models.
| Parameter | Type |
| Geometry | Solid zone |
| Enclosure | Fluid zone |
| Operating Pressure | Atmospheric |
| Viscous Model | k-epsilon (2 eqn) |
| Near-Wall Treatment | Standard Wall Functions |
| Velocity Formulation | Absolute |
| Solver Type | Pressure-Based |
| Time | Steady |
| Gravity | -9.81 m/s2 |
DownLoad: CSVIn order to estimate how much energy a specific turbine will be expected to produce at a given location, the wind resource at that location must be identified. A wind turbine works by extracting kinetic energy out of the wind and converting it to mechanical and then electrical energy. The power that is available in the wind to be converted to electrical energy is defined in equation 3.
| Pwind=12ρAU3 |
(3) |
Where: Pwind is the power available in the wind, is the density of air, A is the swept area of the turbine and U is the wind speed approaching the wind turbine.
Large-scale integration of wind turbines into buildings requires extensive research and development for it to operate at high efficiencies in order to balance out the high cost of installation. The specification of the wind turbines used in this study was mapped on the ones installed on the Bahrain Trade Centre. The fixed horizontal axis wind turbine comprised of a conventional nacelle design containing an enclosure with the gearbox, cooling system and the associated control system. The nominal electrical power rating of the turbine was 225 kW with the rotor diameter measuring 29 m. The rotor speed at full load was 38 rpm. The cut-in wind speed for the wind turbine operation was 4 m/s while the cut-out speed was 20 m/s [1].
Since the potential power production is proportional to the wind speed cubed, the annual mean wind power density cannot be defined by strictly using the mean annual wind speed. However, some knowledge of the wind distribution must be known to estimate the power density. The power density (Pdensity) can be used as a function of the power divided by the area and the expression is displayed in equation 4.
| Pdensity=12ρU3 |
(3) |
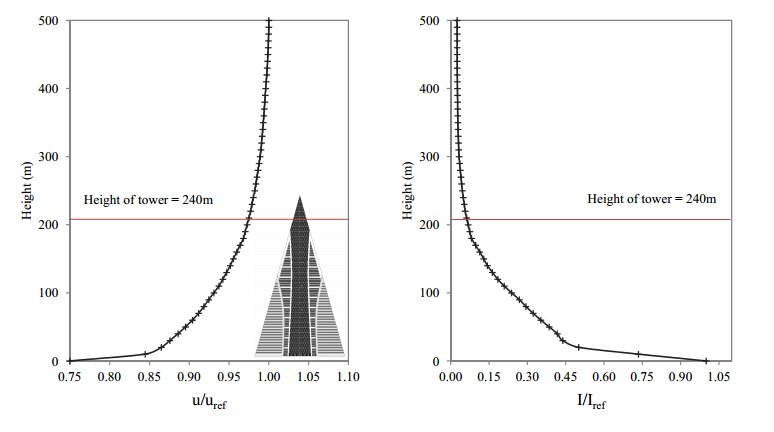
Using the computational domain, a representation of velocity boundary layer profile and turbulence intensity (I) at the windward side of the building is shown in Figure 6 wherein the wind speed is taken from the direction of the sea. The thickness of boundary layer of the atmosphere varies with wind speed, turbulence level and the type of surface. The power law is an empirical equation expressed in equation 5. For neutral stability conditions, α is approximately 1/7, or 0.143, regarded as a reasonable but conservative estimate [19].
| u=uref(zzref)α |
(5) |
Figure 6. Representation of the boundary layer profile and turbulence intensity.
Where: u is the speed at a particular point, uref is the reference speed, z is the height at a particular point and zref is the reference height.
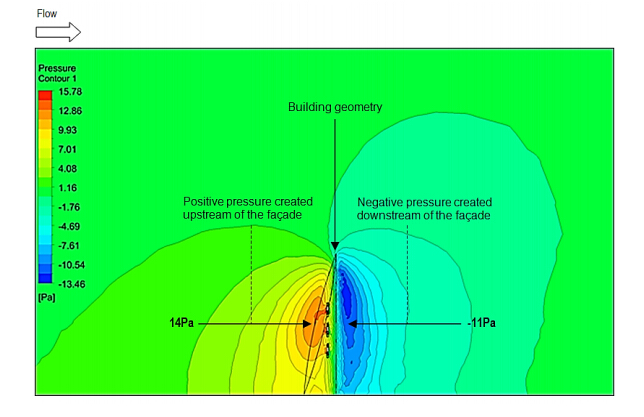
Using the benchmark model, Figure 7 displays the contour levels for static pressure as the air comes in contact with the building. A positive airside pressure was created as the air stream came in direct contact with the building façade. This was due to the force being directly perpendicular to the area of interaction. As a result, a negative pressure was created on the opposite end at the immediate downstream of the building where the air velocity increased due to the streamlined body of the structure. The analysis showed that a total pressure differential of 29.2 Pa was created for the entire geometry.
Figure 7. Contour levels of static pressure formation upstream and downstream of the building.
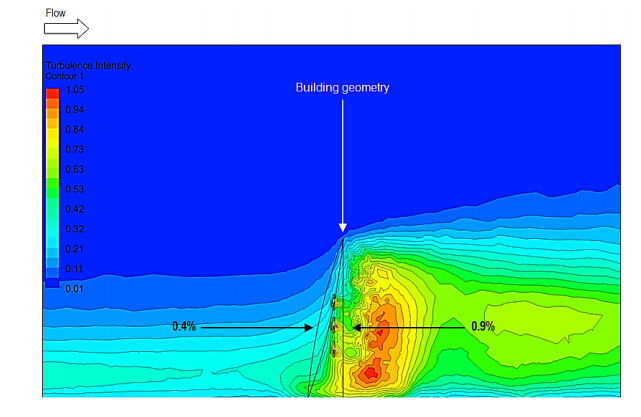
Figure 8 displays the contour levels of turbulence intensity, upstream and downstream of the benchmark model. At the windward side of the building, it was observed that the layers of turbulence intensified in inverse proportion to the height of the building with an average value of 0.45 %. The turbulence intensity was however found to increase (maximum value of 1.05 %) at the leeward side of the building as the wind came in contact and sheared away towards the sides of the structure.
Figure 8. Contour levels of turbulence intensity upstream and downstream of the building.
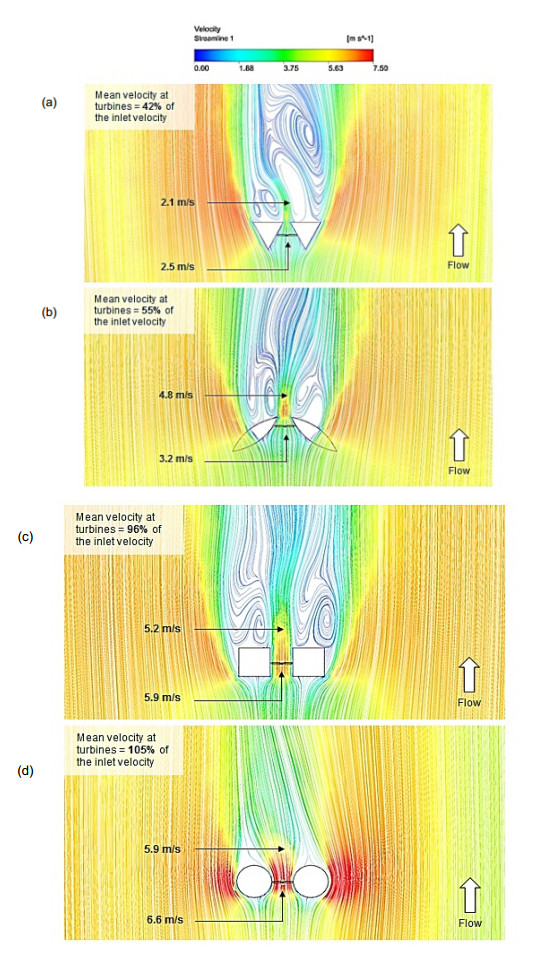
Figure 9. Air velocity streamlines representing the formation of resulting flow using: (a) triangular cross-section (b) benchmark model (c) square cross-section (d) circular cross-section.
Figure 9. displays the formation of air velocity profile for all analysed models in order to illustrate the effect of the building morphology on the wind speed received by the wind turbines. At a reference speed of 6 m/s, the only successful augmentation of the speed was achieved using the circular cross-section with the mean velocity at wind turbines determined at 6.6 m/s. The investigation showed that the mean air velocity at the wind turbines using the configuration of the existing benchmark model was 55 % of the inlet velocity. This was superior to an equilateral triangular cross-section which showed the least recovery in wind speeds with the turbines capturing only 42 % of the inlet velocity.
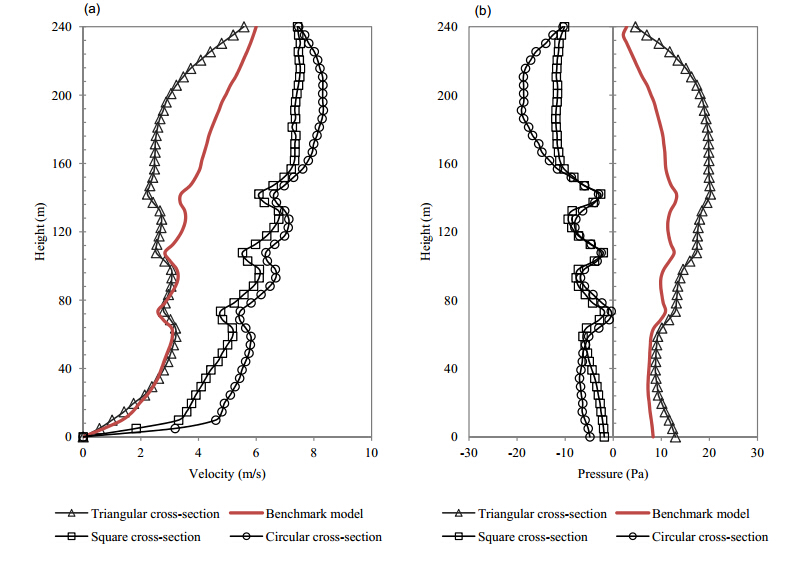
A graphical representation of the variation in velocity and pressure profiles with respect to the height of the building is shown in Figure 10. A periodic increase in air velocity was observed for the square and circular cross-sections with the wind speed augmenting with increasing amplitude. The three regions of distinct peaks represent the elevation levels of the three wind turbines used in this study. The average wind speed across the profile was 6.6 m/s and 6.0 m/s for the circular and square cross-sections, thereby indicating the optimum extraction of the prevailing inlet wind. The average wind speeds for the triangular and benchmark configurations were 2.9 m/s and 3.7 m/s thus confirming the inability of the structural design to capture the incoming wind when blown perpendicular to the building. With regards to the static pressure formations, negative pressure gradients were recorded for the circular and square cross-sections while the other two designs displayed positive pressure profiles, thus confirming the reason for the reduction in wind speed.
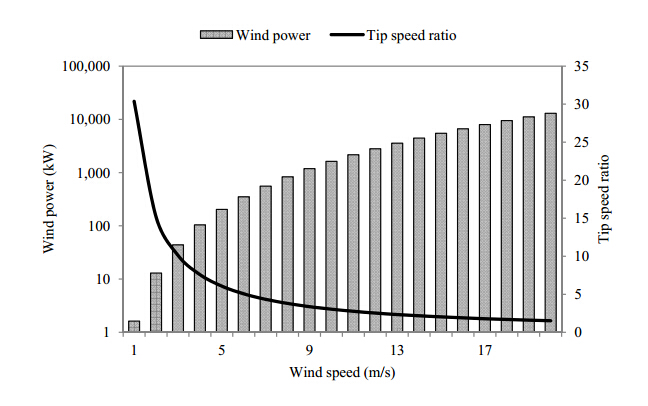
Figure 10. Formation of velocity and pressure layers with periodic rise in altitude. Following the numerical investigation, an estimation of the wind power characteristics was calculated theoretically. Using the rotor diameter of 29 m for the wind turbine used in the Bahrain Trade Centre (the benchmark model), a comparison between power in the wind and the tip speed ratio is illustrated in Figure 11. Wind turbines are designed to operate at their optimum tip speed ratio in order to extract as much power possible from the air stream. For a grid connected wind turbine with three rotor blades, the optimum tip speed ratio is recommended between 6 and 8 [20]. While a linear increase in wind power was obtained with increasing wind speeds, the recommended tip speed ratio values were found to be at 4 m/s and 5 m/s respectively.
Figure 11. Relationship between wind power and tip speed ratio at increasing wind speeds.
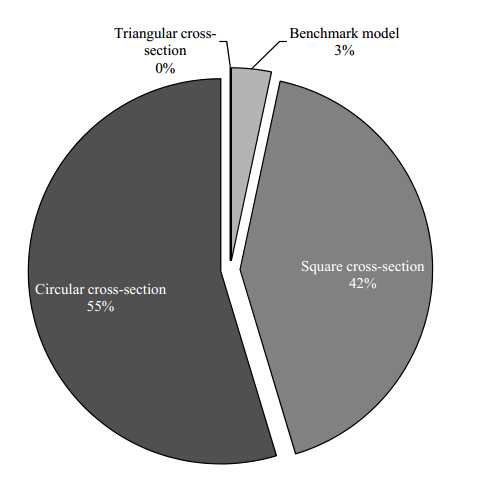
Using the wind speeds obtained from the CFD models, the conservative figures of estimated power generation capability of wind turbines for all analysed cases is displayed in Table 2. Three wind turbines were used on the buildings which were categorised as Turbine 1 (Low-altitude), Turbine 2 (Mid-altitude) and Turbine 3 (High-altitude). For the triangular cross-section, the results showed that none of the wind turbines were able to meet the cut-in wind speed requirement, thereby indicating no production of power. Using the benchmark model, the study quantified an estimate power generation of 6.4 kW indicating a capacity factor of 2.9 %. The square and circular cross-sections however determined greater capacity factors of 12.2 % and 19.9 %, recording an estimated power production capability of 26.9 kW and 35.1 kW and confirming the largest extraction of the incoming wind stream. The results quantified that the wind turbines located between the circular building morphology had the highest power density of 203 W/m2 using the high-altitude turbine. Figure 12 displays the breakdown of results in a pie-chart representation for the estimated power generation capacity of wind turbines integrated in buildings having different structural morphologies.
| Cross-section | Turbine | Velocity (m/s) | Estimated power (W) | Power density (W/m2) | Capacity Factor (%) |
| Triangular cross-section | Wind turbine 1 | 2.8 | - | - | - |
| Wind turbine 2 | 2.5 | - | - | - | |
| Wind turbine 3 | 2.3 | - | - | - | |
| Benchmark model | Wind turbine 1 | 2.6 | - | - | - |
| Wind turbine 2 | 3.3 | - | - | - | |
| Wind turbine 3 | 4.1 | 6, 430 | 43.1 | 2.9% | |
| Square cross-section | Wind turbine 1 | 4.8 | 14, 060 | 69.4 | 6.2% |
| Wind turbine 2 | 5.9 | 27, 470 | 127.2 | 12.2% | |
| Wind turbine 3 | 6.6 | 39, 380 | 179.7 | 17.5% | |
| Circular cross-section | Wind turbine 1 | 5.4 | 21, 200 | 99.2 | 9.4% |
| Wind turbine 2 | 6.6 | 39, 400 | 127.2 | 17.5% | |
| Wind turbine 3 | 6.9 | 44, 700 | 203.1 | 19.9% |
DownLoad: CSV
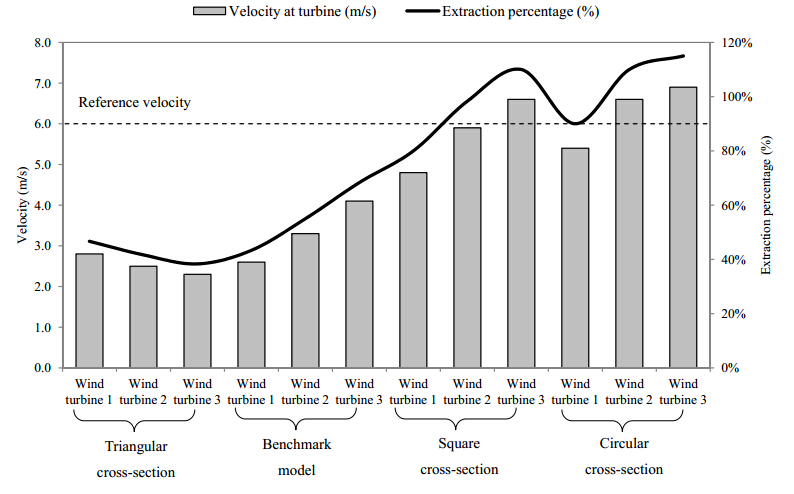
Figure 12. Power generation comparison between the analysed structural morphologies.The extracted wind speeds by the three wind turbines for all four cases is shown in Figure 13. Despite its streamlined façade, the average speed at the wind turbines for the benchmark model was 2.7 m/s lower than the incoming speed of 6 m/s. For the square cross-section, the average speed was only 0.2 m/s lower than the incoming speed this indicating a high percentage of wind extraction. The square cross-sectional configuration indicated a 41 % superior extraction of incoming wind than the benchmark model. However, the optimum cross-sectional configuration for installing wind turbines in high-rise buildings was the circular orientation as the average wind speed at the wind turbines was 0.3 m/s greater than the incoming wind resulting in an average augmentation of 5 %. The maximum wind speed of 6.9 m/s was recorded at wind turbine 3 which was located at an altitude of approximately 160 m from the ground level. The circular configuration depicted a 49 % superior extraction of incoming wind than the benchmark model. In general, the findings of this study highlighted that circular cross-section is the most suitable orientation for integrating wind turbines, particularly suited to regions with a dominant prevailing wind direction.
Figure 13. Wind speeds recorded at individual wind turbines for the four analysed cases.
In this paper, the feasibility of implementing building-integrated wind turbines was determined by investigating the effect of structural morphology on the extraction of prevailing inlet wind. The power generation capacity of wind turbines was determined using the specifications of the Bahrain Trade Centre which was taken as the benchmark model and the findings were compared against triangular, square and circular cross-sections of the same building. The three-dimensional Reynolds - averaged Navier-Stokes (RANS) equations along with the momentum and continuity equations were solved using the commercial CFD code for velocity and pressure field simulations. Using a reference wind speed of 6 m/s, the study quantified an estimate power generation of 6.4 kW indicating a capacity factor of 2.9 % for the benchmark model. The square and circular cross-sections however determined greater capacity factors of 12.2 % and 19.9 %, recording an estimated power production capability of 26.9 kW and 35.1 kW and confirming the highest extraction of the incoming wind stream. The findings from this study highlighted that circular cross-section is the most viable building orientation, particularly suited to regions with a dominant prevailing wind direction as a mean wind speed augmentation of 5 % was achieved at the turbines.
All authors declare no conflicts of interest in this paper.
| [1] | Killa S, Smith RF. (2008) Harnessing Energy in Tall Buildings: Bahrain World Trade Center and Beyond. Council of Tall Buildings and Urban Habitat (CTBUH) 8th World Congress; Dubai, United Arab Emirates. |
| [2] | Chaudhry HN, Hughes BR. (2011) Computational analysis of dynamic architecture. Journal of Power and Energy, P I Mech Eng Part A 225, 85-95. |
| [3] | Hughes BR, Chaudhry HN. (2011) Power generation potential of dynamic architecture, World Acad Sci, Eng Technol 5: 1-24. |
| [4] | Hughes BR, Chaudhry HN, Ghani SA. (2011) A review of sustainable cooling technologies in buildings, Renew Sust Energ Rev 15: 3112-3120. |
| [5] | Chong WT, Yip SY, Fazlizan A, et al. (2013) Design of an exhaust air energy recovery wind turbine generator for energy conservation in commercial buildings. Renew Energ 67: 252-256. |
| [6] | Muller G, Jentsch MF, Stoddart E. (2008) Vertical axis resistance type wind turbines for use in buildings. Renew Energ 34: 1407-1412. |
| [7] |
Sharpe T, Proven G. (2010) Crossflex: Concept and early development of a true building integrated wind turbine. Energ Buildings 42: 2365-2375. doi: 10.1016/j.enbuild.2010.07.032
|
| [8] |
Lu L, Sun K. (2014) Wind power evaluation and utilization over a reference high-rise building in urban area. Energ Buildings 68: 339-350. doi: 10.1016/j.enbuild.2013.09.029
|
| [9] |
Mithraratne N. (2009) Roof-top wind turbines for microgeneration in urban houses in New Zealand. Energ Buildings 41: 1013-1018. doi: 10.1016/j.enbuild.2009.05.003
|
| [10] | Bahaj AS, Myers L, James PAB. (2006) Urban energy generation: Influence of micro-wind turbine output on electricity consumption in buildings. Energ Buildings 39: 154-165. |
| [11] | Lu L, Ip, KY. (2007) Investigation on the feasibility and enhancement methods of wind power utilization in high-rise buildings of Hong Kong. Renew Sust Energ Rev 13: 450-461. |
| [12] |
Li QS, Chen FB, Li YG, et al. (2013) Implementing wind turbines in at all building for power generation: A study of wind loads and wind speed amplifications. J Wind Eng Ind Aerod 116: 70-82. doi: 10.1016/j.jweia.2013.03.004
|
| [13] | Launder BE, Spalding DB. (1972) Lectures in mathematical models of turbulence. London, England: Academic Press. |
| [14] | Chung TJ. (2002) Computational Fluid Dynamics, Cambridge University Press; illustrated edition, ISBN-0521594162. |
| [15] | Calautit JK, Hughes BR, Ghani SA. (2013) Numerical investigation of the integration of heat transfer devices into wind towers. Chem Eng T 34: 43-48. |
| [16] |
Calautit JK, Hughes BR, Ghani SA. (2013) A Numerical Investigation into the Feasibility of Integrating Green Building Technologies into Row Houses in the Middle East. Architectural Sci Rev 56: 279-296. doi: 10.1080/00038628.2012.686433
|
| [17] |
Hughes BR, Calautit JK, Ghani SA. (2012) The Development of Commercial Wind Towers for Natural Ventilation: A Review. Appl Energ 92: 606-627. doi: 10.1016/j.apenergy.2011.11.066
|
| [18] | Wind & weather statistics Bahrain Airport 2014, Available from http://www.windfinder.com/windstatistics/Bahrain. |
| [19] | Kubik ML, Coker PJ, Hunt C. (2011) Using meteorological wind data to estimate turbine generation output: a sensitivity analysis. World Renewable Energy Congress; Linkoping. Sweden. |
| [20] | Cetin NS, Yurdusev MA, Ata R, et al. (2005) Assessment of optimum tip speed ratio of wind turbines. Math Comput Appl 10: 147-154. |
| 1. | Q.S. Li, Z.R. Shu, F.B. Chen, Performance assessment of tall building-integrated wind turbines for power generation, 2016, 165, 03062619, 777, 10.1016/j.apenergy.2015.12.114 | |
| 2. | Ernesto Arteaga-López, Cesar Ángeles-Camacho, Francisco Bañuelos-Ruedas, Advanced methodology for feasibility studies on building-mounted wind turbines installation in urban environment: Applying CFD analysis, 2019, 167, 03605442, 181, 10.1016/j.energy.2018.10.191 | |
| 3. | An-Shik Yang, Ying-Ming Su, Chih-Yung Wen, Yu-Hsuan Juan, Wei-Siang Wang, Chiang-Ho Cheng, Estimation of wind power generation in dense urban area, 2016, 171, 03062619, 213, 10.1016/j.apenergy.2016.03.007 | |
| 4. | Hassam Nasarullah Chaudhry, John Kaiser Calautit, Ben Richard Hughes, Design and aerodynamic investigation of dynamic architecture, 2016, 1, 2364-4176, 10.1007/s41062-016-0002-2 | |
| 5. | Katrina Calautit, Angelo Aquino, John Calautit, Payam Nejat, Fatemeh Jomehzadeh, Ben Hughes, A Review of Numerical Modelling of Multi-Scale Wind Turbines and Their Environment, 2018, 6, 2079-3197, 24, 10.3390/computation6010024 | |
| 6. | Y.-H. Juan, C.-Y. Wen, W.-Y. Chen, A.-S. Yang, Numerical assessments of wind power potential and installation arrangements in realistic highly urbanized areas, 2021, 135, 13640321, 110165, 10.1016/j.rser.2020.110165 | |
| 7. | Samuel P. Evans, Anup KC, David R. Bradney, Tania P. Urmee, Jonathan Whale, Philip D. Clausen, David Goodfield, The suitability of the IEC 61400-2 wind model for small wind turbines operating in the built environment, 2017, 2, 2493-9439, 31, 10.1051/rees/2017022 | |
| 8. | Ted Stathopoulos, Hatem Alrawashdeh, Ayman Al-Quraan, Bert Blocken, Aierken Dilimulati, Marius Paraschivoiu, Pragasen Pilay, Urban wind energy: Some views on potential and challenges, 2018, 179, 01676105, 146, 10.1016/j.jweia.2018.05.018 | |
| 9. | Anup KC, Jonathan Whale, Tania Urmee, Urban wind conditions and small wind turbines in the built environment: A review, 2019, 131, 09601481, 268, 10.1016/j.renene.2018.07.050 | |
| 10. | T. Stathopoulos, H. Alrawashdeh, 2019, Chapter 1, 978-3-030-12814-2, 3, 10.1007/978-3-030-12815-9_1 | |
| 11. | Yu-Hsuan Juan, Abdolrahim Rezaeiha, Hamid Montazeri, Bert Blocken, Chih-Yung Wen, An-Shik Yang, CFD assessment of wind energy potential for generic high-rise buildings in close proximity: Impact of building arrangement and height, 2022, 321, 03062619, 119328, 10.1016/j.apenergy.2022.119328 | |
| 12. | Yee-Ting Lee, Yuan-Lung Lo, Yu-Hsuan Juan, Zhengtong Li, Chih-Yung Wen, An-Shik Yang, Effect of void space arrangement on wind power potential and pressure coefficient distributions for high-rise void buildings, 2023, 75, 23527102, 107061, 10.1016/j.jobe.2023.107061 | |
| 13. | Katrina Calautit, Cameron Johnstone, State-of-the-art review of micro to small-scale wind energy harvesting technologies for building integration, 2023, 20, 25901745, 100457, 10.1016/j.ecmx.2023.100457 | |
| 14. | Yu-Hsuan Juan, Abdolrahim Rezaeiha, Hamid Montazeri, Bert Blocken, An-Shik Yang, Improvement of wind energy potential through building corner modifications in compact urban areas, 2024, 248, 01676105, 105710, 10.1016/j.jweia.2024.105710 | |
| 15. | Xinyu Zhang, Yunting Ge, Raj Vijay Patel, Renewable Energy Integration and Energy Efficiency Enhancement for a Net-Zero-Carbon Commercial Building, 2025, 15, 2075-5309, 414, 10.3390/buildings15030414 | |
| 16. | Jing Wen, Zhengyu Fan, Jiaping Liu, Effects of complex skyscraper geometries on wind energy potentials of high-density urban central business district: a case study of the Lujiazui blocks, 2025, 22106707, 106287, 10.1016/j.scs.2025.106287 |
Figures(13) / Tables(2)
Hassam Nasarullah Chaudhry, John Kaiser Calautit, Ben Richard Hughes. The Influence of Structural Morphology on the Efficiency of Building Integrated Wind Turbines (BIWT)[J]. AIMS Energy, 2014, 2(3): 219-236. doi: 10.3934/energy.2014.3.219
| Parameter | Type |
| Geometry | Solid zone |
| Enclosure | Fluid zone |
| Operating Pressure | Atmospheric |
| Viscous Model | k-epsilon (2 eqn) |
| Near-Wall Treatment | Standard Wall Functions |
| Velocity Formulation | Absolute |
| Solver Type | Pressure-Based |
| Time | Steady |
| Gravity | -9.81 m/s2 |
DownLoad: CSV| Cross-section | Turbine | Velocity (m/s) | Estimated power (W) | Power density (W/m2) | Capacity Factor (%) |
| Triangular cross-section | Wind turbine 1 | 2.8 | - | - | - |
| Wind turbine 2 | 2.5 | - | - | - | |
| Wind turbine 3 | 2.3 | - | - | - | |
| Benchmark model | Wind turbine 1 | 2.6 | - | - | - |
| Wind turbine 2 | 3.3 | - | - | - | |
| Wind turbine 3 | 4.1 | 6, 430 | 43.1 | 2.9% | |
| Square cross-section | Wind turbine 1 | 4.8 | 14, 060 | 69.4 | 6.2% |
| Wind turbine 2 | 5.9 | 27, 470 | 127.2 | 12.2% | |
| Wind turbine 3 | 6.6 | 39, 380 | 179.7 | 17.5% | |
| Circular cross-section | Wind turbine 1 | 5.4 | 21, 200 | 99.2 | 9.4% |
| Wind turbine 2 | 6.6 | 39, 400 | 127.2 | 17.5% | |
| Wind turbine 3 | 6.9 | 44, 700 | 203.1 | 19.9% |
DownLoad: CSV| Parameter | Type |
| Geometry | Solid zone |
| Enclosure | Fluid zone |
| Operating Pressure | Atmospheric |
| Viscous Model | k-epsilon (2 eqn) |
| Near-Wall Treatment | Standard Wall Functions |
| Velocity Formulation | Absolute |
| Solver Type | Pressure-Based |
| Time | Steady |
| Gravity | -9.81 m/s2 |
| Cross-section | Turbine | Velocity (m/s) | Estimated power (W) | Power density (W/m2) | Capacity Factor (%) |
| Triangular cross-section | Wind turbine 1 | 2.8 | - | - | - |
| Wind turbine 2 | 2.5 | - | - | - | |
| Wind turbine 3 | 2.3 | - | - | - | |
| Benchmark model | Wind turbine 1 | 2.6 | - | - | - |
| Wind turbine 2 | 3.3 | - | - | - | |
| Wind turbine 3 | 4.1 | 6, 430 | 43.1 | 2.9% | |
| Square cross-section | Wind turbine 1 | 4.8 | 14, 060 | 69.4 | 6.2% |
| Wind turbine 2 | 5.9 | 27, 470 | 127.2 | 12.2% | |
| Wind turbine 3 | 6.6 | 39, 380 | 179.7 | 17.5% | |
| Circular cross-section | Wind turbine 1 | 5.4 | 21, 200 | 99.2 | 9.4% |
| Wind turbine 2 | 6.6 | 39, 400 | 127.2 | 17.5% | |
| Wind turbine 3 | 6.9 | 44, 700 | 203.1 | 19.9% |
