Non-spatial models of competition between floating aquatic vegetation (FAV) and submersed aquatic vegetation (SAV) predict a stable state of pure SAV at low total available limiting nutrient level, N, a stable state of only FAV for high N, and alternative stable states for intermediate N, as described by an S-shaped bifurcation curve. Spatial models that include physical heterogeneity of the waterbody show that the sharp transitions between these states become smooth. We examined the effects of heterogeneous initial conditions of the vegetation types. We used a spatially explicit model to describe the competition between the vegetation types. In the model, the FAV, duckweed (L. gibba), competed with the SAV, Nuttall's waterweed (Elodea nuttallii). Differences in the initial establishment of the two macrophytes affected the possible stable equilibria. When initial biomasses of SAV and FAV differed but each had the same initial biomass in each spatial cell, the S-shaped bifurcation resulted, but the critical transitions on the N-axis are shifted, depending on FAV:SAV biomass ratio. When the initial biomasses of SAV and FAV were randomly heterogeneously distributed among cells, the vegetation pattern of the competing species self-organized spatially, such that many different stable states were possible in the intermediate N region. If N was gradually increased or decreased through time from a stable state, the abrupt transitions of non-spatial models were changed into smoother transitions through a series of stable states, which resembles the Busse balloon observed in other systems.
Citation: Linhao Xu, Donald L. DeAngelis. Effects of initial vegetation heterogeneity on competition of submersed and floating macrophytes[J]. Mathematical Biosciences and Engineering, 2024, 21(10): 7194-7210. doi: 10.3934/mbe.2024318
Non-spatial models of competition between floating aquatic vegetation (FAV) and submersed aquatic vegetation (SAV) predict a stable state of pure SAV at low total available limiting nutrient level, N, a stable state of only FAV for high N, and alternative stable states for intermediate N, as described by an S-shaped bifurcation curve. Spatial models that include physical heterogeneity of the waterbody show that the sharp transitions between these states become smooth. We examined the effects of heterogeneous initial conditions of the vegetation types. We used a spatially explicit model to describe the competition between the vegetation types. In the model, the FAV, duckweed (L. gibba), competed with the SAV, Nuttall's waterweed (Elodea nuttallii). Differences in the initial establishment of the two macrophytes affected the possible stable equilibria. When initial biomasses of SAV and FAV differed but each had the same initial biomass in each spatial cell, the S-shaped bifurcation resulted, but the critical transitions on the N-axis are shifted, depending on FAV:SAV biomass ratio. When the initial biomasses of SAV and FAV were randomly heterogeneously distributed among cells, the vegetation pattern of the competing species self-organized spatially, such that many different stable states were possible in the intermediate N region. If N was gradually increased or decreased through time from a stable state, the abrupt transitions of non-spatial models were changed into smoother transitions through a series of stable states, which resembles the Busse balloon observed in other systems.
Competition was modeled between floating (FAV) and submersed (SAV) aquatic macrophyte species in a shallow waterbody (Scheffer et al. [1]). FAV was limited by nutrient concentration (assumed nitrogen in their model) in the water column but, when established, could limit the light of the SAV. The authors showed that SAV could always exclude FAV at low nutrient concentrations, at which SAV was a stable state. If the total nutrient of the modeled system, N, was increased sufficiently, FAV could invade such that a mixed SAV-FAV stable state occurred. However, further increase in N could lead to an abrupt shift such that, for all larger values of N, only a stable state of FAV existed. The sudden shift is called a critical transition [1]. If the nutrient amount was then decreased, the critical transition from FAV back to mixed FAV and SAV occurred at a lower nutrient level than the critical transition from the SAV-FAV mixture to pure FAV; that is, there is hysteresis. This situation is described by an S-shaped bifurcation curve as a function of N (Figure 2 in [1]). In the range of values of N between the two critical transitions, there are two alternative stable states, one with pure FAV on one branch of the S-shaped curve and one that is a mixture of the two species on the other branch. The authors successfully tested the model with small tank competition experiments between the FAV, duckweed (L. gibba), and the SAV, Nutall's waterweed (Elodea nuttallii).
The model of [1] is non-spatial, thus implicitly spatially homogeneous. Subsequently, Nes et al. [2] developed spatial models, including a two-dimensional, 50 × 50-pixel grid, representing a spatially explicit system, in order to be able to represent different physical spatial conditions of the waterbody, such as spatially varying water depth. The authors studied three cases, no spatial heterogeneity, a linear gradient in the spatial parameter for water column depth along the lattice, and random assignment of water column depths. The aim of the model was to determine the effects of heterogeneity in the underlying physical environment, such as spatial variations in depth, on the outcome of the competition of SAV and FAV. The authors found that the physical heterogeneity of the system led to the abrupt changes in alternative stable states of SAV and FAV in the model of [1] being replaced by gradual changes from one stable equilibrium to the other as N was changed, though hysteresis still occurred.
Another aspect of spatial heterogeneity can be differences in the initial biomasses of the aquatic vegetation. For example, following a large disturbance of a shallow pond or lake that greatly reduces vegetation, recolonization by aquatic vegetation could occur in some sort of spatially random way. To study how different initial spatial patterns of colonization can affect the long-term outcome, we used a two-dimensional spatial model similar to that of [2], that is, a 50 × 50 grid or lattice. However, we assumed physical homogeneity of depths, and, instead, we assumed that initial conditions of the competing SAV and FAV could differ, including differences both between the initial biomasses of the two species and in their initial spatial distributions. We investigated the effects of initial conditions on the stable equilibria that result, including both amounts and spatial distribution of the biomasses of the SAV and FAV species. Our spatial model was based on an existing cellular automata (CA) model (McCann [3]), which, like the model of [2], was an extension to space of the non-spatial model of [1]. Unlike the model of [2], McCann's model assumes homogeneous depths, which are assumed in our model as well. Xu and DeAngelis [4] adapted the CA model of [3] as a basis for studying competition of SAV and FAV in combination with a biocontrol agent (the weevil Neochetina eichhorniae) feeding on the FAV. However, the competitive interaction of SAV and FAV in the absence of biocontrol was not considered in [4]. Here we show that the initial spatial heterogeneity of colonization of a shallow waterbody by competing SAV and FAV could lead to the emergence of self-organization of the vegetation, which replaced abrupt critical transitions with relatively smooth changes in the species biomasses as a function of the changing nutrient.
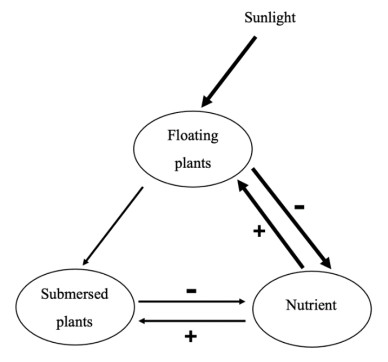
The model simulates competition between a submersed aquatic vegetation (SAV) and floating aquatic vegetation (FAV). The nutrient level, N, is assumed to be limiting to FAV, while light is limiting to SAV [1] (Figure 1).

For the non-spatial model of [1], the equations of competition between the SAV and FAV are,
| dSdt=rsSnn+hs11+asS+bF+W−lsS | (2.1) |
| dFdt=rfFnn+hf11+af∗F−lfF, | (2.2) |
where S and F are dry weight biomasses (g dW m-2), rs and rf are the maximum growth rates, and ls and lf are the loss rates from respiration and mortality. Nutrient concentration in mg liter-1 is given by n and hs and hf are the half-saturation values for nutrient uptake of SAV and FAV. Parameters as and af are the intraspecific competitive effects of SAV and FAV, respectively, while b is the effect of shading of FAV on SAV, and W is the effect of light absorption by the floating plant on submersed plant growth. As in Scheffer et al. [1] and McCann [3], it is assumed here that the water is shallow and clear enough that W = 0.
The total amount of limiting nutrient in the system, N, which is divided among the vegetation and soluble form in the water column, is assumed fixed, as in the models of [1] and [3];
| N=n+nqsS+nqfF. | (2.3) |
Here qs and qf are coefficients of the effect of submerged and floating plants on the nutrient concentration in the water; that is, they represent the fractions of nutrient tied up in the vegetation per unit dry weight biomass. Therefore, the mean amount of nutrient in the water column is
| n=N1+qsS+qFF. | (2.4) |
McCann [3] used the equations of [1] to simulate competition of SAV and FAV in a spatial arena or lattice, using a CA model composed of a block of contiguous spatial cells or pixels. We adopt the model of [3] with some modifications. Unlike the [3] model, which simulates various spatial configurations of pixels, we considered only a 50 × 50 square of 1× 1 m pixels.
Both species are capable of both growing within the pixels they occupy and spreading to adjacent pixels in the model. We simulate spread such that, at each time step, if the biomass in a given pixel is sufficiently large, some fraction of its biomass could spread to any of eight adjacent cells. Vegetation could not spread beyond the limits of the 50 × 50 lattice. The details of the spread are described in Appendix 1.
Nutrient was allowed to spread by symmetric two-dimensional diffusion, but the concentration at any point was also assumed to be influenced by the local biomasses of the two species. If there were no diffusion, local nutrient concentration in each pixel would be given by Eq (2.4); for a given pixel (i, j)
| nij=N1+qsSij+qFFij, | (2.5) |
where Sij and Fij are the biomass concentrations (g dW m-2) in that pixel. If diffusion were very large, nutrient concentration would be evenly spread across the spatial arena. In the absence of specific knowledge, we considered a variety of nutrient diffusion rates.
Our spatial model used the equations above to simulate the growth of floating and submerged plants in a difference equation version of the CA model of [3] for the spatial dynamics of FAV (duckweed) and SAV (Nuttall's waterweed). The parameter values are listed in Table 1 and parametrization is further discussed in [4].
| State variables | Symbol | Values | Units |
| Floating plant biomass, FAV | F | 0 to 900 | g dW m-2 |
| Submersed plant biomass, SAV | S | 0 to 800 | g dW m-2 |
| Nutrient concentration in water | n | 0 to 2 | mg nitrogen l-1 |
| Parameters | |||
| Maximum relative growth rate | r | 0.5 (FAV and SAV) | day-1 |
| Loss rate | l | 0.05 (FAV and SAV) | day-1 |
| Half saturation coefficient for n | h | 0.2 (FAV), 0 (SAV) | mg nitrogen l-1 |
| FAV Light limitations parameter | a | 0.01 (FAV and SAV) | g dW m2 |
| Light attenuation in water | W | 0 | unitless |
| Total nutrient in system | N | 0 to 2 | mg nitrogen l-1 |
| Nutrient diffusion rate | Ndifff | 0.01, 0.05, 0.1, 0.2 | m2 day-1 |
Using these parameters and solving Eqs (2.1)–(2.3) analytically, we first checked that we were able to produce the bifurcation diagram of the non-spatial model of [1]. We found that within the approximate range N = 0.8 to N = 1.35, there are two possible stable equilibrium states, floating species alone or mixed floating and submersed. For N > 1.35, only the FAV exists as a stable state. Between N = 0.55 and 0.8, only the mixed vegetation exists as a stable state, while for N < 0.55 only the SAV exists as a stable state (Figure 2).

The effects of different initial conditions were studied in three scenarios. In the first two scenarios, the system was assumed closed with a fixed total amount of limiting nutrient, N, in the system. In the third scenario, N, was gradually changed through time.
Scenario 1. Spatially homogeneous initial biomasses.
The waterbody was initially empty of vegetation. Then initial biomasses of both SAV (S) and FAV (F) were allowed to colonize homogeneously to all pixels across the 50 × 50-pixel grid, and the resultant equilibrium state that was reached was determined through simulations. Each pixel was initiated with the same amount of biomass for a given species, but the initial biomasses could differ between species. Five cases of the two species were simulated in the model: Case 1, F = 50, S = 50, Case 2, F = 500, S = 5, Case 3, F = 5, S = 500, Case 4. F = 60, S = 30 g dW m-2, and Case 5. F = 30, S = 60 g dW m-2 Also, for each case two levels of nutrient diffusion were used, one a low rate and one a high rate. Here, low nutrient diffusion rate means that every day 1% of the nutrient of a pixel is exchanged with all eight neighboring pixels, intermediate means 10%, (or 5% in some cases) and high diffusion rate means that every day 20% of nutrient is exchanged.
Scenario 2: Spatially heterogeneous initial biomasses.
In the second scenario, again the waterbody was initially empty of vegetation. Certain initial biomasses of SAV and FAV were then spread randomly to some fraction of the pixels. In Cases 1–3, biomasses of each species were added randomly to a mean of 15% of the pixels. That is, each pixel had a 15% chance of being settled by SAV and 15% by FAV. Because overlap was possible, on average 2.5% of pixels were colonized with biomasses of both SAV and FAV. The initial biomasses of SAV and FAV (in g dW m-2) colonizing the randomly selected pixels differed. Five cases were simulated. In Case 1, F = 50, S = 50, in Case 2, F = 500, S = 5, Case 3, F = 5, S = 500 for the two species (we later use the terms F:S = 5:500, 50:50, and 500:5). Two additional cases were simulated. In Case 4, 50% of the pixels were randomly colonized by FAV and 15% for SAV, where F = 500, S = 5, and in Case 5 90% of the pixels were colonized by FAV and 15% by SAV with F = 500, S = 5. For each case two different values of nutrient level, N, were used.
Scenario 3. Changing values of limiting nutrient, N.
The bifurcation analysis of SAV-FAV competition studied in [1] was motivated primarily for predicting changes in the vegetation in shallow lakes as the result of gradually increasing nutrient loadings. Scenarios 1 and 2 focused on the properties of the model in [1] for cases in which total nutrient, N, was fixed and simulations were performed for different starting conditions of FAV and SAV. Here, in Scenario 3, we studied how equilibrium states respond to N changing through time. As in Section 3.2, we started by initializing simulations with different values of FAV and SAV, distributed in a spatially heterogeneous manner. But now, after a stable equilibrium was reached, the total amount of nutrient, N, was gradually changed, both by increasing and decreasing N, with the system being allowed to come to equilibrium, by taking 1000 time steps between each small amount increment in N. Two examples are presented, one with N decreasing and one with N increasing, with starting conditions in the range 0.8 ≤ N ≤ 1.35, where multiple stable equilibria can occur. The intention is not a thorough study, but just to show examples of possible trends in equilibria as total nutrient changes.
The software, MatLab R2022a, was used in all simulations and calculations.
For a series of fixed values of nutrient concentration N, biomasses of F:S = 50:50, F:S = 500:5, F:S = 5:500, and F:S = 60:30 were initiated in each pixel and the simulations were run until stable equilibrium states were reached. The resultant stable FAV (F) and SAV (S) biomasses reached for the four different cases with low nutrient diffusion rate are shown in Figure 3.

In all cases, for N > 1.35, only the FAV existed as a stable state, for 0.55 < N < 0.8 only the mixed state occurred, and for N < 0.55 only the SAV occurred as a stable state. However, in the range 0.8 < N < 1.35, different stable equilibria were reached, depending on the different biomass starting conditions of F:S = 50:50, F:S = 500:5, and F:S = 5:500. For F:S = 5:500, an abrupt change from one branch to another occurred at N = 1.35 (Figure 3(c)). For F:S = 50:50, the abrupt change occurs at N = 1.26 (Figure 3(a)). For F:S = 500:5, the abrupt change occurred at N = 0.82 (Figures 3(b)). For F:S = 60:30 the abrupt change occurs at N = 1.13 Figures 3(d)). An additional case of F:S = 30:60 was also run, and the abrupt occurred at N = 1.33 (not shown). Therefore, the high and low extreme F:S ratios produced jumps between the branches of the bifurcation curve that are the same as those at the high and low ends of Figure 2 (N = 1.35 and 0.8, respectively) and thus correspond to the critical transitions of the model of Scheffer et al. [1]. However, the three cases in which the starting biomass values of FAV and SAV were close produced abrupt changes at intermediate values (N = 1.26, 1.35, and 1.13) The simulations in Figure 3 for low nutrient diffusion rate (0.01) were repeated for high nutrient diffusion rate (0.20). There was no difference in the results, which are not shown here.
The simulations show that under the homogeneous state, results of the spatial model with high F:S (500:5) and low F:S ratios (5:500) of initial homogeneously distributed SAV and FAV species taken together can roughly duplicate the basic results of Scheffer et al. [1] for the branches of the stable states. Starting conditions of 50:50, 60:30, and 30:60 produce results in which the transition of the equilibrium point from one branch to the other occurs at intermediate values of N between the two extremes of 0.8 and 1.35.
For a series of fixed N values, spatially heterogeneous stable equilibria were produced by starting the simulations with different assumed colonization by FAV and SAV biomass scattered randomly in some fractions of the pixels, as described in Section 2.4. Five different cases of amounts of initial colonization of species biomass and different probabilities of pixels being colonized were considered.
For a series of values of total nutrient N, Figure 4 shows that, as in Scenario 1, for the N > 1.40 or N < 0.70, similar to results for the stable equilibrium states were obtained as in the Scheffer et al. [1] non-spatial model; that is, there was only one stable equilibrium state, either FAV for N > 1.40, mixed SAV-FAV for 0.55 < N < 0.70, or SAV, for N < 0.55. However, the values of N such that 0.70 ≤ N ≤ 1.40, the situation is more complicated. Different initial values of the FAV and SAV biomasses resulted in different stable equilibria for values in the range of 0.70 ≤ N ≤ 1.40 when there was spatial heterogeneity in the initial biomasses. These equilibrium points depart from those predicted by the bifurcation curve of Scheffer et al. [1] and Figure 2.

Continua of equilibria were reached in the range 0.8 ≤ N ≤ 1.35 for the five different cases for FAV (Figure 4(a)) and SAV (Figure 4(b)), which are color-coded for the five cases of different heterogeneous starting values of biomasses. All results shown are for the low nutrient diffusion rates, (Ndiff = 0.01). Consider Case 5 (light green) first. In this case FAV was introduced at very high amounts to approximately 90% of the cells and a small amount of SAV was introduced to 15% of the cells. The result was that the simulations came very close to producing the bifurcation branches of the [1] model (our Figure 2), with the FAV biomass declining drastically for decreasing N only when N had decreased to 0.80. In Case 4 (brown), in which the only change from Case 4 was that FAV was introduced to only 50% of cells rather than 90%, the FAV species biomass declined more gradually, starting around the point where N declines slightly below 1.4, far before the rapid drop that occurs in Case 5. At the other extreme, Case 3 (light orange), where the SAV biomass was introduced to pixels at 500 g dW, while FAV was introduced to pixels at 5 g dW in approximately 15% of the cells for both species, the FAV started to decline gradually, but the rapidly, as N decreased below 1.4. The two remaining cases, Cases 1 and 2, fall in between these cases. Precisely the same patterns occurred under the high nutrient diffusion rate (Ndiff = 0.2, results not shown here). All of the points (places connecting straight lines) shown in Figure 4 are stable equilibria, meaning that some sort of heterogeneous stable spatial pattern had been reached, which is explored in the next section.
The reason for the multiple stable equilibrium states that occur in Scenario 2 is that stable heterogeneous patterns of SAV and FAV developed on the spatial grid. Here we show an example of stable spatial patterns produced by initial heterogeneous introductions of SAV and FAV, for the case in which N = 1 and with 15% of the spatial pixels initialized randomly with SAV and 15% initialized randomly with FAV. Initial values of both FAV and SAV in each of the randomly occupied cells was 50 g dW (as in Case 1). An intermediate diffusion rate of (0.1) was used; that is, a daily turnover rate of 10% in a cell.
Under intermediate nutrient concentration (N = 1), a stable state of a mixture FAV and SAV had been formed by day 5000, a steady state had formed with species coexisting heterogeneously across space (Figure 5(a), (b)). with FAV average biomass is 231 g dW m-2 and SAV average biomass is 449 g dW m-2. Figure 5(c) shows changes in mean FAV and SAV biomass through time.
The results Figure 4 show the stable equilibria reached for five different heterogeneous initial conditions on SAV and FAV biomasses over a range of values of total nutrient, N. The effects of the initial conditions by themselves can be studied more systematically. Here, nutrient level was fixed at an intermediate level of N = 1. The initial conditions were varied in the following way. Three different initial values of FAV and SAV biomasses were considered, F:S = 5:50, F:S = 50:50, and F:S = 500:50 (Figure 6). For each ratio (F:S), coverage range (mean fraction of pixels in which vegetation was initialized) was varied from 0.10 to 0.90, increasing by 0.05 each step. A general result of the simulations was that there was continued coexistence for the three cases over the whole range of coverages. As would be expected, SAV dominated for F:S = 5:50 and FAV dominated for F:S = 500:50, at least for higher coverage levels, but the SAV dominated for F:S = 50:50, which implies that there is an advantage for SAV for the value of N = 1.
In the absence of knowledge of the nutrient diffusion rate for the situation modeled, it is useful to explore the consequences of a range of plausible values of diffusion. This was done for the particular case of total nutrient N = 1 and initial biomasses F:S = 50:50, each being initially spread randomly over 50% of the pixels, so there was a lot of overlap of biomasses on pixels. The effect of the diffusion rate was relatively small, though there was some increase in amount of SAV biomass and decrease in FAV biomass for larger values of the diffusion rate (Figure 7).
Case 1: Decreasing values of nutrient amount, N.
The initial values of SAV biomass, S, across the grid were chosen randomly and uniformly between 0 and 10 g dW m-2 on 50% of the cells, and those of FAV biomass, F, were chosen randomly and uniformly between 0 and 600 on 50% of the cells. The total nutrient was started at N = 1.2 mg l-1. The system was first allowed to approach a stable equilibrium and then N was decreased gradually through time in steps of 0.001. Between each step in N there were 1000 steps in time to allow the system to approach a new equilibrium point. The result of decreasing N from 1.2 was that at first F decreased and S increased very gradually. Then, at about N = 0.75 there is a series of a few sharp increases in mean S and drops in mean F, after which the changes were slower (Figure 8(a)). With further decreases in N, F would reach zero. The accompanying changes in the biomass patterns in spatial grid landscape show a changing self-organizing pattern of S and F in the spatial pixels (Figure 9(a)). Each panel in Figure 9(a), is a steady state equilibrium. By the time N = 0.75 was reached, clumped patterns of F and S occurred, and continued to change with further decreases in N. At N = 0.7, both S and F were close to being homogeneously distributed on the grid, with F approaching a small value. The decrease in N was continued to N = 0.65 and then reversed such that N increased. Although the spatial results are not shown for this reversal in Figure 9, the mean values are shown in Figure 10 (compare with Figure 8(a)). The result is hysteresis, with the trajectories of F and S following the bifurcation branch of mixed FAV and SAV when N is reversed (Figure 10).


Case 2. Increasing values of nutrient.
The initial values of S were chosen randomly and uniformly between 0 and 10 g dW m-2 on 50% of the cells, and initial values of F biomass values were chosen randomly and uniformly between 0 and 600 on 70% of the cells. In this case, the initial total nutrient was N = 0.78, and it was increased from that amount over time. As in Case 1, the system was allowed to go to equilibrium between each step of N. After sharp increases in S and drops in F to reach an equilibrium state, there was a more gradual decrease in S and increase in F, followed by a sharp drop in S and sharp increase in F (Figure 8(b)). The remaining changes follow the upper branch bifurcation diagram of Figure 2, for the F-alone stable state. Both the decreasing and increasing N scenarios show that spatial heterogeneity plays a role in moderating the changes in mean SAV and FAV biomass over segments of the changes in N, although the heterogeneity does not completely eliminate the occurrence of sharp changes (Figure 9(b)). The effect of spatial self-organization on smoothing the transitions was stronger for decreasing than for increasing N.
Our study of competition of submersed (SAV) and floating (FAV) aquatic macrophytes shows that the initial conditions of the two competing species could determine the stable equilibrium reached. Three types of scenarios were studied using the 50 × 50 pixel spatially explicit model of [3].
In Scenario 1, each species was initiated with the same biomass as each of the 50 x 50 pixels of the grid, but the starting biomasses of the two species differed. This was done over the whole range of values of nutrient 0 < N < 2. Over the range of values, 0.80 ≤ N ≤ 1.35, [1] found that two alternative states could occur, one along a branch of pure FAV and one along a branch of mixed FAV and SAV. Our results duplicated the existence and biomass values of the two branches but showed that the discontinuous transition from one branch to the other depended on the initial ratios of the biomasses of FAV to SAV. Outside of the range 0.80 ≤ N ≤ 1.35, our results completely agree with those of [1], that only one stable equilibrium occurred outside of the range, pure SAV for N < 0.55, mixed SAV-FAV for the range 0.55 ≤ N ≤ 0.8 and pure FAV for N > 1.35.
In Scenario 2, again the initial values of the two species were initiated at different ratios of the species, but this time the biomasses of the species were initiated randomly and independently to an average of 15% of the pixels on the grid. In this scenario, instead of the equilibria being reached that are always along one of the two alternative branches as in [1], the result is that there are multiple possible stable states in the approximate range 0.65 ≤ N ≤ 1.40, depending on the initial values. As in Scenario 1, only one stable equilibrium occurred outside of that range, pure SAV for N < 0.55, mixed FAV-SAV for 0.55 ≤ N < 0.65 and pure FAV for N > 1.40, but, instead of the abrupt discontinuities, the transitions between alternative stable states were modified so that they were relatively smooth.
In Scenario 3, in which N was gradually decreased or increased after an initial heterogeneous stable state was formed in the approximate range 0.80 < N < 1.35, it was found that increasing N but particularly decreasing N can produce gradual changes of FAV and SAV biomasses, as a series of small jumps, as the system moved from one stable heterogeneous equilibrium state to another. Coexistence could occur outside of the region within the critical transition points of the non-spatial model of [1]. An interesting difference between the increasing and decreasing N cases is that in the latter there appears to be self-organization into spotty spatial patterns of SAV and FAV dominance (Figure 9). As in the models [1,2], there was hysteresis when the direction of N change was reversed (Figure 10).
Our modeling can be compared with other work on competition in aquatic ecosystems. Our spatial model differs from that of [2], in which the physical conditions of the aquatic system, e. g., water depth, were spatially varying, either as a gradient or with random heterogeneity. Depending on the details of physical heterogeneities in [2], they could lead to a smoothing of the discontinuity, though some degree of hysteresis remained. Another way in which physical heterogeneity could be applied to the case of competing floating and submersed vegetation was modeled in Janssen et al. [5]. In their model of a spatially long lake, the way in which nutrient loading was applied, either at the upstream end or through seepage along the longitudinal extent of the lake, could affect the occurrence and spatial location of alternative stable states. Our model is not like either of these examples, as the physical conditions were assumed homogeneous, and instead the initial conditions on vegetation varied, including initial differences in the SAV and FAV spread homogeneously or heterogeneously over the grid. These results are important, as initial conditions of vegetation in a shallow lake, such as those following a disturbance, are likely to be heterogeneous.
Although we know of no model of aquatic vegetation that our model can be directly compared with, it is possible that our results reflect observations and theory of some terrestrial vegetation. Our model simulations resemble some studies of vegetation patterns in semi-arid ecosystems showing that sudden tipping points may be evaded by spatial pattern formation [6,7]. The sequence of stable patterns exhibited in our Figure 9 is similar to what has been observed empirically and studied in models of semi-arid systems. The authors of such studies have related them to what is called the Busse balloon, after Bastiaansen [8,9]. In particular, Rietkerk and Koppel [10] found that changes in some factors such as soil water availability, light, water and nutrient flux, produce sequences of stable states. von Hardenberg et al. [11] found such a vegetation formation pattern transition in water-limited regions, that is bare soil at low precipitation and vegetation at high precipitation. Siteur et al. [12] and Vanselow et al. [13] found that the response of patterned ecosystem depends on both magnitude and rate of environmental change. Sheffer et al. [14] concluded that real landscapes are controlled by the mixture of physical template and self-organization. Dong et al. [15] found that self-organized spatial patterns are caused by scale-dependent feedbacks, coupling short-range positive feedbacks with long-range negative feedbacks.
Our model has some of the characteristics of the models in the papers cited above. At low N levels have short-range positive feedbacks on submerged plants by promoting their dominance, which leaves little nutrient for floating plants to grow due to long-range negative feedbacks. However, high nutrient level provides enough nutrient for both submerged plants and floating plants to grow. When floating plants grow to a sufficiently large size, they will have long-range negative feedbacks on submerged plants by shading light away from the water surface. Patch formations in Figure 10 are the examples of self-organized spatial patterns, for example, when N is equal to 0.74 in Figure 10(a), vegetation pattern forms a dot-stripe-like pattern. The boundary of self-organized pattern is clearer in figure 9(a) than that in figure 9(b), which shows that decreasing N with heterogeneity causes more visible pattern than increasing N with heterogeneity does.
Our modeling extends the work of studies such as [1] and [2] on the competition of floating and submersed vegetation in shallow lakes. In particular, within the range of values of nutrient, N, our modeling shows that the initial conditions on the starting biomasses of the competing species can determine the equilibria reached. The equilibria that are reached can then affect the response of the biomasses of the two species to any gradual changes in nutrient level in the system. Instead of an abrupt discontinuity causing dominance of one species to shift to another, it is more likely that a series of stable states will occur between the two extreme stable equilibria. This result may relate to similar results in models of vegetation patterns in semi-arid regions.
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
We appreciate the helpful comments of Donald Schoolmaster on an earlier version of this manuscript. DLD and LX were supported by U. S. Geological Survey's Greater Everglades Priority Ecosystem Science program, LX on Grant GR106613 to the University of Miami. Any use of trade, firm, or product names is for descriptive purposes only and does not imply endorsement by the U.S. Government.
The authors declare there is no conflict of interest.
Movement algorithm of biota.
FAV colonization
Each day FAV in a given pixel can invade a Moore-adjacent pixel deterministically by adding 1 g dW of biomass into an adjacent pixel if
● There is more than 8 g dW in the donor pixel.
● There is less than 1 g dW in the recipient pixel.
The donor pixel can contribute to more than one recipient pixel and the amount 1 g dW is subtracted for each donation.
SAV colonization
Each day SAV can invade 1 g dW of biomass into an adjacent pixel if
● There is more than 8 g dW in the donor pixel.
● There is less than 1 g dW in the recipient pixel.
That amount is subtracted from the donor pixel.
| [1] |
M. Scheffer, S. Szabo, A. Gragnani, E. Van Nes, S. Rinaldi, N. Kautsky, et al., Floating plant dominance as a stable state, PNAS, 100 (2003), 4040−4045. https://doi.org/10.1073/pnas.0737918100 doi: 10.1073/pnas.0737918100

|
| [2] |
E. van Nes, M. Scheffer, Implications of spatial heterogeneity for catastrophic regime shifts in ecosystems, Ecology, 86 (2005), 1797−1807. https://doi.org/10.1890/04-0550 doi: 10.1890/04-0550

|
| [3] |
M. McCann, Evidence of alternative states in freshwater lakes: A spatially-explicit model of submerged and floating plants, Ecol. Modell., 337 (2016), 298−309. https://doi.org/10.1016/j.ecolmodel.2016.07.006 doi: 10.1016/j.ecolmodel.2016.07.006

|
| [4] |
L. Xu, D. L. DeAngelis, Spatial patterns as long transients in submersed-floating plant competition with biocontrol, Theor Ecol., (2024). https://doi.org/10.1007/s12080-024-00584-6 doi: 10.1007/s12080-024-00584-6

|
| [5] |
A. B. Janssen, D. van Wijk, L. P. Van Gerven, E. S. Bakker, R. J. Brederveld, D. L. DeAngelis, et al., Success of lake restoration depends on spatial aspects of nutrient loading and hydrology, Sci. Tot. Envir., 679 (2019), 248−259. https://doi.org/10.1016/j.scitotenv.2019.04.4430048-9697 doi: 10.1016/j.scitotenv.2019.04.4430048-9697

|
| [6] |
M. Rietkerk, R. Bastiaansen, S. Banerjee, J. van de Koppel, M. Baudena, A. Doelman, Evasion of tipping in complex systems through spatial pattern formation, Science, 374 (2021). https://doi.org/10.1126/science.abj0359 doi: 10.1126/science.abj0359

|
| [7] |
S. Kéfi, A. Génin, A. Garcia-Mayor, E. Guirado, J. S. Cabral, M. Berdugo, et al., Self-organization as a mechanism of resilience in dryland ecosystems, PNAS, 121 (2024), p.e2305153121. https://doi.org/10.1073/pnas.2305153121 doi: 10.1073/pnas.2305153121

|
| [8] |
R. Bastiaansen, O. Jaïbi, V. Deblauwe, M. Eppinga, K. Siteur, E. Siero, et al., Multistability of model and real dryland ecosystems through spatial self-organization, PNAS, 115 (2018), 11256−11261. https://doi.org/10.1073/pnas.1804771115 doi: 10.1073/pnas.1804771115

|
| [9] |
R. Bastiaansen, H. Dijkstra, A. von der Heydt, Fragmented tipping in a spatially heterogeneous world, Environ. Res. Lett., 17 (2022). https://doi.org/10.1088/1748-9326/ac59a8 doi: 10.1088/1748-9326/ac59a8

|
| [10] |
M. Rietkerk, J. van de Koppel, Regular pattern formation in real ecosystems, Trends Ecol. Evol., 23 (2008), 169−175. https://doi.org/10.1016/j.tree.2007.10.013 doi: 10.1016/j.tree.2007.10.013

|
| [11] | J. von Hardenberg, E. Meron, M. Shachak, Y. Zarmi, Diversity of vegetation patterns and desertification, Phys. Rev. Lett., 87 (2001), 198101. https://doi-org.access.library.miami.edu/10.1103/PhysRevLett.87.198101 |
| [12] |
K. Siteur, E. Siero, M. Eppinga, J. Rademacher, A. Doelman, M. Rietkerk, Beyond Turing: The response of patterned ecosystems to environmental change, Ecol. Complex., 20 (2014), 81−96. https://doi.org/10.1016/j.ecocom.2014.09.002 doi: 10.1016/j.ecocom.2014.09.002

|
| [13] |
A.Vanselow, L. Halekotte, P. Pal, S. Wieczorek, U. Feudel, Rate-induced tipping can trigger plankton blooms, Theor. Ecol., 17 (2024), 1−7. https://doi.org/10.1007/s12080-024-00577-5 doi: 10.1007/s12080-024-00577-5

|
| [14] |
E. Sheffer, J. von Hardenberg, H. Yizhaq, M. Shachak, E. Meron, Emerged or imposed: A theory on the role of physical templates and self‐organisation for vegetation patchiness, Ecol. Lett., 16 (2013), 127−139. http://doi.org/10.1111/ele.12027 doi: 10.1111/ele.12027

|
| [15] |
X. Dong, S. Fisher, Ecosystem spatial self-organization: free order for nothing?, Ecol. Complex., 38 (2019), 24−30. https://doi.org/10.1016/j.ecocom.2019.01.002 doi: 10.1016/j.ecocom.2019.01.002

|
| 1. | Linhao Xu, Donald L. DeAngelis, Anatomy of the last days of a long transient spatial pattern: The ecological mechanism by which a traveling wave spatial patterns may end, 2025, 505, 03043800, 111101, 10.1016/j.ecolmodel.2025.111101 |
| State variables | Symbol | Values | Units |
| Floating plant biomass, FAV | F | 0 to 900 | g dW m-2 |
| Submersed plant biomass, SAV | S | 0 to 800 | g dW m-2 |
| Nutrient concentration in water | n | 0 to 2 | mg nitrogen l-1 |
| Parameters | |||
| Maximum relative growth rate | r | 0.5 (FAV and SAV) | day-1 |
| Loss rate | l | 0.05 (FAV and SAV) | day-1 |
| Half saturation coefficient for n | h | 0.2 (FAV), 0 (SAV) | mg nitrogen l-1 |
| FAV Light limitations parameter | a | 0.01 (FAV and SAV) | g dW m2 |
| Light attenuation in water | W | 0 | unitless |
| Total nutrient in system | N | 0 to 2 | mg nitrogen l-1 |
| Nutrient diffusion rate | Ndifff | 0.01, 0.05, 0.1, 0.2 | m2 day-1 |
| State variables | Symbol | Values | Units |
| Floating plant biomass, FAV | F | 0 to 900 | g dW m-2 |
| Submersed plant biomass, SAV | S | 0 to 800 | g dW m-2 |
| Nutrient concentration in water | n | 0 to 2 | mg nitrogen l-1 |
| Parameters | |||
| Maximum relative growth rate | r | 0.5 (FAV and SAV) | day-1 |
| Loss rate | l | 0.05 (FAV and SAV) | day-1 |
| Half saturation coefficient for n | h | 0.2 (FAV), 0 (SAV) | mg nitrogen l-1 |
| FAV Light limitations parameter | a | 0.01 (FAV and SAV) | g dW m2 |
| Light attenuation in water | W | 0 | unitless |
| Total nutrient in system | N | 0 to 2 | mg nitrogen l-1 |
| Nutrient diffusion rate | Ndifff | 0.01, 0.05, 0.1, 0.2 | m2 day-1 |