Mean time to infection by small diffusing droplets containing SARS-CoV-2 during close social contacts

1.   Introduction

Because of small fusion zone and low distortion, laser welding (LW) is gaining industrial importance day by day. Weld quality depends on the weld bead geometry ^[1,2,3]. Titanium alloys are treated as good corrosion resistance and lightweight materials. They are of great demand in automotive, aerospace, nuclear and biomedical industries ^[4]. Researchers are in the continuous process of developing models to simplify the time-consuming simulations. For welding of titanium alloys, laser beam welding (LBW) is opted due to its versatility, high specific heat input, and flexibility. For optimal process conditions, its weld strength is close to that of parent material. However, the potential weldability issues are low elongation, corrosion resistance and inferior fatigue properties ^[5].

Denney and Metzobower have made an interesting discussion on LBW of titanium ^[6]. Du et al. have carried out LBW (laser beam welding) simulations and presented fully penetrated weld bead geometry profiles ^[7]. Benyounis et al. have adopted RSM (response surface methodology) and examined the influence of focal position, speed and laser power on the weld bead geometry of medium steel carbon steel ^[8]. Liao and Yu have examined the weld bead profiles of thin stainless steel sheets performing pulse laser welding by varying the laser energy and incident angle ^[9]. Akman et al. have examined the effect of pulse duration and energy on DOP (depth of penetration) by analyzing microstructures and strength properties ^[10]. ANN (artificial neural network) approach is adopted for investigating the weld geometry ^[11]. Yamashita et al. and Takemori et al. have performed simulations on LW process ^[12,13].

Sathiya et al. have followed the Taguchi approach and found the optimal LW parameters for alloy 904L ^[14]. Shanmugam et al. have utilized ANSYS and performed FEA (finite element analysis) for generating weld bead profiles of AISI 304 varying beam power, incident angle and exposure time ^[15]. Squillace et al. have examined the influence of LBW parameters on morphology, tensile and fatigue properties ^[16]. Cherepanov et al. have performed simulations on the thermo-physical processes at LW of alloys possessing refractory nanoparticles ^[17]. Cao et al. have made investigations on the porosities in the LBW of butt joints ^[18]. Song et al. have analyzed the residual stress distribution in titanium welds ^[19]. Akbari et al. have performed simulations on pulsed LW of Ti–6Al–4V alloy and observed 2% to 17% deviation in temperature distribution and melt pool geometry ^[20]. Gao et al. have examined the influence of LW parameters on porosity formation ^[21]. Gao et al. have achieved better titanium alloy strength properties with medium OLF (overlapping factor) ^[22]. The shapes of the molten pool from numerical simulations of Azizpour et al. are comparable with measured data ^[23]. Akbari et al. have adopted an ANN approach and performed simulations for temperature distribution and melt pool geometry ^[24]. Zhan et al. have made investigations on invar 36 alloy conducting MIG welding and hybrid laser-MIG welding ^[25]. Zhan et al. have made consistent assessments with experiments on the microstructure of Ti–6Al–2Zr–1Mo–1V LBW joints ^[26]. Oliveira et al. have made a survey on the joining of NiTi shape memory alloys ^[27]. LW of NiTi and Ti6Al4V utilizing niobium interlayer is examined in ^[28]. High quality of weld joints can be produced through fiber LW of AA6061-T6 ^[29]. Gursel et al. have observed crack risk in Nd:YAG laser welding ^[30]. Caiazzo et al. have made investigations on LW of 3 mm thick Ti6Al4V alloy plates and recommended optimal LW parameters to lower the undercut and porosity ^[31]. Kumar et al. have reported the effect of the scanning speed and beam power on the fiber LW of Ti6Al4V alloy ^[32]. Kumar et al. have performed simulations and LBW tests on 1 mm thick Ti–6Al–4V alloy sheets varying welding speed and laser power ^[33]. Samples annealed at 980 ℃ yield tensile strength of 1048 MPa, which is above 4% to that of conventional weld samples. Auwal et al. have discussed the effect of LW parameters weld defects ^[34]. Kumar et al. have reported optimal parameters, which yielded high tensile strength in pulsed Nd:YAG LW of Monel 400 and Hastelloy C276 sheets ^[35]. Jiang et al. have carried out simulations and experiments on LW of Ti–6Al–4V alloy varying average power, beam diameter and pulse energy ^[36]. Kumar and Sinha have made investigations on pulsed Nd:YAG LW of Ti6Al4V alloy varying heat input and presented bead profile, micro-hardness and tensile strength ^[37].

LBW process will be generally either in conduction or in keyhole mode ^[38]. Welding in conduction mode is carried out above melting and below vaporization of materials. Thermal convection due to Marangoni flow will be there in addition to heat conduction. In keyhole welding, the surface temperature is above the threshold of boiling point. A hole will be formed in the weld pool after vaporization. Defects (like spatter and blowholes) are introduced upon creation of strong recoil pressure on the melt in the keyhole welding process. Conduction welding is a stable process. It is possible to achieve high quality welds free of pores and spatter ^[39]. To perform good quality of welding, there is a need for reliable simulation tools and weld equipment's ^[40,41]. Numerical simulations are required to minimize the cost and time-consuming trial tests, which provide the temperature field and the weld bead geometry. High-speed video recording is required to examine the process on the weld pool surface.

This paper adopts the Taguchi's L₉ OA (orthogonal array) in the numerical simulations to obtain optimal LBW process parameters for thin Ti–6Al–4V alloy sheets. By utilizing the Taguchi's design of experiments, empirical relations are developed for performance indicators in LBW simulations performing few trial runs. Narrow weld bead width with full depth of penetration is arrived by varying the LBW parameters. Empirical relations represent the weld bead profile. A set of optimal LBW parameters is finalized adopting a multi-objective optimization procedure.

2.   Materials and methods

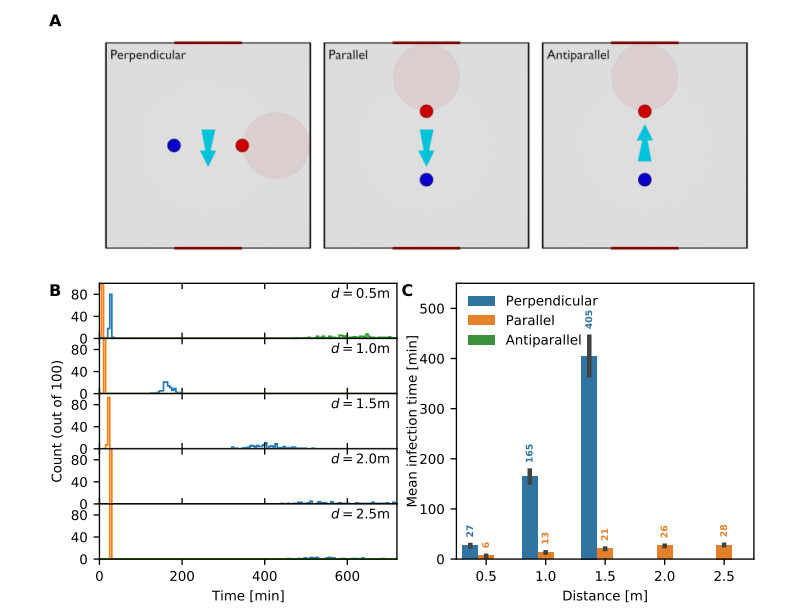
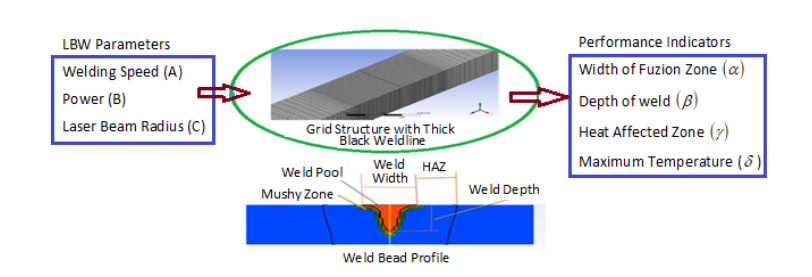
Thermal history in the weld is essential for assessing the strength of weld joint. To improve the quality of weld, selection of optimal LBW parameters plays an important role. The time-consuming trial and error-based methods are expensive. A CFD Model is required for carrying out thermo-fluid analysis to generate the weld bead profile. A 3D model for LBW is developed (incorporating buoyancy and Marnangoni stress). ANSYS Fluent embodied with VC++ code is utilized to assess the generic nature of the model by comparing the measured weld bead profiles of different materials (viz., SS304L, carbon steel, zircoly-4 and Zr-1%Nb) ^{[42,43,44,45,46,47]}. In the present study, 2 mm thick Ti–6Al–4V alloy plates (having 50mm length and 20mm width) are considered to perform LBW simulations. Figure 1 shows the LBW parameters and performance indicators. For the 3 LBW process parameters with 3 levels, full factorial design of experiments requires 27 tests, whereas 9 tests are needed as per the Taguchi's L₉ OA.

Numerical simulations are performed by varying 8 to 12 m/s welding speed; 150 to 250 W power; and 0.5 to 1.5 mm laser beam diameter. As in ^[43], the simulations are based on the solution of N–S (Navier–Stokes) equations, k-𝜀 equation in the regions of mushy zone and weld pool. The temperature dependent properties of Ti–6Al–4V alloy are considered ^[48]. Specific heat of solid is 670 J/(kg·K), whereas in case liquids it is 730 J/(kg·K). Viscosity of liquid is 0.005 kg/(m·s). Melting heat is 370000 J/kg. Solidus temperature (T_s) is 1878 K. Liquidus temperature (T_L) is 1928 K.

Density, ρ (kg/m³) in terms of temperature, T (K) is Eq 1.

The source term (or momentum frictional dissipation) in the mushy zone is Eq 2 ^[49,50].

Here $\overrightarrow{w}$ is the pull velocity and A_mush is a constant of the mushy zone.

Thermal conductivity, $\kappa$ (W·m⁻¹·K⁻¹) in terms of T (K) is Eq 3.

Following the welding process simulations ^{[42,43,44,45,46,47]} and considering the Ti–6Al–4V alloy properties, weld pool cross-section is generated specifying the welding speed (A), power (B) and the laser beam diameter (C) as per Taguchi's L₉ OA. Details on the identification of optimal LBW parameters are presented in the next section.

3.   Results

Taguchi method is useful to design with few welding experiments for the process variables and the assigned levels. Analysis of variance (ANOVA) results will be helpful in identifying the optimal welding parameters. From the experimental data, it is possible to generate the data for the full factorial design of experiments. A simple statistical approach, known as the Taguchi method ^[51] recommends an orthogonal array (OA) to perform few tests for obtaining performance indicators (PIs). From these tests, it is possible to generate PIs for all combinations of the levels of input process variables. That is the possibility of generating data for the full factorial design of experiments. Obviously, this approach minimizes the cost as well as the time-consuming trial and error-based tests. A few of the successfully solved engineering/industrial optimization problems are damages due to drilling of composites ^{[52,53,54,55]}, stage and satellite separation problems in space vehicles ^[56,57,58], performance of heat exchangers ^[59], design of planetary gears ^[60,61], welding process ^{[62,63,64,65,66,67]}, machining process ^{[68,69,70,71,72,73]}, and fuel engine performance ^{[74,75,76,77]}.

Taguchi method ^[51] recommends L₉ OA for LBW process variables, n_pv = 3 with levels, n_vl = 3. The minimum test runs (N_tests) required is Eq 4.

This could be the reason why Taguchi method ^[51] recommends L₉ OA. Tables 1 and 2, Figure 2 present numerical simulations of the PIs (viz., width of fusion zone, α (mm), depth of weld, β (mm), heat affected zone, γ (mm) and maximum temperature, δ (K)) and the simulated weld bead profiles for the nine test runs. Substituting N_tests = 9 and n_vl = 3 in Eq 4, one gets n_pv = 4, which indicates the possibility of accommodating 4 process variables in 9 test runs. Modelling and Numerical simulations (utilizing ANSYS Fluent V16.0 with Vc++ code) are validated by comparing the measured weld bead profiles of different materials (viz., SS304L, carbon steel, zircoly-4 and Zr-1%Nb) ^{[42,43,44,45,46,47]}. As in ^[43], Table 1 introduces a fictitious parameter (D). ANOVA (analysis of variance) results are presented in Table 3. %Contribution of B is significant on the grand mean value of both α and β. %Contribution of A, B and C on α are 8.3%, 88.5% and 2.6% respectively, whereas 26.8%, 52.7% and 19.4% are respectively on β. Sum of the %Contributions of A, B and C on α and β are 99.5% and 99%. Hence, the %Contribution of D on both α and β are 0.5% and 1%, which are nothing but the error (%).

From ANOVA Table 3, the optimal LBW process variables to achieve minimum α (width of fusion zone) are A₃B₁C₃, in which subscripts denote the levels of the process variables. The optimal LBW process variables to achieve maximum β (depth of weld) are A₁B₃C₁. These two sets of optimal LBW process variables are found to be different for achieving minimum α and maximum β. If the set of LBW process variables is not in L₉ OA of Table 2, then confirmation tests to obtain the PIs are mandatory.

Utilizing the additive law ^[51], estimates of PIs from the results of ANOVA Table 3 obtained are as follows. Let $\varPsi$ be the PI and $\widehat{\varPsi }$ is its estimate for the process variables (A_i, B_j, C_k, D_l) in which the levels are indicated by subscripts i, j, k, l varying from 1 to 3. Designating Ψ(A_i), Ψ(B_j), Ψ(C_k) and Ψ(D_l) as mean values of Ψ corresponding to the levels of the respective process variables. Ψ_mean, is the grand mean of the PI for nine test runs. As per the additive law ^[51], estimate $\widehat{\varPsi }$ for the specified (A_i, B_j, C_k, D_l) is Eq 5.

In case of 3 input variables (A_i, B_j, C_k), Eq 5 reduces to Eq 6.

The deviation of the estimates from Eqs 5 and 6 is Ψ(D_l) − Ψ_mean. For 3 levels (l = 1, 2, 3), 3 deviations are obtained. As in ^[43], the range of estimates is obtained through superposition of the minimum and maximum deviations to the estimates of Eq 6. Numerical simulations of α, β, γ and δ in Tables 4–7 are within the range of estimates. The minimum and maximum deviations for α, β, γ and δ are (−0.07, 0.05), (−0.06, 0.04), (−0.029, 0.02) and (−74.8, 98.9) respectively.

Following the concept of additive law, empirical relations for the PIs (α, β, γ and δ) are developed (from the results of ANOVA Table 3) in the form Eqs 7–10.

Here ζ₁ = 0.5A − 5; ζ₂ = 0.02B − 4; and ζ₃ = 2C – 2. The range of estimates for PIs (α, β, γ and δ) from empirical relations Eqs 7–10 is obtained by superimposing the respective minimum and maximum deviations. Figures 3–6 show the estimates of α, β, γ and δ for all possible 27 combinations ((((A_iB_jC_k), k = 1, 2, 3), j = 1, 2, 3), i = 1, 2, 3) of LBW parameters. Numerical simulations in Table 2 for the test runs in these Figures 3–6 are within the expected range (that is within lower and upper bounds).

4.   Results and discussion

(A₃B₁C₃) and (A₁B₃C₁) are two different sets of input process variables identified for minimum α and maximum β. To select a set of input process variables, a multi-objective optimization technique ^[64,65] is followed here by constructing a single objective function (ζ) in terms of α and β (after normalizing with α_max and β_max) and introducing weighing factors ω₁ ∈ [0, 1] and ω₂ = 1 − ω₁.

The single objective function (ζ) is Eq 11.

Minimization of ζ implies maximization of β and minimization of α for a set of input process variables. Table 8 presents the data for ζ generated from Table 8 consider equal weighting (${\omega }_{1}$ = ${\omega }_{2} = \frac{1}{2}$). ANOVA results are also presented in Table 8. The optimal input variables selected for the minimum ζ are A₁B₂C₁. These correspond to welding speed = 8 mm/s; power = 200 W and laser beam diameter = 0.5 mm. The PIs for these input variables are not in the Taguchi L₉ OA of Table 1. Hence, numerical simulations are performed by specifying the identified optimal input variables for obtaining the weld bead profile. Table 9 gives weld bead profiles for the single and multiple objective optimization problems. Numerical simulations are comparable to the range of PIs estimated from empirical relations Eqs 7–10. Figures 7–9 show the weld bead profile for max depth of weld, minimum bead width and optimum depth and width.

5.   Conclusions

Numerical simulations are performed on the laser beam welding (LBW) of 2 mm thick Ti–6Al–4V alloy sheets. Taguchi's design of experiments is followed to conduct few simulations. Following the concept of additive law in Taguchi's approach, the performance indicators (PIs), namely, width of fusion zone (α) and depth of penetration (β) are estimated and validated with simulation results for the input process variables in each test run of the Taguchi's L₉ OA (orthogonal array).

● Empirical relations are developed for PIs.

● Modified Taguchi approach provides the range of estimates for PIs.

● Optimal LBW process parameters are identified through a multi-objective optimization.

● Numerical simulations for the optimal LBW parameters are within the range of estimates.

● Incorporation of Taguchi approach in numerical simulations minimizes the trial and error-based test runs thereby reduction in computational time in selecting the optimal LBW parameters.

Future work is directed towards experimentation for investigating the microstructures and formation of defects in welding of Ti–6Al–4V with different welding processes (viz., electron beam welding, laser beam welding, plasma arc welding and TIG welding), and their influence on the properties.

Acknowledgments

The authors wish to thank the authorities of Koneru Lakshmaiah Education Foundation, India for providing facilities to carry out this work. The authors are grateful to the reviewers for their constructive criticism to improve the quality of presentation.

Conflict of interest

All authors declare no conflicts of interest in this paper.