A discontinuous Galerkin Method based on POD model reduction for Euler equation

1.   Introduction

The presence of an unknown degree of partial consolidation during a piezocone penetration test (CPTU) in silts complicates the interpretation of geotechnical parameters in these soil deposits. It is well established that standard rate (20 mm/s) CPTU tests in clays are carried out under undrained conditions whereas CPTU tests conducted in sands follow a drained penetration behaviour. For intermediate soils such as silts the penetration behaviour is complex and choosing an appropriate penetration rate is not easy due to the development of an unknown degree of partial drainage during standard penetration. Furthermore, the composition and structure of silt deposits impede the collection of high-quality soil samples and hence high-quality laboratory soil data is rather difficult to achieve ^[1]. Neglecting the presence of partial drainage in these materials may lead to a significant risk of over- or underestimating the geotechnical design parameters. Consequently, the improvement of interpretation models of in-situ testing methods becomes even more important in soils where partial drainage is present.

Up to recently, the focus of research interest has been on rate dependency in clayey soils and the influence of penetration rate on derived estimated geotechnical parameters. Recently, attention has been drawn to the field of intermediate soil behaviour focusing mainly on centrifuge and laboratory studies rather than field research sites ^[2,3,4,5,6]. Thus, it appears that existing published field data is rather limited and only a few studies have been documented dealing with the consolidation behaviour of silt deposits and the interpretation of consolidation parameters in these complex soils ^[7,8,9,10].

In order to study the influence of penetration rate in silts on the interpretation of consolidation parameters and to establish recommendations on how to interpret them in partial drained soil deposits a comprehensive field and laboratory testing program has been conducted by the Norwegian University of Science and Technology (NTNU). The field study comprised CPTU tests with penetration rates varying between 0.5 mm/s up to 200 mm/s followed by numbers of dissipation tests at four different depths of interest in the affected silt layer (4 m to 14 m). Supporting the field results, soil samples have been taken in the silt layer using thin walled 54 mm steel sample tubes for the purposes of laboratory consolidation testing.

The present paper focuses on the interpretation of consolidation parameters from the silt site by using corresponding field and laboratory test results. Several methods have been applied to the data in order to establish t₅₀ values (time for 50% dissipation of excess pore pressure) for non-standard dissipation tests ^{[11,12,13,14]}. In order to consider partial drainage effects on the coefficient of consolidation (c_h), the method proposed by DeJong & Randolph ^[15] has been applied to the data set. Furthermore, the procedure proposed by Schnaid et al. ^[16] for intermediate materials has been used in order to study the drainage behaviour and degree of partial consolidation of the soil deposit. Based on the results from the Halsen-Stjørdal study, the recommended procedures have been applied to existing dissipation data from the silt at the Norwegian Geo-Test Site (NGTS) in Halden, Norway in order to support and verify the findings. Recommendations have been made for practicing engineers on how to consider partial drainage in silts when establishing design parameters.

2.   Halsen-Stjørdal test site

2.1.   Site description

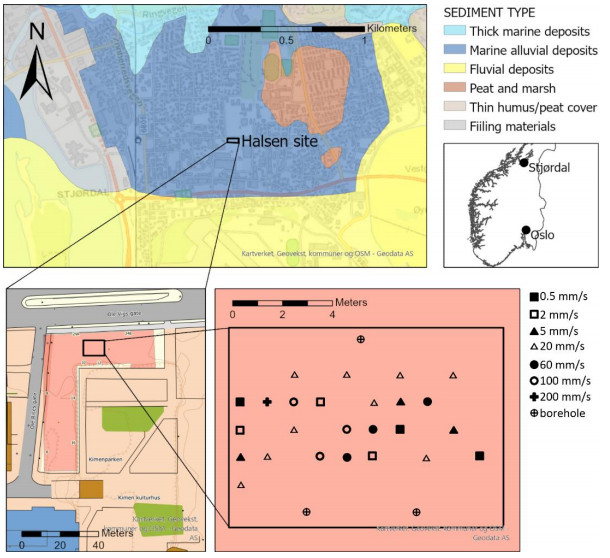
The research investigation test site Halsen-Stjørdal which is used for the current study is situated about 35 km north-east from Trondheim in Norway (Figure 1). The ground conditions are dominated by a thick low plastic silt deposit which is overlain by a stiff, coarse 4 m top layer. The ground water level is at 2.8 m depth and hydrostatic ground conditions prevail. The geological history of the area is defined by the Quaternary period. Enormous masses of fine-grained material were transported by rivers of melt water into the sea during the last de-glaciation. The Halsen-Stjørdal test site is primary characterized by these materials, forming a very irregular soil deposit with layers and lenses of clay and coarser sand. Geological studies carried out in the area indicate a normally to light overconsolidated (OC) soil deposit ^[17]. The current site is about 500 m away from the well-known Halsen test site investigated by Sandven ^[18].

2.2.   Site investigation program

In order to study the material behaviour of the silt deposit an extensive laboratory and field-testing program was conducted. The layout of the test site (Figure 1) covers an area of about 11 m × 8 m. Several CPTU tests were performed using a standard 10 cm² friction cone with measurements of the pore pressure at the u₂ position. The penetration rates were varied between 0.5 mm/s and 200 mm/s throughout the 25 CPTU tests in order to study the drainage behaviour of the silt in detail, aiming to cover all drainage conditions varying from drained, partial drained to undrained. In addition, dissipation tests were carried out at four predetermined depths of interest where the penetration was paused, and the development of the pore pressure was measured over time. To avoid possible movement of the system during a dissipation test, the rods were clamped carefully during each test. In addition to the field measurements, thin walled 54 mm steel sample tubes were used to take series of continuous soil samples.

3.   Laboratory test results

During the field-testing program a series of soil samples were taken from three boreholes down to a sampling depth of 14 m (Figure 1). To ensure highest possible soil sample quality, all samples were extruded and analyzed in the laboratory within 24 hours of sampling time. Bihs et al. ^[20] give a detailed description of the different test methods used, results obtained in the laboratory and discuss sample quality. The results reveal a rather irregular silt deposit with varied soil parameters with depth, reflecting the geological history of the material. The sample quality has been assessed by applying the clay based volume change criteria ^[21] as well as the strain energy compression ratio criteria ^[23], revealing reasonable sample quality for the present silt deposit ^[22].

3.1.   Basic laboratory tests

Figure 2 shows the basic laboratory results indicating an upper and lower silt layer from 4 m to 8 m and from 8 m to 14 m respectively. The water content is rather constant with depth with an average value of about 24%. Sensitivity measurements using the falling cone test indicate a medium sensitive material deposit with slightly increasing values with depth from about 10 at the top of the upper silt layer down to 28 in the lower silt layer.

Grain size distribution measurements reveal a sandy and/or clayey SILT with an average clay, sand and silt content of 7%, 38% and 55% respectively by applying the Norwegian recommendations made by the Norwegian Geotechnical Society (NGF) to identify the soil type ^[24]. Furthermore, the results show an increase of clay and sand content with depth and a slight decrease of silt content.

3.2.   Oedometer tests

A series of 1D consolidation constant rate of strain (CRS) have been carried out on 2 cm thick samples following the standard procedure described by Sandbæ kken et al. ^[25] and applying axial strain rates between 2 %/h to 5 %/h. Due to the silty nature of the material and some possible partial sample disturbance which occurred during sampling and extruding in the laboratory, the stress strain curves of the soil samples are of rather rounded character, not showing a distinct effective preconsolidation pressure (p'_c) which is characteristic for silt deposits. Several researchers stated similar findings in silts, e.g. ^[26,27]. The well-known method proposed by Becker et al. ^[28] was applied to the measured data sets and revealed overconsolidation ratios (OCR) between 1–2, indicating a normally to lightly overconsolidated material deposit. These findings are supported by the geological history of the area and prior analyses carried out by Sandven ^[18] nearby the present test site. Vertical coefficients of consolidation (c_v) were deduced using the method established by Janbu et al. ^[29]. Figure 3 A shows examples of c_v varying with vertical effective stress (σ_v') for two different samples taken between 7.45 m and 9.7 m.

Figure 3B shows the variation of c_v0 (taken at in-situ effective stress (σ_v0')) with depth for all samples analyzed, implying a rather irregular silt deposit. For the upper silt layer c_v0 values are scattered and vary between 80 m²/year and 750 m²/year whereas the results for the lower silt layer are more consistent between 80 m²/year and 300 m²/year. Results from Sandven ^[18] indicate similar varied results stressing the influence of sample disturbance and irregular soil layering.

3.3.   Triaxial tests

By following the procedure proposed by Berre ^[30], several anisotropically consolidated undrained triaxial compression tests (CAUC) have been carried out on samples from Halsen-Stjørdal. To achieve consistent test results, a shearing rate of 4 %/h is used and a backpressure of 200 kPa was applied to most of the samples. Due to the rather dilative behaviour of silts in triaxial compression, no unique maximum shear strength can be defined, resulting in a continuous increase of stress during shear. To establish undrained shear strength (s_u) profiles in these soils, Brandon et al. ^[31] proposed several criteria to determine s_u. Using criteria (5) where s_u is taken at the maximum measured pore pressure appeared to reveal most consistent results for this site and ensures a design strength being well below the fully mobilized strength at high strains ^[31]. Figure 4A shows the s_u profile with depth with an average value of about 55 kPa. Furthermore, values of the effective friction angles (φ') have been determined for the site with an average φ' of 36.9°.

To correctly determine consolidation parameters from CPTU tests, an evaluation of the rigidity index (I_R = G/s_u) is required. A lot of research has been carried out to relate the size of the plastic failure zone that is generated during a CPTU test to I_R ^[14,15]. With increasing I_R the failure zone increases which influences the generation and development of excess pore pressures and in turn c_h. Therefore, it is essential to determine a thorough design profile of I_R for each test site when dealing with the interpretation of dissipation tests from CPTU and it needs to reflect the actual stress distribution around the penetrating cone ^[33]. Although several approaches are available to determine I_R, use of high-quality laboratory data for G and s_u to establish a rigidity index profile is preferred. Shear strength values should represent the average strength around the cone whereas the shear modulus is often taken at 50 % mobilized strength (G₅₀) in the CAUC test as it represents the average soil response of the affected soil volume around the cone ^[32].

A number of different approaches have been published over time to deduce I_R. Keaveny & Mitchell ^[34] proposed an empirical relationship based on triaxial test data using a combination of OCR and plasticity index (IP). Furthermore, Kulhawy & Mayne ^[35] established a relation for I_R based on a Cam-clay derivation. Later Mayne ^[36] reformulated the critical state soil mechanics approach and derived an expression for I_R based on CPTU measurements. Agaiby & Mayne ^[37] formulated an expression for I_R based on post-processing of CPTU data. Krage et al. ^[32] stated that the interpretation of I_R in silty material is demanding due to the presence of partial drainage and the challenge of achieving high quality soil samples. Krage et al. ^[32] established two different methods to estimate I_R. Method A is based on laboratory test results for s_u and empirical estimates for G₅₀/ G_max where G_max represents the tangent modulus at low strains. Method B uses seismic CPTU data.

Figure 4B shows the application of method A and B as well as the laboratory data from triaxial test results for the Halsen-Stjørdal test site. The approaches suggested by Mayne ^[36] and Agaiby & Mayne ^[37] resulted in unreliable low values for I_R and were neglected in the present study. I_R values vary between 100 and 300, with an increasing tendency with depth. Method A falls in between the lower results from method B and the higher values for I_R from triaxial tests. Carroll & Paniagua ^[38] applied the methods proposed by Krage et al. ^[32] to a silt test site and confirmed good agreement with values established from laboratory tests. For the following consolidation analysis, a rigidity index of 200 has been chosen for the upper silt layer whereas an average I_R of 250 is applied to tests below 8 m depth. Table 1 summarizes results from research test sites studying CPTU dissipation tests in silts confirming that the I_R from Halsen-Stjørdal falls in between the intervals used by others dealing with low plastic and lightly overconsolidated silts.

4.   CPTU

4.1.   Standard CPTU tests

During the field-testing program, several standard rate CPTU tests have been carried out with a penetration rate of 20 mm/s down to a depth of about 18 m. All tests were executed by following the international standard procedures according to ISO 22476–1 ^[43]. It was necessary to predrill through a 4 m hard and stiff top layer, so as to keep the pore water filters saturated during the penetration process. The results of the penetration tests are presented in terms of measured cone resistance (q_t) corrected for out of balance pore water pressure effects, pore pressure at the u₂ location (u₂) and measured sleeve friction (f_S). Furthermore, the ratio of measured excess pore pressure to net cone resistance (q_t–σ_v0) is defined as the pore pressure parameter B_q and can be studied in Figure 5.

The results from the standard penetration rate tests reveal an irregular silty soil deposit with small layers and lenses with varying properties and indicating a coarse, sandy silt deposit. Measurements of q_t are rather constant with an average value of about 1.5 MPa, although showing some peak values between 10 m and 12 m. Pore pressure readings are very scattered, measuring values around the hydrostatic line (u₀) and even negative values are recorded. The results from the sleeve friction readings increase with depth, indicating a very irregular and scattered soil deposit. B_q values for the silt layer (4 m to 14 m) are very low and even negative due to the low u₂ readings which make this parameter very sensitive to the measured results. Below 14 m the soil deposit becomes more clayey and less silty which is emphasized by more steady q_t measurements, increasing u₂ and decreasing f_s readings. As a result of higher u₂ values, B_q increases in this layer. Overall findings from the standard CPTU tests confirm the results from the laboratory investigations.

4.2.   Varied rate CPTU tests

In addition to standard penetration rate CPTU tests, series of different rate tests have been carried out at the research test site by changing the rate between 0.5 mm/s and 200 mm/s but kept constant for each single test. By varying the penetration rate, it was aimed to cover all penetration conditions from drained to partially drained and finally undrained. A detailed analysis and evaluation of the varied penetration tests and drainage conditions at the Halsen-Stjørdal site can be found in Bihs et al. ^[10]. Figure 6 presents results for the silt layer between 4 m and 14 m by averaging the results for q_t, excess pore pressure Δu₂ (u₂–u₀) and f_S over the upper and lower silt layer depth and plotting the results over the corresponding penetration rate (v).

The results show a clear rate dependency of the registered q_t and u₂ measurements. The cone resistance increases with decreasing penetration rate, with a maximum of 3.1 MPa for the slower tests. For fast penetration rates q_t readings even out and are about 1.1 MPa at a minimum. The results for excess pore pressures indicate an opposite trend. For slow penetration rates, the values converge to a constant low level representing hydrostatic conditions. On the other hand, for fast penetration rates, Δu₂ readings increase and reveal high negative measures for the fastest penetration rates. Due to the very scattered f_s results, it was difficult to state a rate dependency for this parameter although it seems that f_s decreases in general for higher penetration rates in a similar manner to q_t.

4.3.   Dissipation tests

Various dissipation tests have been conducted during the field program at Halsen-Stjørdal at different depth of interest (Figure 5), covering all rates of penetration. To ensure no movement of the CPTU system, it was important to ensure fixed clamps during each dissipation measurement. For clay soils in undrained conditions typical dissipation behaviour expected would follow a monotonic decrease in pore pressure over time, reaching the hydrostatic pore pressure limit after time. However, researchers have observed several different dissipation curves types especially in high OC soils and intermediate soil deposits that can be categorized into types according to Sully et al. ^[11]. Figure 7 illustrates the types of dissipation curve divided into Type II to V for pore pressure measurements taken at the u₂ position. Type II and V represent dissipation tests that follow a monotonic decay of pore pressure over time although Type V represents the inverse of Type II starting below hydrostatic pore pressure level. Type III dissipation curves start above in-situ pore pressure, increase up to a maximum level and dissipate finally to the equilibrium in-situ condition. Type IV dissipation behaviour is like Type III although starting below in-situ level, increasing above and finally dissipating to the in-situ pore pressure level again. In the literature, dissipation test Type II is named a standard dissipation test whereas Types III to V are defined as non-standard or dilatory tests ^[36].

In normally consolidated soils standard dissipation behaviour is expected whereas in a highly overconsolidated, fissured or intermediate soil deposit, non-standard dissipation curves dominate the results ^[36]. Reasons for the appearance of these non-standard dissipation curves are numerous. Sully et al. ^[11] stated that the main reason for the rise in pore pressure before decay is mainly due to the redistribution of pore pressure directly after a stop in penetration. Usually the pore pressures at the tip are higher than directly behind the cone which result in a gradient of pore pressure towards the u₂ location, causing a drainage flow from the tip to the shaft ^[44]. Factors influencing the rate of drainage are soil permeability and values of the pore pressure gradient. Furthermore, the strength and stiffness of the soil surrounding the cone influence the gradient and hence the rate of dissipation. Another reason for the occurrence of non-standard dissipation curves is the influence of shear induced pore pressures ^[44]. Shear induced dilatancy causes a reduction in excess pore pressure near the shoulder of the cone compared to the adjacent soil. When penetration is halted, the higher excess pore pressures in the adjacent zone will cause a redistribution of pore pressure towards the u₂ position. Some researchers argue that poor saturation of the filter elements can cause the non-standard dissipation curves ^[12,45]. Although poorly saturated filters can cause a slow sensor response, it is now generally accepted that this is unlikely to be a significant reason for this dissipation behaviour ^[44].

Figures 8 to 10 reproduce the dissipation tests carried out at the site sorted by dissipation depth, rate of penetration and dissipation behaviour type. The difference in measured pore pressure before the start of the dissipation test and the first registered reading at the beginning of the test are small and hence neglectable. The y-axis scales are altered for clarity whereas the x-axis scales are kept the same. For dissipation test locations in the silt layer (4–14 m) the non-standard dissipation behaviour prevails whereas below in the more clayey layer, the standard dissipation behaviour dominates the results (Figure 8). The deepest location at 17.8 m is characterized by a monotonic behaviour for the slow and standard penetration rates whereas the fast tests produce non-standard dissipation tests, indicating less rate dependency than the dissipation tests in the more silty layer above (4–14 m). Figure 9 shows the dissipation tests divided into the different penetration rates. In general, the slow tests measure mainly hydrostatic in-situ pore pressures which is defined as drained penetration and supports the findings from the rate study in Bihs et al. ^[10]. Up to penetration rates of about 20 mm/s the standard dissipation curves predominate, whereas the dissipation tests carried out at faster penetration rates are characterized by a non-standard dissipation behaviour. Figure 10 groups the tests into the four different dissipation types. Type III and IV dissipation tests represent about half of the analyzed tests and are for the most part in the silt layer (4–14 m). Type II and V dominate for the soil unit below 14 m indicating that penetration tests carried in the more clayey layer are mainly represented by a monotonic dissipation behaviour.

In order to understand the mechanisms, it is necessary to study the composition of measured penetration pore pressures. It is well recognized that u₂ is a combination of hydrostatic pore pressure (u₀), change in octahedral normal stress or mean total stress (u_oct) and change in shear (u_shear) ^[46,47]. Although it is not possible to separate the measurements into the different components, a theoretical classification is possible according to (1):

Figure 11 represents a few dissipation tests with varied penetration rates from two locations in the silt layer by means of measured Δu₂ over time. Equilibrium pore pressures are measured for the very slow rate test whereas the fastest tests at 100 mm/s and 200 mm/s respectively are characterized by a Type V, starting at a high negative excess pore pressure level and monotonically dissipating towards equilibrium. The medium rate penetration tests at 20 mm/s and 60 mm/s are represented by a Type III and IV dissipation test respectively. In general, it is evident that the negative shear component Δu_{2, shear} increases with increased penetration rate. Schneider et al. ^[3] carried out a centrifuge piezocone study with different soil mixtures and achieved similar results for the normally consolidated samples of silty material. Furthermore, Chow et al. ^[48] presented penetrometer centrifuge studies in a reconstituted, normally consolidated, natural calcareous silt including dissipation tests after varied penetration rates. The investigation revealed comparable varied rate dissipation curves to this study which support the findings from the present study.

5.   Existing interpretation models

Dissipation tests are frequently used in engineering practice to estimate the coefficient of consolidation. However, the interpretation of dissipation tests from a soil deposit is complicated due to several reasons. These include the complexity of estimating the initial pore pressure distribution, soil disturbance due to the penetrating cone, which can create a zone of disturbed soil with lower permeability, and lastly dissipation of pore pressure is often influenced by soil anisotropy ^[49]. Dissipation tests in an undrained situation cause large strains in the adjacent soil immediately next to the CPTU, which is remoulded due to the penetration process, e.g. dissipation takes place in a partially remoulded soil element. In addition to the remoulding effect, large pore pressures are generated (especially in cohesive soils) due to the cavity expansion generated by the cone which causes a reduction in effective stress ^[45]. Upon a stop in penetration these excess pore pressures dissipate over time until reaching an equilibrium state. It is generally recognized that radial consolidation controls the conditions at the u₂ position, concluding that the coefficient of consolidation in the horizontal direction (c_h) dominates the consolidation process.

The interpretation solution most widely used was established by Teh & Houlsby ^[14] for soils in undrained dissipation conditions. The initial pore pressure distribution is idealized by large strain, finite element analysis in combination with the stress path method (SPM). A modified time factor T* is introduced as a theoretical solution for various degrees of consolidation, depending on the cone radius (r) and I_R in the following way

The process involves a plot of normalized excess pore pressure (U = Δu_t/Δu_initial) against log time (t) in order to select the time associated with 50% dissipation (t₅₀) which is usually taken as a representative value for the estimation of c_h.

Due to the existence of non-standard dissipation test curves in silts, it is necessary to adjust the initial pore pressure dissipation curve so that existing theories can be applied to the measured data. A first attempt to account for the non-standard behaviour was made by Burns & Mayne ^[12]. They based their solution on a cavity expansion-critical state model. Some important input parameters to their approach are OCR, I_R and φ. To achieve a best fit of the theoretical curve to the measured data, iteration of c_h and I_R is required.

Furthermore, several correction methods to the original t₅₀ have been established to consider the non-standard behaviour. Sully et al. ^[11] introduced several methods of fitting the measured curve to the theoretical one. The two most common approaches are the square root of time plot correction and the logarithm of time plot correction. The first approach uses extrapolation techniques to adjust the measured pore pressure curve to a new maximum pore pressure value at t = 0 and normalizes all values by this new maximum pore pressure. The later method is based on adjusting the curve to the measured maximum pore pressure value during a test by adjusting the time values according to t_new = 0 at that maximum u₂ point. However, choosing one of the adjusting methods proposed by Sully et al. ^[11], one has to keep in mind, that the initial part of the dissipation curve is not considered. Later Chai et al. ^[13] suggested a new approach to adjust the t₅₀ for non-standard dissipation curves by an empirical correction of the original t₅₀ using cylindrical cavity expansion simulations, including I_R and t₅₀.

Recent research carried out in silty soil deposits reveal, that the presence of partial consolidation contradicts the assumption of undrained conditions during penetration and reduces the initial excess pore pressure compared to the undrained state. The existence of partial drainage causes an incorrect estimate of c_h if undrained solutions are applied ^[15,50]. DeJong & Randolph ^[15] established a method to correct for partial drainage by modifying the original approach from Teh & Houlsby ^[14] for undrained penetration (based on a nonlinear soil model) and applying numerical (finite element analysis and cavity expansion) and field and centrifuge CPTU data. By accounting for different drainage conditions during dissipation tests, an underestimation of c_h can be prohibited. It is recommended to apply the proposed equations if the deduced t₅₀ values are less than 100 s ^[15].

Although the more recent developed methods that account for non-standard dissipation behaviour and partial consolidation are promising, they do not aim to provide a perfect solution to the complex problem. They provide a range of solutions as a framework for practicing engineers to adjust the design parameters according to a specific problem ^[51].

6.   Analysis

6.1.   Evaluation of t₅₀ for Halsen-Stjørdal test site

For further discussion, the layer between 4 m and 14 m will be referred to as one silt layer. Initially the data has been applied to the approach of Teh & Houlsby ^[14] resulting in t₅₀ values for the site presented in Figure 12A for the Type II and V dissipation tests. The t₅₀ values are widespread varying between 20 s and 260 s with an average value of 135 s, reflecting the rather layered and irregular structure of the soil deposit. To evaluate the t₅₀ values for the Type III and IV dissipation tests, the approach proposed by Burns & Mayne ^[12] has been initially used. Unfortunately, the curve fitting procedure which is necessary to match theory with measured data resulted in unrealistic values for I_R and c_h hence this method is not further considered in this study. Paniagua et al. ^[52] and Carroll et al. ^[38] reported similar findings. Furthermore, correction methods by Sully et al. ^[11] and Chai et al. ^[13] have been used to deduce t₅₀ values for the series of Type III and IV dissipation tests.

Figure 12B presents the data including the results for Type III and IV dissipation tests by Teh & Houlsby ^[14] showing an even more irregular profile than for the Type II and V dissipation tests shown in Figure 12A. Values of t₅₀ vary between 30 s and 450 s and it can be seen that the results for the different methods are especially scattered in the silt layer. Below 14 m the results converge but no trend with depth can been recognized. The approach suggested by Chai et al. ^[13] led to a very irregular and widespread t₅₀ profile, concluding that this approach is not as appropriate for the current test site. Centrifuge studies carried out by Mahmoodzadeh & Randolph ^[4] reported inconsistent results from the approach proposed by Chai et al. ^[13]. Comparing the two approaches by Sully et al. ^[11] Figure 12B indicates that the square root correction method revealed the most consistent results for the present site. Several researchers reported that the square root correction plot was the most successful one when dealing with the interpretation of Type III and IV dissipation curves in intermediate soils ^[4,48,53]. Overall, the approach by Teh & Houlsby ^[14] overestimates the t₅₀ compared to the square root correction method by an average factor of 2.1 which emphasizes the fact that this method reveals unrealistic high values for these dissipation tests.

Figure 13 shows examples from the silt layer where the normalized excess pore pressure is plotted against T* demonstrating the fact that the theoretical solution from Teh & Houlsby ^[14] is not able to reproduce the measured results for dissipation curves of Type III and IV. Furthermore, the square root correction plot by Sully et al. ^[11] has been included showing that this method can adopt to the rise in pore pressure even though information about the pore pressure development before the maximum value is not considered.

Figure 14A shows the final design values for the Type III and IV dissipation tests from the square root correction plot together with the results from the Type II and V dissipation tests from Teh & Houlsby ^[14]. About 1/3 of the tests in the silt layer have a t₅₀ < 100 s which is defined by DeJong & Randolph ^[15] as a limiting value for partial consolidation. If ignored, the results from interpreted c_h values may be significantly underestimated. The development of t₅₀ with penetration rate is presented in Figure 14B. Although showing rather scattered results, a clear trend of decreasing t₅₀ with increasing penetration rate is observed. Paniagua et al. ^[52] carried out studies covering results from a natural silt deposit and laboratory studies on reconstituted natural silt samples, indicating the same trend as observed in the present study. Furthermore, Carroll et al. ^[38] reported decreased t₅₀ values with increased rate, suggesting that the high negative excess pore pressures generated during very fast penetration tests lead to a significant increase in dissipation rate compared to the slower tests.

6.2.   Coefficient of consolidation for Halsen-Stjørdal test site

Even though the interpretation of c_h in partial consolidated soils is complicated, an attempt has been made to establish an estimated design profile for the horizontal coefficient of consolidation. The tests influenced by partial consolidation (t₅₀ < 100 s) have been analyzed separately from the remaining ones. First the conventional approach by Teh & Houlsby ^[14] has been applied to the data set. Furthermore, the correction method proposed by DeJong & Randolph ^[15] has been used in order to account for partial consolidation. Figure 15A presents results for the partially consolidated tests analyzed with the common approach by Teh & Houlsby ^[14] indicating values varying between 75 m²/year and 400 m²/year.

Furthermore, the separation line between typical c_h values (95 m²/year) expected for clay and silt has been included in Figure 15, indicating that the approach by Teh & Houlsby ^[14] underestimated the coefficient of consolidation, defining the deposit towards the clayey like behaviour.

Applying the approach by DeJong & Randolph ^[15] to the partial consolidated dissipation tests revealed a c_h profile according to Figure 15B showing minimum and maximum values of about 380 m²/year and 900 m²/year for the silt layer. By taking partial consolidation into account, the values for c_h increase for the silt layer by about 1.3 and are located more in the silt region compared to the results from Figure 15A. It can be concluded, that the application of the approach proposed by Teh & Houlsby ^[14] is not recommendable for silty deposits with partial consolidation taking place during penetration.

DeJong & Randolph ^[15] established a graphical solution including the original theory proposed by Teh & Houlsby ^[14] plotted as straight lines into the logarithmic plot of c_h over t₅₀ together with the new solution of incorporating partial drainage presented in Figure 16 for a 10 cm² cone ^[51]. The different lines represent different levels of I_R. For undrained conditions, e.g. small c_h values, the new method coincides with the method by Teh & Houlsby ^[14]. However, for values of t₅₀ < 100 s partial consolidation increases and with increasing c_h values the solutions diverge.

Dissipation tests with t₅₀ < 100 s have been plotted into Figure 16. Figure 16A presents the solution proposed by Teh & Houlsby ^[14] revealing results plotted around the theoretical line of I_R = 200 as expected. Whereas Figure 16B shows the theory applied by DeJong & Randolph (2012) taking partial consolidation into consideration. As t₅₀ decreases, c_h increases and the results plot close to the I_R = 200 line proposed by DeJong & Randolph ^[15], supporting the fact the c_h is underestimated in partial consolidated materials if drainage is not considered.

An estimated c_h profile with depth has been established from the dissipation tests taken at the site. The results are presented in Figure 17A, indicating a more scattered profile for the silt layer and converging more for the deeper layer below 14 m, emphasizing the rather layered and irregular structure of the silt layer. Figure 17B shows average ratios of c_h/c_v0 which have been determined for the site revealing scattered result varying up to a maximum of 3.1, representing ranges similar to those reported in the literature ^[4,54]. Nevertheless, Randolph ^[55] stated that care needs to be taken when comparing c_v0 from the laboratory with c_h from the field since the link between the elasto-plastic compressional response of the soil and the field values is complicated. An attempt has been made by Mahmoodzadeh & Randolph ^[54] to overcome these issues by introducing an operative coefficient of consolidation. Furthermore, Figure 17C presents the rate dependency of c_h for the deposit. High negative pore pressures recorded for high penetration rates lead to a slightly increased coefficients of consolidation hence an increase in rate of dissipation.

Nevertheless, care has to be taken when evaluating c_h values for a deposit where partial drainage may occur. In the majority of cases, it is challenging to fit the measured results to the theory used which makes the achieved results less reliable. The irregular structure which is often present in natural silt deposits complicates the interpretation of consolidation parameters. The level of layering at the relevant depth of the dissipation test may influence the results significantly, leading to values that might not reproduce design values characterizing the soil deposit altogether ^[18]. A way of avoiding the analysis of the coefficient of consolidation is to directly use methods to deduce estimates of permeability (k) by applying an empirical correlation between t₅₀ and k ^[51,56]. Furthermore, Robertson et al. ^[57] established a diagram which suggests values of k directly for certain values of t₅₀ and normalized cone resistance Q_tn.

6.3.   Rate study

DeJong et al. ^[50] implemented their theoretical solution into a field decision chart to check whether partial drainage is expected during a certain penetration rate with a given c_h. The normalized penetration rate (V) can be defined by the following way ^[58,59]:

Lines for different normalized penetration rates are included as well as areas indicating drained, undrained and partially drained penetration behaviour. Figure 18 shows the data from the present test site (from Figure 17A) plotted into the c_h versus penetration rate chart including the c_h ranges proposed by DeJong & Randolph ^[15] for clay and silt respectively. Initially it can be seen that the majority of the data falls into the silt region, covering mostly partially drained penetration tests as concluded by studies carried out on the silt deposit by Bihs et al. ^[10].

To overcome problems in establishing reliable coefficient of consolidation values in partial consolidated soil deposits such as silts when evaluating the drainage situation of a soil deposit, Schnaid et al. ^[16] proposed a direct formulation of a new normalized penetration rate V_h which is independent of c_h and just relies on penetration rate, diameter of the probe, I_R and t₅₀ in the following way:

The suggested method has been applied to the existing data set in the upper silt layer (4 m to 8 m) presented in Bihs et al. ^[10] using the established t₅₀ values from Figure 14A and a rigidity index of 200. Figure 19A & B show the results in terms of normalized cone resistance Q_t ( = (q_t-σ_v0)/σ'_v0) and normalized excess pore pressure (Δu₂/σ'_v0) respectively as a function of log V_h. The data has been fitted by a hyperbolic fitting equation as suggested by House et al. ^[59] and Chung et al. ^[60]. The standard penetration rate (20 mm/s) has been plotted into Figure 19 corresponding to a V_h of 26. The results prove that the suggested method by Schnaid et al. ^[16] reveals promising and reliable results for soil deposits where partial consolidation during penetration is likely to occur. For V_h < 0.2–0.3 the penetration is likely to be drained whereas for penetration rates of V_h > 40–50 undrained conditions can be expected.

7.   Example from the NGTS silt site in Norway

The consolidation study carried out at Halsen-Stjørdal showed that the square root correction method by Sully et al. ^[11] revealed the most consistent results for the determination of t₅₀ values. In order to establish reliable c_h values for the silt site, where partial drainage influences the results, the approach suggested by DeJong & Randolph has proven to provide reliable results. In order to verify the findings, data from the Norwegian Geo-Test Site (NGTS) for silts in Norway has been used and the methods proposed have been applied. The NGTS research site Halden is located about 120 km south of Oslo. The soil deposit consists of a low plastic, relatively uniform silt layer between 5 m and 15 m being characterized as a sandy, clayey silt. A detailed description about the ground conditions as well as laboratory and field tests carried out can be found in Blaker et al. ^[8]. Previous rate studies carried out on the silt indicate a tendency towards undrained conditions at V = 100 whereas drained conditions seem to occur at V < 1 ^[38].

A series of varied rate, high quality CPTU tests have been conducted supported by various dissipation tests at four different depth of interest in the silt layer (5 m, 6.5 m, 8.5 m and 10 m) ^[38,52]. In order to study the consolidation and drainage behaviour of the silt deposit and the rate dependency of the measured parameters, a few dissipation tests have been selected at depths of 6.5 m, 8.5 m and 10.5 m covering penetration rates varying between 1 mm/s up to 300 mm/s. Figure 20 shows the test data presented as measured pore pressure against registered time.

Overall, the slow dissipation tests show a close to monotonic dissipation behavior whereas the measured pore pressures increase with increased penetration rate, resulting in Type III dissipation curves for all tests except the slow ones. The dissipation tests at 6.5 m depth are quite varied with penetration rate, indicating a strong rate dependency on the consolidation behaviour of the deposit. For the deeper test locations, the dissipation curves converge more and get less dilative compared to the shallower ones. It is interesting to notice that no Type IV or V tests can be identified for the Halden test site, compared to the results presented for the Stjørdal-Halsen silt (Figure 11).

Values of t₅₀ have been established according to the square root correction method by Sully et al. ^[11] for the Type III dissipation curves. Figure 21A shows a summary plot of the t₅₀ values with depth comparing the approach by Teh & Houlsby ^[14] with the one by Sully et al. ^[11] revealing a significant overestimation of t₅₀ by Teh & Houlsby ^[14] (see also Figure 22). Furthermore, a clear reduction of t₅₀ with depth can be seen, indicating the presence of partial consolidation for tests located below 10 m depth as defined by DeJong and Randolph ^[15]. Figure 21B shows results of t₅₀ with penetration rate, indicating a trend of slightly reduced t₅₀ with increased penetration rate but not as clear as for the Halsen test site.

In order to estimate c_h values for Halden silt, a rigidity index of 147 has been used for the tests carried out at 6.5 m depth, whereas a value of 126 has been applied to the deeper tests as reported by Carroll et al. ^[38]. For t₅₀ < 100 s, partial consolidation has to be considered when calculating c_h values for the silt deposit. Hence the approach by DeJong & Randolph ^[15] has been used for the relevant tests. Figure 23 represents a summary plot showing results of c_h versus depth as well as c_h versus penetration rate for the Halden silt deposit. Despite some scatter on the data a slightly increasing c_h value with depth is recognized. Furthermore, no clear rate dependency is visible for the results.

Paniagua et al. ^[52] conducted an analysis of dissipation tests at 6.5 m depth from the same deposit, confirming the results described above. A clear trend of decreasing t₅₀ values with increased penetration rate was also reported by Carroll et al. ^[38] who executed a study of dissipation tests between 5 m to 10 m. The study emphasized the success of applying the square root correction method by Sully et al. ^[11] for the Type III dissipation tests.

Although the rate dependency of the established consolidation parameters for the Halden silt deposit does not show the same clear tendency as for the Halsen-Stjørdal silt site, the methods suggested for silts could be applied successfully confirming the importance of considering the rate dependency of the geotechnical parameters in these deposits.

8.   Summary and conclusions

Existing dissipation models are developed for elastic-plastic material behaviour and homogeneous soil conditions which do not prevail in silty soil deposits. To understand and get an overview over the present partial consolidation conditions in a soil deposit are essential factors in understanding and interpreting dissipation tests in silts ^[18]. Furthermore, studies carried out showed that the inhomogeneous nature of silty material can cause an incorrect estimate of c_h compared to a homogenous deposit as assumed by the theoretical interpretation methods ^[50,61]. In the absence of well-reviewed interpretation models and recommendations for silts together with only few existing field research silt sites, the present research project at NTNU has been conducted. Various field and laboratory investigations have been performed on a low plastic silt deposit at Halsen-Stjørdal in Norway to study the partial consolidation behaviour of the silt.

In order to correctly determine consolidation parameters from CPTU tests, an evaluation of I_R is crucial, which needs to reflect the actual stress distribution around the penetrating cone ^[33]. The two different methods recommended by Krage et al. ^[32] alongside with the well-known approach of using laboratory data revealed consistent values between 200 and 250 for the present silt layer which are in accordance with values presented by other research sites on low plastic, light OC silts ^[7,8,9,39]. Furthermore, the varied CPTU tests indicated a strong rate dependency of the measured q_t and u₂ parameters ^[10].

The analysis of more than 44 dissipation tests revealed predominantly Type III and IV dissipation tests in the silt layer (4–14 m). Whereas in the more clayey zone below 14 m, Type II and V dissipation tests dominate the results. Furthermore, rate dependency of the dissipation test type could be observed. The very slow rate dissipation tests showed almost drained behaviour as already examined by Bihs et al. ^[10] whereas the faster rate dissipation tests showed a Type III and IV dissipation behaviour. Investigations carried out by Schneider et al. ^[3] and Chow et al. ^[48] support the findings from the present dissipation study.

The evaluation of representative t₅₀ values for silt deposits is challenging due to the presence of unknown partial consolidation. For Type II and V dissipation curves, the well-known and accepted approach by Teh & Houlsby ^[14] has been used whereas for Type III and IV dissipation curves, the square root correction method proposed by Sully et al. ^[11] revealed the most consistent and reliable values for the Halsen-Stjørdal silt. The results showed a rather scattered t₅₀ profile especially in the silt layer (4–14 m) with values varying between 30 s and more than 300 s. The lower, clayey silt layer indicated more consistent t₅₀ results with a slightly decreasing trend with depth. Rate dependency studies showed that t₅₀ decreases with increasing penetration rate. Similar trends have been reported by others studying the dissipation behaviour of silts ^[38,52]. Furthermore, the results showed partially drained layers predominantly in the silt layer with t₅₀ values being less than 100 s which represents a limiting value according to DeJong & Randolph ^[15].

To evaluate the consolidation behaviour an attempt has been made to establish values of c_h for the silt deposit. For tests with t₅₀ values > 100 s, the approach by Teh & Houlsby ^[14] has been applied. Partial consolidation must be considered when evaluating c_h values for tests with t₅₀ values below 100 s. Therefore, the model proposed by DeJong & Randolph ^[15] has been successfully used in order to avoid an underestimation of c_h for the layers where partial consolidation is present ^[50]. Opposite rate dependency trends have been reported for c_h compared to t₅₀. A slight increase in c_h has been observed for increased penetration rates. Ratios of c_h to c_v0 have been deduced, showing values of up to 3.1 indicating higher consolidation values from the field tests as expected ^[4,55]. Great care should be taken when considering coefficient of consolidation values in silts due to the missing framework linking c_h from the field to the elasto-plastic compressional soil response ^[54]. To overcome problems in establishing reliable coefficient of consolidation values in partial consolidated soil deposits, Schnaid et al. ^[16] proposed a direct formulation of a new normalized penetration rate V_h which is independent of c_h. The application of V_h to the current test data showed borders for drained and undrained penetration behaviour which are in accordance with the ones established by Bihs et al. ^[10] using the standard approach for V. Finally, the experiences made in the Halsen-Stjørdal silt deposit have been used and the methods proposed have been applied to a dissipation data set available from a NGTS silt site in Norway. The results support the findings from the Halsen-Stjørdal site.

The present comprehensive study contributes to broadening the understanding of partially consolidated materials as silts and their consolidation behaviour. The recommendations and experiences made from two different silt sites are useful for practicing engineers in order to increase the awareness of the importance of considering partially drainage when establishing design consolidation values.

Acknowledgement

The authors would like to acknowledge the Norwegian Geo-Test Site project (No. 245650/F50) funded by the Research Council of Norway (RCN) for sharing the data on the Halden silt site.

Conflict of interest

All authors declare no conflict of interest.