Group decision-making analysis with complex spherical fuzzy $N$-soft sets

1.   Introduction

Multi-attribute group decision-making (MAGDM)^[1,2,3] is an artifice that investigates and resolves decision problems by integrating three basic modules of MAGDM; at least two decision-makers, two decision alternatives and two conflicting attributes. The elementary phenomena of MAGDM is to analyze the problem by combining the valuation of each decision alternative that are assessed by the decision-experts according to incompatible attributes and then results into a pertinent choice. The significant and associated MAGDM techniques are established to help the decision panel in order to solve MAGDM problems. These are frequently employed in various types of factual problems where collection of feasible alternatives are contemplated against some related parameters. The application of MAGDM techniques in poverty and poverty alleviation project has perpetually raised in the literature, readers are referred to ^[4].

1.1.   Related works

Outranking-based techniques ^[5], as an important classification of MAGDM, can be exploited to choose which decision alternative is more suitable, unexceptional or incomparable by comparing the alternatives with each other pursuant to each attribute. In the family of outranking techniques, ELECTRE method ^[6] plays an influential role as it has ability to take incomparable and appropriate thresholds into account and purely ordinal scales can be considered when imitating the imperfect information. The ELECTRE approach, also addressed as ELECTRE I technique is further improved as the ELECTRE-II, ELECTRE-III and ELECTRE-IV techniques efficient at tackling with choice problems and as in the case of ELECTRE-TRI and ELECTRE-A techniques, designed to deal with ranking problems. A detailed analysis was conducted by Figueria et al. ^[7] about the ELECTRE family that inclusively provide ranking of the alternatives by managing the attributes of quantitative nature. The diversity of ELECTRE techniques have been comprehensively utilized to different fields like environmental health, waterwaste management, forest management, energy and supplier selection.

Recently, the ELECTRE approach is applied to pursue the situation in which the assessed information of the MAGDM problems may be ambiguous and hazy, which is due to the limited awareness of decision-experts and also caused by the indistinct situations of real-life. For addressing the haziness contained in MAGDM problems fuzzy set (FS) theory, introduced by Zadeh ^[8], is absolutely suited. Indeed, extensive research has been performed on the expanded ELECTRE techniques in a fuzzy frame of reference, for example, Vahdani et al. ^[9] provided a neoteric ELECTRE approach together with the conception of interval weights and fuzzy information. Kabak et al. ^[10] presented a MADM technique for the selection of a snipper by associating the fuzzy ELECTRE method together with Fuzzy ANP and Fuzzy TOPSIS technique. Alghamdi et al. ^[11], Akram et al. ^[12] and Chen et al. ^[13] expanded ELECTRE I technique under fuzzy, bipolar neutrosophic and hesitant fuzzy context, respectively.

Atanassov ^[14], later added a new component to the description of FSs with the aim to handle the negative response $\nu$ of a member along with the positive response $\alpha.$ The abstraction that manifested is named as intuitionistic fuzzy sets (IFSs). Though FSs illustrate the level of positive response $\alpha$ of a person to the set under discussion, IFSs concede to assign level of truthiness $\alpha$ and falsity $\nu,$ which are interrelated by a marginal condition that $\alpha + \nu \leq 1$ entirely. It has even been extensively implemented in MAGDM and other sectors, like, Chen et al. ^[15] and Rouyendegh ^[16] extended ELECTRE I technique within the domain of IFSs for solving the project manager and site selection problem, respectively.

Pythagorean fuzzy sets $(P_{Y}FSs)$ were presented by Yager ^[17] to suppress the confines of the IFSs by the condition $\alpha^2+ \nu^2\leq 1.$ Akram et al. ^[18] utilized $P_YFSs$ for the development of ELECTRE I method in the context of multi-criteria decision-making, respectively. Furthermore, Akram et al. ^[19] presented the hesitant Pythagorean fuzzy ELECTRE II method and applied it to various case studies within the network of many criteria. In 2013, a neoteric concept of picture fuzzy sets (PFSs) was established by Cuong and Kreinovich ^[20] that demonstrates the level of truthiness $\alpha,$ neutrality $\delta$ and falsity $\nu$ of a person to the set under discussion along with a restriction $\alpha+ \delta+\nu\leq 1.$ Later on, picture fuzzy EDAS-ELECTRE approach was presented by Liang et al. ^[21] to appraise the level of environmental friendly production in gold mines.

Subsequently, Gundogdu and Kahraman ^[22] and Mahmood et al. ^[23] argued that the restriction of PFSs can be suppress by the condition $\alpha^2 + \delta^2 +\nu^2\leq 1$ in conjunction to capture three responses (yes, neutral, no) of human nature. The cogitation that emerged is known as spherical fuzzy sets (SFSs). Many valuable and beneficial advancements have been illustrated to enhance the decision-making techniques under spherical fuzzy environment ^[24,25].

In 2002, Ramot et al. ^[26] was first who revised the idea of fuzzy set theory and introduced an innovative concept of complex fuzzy sets (CFSs) to confront the periodic phenomena as the traditional models of fuzzy set theory are limited to handle the data of non-periodic nature. In CFS, the range of membership function is extended from the unit closed interval $[0, 1]$ to the complex unit disc $\{u| u\in \mathbb{C}, |u|\leq 1\}.$ Moreover, the complex intuitionistic fuzzy sets (CIFSs) were purposed by Alkouri and Salleh ^[27] in order to capture the complex-valued non-membership degree of alternatives. Ullah et al. ^[28] introduced the novel concept of complex Pythagorean fuzzy sets $(CP_{Y}FSs).$ Akram et al. ^[29] developed theory for complex Pythagorean fuzzy-ELECTRE I technique to solve MAGDM problems. One of the modern representations is complex spherical fuzzy sets $CSFSs$ proposed by Akram et al. ^[29]. Furthermore, $CSFSs$ can capture the abstinence data of periodic nature supplementary to constrained conditions on amplitude terms and phase terms. Akram et al. ^[30] worked on the expansion of ELECTRE I approach which is adequate enough to manage $CSF$ information. The $CSF$-ELECTRE I strategy nimbly integrates alternatives but ineffectual to measure MAGDM problems that contain information along the lines of multi-valuation and parameterizations. These infirmities of the figurative $CSF$-ELECTRE I method resolutely stimulate us to broaden ELECTRE I technique in terms of some comprehensive environment.

It is manifested that the vast majority of the research is based on the theories of fuzzy sets ^[8] and soft sets ^[31]. Meanwhile, many problems of real-world are provided with knowledge having a non-binary parameterized structure. Therefore, Fatimah et al. ^[32] introduced the novel theory of $N$-soft set $(N\mathcal{S}_{f}S)$ and constructed some algorithms for real-life decision-making problems. In recent time, the $N\mathcal{S}_{f}S$ is broadened under the productive fuzzy context, like fuzzy $N$-soft set $(FN\mathcal{S}_{f}S)$ ^[33], hesitant fuzzy $N$-soft sets $(HFN\mathcal{S}_{f}S)$ ^[34], Pythagorean fuzzy $N$-soft set $(P_{Y}FN\mathcal{S}_{f}S)$ ^[35], complex Pythagorean fuzzy $N$-soft set $(CP_{Y}FN\mathcal{S}_{f}S)$ ^[36] and so on. Particularly to our concerns, Akram et al. ^[37] investigated the magnificent theory of complex spherical fuzzy $N$-soft set $(CSFN\mathcal{S}_{f}S)$ as well as studied some comprehensive MAGDM techniques under the receptive discipline of complex spherical fuzzy $N$-soft sets.

1.2.   Significance of complex spherical fuzzy $N$-soft sets

The $CSFN\mathcal{S}_{f}S,$ as modern extension, overwhelm the inadequacies of the above-mentioned traditional models, including $CSFS$ and $CP_{Y}FN\mathcal{S}_{f}S.$ The splendid theory of $CSFN\mathcal{S}_{f}S$ comprises of two-dimensional vagueness, parameterizations and multi-nary ranking system. Research articles ^[37,38] briefly describe the significance and prominence of the dazzling $CSFN\mathcal{S}_{f}Ss$ real-life examples and applications by exploiting some fundamental tools and operations. Moreover, the characteristic comparison of the model of our purposes ($CSFN\mathcal{S}_{f}S$) with some existing models is given in Table 1 that ensured the superiority of the mainstream $CSFN\mathcal{S}_{f}$ model.

1.3.   Motivation of presented manuscript

The motivation and importance of the presented theory is described by the following arguments:

$1)$ The existing models from the family of $FN\mathcal{S}_{f}S$ including $IFN\mathcal{S}_{f}S,$ $P_{Y}FN\mathcal{S}_{f}S$ and $CP_{Y}FN\mathcal{S}_{f}S$ are insufficient to interpret the neutral response of individual nature. Therefore, the $CSFN\mathcal{S}_{f}S$ is preferred as the most convenient domain for the proposed method.

$2)$ The ELECTRE I approach is broadly applied on top of group decision-making approach that eliminates the less favorable alternative and designate the outranked results by implementing the pairwise comparison of conceivable choices in terms of concordance and discordance sets.

$3)$ The existing methodologies of decision-making, in particular, fuzzy-ELECTRE I, IF-ELECTRE I, $P_{Y}F$-ELECTRE I, $CP_{Y}F$-ELECTRE I and the latest expansion of ELECTRE I method under CSF environment (CSF-ELECTRE I method) are, however, competent to beneficially manage the ambiguous knowledge but they are unable to handle multi-valuation along with parameterizations. As there are several real-world applications in which relevant data is entailing multi-valuation along with parameterizations. These impotencies of the traditional techniques persistently persuade us to extend ELECTRE I approach in the context of well versed $CSFN\mathcal{S}_{f}Ss.$

$4)$ The additional complications in real-life problems implies that MAGDM can grant most trustworthy and accurate results. As it successfully applies the valuation from decision-makers who have appropriate data about the conflicting components of the crucial problem.

$5)$ Foregoing rationale shifted our interest towards the proposed generalization, whereupon the objective is to take advantage of the neoteric $CSFN\mathcal{S}_{f}S$ within the coherent approach of ELECTRE I in respect of problem-solving strategies.

1.4.   Contribution of presented manuscript

The foremost contributions of this manuscript can be epitomized as follows:

$1)$ This manuscript effectuate an experimental MAGDM strategy, known as $CSFN\mathcal{S}_{f}$-ELECTRE I method, to manage the $CSFN\mathcal{S}_{f}$ information that secures four opinions (Yes, abstinence, No and refusal) of human nature in two-dimensional setting along with multi-valuation parametrization.

$2)$ The proposed $CSFN\mathcal{S}_{f}$-ELECTRE I method deals with distinguishing ideas of concordance (discordance) sets which are modernly determined through the medium of score and accuracy degrees of complex spherical fuzzy $N$-soft numbers. The proposed scheme operates to suggests the supreme alternative by applying the outranking graphs and relations.

$3)$ The practicality and amenability of the presented method are approved through a vigorous numerical example of poverty alleviation from the discipline of social economy.

$4)$ We accomplish our established MAGDM technique by virtue of comparative study with traditional $CSF$-ELECTRE I method. The eventual results from both rationale techniques demonstrate the accountability of the developed strategy.

$5)$ Eventually, the primary insights of the proposed MAGDM approach illustrate it's versatility, proficiency, and distinction over the high-tech group decision-making methodologies.

1.5.   Outline of presented manuscript

Rest of the manuscript is systematized as follows: Section 2 recalls some groundwork of $CSFN\mathcal{S}_{f}S.$ Section 3 invokes a meticulous algorithm of proposed $CSFN\mathcal{S}_{f}$- ELECTRE I method, with a comprehensive overview of all phases, under the settings of complex spherical fuzzy $N$-soft sets. It also illustrates a graphical model of our complex spherical fuzzy $N$-soft concurrent decision supporting system. Section 4 explicates the proposed $CSFN\mathcal{S}_{f}$-ELECTRE I method through an application from the socio-economic field. Section 5 describes the comparative analysis of our proposed strategy with existing CSF-ELECTRE I method. Section 6 comprises the concluding remarks along with some major insights and boundaries of the provided scheme and contains some forthcoming research challenges.

2.   Preliminaries

Definition 2.1. ^[37] Let $\mathrm{U}$ be a non-empty set and $\mathcal{A} \subseteq E,$ whereas $E$ be a set of parameters (or attributes), and $M = \{0, 1, 2, \ldots, N-1\}$ be a set of grades level with $N \in \{2, 3, \ldots \}.$ Then a complex spherical fuzzy $N$-soft set $(CSFN\mathcal{S}_{f}S)$ on $\mathrm{U}$ is denoted by a triplet $(\digamma_{\tau}, \mathrm{A}, N),$ defined as

along with the assumption of $\digamma : \mathrm{A}\rightarrow 2^{ \mathrm{U}\times M},$ where $NS_{f}S$ be defined on $\mathrm{U},$ and $\tau$ is a function from $\mathrm{A}$ to $\mathbb{CSFN}$. The notation $\mathbb{CSFN}$ denotes the collection of all complex spherical fuzzy numbers on $\mathrm{U},$ and $g_{rs},$ $q_{rs},$ $h_{rs},$ indicating the amplitude terms, $\phi_{rs},$ $\eta_{rs}$ and $\gamma_{rs},$ indicating the phase terms, be well taken from unit closed interval within the constraint conditions

$\forall u_{r} \in \mathrm{U}$ and $a_{s} \in \mathrm{A}.$ The term $m^{r}_{s}$ denotes the ranking of the parameter $a_{s}$ for the alternative $u_{r}.$

Definition 2.2. ^[37] Let $\digamma_{\tau}(a_{s}) = (m^{r}_{s}, g_{rs}e^{i2\pi \phi_{rs}}, q_{rs}e^{i2\pi \eta_{rs}}, h_{rs}e^{i2\pi \gamma_{rs}})$ be a $CSFN\mathcal{S}_{f}S.$ Then complex spherical fuzzy $N$-soft number $(CSFN\mathcal{S}_{f}N)$ is defined as:

and the degree of refusal is defined as:

Definition 2.3. ^[37] Let $\kappa_{rs} = (m^{r}_{s}, g_{rs}e^{i2\pi \phi_{rs}}, q_{rs}e^{i2\pi \eta_{rs}}, h_{rs}e^{i2\pi \gamma_{rs}})$ be $CSFN\mathcal{S}_{f}N.$ The score function $\mathrm{Sc}(\kappa_{rs})$ of $CSFN\mathcal{S}_{f}N$ is:

where $\mathrm{Sc}({ \kappa_{rs}}) \in [-2, 3].$ The accuracy function $\mathrm{Ac}({ \kappa_{rs}})$ is:

where $\mathrm{Ac}({ \kappa_{rs}}) \in [0, 3],$ respectively.

Definition 2.4. ^[37] Let $\kappa_{rs} = (m^{r}_{s}, g_{rs}e^{i2\pi \phi_{rs}}, q_{rs}e^{i2\pi \eta_{rs}}, h_{rs}e^{i2\pi \gamma_{rs}})$ and $\kappa_{yx} = (m^{y}_{x}, g_{yx}e^{i2\pi \phi_{yx}}, q_{yx}e^{i2\pi \eta_{yx}}, h_{yx}e^{i2\pi \gamma_{yx}})$ be two $CSFN\mathcal{S}_{f}Ns$

1. If $\mathrm{Sc}({ \kappa_{rs}}) < \mathrm{Sc}({\kappa_{yx}})$, then $\kappa_{rs} \prec \kappa_{yx}$ ($\kappa_{rs}$ is inferior to $\kappa_{yx}),$

2. If $\mathrm{Sc}({ \kappa_{rs}}) > \mathrm{Sc}({\kappa_{yx}})$, then $\kappa_{rs} \succ \kappa_{yx}$ ($\kappa_{rs}$ is superior to $\kappa_{yx}),$

3. If $\mathrm{Sc}({ \kappa_{rs}}) = \mathrm{Sc}({\kappa_{yx}}),$ then

i $\mathrm{Ac}({\kappa_{rs}}) < \mathrm{Ac}({\kappa_{yx}}),$ then $\kappa_{rs} \prec \kappa_{yx}$ ($\kappa_{rs}$ is inferior to $\kappa_{yx}),$

ii $\mathrm{Ac}({\kappa_{rs}}) > \mathrm{Ac}({\kappa_{yx}}),$ then $\kappa_{rs} \succ \kappa_{yx}$ ($\kappa_{rs}$ is superior to $\kappa_{yx}),$

iii $\mathrm{Ac}({\kappa_{rs}}) = \mathrm{Ac}({\kappa_{yx}}),$ then $\kappa_{rs} \sim \kappa_{yx}$ ($\kappa_{rs}$ is equivalent to $\kappa_{yx}).$

Definition 2.5. The normalized Euclidean distance between two $CSFN\mathcal{S}_{f}Ns$ $\kappa_{rs} = (m^{r}_{s}, g_{rs}e^{i2\pi \phi_{rs}}, q_{rs}e^{i2\pi \eta_{rs}}, h_{rs}e^{i2\pi \gamma_{rs}})$ and $\kappa_{xs} = (m^{x}_{v}, g_{xs}e^{i2\pi \phi_{xs}}, q_{xs}e^{i2\pi \eta_{xs}}, h_{xs}e^{i2\pi \gamma_{xs}})$ are calculated as follow:

Definition 2.6. ^[37] Let $\kappa_{rs} = (m^{r}_{s}, g_{rs}e^{i2\pi \phi_{rs}}, q_{rs}e^{i2\pi \eta_{rs}}, h_{rs}e^{i2\pi \gamma_{rs}})$ and $\kappa_{xs} = (m^{x}_{s}, g_{xs}e^{i2\pi \phi_{xs}}, q_{xs}e^{i2\pi \eta_{xs}}, h_{xs}e^{i2\pi \gamma_{xs}})$ be two $CSFN\mathcal{S}_{f}Ns$ and $\varepsilon > 0.$ The operations related with $CSFN\mathcal{S}_{f}Ns$ are:

Definition 2.7. ^[37] Let $\kappa_{rs} = (m^{r}_{s}, g_{rs}e^{i2\pi \phi_{rs}}, q_{rs}e^{i2\pi \eta_{rs}}, h_{rs}e^{i2\pi \gamma_{rs}})$ be a family of $CSFN\mathcal{S}_{f}Ns$ and $\varepsilon = (\varepsilon_{1}, \varepsilon_{2}, \ldots \varepsilon_{w})^{T}$ be the weight vector of $\kappa_{rs}$ with $\varepsilon_{s} > 0$ and $\sum\limits_{s = 1}^{w} \varepsilon_{s} = 1.$ The complex spherical fuzzy $N$ soft weighted average $(CSFN\mathcal{S}_{f}WA)$ operator is defined as:

3.   Algorithm of complex spherical fuzzy $N$-soft ELECTRE I method

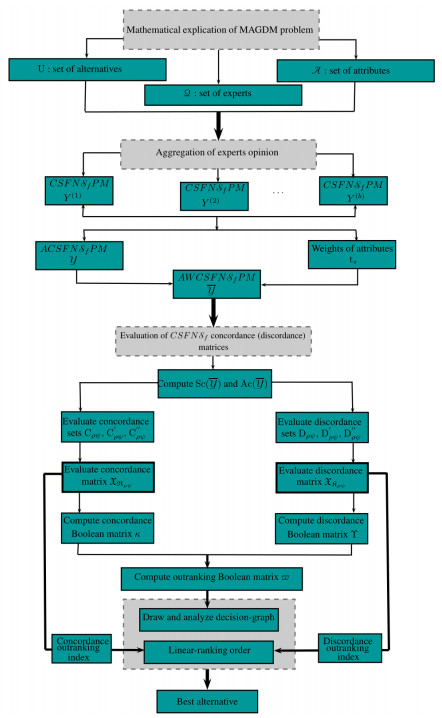
In this section, complex spherical fuzzy $N$-soft ELECTRE I ($CSFN\mathcal{S}_{f}$-ELECTRE I) method is introduced to support the multi-attribute group decision making (MAGDM) problems under $CSFN\mathcal{S}_{f}$ environment. In $CSFN\mathcal{S}_{f}$-ELECTRE I method, $CSFN\mathcal{S}_{f}Ns$ are basically assigned to the alternatives according to the conflicting parameters as well as with respect to the weights of the parameters. The $CSFN\mathcal{S}_{f}$-ELECTRE I method pursue the following procedure:

Consider a MAGDM problem with

$-$ $\mathrm{U} =$ $\{\mathrm{U}_{1},$ $\mathrm{U}_{2},$ $\mathrm{U}_{3},$ $\ldots,$ $\mathrm{U}_{v}\}$ be a discrete set of $v$ alternatives,

$-$ $\mathcal{A}_{s} =$ $\mathcal{A}_{1},$ $\mathcal{A}_{2},$ $\mathcal{A}_{3},$ $\ldots,$ $\mathcal{A}_{w}$ be a set of decision attributes,

$-$ $\mathcal{Q}_{p} =$ $\mathcal{Q}_{1},$ $\mathcal{Q}_{2},$ $\mathcal{Q}_{3},$ $\ldots,$ $\mathcal{Q}_{b}$ be a group of decision experts.

Phase I: Assemblage of Group Evaluation

${\bf Step 1:}$ The decision-makers $\mathcal{Q}_{p}$ specify $CSFN\mathcal{S}_{f}N$ to each ordered grade of the $N\mathcal{S}_{f}S$ that are initially submitted by the decision-making panel. So that the complex spherical fuzzy $N$-Soft performance matrices ($CSFN\mathcal{S}_{f}PMs$) $Y^{(p)}$ with the entities $D^{(p)}_{rs} = ({m^{r}_{s}}^{(p)}, \alpha^{(p)}_{rs}, \delta^{(p)}_{rs}, \nu^{(p)}_{rs}) = ({m^{r}_{s}}^{(p)}, g^{(p)}_{rs}e^{i2\pi \phi^{(p)}_{rs}}, q^{(p)}_{rs}e^{i2\pi \eta^{(p)}_{rs}}, h^{(p)}_{rs}e^{i2\pi \gamma^{(p)}_{rs}})$ are pursuant to each decision-expert $\mathcal{Q}_{p}.$ The MAGDM problem can be expressed as in Table 2 where, $r\in\{1, 2, \ldots, v\},$ $s\in\{1, 2, \ldots, w\}$ and $p\in\{1, 2, \ldots, b\}.$

${\bf Step 2:}$ Construct the aggregated complex spherical fuzzy $N$-soft performance matrix ($ACSFN\mathcal{S}_fPM$) as in Table 3. The intellectual perspectives of decision-experts are required to be summarized in one performance matrix by using the experts opinions along with normalized weight vector $\mathrm{a} = (\mathrm{a}_1, \mathrm{a}_2, \ldots \mathrm{a}_b)^{T}$ of the experts. For this purpose, a ${CSFN\mathcal{S}_{f}WA}$ operator is employed in the following way:

${\bf Step 3:}$ Evaluate the weight matrix for selected attributes as the preference perception of possible choices varies in accordance with the rank of the attributes. The non-binary ranks of the attributes are further developed by decision-experts into $CSFN\mathcal{S}_{f}$-weights $\mathrm{t}^{(p)}_{s} = ((m^{r}_{s})^{(p)}, g^{(p)}_{s}e^{i2\pi \phi^{(p)}_{s}}, q^{(p)}_{s}e^{i2\pi \delta^{(p)}_{s}}, h^{(p)}_{s}e^{i2\pi \gamma^{(p)}_{s}})$ that are aggregated by the $CSFN\mathcal{S}_{f}WA$ operator in the following manner:

${\bf Step 4:}$ Establish the aggregated weighted complex spherical fuzzy $N$-soft performance matrix ($AWCSFN\mathcal{S}_fPM$) $\overline{\mathcal{Y}} = (\overline{\mathcal{Y}}_{rs})_{v \times w} = (\overline{m}^{r}_{s}, \overline{g}_{rs}e^{i2\pi\overline{\phi}_{rs}}, \overline{q}_{rs}e^{i2\pi\overline{\delta}_{rs}}, \overline{h}_{rs}e^{i2\pi\overline{\gamma}_{rs}}),$ as in Table 4, with the help of $ACSFN\mathcal{S}_fPM$ along with the weights of attributes $\mathrm{t}_s.$ Compute each entity of $\overline{\mathcal{Y}}$ by using Eq (3.1).

Phase II: Complex spherical fuzzy $N$-soft ELECTRE I ranking phase

Subsequent to the secured computations from the first phase of the complex spherical fuzzy $N$-soft decision endorse technique, the second phase applies the method of $CSFN\mathcal{S}_f$-ELECTRE I, to conclude the ranking order of decision alternatives.

${\bf Step 5:}$Compute score and accuracy values of $\overline{\mathcal{Y}}_{rs}$ as in Table 5, using Eqs (2.1) and (2.2), respectively. The pair wise comparison of possible choices corresponding to some competent attributes is a central analysis of $CSFN\mathcal{S}_f$-ELECTRE I method. The score degree $\mathrm{Sc}(\overline{\mathcal{Y}}_{rs})$ and the accuracy degree $\mathrm{Ac}(\overline{\mathcal{Y}}_{rs})$ are employed to compare the entities of $AWCSFN\mathcal{S}_fPM$ $\overline{\mathcal{Y}}.$ It is suggested that an adequate alternative likely to have higher $\mathrm{Sc}(\overline{\mathcal{Y}}_{rs})$ or lower $\mathrm{Sc}(\overline{\mathcal{Y}}_{rs})$ as well as may possess higher $\mathrm{Ac}(\overline{\mathcal{Y}}_{rs})$ or lower $\mathrm{Ac}(\overline{\mathcal{Y}}_{rs}).$ The alternative with higher score value implies higher ordered grade along with higher satisfaction degree, whereas the higher score value not always implies higher accuracy value.

${\bf Step 6:}$ For a random pair of choices $(\mathrm{U}_{\rho}, \mathrm{U}_{\psi}),$ ($\rho, \psi = 1, 2, 3, \ldots, v,$ $\rho \neq \psi$), the $CSFN\mathcal{S}_f$ concordance sets comprehend all the indices of the attributes for which the alternative $\mathrm{U}_{\rho}$ is preferable than the alternative $\mathrm{U}_{\psi},$ that is, the alternative $\mathrm{U}_{\rho}$ has higher ordered grade along with higher satisfaction value as compared to the alternative $\mathrm{U}_{\psi}.$ In accordance with the stances of accuracy and score functions defined for $CSFN\mathcal{S}_fNs,$ the $CSFN\mathcal{S}_f$ concordance sets can be classified as the $CSFN\mathcal{S}_f$ strong, mid range and weak concordance sets. The $CSFN\mathcal{S}_f$ concordance sets are established in the following manner:

(i) The complex spherical fuzzy $N$-soft strong concordance set $\mathrm{C}_{\rho\psi}$ is calculated as:

The greater value of score function and accuracy function of the entity $\overline{\mathcal{Y}}_{\rho s}$ corresponds to the greater ordered grade and greater satisfaction value of the alternative $\mathrm{U}_{\rho}$ as compared to the alternative$\mathrm{U}_{\psi}.$ Therefore, the alternative $\mathrm{U}_{\rho}$ is strongly concordant from the alternative $\mathrm{U}_{\psi}.$

(ii) The complex spherical fuzzy $N$-soft mid range concordance set $\mathrm{C}^{'}_{\rho\psi}$ is calculated as:

The alternatives $\mathrm{U}_{\rho}$ and $\mathrm{U}_{\psi}$ are mid range concordant to each other due to the higher accuracy value of the entity $\overline{\mathcal{Y}}_{\psi s}$ from the entity $\overline{\mathcal{Y}}_{\rho s}.$

(iii) The complex spherical fuzzy $N$-soft weak concordance set $\mathrm{C}^{"}_{\rho\psi}$ can be determined as:

The equal value of score function indicates that the alternatives are equivalently significant with respect to the ordered grades and the membership degrees. Whereas the larger value of accuracy function of $\overline{\mathcal{Y}}_{\rho s}$ implies the preference of the alternative $\mathrm{U}_{\rho}$ over the alternative $\mathrm{U}_{\psi}.$

Step 7: For a random pair of choices $(\mathrm{U}_{\rho}, \mathrm{U}_{\psi}),$ ($\rho, \psi = 1, 2, 3, \ldots, v,$ $\rho \neq \psi$), the $CSFN\mathcal{S}_f$ discordance sets encompass all the indices of the attributes for which the alternative $\mathrm{U}_{\rho}$ is not appropriate as compared to the alternative $\mathrm{U}_{\psi}.$ In accordance with the stances of accuracy and score functions defined for $CSFN\mathcal{S}_fNs,$ the $CSFN\mathcal{S}_f$ discordance sets can be classified as the $CSFN\mathcal{S}_f$ strong, mid range and weak discordance sets. The $CSFN\mathcal{S}_f$ discordance sets are established in the following manner:

(i) The complex spherical fuzzy $N$-soft strong discordance set $\mathrm{D}_{\rho\psi}$ can be determined as:

The lesser value of score function and accuracy function of $\overline{\mathcal{Y}}_{\rho s}$ corresponds to the minimum grade and lesser truth membership degree of the alternative $\mathrm{U}_{\rho}$ from the alternative $\mathrm{U}_{\psi}.$ Therefore, the alternative $\mathrm{U}_{\rho}$ is strongly discordant from the alternative $\mathrm{U}_{\psi}.$

(ii) The complex spherical fuzzy $N$-soft mid range discordance set $\mathrm{D}^{'}_{\rho\psi}$ can be determined as:

The alternatives $\mathrm{U}_{\rho}$ and $\mathrm{U}_{\psi}$ are mid range discordant to each other due to the lower accuracy value of the entity $\overline{\mathcal{Y}}_{\psi s}$ from the entity $\overline{\mathcal{Y}}_{\rho s}.$

(iii) The complex spherical fuzzy $N$-soft weak discordance set $\mathrm{D}^{"}_{\rho\psi}$ can be determined as:

The lesser value of accuracy function of $\overline{\mathcal{Y}}_{\rho s}$ implies the preference of the alternative $\mathrm{U}_{\rho}$ as weakly discordant over the alternative $\mathrm{U}_{\psi}.$ Whereas the equal value of score function indicates that the alternatives are equally important with respect to the grades and the membership degrees.

Step 8: The exclusive $CSFN\mathcal{S}_{f}$ concordance matrix is determined by the $CSFN\mathcal{S}_{f}$ concordance indices $\mathfrak{R}_{\rho \psi}$ ($\rho, \psi = 1, 2, 3, \ldots, v,$ $\rho \neq \psi$). The $CSFN\mathcal{S}_{f}$ concordance index is proportional to the sum of the $CSFN\mathcal{S}_{f}$ weights $\mathrm{t}_{s}$ ($s = 1, 2, 3, \ldots, w)$ of the attributes whose indices are confined in the $\mathrm{C}_{\rho\psi},$ $\mathrm{C}^{'}_{\rho\psi}$ and $\mathrm{C}^{"}_{\rho\psi}.$ In $CSFN\mathcal{S}_{f}$-ELECTRE I method the concordance indices $\mathfrak{R}_{\rho \psi} = ({m^{(s)}_{\mathfrak{R}_{\rho \psi}}}, \alpha^{(s)}_{\mathfrak{R}_{\rho \psi}}, \delta^{(s)}_{\mathfrak{R}_{\rho \psi}}, \nu^{(s)}_{\mathfrak{R}_{\rho \psi}}) = ({m^{(s)}_{\mathfrak{R}_{\rho \psi}}}, g^{(s)}_{\mathfrak{R}_{\rho \psi}}e^{i2\pi \phi^{(s)}_{\mathfrak{R}_{\rho \psi}}}, q^{(s)}_{\mathfrak{R}_{\rho \psi}}e^{i2\pi \eta^{(s)}_{\mathfrak{R}_{\rho \psi}}}, h^{(s)}_{\mathfrak{R}_{\rho \psi}}$ $e^{i2\pi \gamma^{(s)}_{\mathfrak{R}_{\rho \psi}}})$ of $\mathrm{U}_{\rho}$ and $\mathrm{U}_{\psi},$ is measured as:

where, the ${\mathfrak{E}}_{\mathrm{C}_{\rho\psi}},$ ${\mathfrak{E}}_{\mathrm{C}^{'}_{\rho\psi}}$ and ${\mathfrak{E}}_{\mathrm{C}^{"}_{\rho\psi}}$ are respectively the weights of $CSFN\mathcal{S}_{f}$ strong concordance set, $CSFN\mathcal{S}_{f}$ mid range concordance set and $CSFN\mathcal{S}_{f}$ weak concordance set relying on the viewpoints of the decision-experts.

The $CSFN\mathcal{S}_{f}$ concordance matrix $\mathfrak{X}_{\mathfrak{R}_{\rho \psi}}$ is estimated as follows:

Step 9: The $CSFN\mathcal{S}_{f}$ discordance matrix is determined by the $CSFN\mathcal{S}_{f}$ discordance indices $\mathfrak{K}_{\rho \psi}$ ($\rho, \psi = 1, 2, 3, \ldots, v,$ $\rho \neq \psi$). The $CSFN\mathcal{S}_{f}$ discordance index is reflective of significant difference of $\mathrm{U}_{\rho}$ with reference to $\mathrm{U}_{\psi}$ from the perspective of discordance attributes whose indices are confined in the $\mathrm{D}_{\rho\psi},$ $\mathrm{D}^{'}_{\rho\psi}$ and $\mathrm{D}^{"}_{\rho\psi}.$ In $CSFN\mathcal{S}_{f}$-ELECTRE I method the discordance index $\mathfrak{K}_{\rho \psi} = ({m^{(s)}_{\mathfrak{K}_{\rho \psi}}}, \alpha^{(s)}_{\mathfrak{K}_{\rho \psi}}, \delta^{(s)}_{\mathfrak{K}_{\rho \psi}}, \nu^{(s)}_{\mathfrak{K}_{\rho \psi}}) = ({m^{(s)}_{\mathfrak{K}_{\rho \psi}}}, g^{(s)}_{\mathfrak{K}_{\rho \psi}}e^{i2\pi \phi^{(s)}_{\mathfrak{K}_{\rho \psi}}}, q^{(s)}_{\mathfrak{K}_{\rho \psi}}e^{i2\pi \delta^{(s)}_{\mathfrak{K}_{\rho \psi}}}, h^{(s)}_{\mathfrak{K}_{\rho \psi}}$ $e^{i2\pi \gamma^{(s)}_{\mathfrak{K}_{\rho \psi}}})$ is defined as:

where, ${\mathfrak{E}}_{\mathrm{D}_{\rho\psi}},$ ${\mathfrak{E}}_{\mathrm{D}^{'}_{\rho\psi}}$ and ${\mathfrak{E}}_{\mathrm{D}^{"}_{\rho\psi}}$ are respectively the weights of $CSFN\mathcal{S}_{f}$ strong discordance set, $CSFN\mathcal{S}_{f}$ mid range discordance set and $CSFN\mathcal{S}_{f}$ weak discordance set relying on the stances of the decision-experts and $d(\overline{\mathcal{Y}}_{\rho s}, \overline{\mathcal{Y}}_{\psi s})$ denotes the $CSFN\mathcal{S}_{f}$ normalized Euclidean distance. The $CSFN\mathcal{S}_{f}$ normalized Euclidean distance $d(\overline{\mathcal{Y}}_{\rho s}, \overline{\mathcal{Y}}_{\psi s})$ between $\overline{\mathcal{Y}}_{\rho s}$ and $\overline{\mathcal{Y}}_{\psi s}$ is calculated as:

The $CSFN\mathcal{S}_{f}$ discordance matrix $\mathfrak{X}_{\mathfrak{K}_{\rho \psi}}$ is defined as:

Step 10: The $CSFN\mathcal{S}_{f}$ dominance concordance matrix $\Im$ is established according to the threshold value $\varsigma$ of $CSFN\mathcal{S}_{f}$ concordance indices. The dominance degree of the alternative $\mathrm{U}_{\rho}$ increases if the score value of $CSFN\mathcal{S}_{f}$ concordance index $\mathfrak{R}_{\rho \psi}$ of $\mathrm{U}_{\rho}$ with respect to $\mathrm{U}_{\psi}$ is over the threshold value $\varsigma$ can be determined as:

$(\rho, \psi = 1, 2, 3, \ldots, v,$ $\rho \neq \psi).$

The $CSFN\mathcal{S}_{f}$ concordance dominance matrix $\Im$ $= (\Im_{\rho \psi})_{v\times v}$ can be determined as:

whose entities satisfy

Step 11: Similarly, the $CSFN\mathcal{S}_{f}$ discordant dominant matrix are also evaluated by the discordant level $\tau,$ which is basically the average of all the entities in the $CSFN\mathcal{S}_{f}$ discordance matrix and can be defined as:

The dominance discordance matrix $\Upsilon$ $= (\Upsilon_{\rho \psi})_{b\times b}$ can be compiled as:

whose entities satisfy

The entities of the dominance discordance matrix $\Upsilon$ indicates the intensity of the discordance. For an instance, the discordant argument would no more valid if $\tau < \mathfrak{K}_{\rho \psi},$ however the matrix entity with value 1 indicates the dominant relation together with other alternatives.

Step 12: The aggregated dominance matrix is obtained by unifying the $CSFN\mathcal{S}_{f}$ dominance concordance and discordance matrices in the following manner:

So that aggregated dominance matrix $\varpi$ is constructed as:

where, $\varpi_{\rho \psi} = \Im _{\rho \psi} \times \Upsilon_{\rho \psi}.$ The aggregated dominance matrix provided supreme resistance to alternative $\mathrm{U}_{\rho}$ if $\varpi_{\rho \psi} = 1.$

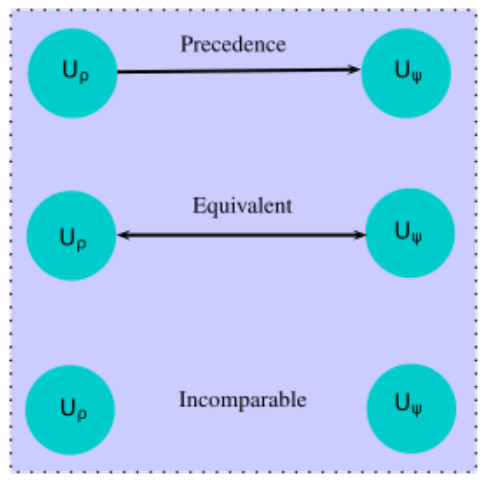
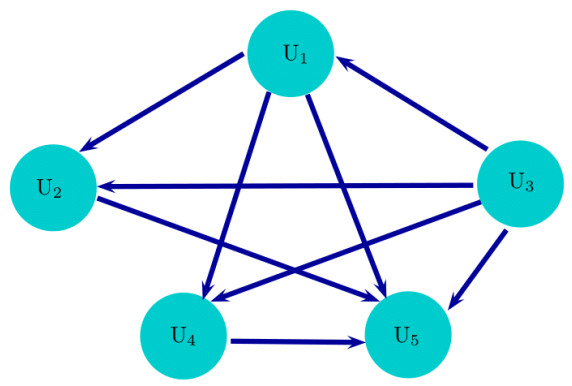
Step 13: In the final round of the $CSFN\mathcal{S}_{f}$-ELECTRE I method, a directed graph is composed to secure the supreme alternative among the probable choices. To construct directed graph specific details are depicted by Figure 1 and also elaborated by the following cases:

1. If $\varpi_{\rho\psi} = 1,$ then $\mathrm{U}_{\rho}$ is strictly superior from $\mathrm{U}_{\psi}$ or $\mathrm{U}_{\psi}$ is strictly inferior from $\mathrm{U}_{\rho},$ i.e., ($\mathrm{U}_{\rho} \succ \mathrm{U}_{\psi}$).

2. If $\varpi_{\rho\psi} = 1$ and $\varpi_{\psi\rho} = 1,$ then $\mathrm{U}_{\rho}$ and $\mathrm{U}_{\psi}$ depicted indifferent association, i.e., ($\mathrm{U}_{\rho} \approx \mathrm{U}_{\psi}$).

3. If $\varpi_{\rho\psi} = 0,$ then $\mathrm{U}_{\rho}$ is not comparable to $\mathrm{U}_{\psi}$.

Step 14: The linear ranking order of the alternatives can be evaluated using the net outranking index to strengthen the proposed ELECTRE I method. The net outranking index is calculated as follow:

where, $\overline{J}_{r}$ represents the concordant outranking index and $\underline{J}_{r}$ indicates the discordant outranking index. The concordant outranking index $\overline{J}_{r}$ and the discordant outranking index $\underline{J}_{r}$ can be computed by the Eqs (3.16) and (3.17), respectively.

The values of $\Re_r$ are arranged in descending order and the alternative with largest net outranking index stated as more adequate alternative from the probable choices.

The $CSFN\mathcal{S}_{f}$-ELECTRE I algorithm is graphically visualized through a flow diagram presented in Figure 2.

4.   Application

In this section, we describe a case study from socio-economic field related to the "Poverty alleviation" that illustrate the applicability of proposed $CSFN\mathcal{S}_{f}$-ELECTRE I method.

4.1.   Case study: Best poverty alleviation program

4.1.1.   Problem prominence

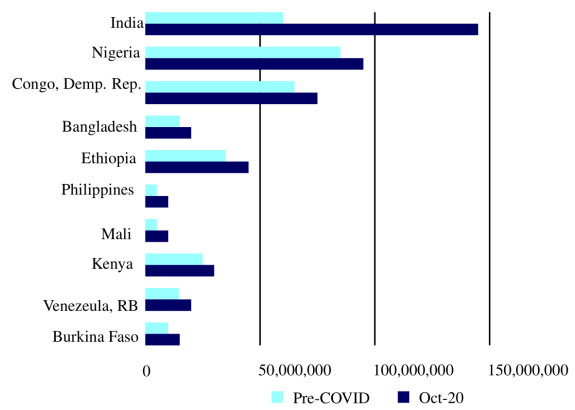
Currently, an estimation reveals that COVID-19 caused the biggest rise in global poverty since 1998 and this can be observes through Figure 3 in which poverty rates are compared before and after this pandemic disease, (https://en.wikipedia.org/wiki/Brookings_Institution). This worldwide disease impelled 49 million population into utmost poverty due to the sudden lock downs in major cities. Unfortunately, India, Nigeria, Central African Republic, Bangladesh etc., are among the countries whose poverty level is highly increased by COVID-19 as this pandemic dragged millions of people of these countries into poverty. This international issue of poverty badly influence the economy of the developing countries. However, the poorest people are predominantly at substantial risk from polluted environmental, climate crisis and struggle for resources. As reported by UNICEF, about 22,000 children pass away daily due to poverty, therefore, it is necessary to counter the poverty problem before massive losses in the world.

4.1.2.   Problem description

It is necessary for poor countries to make some poverty alleviation policies that might enhance the socio-economic growth of the countries. Since the poverty alleviation is perceived by the worldwide community as a substantial part of the socio-economic legislative framework for all the countries. The selection of strategy for poverty alleviation is the most complex and difficult task. For the compilation of best poverty alleviation strategy, $\mathcal{K}_{1},$ $\mathcal{K}_{2}$ and $\mathcal{K}_{3}$ are the decision-experts from socio-economic field. In the global campaign against poverty, there have been numerous strategies that are successfully rationalize the widespread problem. The five topmost poverty alleviation strategies, selected by the decision-experts from the source, https://www.borgenproject.org, are given as:

Brazil's poverty alleviation program ($\mathrm{U}_{1}$): During the time period of COVID-19, a poverty index decrease in Brazil demonstrates Brazil's victorious attempts with its corona voucher program.

United states poverty alleviation program ($\mathrm{U}_{2}$): The government policies of United states were still retained as of successfully which have reduced poverty on Native American.

China's poverty alleviation program ($\mathrm{U}_{3}$): China's poverty elimination campaign amid this unpredictable pandemic are commendable. The poverty reduction efforts indeed enhanced the living standard of many poor families in rural China.

Canada's poverty alleviation program ($\mathrm{U}_{4}$): Canada has applied poverty alleviation programs like the Guaranteed Income Supplement and the National Housing Strategy and consistently reduced poverty with these poverty elimination campaign.

Denmark's poverty alleviation program ($\mathrm{U}_{5}$): The social welfare system of Denmark provides supports to the unwaged, the disabled and the aged among others, therefore, the people in Denmark have good health, low child death rates and have approach to free education.

4.1.3.   Attribute selection

This section re-considers the attributes discussed by Meng et al. ^[4] for poverty alleviation, which helps to determine appropriate program to reduce poverty. The selection of prime poverty alleviation program is based on a number of factors like: micro-financing, local benefits, social security, flexibility, personnel demands, good governance, society benefit, economic benefit, etc. However, Meng et al. ^[4] allocated a poverty alleviation project based on eight conflicting attributes. But according to the socio-economic conditions of countries, four significant and preferable attributes are:

Flexibility($\mathcal{A}_{1}:$) It would require to insure that the program can be flexibly funded and pursued to such extent that it does not jeopardize socio-economic stability of a country. The most flexible poverty alleviation program is favored.

Operability ($\mathcal{A}_{2}:$) In the context of poverty alleviation strategy, operatability is a measure of how well a poverty reduction program minimizes the energy and time required for unexpected interventions. A highly operable poverty alleviation and socio-economic strategy is preferable.

Society benefit($\mathcal{A}_{3}:$) The poverty alleviation strategy also comprehends some priority measures like society benefits which further include personnel demands, local benefits and social security. Therefore, experts integrate poverty reduction programs into a uniform framework.

Economic growth($\mathcal{A}_{4}:$) Economic growth is an effective factor for poverty eradication and enhancing the standard of living in poor countries. It is required to see that the selected strategy implemented in such a way that it does not put growth objectives in danger. A successful poverty eradication program certainly have at its focus to boost swift and robust economic growth.

The non-binary evaluation are kept in Table 7 that are applied by the decision-experts to analyze the importance of the alternatives along with related attributes. Decision-experts associated a complex spherical fuzzy number with each ordered grade, however, initially data is collected by the socio-economic researchers.

4.1.4.   Evaluation process

The sequential procedure to identify the best poverty alleviation program for the country of Madagascar by $CSFN\mathcal{S}_{f}$-ELECTRE I method contains the following steps:

Step 1: Acknowledging the behavior of attributes in the concerned problem, experts framed $6$-soft set that is organized in Table 7, where

Rank '5' indicates Remarkably Good ($\mathrm{RG}$),

Rank '4' indicates Very Good ($\mathrm{VG}$),

Rank '3' indicates Fairly Good ($\mathrm{FG}$),

Rank '2' indicates Fairly Bad ($\mathrm{FB}$),

Rank '1' indicates Very Bad ($\mathrm{VB}$),

Rank '0' indicates Remarkably Bad ($\mathrm{RB}$).

Likewise, the experts provided grading criteria, arranged in Table 6, for expressing the non-binary assessments in the form of $C\mathcal{S}FNS_{f}PMs$ $\mathcal{Y}^{1},$ $\mathcal{Y}^{2}$ and $\mathcal{Y}^{3}$ that are organized in Tables 8–10, respectively. Table 6 impersonate as descriptor which is thereby given a clear guidance about the rationing of $CSF6\mathcal{S}_{f}Ns$ that what $CSF6\mathcal{S}_{f}Ns$ must be assigned to the initial grades (given in Table 7).

Step 2: The $CSFN\mathcal{S}_{f}AW$ operator and the experts weight vector $\mathrm{a} = [0.3595, 0.3512, 0.2893]^{T}$ are used for the development of $ACSFN\mathcal{S}_{f}PM$ $\mathcal{Y} = (\mathcal{Y}_{rs})_{v\times v},$ given in Table 11.

Step 3: The $CSFN\mathcal{S}_{f}$-weights of attributes are evaluated by employing the non-binary assessment of experts about attributes that are pinned up in Table 12. The weight vectors of attributes are aggregated by $CSFN\mathcal{S}_{f}AW$ operator is given as:

Step 4: The $AWCSFN\mathcal{S}_{f}PM$ $\overline{\mathcal{Y}} = (\overline{\mathcal{Y}}_{rs})_{v \times w}$ is figured out in Table 13 and aggregated by Eq (3.1).

Step 5: The score and accuracy values of $\overline{\mathcal{Y}}_{rs}$ are organized in Table 14. The score and accuracy values of $AWCSFN\mathcal{S}_{f}PM$ are exploited for $CSFN\mathcal{S}_{f}$ concordance and discordance sets.

Step 6: The $CSFN\mathcal{S}_{f}$ concordance sets $\mathcal{C}_{\rho\psi},$ $\mathcal{C}^{'}_{\rho\psi},$ and $\mathcal{C}^{"}_{\rho\psi}$ are manifested by employing the Eqs (3.2)–(3.4). The $CSFN\mathcal{S}_{f}$-strong concordance set $\mathcal{C}_{\rho\psi},$ $CSFN\mathcal{S}_{f}$-mid range concordance set $\mathcal{C}^{'}_{\rho\psi}$ and $CSFN\mathcal{S}_{f}$-weak concordance set $\mathcal{C}^{"}_{\rho\psi}$ accorded as:

Step 7: The $CSFN\mathcal{S}_{f}$ discordance sets $\mathcal{D}_{\rho\psi},$ $\mathcal{D}^{'}_{\rho\psi}$ and $\mathcal{D}^{"}_{\rho\psi}$ are calculated using Eqs (3.5)–(3.7). The $CSFN\mathcal{S}_{f}$-strong discordance set $\mathcal{D}_{\rho\psi},$ $CSFN\mathcal{S}_{f}$-mid range discordance set $\mathcal{D}^{'}_{\rho\psi}$ and $CSFN\mathcal{S}_{f}$-weak discordance set $\mathcal{D}^{"}_{\rho\psi}$ given as:

Step 8: The $CSFN\mathcal{S}_{f}$ concordance matrix $\mathfrak{X}_{\mathfrak{R}_{\rho \psi}}$ is computed by utilizing the rationed weights $({\mathfrak{E}}_{\mathrm{C}_{\rho\psi}}, {\mathfrak{E}}_{\mathrm{C}^{'}_{\rho\psi}}, {\mathfrak{E}}_{\mathrm{C}^{"}_{\rho\psi}})$ and concordance indices $\mathfrak{R}_{\rho \psi}$ that are organized in Eq (4.1) and in Table 15, respectively. The $CSFN\mathcal{S}_{f}$ concordance indices $\mathfrak{R}_{\rho \psi}$ are calculated with the help of Eq (3.8).

The score values of $CSFN\mathcal{S}_{f}$ concordance matrix $\mathfrak{X}_{\mathfrak{R}_{\rho \psi}}$ are given by:

Step 9: The $CSFN\mathcal{S}_{f}$ discordance matrix $\mathfrak{X}_{\mathfrak{K}_{\rho \psi}}$ is composed of discordance indices that are computed by employing the rationed weights $({\mathfrak{E}}_{\mathrm{D}_{\rho\psi}}, {\mathfrak{E}}_{\mathrm{D}^{'}_{\rho\psi}}, {\mathfrak{E}}_{\mathrm{D}^{"}_{\rho\psi}})$ and normalized Euclidean distances that are sorted in Eq (4.3) and in Table 16, respectively, along with Eq (3.9).

The $CSFN\mathcal{S}_{f}$ discordance matrix $\mathfrak{X}_{\mathfrak{K}_{\rho \psi}}$ is constituted as follow:

Step 10: The concordance threshold value (estimated by Eq (3.10)) is $0.1495$. The score values of $\mathfrak{R}_{\rho \psi},$ pinned up in Eq (4.2) are employed for the construction of the $CSFN\mathcal{S}_{f}$ dominance concordance matrix that is as follow:

Step 11: The items of the $CSFN\mathcal{S}_{f}$ discordance matrix are collated with the discordance threshold value $\tau = 0.4941$ (evaluated by Eq (3.12)) for the constitution of $CSFN\mathcal{S}_{f}$ dominance discordance matrix $\Upsilon$, given as:

Step 12: The aggregated outranking Boolean matrix by unifying the entities of $CSFN\mathcal{S}_{f}$ Boolean concordance and discordance matrices. The aggregated outranking Boolean matrix $\Re$ is given by:

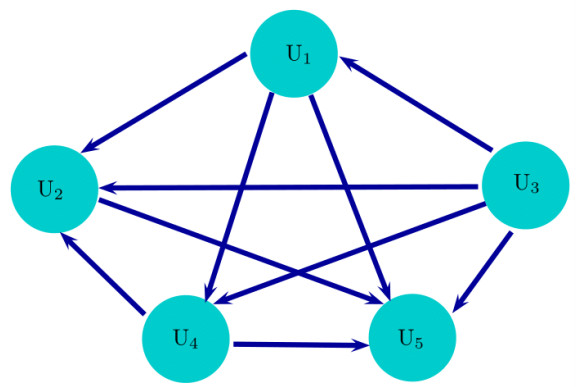
Step 13: The outranking graph (shown in Figure 4) depicts the MAGDM problem clearly as well as stated that $\mathrm{U}_{3}$ outperform from all the other alternatives. A descriptive analysis about alternatives from Figure 4 is pinned up in Table 17 and indicate that the alternative $\mathrm{U}_{3}$ is best strategy for the affected countries.

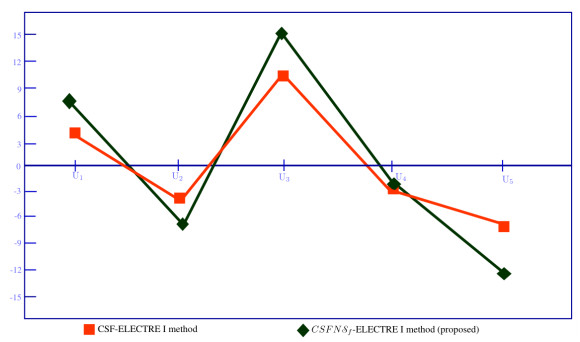
Step 14: The concordant outranking index $\overline{J}_{r},$ discordant outranking index $\underline{J}_{r}$ and net outranking index $\Re_r$ are in Table 18. Table 18 indicates that $\mathrm{U}_3$ is best choice as well as the linear ranking of the alternatives is given as: $\mathrm{U}_3\succ \mathrm{U}_1\succ \mathrm{U}_4\succ \mathrm{U}_2\succ \mathrm{U}_5.$

5.   Comparative study

Here, we demonstrate a detailed comparison of our proposed model with the existing complex spherical fuzzy ELECTRE I ($CSF$-ELECTRE I) method, proposed by Akram et al. ^[30].

5.1.   Comparison with $CSF$-ELECTRE I approach

We accomplish the tremendous $CSF$-ELECTRE I method to identify the best poverty alleviation program for the poor countries as well as assimilate the results to endorse the legitimacy and veracity of the contemplated technique. To address the $CSF$-ELECTRE I methodology for the solution of considered MAGDM problem, the non-binary evaluation is withdrawn from each $CSFN\mathcal{S}_{f}N.$ Consequently, $CSFPMs$ are originated corresponding to each expert $\mathcal{Q}_{b}$ along with the normalized weights $\mathrm{a} = [0.3595, 0.3512, 0.2893]^{T}$ of of decision-experts.

Step 1: The non-binary evaluation of the alternatives by the experts are classified in Table 7, in which each ordered grade represents a linguistic term that is further superseded by the $CSFNs.$ Tables 19–21 indicate the complex spherical fuzzy performance matrix (CSFPM) of the decision-expert $\mathcal{Q}_{1},$ $\mathcal{Q}_{2}$ and $\mathcal{Q}_{3},$ respectively.

Step 2: The collective measures of all decision-experts is attained by integrating the self-sufficient judgment of each decision-expert through complex spherical fuzzy weighted average $(CSFWA)$ operator in the following manner:

The aggregated complex spherical fuzzy performance matrix (ACSFPM) is accounted via Eq (5.1) and set out in the Table 22.

Step 3: The CSF-weight vector of attributes is aggregated by $CSFWA$ operator as follow:

where, $\mathrm{t}^{(p)}_{s}, (p = 1, 2, 3)$ is a CSF-weight vector of $s^{th}$ attribute which is assessed by $p^{th}$ decision-expert using Table 12. Consequently, the CSF-weight vector $\mathrm{t} = (\mathrm{t}_1, \mathrm{t}_2, \ldots, \mathrm{t}_w)^{T}$ is contoured as:

Step 4: To summarize the $ACSFPMs$ with respect to the CSF-weights $\mathrm{t}_s$ of the attributes aggregated weighted complex spherical fuzzy performance matrix $(AWCSFPM)$ is constructed whose entities are quantified as follow:

The $AWCSFPM$ is sorted in Table 23.

Step 5: The score, accuracy and refusal values of $\overline{\mathcal{Y}}_{rs}$ are organized in Table 24. The score, accuracy and refusal values of $AWCSFPM$ are applied for $CSF$ strong, mid range and weak concordance (discordance) sets that can be computed by virtue of Eqs (5.2)–(5.7), respectively.

Step 6: The $CSF$-strong concordance set $\mathcal{C}_{\rho\psi},$ $CSF$-mid range concordance set $\mathcal{C}^{'}_{\rho\psi}$ and $CSF$-weak concordance set $\mathcal{C}^{"}_{\rho\psi}$ are computed through the conventions of Eqs (5.2)–(5.4) that are contoured as follow:

Step 7: The $CSF$-strong discordance set $\mathcal{D}_{\rho\psi},$ $CSF$-mid range discordance set $\mathcal{D}^{'}_{\rho\psi}$ and $CSF$-weak discordance set $\mathcal{D}^{"}_{\rho\psi}$ are figured out by dint of Eqs (5.5)–(5.7) that are organized as follow:

Step 8: The $CSF$ concordance matrix is computed by using the empirical weights of concordance sets and wit help of $CSF$ concordance indices that are arranged in Eq (4.1) and in Table 25, respectively. The $\mathfrak{R}_{\rho \psi}$ are calculated by virtue of Eq (3.8). The score values of $CSF$ concordance matrix are as follow:

Step 9: The discordance indices are evaluated by employing the Eq (3.9), where the weights of discordance sets and the normalized Euclidean distances are organized in Eq (4.3) and in Table 26, respectively. The normalized Euclidean distance $d(\overline{\mathcal{Y}}_{\rho v}, \overline{\mathcal{Y}}_{v \psi})$ is computed by the following convention:

The $CSF$ discordance matrix is arranged as follow:

Step 10: The CSF effective concordance matrix is evaluated by comparing the score values of CSF concordance matrix with the threshold value$= 0.0987$ that is computed by employing the Eq (3.10). The CSF effective concordance matrix is as follow:

Step 11: The CSF effective discordance matrix is constituted by means of discordance level $0.2425$ and by virtue of $CSF$ discordance matrix, where the discordance level is computed by Eq (3.12). Consequently, the CSF effective discordance matrix is given as:

Step 12: The ordinary multiplication of the corresponding entities of CSF effective concordance and discordance matrices are help out for the formation of aggregated outranking Boolean matrix that is given as:

Step 13: As it is illustrated in aggregated outranking Boolean matrix $\mathrm{U}_{3}$ outrank from $\mathrm{U}_{1},$ $\mathrm{U}_{2},$ $\mathrm{U}_{4}$ and $\mathrm{U}_{5}.$ A narrative analysis about alternatives are portrayed in Figure 5 and also delineated in Table 27.

Step 14: Table 27 ensures that the alternatives $\mathrm{U}_2$ and $\mathrm{U}_4$ are not comparable, therefore, the net outranking index is evaluated for linear ranking order that are sorted in Table 28. In accordance to Table 28 the linear ranking of the alternatives is as follow: $\mathrm{U}_3\succ \mathrm{U}_1\succ \mathrm{U}_4\succ \mathrm{U}_2\succ \mathrm{U}_5.$

Thus, the poverty alleviation strategy $\mathrm{U}_{3}$ is the most appropriate and suitable choice.

5.2.   Comparative discussion

$\bullet$ We have scrutinized the corrective MAGDM problem through the subsisting CSF-ELECTRE I method. The inferring assessment of two methodologies, inclusively the linear ranking and best project, are provided in Table 29. $\bullet$ The CSF-ELECTRE I ^[30] technique was expanded by virtue of the innovative idea of (weak, midrange and strong) concordance and discordance sets which were premised on score, accuracy and refusal values. In CSF-ELECTRE I method linguistic terms are employed to determine the comparative strength and eminence ratings of alternatives but capitulates to handel the instances in which the decision-makers confronted given problem with modern evaluation based on non-binary parameterized information.

$\bullet$ To subdue this inconvenience, $CSFN\mathcal{S}_{f}$-ELECTRE I method is developed and certificated to decision-making. In the developed approach, multiple parameters as well as finite ordered grades are manifested through $CSFN\mathcal{S}_{f}Ss$ that demonstrates the stimulus generalization of the intended model.

$\bullet$ The intended model comprises more information by merging the $CSFN\mathcal{S}_{f}Ss$ and ELECTRE I method, that is more persuasive in the origination of outranking correlations between the plausible alternatives. The comparative consequences yielded by invoking the poverty alleviation problem, the proposed ELECTRE-based outranking method secures more decision endorse information than does the CSF-ELECTRE I method.

$\bullet$ The presented visionary model even manage one-dimensional problems under the auspices of spherical fuzzy and picture fuzzy information by employing the phase terms and multi-valuation zero and consequently lifts the persuasion and stability of the presented work.

The pictorial representation of comparison of net outranking index between CSF-ELECTRE I method ^[30] and our proposed $CSFN\mathcal{S}_{f}$-ELECTRE I method is provided in Figure 6.

6.   Conclusions

The theory of $CSFN\mathcal{S}_{f}S$ (proposed by Akram et al. ^[37]) is emerging as a valuable extension of $N$-soft sets which support real-life decision-making problems. In the present study, we have enhanced the theoretical basis of $CSFN\mathcal{S}_{f}S$ in directions that are endorsed by their consequences on specific context and their capacity in number of opinions. From this perspective, we have established a creative assorted technique, namely, $CSFN\mathcal{S}_{f}$-ELECTRE I technique. Eventually, this article improves the ELECTRE-based outranking methods to pursue concerted $CSFN\mathcal{S}_{f}$ data. We employed the score and distance approach to specify the concordance and discordance indices, respectively, for each pair of plausible choices. With respect to the aggregated outranking Boolean matrix, the decision graph was applied to illustrate the partial ordering of the plausible choices and the consistencies of the outranked results are also clarified through linear-ranking ordering of the feasible alternatives. The presented approach provides a conventional generalization of several existing techniques. The primary scheme of $CSFN\mathcal{S}_{f}$-ELECTRE I method is established with a definite stepwise algorithm which has two phases: $(i)$ accumulation of group valuations, $(ii)$ ranking process. A detailed explanation of the $CSFN\mathcal{S}_{f}$-ELECTRE I method is elaborated properly and employed in MAGDM. We have performed a numeral computations for poverty alleviation problem and a comparison with previous techniques, which verifies that the $CSFN\mathcal{S}_{f}$-ELECTRE I method can not only anticipate the compatible outcomes, but also substantially relieve endeavors for non-binary evaluation. Some significant insights and boundaries of the proposed $CSFN\mathcal{S}_{f}$-ELECTRE I technique and some future targets can be accounted as: Advantages

$\bullet$ The $CSFN\mathcal{S}_{f}$-ELECTRE I technique successfully interpret advanced means of non-binary evaluation along with multiple parameters and, therefore, competent to decision-making. The proposed method properly figures out the level of feasible choices and then adequately fuses with a two dimensional paradigm of $CSFN\mathcal{S}_{f}$ information in accordance with the relevant MAGDM problem.

$\bullet$ The $CSFN\mathcal{S}_{f}$-ELECTRE I method provides potent and extensive structures for classifying prospective alternatives in decision-making problem as it's working principles based on $CSFN\mathcal{S}_{f}$ concordance and discordance sets in which score and accuracy functions are employed for the comparative purposes.

$\bullet$ The attributes weights and experts valuations are evaluated by the easiest aggregating valuations operators.

$\bullet$ The frequent process of investigating the outranking graph in ranking procedure of ELECTRE I is described in more focused way, which provides a frame of profound knowledge for reader.

Limitations

$\bullet$ The $CSFN\mathcal{S}_{f}$-ELECTRE I method is incompetent to address the problem in which the amplitude terms and the phase terms are highly ambiguous that their square sum exceeds 1.

$\bullet$ The abundance of alternatives along with attributes complicates the analysis of the given problem specifically, the calculation becomes more hard and time consuming.

Future targets

$\bullet$ As future research targets, we can apply the presented method for major MAGDM problems of real-life, like, water waste management, forest management, medical sciences and so forth.

$\bullet$ Furthermore, the presented work can be prolong for the most generalized complex $T$-spherical fuzzy $N$-soft environment as well as, due to the versatility of $CSFN\mathcal{S}_{f}$ model, we can introduce the $CSFN\mathcal{S}_{f}$-ELECTRE II group decision supporting scheme.

Acknowledgments

The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through General Research Project under grant number (R.G.P.1/258/43).

Conflict of interest

The authors declare there is no conflict of interest.