1.
Introduction
Primitive semigroups have been an important topic of semigroup researches since the 1950s. In fact, as early as 1954, Preston who is one of the founders of the algebraic theory of semigroups studied primitive inverse semigroups in [16], and then he gave the characterization of primitive regular semigroups and applied it to the study of matrix representations of inverse semigroups in [17]. In particular, he pointed out that a regular semigroup (resp. an inverse semigroup) with zero is primitive if and only if it is the $ 0 $-direct union of a family of completely $ 0 $-simple semigroups (resp. Brandt semigroups) (See also the monographs [5,12,18]). In addition, from the view of category Lawson [12] showed that an inverse semigroup with zero is primitive if and only if it is isomorphic to a groupoid with zero adjoined. On the other hand, Theorem Ⅲ.3.5 and Corollary Ⅲ.3.6 in [5] together give that a regular semigroup (resp. an inverse semigroup) without zero is primitive if and only if it is a completely simple semigroup (resp. a group). Furthermore, primitive orthodox semigroups were also concerned in Venkatesan [21].
As generalizations of regular semigroups, abundant semigroups were introduced and investigated in 1982 by Fountain in [2] where the class of primitive abundant semigroups and its several subclasses, such as primitive abundant semigroups with regularity condition, primitive quasi-adequate semigroups and primitive adequate semigroups etc., were also characterized. We observe that the roles of quasi-adequate semigroups and adequate semigroups in the range of abundant semigroups are similar to those of orthodox semigroups and inverse semigroups in the range of regular semigroups, respectively.
In 1991, Lawson [13] went a further step to generalize abundant semigroups to $ U $-semiabundant semigroups where $ U $ is a nonempty subset of the set of idempotents and correspondingly generalize quasi-adequate semigroups and adequate semigroups to weakly $ U $-orthodox semigroups and Ehresmann semigroups, respectively. The class of Ehresmann semigroups and its special subclasses (for example, the class of restriction semigroups) now form a hot research topic, and a lot of achievements in this line have been obtained by many semigroup experts, for example, see [3,4,6,8,10,11,13,20] and the references therein. In particular, Gould [3,4] gave the equivalent definition of Ehresmann semigroups from the view of variety, and Jones explicitly introduced the notion of primitive Ehresmann semigroups in [8] and by using small categories obtained a construction of primitive Ehresmann semigroups with zero in [10] which is analogous to that of primitive inverse semigroups with zero given in Lawson [12] by using groupoids. We also observe that Lawson [14] investigated a class of primitive $ U $-semiabundant semigroups named Rees semigroups and Wang [22] characterized primitive weakly $ U $-orthodox semigroups, which generalize the corresponding results of primitive abundant semigroups provided in [2].
On the other hand, Jones [7] generalized Ehresmann semigroups to $ P $-Ehresmann semigroups from a varietal perspective and provided a common framework for Ehresmann semigroups and regular *-semigroups. Regular *-semigroups first appeared in Nordahl and Scheiblich [15] and a generalization of this class of semigroups was investigated in the author [23]. For more details for regular $ ^\ast $-semigroups, the reader may consult the texts[1,7,15,19,23] and their references. At present, some valuable results have been obtained on $ P $-Ehresmann semigroups. For instance, the constructions of $ P $-Ehresmann semigroups have been considered by "fundamental approach" in [7] and [25,26] by "categorical approach", respectively. Variety properties, semigroup algebras and completions of $ P $-Ehresmann semigroups have been explored in Jones [8], Wang [24] and Yan and Wang [27], respectively.
From the above discussions, the following problem is natural: How to introduce and characterize primitive $ P $-Ehresmann semigroups? The aim of this paper is to solve the above problem. We have introduced the notion of projection-primitive $ P $-Ehresmann semigroups and established the structures of projection-primitive $ P $-Ehresmann semigroups. In particular, we show that projection-primitive $ P $-Ehresmann semigroups are always $ P $-restriction. Our work may be regarded as extending primitive Ehresmann semigroups introduced and investigated by Jones in [8] and [10], respectively.
2.
Preliminaries
In this section, after recalling some necessary notions and results on $ P $-Ehresmann semigroups, we shall introduce projection-primitive $ P $-Ehresmann semigroups and explore their basic properties.
For a semigroup $ S $, we always denote the set of idempotents in $ S $ by $ E(S) $. From Lemma 2.2 and its dual in Gould [3], a bi-unary semigroup $ (S, \cdot, ^+, ^\ast) $ is called an Ehresmann semigroup if the following identities hold:
To extend Ehresmann semigroups, $ P $-Ehresmann semigroups were introduced in Jones [7] from the view of variety. A bi-unary semigroup $ (S, \cdot, ^+, ^\ast) $ is called a P-Ehresmann semigroup if the following identities hold:
A $ P $-Ehresmann semigroup $ (S, \cdot, ^+, ^\ast) $ is called $ P $-restriction if
In a $ P $-Ehresmann semigroup $ (S, \cdot, ^+, ^\ast) $, the set of projections is $ P_{S} = \{a^+\mid a\in S\} $ which is equal to $ \{a^\ast\mid a\in S\} $ by (ⅴ) and (ⅴ)$ ' $. The following lemmas collect some basic properties of $ P $-Ehresmann semigroups first given in Jones [7].
Lemma 2.1 ([7]). A bi-unary semigroup $ (S, \cdot, ^+, ^\ast) $ is Ehresmann (resp. restriction) if and only if $ (S, \cdot, ^+, ^\ast) $ is $ P $-Ehresmann (resp. $ P $-restriction) and $ P_{S} $ is a subsemilattice of $ {S} $.
Lemma 2.2 ([7]). Let $ (S, \cdot, ^+, ^\ast) $ be a $ P $-Ehresmann semigroup and $ x, y \in S, \; e, f\in P_{S} $.
(1) $ (x^+y)^+ = x^+y^+x^+, \; x^{++} = x^+, \; x^+(xy)^+x^+ = (xy)^+ $.
(2) $ (xy^\ast)^\ast = y^\ast x^\ast y^\ast, \; x^{\ast\ast} = x^\ast, \; y^\ast(xy)^\ast y^\ast = (xy)^\ast $.
(3) $ (ef)^2 = ef, \; e^+ = e = e^\ast, \; (ef)^+ = efe = (fe)^\ast \in P_{S} $.
(4) $ ef\in P_{S} $ if and only if $ ef = fe $.
Let $ (S, \cdot, ^+, ^\ast) $ be a $ P $-Ehresmann semigroup. Define a relation on $ P_S $ by the rule
Then it is easy to see that $ \leq $ is a partial order on $ P_S $. By Lemma 2.2, the following corollary is obvious.
Corollary 2.3. Let $ (S, \cdot, ^+, ^\ast) $ be a $ P $-Ehresmann semigroup and $ x, y \in S, e, f\in P_{S} $. Then $ (xy)^+\leq x^+, \; (xy)^\ast\leq y^\ast $ and $ efe\leq e $.
Similar to the case of restriction semigroups appeared in Jones [8], we call a $ P $-Ehresmann semigroup $ (S, \cdot, ^+, ^\ast) $ without zero or with zero $ 0 $ satisfying $ 0\not\in P_S $ projection-primitive if
while call a $ P $-Ehresmann semigroup $ (S, \cdot, ^+, ^\ast) $ with zero $ 0 $ satisfying $ 0\in P_S $ projection-primitive if
Observe that a primitive Ehresmann semigroup without zero is just a momoid in which the identity is the only projection by Lemma 2.1. We first characterize projection-primitive $ P $-Ehresmann semigroups without zero.
Proposition 2.4. Let $ (S, \cdot, ^+, ^\ast) $ be a $ P $-Ehresmann semigroup without zero. Then the following statements are equivalent:
(1) $ S $ is projection-primitive.
(2) $ (xy)^+ = x^+ $ for all $ x, y\in S $.
(3) $ (xy)^\ast = y^\ast $ for all $ x, y\in S $.
Proof. We only show that (1) is equivalent to (2), and one can prove that (1) is equivalent to (3) by similar arguments. If $ S $ is projection-primitive and $ x, y\in S $, then $ (xy)^+\leq x^+ $ by Corollary 2.3. This implies that $ (xy)^+ = x^+ $. Conversely, let $ e, f\in P_S $ and $ e\leq f $. Then $ ef = fe = e $. By the given condition and Lemma 2.2, we have $ f = f^+ = (fe)^+ = e^+ = e $. This gives the projection-primitivity of $ S $.
From Jones [9], a $ P $-Ehresmann semigroup $ (S, \cdot, ^+, ^\ast) $ is called reduced if $ P_S $ contains exactly one element. By the identities (ⅰ) and (ⅰ)$ ' $, in this case $ S $ is a monoid with the only projection as its identity. Obviously, reduced $ P $-Ehresmann semigroups are always projection-primitive. In fact, we have the following result.
Proposition 2.5. Let $ (S, \cdot, ^+, ^\ast) $ be a $ P $-Ehresmann semigroup with zero $ 0 $ and $ 0\not\in P_S $. Then the following statements are equivalent:
(1) $ S $ is projection-primitive.
(2) $ x^+ = 0^+ $ for all $ x\in S $.
(3) $ x^\ast = 0^\ast $ for all $ x\in S $.
In this case, $ S $ is a reduced $ P $-Ehresmann semigroup with the identity $ 0^+ $ and so is an Ehresmann semigroup.
Proof. We only show that (1) is equivalent to (2), and one can prove that (1) is equivalent to (3) by similar arguments. Let $ S $ be projection-primitive and $ x\in S $. Then $ 0^+ = (x0)^+\leq x^+ $ by Corollary 2.3, and so $ 0^+ = x^+ $. Conversely, the given condition (2) implies that $ P_S = \{x^+\mid x\in S\} = \{0^+\} $. This gives that $ S $ is reduced and has identity $ 0^+ $, and so is projection-primitive certainly.
Remark 2.6. By Proposition 2.5, a projection-primitive $ P $-Ehresmann (or Ehresmann) semigroup $ (S, \cdot, ^+, ^\ast) $ with zero $ 0 $ and $ 0\not\in P_S $ is reduced and is exactly a monoid with zero containing at least two elements.
Now we consider projection-primitive $ P $-Ehresmann semigroups with zero $ 0 $ as a projection.
Proposition 2.7. Let $ (S, \cdot, ^+, ^\ast) $ be a projection-primitive $ P $-Ehresmann semigroup with zero $ 0 $ and $ 0\in P_S $.
(1) For all $ x\in S $, $ x^+ = 0 \Longleftrightarrow x = 0 \Longleftrightarrow x^\ast = 0. $
(2) For all $ x, y\in S\setminus \{0\} $, $ xy\not = 0 \Longleftrightarrow x^\ast y^+x^\ast = x^\ast\Longleftrightarrow y^+x^\ast y^+ = y^+ $.
Proof. (1) Let $ x\in S $. We only prove that $ x^+ = 0 $ if and only if $ x = 0 $. The other equivalence can be showed by symmetry. In fact, if $ x^+ = 0 $, then $ x = x^+ x = 0x = 0 $ by (ⅰ). To show the converse, we first observe that $ 0^+ = (a0)^+\leq a^+ $ for all $ a\in S $ by Corollary 2.3. This implies that $ 0^+ $ is the minimum element in $ P_S $. Since $ 0\in P_S $, it follows that $ 0^+ = 0^+ 0 = 0 $.
(2) Let $ x, y\in S\setminus \{0\} $. We only prove that $ xy\not = 0 $ if and only if $ x^\ast y^+x^\ast = x^\ast $. The other equivalence can be showed by symmetry. If $ xy\not = 0 $, then $ xx^\ast y^+ y = xy\not = 0 $ by the identities (ⅰ) and (ⅰ)$ ' $. This implies that $ x^\ast\not = 0 $ and $ x^\ast y^+\not = 0 $. By item (1) we have $ x^{\ast+}\not = 0 $ and $ (x^\ast y^+)^+\not = 0 $. But Corollary 2.3 gives that $ (x^\ast y^+)^+\leq x^{\ast+} $, and so $ (x^\ast y^+)^+ = x^{\ast+} $ by the projection-primitivity of $ S $. Moreover, Lemma 2.2 provides that $ x^\ast y^+ x^\ast = (x^\ast y^+)^+ = x^{\ast+} = x^\ast $. Conversely, if $ x^\ast y^+x^\ast = x^\ast $, then by using (ⅱ), (ⅰ)$ ' $, (ⅱ), Lemma 2.2 (3), (ⅰ)$ ' $ and item (1) of the present lemma in order, we have
which implies that $ xy\not = 0 $ by item (1) of the present lemma again. To end this section, we observe the following interesting result.
Theorem 2.8. A projection-primitive $ P $-Ehresmann semigroup is always $ P $-restriction.
Proof. Let $ (S, \cdot, ^+, ^\ast) $ be a projection-primitive $ P $-Ehresmann semigroup and $ x, y\in S $. Firstly, if $ S $ contains no zero, then $ (xy)^+x = x^+x = x $ by Proposition 2.4. By Corollary 2.3, we have $ x^\ast y^+ x^\ast\leq x^\ast $, and so $ x^\ast y^+ x^\ast = x^\ast $ by the projection-primitivity of $ S $. This implies that $ xy^+x^\ast = xx^\ast y^+ x^\ast = xx^\ast = x $ by (ⅰ)$ ' $. Thus $ (xy)^+x = xy^+x^\ast $. Dually, we have $ x(yx)^\ast = x^+y^\ast x $. Secondly, if $ S $ contains a zero $ 0 $ and $ 0\not\in P_S $, then it is obvious that $ (xy)^+x = xy^+ x^\ast $ and $ x(yx)^\ast = x^+y^\ast x $ by Proposition 2.5. Finally, assume that $ S $ contains a zero $ 0 $ and $ 0 \in P_S $. If $ xy = 0 $, then by Proposition 2.7 (1) and (ⅱ) we have $ 0 = (xy)^+ = (xy^+)^+ $ and $ xy^+ = 0 $. This implies that $ (xy)^+x = 0 = xy^+ x^\ast $. If $ xy\not = 0 $, then $ (xy)^+\not = 0 $ and $ x^\ast = x^\ast y^+ x^\ast $ by Proposition 2.7. Since $ (xy)^+\leq x^+ $ by Corollary 2.3, the projection-primitivity of $ S $ gives that $ (xy)^+ = x^+ $. This implies that
by (ⅰ) and (ⅰ)$ ' $. Therefore, $ (xy)^+x = xy^+ x^\ast $. Dually, we have $ x(yx)^\ast = x^+y^\ast x $. Thus, $ S $ is $ P $-restriction in all cases.
3.
Projection-primitive $ P $-Ehresmann semigroups without zero or with zero which is not a projection
In the remainder of this paper, we shall establish the structures of projection-primitive $ P $-Ehresmann semigroups. The present section is devoted to projection-primitive $ P $-Ehresmann semigroups without zero or with zero which is not a projection. The following theorem characterize these semigroups completely.
Theorem 3.1. Let $ I $ and $ \Lambda $ be two sets and $ \phi:I\rightarrow \Lambda, i\mapsto i\phi $ be a bijection. Assume that $ M $ is a monoid, $ |I\times M\times \Lambda|\not = 1 $ and $ P = (p_{\lambda i})_{\Lambda\times I} $ is a $ \Lambda\times I $-matrix over $ M $ satisfying $ p_{i\phi, i} = e = p_{i\phi, j}p_{j\phi, i} $ for all $ i, j\in I $, where $ e $ is the identity of $ M $. Define a binary and two unary operations on the set
as follows:
Then $ (S, \cdot, ^+, ^\ast) $ is a projection-primitive $ P $-Ehresmann semigroup without zero or with zero which is not a projection. Conversely, every such semigroup can be obtained in this way.
Proof. Direct part. By hypothesis, $ S^0 $ can be regarded as a Rees matrix semigroup over the monoid $ M^0 $. Denote $ P(S^0) = \{(i, p^{-1}_{\lambda i}, \lambda)\mid i\in I, \lambda\in \Lambda\}\cup \{0\} $ and $ U = \{(i, e, i\phi)\mid i\in I\} $. Then by Proposition 1.5 in Lawson [14], we can easily show that for all $ (i, x, \lambda), (j, y, \mu)\in S $,
Moreover, $ \widetilde{\cal R}^{U} $ (resp. $ \widetilde{\cal L}^{U} $) is a left congruence (resp. a right congruence) on $ S $ by Lemma 1.9 in Lawson [14]. By the given condition on the matrix $ P $, it is easy to see that $ U $ is both a right projection-set and a left projection-set of $ S $ in the sense of Jones [7] (see page 629). According to Theorem 6.1 of Jones [7] and its dual, $ (S, \cdot, ^+, ^\ast) $ is a $ P $-Ehresmann semigroup and $ P_S = U $. Moreover, in view of Proposition 1.7 of Lawson [14], no two different elements in $ P_S $ can be compatible. Thus $ S $ is projection-primitive. If $ (i, z, \lambda) $ is the zero element of $ S $, then for all $ (j, y, \mu)\in S $, we have $ (i, z, \lambda)(j, y, \mu) = (i, z, \lambda) = (j, y, \mu)(i, z, \lambda) $. This implies that $ i = j $ and $ \lambda = \mu $. In this case, $ |I| = |\Lambda| = 1 $ and so $ P_S $ contains only one element. By hypothesis, $ S $ has at least two elements and so the zero is not a projection.
Converse part. Let $ (M, \cdot, ^+, ^\ast) $ be a projection-primitive $ P $-Ehresmann semigroup with zero which is not a projection. Then by Proposition 2.5 and Remark 2.6, $ M $ has at least two elements and is a monoid with the only projection $ e $ as its identity. In this case, $ M $ has the form in the theorem certainly.
Now let $ (T, \cdot, ^+, ^\ast) $ be a projection-primitive $ P $-Ehresmann semigroup without zero. Then it is easy to see that $ T^0 $ is a Rees semigroup with respect to $ U = P_T^0 $ in the sense of Lawson [14], and $ \widetilde{\cal L}^U = \{(a, b)\in T^0\times T^0\mid a^\ast = b^\ast\}\cup \{(0, 0)\} $ and $ \widetilde{\cal R}^U = \{(a, b)\in T^0\times T^0\mid a^+ = b^+\}\cup \{(0, 0)\} $ (see page 28 in [14]). Fix an element $ e\in P_T $ and denote $ I = \{xe\mid x\in P_T\}, \; \Lambda = \{ex\mid x\in P_T\} $. Define $ \phi: I\rightarrow \Lambda, \; xe\mapsto ex $ for all $ x\in P_T $. Then $ \phi $ is a bijection. In fact, if $ x, y\in P_T $ and $ xe = ye $, then $ x = x^+ = (xe)^+ = (ye)^+ = y^+ = y $ by Lemma 2.2 and Proposition 2.4, and so $ ex = ey $. This fact and its dual give that $ \phi $ is bijection. We assert that $ p_{i\phi, i} = e = p_{i\phi, j}p_{j\phi, i} $ for all $ i, j\in I $. In fact, take $ i = xe, j = ye\in I $ where $ x, y\in P_T $. Then $ i\phi = ex $ and $ j\phi = ey $. This implies by Lemma 2.2 and Proposition 2.4 that $ p_{i\phi, i} = (i\phi) i = (ex)(xe) = exe = (ex)^+ = e^+ = e $ and
On the other hand, for every $ t\in T $, we have $ (t^+e)^+ = t^+ $ and $ (et^\ast)^\ast = t^\ast $ by Proposition 2.4. In view of Lemma 2.2 (4), $ I $ and $ \Lambda $ can index the non-zero $ \widetilde{\cal R}^U $-classes and $ \widetilde{\cal L}^U $-classes of $ T^0 $, respectively. Denote $ M = \{a\in T\mid a^+ = a^\ast = e\}\cup \{0\} $. For $ i\in I $ and $ \lambda\in \Lambda $, let $ r_i = i $ and $ q_\lambda = \lambda $ and denote $ p_{\lambda i} = q_\lambda r_i = \lambda i $. Since $ (t^+e)^+ = t^+ $, $ (et^\ast)^\ast = t^\ast $, $ (ete)^+ = (ete)^\ast = e $ and $ t = (t^+ e)ete(et^\ast) $ by Lemma 2.2 and Proposition 2.4, in view of the proof of Theorem 3.6 in Lawson [14],
is a semigroup isomorphism. Moreover, if we define
on $ S $, then we can see that $ \theta $ also preserves $ ^+ $ and $ ^\ast $ by Lemma 2.2 and Proposition 2.4. By the construction of $ P = (p_{\lambda i}) $, $ \theta|_{T} $ is a $ (2, 1, 1) $-isomorphism from $ T $ onto $ {\cal M}(I, \Lambda, M, P) $.
In Theorem 3.1, if we identify $ i $ with $ i\phi $ for all $ i\in I $, we can assume that $ I = \Lambda $. So we have the following corollary.
Corollary 3.2. Let $ I $ be a set and $ M $ a monoid with $ |I\times M|\not = 1 $. Assume that $ P = (p_{\lambda i})_{I\times I} $ is an $ I\times I $-matrix over $ M $ satisfying $ p_{ii} = e = p_{ij}p_{j, i} $ for all $ i, j\in I $, where $ e $ is the identity of $ M $. Define a binary and two unary operations on the set
as follows:
Then $ (S, \cdot, ^+, ^\ast) $ is a projection-primitive $ P $-Ehresmann semigroup without zero or with zero which is not a projection. Conversely, every such semigroup can be obtained in this way.
4.
Projection-primitive $ P $-Ehresmann semigroups with zero as a projection
In this section, we consider the structures of projection-primitive $ P $-Ehresmann semigroups with zero as a projection. To this aim, we need to recall some necessary notions and results. From Jones [7], a left projection algebra consists of a nonempty set $ P $ and a binary operation $ "\times" $ satisfying the following axioms:
(P1) $ e\times e = e $.
(P2) $ e\times(e\times f) = (e\times f)\times e = e\times f $.
(P3) $ (e\times f)\times g = e\times (f\times(e\times g)) $.
(P4) $ e\times(f\times g) = (e\times f)\times (e\times (f\times g)) $.
For simplicity, we use the words "projection algebra" to replace "left projection algebra" in the sequel. Let $ (P, \times) $ be a projection algebra. Define a relation $ "\leq_P" $ on $ P $ by the rule that for all $ e, f\in P $, $ e\leq_P f \;{\rm{ if \;and\; only\; if }}\;e = f\times e. $ Then $ \leq_P $ is a partial order on $ P $ by (P1)–(P4). Moreover, by (P2) it is easy to see that
for all $ e, f\in P $. A projection algebra $ (P, \times) $ with the least element $ 0 $ with respect to $ \leq_P $ is called primitive if no two different elements in $ P\setminus\{0\} $ can be compatible. On primitive projection algebras, we have the following simple results.
Proposition 4.1. A primitive projection algebra $ (P, \times) $ is just a (2, 0)-type algebra $ (P, \times, 0) $ satisfying the following conditions: For all $ e, f\in P $,
(Pr1) $ e\times e = e $.
(Pr2) $ 0\times e = 0 = e\times 0 $.
(Pr3) $ e\times f = 0 \;\mathit{{or}}\; e\times f = e $.
(Pr4) $ e\times f = 0 \;\mathit{{if \;and \;only\; if}} \;f\times e = 0 $.
In particular, if $ e\times f = f\times e $ for all $ e, f\in P $, then $ e\times f\not = 0 $ if and only if $ e = f\not = 0 $.
Proof. Let $ (P, \times) $ be a primitive projection algebra with the least element $ 0 $. We only need to show that (Pr2)–(Pr4) hold. Let $ e, f\in P $. Since $ 0\leq_P e $, we have $ e\times 0 = 0 $, and so $ 0\times e = (e\times 0)\times e = e\times 0 = 0 $ by (P2). This proves (Pr2). In view of (4.1), (Pr3) is true. Finally, if $ e\times f = 0 $ and $ f\times e\not = 0 $, then $ f\times e = f\not = 0 $ by (Pr3). However,
by (P3) and (Pr2). This is a contradiction. So (Pr4) holds.
Conversely, let $ (P, \times, 0) $ be a (2, 0)-type algebra satisfying the given conditions. We only need to show that (P2)–(P4) hold. Let $ e, f, g\in P $. By (Pr3), $ e\times f = 0 $ or $ e\times f = e $. In the former case, all items in (P2) are equal to $ 0 $ by (Pr2). In the latter case, all items in (P2) are equal to $ e $ by (Pr1). This shows (P2). Moreover, we also have $ e\times g = 0 $ or $ e\times g = e $. Then the following four cases may occur:
In case (1), $ (e\times f)\times g = e\times g = e $ and $ e\times(f\times (e\times g)) = e\times(f\times e) $. By (Pr3) and (Pr4), $ f\times e = f $ in the case. So $ e\times(f\times e) = e\times f = e $. This proves (P3) for case (1). The other cases can be showed similarly. Finally, we consider (P4). By (Pr3), $ f\times g = f $ or $ f\times g = 0 $. In the former case, the left side of (P4) is $ e\times f $, the right side of (P4) is $ (e\times f)\times (e\times f) = e\times f $ by (Pr1), and so they are equal. In the latter case, the two sides of (P4) are both $ 0 $ by (Pr2). The final result of the proposition follows from (Pr1), (Pr3) and (Pr4).
By the dual of Proposition 2.4 in [7], and Propositions 2.7 and 4.1, we have the following result easily.
Lemma 4.2. Let $ (S, \cdot, ^+, ^\ast) $ be a primitive $ P $-Ehresmann semigroup with zero $ 0 $ and $ 0\in P_S $. Define a binary operation $ "\times_{S}" $ on $ P_{S} $ as follows: For all $ e, f\in P_{S} $, $ e\times_{S} f = (ef)^+ = efe $. Then $ (P_{S}, \times_{S}, 0) $ forms a primitive projection algebra. In particular, if $ S $ is Ehresmann, then $ e\times_S f = f\times_S e $ for all $ e, f\in P_S $ by Lemma 2.1.
Let $ C $ be a nonempty set with a partial binary operation $ \cdot $ and $ (P, \times, 0) $ a primitive projection algebra with $ (P\setminus\{0\})\subseteq C $. Assume that $ {\bf d}: C\rightarrow P, x\mapsto {\bf d}(x), \ \ {\bf r}: C\rightarrow P, x\mapsto {\bf r}(x) $ are maps such that $ {\bf d}(C)\cup {\bf r}(C)\subseteq (P\setminus\{0\}) $ and
for all $ e\in (P\setminus\{0\}) $. According to Wang [26], $ {\bf C} = (C, \cdot, {\bf d}, {\bf r}, P) $ is called a generalized category over $ (P, \times, 0) $ if the following conditions hold:
(G1) For all $ x, y\in C $, $ x\cdot y $ is defined if and only if $ {\bf r}(x)\times {\bf d}(y)\not = 0 $ and then $ {\bf d}(x\cdot y) = {\bf d}(x) $ and $ {\bf r}(x\cdot y) = {\bf r}(y) $.
(G2) If $ x, y, z\in C $ such that both $ x\cdot y $ and $ y\cdot z $ are defined, then $ (x\cdot y)\cdot z = x\cdot(y\cdot z) $.
(G3) For all $ x\in C $, $ {\bf d}(x)\cdot x $ and $ x\cdot {\bf r}(x) $ are defined and $ {\bf d}(x)\cdot x = x = x\cdot {\bf r}(x) $.
(G4) If $ e, f\in P $ and $ e\times f\not = 0 $, then $ (e\cdot f)\cdot e = e $.
If $ e\times f = f\times e $ for all $ e, f\in P $, then $ e\times f\not = 0 $ if and only if $ e = f $, and so (G4) is always satisfied by (4.2), (G3) and Proposition 4.1. In this case, $ {\bf C} = (C, \cdot, {\bf d}, {\bf r}, P) $ is a category in usual sense.
Proposition 4.3. Let $ {\bf C} = (C, \cdot, {\bf d}, {\bf r}, P) $ be a generalized category over the primitive projection algebra $ (P, \times, 0) $. Put $ C^0 = C\cup \{0\} $. Define a binary operation on $ C^0 $ as follows: If $ x, y\in C $ and $ x\cdot y $ is defined in $ C $, then $ xy = x\cdot y $; all other products in $ C^0 $ are $ 0 $. Moreover, define two unary operations on $ C^0 $ as follows: $ 0^\clubsuit = 0^\spadesuit = 0 $ and $ x^\clubsuit = {\bf d}(x), x^\spadesuit = {\bf r}(x) $ for all $ x\in C $. With these operations $ C^0 $ is a projection-primitive $ P $-Ehresmann semigroup with $ 0 $ as a projection. In the sequel, we call $ (C^0, \cdot, \clubsuit, \spadesuit) $ a generalized category with zero adjoined.
Proof. Let $ x, y, z\in C^0 $. It is routine to check that $ (xy)z = 0 $ precisely when $ x(yz) = 0 $. Thus $ C^0 $ is a semigroup by (G2). We shall show that the identities (ⅰ)–(ⅴ) and (ⅰ)$ ' $–(ⅴ)$ ' $ are satisfied. Let $ x, y\in C^0 $. If $ 0\in \{x, y\} $, the identities (ⅰ)–(ⅴ) and (ⅰ)$ ' $–(ⅴ)$ ' $ are satisfied obviously. So we assume that $ x, y\in C $. Firstly, since $ {\bf d}(x)\cdot x = x $ by (G3), we have $ x^\clubsuit x = x $. This gives (ⅰ). Dully, we have (ⅰ)$ ' $. Secondly, since $ {\bf d}(y^\clubsuit) = {\bf d}({\bf d}(y)) = {\bf d}(y) $ by (4.2), it follows that $ xy^\clubsuit\not = 0 $ if and only if $ xy\not = 0 $ by (G1). If this is the case, we have
by (G1) again. This is exactly the identity (ⅱ). Dually, (ⅱ)$ ' $ is also true. Thirdly, by (4.2), (G1) and (Pr4), we can see that
In this case, we have
by (G1) and $ x^\clubsuit y^\clubsuit x^\clubsuit = {\bf d}(x) {\bf d}(y) {\bf d}(x) = {\bf d}(x) $ by (G4). This implies that the identity (ⅲ) is true. Dually, (ⅲ)$ ' $ is valid. Moreover, by (4.2), (G1) and (G3) we have
This gives (ⅳ). Similarly, we have (ⅳ)$ ' $. The identities (ⅴ) and (ⅴ)$ ' $ follow from the fact $ (x^\clubsuit)^\spadesuit = {\bf r}({\bf d}(x)) = {\bf d}(x) = x^\clubsuit $ by (4.2) and its dual. We have shown that $ (C^0, \cdot, \clubsuit, \spadesuit) $ is a $ P $-Ehresmann semigroup with the set of projections
Finally, let $ e, f\in P_{C^0} $ and $ e\leq f $. Then $ e = ef = fe $. If $ e\not = 0 $, then $ f\cdot e $ is defined and so $ e = {\bf d}(e) = {\bf d}(fe) = {\bf d}(f) = f $ by (4.2) and (G1). Thus, $ (C^0, \cdot, ^\clubsuit, ^\spadesuit) $ is projection-primitive.
Remark 4.4. Let $ {\bf C} = (C, \cdot, {\bf d}, {\bf r}, P) $ be a generalized category over the primitive projection algebra $ (P, \times, 0) $. If $ P $ contains at least three elements and $ e\times f\not = 0 $ for all $ e, f\in P\setminus\{0\} $, then $ x\cdot y $ is defined for all $ x, y\in C $. By Propositions 4.3 and 2.5, $ (C, \cdot, ^\clubsuit, ^\spadesuit) $ is a projection-primitive $ P $-Ehresmann semigroup without zero. On the other hand, if $ P $ contains two elements, say, $ P = \{0, 1\} $, then $ (C, \cdot, ^\clubsuit, ^\spadesuit) $ is a reduced $ P $-Ehresmann semigroup. In fact, $ (C, \cdot) $ is a monoid with $ 1 $ as identity, and $ (C^0, \cdot) $ is a monoid with zero adjoined. Thus we can think that generalized categories with zero adjoined covers the semigroups considered in the last section.
Now we can give the main result of this section, which is a generalization of a result on restriction semigroups obtained by Jones in Section 4 of [10].
Theorem 4.5. Let $ (S, \cdot, ^+, ^\ast) $ be a $ P $-Ehresmann semigroup with zero as a projection and $ |S| > 1 $. Then $ S $ is projection-primitive if and only if $ S $ is (2, 1, 1)-isomorphic to a generalized category with zero adjoined.
Proof. We have proved in Proposition 4.3 that every generalized category with zero adjoined is a projection-primitive $ P $-Ehresmann semigroup with zero as a projection. To prove the converse, let $ (S, \cdot, ^+, ^\ast) $ be a projection-primitive $ P $-Ehresmann semigroup with zero $ 0 $ and $ 0\in P_S $. By Lemma 4.2, $ (P_{S}, \times_{S}, 0) $ forms a primitive projection algebra. Denote $ C = S\setminus\{0\} $. Define a partial binary operation $ "\cdot" $ as follows:
where $ xy $ denotes the multiplication of $ x $ and $ y $ in the semigroup $ S $. Define maps
Then we have $ {\bf d}(C)\cup {\bf r}(C)\subseteq (P_S\setminus \{0\}) $ by Proposition 2.7 (1), and $ {\bf d}(e) = e = {\bf r}(e) $ for all $ e\in P_S\setminus \{0\} $ by Lemma 2.2, respectively.
We assert that $ (C, \cdot, {\bf d}, {\bf r}, P_S) $ is a generalized category over the primitive projection algebra $ (P_S, \times_S, 0) $. First, let $ x, y\in C $. By Proposition 2.7 (2) and (Pr3), (Pr4),
In this case, by the identities defining $ P $-Ehresmann semigroups and Lemma 2.2 we have
Dually, we have $ {\bf r}(x\cdot y) = {\bf r}(y) $. Thus (G1) holds. Next, let $ x, y, z\in C $, and $ x\cdot y $ and $ y\cdot z $ be defined. Since $ {\bf r}(x\cdot y) = {\bf r}(y) $ and $ {\bf d}(y\cdot z) = {\bf d}(y) $, $ (x\cdot y) \cdot z $ and $ x\cdot (y \cdot z) $ are defined, and so $ (x\cdot y)\cdot z = (xy)z = x(yz) = x\cdot(y\cdot z) $. This gives (G2). Moreover, for $ x\in C $, since $ x^+x = x\not = 0 $, it follows that $ x^+\cdot x $ is defined and $ {\bf d}(x)\cdot x = x $. Dually, $ x\cdot x^\ast $ is defined and $ x\cdot {\bf r}(x) = x $. Thus (G3) is true. Finally, let $ e, f\in P_S $ and $ e\times_S f\not = 0 $. Then $ f\times_S e\not = 0 $ by (Pr4) and $ e = e\times_S f = efe $ by (Pr3). In view of (G2), $ (e\cdot f)\cdot e $ is defined and $ (e\cdot f)\cdot e = (ef)e = efe = e $. Thus (G4) is valid.
By Proposition 4.3, we have a generalized category with zero adjoined $ (C^0, \cdot, ^\clubsuit, ^\spadesuit) $. We shall show that $ S $ is (2, 1, 1)-isomorphic to $ C^0 $. Define a map $ \psi: S\rightarrow C^0 $ by assigning $ 0\psi = 0 $ and $ x\psi = x $ for all $ x\in C = S\setminus\{0\} $. Obviously, $ \psi $ is a bijection. Let $ x, y\in S $. If $ x = 0 $ or $ y = 0 $, then $ x\psi = 0 $ or $ y\psi = 0 $, whence $ (xy)\psi = 0\psi = 0 = (x\psi)(y\psi) $. Assume that $ x, y\in C = S\setminus\{0\} $. Then $ xy = 0 $ in $ (S, \cdot, ^+, ^\ast) $ if and only if $ x\cdot y $ is not defined in the generalized category $ (C, \cdot, {\bf d}, {\bf r}, P_S) $, if and only if $ xy = 0 $ in $ (C^0, \cdot, ^\clubsuit, ^\spadesuit) $ by (4.3) and Proposition 4.3. This implies that $ (xy)\psi = (x\psi)(y\psi) $ for all $ x, y\in C $. Thus $ \psi $ is a semigroup homomorphism. Furthermore, observe that $ 0^+ = 0 $ by Proposition 2.7 (1) and $ 0^\clubsuit = 0 $ by Proposition 4.3, it follows that $ (0\psi)^\clubsuit = 0^\clubsuit = 0 = 0\psi = 0^+\psi $. Dually, we have $ (0\psi)^\spadesuit = 0^\ast\psi $. If $ x\in C = S\setminus\{0\} $, then $ x^+\in C $ by Proposition 2.7 (1), this implies that $ (x\psi)^\clubsuit = x^\clubsuit = {\bf d}(x) = x^+ = x^+\psi $ by Propositions 4.3 and (4.4). Dually, we have $ (x\psi)^\spadesuit = x^\ast\psi $ for all $ x\in C $. We have shown that $ \psi $ is a (2, 1, 1)-isomorphism. By Lemma 4.2 and the statements before Proposition 4.3, we have the following result appeared in Jones [10].
Corollary 4.6 ([10]). Let $ (S, \cdot, ^+, ^\ast) $ be an Ehresmann semigroup with zero as a projection and $ |S| > 1 $. Then $ S $ is projection-primitive if and only if $ S $ is (2, 1, 1)-isomorphic to a category with zero adjoined.
Remark 4.7. Let $ (S, \cdot, ^+, ^\ast) $ be a primitive $ P $-Ehresmann semigroup without zero or with zero 0 but $ 0\not\in P_S $. Let $ \diamond\not\in S $ and define additionally $ x\diamond = \diamond x = \diamond = \diamond\diamond $ and $ \diamond^+ = \diamond^\ast = \diamond $. Then $ (S^\diamond, \cdot, ^+, ^\ast) $ forms a primitive $ P $-Ehresmann semigroup with zero $ \diamond $ and $ \diamond\in P_{S^\diamond} $. In this case, the generalized category associated with $ S^\diamond $ constructed in the proof of Theorem 4.5 is just $ (S, \cdot, ^+, ^\ast) $ and the corresponding generalized category with zero adjoined is just $ (S^\diamond, \cdot, ^+, ^\ast) $. By Remark 4.4, we can think that Theorem 4.5 also works for the semigroups considered in the last section. However, it is trivial certainly in the case.
5.
Conclusions
In this paper, we have obtained the structures of projection-primitive $ P $-Ehresmann semigroups. As a future work, one can investigate the associative algebras of these semigroups by using the results obtained in the present paper.
Acknowledgments
The author expresses his profound gratitude to the referees for the valuable comments and suggestions, which improve greatly the content and presentation of this article. In particular, according to the advices of one of the referees, we rewrite Section 3 (with the help of the results of Lawson [14] provided by the referee) and Section 4. This research is supported by the National Natural Science Foundation of China (11661082). Thanks also go to the editor for the timely communications.
Conflict of interest
The author declares there is no conflict of interest.









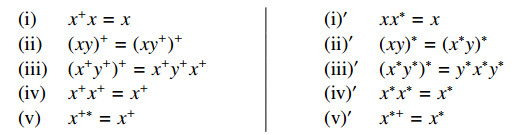









 DownLoad:
DownLoad: