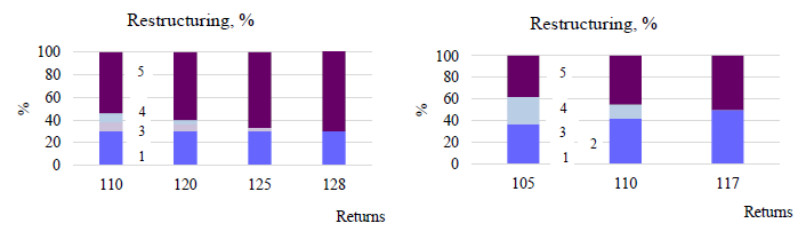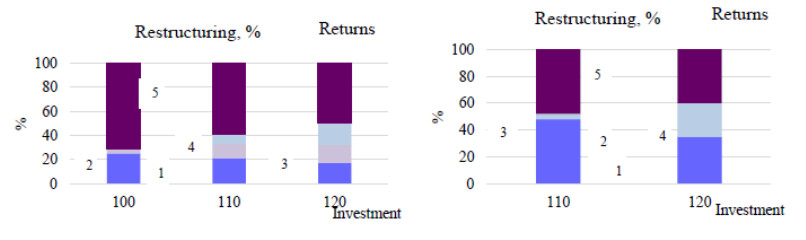The restructuring of the investment portfolio: the risk and effect of the emergence of new combinations

1.   Introduction

Portfolio theory from the time of priority works of J. Tobin (Tobin and Hester, 1967; Brainard and Tobin, 1992), Markowitz (Markowitz, 1952, 1991; Markowitz and Dijk, 2008) and Sharpe (Sharpe, 1970; Sharpe et al., 1998) gained wide popularity not only in the study of the distribution of investment in financial assets (securities). Its significance is usually presented in the broader context in relation to the savings and investment distribution in the economy as a whole, the selection of assets, the study of decision-making by economic agents regarding new and old assets, the distribution of return, decision-making in conditions of comparable and non-comparable risks, etc.

The popularity of portfolio theory is also evident in recent researches on the formation of portfolios based on risk and diversification (Lhabitant, 2017), the forecast of changes in global financial markets with an assessment of the profitability of a multi-factor risk-managed portfolio (Guard et al., 2015), the choice of alternative risks (Markowitz and Dijk, 2008) for effective portfolios, etc. Portfolio theory is used in open macroeconomic models (Brainard and Tobin, 1992), as well as in the analysis of sectoral interactions, such as the financial and fixed asset market (Nkeki, 2018), taking into account the risk of investment strategies and changes in the risk profile of the investor in the financial crisis. In addition, there is investigation the correlation of the statistical properties of portfolio models and empirical evidence (Li and Mei, 2014), the conditions of minimal risk, the stability of portfolio returns. There are works on psychometric risk perception, which are useful in the framework of portfolio theory in that they allow to link different institutional parameters of the economy with the perception of risk by agents engaged in portfolio selection (Sachse et al., 2012). Sources of financing have the impact on investment risk (Wang et al., 2016), especially in the field of high-tech developments, so the formation of the portfolio in each case has its own specifics, due to the state of the portfolio objects.

Most of these studies are devoted to the financial market and financial assets, although portfolio theory takes a much wider range of issues for research. The application of portfolio theory to the study of the distribution effects of different types of capital—human, financial, service, etc. (Byers et al., 2015) can be considered promising. In contrast to the above directions of application of the portfolio theory, the attempt will be made to use the optimization models of the portfolio by return and risk with a demonstration of the effect of restructuring the investment portfolio, provoking uncertainty of portfolio choice. The effect of investment portfolio restructuring is understood as the change in the distribution of resources on the portfolio objects when a new object appears, when the value of the return on the previous set of objects remains the same at the considered time interval, and the resource distributed among the objects changes. The emergence of a new portfolio object leads to the redistribution of the allocated resource according to the existing at the moment the portfolio object. In addition, the restructuring effect is the change in the structure of resource allocation between portfolio objects without the appearance of a new object (a new combination), but according to different optimization models—maximizing return and minimizing portfolio risk. Distribution structures are different and there is a problem of choosing the structure. It also shows the possibility of applying portfolio theory and models in the design of reforms as control effects on the economy, the directions of which can be considered as portfolio objects. In other words, reforms are peculiar projects, portfolio objects. They are optimized to find out how the resource is distributed between the directions of reform (these areas are portfolio objects)¹. Particular emphasis is placed on the emergence of the new portfolio object is combination that generates some effects that require consideration in the implementation of portfolio selection and economic policy planning.

¹ Reform is understood as a certain government project, characterized by the investment of resources, the distribution of them between the directions of reforms and the reforms themselves, and giving some returns per unit investment of resources in these reforms. Under the reform is understood as a kind of transformation, a change in the subsystems of the economy during a certain period of time, requiring a resource and characterized by a return per unit of resource.

The concept of the new combination in the article is used according to J. Schumpeter, who identified five types of new combinations (making a new good/new quality of the good, introducing a new mode of production, developing a new market for these products, obtaining a new source of raw materials or semi-finished products, conducting the corresponding reorganization of the market/enterprise). As an object of a portfolio, this is not necessarily an innovation, but simply a new combination for portfolio. It may not bring with it a novelty in the Schumpeter sense.

The portfolio consisting of objects that are invested, defined by the amount of return and risk, is usually considered static, as consisting of a given set of objects are combinations, if you apply the vocabulary of J. Schumpeter (Schumpeter, 2008). However, the emergence of the new object (combination) generates a dynamic effect of investment redistribution (resources), including existing combinations. Such effects have been studied not so well and are a reason to deepen research in the framework of neo-shumperian areas of economic science (Saviotti et al., 2016; Hanusch and Pyka, 2007; Hanusch et al., 2017).

The emergence of new combinations in the economy is not only due to the diversion of investment from existing combinations (borrowing), but also due to the opening of new combinations (resources). This fundamental refinement of the Schumpeterian representation and modeling of economic development makes it possible to expand the possibilities of studying the evolution of economic structures and its restructuring.

The portfolio can be considered an analogue of the economic system (Serletis, 2001) in the model sense, since it consists of objects, as well as the economy, and the problem of investment (resources) distribution between these objects, given the return and risk. At the same time, there is a total return on the portfolio (the current distribution structure) and the total risk of the portfolio, as well as a choice within the portfolio and between different portfolios. The problem of choosing between different portfolios is the assessment of restructuring, when the new combination is introduced into the portfolio (there were, for instants, five objects, i.e. combinations, it became six). It seems to be two portfolios, but there is one problem—a reasonable distribution of investment between objects-portfolio combinations.

For the demonstration of restructuring due to the effect of the new combinations emergence, you can use optimization models (Shinzato, 2018). We are talking about the formulation of the problem of conditional optimization for different target functions (return and risk), reflecting the different motivation of choice and economic development (rational and limited rational). With a rational motive, interest causes the greatest return. With a limited rational motive, the least risk (although this is not quite accurate, because the objective function of minimizing the parameter, in General, rational).

Through such models, it is possible to simulate the appearance of the new portfolio object—a combination, in order to assess the effect of resource allocation and borrowing when the optimization objective function is set. By changing the constraints on the target function, it is possible to assess the impact of institutional constraints, which are embodied in mathematical inequalities (optimization conditions), on economic dynamics and the achievement of optimum.

Consider the portfolio consisting of five objects, i.e. combinations and the situation with the appearance of the sixth object. Moreover, the objects of the portfolio have different dynamics of return per unit of investment. Some of them are characterized by decreasing, others are increasing returns. The gradient projection method used for optimization allows us to design a step-by-step optimization algorithm that reflects the change in the structure of the portfolio investment distribution regarding the direction of the main goal (maximum portfolio return or minimum risk). These goals are considered to be at this time interval not changeable, the interval of consideration is stable, as well as the value of return on it and other imposed restrictions (on the total amount of distributed investment on objects). By changing the purpose, restrictions, you can get a different solution, revealing how the different goal setting or other restrictions on the restructuring of the portfolio when moving to the goal. We will assume that the value of the return on the portfolio objects is not related, that is, the combination objects are independent of this indicator.

We will check to what extent the effects of borrowing (redistribution) of investment and how important it is to increase new investment (resources) for the purpose of ensuring a rational portfolio choice. Thus, it will be possible at the theoretical level of analysis to check how the principle of Schumpeter's "creative destruction" (Schumpeter, 2008) (borrowing, resource diversion) and the principle of "build-up", which is associated with the creation of new combinations at the expense of not distracted, but newly introduced resource. We will formulate the optimization models necessary for the study and test them. Then consider the portfolio, consisting of five available and one created combinations. We will study on optimization models, what happens to the return, risk, investment distribution between objects-combinations. Let us assess how the growing diversification is connected with risk and profitability. We will conclude the study by considering the problem of portfolio selection within the portfolio of reforms with the definition of the characteristic point of investment distribution in the areas of reform, requiring non-trivial additional selection procedures within this portfolio task.

2.   Research methodology

In the research to optimize the investment portfolio uses the optimization model (maximization of the portfolio return and minimizing of the portfolio risk) (Ravindran et al., 1983). The use of such models allows us to analyze the investment distribution between the objects of the portfolio, which in general can be interpreted as elements of the economic system (sectors). This approach allows us to identify relevant to the understanding systemic qualities or properties of the economy.

The mathematical formulation of the models takes the form:

1) Maximizing portfolio return: $D = \sum\limits_{j = 1}^{N} \mu_{j} z_{j} \rightarrow \max$, under restrictions: $\sum\limits_{j = 1}^{N} z_{j} \leq Q, z_{j} \geq 0$,

where D is the total return of the portfolio; z_j is the investment in the j-th portfolio object;

$\mu_{j} = \frac{1}{T} \sum\limits_{t = 1}^{T} r_{j}(t)$ is the average expected return on the j-th sector or type of economic activity;

r_j is the amount of return in term t on the j-th object of the portfolio;

Т is the time period of implementation of the model;

Q is total investment (resources);

N is the number of objects portfolio.

The mathematical formulation of the model of minimizing the total risk has the form:

2) Portfolio risk minimization: $R = z^{T} H z \rightarrow \min$, under restrictions: $\sum\limits_{j = 1}^{N} z_{j} \leq Q, \quad z_{j} \geq 0, \mu^{T} z \geq D_{0}$, where $H = \left[\sigma_{i j}^{2}\right]$ is the covariance matrix for N portfolio objects, D₀ is the minimum average expected return (which can be obtained in the future, which is calculated by the agent who decides on the investment distribution and the choice of the portfolio structure), R – the total risk of the portfolio².

²The magnitude of the risk of the portfolio measured by the value of the covariance $\sigma_{\mathrm{ij}}^{2} = \frac{1}{T} \sum\limits_{i = 1}^{T}\left(r_{i}(t)-\mu_{i}\right)\left(r_{j}(t)-\mu_{j}\right)$

The method of gradient projections (Ravindran et al., 1983) is used as the method of optimization of the above models. It has a good speed of convergence and a simple mathematical algorithm (which is not given in the research, as it is known in the research).

To demonstrate the models and procedures for its coordination, we formulate the test example of these models and optimization method. The main idea of the application of these models is that they will need to be agreed, because it is during this procedure that you can get an answer to the question of choosing the structure of the investment distribution within the boundaries of the portfolio with the given restrictions.

Let the objects of the investment portfolio are denoted by the letters A, B, C, D, E. Moreover, the return per unit of cost is known. This can be both the planned value of some production projects (or the expected return of economic sectors) and the actual value of the return of securities for the certain period (if the portfolio consists of securities), which is the same for all portfolio objects.

Let that the return per 1 monetary unit of investment for different periods of time for the investment portfolio objects is given by such values:

А 1. 0.7 1.2

B -0.8 -1.5 -2.1

C 0. 0.7 1.4

D 0.4 0.6 1.

E 1.2 3.0 2.2

In the form of the initial point of investment distribution by portfolio objects in the first model (maximization of total return), we take the uniform distribution, namely: {20, 20, 20, 20, 20}. Let the total return of investment is Qo = 100 (one hundred conventional monetary units) ³.

³ To test models, we assign conditional values, assuming that in practice monetary units are used.

For the model of minimizing the risk of the portfolio in the form of initial points of investment, distribution in portfolio objects adopted a distribution close to that, which according to the first model maximize return. In the following test example for the implementation of the optimization model, we set the initial distribution point by the following resource values for portfolio objects, totaling one hundred units:{2.5 2.5 2.5 2.5 90}.

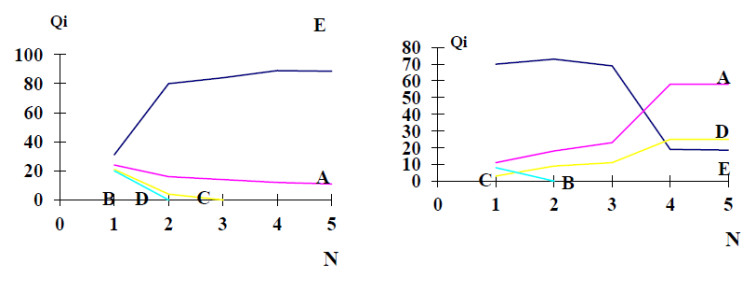
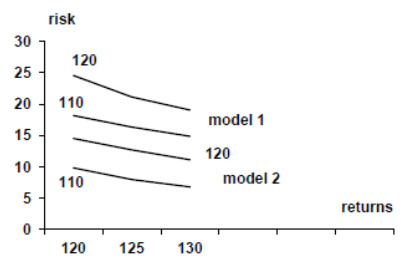
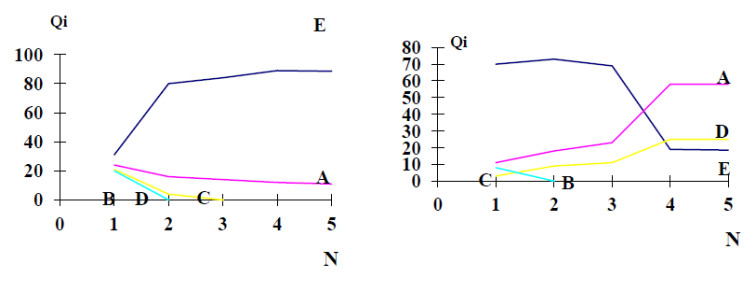
Further calculations are carried out according to the developed optimization program (using the gradient projection method). Changes in the value of the expected return of the investment portfolio. The iterative change in the value of investment for portfolio objects is given for each model in figure 1. Figure 2 shows the return and risk on the investment portfolio for each model.

Figure 1.  The iterative change of investment in portfolio objects, model of return maximization (on the left), risk minimizing (right).

DownLoad: Full-Size Img PowerPoint

Figure 2.  Total return and risk of the portfolio by iterations (Ⅰ-model of profit maximization, Ⅱ - the model of minimizing the risk).

DownLoad: Full-Size Img PowerPoint

Figure 1 shows the iterative changes in project investment for the first (left) and second (right) models. Figure 2 shows the change in total return and risk. For the first model (maximizing portfolio return), the expected return grows to 200 units as the number of iterations increases, but so does the risk to 60 units. At the first iteration, there is a race, and then a relatively systematic growth, which ends at the fourth iteration of the maximum return. investment in the portfolio object B are reset at the first iteration, in the project D at the second iteration, in the project C at the third. The total amount of investment equal to 100 units is distributed between the objects of portfolio A and E at the fourth iteration. For the portfolio risk minimization model for the same objects and the expected return of 110 monetary units (total investment amount of 100 units) and the starting point, which is close to the portfolio structure, giving the maximum return for the first model, we have the situation shown in figure 1 (right). As the result of optimization with the increase in the number of iterations, the total risk decreases and reaches an acceptable minimum with the return of 110 units. Investment is distributed among the portfolio objects A, D, E.

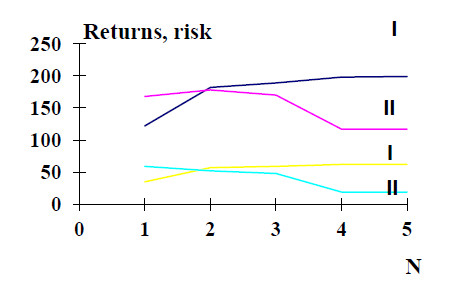
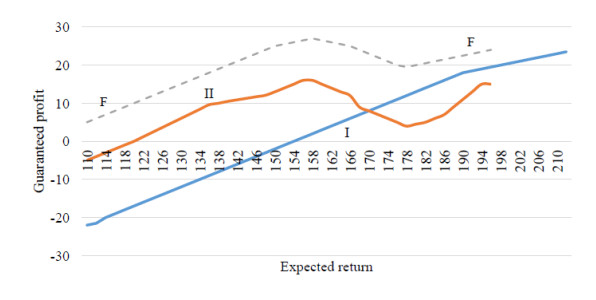
Figure 3 shows the change in the guaranteed profit for this portfolio from the expected return according to the model of return maximization and risk minimization. This chart can be considered as the result, as it outlines the range of acceptable solutions and determines the options of the portfolio structure for different values of expected return.

Figure 3.  Guaranteed profit and expected return on optimization models (Ⅰ and Ⅱ).

DownLoad: Full-Size Img PowerPoint

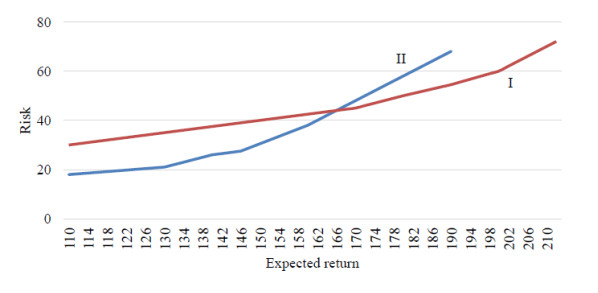
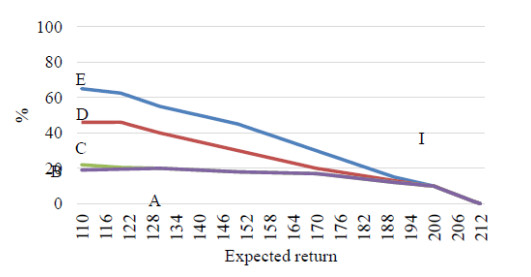
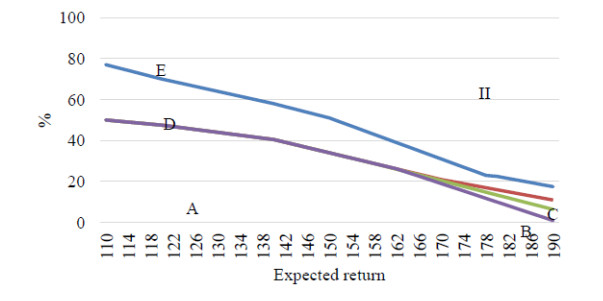
Figure 4 shows that with the increase in expected return, the risk increases for both models, but the nature of this change is different and determines the type of guaranteed profit curves in figure 3. The FF envelope curve for the two models in figure 3 shows the overall trend of the guaranteed profit increase with the increase in the expected return for this portfolio. Figure 5–6 shows the structure of the investment funds distribution between the five objects-combinations of the portfolio according to the specified models depending on the expected return. It should be noted that according to the structural diagram of figure 5, there is the decrease in the level of portfolio diversification with the increase in expected return by the model of maximizing return.

Figure 4.  Portfolio risk and expected return on optimization models (Ⅰ and Ⅱ).

DownLoad: Full-Size Img PowerPoint

Figure 5.  Structure of the investment portfolio according to the return maximization model.

DownLoad: Full-Size Img PowerPoint

Figure 6.  Structure of the investment portfolio according to the risk minimization model.

DownLoad: Full-Size Img PowerPoint

By the model of portfolio risk minimization, on the contrary, with the growth of return, the level of diversification will increase and the total risk will be less (figure 6). Figure 6 shows the opposite effect. The degree of diversification is higher if we expect a higher return on the second model while minimizing the total risk.

This will not be the case for all types of portfolio distributions. Further, it will be shown, using the same optimization models that the emergence of the new combination and portfolio diversification associated with it does not lead to a decrease in the portfolio risk.

The given test case of optimizing the investment portfolio by return and risk shows the possibility of applying these models not only in the field of portfolio investment decisions, but also in the process of investment distribution, as well as the restructuring of the portfolio, especially when new combinations appear (Schumpeter, 2008)—portfolio objects. Portfolio theory covers assets much more widely than securities (financial assets). Its logic can be applied to the invested objects—sectors of the economy. This is a resource allocation problem that can be addressed by different methods and procedures, including portfolio analysis. The use of optimization models and the use of the optimization algorithm by the gradient projection method allows not only obtaining an acceptable optimal solution, but also using the advantage of the algorithm of this optimization method, to see the iterative process of changing the relevant parameters when moving to the optimal point.

3.   The change in the profitability and risk of the portfolio when the new combination

Within the framework of portfolio theory, solutions are quite common when the number of elements composing a portfolio is known. However, it is important to study structural changes, as within the portfolio, investment (resources) are distributed between its objects, which occurs when the new combination appears. The resulting distribution effect changes relative to what was available when the number of portfolio objects is stable. Optimization models can be used to show changes in the distribution effect and the fact that investment diversification may not lead to lower risk, as is commonly believed.

Let us consider the portfolio, within which it is possible not only to compensate for the investment volume of 100 units, but also to exceed it, creating additional return. Let us set the value of return on investment for the five and the emerging sixth portfolio objects (in our case this new portfolio object is the new combination by J. Schumpeter) (table 1).

Table 1.  Initial data on the portfolio structure.

Portfolio object number-combinations	Return per unit of investment for equal periods of time
First	1.0 0.7 1.2
Second	-0.8 -1.5 -2.1
Third	0.0 0.7 1.4
Fourth	0.4 0.6 1.0
Fifth	1.2 1.7 1.3
Sixth	0.6 0.9 1.1

---

 | Show Table

DownLoad: CSV

In table 1, the first five objects demonstrate the existing portfolio composition, characterized by the value of return on the invested dollar. The sixth object appears with some return and is perceived as the new combination. We will further call the portfolio object the term "combination", meaning that initially there were five combinations, then there is the sixth combination (number 6 in table 1).

Consider the situation where the resource is set to 100,110, and 120 units. In the first case, the starting point of the investment distribution in the portfolio items {20; 20; 20; 20; 20} for the five combinations, in the second is {20; 20; 20; 20; 30}, in the third is{20; 20; 20; 30; 30}. If there are six combinations, the initial point for each resource value is accepted by the given: {20; 20; 20; 20; 10; 10}, {20; 20; 20; 20; 20; 10}, {20; 20; 20; 20; 20; 20}.

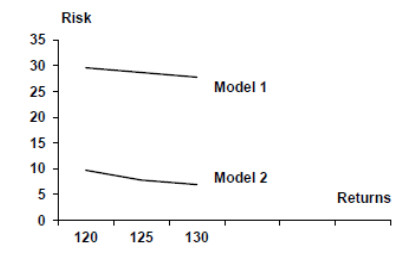
For five combinations with the growth of investment from 110 to 120 units, according to the optimization model 1 (return) and 2 (risk), we have the following type of return-risk chart (figure 7).

Figure 7.  Return-risk with growth of investment by model 1 and model 2 (five objects-combinations).

DownLoad: Full-Size Img PowerPoint

As we can see from figure 7, with the growth of expected return, the agammaegate risk is reduced, which is provided by the specific combination of the return to the portfolio objects. However, model 1 is less attractive because for the same expected return the agammaegate risk is greater for any investment, in both 110 and 120 units. Therefore, the choice of the structure of investment distribution within the boundaries of the portfolio will require additional analysis, especially when we consider that when resource 110 units in model 1 and 120 units of model 2 are quite close to the risk level for the given amount of return. It is this proximity that makes the choice of the investment distribution structure almost equivalent. If we strictly follow the comparison of risk values, model 2 and the corresponding structure of investment distribution in the portfolio will be preferable. In view of the foregoing, there is the problem of restructuring the investment portfolio, the value of which is updated when the new portfolio object is combination.

We show the portfolio restructuring with the growth of return on the model 1 (figure 8, left) (maximization of return), when investment are stable in size and amount to Q = 100 units and on the model 2 (figure 8, right) (risk minimization).

Figure 8.  Portfolio restructuring by model 1 (left) and model 2 (right) with investment Q = 100 (five portfolio combination-objects).

DownLoad: Full-Size Img PowerPoint

As can be seen from figure 8, the two models show the increase in investment in the fifth combination and investment in the first combination. However, according to model 2, this is more intense, since the risk of activity on these objects-combinations is lower relative to other portfolio objects. The second combination to model 1 does not receive investment, to model 2 the third combination does not receive them, and the second, despite the growing loss ratio, receives a very small amount of investment (model 2), but with further growth of return gives it in favor of the dominant portfolio objects (combinations). It should be noted that the portfolio considered in the presented simulation demonstrates such ratios of return that with the growth of return at the selected time interval on the model 1 and 2, the decrease in risk is detected, and the risk on the model 1 exceeds the risk on the model 2 (so that the model 2 is preferable for any return). If there is the sixth combination within this portfolio, then this ratio of changes in return and risk for the portfolio remains.

Now let's assess the situation when the portfolio restructuring occurs with an increase in the total investment of 100,110,120 units according to model 1 and 2, and the expected return, which we have to count is 125 units. We obtain the change in the portfolio structure with the increase in the investment volume in the model 1 (figure 9, left) and model 2 (figure 9, right).

Figure 9.  Portfolio restructuring according to model 1 (left) and model 2 (right) with variable investment volume (expected return level is 125 units).

DownLoad: Full-Size Img PowerPoint

Based on figure 9, it can be seen that with the growth of investment, their value for the first and fifth combinations decreases, but increases for the third and fourth (according to model 1). According to model 2, the same situation is observed, only more smoothed and the third portfolio object does not receive investment, but the fourth receives the significant amount of investment due to lower risk.

Let us imagine that the sixth object appears in the portfolio is the new combination with increasing returns. The change in returns will be 0.6; 0.9; 1.1. (table 1). According to the model with high risk investment in this new combination are practically not made. However, in practice, it is quite a situation that this combination is invested, which indicates the neglect of high risk by decision-making agents, or the presence of such interspecific properties of this combination that they are invested, despite the risk.

When investing in 100,110 or 120 units with the growth of return, the total portfolio risk with the sixth combination decreases (as shown in figure 10 for Q = 110) according to models 1 and 2.

Figure 10.  Chart "return-risk" in the total investment in the portfolio Q = 110 for model 1 and model 2 (six portfolio combinations).

DownLoad: Full-Size Img PowerPoint

The appearance of the sixth combination, with the investment of 110 units, increased the risk for the same level of expected return of 120,125 and 130 units on model 1, but did not increase the risk or even slightly reduced it on model 2 (comparative analysis of figure 9 and 10). Thus, it can be noted that the predominance of the behavior model aimed at the highest return, accompanied by the emergence of the risky new combination, will increase the total risk. If the agents making the portfolio choice prefer low risk, then the emergence of the new combination (portfolio object) can contribute to the investment redistribution between other portfolio objects. This circumstance can slightly increase the risk or even reduce the total risk.

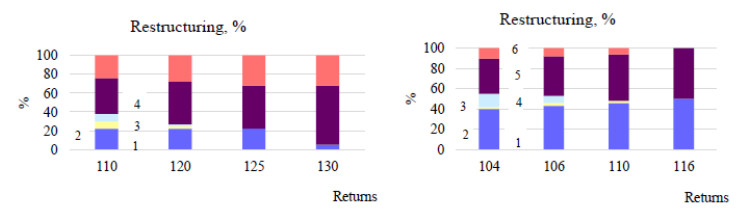
With the growth of total investment Q from 110 to 130 units in the model 1, there is the increase in the investment of the new sixth combination from 23.35 to 31.5 units, but in the model 2 with the growth of expected return from 104 to 116 units, investment in the sixth combination are reduced from 11.78 to 0, 83. The appearance of the new sixth combination is the meaning of restructuring and significantly changes the nature of restructuring with five objects (portfolio combinations). The result of this change is shown in figure 11 compared to figure 10.

Figure 11.  The portfolio rebalancing model 1 (left) and model 2 (right) with the investment of Q = 100 (six-combinations of portfolio).

DownLoad: Full-Size Img PowerPoint

The result of the presented optimization models is that for six combinations of model 1 the fifth and sixth combinations increase investment, the fourth and third combinations decrease its, without receiving investment with the expected return from the investment portfolio of 130 units. With the existing ratios of return on the objects-combinations of the portfolio, it is not possible to obtain the total expected return of 130 units in any other way. investment in the first object-combination are reduced.

With five combinations for an expected return of 130 units the third and fourth combinations also lose investment. Investment are distributed between the first and fifth combinations with the dominance of the fifth combination to receive investment. Due to the sixth combination the risk with an return of 130 units is higher for the portfolio of six combinations than for five combinations and more than 2 times (11 against 26 units). Due to the sixth combination the dominance of the first and fifth combinations is reduced by 3 and 1.2 times respectively. The level of system diversification increases (due to the appearance of the sixth combination) and this increases the total risk (but does not reduce as is commonly believed in other approaches). According to model 2 for six combinations as well as for five combinations there is the reduction in the diversification level of the system with the increase in expected return. Investment is made at the expense of the first and fifth objects-combinations of the portfolio, displacing other combinations, including the sixth sector. However, for the same return, for instants 110 units, the risk is slightly less for the portfolio with six combinations compare to the portfolio with five combinations. However, the distribution (restructuring) takes place in such a way that the first sector receives more resources with six combinations than for the portfolio with five combinations with the expected return of 110 units. The fourth and fifth combinations receive more investment in the portfolio with five combinations than with six combinations.

If the portfolio choice is dominated by model 2 (limited rationality and minimizing portfolio risk), then the desire to focus the system on the highest return can eliminate new combinations that are more risky. The new combination is deprived of investment. Limited rationality here can understand the type of risk fear or institutional blocking of risky activities. In order for the new combination to receive investment for development, it is necessary to focus on real goals, that is to want to receive the return of 110 units from investment of 100 units or 105 units. Then the sixth combination will receive investment of 5.85 or 11.78 units respectively.

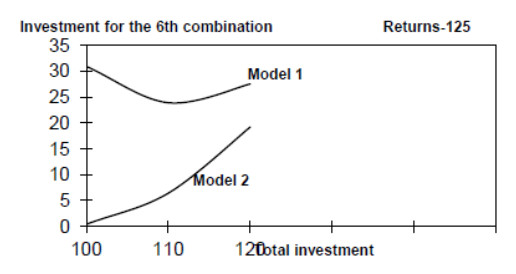
With the growth of investment its value for the sixth combination changes in different ways for model 1 and 2. Let's show this for the expected return of 125 units for model 1 and 2 respectively. The system risk with the growth of the allocated resource increases in both models. However, if in model 2 with the investment growth by the sixth combination the allocated volume of investment for this level of return increases, then in model 1 the change for this expected return of 125 units (with the risk growth) is the following: first, investment decrease slightly, then increase (figure 12).

Figure 12.  Dynamics of changes in total investment by the 6th combination with the investment growth (return 125 units) on the model 1 and 2.

DownLoad: Full-Size Img PowerPoint

If agents make a portfolio choice rationally, that is, seek to get more return from the investment distribution within this portfolio with the growth of investment, as shown by the computer implementation of optimization models, investment will first fall to the new combination, then increase. The calculation was carried out under the assumption that the value of the return on the objects-combinations of the portfolio is not related, and in the considered period of time the return does not change much on the average.

Now let's see how the process of investment diversion in favor of the sixth combination and what happens when the total investment increases from 100 to 110 units (according to the model 1 agents do not consider the risk increase). To do this, we will use the data on the portfolio from table 1, carrying out the model simulation for return of 120 units with investment of 100 and 110 units respectively. First, there are five objects-combinations in the portfolio, then the sixth combination appears in it (the results of the restructuring are presented in table 2).

Table 2.  Results of restructuring: investment distraction and accretion.

Investment 100, return 120, 5 combinations	Investment 100, return 120, 6 combinations	Investment diversion	Investment 110, return 120, 6 combinations	The difference for 6 combinations when increasing investment to 110 units
1	2	3 (column 1 –column 2)	4 (created the investment)	5 (column 4–column 2)
27.58	22.7	4.88	29.19	+6.49
0.0	0.0	0.0	0.0	0.0
6.93	5.43	1.5	13.4	+7.87
4.35	3.27	1.08	12.05	+8.78
61.12	48.7	12.42	39.71	-8.89
–	19.8	+19.8	15.6	-4.2

---

 | Show Table

DownLoad: CSV

The results of the model simulation are collected in table 2 and make it possible to state that the emergence of the sixth combination with investment in 100 units leads to the system restructuring by diverting the resource from the old existing combinations (portfolio objects). For the return of 120 units this distraction will be +19.8 (column 3). If the investment increases to 110, that is, by 10 units (six combinations and the expected return of 120 units), then the system restructuring is described in column 4. With the constant value of total investment the new combination appeared only at the expense of other combinations diverted 19.8 units of investment in them. But with the investment increase the new combination of them is less (15.6) than it distracted (19.8) for the resource of 100 units. Consequently, 4.2 units of investment in the expansion of the total investment portfolio went from the new combination to the old combinations, as well as 10 units of newly increased investment. Moreover, the fifth combination of the same gave investment in favor of other old combinations in the amount of 8.89 units (column 5). In total, the old combinations with the investment expansion received 23.1 units of investment. The fifth and sixth combinations gave 13.1, the difference is 10 units, that is, just the increase in investment, which was taken by the old combinations (by numbers 1, 3 and 4).

Thus, the old combinations with the expansion of the total investment portfolio received 10 units of increased investment and the new combination, which diverted 19.8 units of investment gave 4.2 units of investment in favor of the old combinations. Therefore, the position of the new combination in the portfolio due to the allocation and increase of resources, decreased (the value of the impact for each activity, table 1).

Summarizing, we note that the tested models show the situation of portfolio restructuring with the consequent change in portfolio choice due to changes in investment within the portfolio structure under the assumption that the return of objects-combinations portfolio does not change in the considered time interval. There are two types of mechanism are diverting investment from the previous feature combinations and compounding of investment. The new combination can get as much value investment and less. The result is determined by the amount of efficiency and risk associated with this new combination, as well as the investment distribution between the old combinations.

Structural analysis of the portfolio expands the possibilities of the "portfolio" theory, which can be applied to select the structure of investment or resources allocation for the implementation of certain economic (institutional) reforms. In this case, we can talk about the portfolio of reforms and the choice of its structure. Let us consider such the problem in the truncated version on the basis of the above models of return optimization and minimizing the total risk of the portfolio. Let the portfolio objects are represented by some variants of reforms (for simplicity we introduce the assumption that the return on each portfolio object does not depend on the return of other objects, that is, the reforms are some alternatives and can be carried out independently from each other). Investment in this case will be considered as resources allocated to each reform within the portfolio.

4.   "Portfolio" of economic reforms—structure choice

For example, the government is planning to implement eight reforms at the same time with the expected estimated impact for the next four years determined by the average rate of return on each reform. Table 3 shows these coefficients for each reform direction (taken arbitrarily). Using the data in table 3, we obtain the risk change in the reform portfolio for eight objects (A, B, C, D, E, F, G, H) depending on the expected return for the two models presented above. We will take the initial amount of resources available to the government as, for example, ＄27.9 million (the number is arbitrary).

Table 3.  Expected return on the objects of the reform portfolio.

Reform/ time period	1	2	3	4
А	1.233	1.066	1.206	1.15
B	0.923	0.881	0.535	0.796
C	0.128	0.204	0.176	0.292
D	0.354	1.294	0.577	0.701
E	1.39	1.4	1.33	1.1
F	2.6	2.34	2.01	1.98
G	0.41	0.519	0.435	0.458
H	0.902	1.253	0.72	0.849

---

 | Show Table

DownLoad: CSV

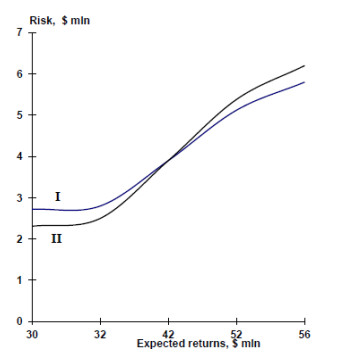
Then we get the following ratio of risk and return on the implementation of the portfolio of reforms by model Ⅰ and Ⅱ (figure 13).

Figure 13.  Risk of implementation of the "portfolio" of reforms depending on expected return.

DownLoad: Full-Size Img PowerPoint

The observed risk trend for each model (Ⅰ and Ⅱ) confirms their growth with increasing expected return. With the expected return of ＄42 million there is the point of intersection of risk graphs on the return maximization (Ⅰ) and risk minimization (Ⅱ) model. With other expected return values the calculated risk indicators for the models are different. To the point of intersection of the graphs the risk for the return maximization model is higher for this level of return than for the risk minimization model and after the intersection point is lower. A characteristic point of intersection is of particular interest in that its economic meaning can be described as "ambiguous portfolio choice" since the same combination of expected return and total portfolio risk is provided by different structures of investment (resources) distribution. With regard to the choice of economic reforms additional decision—making procedures are required. What investment (resources) structure and economic policy efforts to choose. These may be fundamentally different options for strategic decisions. They relate to different portfolio structures, that is, different investment (resources) distribution, for this reason, and different efficiency, which should be evaluated separately. Therefore, the choice of the best option at this point in the portfolio structure requires procedures, assessment of the quality of institutions, the current distribution structure. In addition, it may be necessary to work out the probably scenarios for achieving results for each portfolio object.

Figure 14.  Structure of distribution of the reform portfolio according to expected return by model Ⅰ.

DownLoad: Full-Size Img PowerPoint

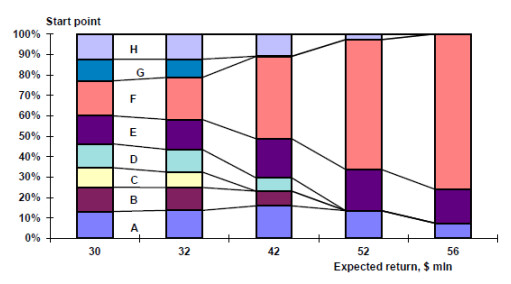
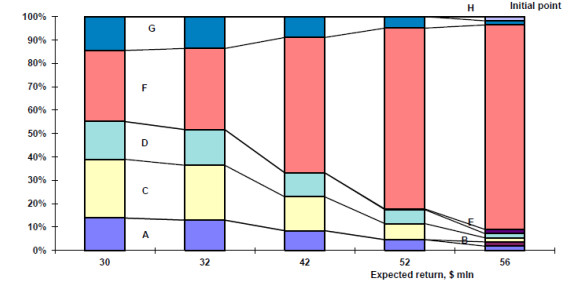
The dynamics of the structure of the "portfolio" of reforms (economic policy priorities) is shown in figures 14–15, where the expected return is ＄42 million (characteristic point). There are obvious differences in investment in each direction, but giving the same risk of such economic policy for this expected return.

Figure 15.  Structure of distribution of the reform portfolio from expected return by model Ⅱ.

DownLoad: Full-Size Img PowerPoint

There is the different risk and structure for the investment distribution of across the reform portfolio for different expected return. However, not only for the characteristic point where risk and expected return are the same, and the distribution structure is different, but also for other expected return values, where risk and distribution structure are different, the question of additional distribution selection criteria also remains.

For instants, after analyzing the investment (resources) distribution in the areas of reform, it is possible to select those, the possibility of allocating funds for which is consistent with their high ratings (including with the help of expert assessments). This may be one of the criteria (expert assessment of the investment distribution structure in the areas of reforms).

Thus, with the help of optimization models it is shown that investing in some areas of development (reforms) can weaken other areas, or sharply narrow their "investment window" of opportunities. Such restructuring is the essence of the evolution not only of the investment portfolio, but also of the economic system with the permanent change in its structural quality. In reality, the rates of return for each direction change dynamically over the monitored period of time. This change is related to the nature of the interaction of the directions or types of policies and the effectiveness/inefficiency of actions within the framework of this economic policy. This will require mine-grade models, but the models applied here already provide the very important conclusion about the presence of the structural distribution point in the portfolio, as well as the impact of risk and return on the distribution itself.

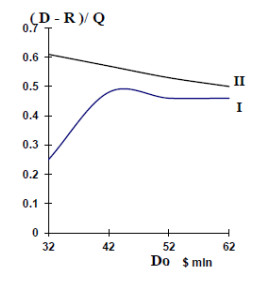
Find the share of the difference between total return (D) and risk (R) in the total amount of investment (Q) allocated to reforms. The change in this share according to expected return (Do) by models Ⅰ and Ⅱ is shown in figure 16.

Figure 16.  Share of difference between total return and portfolio risk in total investment and expected return (model Ⅰ and Ⅱ).

DownLoad: Full-Size Img PowerPoint

The dependences of figure 16 are based on the same data as figures 14–15. From figure 16 it is seen that the curve Ⅰ in the characteristic point of expected return (＄42 million) has the extremum. In the first model the rate of change in return is first higher than the rate of change in risk, but after the characteristic point the risk begins to grow faster than return and the value of the share decreases. According to the second model there is the systematic decrease in the share of the difference in return and risk in the amount of investment due to the monotonous increase in risk and return. Therefore, the risk curves for model Ⅰ and Ⅱ in this case will not have the intersection point and the characteristic point looks like the break point of curve Ⅰ. Therefore, it makes sense to calculate the structures of investment distribution in the areas of reforms in accordance with the optimization models used, but only for the characteristic point. The results are shown in table 4.

Table 4.  Investment allocation structure for the characteristic point (＄42 million).

The direction of economic policy	Model Ⅰ	Model Ⅱ
A	4.9	4.67
B	3.45	3.08
C	3.3	4.09
D	3.46	4.4
E	3.4	4.61
F	3.15	2.08
G	3.15	2.6
H	3.06	2.33

---

 | Show Table

DownLoad: CSV

The result allows us to demonstrate the problem of choosing the reform directions (within the existing reform portfolio) in order to further apply the reasonable algorithm of decision-making for the behavior of effective reforms. This helps to overcome inefficiencies in resource allocation. For example, if the investment distribution in the reforms was outside any criteria, the choice of distribution structure would be random. This is what happens if you do not take into account neither the structure of the distribution of investment (resources), nor the characteristic distribution point associated with the ratio of risk and expected return of the portfolio. Random selection of the distribution structure can give the following: a) for the distribution vector {0.4, 0.4, 9.3, 0.4, 0.4, 3.5, 7.0, 7.0} or (b) vectors {0, 0, 18.0, 0, 0, 0, 0.9, 9.0} total return from such distribution for (a) ＄19 million, for (b) ＄19.3 million, that is, significantly less than the initial total investment of ＄27.9 million. When distributing investment in the different proportion, for example, in the form of the vector {4.9, 3.45, 3.3, 3.3, 3.4, 3.15, 3.15, 3} the total return will amount to ＄42 million, which for the same period of time is a fairly high return, covering the excess of initial investment, provided that there are no unforeseen institutional and financial risks.

5.   Discussion of the results

In the course of the theoretical study on optimization models of the investment portfolio (maximizing return and minimizing risk) solved by the gradient projection method, it was shown that the nature of the distribution of resources within the portfolio changes when a new object appears and depending on the profitability of this new combination. A completely different resource is received by the old portfolio objects (old combinations).

This approach mimics the emergence of a new combination and shows, in contrast to the known applications of portfolio theory (Matthies et al., 2019; Way et al., 2019; Paut et al., 2019; Barnes et al., 2019; Zhang et al., 2018) that the emergence of a new combination not only changes the dynamics of previously existing combinations, but also shows the effect that greater portfolio diversification does not always lead to less risk. This conclusion is consistent with models from evolutionary game theory (Sohrabi et al., 2019; Yi et al., 2019; Babu et al, 2018; Elsner et al., 2018; Ozkan-Canbolat et al., 2016; Adami et al., 2016; Herbert, 2009; Bowles, 2006), but obtained in a class of optimization models.

In addition, when implementing optimization models and combining their results, a point was obtained at which different structures of resource distribution among portfolio objects give the same combination of risk and return. This characteristic point problem leads to uncertainty in the choice of distribution structure. However, in the case when the risk is less, the return is greater, or the risk is greater, the return is less, the problem of choosing a structure also exists. However, in this case, the agent may prefer either more risk and more return, or less risk and less return, with the resulting choice of a distribution structure that corresponds to some ratio of risk and return.

The emergence of the new combination can shift the characteristic point, or even become the condition for its absence, however, the problem of choosing for different risks and the same expected return with different structures of investment distribution remains. Moreover, the very new combination within the portfolio, depending on the size of the yield and its risk, can create the special regime for the distribution of investment (resources) between existing objects and for itself it can be the limiting effect.

Thus, with the help of portfolio theory and optimization models (maximization of return and minimizing the risk of the investment portfolio) it is possible to show the effect of the new combination determined not only by the amount of risk, but also by the initial structure of the investment distribution. The 'novelty' of the resulting combination, generating its risk and expected return in comparison with expected return and risk for other objects-combinations of the portfolio is also of significant importance. Thus, it is possible to reveal the mechanism of the emergence of the new combination in the sense of J. Schumpeter and show the internal process of evolution of the portfolio structure, which acts as the kind of economy model, consisting of various elements. In practice, there is the more complex distribution process, which is determined by the institutions and the connectivity of the various elements of the economic structure (including the dependence of the yield of different elements). However, already this model demonstration shows the presence of very relevant properties of portfolio diversification and investment distribution in it.

6.   Conclusion

Let us formulate the main conclusions obtained in the research.

First, the diversion of investment from one portfolio object to another when the new object (the new combination) appears has the internal limitation due to the fact that this process can occur until the reduced resource for the already existing portfolio objects leads to the change in their profitability. The creation of the new object (combination) does not guarantee the possibility of increasing investment in this new object (combination).

Secondly, if only investment can be used only by this object (the new combination), then the very fact of such use will contribute to the increase of investment in this object of the portfolio.

In this research the data interspecifically properties investment (invest in the resource object) is not considered.

Third, the emergence of the new portfolio object, the new combination, in some way affects the portfolio structure and in such the way that it contributes the an increase in investment in the old objects (old combinations), especially with the expansion of the total resource (investment).

The result is useful for understanding the patterns of investment distribution within the boundaries of the existing portfolio choice, including through the restructuring of the portfolio itself. Moreover, the portfolio is the analogue of the economic system, in this connection, the conclusions are useful in the research of economic restructuring, as they allow to take into account the effect of the emergence of the new combination for the development of its own and already existing and functioning combinations (portfolio object).

Acknowledgments

This manuscript benefited from the valuable comments of two anonymous reviewers.

Conflict of interest

The author declares no conflict of interest in this paper.