Attention based residual network for medicinal fungi near infrared spectroscopy analysis

1.   Introduction

Medicinal fungi, such as Cordyceps, Reishi, Antrodia Camphorata and Matsutake, can enhance human immunity, anti-tumor and anti-cancer. The active ingredients in medicinal fungi are useful in a wide range of clinical therapies and these ingredients can be detected quickly by near infrared spectroscopy (NIRS). NIRS is a convenient, fast and non-intrusive analysis method which has been applied to quantitative analysis of medicinal fungi data. In organic molecules, the vibration frequency and the frequency multiplier at all levels of hydrogen-containing groups (O-H, N-H, C-H), these absorption regions are consistent with near infrared spectrum regions. By scanning the near infrared spectrum of the sample, the frequency information of one single chemical bond in molecule can be recorded. Due to the advantage of NIRS, researchers can quickly and accurately analyze the content of various active ingredients in medicinal fungi, and the NIRS has been widely used in qualitative and quantitative analysis in medicinal fungi domains such as chemical and pharmaceutical industries ^[1,2]. As a secondary analysis method, NIRS needs to build a mathematical method to explain the relation between spectra data and reference value.

Many traditional NIRS analysis methods, such as partial least squares (PLS) and radial basis function neural network (RBFNN), show a good prediction accuracy and performance. However, due to the high dimensionality and multiple information mixture of NIRS data, these methods require feature spectral wave band selection which depends on experts' experience to reduce the dimensions and improve the prediction accuracy. The artificial selection of feature wave bands from high dimensional spectral data may lose some tiny but significant feature peaks in original spectral curves and also be consuming.

Recently, with the popularity and development of deep learning technologies, convolutional neural network, as a typical model of deep learning, can rapidly extract feature information from high dimensional data. Compared with the artificial feature selection depends on experts' experience, convolutional neural network can autonomously learn and extract every local feature of data through multiple convolution layers and iterations. Meanwhile, a deep structure with nonlinear activation function makes the model more suitable for big data, especially for those with high dimension and non-linearity, such as NIRS.

In this paper, we provide an NIRS analysis method, attention based residual network (ABRN) for NIRS. ABRN is based on convolutional neural network. In ABRN, we add attention module to enhance the feature wave bands and to reduce the noise bands in original NIRS vectors, and then use residual network to autonomously extract each dimension features in spectral vectors. Finally, ABRN will output the predicted value corresponding to the spectrum. To verify ABRN, we predict the content of several active ingredients in medicinal fungus (Antrodia Camphorata and Matsutake), compare the result with current popular NIRS analysis methods.

2.   Related work

There are many developed methods in analyzing NIRS data. There are three categories: (1) Linear regression method based on principal component analysis and PLS; (2) Nonlinear machine learning methods, such as artificial neural network (ANN), RBFNN, support vector machine (SVM), and so on; (3) Feature extraction and value prediction from high-dimensional NIRS data methods based on deep learning methods.

Here are detailed summarizations of NIRS analysis methods.

2.1.   PLS method

PLS regression method is a traditional NIRS analysis method. It maps predicted values and actual values into a new common space through linear regression method. A satisfactory calibration method has been built with PLS via adopting optimum wavelength ^[3]. Due to the potential interferences and noises in NIRS, the successive projection algorithm for interval selection in PLS (iSPA-PLS) ^[4,5] is used to eliminate the unrelated variables. The wavelength selection and data preprocessing on NIRS, such as smoothing, derivative, multiplicative scattering correction ^[6,7] etc., also affect the PLS's accuracy of predictions. Kim G. et al. use maximum normalized preprocessing to eliminate extraneous noise in the spectrum ^[8]. Magalhães A. F. B. et al. obtain better results by reducing the range of original spectra ^[9]. However, these traditional NIRS linear analysis methods need to artificially extract the spectral crests which reflect some of features in original spectrum. The accuracy of prediction depends on if the feature wave bands are typical. Furthermore, PLS is a linear regression method, which there may be some limitations in solving nonlinear problems such as NIRS.

2.2.   Nonlinear machine learning method

Using nonlinear neural network can retrieval and extract relationships from biomedical data or literatures ^{[10,11,12,13,14]}. One of the most popular nonlinear machine learning methods of analyzing biomedical NIRS data is through RBFNN ^[15]. For example, Lu J H et al. ^[16] use wavelet transform preprocessing based RBFNN to analyze NIRS. Meanwhile, moving window method ^[17] is part of pre-processing in RBFNN to select the feature wave bands by using the degree approximation ^[18,19,20]. Jintao X et al. use ANN to extract main components and compare PLS with ANN to verify that ANN has better nonlinear fitting performance ^[21,22]. Other machine learning methods ^[25,26], such as SVM ^[23,27] also shows good performance and predictive accuracy in NIRS analysis. As the input of these machine learning methods, the original NIRS data requires pre-processing ^[24] such as dimensionality reduction ^[28], denoising and feature wave bands selection, to improve the accuracy of prediction ^[29]. Artificial feature selection, which relies on experts' experience, may lose some tiny feature peaks in NIRS. In original high-dimensional spectral data, many unrelated noise bands also affect the accuracy of prediction.

2.3.   Deep learning method

Deep learning methods have good performance in extracting relationships ^[30] and features from high-dimensional biomedical data ^[31]. Unsupervised learning method, deep automatic encoder (DAE), can extract valid features from NIRS by transforming high dimensional data into low-dimensional codes with linear and nonlinear combination features ^[32]. Deep belief network with dropout can prevent overfitting and cost less training time compared with DAE ^[33]. Convolutional neural network also shows good performance by converting one dimensional vector of NIRS into two-dimensional information matrix ^[34]. The accuracy of previous methods in analyzing NIRS depends on artificial feature wave bands selection. One of the biggest advantages of deep learning methods is that it can autonomously extract features from high dimensional data through multiple iterations. However, due to the complexity of original spectral data, irrelevant information and noise will affect the extraction of feature wave bands. Therefore, current deep learning methods in NIRS analysis require artificial denoising and compression of original spectral data.

The above NIRS analysis methods rely on experts' experience to perform preprocessing of artificial feature wave bands selection. Even with deep learning methods, only a small number of feature wave bands are available in original spectral data, and many noise wave bands affect the extraction of key feature wave bands. The proposed ABRN can directly use original spectral data as input vectors, redistribute the weights of feature wave bands and reduce irrelevant wave bands through attention module in ABRN. The residual network in ABRN, which is proposed by Kaiming He et al. ^[35], performs autonomous extraction of features and content prediction. Our ABRN is accelerated by NVIDIA GeForce GTX 1080. Compared with traditional NIRS analysis methods, ABRN can improve computational and time efficiency and maintain high accuracy.

3.   Method

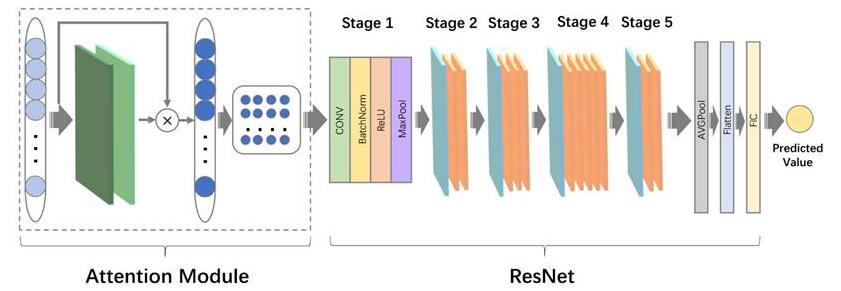
To reduce the impact of human factors and achieve an autonomous analysis of original NIRS data, we propose ABRN which based on residual network. Traditional NIRS analysis methods rely on human experience to select feature wave bands, while ABRN can realize autonomous selection of feature wave bands in original NIRS vectors through multiple convolutional layers. We adopt attention module in ABRN to autonomously enhance the features to improve the accuracy of prediction. Figure 1 shows the structure of ABRN.

Figure 1.  The architecture of ABRN.

DownLoad: Full-Size Img PowerPoint

3.1.   The residual network architecture

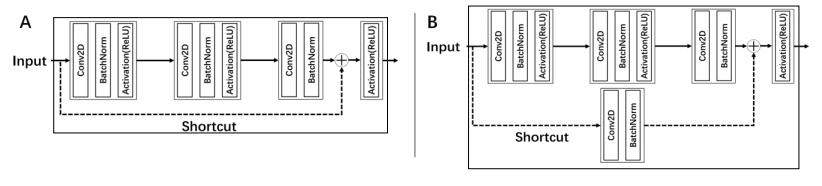
Convolutional neural network has been successfully applied in image recognition tasks and has achieved good performance due to its advantages of extracting local features in the images. With the increasing of convolutional layers, a deeper traditional convolutional neural network may have degradation problem, which causes feature disappear during multiple nonlinear layers. In this paper, we use residual convolutional network to solve degradation problem. ResNet adds a shortcut branch in the forward propagation to build two kinds of residual blocks: identity block and convolutional block, which are to fix the gradient disappearance and accuracy decline. Figure 2 shows that shortcut branch combines the input and the output of multiple convolution.

Figure 2.  Identity block (A): represents the main path of network propagation, and the shortcut which skips three layers. Convolutional block (B): add convolution (Con2D) and normalization layer (BatchNorm) to the shortcut based on identity block. Both of them have convolution with activation function of rectified linear unit (ReLU) in each layer of block.

DownLoad: Full-Size Img PowerPoint

The network is divided into five different stages: Stage 1 is a standard convolution; Stage 2 is one convolutional block followed by two identity blocks; Stage 3 is one convolutional block followed by three identity blocks; Stage 4 is one convolutional block followed by five identity blocks; Stage 5 is the same as Stage 2. Eventually, fully connected layer with a unit acts as output layer. In the following we consider a ResNet-50 as basic building block of ABRN due to the advantages of autonomous feature extraction and prediction.

3.2.   Attention based residual network

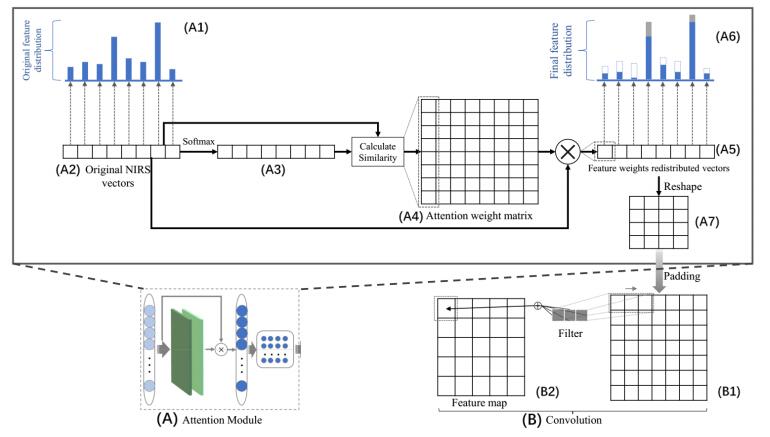
There are many irrelevant wave bands and noise wave bands in the original spectral data, which would interfere with feature extraction and decline prediction accuracy. A small number of effective feature wave bands are unevenly distributed in the original high-dimensional spectral vector. To solve this problem, we add an attention module before the basic residual network, which is showed in Figure 3, to be an automatic preprocessing of feature weights redistribution.

Figure 3.  Attention module in ABRN. (A) shows the architecture of attention module: A1 and A6 are the feature distribution before and after attention module; A3 is the result of original NIRS vectors A1 processed by softmax; A4 is the attention weight matrix calculated by A2 and A3; A5 is calculated by matrix multiplication of A4 and A2. A7 is to adapt the input format by reshaping A5 to a matrix. (B) is an example of convolution: B1 keeps the original dimension by padding and B2 is feature map after convolution.

DownLoad: Full-Size Img PowerPoint

We will take one single sample as an example to introduce the principle of the proposed attention module in ABRN. We define the feature weights (ω_atn) in attention module and original long sequence spectral input vector (X_SD) as

where ω_atn is a square matrix and the size of which is consistent with the dimension of the input vector, showed in Figure 3 (A4). n is the dimension of one sample and num is the number of samples.

Attention module can enhance the feature wave bands and weaken the noise wave bands in the original spectral vector to increase the accuracy of the model, and attention module is defined as:

where iϵn and ${X_{SD}^i}$ is the ith dimension of single original spectral sample's vector. We use softmax function on ${X_{SD}^i}$ to get ${y_{atn}^i}$. ${y_{atn}^i}$ interacts with ${X_{atn}^i}$ via dot product to calculate the similarity by Eq (4). $\omega _{atn}^i$ is a n×n matrix, where each row represents a vector corresponding to each dimension of X_SD, and the size n is consistent with the dimension of single sample X_SD. Finally, we calculate the feature weights redistributed vectors C_atn corresponding to each dimension of X_SD as follows:

where $C_{atn}^j$ is the jth dimension of vector after weights redistributed and iϵn.

We apply the feature enhancement spectral vector as the new input of ResNet. The new spectral vector via attention module's autonomous processing can reduce the impact of noise, optimize the extraction of feature wave bands and improve the prediction accuracy. Experiments in section 4 shows the validity of ABRN.

After automatic preprocessing of attention module, we input the new spectral vectors to ResNet to extract the feature wave bands autonomously. In each convolution layer showed in Fig 3 (B), we apply moving convolutional operation by multiple convolutional kernel to obtain feature maps. Each map represents a feature in original spectral vectors. In order to adapt to the original samples' property of a one-dimensional vector, we modify the size of convolutional kernel to 1×3 with stride 1. The kernel scans each dimension of the vector X_i and convolution is defined as

where W₁, W₂, W₃ are the weights of kernel. After convolutional operation, we will obtain the feature map y_i in which the feature wave band represented by the kernel is highlighted. The weights of kernel are initialized randomly.

We use Root Mean Squared Error (RMSE) as loss function of ABRN to find feature weights for each convolutional kernel through iterations, which is defined as

where y_pre is predicted value and y_label is actual value. num is the number of samples.

4.   Experiments

4.1.   Design

In this section, we experiment with our proposed ABRN for predicting the active ingredient content in Antrodia Camphorata and Matsutake NIRS datasets, and compare the result with current popular NIRS analysis methods.

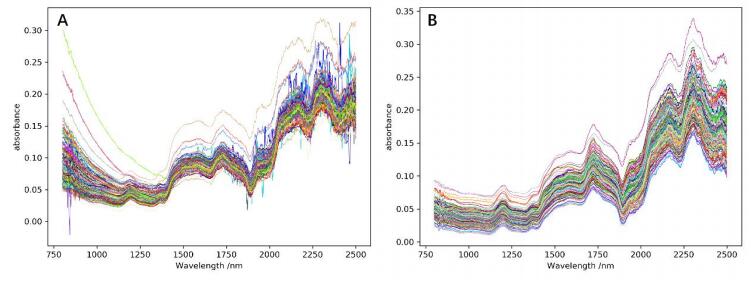
We collect 165 Antrodia Camphorata samples and 200 Matsutake samples as our experiment datasets. The samples are processed by fermentation, centrifugation, freezing, filtration to obtain the final powder as an experimental sample. The spectral data of Antrodia Camphorata and Matsutake are obtained by scanning the NIRS of samples with Shimadzu UV-3150 UV-visible near infrared spectrophotometer and Japanese Shimadzu ISR-3100 integrating sphere accessory. The range of spectrophotometer is from 800 nm to 2500 nm. The scanned interval is 1 nm and the entrance slit width is 12 nm. We use barium sulfate product as a blank reference. Each sample is subjected to 3 spectral scans, and we take the average spectral data as datasets. The NIRS of Antrodia Camphorata and Matsutake are shown in Figure 4. Different color curves in Figure 4 (A) and (B) represent different samples and the absorbance in Figure 4 reflects that different substances in samples have different reflection for the near infrared. Active ingredients in Antrodia Camphorata and Matsutake are determined by invasive analysis using chemical reagents.

Figure 4.  (A):165 Antrodia Camphorata samples NIRS; (B):200 Matsutake samples NIRS.

DownLoad: Full-Size Img PowerPoint

In our experiments, 155 samples were selected randomly for model training to predict the content of polysaccharide and triterpenoid in Antrodia Camphorata, and the rest 10 samples were served as validation set. Meanwhile, 185 samples were selected randomly for model training to predict the content of polysaccharide and ergosterol in Matsutake, and the rest 15 samples were validation set. Due to uneven distribution of input data, we also normalized them before input into the model by subtracting the mean of input vectors and dividing by the variance to make the data conform to the standard normal distribution.

Adam algorithm ^[36] has faster learning rate and convergence rate than stochastic gradient descent, so we adopted it to optimize our ABRN. In the experiments, hyperparameters were set as follows: we set learning_rate = 0.001, beta_1 = 0.9, beta_2 = 0.999, epsilon = 1e-08, batch_size = 10. Due to the small number of samples, we added regularization layers and dropout mechanism to overcome over-fitting problem during the model training. Finally, we evaluate the performance of ABRN by calculating the coefficient of determination (R²) between the predicted value and the actual value, which is defined as follows:

4.2.   Results and analysis

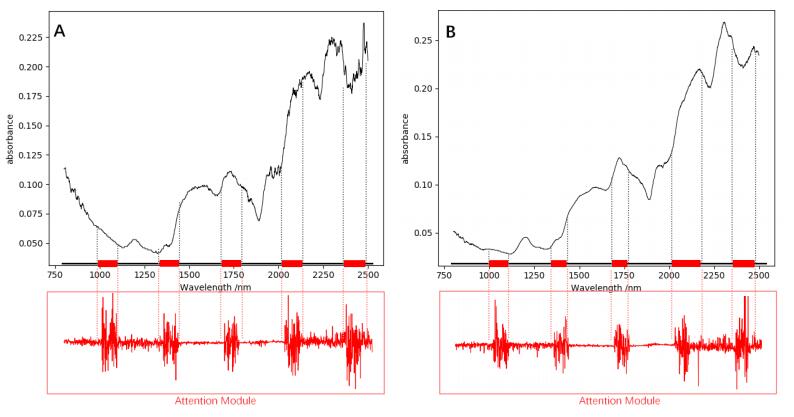
In our experiments, we evaluate the performance of ABRN by analyzing original NIRS vectors without preprocessing of artificial feature wave bands selection. We take polysaccharide from Antrodia Camphorate and ergosterol from Matsutake as examples to present the intermediate results of attention module in ABRN shown in Figure 5.

Figure 5.  The black curves in (A) and (B) represent original NIRS of one Antrodia Camphorate sample and one Matsutake sample. The red regions in (A) and (B) represent feature wave bands selected by attention module in ABRN.

DownLoad: Full-Size Img PowerPoint

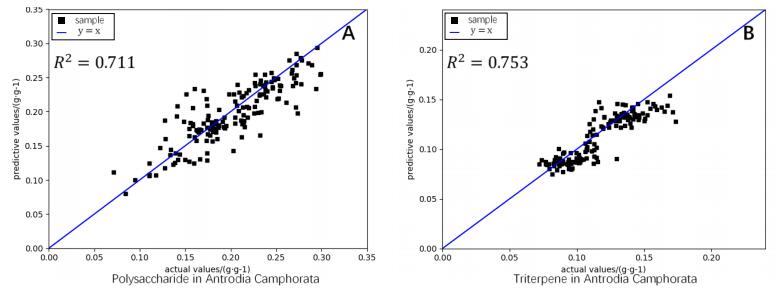
The we predict the content of various active ingredients in 165 Antrodia Camphorata samples and 200 Matsutake samples. Each group of experiments was repeated 10 times. The ABRN results of polysaccharide and triterpene in Antrodia Camphorata are shown in Figure 6. Meanwhile, the ABRN results of polysaccharide and ergosterol in Matsutake are shown in Figure 7 and Figure 8.

Figure 6.  (A) and (B) are fitting between actual values and predictive values of ABRN in predicting the content of polysaccharide and triterpenoid in Antrodia Camphorata.

DownLoad: Full-Size Img PowerPoint

Figure 7.  Fitting results of PLS, RBFNN, ResNet and ABRN in predicting polysaccharide content in Matsutake, where the horizontal axis indicates actual values and the vertical axis indicates predictive values.

DownLoad: Full-Size Img PowerPoint

Figure 8.  Fitting results of PLS, RBFNN, ResNet and ABRN in predicting ergosterol content in Matsutake, where the horizontal axis indicates actual values and the vertical axis indicates predictive values.

DownLoad: Full-Size Img PowerPoint

Figure 6 shows the fitting results with actual values and predictive values using ABRN. It can be seen from A and B in Figure 6 that points are close to the blue line indicates ABRN has a high accuracy in predicting the content of active ingredients in Antrodia Camphorata samples.

Comparative experiments

We also compared ABRN with multiple linear regression with successive projections algorithm (SPA-MLR) ^[37], PLS ^[8], RBFNN ^[17], residual network (ResNet) ^[35] in analyzing original NIRS vectors. RMSET indicates the root mean square errors of training set and RMSEV indicates the root mean square errors of validation set. Table 1 shows the comparative results.

Table 1.  Results of predicting active ingredients of Antrodia Camphorata and Matsutake by different NIRS methods.

Method	Evaluation Metrics	Antrodia Camphorata		Matsutake
		Polysaccharide	Triterpene	Polysaccharide	Ergosterol
SPA-MLR	RMSET/(g∙g-1)	0.0571	0.0424	0.4047	0.0716
	RMSEV/(g∙g-1)	0.1129	0.0383	0.4151	0.0948
	$R_{total}^2$	0.419	0.433	0.325	0.373
PLS	RMSET/(g∙g-1)	0.0537	0.0404	0.3164	0.0672
	RMSEV/(g∙g-1)	0.0439	0.0329	0.2816	0.0929
	$R_{total}^2$	0.585	0.484	0.576	0.407
RBFNN	RMSET/(g∙g-1)	0.0233	0.0166	0.2231	0.0437
	RMSEV/(g∙g-1)	0.0453	0.0261	0.3790	0.0586
	$R_{total}^2$	0.569	0.575	0.551	0.469
ResNet	RMSET/(g∙g-1)	0.0272	0.0202	0.1548	0.0345
	RMSEV/(g∙g-1)	0.0441	0.0338	0.2341	0.0510
	$R_{total}^2$	0.696	0.724	0.723	0.550
ABRN	RMSET/(g∙g-1)	0.0229	0.0173	0.1343	0.0328
	RMSEV/(g∙g-1)	0.0349	0.0189	0.2472	0.0445
	$R_{total}^2$	0.711	0.753	0.847	0.807

---

 | Show Table

DownLoad: CSV

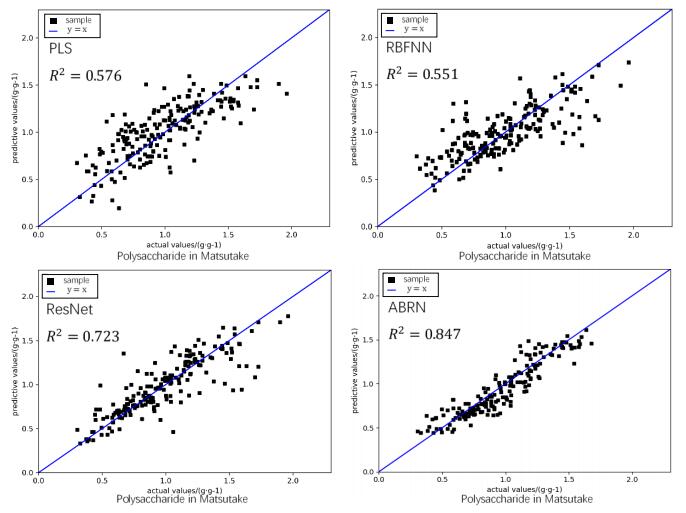
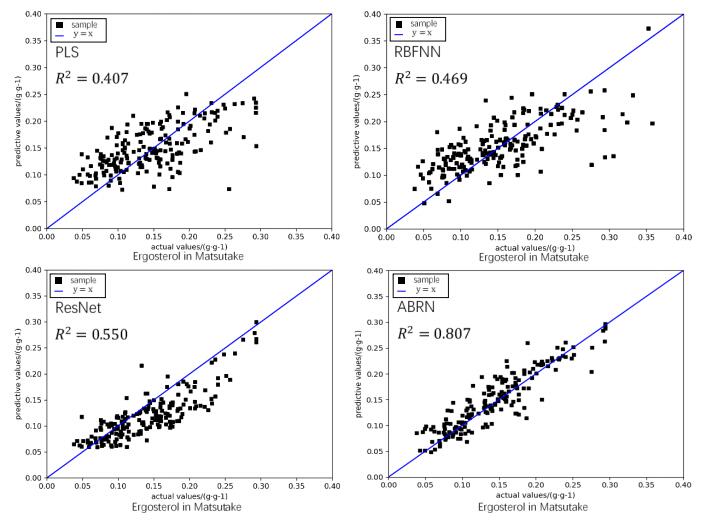
In the comparative experiments, SPA-MLR uses successive projections algorithm as a preprocessing method, PLS uses principal component analysis as a preprocessing method and RBFNN use sliding window as preprocessing on original NIRS vectors to select feature wave bands. We can find in Table 1 that SPA-MLR, PLS and RBFNN both have higher RMSE and lower fitting than deep learning methods (ResNet and ABRN). As for deep learning methods, we compare ResNet with the proposed ABRN, both of them directly input the original spectral data instead of any artificial selected features, and achieve autonomous feature extraction. Unlike ResNet, we adopt attention module in ABRN to enhance feature wave bands and reduce noise wave bands. The results show that ABRN has the lowest RMSE in both training sets and validation sets. ABRN also has the best fitting: for Antrodia Camphorata, the coefficient of fitting between predictive values and actual values in predicting polysaccharide R² = 0.711 and in predicting triterpene R² = 0.753; for Matsutake, the coefficient of fitting between predictive values and actual values in predicting polysaccharide R² = 0.847 and in predicting ergosterol R² = 0.807. ABRN shows the best performance among the four methods.

Furthermore, we take PLS, RBFNN, ResNet and ABRN as examples to plot the fitting points of predictive values and actual values which is shown in Figure 7 and Figure 8. Due to the poor fitting result of SPA-MLR, we do not show SPA-MLR figure in this manuscript. The prediction of polysaccharide and ergosterol content in Matsutake is taken as examples to visually show the fitting results of these 4 different methods.

From Figure 7, we can find that ResNet and ABRN both have more points close to the blue line compared with PLS and RBFNN in predicting polysaccharide in Matsutake. Furthermore, ABRN shows a better fitting result than ResNet.

In predicting ergosterol content in Matsutake, PLS, RBFNN and ResNet all have lower fitting results. As for ResNet, though the most points are pretty concentrated, some of them are still deviate from the blue line. In fitting Figure 8 of ABRN, most of the points concentrate near the blue line which means that it has better fitting.

In all groups of experiments, ABRN shows the best RMSE and R² among four methods. It is because that compared with SPA-MLR, PLS and RBFNN which use preprocessing of common artificial feature wave bands selection, deep learning methods (ResNet and ABRN) can autonomously extract feature wave bands based on the characteristics of data itself in multiple iterations. The advantage is to avoid the loss of some tiny feature peaks in original spectral data. Meanwhile, the attention module we added in ABRN can reduce the influence of noise bands and increase the weights of feature wave bands, which can further improve the accuracy of feature wave bands extraction in the convolution. Therefore, the proposed ABRN has an outstanding and distinct advantage in medicinal fungi active ingredients NIRS analysis.

5.   Conclusion

In this paper, we propose a NIRS of medicinal fungi analysis method, ABRN, which is based on ResNet. Compared with traditional NIRS analysis methods such as SPA-MLR, PLS and RBFNN, ABRN does not rely on experts' experience for artificial feature wave bands selection. ABRN can directly use original NIRS vectors and autonomously extract feature wave bands from original NIRS vectors in multiple iterations, which can decrease the loss of tiny feature peaks. We add attention module in ABRN to do an automatic preprocessing of feature wave bands enhancement and noise wave bands decrement. We make comparative experiments in predicting the polysaccharide and triterpenoid content in Antrodia Camphorata and the polysaccharide and ergosterol content in Matsutake. The results show that ABRN has better fitting results (R² and RMSE) than PLS, RBFNN and ResNet.

Acknowledgments

This work is supported by the National Natural Science Foundation of China (Grant Nos. 61702214, 61772227). This work is also supported in part by Jilin Provincial Key Laboratory of Big Data Intelligent Computing (20180622002JC), Development Project of Jilin Province of China (20170101006JC, 20170203002GX, 20190201293JC), Premier‐Discipline Enhancement Scheme supported by Zhuhai Government, Premier Key‐Discipline Enhancement Scheme supported Guangdong Government Funds.

Conflict of interest

All authors declare there is no conflict of interest.