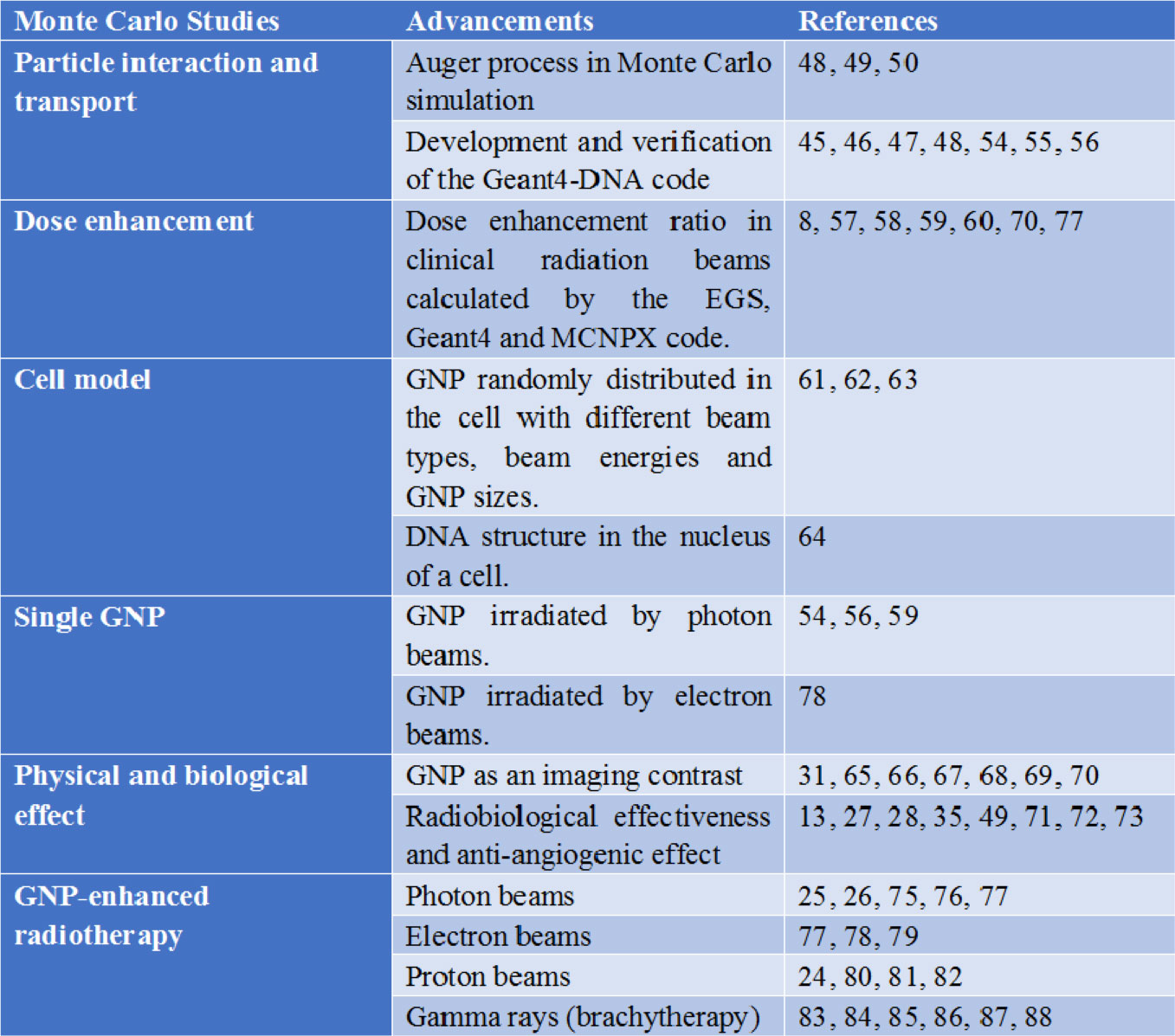
Gold nanoparticles (GNPs) are proven effective heavy-atom radiosensitizers to produce imaging contrast and dose enhancement in radiotherapy. To understand the physical and biological effect of adding GNPs to the tumour cells, Monte Carlo simulation based on particle tracking and transport, is employed to predict the dosimetry in the cellular and DNA scale. In this review, we first explore the recent advances in Monte Carlo simulation on GNP radiosensitisation. The development of particle tracking algorithm for very low energy electron in the simulation is discussed, followed by some results regarding the prediction of dose enhancement (microscopic and macroscopic). We then review different Monte Carlo cell models with GNPs in the simulation, the biological effect resulting from DNA damage, and the effects of increasing imaging contrast in the tumour cell due to photoelectric enhancement. Moreover, we explain and look at different studies and results on GNP-enhanced radiotherapy using gamma rays (brachytherapy), megavoltage photon, kilovoltage photon, electron and proton beams.
1.
Introduction
In this paper, a fundamental problem such as how to optimize currency portfolios over time will be considered under a given sequence of the foreign exchange rate matrices. An intrinsic robust approach is proposed for currency portfolio optimization, which is based on the rank one approximation to foreign exchange rates. Usually, the term foreign exchange, abbreviated as forex, expresses the exchange of one currency for another. A foreign exchange rate, also known as a forex rate or exchange rate, is the price of a nation's currency in terms of another currency. Hence, the forex rate matrices over time often describe the time-varying states of the currency market. In addition, the currency market is a decentralized market for the trading of currencies in the business world and possesses the characteristics of big data such as 3Vs(volume, variety and velocity). According to a report of Global Financial Centres Index (GFCI) published in March, 2016, there are 86 main financial centres around the world, whose profiles, rating and rankings are included in the index report together with 16 `associate centres' receiving sufficient assessments (Yeandle, 2016). All participants around the world are able to buy, sell, exchange or speculate different currencies in the currency market in order to make a profit from various investments and maximize their wealth within a controllable risk. For example, an institution having a pre-existing exposure to foreign currencies usually seeks to limit the risk from adverse movements in exchange rates (i.e., foreign exchange hedging) and attempts to profit from tactical foreign exchange views (i.e., foreign exchange speculating). The currency overlay is a typical financial trading strategy conducted by specialist firms who manage the currency exposures of institutions such as pension funds, endowments and corporate equities (Record, 2014). The strategy can be used in international investment portfolios to separate the management of currency risk from the asset allocation and security selection decisions of investors.
A portfolio often refers to a grouping of financial assets, including stocks, bonds and cash equivalents, as well as their fund counterparts. All currencies in an exchange trade can be considered as a currency portfolio. Because every asset class such as equities, fixed-incomes, real estates, real options, futures etc. could be essentially valued by the amount of a certain currency dependent of a medium of exchange used in the market, a currency portfolio is one of basic forms of wealth that an entity owns. Harry M. Markowitz was a pioneer who studied the portfolio selection problem and published a seminal paper about it (Markowitz, 1952). He also discussed the normative portfolio analysis (i.e., mean-variance portfolio analysis) up to 1990 (Markowitz, 1990). The normative portfolio analysis usually describes a norm of behavior that investors should pursue in construction of a portfolio rather than a prediction concerning actual behavior. In the money market, the currency portfolio optimization is a typical variant of portfolio managements. Note that the approaches for portfolio selection and asset pricing provide the building blocks for portfolio optimizations. Various approaches for asset pricing can be found in the related references (Fabozzi, 2009; Pennacchi, 2008).
In the field of portfolio management, the traditional portfolios usually are priced by the same currency. In contrast, when assets in different countries or economic zones are priced by different currencies, it is an important but open problem how to objectively measure the real value of an asset portfolio. No matter which one of real currencies is chosen as a yardstick in the financial market, it is a subjective setting related to people's behavior. Even though a currency portfolio is evaluated by putting different weight on different currencies according to the corresponding exchange rates, it is essentially a more subjective judgement than an objective measurement. It is preferred that an objective measurement of the value of a currency portfolio is dependent on the whole foreign exchange rates instead of a small set of pairwise forex ones. The virtual standard currency is proposed so that a corresponding measurement is independent of the choice of a specific currency and the exchange operations on real currencies for buying or selling (Huang, 2016).
Based on the virtual standard currency and rank one approximation to approximate forex rate matrices, an intrinsic robust approach will be explored in this paper to optimize currency portfolios over time. Note that the rank one approximation has been used to study such a well-known combinatorial optimization problem as the maximum-edge biclique problem (i.e., finding large complete subetaaphs in bipartite graphs), which has many applications in web community discovery, biological data analysis, text mining and linear dimensionality reduction (Gillis, 2011, 2014). In general, the rank one approximation of a nonnegative matrix is a special data analysis technique closely related to nonnegative matrix factorization (NMF), i.e., to approximate a matrix with a product of two nonnegative factors. The relevant properties or applications about nonnegative matrix can be found in References (Bapat, 1997; Naik, 2016). In the literature involving nonnegative matrix factorization and approximation, the Frobenius norm (i.e., the summation of the squares of available errors) is widely used, which induces an optimization problem as follows
where $A$ is $m\times n$ (nonnegative) real matrix and a factorization rank index $k$ satisfying that $1\leq k\leq \min\{m, n\}$. For recommender systems with the implicit and explicit ratings, several bounded matrix low rank approximation algorithms were studied, where the elements of approximation matrices are bounded and the Frobenius norm is adopted for measuring the residual matrix $A-PQ$ (Kannan, 2016). For the computation of nonnegative matrix factorization, multiplicative algorithms and their updates were also proposed together with global convergence analysis (Lee, 2001; Takahashi, 2014). It should also be noted that the exact nonnegative matrix factorization is NP-hard, which leads to a problem for finding an optimal solution to (1) with the minimum zero (Vavasis, 2009).
To the best of our knowledge, there does not exist any significant factors in the forex rate matrix approximation, and let alone the related application to the currency portfolio optimization. In fact, any variant of matrix low rank approximations depends on properties of elements in the matrix $A$, the constraints on the factors and the measure for the difference between the matrix $A$ and $PQ$. This paper is mainly concerned with an intrinsic robust approach for optimizing the currency portfolios over time. It could decrease the gap between the theory and algorithms of nonnegative matrix factorization for the analysis of forex rate matrices and the currency portfolio optimization. The remaining parts of the paper are arranged as follows: Firstly, a basic model for the currency portfolio optimization problem is formulated in Section 2, which includes two kinds of variables for describing currency amounts in portfolios and the amount of one currency exchanged for another. Then, the intrinsic robust property of the rank one approximation problem is explored in Section 3, which induces an objective measurement of the value of wealth in a currency portfolio and a technique of variables reduction for currency portfolio optimization. Some properties and the modified power method about the rank one approximation problem are summarized together with the existence of the virtual exchange rates hidden in the currency market. Thirdly, two variants for variables reduction are presented for attacking the currency portfolio optimization in Section 4. One is to solve the ROA model that is based on rank one approximations. The other is to generate a feasible solution to the basic model by coupling a solution to the ROA model with practical forex rates. In Section 5, in order to verify the feasibility and efficiency of the intrinsic robust rank one approximation approach, practical examples are presented for approximating forex rate matrices and optimizing currency portfolios over time. Finally, conclusions are given in the last section.
2.
The currency portfolio optimization problem
In this section, a basic model for the currency portfolio optimization problem will be formulated under several assumptions about the currency market, where there are two types of variables describing the amount of various currencies in a portfolio and the amount of every currency exchanged for others.
2.1. Assumptions and notations
The first assumption for the currency portfolio optimization is that every real currency in a portfolio can be freely exchanged into others in the currency market at any stage. For example, currencies in the basket of the Special Drawing Right (SDR) can be exchanged mutually and freely in the international monetary market (International Monetory Fund, 2016). Without loss of generality, suppose that there are $n$ currencies exchanged mutually and freely in the currency market and denoted by the set $M = \{1, 2, \cdots, n\}$.
Another assumption is that the financial market is perfect without transaction costs for currency exchanges except for the difference between the bid and ask prices of a foreign currency. A foreign exchange rate usually has two currency components such as a base currency and a counter currency. Either a "domestic" currency $D$ or a foreign currency $F$ can act as a base currency or a counter currency. The direct quotation of the forex rate $F/D$ between $F$ and $D$ is expressed by $F $ 1 = D$ \lambda $, where $\lambda$ is the bid price of one unit of the currency $F$ in terms of $D$. In the mean time, the ask price of one unit of currency $F$, denoted by $F $ 1 = D$ (\lambda+\delta)$, usually is greater than its bid price, where $\delta>0$. It corresponds to the indirect quotation of the forex rate $F/D$ given by $D$ 1 = F$ \frac{1}{\lambda+\delta}$.
The third assumption is that the forex rates are known or could be forecasted or hedged in a certain forward period. The certainty assumption is presented in order to explore the essential properties associated with the currency portfolio optimization. In addition, by simplicity any interest rate is not considered for any currency during the maximization of currency portfolios. The uncertainty of the foreign exchange rates and the impacts of the interest rates may be analyzed in the future research.
Suppose all forex exchange rates over time are grouped by a sequence of matrices $A^k, k = 1, 2, \cdots, N$, where $k$ is the index of time periods, $N$ is the number of time periods and the element $a_{ij}^k$ in the matrix $A^k$ is the bid price of a unit of the currency $i$ in terms of the currency $j$, i.e., the direct quotation of the forex exchange rate $i/j$. Note that it can be proved that the ask price of the currency $i$ is equal to $1/a_{ji}^k$. At the period $k$, let us denote the initial currency portfolio by $x^{k-1}$. At the end of the same period, $x^{k-1}$ is transformed into another currency portfolio $x^k$. Furthermore, let the decision variable $y_{ij}^k$ denote the amount of the currency $i$ exchanged into the currency $j$ during the period $k$, where $i, j = 1, 2, \cdots, n$, $k = 1, 2, \cdots, N$.
2.2. The basic model for the currency portfolio optimization
Assume that an investor's goal is to maximize the amount of a particular currency $m\in \{1, 2, \cdots, n\}$ over $N$ periods. That is, the objective function in the currency portfolio optimization problem is defined by $x_m^N$, an element of the currency portfolio $x^N$ at the end of period $N$. In addition, the relationship among the decision variables $y_{ij}^k$, currency portfolios $x^{k-1}$ and $x^{k}$ is expressed by the following constraints:
where $k = 1, 2, \cdots, N$. Hence, the basic model for the currency portfolio maximization can be formulated by the following optimization problem
where the vector $e = (1, 1, \cdots, 1)^T\in \Re^n$, $x^0$ is an initial currency portfolio, $A^k = (a_{ij}^k)\in \Re^{n\times n}_{++}$ is a forex rate matrix (i.e., cross currency rate matrix) at the period $k$, $Y^k = (y^k_{ij})\in \Re^{n\times n}_+$ is a decision matrix where any component corresponds to the amount of a currency exchanged into another at the period $k$, $x^k$ describes a currency portfolio at the period $k$, and the operator $\circ$ indicates the Hadamard product of two matrices. Note that the Hadamard product $A^k\circ Y^k$ of two matrices $A^k$ and $Y^k$ is also known as the Schur product or the entrywise product, that is, $\left(A^k\circ Y^k\right)_{ij} = a_{ij}^ky_{ij}^k$ for all $i, j = 1, 2, \cdots, n$, $k = 1, 2, \cdots, N$.
In the basic model (4)$\sim$(7), there are $nN$ decision variables $x_i^k$, and $n^2N$ decision variables $y_{ij}^k$ together with $2nN$ linear equality constraints. If the high frequency data about forex rates are used for the currency portfolio optimization, then the number of the time periods $N$ will be so huge that there is a large requirements for the memory space and computer time. This motivates the needs of variables reduction for the basic model (4)$\sim$(7). In addition, the objective function in the basic model is easy to understand, but it seems to be lack of generality. For instance, one may argue that a fixed allocation of the final currency portfolio could be more appealing, while the current setting is a special case. In fact, there exists a generality (next subsection) in the basic model for the currency portfolio optimization.
2.3. The generality implied in the basic model
Suppose that the wealth at the beginning of the final period $N$ is denoted by $W^{N-1}$ and the amount of currency $i$ has a proportion $y_i\in [0, 1]$ of such a wealth. Without loss of generality, suppose that the amount of currency $i$ is equal to $y_iW^{N-1}_i$, where $W^{N-1}_i$ represents the amount of wealth $W^{N-1}$ in terms of the currency $i$. Note that the amount $W^{N-1}_i$ still needs to be maximized such as the maximization of $W^{N-1}$(This also indicates that an objective measure of the wealth is useful in similar cases). By these notations, the objective function in the basic model (4)$\sim$(7) is equivalent to a function as follows
where $a_{im}^N$ is a component in the forex matrix $A^N$, associated with the final period $N$. On the one hand, the basic model (4)$\sim$(7) is equivalent to the following optimization problem
where $x^{N-1}_i$, $i = 1, 2, \cdots, n$, satisfy the constraints (5)$\sim$(7). On the other hand, under the assumption of a given representation of the wealth $W^{N-1}$ such as $(W^{N-1}_1, W^{N-1}_2, \cdots, W^{N-1}_n)$, the inner optimization problem withe respect to variable $y_i$ ($i = 1, 2, \cdots, n$) has an optimal solution $y^*_{i_{N-1}} = 1$, $y^*_{j} = 0$($j\not = i_{N-1}$), where
The theoretical explanation is similar to the result in Lemma 4.1 below. Since $A^N$ is given in advance, the maximization of $x_m^N$ in the basic model is related to the similar problems associated with $x_i^{N-1}$, $i = 1, 2, \cdots, n$. Furthermore, the maximization of a portfolio of currencies such as $x^N = (x_1^N, x_2^N, \cdots, x_n^N)^T$ with weights $c = (c_1, c_2, \cdots, c_n)^T$ can be replaced by maximizing an equivalent function as follows:
where $y_i\geq 0, \sum_iy_i = 1$. It is also related to optimization problems associated with $W^{N-1}_i = x_i^{N-1}$, $i = 1, 2, \cdots, n$, which are similar to the basic model (4)$\sim$(7). Therefore, the basic model as a special case also implies a general approach to the currency portfolio optimization.
In order to objectively measure and optimize the wealth such as $W^{N-1}$(i.e., independent of any real currency), the approach of rank one approximations is proposed to approximate the time series of forex rates and deal with the currency portfolio optimization. Suppose that foreign exchange rates are fixed temporarily (for example, the cross section of the forex rate processes at a particular time) and grouped by a forex rate matrix $A = (a_{ij})$, where $a_{ij}$ is the price of one unit of the currency $i$ in terms of the currency $j$. The rank one approximation to the matrix $A$ plays a fundamental role for developing an approach to reduce the number of decision variables and attack the currency portfolio optimization problem.
Next we will formulate the rank one approximation (ROA) problem and prove its intrinsic robustness to approximate a forex rate matrix. The ROA approach is also related to an objective measurement of wealth in a currency portfolio during the process of optimization over time. Although the ROA approach is not sufficient for solving the basic model (4)$\sim$(7), it is helpful to explore the invariant structure associated with the model. On the one hand, the ROA approach will induce an excellent feasible solution to the basic model (4)$\sim$(7); on the other hand, it also explores a wonderful structure in the sequence of optimal strategies for attacking it. Actually, the currency portfolio optimization is independent of the specified currency $m$ in the objective function.
3.
The rank one approximation problem and its properties
An intrinsic robust approach for variables reduction is based on the rank one approximations to forex rate matrices. In this section, we will formulate two variants of the rank one approximation problem whose objective function is defined by the Frobenius norm or the $2$-norm of the residual matrix. The intrinsic robustness of the rank one approximation is proved by the method of robust optimization. In addition, some properties of the rank one approximation problem are summarized together with a modified power method for solving the ROA problem, which aims at searching for the largest singular value of a forex rate matrix and its corresponding singular eigenvectors. An optimal solution to the basic ROA problem induces an objective measurement of the value of wealth in a currency portfolio.
3.1. The rank one approximation problem and its variants
In order to evaluate the value of a currency portfolio $c\in \Re^n_+$, where $c_i$ denotes the amount of the currency $i$, it is supposed to choose a particular currency, for example, the currency $j$ as a yardstick. If the exchange rates of all currencies to the currency $j$ in a forex rate matrix $A$ is described by the $j$-th column vector, denoted by $A^j = (a_{1j}, a_{2j}, \cdots, a_{nj})^T$, $j = 1, 2, \cdots, n$, then the corresponding value of the currency portfolio $c$ is given by $(A^j)^Tc$. In general, the exchange process of two currencies for any market maker usually involves two different operations such as bank buying or bank selling, which corresponds to the bid and ask price of a currency, respectively. In particular, there is a gap between the bid and ask prices of the currency $i$ against $j$. Therefore, the element $a_{ij}$ is often less than ${1}/{a_{ji}}$.
For each real currency $i\in M$, $i = 1, 2, \cdots, n$, let us introduce a virtual variable $u_i$, which acts as a virtual exchange rate from the currency $i$ to a virtual currency, and denote the value of a currency portfolio $c$ by $c^Tu = \sum_{i = 1}^nc_iu_i$. Furthermore, if another variable $v_i$($i = 1, 2, \cdots, n$) is introduced to denote a virtual exchange rate from the virtual currency to the currency $i$, then any element $a_{ij}$ in the matrix $A$ could be approximated by the product of two virtual exchange rates $u_i$ and $v_j$ ($i, j = 1, 2, \cdots, n$). In such a case, the matrix $A$ could be approximated by a rank one matrix $uv^T$ consisting of two vectors $u = (u_1, \cdots, u_n)^T$ and $v = (v_1, \cdots, v_n)^T$. Therefore, the approximation to the forex rate matrix $A$ can be formulated as the following optimization problem
where $u$ and $v$ are decision variables, $\|\cdot\|$ denotes the Frobenius norm or the $2$-norm in $\Re^{n\times n}$, and $\Re^n_{++} = \{x\in \Re^n \mid x = (x_1, x_2, \cdots, x_n)^T, x_i>0, i = 1, 2, \cdots, n\}$ is the set of all positive vectors in the $n$-dimensional Euclidean space. Since the problem (14) uses a rank one matrix to approximate a positive matrix $A$, it is referred to as a basic rank one approximation(BROA) problem. Note that the virtual exchange rates are related to the concept of the virtual standard currency (VSC), which has been analyzed in details in Reference (Huang, 2016).
Another variant of the rank one approximation assumes that the virtual bid price of a real currency against the VSC is less than or equal to its virtual ask price, that is,
Thus, a constrained rank one approximation(CROA) problem is formulated as follows
It is obvious that the BROA problem (14) is a relaxation of the CROA problem (16). For simplicity, each of them may be called by the rank one approximation(ROA) problem if it does not cause any misunderstanding.
Since the inequality (15) is concerned with forex rates in terms of the VSC, this unique feature distinctly separates our research from existing researches involving the rank one approximations. In addition, this paper does not directly design an optimal algorithm for solving two variants of the ROA problem, (14) and (16). Instead, we analyze the properties of their optimal solutions and design an alternative algorithm to search for them.
3.2. The robustness of the rank one approximation
The idea of robustness in the field of optimization has been introduced to deal with the issues on sensitivity analysis for the least squares problem (EI Ghaoui, 1997). It focuses on finding a solution to the related optimization problem in spite of the uncertainty of parameters. Usually the parameters are uncertain but fall in a bounded region. It will be shown that the formulation (14) is a robust rank one approximation to the forex rate matrix $A$. The similar assertion can be concluded for the formulation (16).
Suppose that the forex rate matrix $A$ has an unknown but bounded perturbation $\Delta A$ satisfying
where $\rho$ is a positive real number bounding the norm of the perturbation, and $\|\cdot\|$ denotes the $2$-norm or the Frobenius norm of a matrix. The robust rank one approximation problem is to find two vectors $u$ and $v$ such that the rank one matrix $uv^T$ minimizes the worst-case norm of the residual matrix $(A+\Delta A) -uv^T$. It can be formulated as follows
On one hand, by using the triangle inequality property of the matrix norm (Golub, 1996), the inner objective function in the problem (18) has a upper bound such that
On the other hand, if a special perturbation matrix $\Delta A$ is chosen by
where $\tilde{E}$ is any matrix in $\Re^{n\times n}$ with $\|\tilde{E}\| = 1$, then it satisfies the equality $\|\Delta A\| = \rho$ and corresponds to the above upper bound. Therefore, the maximization value of the inner problem in (18) satisfies
In particular, if we define the parameter $\rho = \|A -uv^T\|$, the robust minimization problem (18) induces a similar rank one approximation problem to (14) as follows
In this case, the bound of the perturbation $\Delta A$ is dependent of both vectors $u$ and $v$. It is obvious that the optimal value of the problem (19) is two times as the square root of the minimum in (14). A similar result can be concluded for the constrained rank one approximation (16). Therefore, both problems (14) and (16) are robust rank one approximations to the forex rate matrix $A$. The intrinsic robustness of the rank one approximation to a forex rate matrix $A$ is summarized in the following proposition.
Proposition 3.1. Given any forex rate matrix $A\in \Re^{n\times n}_{++}$, let the vector $(u^*, v^*)$ be an optimal solution to the problem (14) and denote $\rho^* = \|A -(u^*)(v^*)^T\|$. Then, for any perturbation $\Delta A$ of the matrix $A$ satisfying $\|\Delta A\|\leq \rho^*$, the error arising from approximating the matrix $A+\Delta A$ by the rank one matrix $(u^*)(v^*)^T$ is not greater than 2$\rho^*$.
3.3. Properties of the basic rank one approximation problem
In this subsection, a lemma is firstly presented in the Frobenius norm. Then the properties about optimal solutions to the basic rank one approximation problem are explored for any nonzero matrix $A\in \Re^{n\times n}$ in the Frobenius norm and the $2$-norm, respectively. The uniqueness of the virtual exchange rates is also presented, which is related to the concept of the virtual standard currency and the convergence of the modified power method below.
Lemma 3.1. Given a nonzero diagonal matrix $D = diag(\sigma_1, \sigma_2, \cdots, \sigma_n)\in \Re^{n\times n}$, where $\sigma_1 \geq \sigma_2\geq \cdots\geq \sigma_n\geq 0$, if the basic rank one approximation problem such as
is considered with the Frobenius norm for measuring the performance of a residual matrix, then each solution to the optimization problem (20) satisfies $u_1v_1 = \sigma_1$, $u_i = v_j = 0$ for all $i, j>1$.
Lemma 3.1 and its proof can be found in Reference (Huang, 2016), which is omitted here. It should be noted that two vectors $u^* = (\sqrt{\sigma_1}, 0, \cdots, 0)^T$ and $v^* = (\sqrt{\sigma_1}, 0, \cdots, 0)^T$ satisfy the property $\|u^*\| = \|v^*\|$ and correspond to a special optimal solution $(u^*, v^*)$ to the problem (20) with the optimal value $\| D-u^*(v^*)^T\|_F^2 = \sum_{i = 2}^n\sigma_i^2$.
Based on Lemmas 3.1, the following theorem describes an optimal rank one matrix to approximate a nonzero matrix with the minimum of the Frobenius norm of the residual matrix.
Theorem 3.1. Given a nonzero matrix $A\in \Re^{m\times n}$ with a singular value decomposition such as (63) in Appendix A.1, where the singular values of $A$ satisfy $\sigma_1\geq \sigma_2\geq \cdots\geq \sigma_r>0$, $U = (u^1, \cdots, u^m)\in \Re^{m\times m}$ and $V = (v^1, \cdots, v^n)\in \Re^{n\times n}$ are orthogonal matrices. Then the matrix $A_1 = \sigma_1u^1(v^1)^T$ is the optimal solution to the following rank one approximation problem
whose optimal value is equal to $\|A-A_1\|_F = \left(\sigma_{2}^2+\cdots+\sigma_r^2\right)^{1/2}$.
The proof of Theorem 3.1 is (in supplementary materials available online) in Appendix B.1. A similar result can also be obtained for the rank one approximation involving the $2$-norm of the residual matrices, whose proof is given in Appendix B.2.
Theorem 3.2. Suppose that a nonzero matrix $A\in \Re^{m\times n}$ has a singular value decomposition such as (63) in Appendix A.1, where $U = (u^1, \cdots, u^m)\in \Re^{m\times m}$ and $V = (v^1, \cdots, v^n)\in \Re^{n\times n}$ are orthogonal matrices. Then the matrix $A_1 = \sigma_1u^1(v^1)^T$ is the optimal solution to the following rank one approximation problem
whose optimal value is equal to $\|A-A_1\|_2 = \sigma_{2}$.
Although both Theorem 3.1 and Theorem 3.2 describe an optimal solution to the rank one approximation problems (21) and (22), respectively, the rank one matrix $A_1 = \sigma_1u^1(v^1)^T$ may not be nonnegative or unique for any forex rate matrix $A$. Hence, it is still necessary to explore the properties of the rank one component $A_1$ in the singular value decomposition of a forex rate matrix $A$.
Here, it is sufficient to show that both vectors $u^1$ and $v^1$ in the rank one matrix $A_1 = \sigma_1u^1(v^1)^T$ in Theorem 3.1 and Theorem 3.2 are positive for any forex rate matrix $A$. For simplicity, some properties about positive matrix and its uniqueness of positive eigenvector(except for a scalar multiplier) are summarized in Appendix A.2, which answers such concerns and presents a theoretical background for the existence and uniqueness of a special optimal solution to the basic ROA problem in the measurement of both the Frobenius norm and the $2$-norm.
In fact, the concept of the virtual standard currency (VSC) is related to the virtual exchange rates $u^*$ and $v^*$ in Theorem 3.3, whose definition and properties are discussed in the reference (Huang, 2016). It is also a base for designing the modified power method in the next subsection.
Theorem 3.3. Given a forex rate matrix $A\in \Re^{n\times n}$ with all entries $a_{ij}>0, i, j = 1, 2, \cdots, n$, if two vectors $u^*, v^*\in \Re^n$ satisfy the following conditions:
(C1) $v^*$ is an eigenvector of the matrix $A^TA$ with a positive component, and corresponds to its positive eigenvalue with the greatest modulus;
(C2) The equality $Av^* = \sigma_1 u^*$ holds, where $\sigma_1$ is the largest singular value of the matrix $A$;
(C3) The Euclidean length of the vector $u^*$ is $\sqrt{\sigma_1}$;
then both $u^*$ and $v^*$ are positive vectors such that $u^* = \sqrt{\sigma_1}u^1$ and $v^* = \sqrt{\sigma_1}v^1$, where $\sigma_1$ is the largest singular value of the matrix $A$, both $u^1$ and $v^1$ are positive unit eigenvectors of the matrices $AA^T$ and $A^TA$, respectively, corresponding to the same positive eigenvalue with the greatest modulus $\sigma_1^2$.
For any forex rate matrix $A$, based on its singular value decomposition (64) in Appendix A.1, Lemma A.1 and Theorem 3.3, it is known that two positive unit eigenvectors $u^1$ and $v^1$ are unique and the rank one matrix $A_1$ in Theorem 3.1 and Theorem 3.2 is positive and equal to $u^*(v^*)^T$. Furthermore, according to the properties of $A_1$, the vectors $u^*$ and $v^*$ lead to an optimal rank one approximation to the forex matrix $A$ with the $2$-norm and the Frobenius norm of the residual matrix, respectively. The minimum norm of the residual matrix satisfies
and
It is easy to see that the positive vector $(u^*, v^*)$ in Theorem 3.3 also corresponds to the unique optimal solution to a variant of the basic ROA problem as follows
where $\|\cdot\|$ in the objective function denotes either the $2$-norm or the Frobenius norm.
3.4. The modified power method for the rank one approximation
The power method is one of important iterative algorithms for computing the dominant eigenvalue of a matrix (Golub, 1996). An eigenvector corresponding to the dominant eigenvalue can also be obtained during the iterative process. Since a forex rate matrix $A$ is positive and it corresponds to two positive semidefinite matrices $A^TA$ and $AA^T$, each of them possesses a dominant eigenvalue together with its corresponding positive eigenvector (see Lemma A.1 in Appendix A.2).
By applying the power method to the matrices $A^TA$ and $AA^T$ simultaneously, it will induce an algorithm for computing the optimal rank one approximation to the forex rate matrix $A$, which is referred to as the modified power method. It is not only a powerful tool to compute the largest singular value of any forex rate matrix $A$, but also a practical algorithm to generate the positive vectors $u^*$ and $v^*$ satisfying the following nonlinear systems
where $\sigma_1$ is the largest singular value of $A$. Note that for any forex rate matrix $A\in \Re^{n\times n}_{++}$, Theorem 3.3 ensures that the vector $(u^*, v^*)$ is unique as one of optimal solutions to the basic ROA problem.
The modified power method
Given any nonnegative vector but not zero $x^{0}\in \Re^{n}_{++}$, denote its corresponding nonnegative unit vector by $v^{0} = x^{0}/\|x^{0}\|_2$. The modified power method is designed as follows, which produces two sequences of unit vectors $\{u^{k}\}$ and $\{v^{k}\}$, together with two sequences of positive real numbers $\{\sigma_u^k\}$ and $\{\sigma_v^k\}$:
BEGIN
Initialization:
to input the vector $x^0\geq 0$($x^0\not = 0$),
or the unit vector $v^0 = x^0/\|x^0\|_2$;
For $k = 1, 2, \cdots, $
$y^k = Av^{k-1}$;
$\sigma_u^k = \|y^k\|_2$;
$u^k = y^k/\sigma_u^k$;
$x^k = A^Tu^k$;
$\sigma_v^k = \|x^k\|_2$;
$v^k = x^k/\sigma_v^k$;
END
The proof of the convergence of the modified power method is based on the properties of positive matrices, the singular value decomposition and the power method, etc. According to the iterative scheme of the modified power method, we have
The continuity of $\|\cdot\|_2$ assures that the convergence of the sequence $\{v^k\}$ implies those of $\{u^k\}$, $\{\sigma_u^k\}$ and $\{\sigma_v^k\}$. In addition, the limit of $\{\sigma_u^k\}$ is the same as that of $\{\sigma_v^k\}$ if the sequence $\{v^k\}$ has a limit. The focus on the convergence of the modified power method is reduced to prove that the limit of $\{v^k\}$ is a positive vector. Since the last assertion can be proved from the convergence of the power method, the reader may refer to such a content in Reference (Golub, 1996). Here a property is presented about the convergence of the modified power method for any positive matrix, whose proof can be found in Reference (Huang, 2016).
Theorem 3.4. Given a positive matrix $A\in \Re^{n\times n}_{++}$, i.e., $a_{ij}>0, i, j = 1, 2, \cdots, n$(e.g., a forex rate matrix), if the modified power method is applied to the matrix $A$ such that two sequences of vectors $\{u^{k}\}$ and $\{v^{k}\}$ are generated, together with two sequences of positive real numbers $\{\sigma_u^k\}$ and $\{\sigma_v^k\}$, then the sequence $\{v^{k}\}$ converges to a positive unit vector $\bar{v}$ satisfying the condition (24), where $\sigma_1^2$ is the unique maximal eigenvalue of $A^TA$ in modulus. Similarly, the sequence $\{u^{k}\}$ converges to a positive unit eigenvector $\bar{u}$ of $AA^T$ corresponding to the unique maximal eigenvalue $\sigma_1^2$ of $AA^T$ in modulus.
Furthermore, both sequences of $\{\sigma_u^k\}$ and $\{\sigma_v^k\}$ converge to $\sigma_1$, i.e., the largest singular value of $A$(or $A^T$).
Note that the iterative error for estimating the largest eigenvalue of the matrix $A^TA$ is given by (Golub, 1996)
This indicates that for a sufficient large $k$, the solution to the optimization problem (23) can be estimated by
Hence, the robust rank one approximation to a forex rate matrix $A$ is estimated by
Finally, an updating strategy is presented to numerically solve the constrained ROA problem (16). During the iterative process of the modified power method, for a sufficient large $k$, it also generates sequences of iterative solutions to the constrained ROA problem (16), defined by
where $\sigma_u^k$, $\sigma_v^k$, $u^k$ and $v^k$ are the same as those in Theorem 3.4, and $\delta^k$ is the updating parameter defined by
Therefore, for the constrained rank one approximation problem (16), the forex matrix $A$ is approximated by
which corresponds to the $2$-norm and the Frobenius norm of the residual matrix such as
and
respectively.
4.
The robust ROA approach to currency portfolio optimization
In this section, the robust rank one approximation approach is extended to attack the currency portfolio optimization problem, which can significantly reduce the number of decision variables and attain the exact optimal solution under the assumption of forex rate matrices with the rank one structure. In other cases, it usually induces a better feasible solution to the currency portfolio optimization problem by integrating optimal forex operations of the ROA model with practical forex rate matrices. The intrinsic robustness of the ROA approach ensures its feasibility together with a high performance, which is illustrated by practical examples next section.
4.1. The ROA model for the currency portfolio optimization
Suppose that each cross currency rate matrix $A^k$ at the stage $k$ can be represented (or approximated) by a positive rank one matrix $u^k(v^k)^T$, that is, $a^k_{ij} = \mbox{or $\approx$ } u^k_iv^k_j$, where both $u^k$ and $v^k$ are positive vectors in $\Re^n$ and referred to as virtual exchange rates, $k = 1, 2, \cdots, N$. In this case, the constraint (3), or equivalently (6) in the basic model, is equivalent to (or approximated by)
In the matrix form, we have
where $V^k = diag(v^k)$ is a diagonal matrix with entries $v^k_i, i = 1, 2, \cdots, n$. In the mean time, the constraint (2), or equivalently (5) in the basic model, is equivalent to
Similarly, we get a constraint in a matrix form as follows
where $U^k = diag(u^k)$ is a diagonal matrix with entries $u^k_i, i = 1, 2, \cdots, n$.
Since the objective function $x_m^N$ (i.e., the amount of the currency $m$ at the end of the period $N$) is not directly dependent on any decision variable $y_{ij}^k$ ($k < N$), these variables $y_{ij}^k, i, j = 1, 2, \cdots, n, k = 1, 2, \cdots, N$ can be discarded from the transformed model during searching for an optimal or near-optimal value of $x_m^N$. For example, after performing the inner product between the vector $e$ with all entries $1$ and each vector on both sides of constraints (41) and (42), all decision variables $y_{ij}^k$ will be discarded, which leads to a rank one approximation model (abbreviated by the ROA model) for the currency portfolio optimization problem:
where $x^0$ is the initial currency portfolio and $\Re^n_+ = \{x\in \Re^n\mid x\geq 0\}$ is the nonnegative orthant in the $n$-dimensional Euclidean space. Note that the ROA model involves only $nN$ decision variables $x_i^k$, and $N$ linear equality constraints.
The technique for variables reduction above is based on the robust rank one approximations to the forex rate matrices. The smaller the norm of the residual matrix $\|A^k-(u^k)(v^k)^T\|$ is, the better the matrix $A^k$ is approximated by $(u^k)(v^k)^T, k = 1, 2, \cdots, N$. In particular, for a fixed number of time periods $N$, the total number of decision variables in the basic model (4)$\sim$(7), which is a quadratic function $n(n+1)N$ with respect to the number of currencies $n$, is reduced to a linear function $nN$ in the ROA model (43)$\sim$(45). The reduction of decision variables is very significant for high frequency sequence of forex rate matrices and a large basket of currencies.
4.2. An optimal solution to the ROA model
In this subsection, a theorem will be presented to characterize an optimal solution to the ROA model (43)$\sim$(45). Before analyzing the optimality of the ROA model, we first present Lemma 4.1 about an optimal solution to a special linear programming problem, whose proof is straightforward and omitted here.
Lemma 4.1. Given a nonnegative vector $c\in \Re^n$, let us consider a linear programming problem
where $c\in \Re^{n}_+$, $e = (1, 1, \cdots, 1)^T\in \Re^n$. Then one of its optimal solutions is given by $x^* = e^p$, where $e^p$ is a unit vector in $\Re^{n}$ such that $e_p^p = 1$, $e_i^p = 0, \forall i\not = p$ and
Theorem 4.1. Given a finite sequence of cross currency rate matrices $\{A^k\}$, suppose that there are two sequences of vectors $\{u^k\}$ and $\{v^k\}$ such that the matrix $(u^k)(v^k)^T$ is the robust rank one approximation to $A^k$, $k = 1, 2, \cdots, N$. For the ROA model (43)$\sim$(45), if we introduce a sequence of intermediate variables $\{t_k\}$ by defining
then there exists an optimal sequence of currency portfolios $\{(x^*)^k\}$ to the ROA model that satisfies
where $t^*_1 = (u^1)^Tx^0$,
and $p_N = m$, where the currency $m$ is specially selected in advance to evaluate the wealth in currency portfolios.
Proof. In order to prove the result of this theorem, the mathematical induction will be modified and applied below in an inverse form.
Firstly, by the constraint (44) and the definition (49) for the case of $k = N$, we have an equivalent expression of the objective function (43) in the ROA model as follows
Thus, the maximum of $x_m^N$ will be obtained by maximizing $t_N$ together with setting the variables $x_i^N = 0(i\not = m)$. This is also the optimality of the ROA model involving the variables $x^N$ and $t_N$.
Secondly, suppose that the maximization of $x_{p_k}^k$ is equivalent to the maximization of the variable $t_k$ under the assumption of $x_j^{k} = 0(j\not = p_k)$, we will show that the maximization of $t_k$ is equivalent to maximize $t_{k-1}$ which also accordingly induces the maximization of the variable $x_{p_{k-1}}^{k-1}$ by setting $x_j^{k-1} = 0(j\not = p_{k-1})$.
Based on the constraint (44) and the definition (49) for the case of $k-1\rightarrow k$, we have the following equality
where $k = N, \cdots, 3, 2$. After substituting the variable $x_i^{k-1}$ into the expression $t_k$ defined by (49), we obtain a recursive equality
where
It is obvious from the constraint (44) that the following equality holds
This implies that for a given value of the variable $t_{k-1} $, the maximization of $t_k$ can be formulated as the following linear programming problem
where $c^{k-1}$ and $c_i^{k-1}$ are positive parameters defined above at the stage $k-1$ for $k = N, \cdots, 3, 2$, and $i = 1, 2, \cdots, n$.
According to Lemma 4.1, an optimal solution to the problem (52)$\sim$(54) can be obtained by setting the variable
where $p_{k-1} = arg\min_i c_i^{k-1}$ is the optimal index of the following maximization
and the optimal value $t_k = u_{p_{k-1}}^kv_{p_{k-1}}^{k-1}t_{k-1} = u_{p_{k-1}}^kx_{p_{k-1}}^{k-1}$. This indicates that the maximization of $t_k$ is equivalent to the maximization of $t_{k-1}$ together with an optimal selection of the index $p_{k-1}$, or the maximization of the variable $x_{p_{k-1}}^{k-1}$ under a given parameter $u_{p_{k-1}}^k$. In particular, the maximization of $t_k$ includes essentially the maximization of $t_{k-1}$ during the subprocess starting from the first stage and ending at the stage $k$.
Finally, we have an initial value of the parameter $t_1 = \sum_i u_i^1x^0_i$ at the first stage, which corresponds to the initial currency portfolio $x^0$, where $u^1$ is the vector in the robust rank one approximation $u^1(v^1)^T$ to the first foreign exchange rate matrix $A^1$. Based on the principle of the mathematical induction, the conclusion holds for all stages $k = N, N-1, \cdots, 1$.
4.3. A feasible solution to the basic model
The solution to the ROA model (43)$\sim$(45) can also induce a near-optimal feasible solution to the basic model (4)$\sim$(7) for the currency portfolio optimization problem without rank one structures. In this subsection, a near-optimal feasible solution to the basic model (4)$\sim$(7) is generated by integrating the sequence of optimal forex operations in the ROA model with practical forex rate matrices $A^k$, $k = 1, 2, \cdots, N$. Certainly, when all forex rate matrices $A^k$ have the rank one structure, the feasible solution induced is also optimal. The following proposition describes the structure of the near-optimal feasible solution.
Proposition 4.1. Given a finite sequence of cross currency rate matrices $\{A^k\}$, suppose that there are two sequences of robust rank one approximation vectors $\{u^k\}$ and $\{v^k\}$, where $k = 1, 2, \cdots, N$. If the indices of optimal foreign exchange operations in the ROA model (43)$\sim$(45) are defined by $p_N = m$ and
where the currency $m$ is specially selected in advance to evaluate the wealth in currency portfolios, then there exists a near-optimal feasible sequence of currency portfolios $\{(x^*)^k\}$ to the basic model (4)$\sim$(7) that satisfies
where $x^0$ is the initial currency portfolio.
5.
Numerical verification for the intrinsic robust ROA approach
In this section, numerical examples will be presented to verify the performance of the intrinsic robust ROA approach for approximating practical forex rate matrices and optimizing currency portfolios over time. All of numerical experiments were conducted in the Lenovo computer X220i with 2.30GHz Intel(R) Core(TM) i3-2350M CPU and 6.0GB memory.
5.1. Source of data about the forex rates
Data about forex rates are collected from the Bloomberg professional service (the Terminal), which spreads from September 6,2016 to December 15,2016 except for holidays and weekends. There are seven currency baskets in the Bloomberg database, such as Majors, G10, Asia, EMEA, Latin America, Middle East and Precious Metals. For example, the basket of G10 includes currencies corresponding to countries (or currency zones) in the Group of Ten. Note that the Group of Ten is a famous organization consisting of eleven industrialized countries (Belgium, Canada, France, Germany, Italy, Japan, the Netherlands, Sweden, Switzerland, the United Kingdom and the United States) across the world. These countries usually organize the meetings of the Ministers of Finance and the Central Bank Governors for consulting each other and co-operating on economic, monetary and financial matters as needed in connection with the International Monetary Fund and the World Bank (Bank for International Settlements, 2016). There is only one different currency in the baskets between Majors (including the Hong Kong Dollar, HKD instead of the Danish Krone, DKK) and G10 (including DKK instead of HKD). The meaning of currency and precious metal codes can also be found in current currency and funds code list 4217-2015 (Swiss Association for Standardization, 2016).
In this section, the basket of Majors is selected to verify the performance of the ROA approach for approximating the cross currency rate matrix. In addition, the extended analysis is conducted for approximating the forex rates and the corresponding currency portfolio optimization involving five major currencies — as a currency basket consisting of the U.S. dollar, euro, the Japanese yen, pound sterling, and the Chinese renminbi (RMB) — which determines the value of the special drawing right(SDR). Note that the SDR was created by the International Monetary Fund (IMF) in 1969. It is an international reserve asset to supplement its member countries' official reserves, which can be exchanged for freely usable currencies. Until March 2016,204.1 billion SDRs (equivalent to about $285 billion) had been created and allocated to members (International Monetory Fund, 2016). Since the RMB was included as the fifth currency in the SDR basket, effective October 1,2016, the authors collected data about the cross currency rates of five currencies in the SDR from October 10,2016 to December 15,2016 in order to verify the performance of the ROA approach for the approximation to a forex rate matrix and the currency portfolio optimization.
In the Bloomberg service system, there are six categories of currency market data, i.e., Bloomberg BGN(NY), Bloomberg BGN(Ldn), Bloomberg BGN(Toyko), Composite(NY), Composite(Ldn) and Composite(Tokyo). These data are indexed by BGN, BGNL, BGNT, CMPN, CMPL, and CMPT, respectively. Each category of data corresponds to three types such as Spot, Forward and Fixing. In numerical examples below, the Fixing data including the bid and ask prices were downloaded and used as the benchmark for foreign exchange rates, which was set in London time 4p.m. daily and determined on the basis of actual transactions conducted by forex traders in the interbank market during a 60-second window (30 seconds either side of 4p.m.).
5.2. Examples for the robust rank one approximation
In this subsection, a sequence of examples is solved to verify the performance of the rank one approximation to the cross currency rates. The currencies belong to the basket of Majors, including eleven currencies such as USD, EUR, JPY, GBP, CHF, CAD, AUD, NZD, HKD, NOK and SEK. Data in examples range more than five years from September 6,2011 to December 15,2016 except for holidays and weekends, which includes the bid and ask prices in the type of Fixing. There are $1378$ records that include both the ask and bid prices for every pair of currencies in the basket.
In each example associated with the time index $k$, the cross currency rate matrices can be constructed from both ask and bid prices, denoted by $A^k$ and $B^k$, respectively. Data uncertainties between $A^k$ and $B^k$ are summarized in Table 1. For each difference $A^k-B^k$ of two matrices $A^k$ and $B^k$, the maximum, minimum, average and standard deviation of all errors are computed at the stage $k$, which leads four sequences of errors with the same length $1378$. The estimated values for each sequence are summarized in a column in Table 1. It is easy to see that average of extreme errors between two cross currency rate matrices has an order about $10^{-3}$ and the average of the sequence of daily average errors has an order about $10^{-6}$. The standard deviation for each sequence of estimated values over time has an order about $10^{-3}$ with the extreme estimated values or $10^{-4}$ with the average estimator. It can be concluded that the difference between $A^k$ and $B^k$ represents the uncertainty of the cross currency rate matrix associated with the basket of Majors.
For each of numerical examples, it has the same stopping rule below during the iterative process of the modified power method. When the modified power method is applied to each instance of the rank one approximations involving $A^k$ or $B^k$, it generates two sequences of vectors $\{u^{k_i}\}$ and $\{v^{k_i}\}$ together with the sequence of parameters $\{\delta^{k_i}\}$. The iterative process terminates whenever the $2$-norm of a difference vector between two successive iterates satisfies $\|v^{k_i}-v^{k_i-1}\|_2\leq \epsilon$ or the number of iteration is greater or equal to $ITER$. In each case of numerical verification, both control parameters are set by $\epsilon = 10^{-10}$ and $ITER = 1000$. The final product matrix $u^{k_i}(v^{k_i})^T$ is a positive rank-one approximation to the cross currency rate matrix. In the mean time, the matrix $\delta^{k_i}u^{k_i}(v^{k_i})^T$ is an optimal approximately solution to the constrained ROA problem(see (16) and (38)). In addition, the initial vector $x^0$ is set randomly, in which every component distributes uniformly in the interval $(0, 1)$. The vector $x^0$ is also scaled to a positive unit vector $v^0 = x^0/\|x^0\|_2$ triggering the iterative process of the modified power method.
For each cross currency rate matrix $A^k$ or $B^k$, the robust ROA approach searches for optimal solutions such as the rank one matrices to both the basic and constrained ROA problems, respectively. The estimated values associated with errors in the residual matrices are summarized in Tables 2~5. The average extreme estimated values of the residual matrices has the same order of $10^{-3}$ as those of $A^k-B^k$ except for the average minimum estimated values in Table 4 and Table 5 with such an even better order as $10^{-4}$. Note that the performance of the rank one approximation is measured by the $2$-norm and the Frobenius norm of the residual matrices. It is known that for each example, an approximately optimal solution to the corresponding CROA problem (16) can be obtained by multiplying each of vectors $u^k$ and $v^k$ with the square root of the parameter $\delta^k$. Hence, the values of the parameter $\delta^k$ displayed in Table 3 and Table 5 indicate the quality of the final updating solutions to the problem (16). As indicated by the robust ROA properties above, it is easy to see that the performance of the basic ROA is better than that of the constrained ROA. Since the minimum of parameters $\delta^k$ is about $0.9996$ for both matrices $A^k$ and $B^k$ over time, together with an average such as $0.99997$ in Table 3 or $0.99999$ in Table 5, there is an order of $10^{-5}$ in general for the residual errors $1-\delta^k$, which ensures that the optimal solution to the CROA problem has a similar property to that of the BROA problem with respect to the magnitude of the largest singular value $\sigma_1^k$ given in Tables 2~5.
In particular, it is easy to see from Tables 2~5 that the largest singular value $\sigma_1^k$ is significantly greater than the second largest one of any cross currency rate matrix (i.e., the $2$-norm of the residual matrix for the basic rank one approximation). Hence, the robust rank one approximation and the modified power method are efficient approaches for approximating cross currency rate matrices. The iteration numbers of the modified power method in Table 2 and Table 4 are 2 or 3 when satisfiable solutions are obtained for these examples.
5.3. Examples for the currency portfolio optimization
In order to verify the performance of the rank one approximation approach to the currency portfolio optimization problem, three steps are adopted from the data collection to the comparison of different optimization strategies.
Firstly, records about the cross currency rates with the basket of SDR were collected in the type of Fixing, which ranged from October 10,2016 to December 15,2016 except for holidays and weekends. Total number of records is $49$, each of which includes both the ask and bid prices for every pair of currency in the SDR basket consisting of the currencies such as USD, EUR, JPY, GBP, and CNY. Note that the cross currency rate matrices can also be constructed from either the ask or bid prices, denoted by $A^k$ or $B^k$, respectively, where $k$ is the time index of records.
Data uncertainties between matrices $A^k$ and $B^k$ are summarized in Table 6. By comparing the estimated values in Table 1 and Table 6, it can be concluded that errors between $A^k$ and $B^k$ for the SDR basket have the similar order to those for the basket of Majors. For example, the average of extreme errors has an order of $10^{-3}$ for two cross currency rate matrices coming from the bid and ask prices, respectively. The average of the sequence of the daily average errors has an order of $10^{-6}$ or $10^{-5}$. The standard deviation of each sequence of estimated values has an order of $10^{-3}$ with the extreme estimated values or $10^{-4}$ with the average ones.
In addition, for each element (a pair of currencies) in the difference matrix $A^k-B^k$, four kinds of statistic estimated values are summarized in Table 7, which corresponds to the Maximum, Minimum, Average and Standard Deviation of errors for each pairwise sequence of foreign exchange rates with the SDR basket over time. Note that the extreme estimated values of the errors related to the foreign exchange rates USD/JPY, EUR/JPY and GBP/JPY have a precision order of $10^{-3}$ or $10^{-2}$ and other estimated values are closer to zero. Note that the foreign exchange rate $CNY/GBP$ was not stored in the Bloomberg terminal at the time of data collection. The foreign exchange rate $CNY/GBP$ in Table 7 comes from the ask price of one unit of $GBP$ in terms of $CNY$, which is used twice in the construction of $A^k$ and $B^k$. The bid prices of $GBP$ against $CNY$ are also used twice in both $A^k$ and $B^k$. These kinds of replacements imply that there exists no difference for the corresponding estimated values in Table 7. The last and fifth lines counted from the bottom consist of zeros in Table 7.
Secondly, the ROA approach is applied to approximate the sequences of cross currency rate matrices (i.e., $\{A^k\}$ and $\{B^k\}$), respectively. That is, at each stage $k$, rank one matrices with respect to variants such as the BROA and CROA are generated to approximate $A^k$ and $B^k$, respectively. Statistical estimated values of errors in the residual matrices are summarized in Tables 8~11. Each average for four estimated values of the residual matrices has an order of $10^{-2}$ with the basic ROA matrices in Table 8 and Table 10, which has a less precision than that of the sequence of $\{A^k-B^k\}$. Note that the performance of the rank one approximation to $A^k$ in Table 8 (or Table 9) is similar to that of the ROA to $B^k$ in Table 10 (or Table 11), which is measured by the $2$-norm and the Frobenius norm of the residual matrices.
In particular, a solution to the corresponding CROA problem (16) is obtained by multiplying vectors $u^k$ and $v^k$ with the square root of the parameter $\delta^k$, respectively. By comparing the $2$-norm and the Frobenius norm of the residual matrices, it is obvious that the performance of the basic ROA approach in Table 8(or Table 10) is much better than that of the constrained ROA approach in Table 9 (or Table 11). Note that the values of the parameter $\delta^k$ for currencies in the SDR basket in Table 9 and Table 11 have a larger standard deviation than those for currencies in the basket of Majors in Table 3 and Table 5. It indicates that the quality of the final updating solutions to the problem (16) with the SDR basket is not better than that with the basket of Majors.
Furthermore, the minimum of parameters $\delta^k$ over time is $0.99470$ in Table 9 or $0.99473$ in Table 11, which corresponds to the largest $2$-norm and Frobenius norm of the residual matrices. The largest norm of the residual matrices in Table 9 and Table 11 are associated with the constrained ROA data on December 5,2016. For example, for the cross currency rate matrix $A^k$, which is generated from the ask prices on December 5,2016, the residual matrix $A^k-u^k(v^k)^T$ of the basic ROA is given by
The updating parameter $\delta^k$ causes a significant change of the third column vector in the residual matrix. For example, the third column vector in the residual matrix $A^k-\delta^k u^k(v^k)^T$ of the constrained ROA is given by $(0.60344$, $0.65065$, $0.00533$, $0.76834$, $0.08872)^T$, which corresponds to the minimum of updating parameters $\delta^k = 0.99470$ and the maximal error $0.76834$ in Table 9. In particular, the maximum of errors, $0.76834$, is at the position of the foreign exchange rate $GBP/JPY$. This is the main reason why the maximum of the $2$-norm and Frobenius norm of residual matrices is larger than $1.179$ in Table 9 and $1.171$ in Table 11 for the constrained rank one approximation.
Finally, the numerical results of three optimization strategies are compared for optimizing the currency portfolios. These strategies include the basic model (4)$\sim$(7) in the subsection 2.2, the ROA model (43)$\sim$(45) in the subsection 4.1 and a variant of the ROA model in Theorem 4.1. The third model integrates the optimal solution to the ROA model with the practical cross currency rates, which is presented in Proposition 4.1 in the subsection 4.3. It usually induces a feasible solution to the currency portfolio optimization problem, which is referred to as the VSC variant in Table 12 and Table 13. Two tables summarize numerical results and the properties related to three models for optimizing the currency portfolios with the SDR basket. In the captions of two tables, $\{A^k\}$ and $\{B^k\}$ represent the sequences of cross currency rate matrices generated from data about the ask and bid prices of currencies in the SDR basket, respectively.
In comparing the performance of three optimization strategies, the same initial currency portfolio $x^0$ is used, in which each element is uniformly distributed in the interval $[0, 10]$ and corresponds to the amount of a currency in the SDR basket. The subroutine linprog.m in the MATLAB is called to solve the basic model (4)$\sim$(7) in the subsection 2.2 under the assumption of the given cross currency rates. For each currency in the SDR basket, the goal is set to maximize its amount at the last stage $N = 49$. The control parameter options.MaxIter in the optimization toolbox of MATLAB is set to the maximum between the integer $85$ and the number of decision variables (i.e., all of $x_i^k$ and $y_{ij}^k$) in the basic model. Other parameters are defaults of the subroutine. As a verification, the subroutine linprog.m is also called to solve the instances generated from the rank one approximations to the cross currency rate matrices. The similar control strategies are adopted to solve the ROA model (43)$\sim$(45) in the subsection 4.1 except for the lack of variables $y_{ij}^k$ in the basic model. One of advantages with the ROA model is that its instance can be solved in a larger size than that of the basic model. In addition, it is easy to integrate the optimal solution to the ROA model with the original foreign exchange rates and construct a feasible solution to the currency portfolio optimization problem.
In Table 12 and Table 13, two initial currency portfolios are $5$-dimensional uniformly distributed vectors in the box domain $[0, 10]^5$, in which every element is not definitely greater or less than another. The initial objective values, the optimal values or the near-optimal values are presented for three optimization strategies, together with the relevant ratios of the final values to the corresponding initial ones. It should be mentioned that optimal values on $A^N$ or $B^N$ for the basic model, on $u^N(v^N)^T$ for the ROA model and on $u^N$ for the VSC variant are obtained by calling the subroutine linprog.m in the MATLAB. The optimal values of the ROA model are slightly greater than those of the basic model for the corresponding selected currencies. In contrast, the objective values of the VSC variant are slightly less than those of the basic model for real currencies, which implies that the former values are near-optimal to the basic model on $A^N$ or $B^N$, respectively. Although each currency in the SDR basket is selected as a goal for optimization with the different ratios of improvement, there exists a common scale that is described by the VSC ratio. The VSC ratio is similar to the transformed ratios under the consideration of the virtual exchange rates at the first and the last stages. It is easy to check that the transformed ratios of the basic model are about $1.273\sim 1.274$ in Table 12 and Table 13, which have errors within $0.002$ in comparing the VSC ratio $1.275$. Even for the feasible solution given by the VSC variant, the transformed ratios range from $1.253\sim 1.256$ with an error about $0.02$. These results indicate that the ROA model and its VSC variant are feasible and efficient tools to solve the currency portfolio optimization problem. In particular, they also possess advantages of reducing decision variables and providing a yardstick independent of currencies in the SDR basket for the currency portfolio optimization problem.
5.4. Theoretical explanation of the basic model and the VSC variant
In this subsection, a theoretical explanation is presented about the relationship between the optimal value of the basic model and a feasible objective value of the VSC variant. Although it is intuitive and not rigorous, it still provides a potential for analyzing the property of the VSC variant compared with an optimal solution to the basic model.
According to the exploration in the subsection 2.3, the optimal value of the basic model (4)$\sim$(7) can be described by
where $i_k, \cdots, i_{N}$ are indices of the target currencies at the end of periods in an optimal solution, $i_N = m$, and $W_{i_k}^k$ is a representation of the wealth $W^k$ in terms of the currency $i_k$. Without loss of generality, suppose that the optimal ratio in the basic model is given by
which corresponds to a certain amount of currency $i_0$ as the initial wealth. Similarly, the optimal ratio in the ROA model (43)$\sim$(45) is given by
where $k_0 = i_0$ and $k_N = i_N = m$. Furthermore, the optimal solution to the ROA model corresponds to a feasible solution as the VSC variant with a ratio defined by
In order to analyze the relationship between the ratios $\rho_m^N$ and $\lambda_m^N$, a lemma about the function $\ln(1+x)$ is needed, whose proof comes from the methods in the calculus and is omitted here.
Lemma 5.1. For any real number $x>-1$, the following inequalities hold
For any forex rate matrix $A^t$, $t = 1, 2, \cdots, N$, there is a rank one approximation such as $u^t(v^t)^T$. Hence, every component $a_{ij}^t$ can be represented by
where $\delta_{ij}^t$ denotes an error in approximating $a_{ij}^t$ by $u_i^tv_j^t$. By using (57)$\sim$(59) and Lemma 5.1, some equalities or inequalities are obtained as follows:
Since the optimality of $\sigma_m^N$ in the ROA model implies
we have the relationship between $\rho_m^N$ and $\lambda_m^N$ as follows:
that is,
It is noted that the rank one approximation errors $\delta_{ij}^t$ may be positive or negative (See also Table 2, Table 4, Table 8 and Table 10). There are possibilities that factors at the right hand side of (61) are greater than or less than $1$. The last three rows in Table 12 and Table 13 indicate that the factors $\exp(\cdot)$ on the right hand side are less than $1$. If the opposite phenomena appear in some numerical experiments, then non-linear structures may exist, which are associated with the original currency portfolio optimization problem (not represented in the basic model) and explored by the rank one approximation approach.
6.
Conclusions
A currency portfolio is one of basic forms of wealth whose value fluctuates with foreign exchange rates over time in the currency market. An approach based on the rank one approximation is proposed in this paper to attack the currency portfolio optimization problem, which aims at maximizing the wealth in currency portfolios evaluated by a specially selected currency. The intrinsic robustness of the rank one approximation to foreign exchange rates is proved together with exploring its properties and developing a modified power method to search for virtual exchange rates. The main results of the paper are summarized as follows: Firstly, under the assumptions about the currency market, the currency portfolio optimization problem is formulated as the basic model, in which there are two types of variables describing currency amounts in portfolios and the amount of each currency exchanged into another, respectively. Secondly, the rank one approximation problem and its variants are also formulated to approximate a foreign exchange rate matrix, whose performance is measured by the Frobenius norm or the $2$-norm of a residual matrix. The intrinsic robustness of the rank one approximation is proved together with its optimality and an algorithm developed to search for virtual exchange rates. Thirdly, the intrinsic robust rank one approximation approach is extended to attack the currency portfolio optimization problem by the technique of decision variables reduction. The reduced formulation is referred to as the ROA model, which keeps only variables describing currency amounts in portfolios. The optimal solution to the ROA model also induces a feasible solution to the basic model of the currency portfolio problem by integrating forex operations from the ROA model with practical forex rates. Finally, numerical examples are presented to verify the feasibility and efficiency of the intrinsic robust rank one approximation approach for approximating forex rate matrices and optimizing currency portfolios over time. There exists an invariant property in the objective function of currency portfolio optimization problem, which is related to the virtual standard currency and independent of any specially selected real currency except for the virtual exchange rates at the first and last stages.
Acknowledgments
The research of the first author is supported by the China Scholarship Council while he visits the Department of Statistics, University of Wisconsin-Madison. The first author is also supported in part by National Natural Science Foundation of China(NSFC) under Project 71031005/G0103. The research of the second author is supported by US National Science Foundation under Project CMMI-1536978.
Conflict of Interest
All authors declare no conflicts of interest in this paper.








 DownLoad:
DownLoad: