1. Introduction
The US housing boom and bust in the first decade of this century led to the worst financial crisis and severe recession since the Great Depression. The estimated cost of this dire situation is $6 trillion to $14 trillion, which translates into $50,000 to $120,000 for every household. At the same time, household net worth plunged $19 trillion. Beyond these monetary costs are the psychological consequences of the high and extended unemployment associated with the crisis and recession (Luttrell et al., 2013).
The federal government responded to the downturn in financial and economic activity in the fall of 2008 by providing extraordinary assistance, including bailouts to hundreds of financial institutions. The estimated direct government support for the financial sector totaled approximately $12.6 trillion (Luttrell et al., 2013). These and other efforts by both the government and private sector prevented a complete collapse and contributed to the subsequent growth in the economy and the improvement in the health of financial institutions.
In an attempt to prevent similar episodes from occurring in the future, the government enacted the Dodd-Frank Wall Street Reform Act (Dodd-Frank Act) in July 2010. The new law, which is the most comprehensive financial reform since the 1930s, aims to promote a safer and sounder financial system. If successful, the Dodd-Frank Act—through the implementation of stricter regulations and supervisory practices—will help prevent another system-wide banking crisis. Of course, banks will always incur some losses insofar as such institutions are by their very nature engaged in risky activities. However, the goal of banks and their regulators is to allow for losses that will inevitably occur but not so large and/or widespread that the entire banking sector finds itself so deeply in trouble that government bailouts are deemed necessary.
The purpose of this paper is to focus on the losses of two very big banks, Citigroup (Citi) and Wells Fargo & Company (Wells Fargo), and two very small banks, First Busey Corporation (Busey) and Capital City Bank Group (Capital), over the period 1991–2016. The federal government actually bailed out the two big banks, as measured by total assets, whereas neither of the two small banks required a bail out. Clearly, if one is able to use a variety of predictor variables to accurately forecast the losses of banks which have various sizes and operate in different geographical location with a variety of business models, this may help identify potential causes of future banking problems and thereby lessen, if not eliminate, the need for future bailouts. This is important for both the banks and the bank regulatory authorities. In particular, those banks expected to suffer significant losses on loans may be in a position to increase their provisioning and thus loan loss allowances. If such banks are unable to take this type of action or other corrective action to address expected losses, regulatory action may become necessary in response to this situation. The motivation for our paper is this very issue: Can one obtain accurate forecasts of losses, or the net charge-off rates, of banks? We provide an answer to this question by examining the four banks mentioned using several hundred predictor variables and several different forecast techniques.
The remainder of the paper proceeds as follows. In the next section, we discuss the importance of recent regulatory and other developments in the banking sector that underscore the need for banks to devote more effort to obtaining accurate forecasts of net charge-off rates, among other on- and off-balance sheet items as well as income statement items. In Section 3, we describe and discuss several important regression models that are used for forecasting purposes, including some models that allow for situations in which the number of predictor variables exceeds the number of observations. Section 4 follows with a presentation and discussion of our empirical findings regarding forecast accuracy based on the different regression models. As discussed in more detail later, we find that the ridge regression model and elastic net model outperform the other models over forecast horizons of four or more quarters. The other models examined, however, outperform a benchmark random walk model over various forecast horizons. This section also identifies the best model as well as the explanation for its choice. The last section contains the conclusions.
2. Pressure for improved bank forecast accuracy grows
A variety of factors in recent years have led to an increase in the pressure on a bank to improve the accuracy of its forecasts for the key variables that ultimately determine whether it will remain profitable or be forced to merge with a healthier bank, if not seized by a bank regulatory agency. Clearly, the more accurate the forecasts the better positioned will be a bank to compete in an increasingly competitive financial marketplace. Banks not only compete with one another but also compete in various ways with financial firms. For example, they compete with firms in the so-called shadow banking sector, where shadow banks are similar to traditional banks, but are not subject to traditional bank regulations and do not have traditional depositors whose funds are covered by insurance, they are in the "shadow" (Adrian and Ashcraft, 2016). Banks also compete with the more recently established and growing FinTech companies, which also are involved in the financial sector by facilitating payments and loans. Banks are facing increasing competition from FinTech start-ups such as Stripe and Square as well as established IT companies such as PayPal, Facebook, Apple, Google, and Amazon that are offering some traditional banking services (Jakšič and Marinč, 2017). For example, Stripe utilizes its business software to help companies take and track digital payments, and has been valued at $9.2 billion (Fitzpatrick et al., 2017). Numerous other startups such as SoFi and GreenSky are also altering the financial services industry by providing personal loans through new technology platforms. Moreover, Facebook, as an established IT company, supports money transfers, and Apple, Samsung, and Google provide for mobile payments in the form of Apple Pay, Samsung Pay, and Google Wallet.
Competition necessarily provides the incentive for banks to operate more efficiently and to undertake actions that enable them to remain profitable on an ongoing basis. This requires a balancing of risk and return over time. Too much risk can lead to excessive losses, but too little risk can lead to inadequate profitability. It is for this reason that forecasting losses or net charge-offs is important. Since there will always be loans that must be charged off, obtaining accurate forecasts is not only to assess the magnitude of expected future losses, but also identify some of the key factors that contribute to those losses.
As already noted, the Dodd-Frank Act increased the restrictions imposed on various activities and operations of banks. The Act also mandated an annual assessment by the Federal Reserve of banks with $50 billion or more in total assets in terms of their ability to absorb losses. In particular, the Comprehensive Capital Analysis and Review (CCAR) and Dodd-Frank Act Stress Testing (DFAST) programs were established to determine whether such big banks have effective capital adequacy processes and sufficient capital to absorb losses under stressful conditions. CCAR and DFAST are complementary exercises. In the case of CCAR, the Federal Reserve evaluates institutions' capital adequacy, their internal capital adequacy assessment processes, and their individual plans to make capital distributions, such as dividend payments or stock repurchases. As regards, DFAST is a forward-looking quantitative evaluation of the effect of stressful economic and financial market conditions on a bank's capital (Barth and Miller, 2017).
In 2012, the Federal Reserve finalized the rules that implement the stress test requirements under the Dodd-Frank Act. Banks with $10 billion or less are exempt from CCAR and DFAST. However, all banks with $10 billion or more in total assets are required to conduct an annual firm-run stress test. Banks with assets greater than $50 billion, moreover, must conduct semiannual firm-run stress tests and are subject to stress tests conducted by the Federal Reserve (i.e., CCAR and DFAST). The estimated losses resulting from these tests are subtracted from a bank's capital to determine the financial buffer that a bank has to insulate itself from losses. A bank effectively fails the tests if its capital falls below a required minimum level after the theoretical losses (Barth and Miller, 2017).
The goal of stress tests conducted under the Dodd-Frank Act is to provide forward-looking information to banks supervisory authorities to assist in their overall assessments of a bank's capital adequacy and to aid in identifying downside risks and the potential impact of adverse outcomes on the bank. Furthermore, these stress tests support ongoing improvement in a bank's internal assessments of capital adequacy and overall capital planning.
It is clear that CCAR and DFAST put additional pressure on large financial institutions subject to such stress tests to obtain forward-looking information on potential losses or net charge-off rate to determine whether there will be sufficient capital to meet the minimum requirements. Since it is costly for banks to hold excess capital, accurate predictions of net charge-offs of loan portfolios enable banks to assess whether they will satisfy, for instance, the minimum required tier 1 common regulatory capital ratio (Covas et al., 2014). More generally, even those banks not subject to CCAR and DFAST would want to obtain accurate forward-looking information to help ensure their profitability and even ongoing survivability in the financial marketplace.
In the next section, the different models that are used to forecast the net charge-off rates over three-year horizons for our four banks mentioned are discussed.
3. Forecasting models
3.1. Factor model
Assume information is available for a large number of predictor variables as follows, x=[x1,x2,…,xN], where xi=[xi,1,xi,2,…,xi,T]′, i=1,2,…,N, and t=1,2,…,T. Assume further that y is the corresponding vector for the target variable and that:
In this equation, h≥0 indicates the forecast horizon for the target variable using the predictor variables. We estimate a vector of the latent common factors, ft, and the associated loading coefficients, λi, via the principal component method. In particular, as suggested by Bai and Ng (2004), since εit may be an integrated process, first-differences of the predictors are used. Assuming that Δxit contains information about Δft, this relationship can be expressed as:
This is the factor representation of the data, where Δft=[Δft1,Δft2,…,ΔftR]′ is a R×1 vector of the common factors, λi=[λi,1,λi,2,…,λi,r]′ is the corresponding vector of factor loadings, and eit is an idiosyncratic error term. We treat ft as the common shocks that cause co-movements in the predictors. Using a principal component estimator, yt+h is regressed on ft to yield estimates of α′ and β in Equation 1. The factor model assumes the target variable follows a random walk when β=1. In this particular case, we refer to the model as a factor-model random walk, in contrast to simply a factor model.
3.2. Partial least squares
Similar to the factor model, the linear partial least square (PLS) regression approach is used to extract factors from the vector of predictor variables, or x matrix, that are used in predicting yt+h Referring to Equation 1, let Δft1,Δft2,…,ΔftR, with R<N, represent a linear combination of the original predictor variables. That is:
Where t=1,2,…,T and Δftr (r=1,…,R). The estimated latent common factors are referred to as x-scores1 and constants. They are estimated as linear combinations of the original predictors Xti, with weights w∗tr. The x-scores have the following two properties:
1 The x-scores are orthogonal predictors of both y and x.
● The matrix x can be expressed as x = ΔFP′+E, where ΔF is a matrix whose columns are x-scores, P is a matrix whose columns are called x-loadings, and E is a matrix of idiosyncratic error terms. In other words, x-scores are multiplied by the loadings pri, which provides sufficient summaries of x, so that the residuals of X, eti, are minimized in the following equation:
● yt+h is modeled as a linear regression on the x-scores2. Then the x-scores are used as predictors of yt+h based on the following equation:
2 In many cases, the goal is to model x and y with a small number of factors, so that the matrix x is never fully decomposed.
|
yt+h=∑RrcrΔftr+βyt+ξt+j
|
(5)
|
Where h=1,2,…H, cr's are y-weights, and the y-residuals, ξt, represent the deviations between the observed values and estimated model values. It is important to note that nonlinear iterative partial least squares (NIPALS) does not estimate all the principal components at once. Since the y-residuals may contain information that is not captured from previous components, Δfr−1p′r−1, we use the residuals to calculate Δftr and p′r (see the appendix for more detail regarding the algorithm used in the estimation). The factor model assumes a random walk process for the target variable, yt, when β=1. In this particular case, we refer to model as a PLS random walk model. This model may also be estimated with and without a lagged target variable. When yt is included as a common factor in the estimation, we refer to this model as a Pure PLS model, whereas when it is included as a separate explanatory variable we refer to the model as a PLS model.
Based on the above equations, we can now express our regression model as the following multiple-variable regression model:
|
yt+h=∑Rr=1cr∑Ni=1w∗trxti+βyt+ξt+j
|
(6)
|
If the constants wtr's are chosen judiciously, then partial least squares regression approaches can often outperform a two-stage factor model approach, as discussed in the previous section, as well as a least squares regression approach (Geladi and Kowalski, 1986 and Barth et al., 2018).
3.3. Ridge regression, LASSO regression, and elastic net
Ridge regression. A basic linear regression model can be used to predict a target variable over h horizons, y, with a large number of predictors, x, as follows:
Where β is the vector of the regression coefficients of the predictors and εi is a random error term. However, a ridge regression model is ideal when there are many predictors and all have non-zero coefficients. Moreover, such a model performs well with many predictors and a relatively high degree of multicollinearity among them. Furthermore, a ridge regression model does not force any of the coefficients to equal zero, thereby avoiding including only the most relevant subset of predictors.
The estimation of a ridge regression model relies on the following penalized least squares approach:
|
ˆβridge=argminβ‖y−xβ‖2+λ‖β‖2
|
(8)
|
Where ‖y−xβ‖2=∑ni=1(yi−xiβ)2 is a quadratic loss function, xi is the i-th row of x, ‖β‖=∑nj=1(βj)2 is the quadratic penalty imposed on β, and λ≥0 is the penalty parameter which determines the degree of the linear shrinkage in the coefficients. The higher the value of λ, the greater is the amount of shrinkage. The regularization parameter lambda is chosen based on the data in order to minimize the residual sum of squares. In this setting, if lambda is set to 0, one simply obtains the least squares solution.
LASSO regression. As with ridge regression, the LASSO (Least Absolute Shrinkage Selection Operator) shrinks some coefficient estimates towards zero, while setting others exactly to zero (Tibshirani, 1996). The LASSO attempts to balance the benefit of dimension reduction against the cost of including all predictors. For some values of λ, the norm penalty function of the LASSO has the effect of forcing some of the coefficient estimates to be set exactly to zero. Therefore, models estimated by LASSO include only a subset of predictors and thereby naturally performs feature selection, or variable selection (Zou and Hastie, 2010). It is clear that the lasso has an edge over ridge regression, in that it yields simpler and more interpretable models than those estimated by ridge regression. Unlike the LASSO, ridge regression does not perform feature selection. In other words, ridge regression will include all predictors in the final model and will not set any of predictors exactly to zero. Such a characteristic may not be a problem for prediction accuracy but can make it difficult to interpret models in settings in which the number of predictors is large. However, the LASSO regression approach is not robust to a high degree of correlation among a large number of predictors. The result is that some predictors are included, while others may be arbitrarily omitted.
A basic linear regression model can be used to predict a target variable with a large number of predictors, x, as follows:
Where β is the vector of the regression coefficients of the predictors. Similar to the ridge regression approach a LASSO regression model also relies on a penalized least squares approach. In particular, the estimation of a LASSO regression relies on the following penalized least squares equation:
|
ˆβLASSO=argminβ‖y−xβ‖2+λ‖β‖
|
(10)
|
Where ‖β‖=∑pj=1|βj| is the norm penalty function on β, which induces sparsity in the optimization procedure, and λ≥0 is a penalty parameter. The penalty term in the LASSO regulates the degree of the linear shrinkage in the least squares fit and sets some components of ˆβLASSO to zero for some arbitrarily chosen value of λ. The particular value is chosen based on a data-driven method, such as cross-validation.
Elastic net. As with ridge and LASSO, the elastic net simultaneously does automatic variable selection and continuous shrinkage, and it can select groups of correlated variables (Zou and Hastie, 2010). Ridge and LASSO work on the same principle. Both methods penalize the beta coefficients so that one can identify the important variables. Ridge and LASSO shrink the beta coefficient towards zero for meaningless variables. As noted in the previous sections, these methods are commonly used when one has more predictors than observations. The only difference between these two techniques is whether alpha is set equal to one or zero. Based on the generalized formula in Eq 11, the importance of alpha becomes clear. When alpha is equal to one, Lasso is the result, whereas when it is equal to zero, ridge is the result. For values of alpha between zero and one, elastic net is the result.
|
minβ0,β1N∑Ni=1wil(yi,β0+βTxi)+λ[(1−α)β22/2+α‖β‖1],
|
(11)
|
Where λ is the penalty parameter. Thus, when α=0, it will become Ridge and when α=1, it will become LASSO. The elastic net with α=1−ε for some small ε>0 performs much like the LASSO. More generally, the elastic net compromises between ridge and LASSO.
3.4. Random walk model as a benchmark
We use the random walk model as a benchmark by which to assess the forecast accuracy of the models discussed in the previous sections. According to this model, the best forecast of the next quarter charge-off rate is this quarter's observed charge-off rate. The random walk model can be expressed as follows:
A random walk is a common benchmark model used to compare the forecast accuracy of competing forecast models (Hyndman and Koehler, 2006).
4. Empirical findings
This section presents and discusses our empirical findings regarding forecasting the net charge-off rates for four banks (Citi, Wells Fargo, Busey, and Capital) using the techniques described in the previous sections. Figure 1 shows the charge-off rates for each of these banks. As may be seen, there is substantial variation in the rates over the nearly 30-year period. All four banks tend to experience relatively high charge-off rates for several quarters following the banking crisis of 2007–2008 and the severe recession from late 2007 to the summer of 2009. With a few quarterly exceptions, Citi tended to have the highest rates over the entire period.
We begin with a description of the predictor variables used in our analysis to forecast the net charge-off rates for the four banks. This is followed by a discussion of the basis for choosing the best forecasting model that is obtained when using nine different empirical techniques. This section also compares and contrasts the forecasting performance of the different techniques, which enables us to identify the best forecasting model. The last section presents the out-of-sample forecasts for the selected banks as well as discusses the relative importance of the various predictor variables used in obtaining the forecasts.
The important advantage of the techniques employed is that they allow for more predictors than observations through a dimension reduction approach. Although we are interested in prediction accuracy, we are choosing predictor variables based upon their importance to understanding banking-sector performance. This enables us to not only interpret the relationship of the predictors to the target variable, but also to discuss the importance of the relationship for specific predictor variables.
Of course, there are other studies in which various forecast techniques are used to gauge the way in which selected factors are expected to influence future bank performance. Some of these studies include the following: (1) Covas et al. (2014) estimate capital shortfalls of banks during periods of financial stress using a fixed effects quantile autoregressive model with exogenous macroeconomic covariates; (2) Bernoth and Pick (2011) use unobserved common factors in addition to macroeconomic variables to forecast the fragility of banks and insurance companies based on the CCE estimator of Pesaran (2006); (3) Drehmann and Juselius (2014) assess the performance of different early warning indicators in terms of the accuracy of their forecast regarding the likelihood that a banking crisis will occur, given a set of covariates, from the sector of macroprudential policy; (4) Guerrieri and Welch (2012) examine the forecast accuracy of combination models (i.e., an equal-weighted average of simple models) as compared to a random walk model for three classes of bank variables, credit measures, revenue measures, and capital measures; (5) Hirtle et al. (2016) examine the impact of macroeconomic conditions on banks using a "top-down" model of the banking industry that generates projections of bank income and capital based on regression models of components of bank income, expense and loan performance, combined with assumptions about provisioning, dividends, asset growth and other factors; (6) Crook and Banasik (2012) model aggregate consumer default rates over a twenty year period using a cointegration technique and compare the forecasting performance of this econometric technique with ARIMA models; (7) Bastos (2010) evaluates the performance of a fractional response regressions and a nonparametric and nonlinear regression tree model in forecasting recovery rates of bank loans; and (8) Kupiec (2018) uses the 2008 financial crisis to assess the forecast accuracy of competing stress test models for an average or representative bank from March 1993 through June 2008.
As just discussed, there are these and other studies that focus on forecasting various measures of bank performance as well as examining the forecast accuracy of different forecasting models. Our contribution to this literature is to examine the forecasting performance using nine different models based on two big banks and two small banks. To our knowledge, no study has conducted such an examination.
4.1. Data description
As Table 1 shows, there are 364 predictors employed in our analysis. They are grouped into bank, national, and state categories. The reason for choosing these three categories is that we have selected four banks that differ substantially in asset size. In the case of the two biggest banks, Citi and Wells Fargo, that operate across many geographical areas we expect that the national variables might be more important for improving forecast accuracy than the state variables. Conversely, for the two smaller banks, Busey and Capital, that mainly operate in single states we expect that the state variables might be more important.
Table 1. Categories of bank, national, and state predictor variables.
| Group ID |
Variable ID |
Categories |
| #1 |
1-27 |
Bank variables |
| #2 |
28-40 |
National variables—Employment |
| #3 |
41-48 |
National variables—Housing |
| #4 |
49-55 |
National variables—Industrial |
| #5 |
56-81 |
National variables—GDP and personal income |
| #6 |
82-112 |
National variables—Consumer prices indices, interest rates, and financial markets |
| #7 |
113-162 |
State variables—Unemployment rate |
| #8 |
163-313 |
State variables—Housing |
| #9 |
314-364 |
State variables—Personal income |
The empirical analysis is based on quarterly data for the period 1991 to 2016 obtained from FRY-9C reports.3 We used R to estimate all models presented in our paper. We also did the coding of the models, except for ridge, LASSO, and elastic net. Specifically, we used the glmnet package available in R to estimate the ridge, LASSO, and elastic net models. A detailed description of each of the predictor variables is provided in Appendix A.
3 The FRY-9C reports provide basic financial information for banks. The reports are prepared by the Federal Reserve based on information required of banks and then made publicly available on a quarterly basis. The FRY-9C is a primary analytical tool used by the Federal Reserve to monitor financial institutions between on-site inspections. For more detail on these reports, see https://www.federalreserve.gov/apps/reportforms/reportdetail.aspx?sOoYJ+5BzDal8cbqnRxZRg==.
4.2. Choosing the best forecasting model
The basis for choosing the best forecasting model over the 12-quarter horizons employed here is to compare the nine techniques to two benchmark models (BM), the autoregressive (AR) model and the random walk (RW) model. In particular, we calculate the ratio of the root mean squared prediction errors (RMSE) for both the AR and RW models divided by the RMSE for each model (CM) using the nine techniques discussed earlier in Section 3. The actual equation is as follows:
|
RRMSPE(j)=√1T−T0−J∑Tt+T0+j(εBMt+j|t)2√1T−T0−J∑Tt+T0+j(εCMt+j|t)2
|
(13)
|
Where εBMt+j|t=yt+j−ˆyBMj|t, εCMt+j|t=yt+j−ˆyCMj|t, BM = AR or RW, CM = Factor model, Factor RW, Pure PLS, PLS, PLS RW without lagged target variable, PLS RW with lagged target variable, Ridge, LASSO, or Elastic Net with α = 0.3, 0.5, and 0.7.4
4 Alternatively, one can, through numerous iterations, allow alpha to be determined as that value which produces the best forecast. Here, we simply wish to choose values that are close to the ridge model, the LASSO model, and the midpoint between the two models.
Using this equation, we are able to determine which of the two benchmark models, AR or RW, provides the best forecast of the net charge-off rate for each of the four selected banks. Table 2 indicates that for each of the banks the RW model outperforms the AR model, since the ratio of AR to RW is greater than one for all 12 quarters of the forecast horizon. This means that the RMSE for the RW model is lower than the RMSE for the AR model. The table also indicates that the ridge and elastic net models outperform the RW model in terms of forecast accuracy after two or four quarters, depending upon the bank. More specifically, the elastic net regression, in general, is the best for Citi, Wells Fargo, and Capital in the fourth quarter and thereafter. Interestingly enough in the case of Busey, the ridge estimator produces the best forecast accuracy of the net charge-off rate as compared to the RW model in the second quarter and thereafter. The RW model provides the best forecast for the shorter horizons in the case of all four banks.
Table 2. Net charge-off rates for selected banks: Comparison of AR/RW to ridge and elastic net (α = 0.5).
| Citi Bank |
RRMSPE |
|
|
Wells Fargo |
RRMSPE |
|
|
| h |
AR/RW |
RW/Ridge |
RW/Elastic Net (α = 0.5) |
h |
AR/RW |
RW/Ridge |
RW/Elastic Net (α
= 0.5) |
| 1 |
1.672 |
0.435 |
0.596 |
1 |
3.395 |
0.409 |
0.418 |
| 2 |
1.445 |
0.689 |
0.912 |
2 |
2.435 |
0.625 |
0.671 |
| 3 |
1.290 |
0.944 |
1.215 |
3 |
2.062 |
0.819 |
0.780 |
| 4 |
1.174 |
1.296 |
1.496 |
4 |
1.721 |
1.047 |
1.015 |
| 5 |
1.208 |
1.563 |
1.832 |
5 |
1.662 |
1.120 |
1.194 |
| 6 |
1.219 |
1.879 |
1.950 |
6 |
1.600 |
1.202 |
1.286 |
| 7 |
1.248 |
1.857 |
1.942 |
7 |
1.500 |
1.568 |
1.661 |
| 8 |
1.269 |
1.926 |
1.948 |
8 |
1.354 |
1.837 |
1.896 |
| 9 |
1.335 |
1.943 |
1.831 |
9 |
1.429 |
1.675 |
1.610 |
| 10 |
1.403 |
1.903 |
1.828 |
10 |
1.420 |
1.594 |
1.522 |
| 11 |
1.455 |
1.968 |
1.990 |
11 |
1.389 |
1.721 |
1.725 |
| 12 |
1.486 |
1.860 |
1.878 |
12 |
1.360 |
1.784 |
1.929 |
| First Busey (IL) |
RRMSPE |
|
|
Capital City (FL) |
RRMSPE |
|
|
| h |
AR/RW |
RW/Ridge |
RW/Elastic Net (α
= 0.5) |
h |
AR/RW |
RW/Ridge |
RW/Elastic Net (α
= 0.5) |
| 1 |
1.714 |
0.846 |
0.557 |
1 |
1.221 |
0.652 |
0.754 |
| 2 |
1.620 |
1.243 |
1.035 |
2 |
1.273 |
0.828 |
0.921 |
| 3 |
1.536 |
1.356 |
1.094 |
3 |
1.204 |
0.981 |
0.977 |
| 4 |
1.290 |
1.303 |
1.143 |
4 |
1.148 |
1.062 |
1.210 |
| 5 |
1.230 |
1.387 |
1.293 |
5 |
1.140 |
1.269 |
1.347 |
| 6 |
1.044 |
1.477 |
1.227 |
6 |
1.128 |
1.347 |
1.384 |
| 7 |
1.071 |
1.388 |
1.254 |
7 |
1.116 |
1.449 |
1.480 |
| 8 |
0.912 |
1.423 |
1.200 |
8 |
1.012 |
1.447 |
1.336 |
| 9 |
0.802 |
1.422 |
1.356 |
9 |
1.079 |
1.397 |
1.392 |
| 10 |
0.793 |
1.422 |
1.302 |
10 |
1.113 |
1.497 |
1.522 |
| 11 |
0.789 |
1.465 |
1.295 |
11 |
1.169 |
1.409 |
1.370 |
| 12 |
0.782 |
1.575 |
1.648 |
12 |
1.180 |
1.520 |
1.457 |
| Note: RRMSPE refers to the ratio of the root mean squared prediction error. We calculate RRMSPE based on the mean squared prediction error (RMSPE) from the RW model (benchmark model) divided by the RMSPE from the ridge regression model and elastic net model (competing models), respectively. Note that the ridge regression model or the elastic net model outperform the benchmark model when RRMSPE is greater than 1. We implement a fixed-sized rolling window method and use the first 50% observations as a training set to evaluate out-of-sample forecasting performance. |
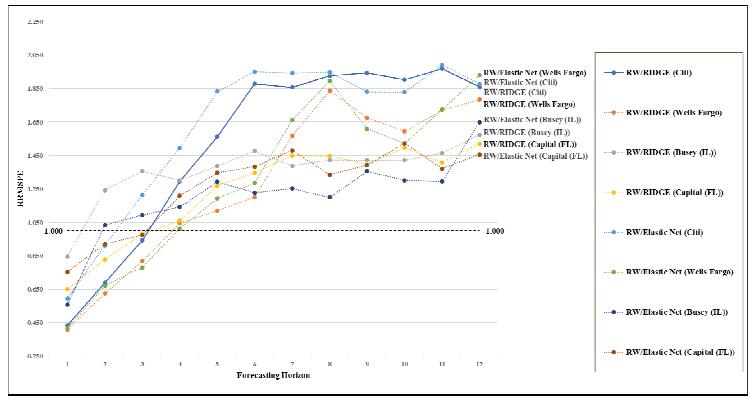
Figure 2 shows the forecast accuracy for each of the four banks based on the ridge and the elastic net (α = 0.5) regression models as compared to the random walk model. As may be seen, no one bank dominates over all 12 forecast horizons. When the elastic net is used, the forecast accuracy is greatest for Wells Fargo after four quarters, followed by Citi. Yet, when the ridge regression is implemented, the forecast accuracy is greatest for Citi after four quarters, while Wells Fargo is second after seven quarters. The two quite small banks rank about equally after seven quarters.
We now discuss in more detail in the next section how the ridge and the elastic net regressions compare in terms of forecast accuracy to the other seven regression techniques used in our analysis. The comparison is based on the out-of-sample forecasting accuracy for each of the four banks.
4.3. Out-of-sample forecasting
In the case of Citi and the other banks, the RRMSPE is calculated for each of the nine models. As Table 3 shows, the best models in terms forecasting accuracy for Citi are the ridge and the elastic net models, but only after three quarters. Except for nine and ten quarters, the elastic net model outperforms the ridge regression. However, it is important to note that every other model provides more accurate forecasts over some horizons than the RW benchmark model. The ranking of the other models in terms RRMSPE is as follows: The Factor model with one factor performs best over horizons of four to seven quarters; the LASSO model performs best over horizons of eight to eleven quarters; and the Pure PLS model with one factor performs best over a horizon of twelve quarters.
Table 3. Citi—best forecasting model based on RW benchmark.
|
|
Pure PLS |
PLS |
Factor Model |
Factor RW |
PLS RW w/o Lagged DV |
PLS RW w/Lagged DV |
Ridge |
Lasso |
Elastic Net (α = 0.3) |
Elastic Net (α = 0.5) |
Elastic Net (α = 0.7) |
Best |
| No. of Factors |
Forecasting Horizon |
RRMSPE |
|
| j |
h |
|
| 1 |
1 |
0.301 |
0.323 |
0.873 |
0.977 |
0.971 |
0.959 |
0.435 |
0.294 |
0.559 |
0.596 |
0.555 |
RW |
|
2 |
0.442 |
0.477 |
0.931 |
0.974 |
0.956 |
0.941 |
0.689 |
0.434 |
0.867 |
0.912 |
0.925 |
RW |
|
3 |
0.597 |
0.605 |
0.993 |
0.977 |
0.969 |
0.993 |
0.944 |
0.580 |
1.220 |
1.215 |
1.262 |
EN (0.7) |
|
4 |
0.738 |
0.765 |
1.024 |
0.970 |
0.964 |
0.995 |
1.296 |
0.723 |
1.385 |
1.496 |
1.469 |
EN (0.5) |
|
5 |
0.888 |
0.891 |
1.070 |
0.966 |
0.964 |
0.982 |
1.563 |
0.860 |
1.895 |
1.832 |
1.939 |
EN (0.7) |
|
6 |
0.991 |
0.989 |
1.102 |
0.958 |
0.958 |
0.908 |
1.879 |
0.986 |
1.944 |
1.950 |
1.932 |
EN (0.5) |
|
7 |
1.071 |
1.060 |
1.143 |
0.964 |
0.963 |
0.887 |
1.857 |
1.105 |
1.995 |
1.942 |
1.804 |
EN (0.3) |
|
8 |
1.146 |
1.125 |
1.160 |
0.974 |
0.969 |
0.971 |
1.926 |
1.202 |
1.924 |
1.948 |
1.880 |
EN (0.5) |
|
9 |
1.237 |
1.205 |
1.243 |
0.981 |
0.980 |
0.979 |
1.943 |
1.286 |
1.846 |
1.831 |
1.839 |
RIDGE |
|
10 |
1.316 |
1.286 |
1.304 |
0.999 |
1.001 |
0.994 |
1.903 |
1.357 |
1.863 |
1.828 |
1.805 |
RIDGE |
|
11 |
1.374 |
1.303 |
1.341 |
1.007 |
1.014 |
1.005 |
1.968 |
1.398 |
1.973 |
1.990 |
2.030 |
EN (0.7) |
|
12 |
1.393 |
1.335 |
1.352 |
1.032 |
1.046 |
1.055 |
1.860 |
1.388 |
1.878 |
1.878 |
1.827 |
EN (0.3) |
| 2 |
1 |
0.287 |
0.322 |
0.841 |
0.940 |
0.944 |
0.876 |
0.435 |
0.294 |
0.559 |
0.596 |
0.555 |
RW |
|
2 |
0.423 |
0.471 |
0.863 |
0.905 |
0.946 |
0.883 |
0.689 |
0.434 |
0.867 |
0.912 |
0.925 |
RW |
|
3 |
0.552 |
0.591 |
0.914 |
0.889 |
0.904 |
0.857 |
0.944 |
0.580 |
1.220 |
1.215 |
1.262 |
EN (0.7) |
|
4 |
0.661 |
0.759 |
0.958 |
0.903 |
0.933 |
0.878 |
1.296 |
0.723 |
1.385 |
1.496 |
1.469 |
EN (0.5) |
|
5 |
0.790 |
0.889 |
1.019 |
0.917 |
0.941 |
0.845 |
1.563 |
0.860 |
1.895 |
1.832 |
1.939 |
EN (0.7) |
|
6 |
0.879 |
0.992 |
1.056 |
0.924 |
0.944 |
0.808 |
1.879 |
0.986 |
1.944 |
1.950 |
1.932 |
EN (0.5) |
|
7 |
0.959 |
1.062 |
1.093 |
0.927 |
0.935 |
0.777 |
1.857 |
1.105 |
1.995 |
1.942 |
1.804 |
EN (0.3) |
|
8 |
1.043 |
1.121 |
1.133 |
0.943 |
0.955 |
0.831 |
1.926 |
1.202 |
1.924 |
1.948 |
1.880 |
EN (0.5) |
|
9 |
1.104 |
1.191 |
1.203 |
0.956 |
0.949 |
0.858 |
1.943 |
1.286 |
1.846 |
1.831 |
1.839 |
RIDGE |
|
10 |
1.162 |
1.262 |
1.263 |
0.982 |
0.961 |
0.904 |
1.903 |
1.357 |
1.863 |
1.828 |
1.805 |
RIDGE |
|
11 |
1.170 |
1.258 |
1.300 |
1.001 |
0.955 |
0.923 |
1.968 |
1.398 |
1.973 |
1.990 |
2.030 |
EN (0.7) |
|
12 |
1.247 |
1.244 |
1.321 |
1.056 |
0.994 |
1.005 |
1.860 |
1.388 |
1.878 |
1.878 |
1.827 |
EN (0.3) |
| 3 |
1 |
0.285 |
0.254 |
0.805 |
0.878 |
0.886 |
0.822 |
0.435 |
0.294 |
0.559 |
0.596 |
0.555 |
RW |
|
2 |
0.429 |
0.377 |
0.831 |
0.891 |
0.941 |
0.847 |
0.689 |
0.434 |
0.867 |
0.912 |
0.925 |
RW |
|
3 |
0.529 |
0.472 |
0.883 |
0.861 |
0.896 |
0.769 |
0.944 |
0.580 |
1.220 |
1.215 |
1.262 |
EN (0.7) |
|
4 |
0.701 |
0.624 |
0.937 |
0.894 |
0.945 |
0.832 |
1.296 |
0.723 |
1.385 |
1.496 |
1.469 |
EN (0.5) |
|
5 |
0.847 |
0.743 |
1.000 |
0.901 |
0.940 |
0.822 |
1.563 |
0.860 |
1.895 |
1.832 |
1.939 |
EN (0.7) |
|
6 |
0.915 |
0.811 |
1.020 |
0.900 |
0.918 |
0.801 |
1.879 |
0.986 |
1.944 |
1.950 |
1.932 |
EN (0.5) |
|
7 |
1.000 |
0.883 |
1.064 |
0.899 |
0.899 |
0.820 |
1.857 |
1.105 |
1.995 |
1.942 |
1.804 |
EN (0.3) |
|
8 |
1.045 |
1.134 |
1.100 |
0.904 |
0.948 |
0.866 |
1.926 |
1.202 |
1.924 |
1.948 |
1.880 |
EN (0.5) |
|
9 |
1.170 |
1.188 |
1.168 |
0.915 |
0.921 |
0.897 |
1.943 |
1.286 |
1.846 |
1.831 |
1.839 |
RIDGE |
|
10 |
1.261 |
1.246 |
1.223 |
0.938 |
0.929 |
0.914 |
1.903 |
1.357 |
1.863 |
1.828 |
1.805 |
RIDGE |
|
11 |
1.274 |
1.236 |
1.266 |
0.944 |
0.907 |
0.961 |
1.968 |
1.398 |
1.973 |
1.990 |
2.030 |
EN (0.7) |
|
12 |
1.320 |
1.225 |
1.292 |
1.010 |
0.940 |
1.057 |
1.860 |
1.388 |
1.878 |
1.878 |
1.827 |
EN (0.3) |
| Note: RRMSPE refers to the ratio of the root mean squared prediction error. We calculate RRMSPE based on the root mean squared prediction error (RMSPE) from the RW model (benchmark model) divided by the RMSPE from the corresponding competing model. Note that the competing model outperforms the benchmark model when RRMSPE is greater than 1. We implement a fixed-sized rolling window method and use the first 50% observations as a training set to evaluate out-of-sample forecasting performance. |
Table 4. Wells Fargo—best forecasting model based on RW benchmark.
|
|
Pure PLS |
PLS |
Factor Model |
Factor RW |
PLS RW w/o Lagged DV |
PLS RW w/Lagged DV |
Ridge |
Lasso |
Elastic Net (α = 0.3) |
Elastic Net (α = 0.5) |
Elastic Net (α = 0.7) |
Best |
| No. of Factors |
Forecasting Horizon |
RRMSPE |
|
| j |
h |
|
| 1 |
1 |
0.276 |
0.305 |
0.505 |
0.418 |
0.466 |
0.107 |
0.409 |
0.308 |
0.419 |
0.418 |
0.418 |
RW |
|
2 |
0.367 |
0.443 |
0.547 |
0.445 |
0.511 |
0.146 |
0.625 |
0.480 |
0.653 |
0.671 |
0.675 |
RW |
|
3 |
0.543 |
0.562 |
0.764 |
0.657 |
0.722 |
0.194 |
0.819 |
0.619 |
0.824 |
0.780 |
0.791 |
RW |
|
4 |
0.719 |
0.685 |
0.801 |
0.671 |
0.739 |
0.224 |
1.047 |
0.745 |
1.024 |
1.015 |
1.018 |
RIDGE |
|
5 |
0.634 |
0.770 |
0.853 |
0.712 |
0.791 |
0.244 |
1.120 |
0.856 |
1.216 |
1.194 |
1.189 |
EN (0.3) |
|
6 |
0.400 |
0.897 |
0.920 |
0.751 |
0.854 |
0.249 |
1.202 |
0.967 |
1.319 |
1.286 |
1.298 |
EN (0.3) |
|
7 |
0.511 |
1.041 |
1.105 |
0.874 |
0.962 |
0.267 |
1.568 |
1.091 |
1.655 |
1.661 |
1.626 |
EN (0.5) |
|
8 |
0.921 |
1.161 |
1.213 |
0.934 |
0.968 |
0.346 |
1.837 |
1.198 |
1.878 |
1.896 |
1.906 |
EN (0.7) |
|
9 |
1.045 |
1.240 |
1.257 |
0.921 |
0.953 |
0.364 |
1.675 |
1.300 |
1.748 |
1.610 |
1.621 |
EN (0.3) |
|
10 |
1.198 |
1.213 |
1.155 |
0.936 |
0.946 |
0.388 |
1.594 |
1.385 |
1.548 |
1.522 |
1.350 |
RIDGE |
|
11 |
1.407 |
1.325 |
1.241 |
0.946 |
0.958 |
0.387 |
1.721 |
1.447 |
1.709 |
1.725 |
1.772 |
EN (0.7) |
|
12 |
1.459 |
1.380 |
1.254 |
0.934 |
0.936 |
0.388 |
1.784 |
1.485 |
1.975 |
1.929 |
2.018 |
EN (0.7) |
| 2 |
1 |
0.278 |
0.263 |
0.214 |
0.113 |
0.133 |
0.102 |
0.409 |
0.308 |
0.419 |
0.418 |
0.418 |
RW |
|
2 |
0.487 |
0.302 |
0.249 |
0.149 |
0.187 |
0.145 |
0.625 |
0.480 |
0.653 |
0.671 |
0.675 |
RW |
|
3 |
0.481 |
0.464 |
0.390 |
0.206 |
0.219 |
0.183 |
0.819 |
0.619 |
0.824 |
0.780 |
0.791 |
RW |
|
4 |
0.579 |
0.475 |
0.313 |
0.230 |
0.290 |
0.221 |
1.047 |
0.745 |
1.024 |
1.015 |
1.018 |
RIDGE |
|
5 |
0.809 |
0.468 |
0.335 |
0.253 |
0.292 |
0.241 |
1.120 |
0.856 |
1.216 |
1.194 |
1.189 |
EN (0.3) |
|
6 |
0.747 |
0.432 |
0.318 |
0.264 |
0.260 |
0.250 |
1.202 |
0.967 |
1.319 |
1.286 |
1.298 |
EN (0.3) |
|
7 |
0.885 |
0.446 |
0.358 |
0.293 |
0.271 |
0.292 |
1.568 |
1.091 |
1.655 |
1.661 |
1.626 |
EN (0.5) |
|
8 |
0.977 |
0.660 |
0.583 |
0.385 |
0.423 |
0.393 |
1.837 |
1.198 |
1.878 |
1.896 |
1.906 |
EN (0.7) |
|
9 |
1.077 |
0.716 |
0.921 |
0.405 |
0.445 |
0.418 |
1.675 |
1.300 |
1.748 |
1.610 |
1.621 |
EN (0.3) |
|
10 |
1.276 |
0.982 |
1.199 |
0.439 |
0.465 |
0.485 |
1.594 |
1.385 |
1.548 |
1.522 |
1.350 |
RIDGE |
|
11 |
1.237 |
1.077 |
1.208 |
0.428 |
0.448 |
0.468 |
1.721 |
1.447 |
1.709 |
1.725 |
1.772 |
EN (0.7) |
|
12 |
1.182 |
1.078 |
1.196 |
0.425 |
0.446 |
0.468 |
1.784 |
1.485 |
1.975 |
1.929 |
2.018 |
EN (0.7) |
| 3 |
1 |
0.275 |
0.182 |
0.199 |
0.108 |
0.082 |
0.100 |
0.409 |
0.308 |
0.419 |
0.418 |
0.418 |
RW |
|
2 |
0.397 |
0.361 |
0.294 |
0.149 |
0.126 |
0.149 |
0.625 |
0.480 |
0.653 |
0.671 |
0.675 |
RW |
|
3 |
0.427 |
0.246 |
0.375 |
0.198 |
0.163 |
0.174 |
0.819 |
0.619 |
0.824 |
0.780 |
0.791 |
RW |
|
4 |
0.632 |
0.485 |
0.342 |
0.229 |
0.185 |
0.212 |
1.047 |
0.745 |
1.024 |
1.015 |
1.018 |
RIDGE |
|
5 |
0.544 |
0.501 |
0.398 |
0.256 |
0.216 |
0.231 |
1.120 |
0.856 |
1.216 |
1.194 |
1.189 |
EN (0.3) |
|
6 |
0.525 |
0.444 |
0.369 |
0.267 |
0.258 |
0.239 |
1.202 |
0.967 |
1.319 |
1.286 |
1.298 |
EN (0.3) |
|
7 |
0.679 |
0.467 |
0.479 |
0.303 |
0.306 |
0.266 |
1.568 |
1.091 |
1.655 |
1.661 |
1.626 |
EN (0.5) |
|
8 |
1.169 |
0.670 |
0.867 |
0.397 |
0.352 |
0.346 |
1.837 |
1.198 |
1.878 |
1.896 |
1.906 |
EN (0.7) |
|
9 |
1.178 |
0.694 |
1.094 |
0.422 |
0.375 |
0.368 |
1.675 |
1.300 |
1.748 |
1.610 |
1.621 |
EN (0.3) |
|
10 |
1.040 |
0.590 |
1.007 |
0.450 |
0.419 |
0.411 |
1.594 |
1.385 |
1.548 |
1.522 |
1.350 |
RIDGE |
|
11 |
1.004 |
0.484 |
1.138 |
0.436 |
0.417 |
0.408 |
1.721 |
1.447 |
1.709 |
1.725 |
1.772 |
EN (0.7) |
|
12 |
1.317 |
0.533 |
1.196 |
0.435 |
0.413 |
0.432 |
1.784 |
1.485 |
1.975 |
1.929 |
2.018 |
EN (0.7) |
| Note: RRMSPE refers to the ratio of the root mean squared prediction error. We calculate RRMSPE based on the root mean squared prediction error (RMSPE) from the RW model (benchmark model) divided by the RMSPE from the corresponding competing model. Note that the competing model outperforms the benchmark model when RRMSPE is greater than 1. We implement a fixed-sized rolling window method and use the first 50% observations as a training set to evaluate out-of-sample forecasting performance. |
Turning to Wells Fargo, the best models are the ridge and the elastic net models, but only after two quarters. As in the case of Citi, the elastic net outperforms the ridge regression over most forecast horizons, except for four and ten quarters. However, as in the case of Citi, every other model provides more accurate forecast over some horizons than the RW benchmark model. The ranking of the other models in terms RRMSPE is as follows: The Factor model with one factor performs best over horizons of four to seven quarters; the LASSO model performs best over horizons of eight to eleven quarters; and the Pure PLS with one factor performs best over a horizon of twelve quarter.
As shown in Table 5 for Busey, the best models are the ridge and the elastic net models, but in this case it does so after the very first quarter. Unlike the previous two big banks, the ridge regression outperforms the elastic net model over most forecast horizons, except for nine and twelve quarters. However, as is the case for the two biggest banks, every other model provides more accurate forecast over some horizons than the RW benchmark model. In particular, the ranking of the other models is as follows: The Pure PLS model with one factor performs best over a horizon of three quarters and the LASSO model performs best after the first quarter, as is the case of the ridge model.
Table 5. Busey (IL)—best forecasting model based on RW benchmark.
|
|
Pure PLS |
PLS |
Factor Model |
Factor RW |
PLS RW w/o Lagged DV |
PLS RW w/Lagged DV |
Ridge |
Lasso |
Elastic Net (α = 0.3) |
Elastic Net (α = 0.5) |
Elastic Net (α = 0.7) |
Best |
| No. of Factors |
Forecasting Horizon |
RRMSPE |
|
| j |
h |
|
| 1 |
1 |
0.677 |
0.666 |
0.565 |
0.975 |
0.968 |
0.967 |
0.846 |
0.675 |
0.568 |
0.557 |
0.535 |
RW |
|
2 |
1.023 |
0.875 |
0.676 |
0.944 |
0.910 |
0.946 |
1.243 |
1.033 |
1.068 |
1.035 |
0.752 |
RIDGE |
|
3 |
1.123 |
0.933 |
0.732 |
0.961 |
0.936 |
0.962 |
1.356 |
1.117 |
1.115 |
1.094 |
1.027 |
RIDGE |
|
4 |
1.054 |
0.998 |
0.773 |
0.920 |
0.898 |
0.907 |
1.303 |
1.151 |
1.079 |
1.143 |
1.129 |
RIDGE |
|
5 |
1.083 |
1.103 |
0.759 |
0.927 |
0.929 |
0.932 |
1.387 |
1.233 |
1.312 |
1.293 |
1.265 |
RIDGE |
|
6 |
1.189 |
1.180 |
0.893 |
0.974 |
0.976 |
1.033 |
1.477 |
1.293 |
1.257 |
1.227 |
1.260 |
RIDGE |
|
7 |
1.172 |
1.197 |
0.878 |
0.984 |
0.978 |
0.989 |
1.388 |
1.293 |
1.228 |
1.254 |
1.253 |
RIDGE |
|
8 |
1.210 |
1.291 |
1.075 |
0.984 |
0.987 |
0.941 |
1.423 |
1.309 |
1.188 |
1.200 |
1.164 |
RIDGE |
|
9 |
1.188 |
1.321 |
1.295 |
0.986 |
0.986 |
0.934 |
1.422 |
1.338 |
1.462 |
1.356 |
1.356 |
EN (0.3) |
|
10 |
1.233 |
1.330 |
1.297 |
0.999 |
0.994 |
0.981 |
1.422 |
1.354 |
1.366 |
1.302 |
1.346 |
RIDGE |
|
11 |
1.281 |
1.352 |
1.297 |
0.999 |
0.996 |
0.992 |
1.465 |
1.375 |
1.283 |
1.295 |
1.405 |
RIDGE |
|
12 |
1.366 |
1.385 |
1.347 |
1.010 |
1.010 |
1.010 |
1.575 |
1.393 |
1.634 |
1.648 |
1.651 |
EN (0.7) |
| 2 |
1 |
0.658 |
0.470 |
0.563 |
0.966 |
0.794 |
0.950 |
0.846 |
0.675 |
0.568 |
0.557 |
0.535 |
RW |
|
2 |
0.965 |
0.798 |
0.650 |
0.941 |
0.678 |
0.927 |
1.243 |
1.033 |
1.068 |
1.035 |
0.752 |
RIDGE |
|
3 |
1.060 |
1.035 |
0.721 |
0.953 |
0.853 |
0.925 |
1.356 |
1.117 |
1.115 |
1.094 |
1.027 |
RIDGE |
|
4 |
1.040 |
0.757 |
0.764 |
0.913 |
0.887 |
0.895 |
1.303 |
1.151 |
1.079 |
1.143 |
1.129 |
RIDGE |
|
5 |
1.111 |
0.756 |
0.748 |
0.918 |
0.852 |
0.938 |
1.387 |
1.233 |
1.312 |
1.293 |
1.265 |
RIDGE |
|
6 |
1.333 |
0.760 |
0.884 |
0.946 |
0.829 |
1.036 |
1.477 |
1.293 |
1.257 |
1.227 |
1.260 |
RIDGE |
|
7 |
1.335 |
0.903 |
0.874 |
0.960 |
0.947 |
1.004 |
1.388 |
1.293 |
1.228 |
1.254 |
1.253 |
RIDGE |
|
8 |
1.183 |
1.136 |
1.079 |
0.972 |
0.960 |
0.905 |
1.423 |
1.309 |
1.188 |
1.200 |
1.164 |
RIDGE |
|
9 |
1.165 |
1.138 |
1.266 |
0.967 |
0.947 |
0.896 |
1.422 |
1.338 |
1.462 |
1.356 |
1.356 |
EN (0.3) |
|
10 |
1.240 |
1.227 |
1.245 |
0.967 |
0.966 |
0.939 |
1.422 |
1.354 |
1.366 |
1.302 |
1.346 |
RIDGE |
|
11 |
1.353 |
1.375 |
1.282 |
0.982 |
0.994 |
0.976 |
1.465 |
1.375 |
1.283 |
1.295 |
1.405 |
RIDGE |
|
12 |
1.413 |
1.382 |
1.345 |
1.004 |
0.997 |
0.991 |
1.575 |
1.393 |
1.634 |
1.648 |
1.651 |
EN (0.7) |
| 3 |
1 |
0.654 |
0.524 |
0.568 |
0.965 |
0.855 |
0.889 |
0.846 |
0.675 |
0.568 |
0.557 |
0.535 |
RW |
|
2 |
0.993 |
0.764 |
0.650 |
0.936 |
0.646 |
0.919 |
1.243 |
1.033 |
1.068 |
1.035 |
0.752 |
RIDGE |
|
3 |
1.089 |
0.926 |
0.713 |
0.946 |
0.788 |
0.927 |
1.356 |
1.117 |
1.115 |
1.094 |
1.027 |
RIDGE |
|
4 |
1.003 |
0.852 |
0.766 |
0.914 |
0.908 |
0.846 |
1.303 |
1.151 |
1.079 |
1.143 |
1.129 |
RIDGE |
|
5 |
1.038 |
0.829 |
0.779 |
0.941 |
0.871 |
0.864 |
1.387 |
1.233 |
1.312 |
1.293 |
1.265 |
RIDGE |
|
6 |
1.372 |
0.851 |
0.946 |
0.989 |
0.872 |
1.003 |
1.477 |
1.293 |
1.257 |
1.227 |
1.260 |
RIDGE |
|
7 |
1.266 |
0.996 |
0.900 |
0.976 |
0.978 |
0.941 |
1.388 |
1.293 |
1.228 |
1.254 |
1.253 |
RIDGE |
|
8 |
1.165 |
1.165 |
1.099 |
0.975 |
0.969 |
0.897 |
1.423 |
1.309 |
1.188 |
1.200 |
1.164 |
RIDGE |
|
9 |
1.096 |
1.188 |
1.257 |
0.961 |
0.978 |
0.898 |
1.422 |
1.338 |
1.462 |
1.356 |
1.356 |
EN (0.3) |
|
10 |
1.040 |
1.193 |
1.235 |
0.962 |
0.975 |
0.850 |
1.422 |
1.354 |
1.366 |
1.302 |
1.346 |
RIDGE |
|
11 |
1.176 |
1.294 |
1.269 |
0.979 |
0.988 |
0.901 |
1.465 |
1.375 |
1.283 |
1.295 |
1.405 |
RIDGE |
|
12 |
1.366 |
1.240 |
1.330 |
0.997 |
1.003 |
0.987 |
1.575 |
1.393 |
1.634 |
1.648 |
1.651 |
EN (0.7) |
| Note: RRMSPE refers to the ratio of the root mean squared prediction error. We calculate RRMSPE based on the root mean squared prediction error (RMSPE) from the RW model (benchmark model) divided by the RMSPE from the corresponding competing model. Note that the competing model outperforms the benchmark model when RRMSPE is greater than 1. We implement a fixed-sized rolling window method and use the first 50% observations as a training set to evaluate out-of-sample forecasting performance |
As shown in Table 6 for Capital, the RRMSPE is calculated for each of the nine models. The best model for Capital, as shown in Table 6, is the PLS RW model with lagged dependent variable in the second quarter when one and three factors are extracted. The ridge and the elastic net models are the best models only after two quarters. In general, the elastic net regression outperforms the ridge regression over shorter forecast horizons. Once again, every other model provides more accurate forecast over some horizons than the RW benchmark model. The ranking of the other models is as follows: (1) the Factor RW model with one factor performs best over horizons of three and five quarters; (2) PLS RW with lagged target variable and one factor performs best over a horizon of four quarter; (3) the LASSO model performs best over horizons of six, seven, ten, eleven, and twelve quarters; (4) the Pure PLS model with one factor performs best over a horizon of eight quarters; and (5) the Factor model with one factor performs best over a horizon of nine quarters.
Table 6. Capital (IL)—best forecasting model based on RW benchmark.
|
|
Pure PLS |
PLS |
Factor Model |
Factor RW |
PLS RW w/o Lagged DV |
PLS RW w/Lagged DV |
Ridge |
Lasso |
Elastic Net (α = 0.3) |
Elastic Net (α = 0.5) |
Elastic Net (α = 0.7) |
Best |
| No. of Factors |
Forecasting Horizon |
RRMSPE |
|
| j |
h |
|
| 1 |
1 |
0.502 |
0.481 |
0.847 |
0.972 |
0.964 |
0.970 |
0.652 |
0.509 |
0.749 |
0.754 |
0.746 |
RW |
|
2 |
0.601 |
0.574 |
0.825 |
1.008 |
1.001 |
1.012 |
0.828 |
0.599 |
0.919 |
0.921 |
0.895 |
PLSRWw/Lag |
|
3 |
0.722 |
0.663 |
0.894 |
0.975 |
0.966 |
0.967 |
0.981 |
0.733 |
1.021 |
0.977 |
1.072 |
EN (0.7) |
|
4 |
0.801 |
0.707 |
0.949 |
0.966 |
0.954 |
0.976 |
1.062 |
0.800 |
1.169 |
1.210 |
1.224 |
EN (0.7) |
|
5 |
0.833 |
0.768 |
0.920 |
0.937 |
0.934 |
0.933 |
1.269 |
0.864 |
1.368 |
1.347 |
1.293 |
EN (0.3) |
|
6 |
0.917 |
0.874 |
0.911 |
0.927 |
0.921 |
0.896 |
1.347 |
0.966 |
1.419 |
1.384 |
1.389 |
EN (0.3) |
|
7 |
0.868 |
0.921 |
0.950 |
0.949 |
0.940 |
0.864 |
1.449 |
1.010 |
1.436 |
1.480 |
1.468 |
EN (0.5) |
|
8 |
1.188 |
1.034 |
1.095 |
0.970 |
0.960 |
0.882 |
1.447 |
1.082 |
1.393 |
1.336 |
1.433 |
RIDGE |
|
9 |
1.080 |
1.044 |
1.108 |
0.970 |
0.965 |
0.904 |
1.397 |
1.077 |
1.357 |
1.392 |
1.344 |
RIDGE |
|
10 |
1.141 |
1.109 |
1.132 |
0.978 |
0.973 |
0.927 |
1.497 |
1.143 |
1.453 |
1.522 |
1.466 |
EN (0.5) |
|
11 |
1.031 |
1.144 |
1.124 |
0.975 |
0.968 |
0.931 |
1.409 |
1.180 |
1.364 |
1.370 |
1.352 |
RIDGE |
|
12 |
1.092 |
1.188 |
1.127 |
1.002 |
0.999 |
0.983 |
1.520 |
1.216 |
1.478 |
1.457 |
1.499 |
RIDGE |
| 2 |
1 |
0.517 |
0.388 |
0.858 |
0.978 |
0.932 |
0.966 |
0.652 |
0.509 |
0.749 |
0.754 |
0.746 |
RW |
|
2 |
0.585 |
0.409 |
0.822 |
0.998 |
0.998 |
0.943 |
0.828 |
0.599 |
0.919 |
0.921 |
0.895 |
RW |
|
3 |
0.706 |
0.416 |
0.893 |
0.961 |
0.853 |
0.925 |
0.981 |
0.733 |
1.021 |
0.977 |
1.072 |
EN (0.7) |
|
4 |
0.745 |
0.386 |
0.930 |
0.948 |
0.831 |
0.860 |
1.062 |
0.800 |
1.169 |
1.210 |
1.224 |
EN (0.7) |
|
5 |
0.814 |
0.522 |
0.918 |
0.933 |
0.917 |
0.915 |
1.269 |
0.864 |
1.368 |
1.347 |
1.293 |
EN (0.3) |
|
6 |
0.912 |
0.625 |
0.893 |
0.911 |
0.943 |
0.877 |
1.347 |
0.966 |
1.419 |
1.384 |
1.389 |
EN (0.3) |
|
7 |
1.005 |
0.670 |
0.920 |
0.924 |
1.026 |
0.955 |
1.449 |
1.010 |
1.436 |
1.480 |
1.468 |
EN (0.5) |
|
8 |
1.205 |
0.962 |
1.094 |
0.957 |
1.189 |
0.995 |
1.447 |
1.082 |
1.393 |
1.336 |
1.433 |
RIDGE |
|
9 |
1.039 |
0.953 |
1.085 |
0.951 |
1.038 |
0.902 |
1.397 |
1.077 |
1.357 |
1.392 |
1.344 |
RIDGE |
|
10 |
1.160 |
1.074 |
1.155 |
0.984 |
1.085 |
0.978 |
1.497 |
1.143 |
1.453 |
1.522 |
1.466 |
EN (0.5) |
|
11 |
1.083 |
1.089 |
1.099 |
0.950 |
1.023 |
0.920 |
1.409 |
1.180 |
1.364 |
1.370 |
1.352 |
RIDGE |
|
12 |
1.221 |
1.249 |
1.160 |
1.009 |
1.086 |
1.022 |
1.520 |
1.216 |
1.478 |
1.457 |
1.499 |
RIDGE |
| 3 |
1 |
0.528 |
0.382 |
0.851 |
0.973 |
0.935 |
0.961 |
0.652 |
0.509 |
0.749 |
0.754 |
0.746 |
RW |
|
2 |
0.589 |
0.409 |
0.813 |
0.987 |
1.036 |
0.958 |
0.828 |
0.599 |
0.919 |
0.921 |
0.895 |
PLSRWw/oLag |
|
3 |
0.735 |
0.433 |
0.870 |
0.938 |
0.895 |
0.916 |
0.981 |
0.733 |
1.021 |
0.977 |
1.072 |
EN (0.7) |
|
4 |
0.797 |
0.408 |
0.918 |
0.933 |
0.867 |
0.897 |
1.062 |
0.800 |
1.169 |
1.210 |
1.224 |
EN (0.7) |
|
5 |
0.811 |
0.563 |
0.925 |
0.933 |
0.921 |
0.851 |
1.269 |
0.864 |
1.368 |
1.347 |
1.293 |
EN (0.3) |
|
6 |
0.944 |
0.719 |
0.916 |
0.906 |
1.057 |
0.877 |
1.347 |
0.966 |
1.419 |
1.384 |
1.389 |
EN (0.3) |
|
7 |
1.035 |
0.775 |
1.008 |
0.951 |
1.138 |
0.945 |
1.449 |
1.010 |
1.436 |
1.480 |
1.468 |
EN (0.5) |
|
8 |
1.192 |
0.991 |
1.159 |
0.966 |
1.243 |
0.919 |
1.447 |
1.082 |
1.393 |
1.336 |
1.433 |
RIDGE |
|
9 |
1.005 |
1.005 |
1.117 |
0.949 |
1.117 |
0.839 |
1.397 |
1.077 |
1.357 |
1.392 |
1.344 |
RIDGE |
|
10 |
1.117 |
1.062 |
1.164 |
0.978 |
1.088 |
0.931 |
1.497 |
1.143 |
1.453 |
1.522 |
1.466 |
EN (0.5) |
|
11 |
1.022 |
1.091 |
1.098 |
0.945 |
1.071 |
0.906 |
1.409 |
1.180 |
1.364 |
1.370 |
1.352 |
RIDGE |
|
12 |
1.083 |
1.139 |
1.161 |
1.008 |
1.063 |
0.975 |
1.520 |
1.216 |
1.478 |
1.457 |
1.499 |
RIDGE |
| Note: RRMSPE refers to the ratio of the root mean squared prediction error. We calculate RRMSPE based on the root mean squared prediction error (RMSPE) from the RW model (benchmark model) divided by the RMSPE from the corresponding competing model. Note that the competing model outperforms the benchmark model when RRMSPE is greater than 1. We implement a fixed-sized rolling window method and use the first 50% observations as a training set to evaluate out-of-sample forecasting performance. |
In addition to comparing the performance of the different forecasting models, it is useful to examine the relative importance of the various predictor variables for the model that most accurate forecast. In particular, beyond a few quarters, one of the best models for forecasting the net charge-off rates is the ridge regression model. We may therefore assess the rankings of the three groups of predictors in terms of their importance in obtaining the most accurate forecast as well as the rankings of the predictors with each of the groups. Although there are four banks, we only do this exercise for two of the banks, one of the two biggest and one of the two smallest, since the results are quite similar in terms of corresponding size for the other two banks.
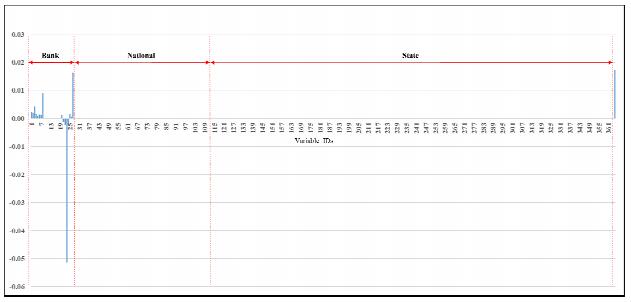
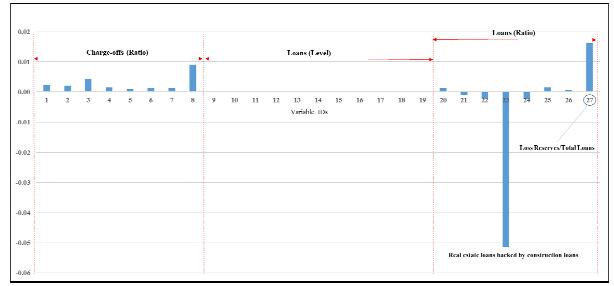
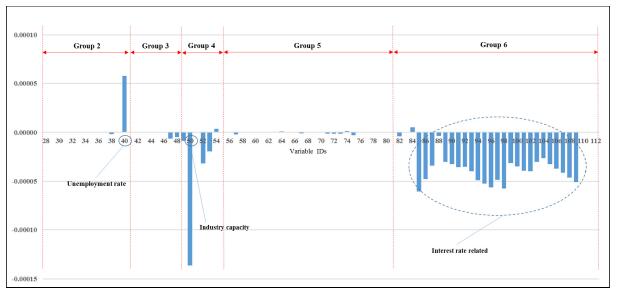
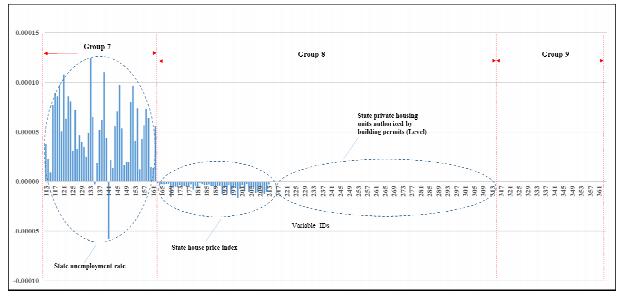
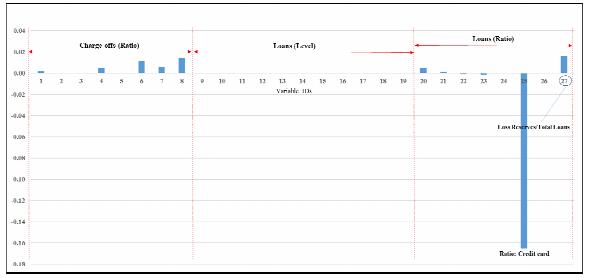
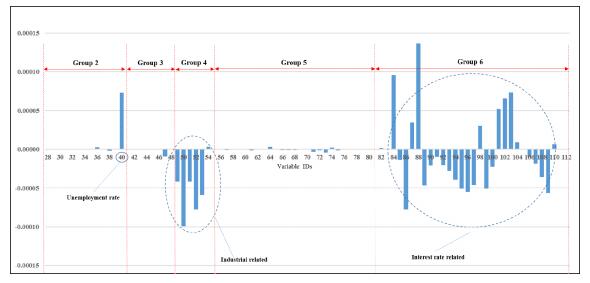
Starting with Citi, Figure 3 shows the relative importance of all 364 predictor variables used in forecasting the net charge-off rate. It is clear that the bank predictors dominate all of the national and state predictors, as shown by the magnitude of their coefficients. Of the 27 bank predictors, moreover, only the net charge-off rates on the various types of loans and the loan ratios matter, not the levels of the types of loans, as shown in Figure 4. When the charge-off rates for the different types of loans are omitted, moreover, the results remain unchanged. Furthermore, the two predictors having the biggest impact are real estate loans backed by construction loans and loan loss reserves, and in that order of importance. Decreases in the former variable are associated with a lower net charge-off rate, while the opposite is the case for loan loss reserves. As regards the national predictors, Figure 5 shows that the two most important predictors are the unemployment rate and industrial capacity, with former having a positive relationship and the latter a negative relationship. Interestingly, almost all the interest-related predictors have some impact and negative relationships with the net charge-off rate. The impact in all these cases, however, tends to be de minimas. Lastly, Figure 5 shows the relative importance of the state predictors. Clearly, the only predictors that matter are the state unemployment rates, although their relative importance overall is also relatively minor. Yet, the impact of the state predictors generally dominates that of the national predictors.
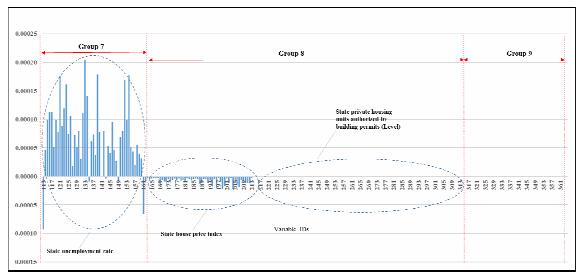
As regards Busey, Figure 7 shows the relative importance of the same 364-predictor variables used in forecasting the net charge-off rate. As is the case with Citi, the bank predictors dominate all of the national and state predictors, as shown by the magnitude of coefficients. Of the 27 bank predictors, in contrast to Citi, not all of the net charge-off rates on the various types of loans matter, as shown in Figure 8. In addition, once again, the levels of the types of loans do not have a meaningful impact. Furthermore, as with Citi, the two predictors having the biggest impact and the same association with the net charge-off rate are real estate loans backed by construction loans and loan loss reserves, and in that order of importance. As regards the national predictors, Figure 9 shows that the findings for Busey contrast fairly sharply with those for Citi. The two most important predictors are the unemployment rate and industrial capacity, with former having a positive relationship and the latter a negative relationship. Interestingly, almost all the interest-related predictors have some impact, albeit relatively minor, and negative relationships with the net charge-off rate. Lastly, Figure 5 shows the relative importance of the state predictors. Clearly, the only predictors that matter are the state unemployment rates, although their relative importance overall is de minimas as compared to the bank predictors. The state unemployment rates, however, are more important than all the national variables.
5. Conclusions
As discussed, recent regulatory and other developments in the banking sector underscore the need for banks to devote more effort to obtaining accurate forecasts of net charge-off rates, among other important banking variables. We have discussed several important regression models that are used for forecasting purposes, including some models that allow for situations in which the number of predictor variables exceeds the number of observations, and use these models to forecast net charge-off rates for four banks. Two of the banks are among the biggest banks in the country, while the other two banks are among the smallest banks. Based upon our empirical findings regarding the forecast accuracy of the different regression models, we find that the ridge regression model or the elastic net model outperform the other models over forecast horizons of four and more quarters. The other models examined, however, outperform a benchmark random walk model over various forecast horizons.
As far as we know, no other study has used as many forecasting models to examine which model performs best in terms of forecasting accuracy over various horizons in the banking literature focusing on an extremely important banking variable, the net charge-off rate. In future research, one might consider using the types of forecasting models employed here for forecasting other banking variables. This would include such variables as the return on assets (ROA), return on equity (ROE), z-score (the return on assets plus the capital asset ratio divided by the standard deviation of return on assets—the z-score measures the distance from insolvency (Roy, 1952)), stock return or price, volatility of stock return, bank earnings, price-earnings (P/E) ratio, nonperforming loans, and loan loss provision.
Our findings have important policy implications. In particular, bank regulatory authorities are able to assess the forecast models used by individual banks and the associated results to assist them in evaluating the expected future performance of banks. Depending upon the forecast models and results as well as their own independent assessment, the regulators will be in a better position to decide upon any actions that might be appropriate to promote safer and sounder banks. This might include requiring modifications in or better explanations for the models used. But it might even include supervisory actions to the extent that the forecast results coupled with the regulators' own assessment suggest the likelihood of emerging problems at a particular bank or a set of banks more generally.
Conflict of interest
The authors declare no conflict of interest.
Appendix
Appendix A. Variable ID description
| Group ID |
Variable ID |
Data description |
| #1 |
1 |
Sum(CO-RE-multifamily, CO-IPRE, CO-construction)/sum(RE-multifamily, IPRE, construction) |
|
2 |
CO-CI/CI |
|
3 |
Sum(CO-credit card, CO-other consumer)/sum(credit card other consumer) |
|
4 |
Income producing real estate |
|
5 |
CO-construction/construction |
|
6 |
CO-Open-end residential loans/Open-end residential loans |
|
7 |
CO-multifamily/multifamily |
|
8 |
CO-close-end residential loans/close-end residential loans |
|
9 |
Total loans (net of unearned income) |
|
10 |
Total assets |
|
11 |
Loans backed by real estate |
|
12 |
Sum (multifamily, construction, IPRE) |
|
13 |
Real estate loans backed by income producing real estate |
|
14 |
Real estate loans backed by construction loans |
|
15 |
Real estate loans backed by residential properties (open-end) |
|
16 |
Real estate loans backed by multifamily loans |
|
17 |
Real estate loans backed by residential properties (close-end) |
|
18 |
Commercial and Industrial Loans |
|
19 |
Loans to consumers: Sum (credit card, other consumer) |
|
20 |
Ratio: Loans to consumers: Sum (credit card, other consumer) |
|
21 |
Ratio: Real estate loans backed by residential properties (close-end) |
|
22 |
Ratio: Sum(multifamily, construction, IPRE) |
|
23 |
Ratio: Real estate loans backed by construction loans |
|
24 |
Ratio: Commercial and Industrial Loans |
|
25 |
Ratio: Credit card |
|
26 |
Total Loans/Total Assets |
|
27 |
Loss Reserves/Total loans |
| #2 |
28 |
All Employees: Private Service-Providing |
|
29 |
All Employees: Government: Federal |
|
30 |
All Employees: Manufacturing |
|
31 |
All Employees: Construction |
|
32 |
All Employees: Education and Health Services |
|
33 |
All Employees: Goods-Producing Industries |
|
34 |
All Employees: Government |
|
35 |
All Employees: Leisure and Hospitality |
|
36 |
All Employees: Mining and logging |
|
37 |
All Employees: Total Private Industries |
|
38 |
All Employees: Other Services |
|
39 |
All Employees: Trade, Transportation and Utilities |
|
40 |
Civilian Unemployment Rate |
| #3 |
41 |
New Privately-Owned Housing Units Completed: 1-Unit Structures |
|
42 |
New Privately-Owned Housing Units Completed: Total |
|
43 |
Housing Starts: Total: New Privately Owned Housing Units Started |
|
44 |
Privately Owned Housing Starts: 1-Unit Structures |
|
45 |
New Private Housing Units Authorized by Building Permits |
|
46 |
New Private Housing Units Authorized by Building Permits—in Structures with 1 Unit |
|
47 |
All-Transactions House Price Index for the United States |
|
48 |
Commercial Real Estate Price Index (Level) |
| #4 |
49 |
Industrial Production Index |
|
50 |
Industrial Capacity: Total index |
|
51 |
Capacity Utilization: Total Industry |
|
52 |
Motor Vehicle Retail Sales: Light Weight Trucks |
|
53 |
Light Weight Vehicle Sales: Autos and Light Trucks, Seasonally Adjusted Annual Rate |
|
54 |
Producer Price Index by Commodity for Final Demand: Finished Goods |
|
55 |
Real Final Sales to Private Domestic Purchasers |
| #5 |
56 |
Compensation of employees: Wages and salaries: Private industries |
|
57 |
Compensation of employees: Wages and salaries: Government |
|
58 |
Compensation of Employees: Wages and Salary Accruals |
|
59 |
Real Exports of Goods and Services |
|
60 |
Real imports of goods and services |
|
61 |
Real Exports of services |
|
62 |
Real Exports of Goods |
|
63 |
Real Imports of Goods |
|
64 |
Real Imports of Services |
|
65 |
Real Net Exports of Goods and Services |
|
66 |
Real Private Nonresidential Fixed Investment |
|
67 |
Real Private Residential Fixed Investment |
|
68 |
Real Fixed Private Investment |
|
69 |
Change in Real Private Inventories |
|
70 |
Real Gross Private Domestic Investment |
|
71 |
Real Personal Consumption Expenditures: Durable Goods |
|
72 |
real Personal Consumption Expenditures: Services |
|
73 |
Real Personal Consumption Expenditures: Nondurable Goods |
|
74 |
Real Federal Consumption Expenditures and Gross Investment |
|
75 |
Real State and Local Consumption Expenditures & Gross Investment |
|
76 |
Real Gross Domestic Product |
|
77 |
Real Final Sales to Private Domestic Purchasers |
|
78 |
Real Personal Income |
|
79 |
Corporate Profits After Tax (without IVA and CCAdj) |
|
80 |
Real Disposable Personal Income |
|
81 |
Real Disposable Personal Income: Per Capita |
| #6 |
82 |
Consumer Price Index for All Urban Consumers: All Items |
|
83 |
Consumer Price Index for All Urban Consumers: Energy |
|
84 |
Consumer Price Index for All Urban Consumers: Food and Beverages |
|
85 |
Consumer Price Index for All Urban Consumers: All Items Less Food and Energy |
|
86 |
Effective Federal Funds Rate |
|
87 |
Moody's Seasoned Aaa Corporate Bond Yield |
|
88 |
Moody's Seasoned Baa Corporate Bond Yield |
|
89 |
3-month Treasury Constant Maturity Rate |
|
90 |
6-month Treasury Constant Maturity Rate |
|
91 |
1-Year Treasury Constant Maturity Rate |
|
92 |
2-Year Treasury Constant Maturity Rate |
|
93 |
3-Year Treasury Constant Maturity Rate |
|
94 |
5-Year Treasury Constant Maturity Rate |
|
95 |
7-Year Treasury Constant Maturity Rate |
|
96 |
10-Year Treasury Constant Maturity Rate |
|
97 |
Bank Prime Loan Rate |
|
98 |
30-Year Fixed Rate Mortgage Average in the United States, Percent, Quarterly, Not Seasonally Adjusted |
|
99 |
3-Month Treasury Bill: Secondary Market Rate |
|
100 |
6-Month Treasury Bill: Secondary Market Rate |
|
101 |
3-Month London Interbank Offered Rate (LIBOR), based on U.S. Dollar |
|
102 |
6-Month London Interbank Offered Rate (LIBOR), based on U.S. Dollar |
|
103 |
12-Month London Interbank Offered Rate (LIBOR), based on U.S. Dollar |
|
104 |
2-year swap |
|
105 |
3-year swap |
|
106 |
4 year swap |
|
107 |
5-year swap |
|
108 |
7-year swap |
|
109 |
10-year swap |
|
110 |
U.S Market Volatiliry Index |
|
111 |
Dow Jones Total Stock Market |
|
112 |
S & P 500 Index |
| #7 |
113 |
Unemployment Rate in Alaska |
|
114 |
Unemployment Rate in Alabama |
|
115 |
Unemployment Rate in Arkansas |
|
116 |
Unemployment Rate in Arizona |
|
117 |
Unemployment Rate in California |
|
118 |
Unemployment Rate in Colorado |
|
119 |
Unemployment Rate in Connecticut |
|
120 |
Unemployment Rate in the District of Columbia |
|
121 |
Unemployment Rate in Delaware |
|
122 |
Unemployment Rate in Florida |
|
123 |
Unemployment Rate in Georgia |
|
124 |
Unemployment Rate in Hawaii |
|
125 |
Unemployment Rate in Iowa |
|
126 |
Unemployment Rate in Idaho |
|
127 |
Unemployment Rate in Illinois |
|
128 |
Unemployment Rate in Indiana |
|
129 |
Unemployment Rate in Kansas |
|
130 |
Unemployment Rate in Kentucky |
|
131 |
Unemployment Rate in Louisiana |
|
132 |
Unemployment Rate in Massachusetts |
|
133 |
Unemployment Rate in Maryland |
|
134 |
Unemployment Rate in Maine |
|
135 |
Unemployment Rate in Michigan |
|
136 |
Unemployment Rate in Minnesota |
|
137 |
Unemployment Rate in Missouri |
|
138 |
Unemployment Rate in Mississippi |
|
139 |
Unemployment Rate in Montana |
|
140 |
Unemployment Rate in North Carolina |
|
141 |
Unemployment Rate in North Dakota |
|
142 |
Unemployment Rate in Nebraska |
|
143 |
Unemployment Rate in New Hampshire |
|
144 |
Unemployment Rate in New Jersey |
|
145 |
Unemployment Rate in New Mexico |
|
146 |
Unemployment Rate in Nevada |
|
147 |
Unemployment Rate in New York |
|
148 |
Unemployment Rate in Ohio |
|
149 |
Unemployment Rate in Oklahoma |
|
150 |
Unemployment Rate in Oregon |
|
151 |
Unemployment Rate in Pennsylvania |
|
152 |
Unemployment Rate in Rhode Island |
|
153 |
Unemployment Rate in South Carolina |
|
154 |
Unemployment Rate in South Dakota |
|
155 |
Unemployment Rate in Tennessee |
|
156 |
Unemployment Rate in Texas |
|
157 |
Unemployment Rate in Utah |
|
158 |
Unemployment Rate in Virginia |
|
159 |
Unemployment Rate in Washington |
|
160 |
Unemployment Rate in Wisconsin |
|
161 |
Unemployment Rate in West Virginia |
|
162 |
Unemployment Rate in Wyoming |
| #8 |
163 |
All-Transactions House Price Index for California |
|
164 |
All-Transactions House Price Index for Florida |
|
165 |
All-Transactions House Price Index for New York |
|
166 |
All-Transactions House Price Index for New Jersey |
|
167 |
All-Transactions House Price Index for Hawaii |
|
168 |
All-Transactions House Price Index for Massachusetts |
|
169 |
All-Transactions House Price Index for Texas |
|
170 |
All-Transactions House Price Index for Utah |
|
171 |
All-Transactions House Price Index for Colorado |
|
172 |
All-Transactions House Price Index for Michigan |
|
173 |
All-Transactions House Price Index for Connecticut |
|
174 |
All-Transactions House Price Index for Illinois |
|
175 |
All-Transactions House Price Index for Wisconsin |
|
176 |
All-Transactions House Price Index for Alabama |
|
177 |
All-Transactions House Price Index for Pennsylvania |
|
178 |
All-Transactions House Price Index for Arizona |
|
179 |
All-Transactions House Price Index for North Carolina |
|
180 |
All-Transactions House Price Index for Minnesota |
|
181 |
All-Transactions House Price Index for Georgia |
|
182 |
All-Transactions House Price Index for Rhode Island |
|
183 |
All-Transactions House Price Index for Nevada |
|
184 |
All-Transactions House Price Index for New Hampshire |
|
185 |
All-Transactions House Price Index for Maine |
|
186 |
All-Transactions House Price Index for Maryland |
|
187 |
All-Transactions House Price Index for Idaho |
|
188 |
All-Transactions House Price Index for Ohio |
|
189 |
All-Transactions House Price Index for Missouri |
|
190 |
All-Transactions House Price Index for Oregon |
|
191 |
All-Transactions House Price Index for Washington |
|
192 |
All-Transactions House Price Index for North Dakota |
|
193 |
All-Transactions House Price Index for South Carolina |
|
194 |
All-Transactions House Price Index for Louisiana |
|
195 |
All-Transactions House Price Index for Virginia |
|
196 |
All-Transactions House Price Index for Oklahoma |
|
197 |
All-Transactions House Price Index for Alaska |
|
198 |
All-Transactions House Price Index for New Mexico |
|
199 |
All-Transactions House Price Index for Iowa |
|
200 |
All-Transactions House Price Index for Indiana |
|
201 |
All-Transactions House Price Index for Delaware |
|
202 |
All-Transactions House Price Index for Tennessee |
|
203 |
All-Transactions House Price Index for Vermont |
|
204 |
All-Transactions House Price Index for Kansas |
|
205 |
All-Transactions House Price Index for Kentucky |
|
206 |
All-Transactions House Price Index for West Virginia |
|
207 |
All-Transactions House Price Index for Nebraska |
|
208 |
All-Transactions House Price Index for South Dakota |
|
209 |
All-Transactions House Price Index for Montana |
|
210 |
All-Transactions House Price Index for Wyoming |
|
211 |
All-Transactions House Price Index for Arkansas |
|
212 |
All-Transactions House Price Index for Mississippi |
|
213 |
All-Transactions House Price Index for the District of Columbia |
|
214 |
New Private Housing Units Authorized by Building Permits for Alaska |
|
215 |
New Private Housing Units Authorized by Building Permits for Alabama |
|
216 |
New Private Housing Units Authorized by Building Permits for Arkansas |
|
217 |
New Private Housing Units Authorized by Building Permits for Arizona |
|
218 |
New Private Housing Units Authorized by Building Permits for California |
|
219 |
New Private Housing Units Authorized by Building Permits for Colorado |
|
220 |
New Private Housing Units Authorized by Building Permits for Connecticut |
|
221 |
New Private Housing Units Authorized by Building Permits for Delaware |
|
222 |
New Private Housing Units Authorized by Building Permits for Florida |
|
223 |
New Private Housing Units Authorized by Building Permits for Georgia |
|
224 |
New Private Housing Units Authorized by Building Permits for Hawaii |
|
225 |
New Private Housing Units Authorized by Building Permits for Iowa |
|
226 |
New Private Housing Units Authorized by Building Permits for Idaho |
|
227 |
New Private Housing Units Authorized by Building Permits for Illinois |
|
228 |
New Private Housing Units Authorized by Building Permits for Indiana |
|
229 |
New Private Housing Units Authorized by Building Permits for Kansas |
|
230 |
New Private Housing Units Authorized by Building Permits for Kentucky |
|
231 |
New Private Housing Units Authorized by Building Permits for Louisiana |
|
232 |
New Private Housing Units Authorized by Building Permits for Massachusetts |
|
233 |
New Private Housing Units Authorized by Building Permits for Maryland |
|
234 |
New Private Housing Units Authorized by Building Permits for Maine |
|
235 |
New Private Housing Units Authorized by Building Permits for Michigan |
|
236 |
New Private Housing Units Authorized by Building Permits for Minnesota |
|
237 |
New Private Housing Units Authorized by Building Permits for Missouri |
|
238 |
New Private Housing Units Authorized by Building Permits for Mississippi |
|
239 |
New Private Housing Units Authorized by Building Permits for Montana |
|
240 |
New Private Housing Units Authorized by Building Permits for North Carolina |
|
241 |
New Private Housing Units Authorized by Building Permits for North Dakota |
|
242 |
New Private Housing Units Authorized by Building Permits for Nebraska |
|
243 |
New Private Housing Units Authorized by Building Permits for New Hampshire |
|
244 |
New Private Housing Units Authorized by Building Permits for New Jersey |
|
245 |
New Private Housing Units Authorized by Building Permits for New Mexico |
|
246 |
New Private Housing Units Authorized by Building Permits for Nevada |
|
247 |
New Private Housing Units Authorized by Building Permits for New York |
|
248 |
New Private Housing Units Authorized by Building Permits for Ohio |
|
249 |
New Private Housing Units Authorized by Building Permits for Oklahoma |
|
250 |
New Private Housing Units Authorized by Building Permits for Oregon |
|
251 |
New Private Housing Units Authorized by Building Permits for Pennsylvania |
|
252 |
New Private Housing Units Authorized by Building Permits for Rhode Island |
|
253 |
New Private Housing Units Authorized by Building Permits for South Carolina |
|
254 |
New Private Housing Units Authorized by Building Permits for South Dakota |
|
255 |
New Private Housing Units Authorized by Building Permits for Tennessee |
|
256 |
New Private Housing Units Authorized by Building Permits for Texas |
|
257 |
New Private Housing Units Authorized by Building Permits for Utah |
|
258 |
New Private Housing Units Authorized by Building Permits for Virginia |
|
259 |
New Private Housing Units Authorized by Building Permits for Vermont |
|
260 |
New Private Housing Units Authorized by Building Permits for Washington |
|
261 |
New Private Housing Units Authorized by Building Permits for Wisconsin |
|
262 |
New Private Housing Units Authorized by Building Permits for West Virginia |
|
263 |
New Private Housing Units Authorized by Building Permits for Wyoming |
|
264 |
New Private Housing Units Authorized by Building Permits: 1-Unit Structures for Alaska |
|
265 |
New Private Housing Units Authorized by Building Permits: 1-Unit Structures for Alabama |
|
266 |
New Private Housing Units Authorized by Building Permits: 1-Unit Structures for Arkansas |
|
267 |
New Private Housing Units Authorized by Building Permits: 1-Unit Structures for Arizona |
|
268 |
New Private Housing Units Authorized by Building Permits: 1-Unit Structures for California |
|
269 |
New Private Housing Units Authorized by Building Permits: 1-Unit Structures for Colorado |
|
270 |
New Private Housing Units Authorized by Building Permits: 1-Unit Structures for Connecticut |
|
271 |
New Private Housing Units Authorized by Building Permits: 1-Unit Structures for Delaware |
|
272 |
New Private Housing Units Authorized by Building Permits: 1-Unit Structures for Florida |
|
273 |
New Private Housing Units Authorized by Building Permits: 1-Unit Structures for Georgia |
|
274 |
New Private Housing Units Authorized by Building Permits: 1-Unit Structures for Hawaii |
|
275 |
New Private Housing Units Authorized by Building Permits: 1-Unit Structures for Iowa |
|
276 |
New Private Housing Units Authorized by Building Permits: 1-Unit Structures for Idaho |
|
277 |
New Private Housing Units Authorized by Building Permits: 1-Unit Structures for Illinois |
|
278 |
New Private Housing Units Authorized by Building Permits: 1-Unit Structures for Indiana |
|
279 |
New Private Housing Units Authorized by Building Permits: 1-Unit Structures for Kansas |
|
280 |
New Private Housing Units Authorized by Building Permits: 1-Unit Structures for Kentucky |
|
281 |
New Private Housing Units Authorized by Building Permits: 1-Unit Structures for Louisiana |
|
282 |
New Private Housing Units Authorized by Building Permits: 1-Unit Structures for Massachusetts |
|
283 |
New Private Housing Units Authorized by Building Permits: 1-Unit Structures for Maryland |
|
284 |
New Private Housing Units Authorized by Building Permits: 1-Unit Structures for Maine |
|
285 |
New Private Housing Units Authorized by Building Permits: 1-Unit Structures for Michigan |
|
286 |
New Private Housing Units Authorized by Building Permits: 1-Unit Structures for Minnesota |
|
287 |
New Private Housing Units Authorized by Building Permits: 1-Unit Structures for Missouri |
|
288 |
New Private Housing Units Authorized by Building Permits: 1-Unit Structures for Mississippi |
|
289 |
New Private Housing Units Authorized by Building Permits: 1-Unit Structures for Montana |
|
290 |
New Private Housing Units Authorized by Building Permits: 1-Unit Structures for North Carolina |
|
291 |
New Private Housing Units Authorized by Building Permits: 1-Unit Structures for North Dakota |
|
292 |
New Private Housing Units Authorized by Building Permits: 1-Unit Structures for Nebraska |
|
293 |
New Private Housing Units Authorized by Building Permits: 1-Unit Structures for New Hampshire |
|
294 |
New Private Housing Units Authorized by Building Permits: 1-Unit Structures for New Jersey |
|
295 |
New Private Housing Units Authorized by Building Permits: 1-Unit Structures for New Mexico |
|
296 |
New Private Housing Units Authorized by Building Permits: 1-Unit Structures for Nevada |
|
297 |
New Private Housing Units Authorized by Building Permits: 1-Unit Structures for New York |
|
298 |
New Private Housing Units Authorized by Building Permits: 1-Unit Structures for Ohio |
|
299 |
New Private Housing Units Authorized by Building Permits: 1-Unit Structures for Oklahoma |
|
300 |
New Private Housing Units Authorized by Building Permits: 1-Unit Structures for Oregon |
|
301 |
New Private Housing Units Authorized by Building Permits: 1-Unit Structures for Pennsylvania |
|
302 |
New Private Housing Units Authorized by Building Permits: 1-Unit Structures for Rhode Island |
|
303 |
New Private Housing Units Authorized by Building Permits: 1-Unit Structures for South Carolina |
|
304 |
New Private Housing Units Authorized by Building Permits: 1-Unit Structures for South Dakota |
|
305 |
New Private Housing Units Authorized by Building Permits: 1-Unit Structures for Tennessee |
|
306 |
New Private Housing Units Authorized by Building Permits: 1-Unit Structures for Texas |
|
307 |
New Private Housing Units Authorized by Building Permits: 1-Unit Structures for Utah |
|
308 |
New Private Housing Units Authorized by Building Permits: 1-Unit Structures for Virginia |
|
309 |
New Private Housing Units Authorized by Building Permits: 1-Unit Structures for Vermont |
|
310 |
New Private Housing Units Authorized by Building Permits: 1-Unit Structures for Washington |
|
311 |
New Private Housing Units Authorized by Building Permits: 1-Unit Structures for Wisconsin |
|
312 |
New Private Housing Units Authorized by Building Permits: 1-Unit Structures for West Virginia |
|
313 |
New Private Housing Units Authorized by Building Permits: 1-Unit Structures for Wyoming |
| #9 |
314 |
Total Personal Income in Alaska |
|
315 |
Total Personal Income in Alabama |
|
316 |
Total Personal Income in Arkansas |
|
317 |
Total Personal Income in Arizona |
|
318 |
Total Personal Income in California |
|
319 |
Total Personal Income in Colorado |
|
320 |
Total Personal Income in Connecticut |
|
321 |
Total Personal Income in Delaware |
|
322 |
Total Personal Income in Florida |
|
323 |
Total Personal Income in Georgia |
|
324 |
Total Personal Income in Hawaii |
|
325 |
Total Personal Income in Iowa |
|
326 |
Total Personal Income in Idaho |
|
327 |
Total Personal Income in Illinois |
|
328 |
Total Personal Income in Indiana |
|
329 |
Total Personal Income in Kansas |
|
330 |
Total Personal Income in Kentucky |
|
331 |
Total Personal Income in Louisiana |
|
332 |
Total Personal Income in Massachusetts |
|
333 |
Total Personal Income in Maryland |
|
334 |
Total Personal Income in Maine |
|
335 |
Total Personal Income in Michigan |
|
336 |
Total Personal Income in Minnesota |
|
337 |
Total Personal Income in Missouri |
|
338 |
Total Personal Income in Mississippi |
|
339 |
Total Personal Income in Montana |
|
340 |
Total Personal Income in North Carolina |
|
341 |
Total Personal Income in North Dakota |
|
342 |
Total Personal Income in Nebraska |
|
343 |
Total Personal Income in New Hampshire |
|
344 |
Total Personal Income in New Jersey |
|
345 |
Total Personal Income in New Mexico |
|
346 |
Total Personal Income in Nevada |
|
347 |
Total Personal Income in New York |
|
348 |
Total Personal Income in Ohio |
|
349 |
Total Personal Income in Oklahoma |
|
350 |
Total Personal Income in Oregon |
|
351 |
Total Personal Income in Pennsylvania |
|
352 |
Total Personal Income in Rhode Island |
|
353 |
Total Personal Income in South Carolina |
|
354 |
Total Personal Income in South Dakota |
|
355 |
Total Personal Income in Tennessee |
|
356 |
Total Personal Income in Texas |
|
357 |
Total Personal Income in Utah |
|
358 |
Total Personal Income in Virginia |
|
359 |
Total Personal Income in Vermont |
|
360 |
Total Personal Income in Washington |
|
361 |
Total Personal Income in Wisconsin |
|
362 |
Total Personal Income in West Virginia |
|
363 |
Total Personal Income in Wyoming |
|
364 |
Total Personal Income in the District of Columbia |
Appendix B. The Nonlinear Iterative Partial Least Squares (NIPALS) algorithm
In contrast to the two stages factor model5, for the partial least squares regression, the latent component variables are obtained iteratively. In other words, to identify the second component PLSR direction we first adjust each of the variables for ΔF1, by regressing each variable on ΔF1 and taking residuals. We believe these residuals contain the remaining information and can be explained by introducing another component in the model.
5 It is well known that two-stage approach the first component always captures most of the variance, the second component most and so on until all the variance is accounted for. Since the first capture most of the variance, they are typically of focus.
The Nonlinear Iterative Partial Least Squares (NIPALS) algorithm is shown below. It starts with scaled and centered data.
● The x-weights, wN×1:
|
wN×1=X′N×TuT×1/u′1×TuT×1(Gettingastartingvectorofu,usuallyu=y)
|
(B1)
|
● Calculate X-scores, ΔFT×1:
● The y-weights, c:
|
c=y′1×T,ΔFT×1/ΔF′1×TΔFT×1
|
(B3)
|
● Update set of Y-scores, u:
● Convergence is tested on the change in u, i.e., ‖uold−unew‖‖unew‖<10−8. If the convergence hast not reached, return to step 2, otherwise continue with step 5.
● Remove the present component from X and y use these deflated matrices as X and y in the next component6:
6 It is important to note that after each component, r, the design matrix XT×N is deflated by subtracting ΔFT×1p′1×N from XT×N. Hence, the weights, wN×1, is referred to the residuals after previous dimension, eti,a−1, instead of relating to the X-variables themselves. Therefore, the equation, ΔFtr=∑Ni=1w∗irXti, becomes ΔFtr=∑Ni=1wireti,a−1, where eti,a−1=eti,a−2−ΔFt,a−1pa−1,i. When a=1, eti,0=Xti. However, the weights, w, can be transformed to w*, which directly related to X, given the equation ΔFtr=∑Ni=1w∗irXti. Manne (1987) showed that the relationship between above two is expressed by W∗N×R=WN×R(P′R×NWN×R)−1.
|
XT×N=XT×N−ΔFT×1p′1×N,wherepN×1=X′N×TΔFT×1/(ΔF′1×TΔFT×1)
|
(B5)
|
● Continue with next component (i.e., back to step 1 with the deflated y and X) until we think that there is no more significant information in X about y.









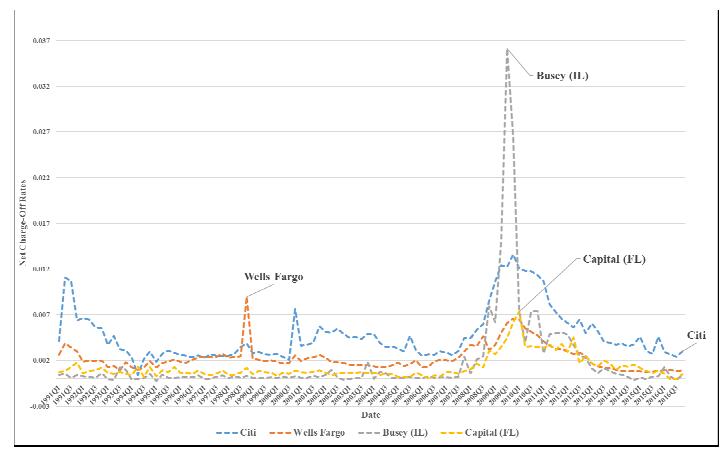
 DownLoad:
DownLoad: