Pressurized Carbon Dioxide as Heat Transfer Fluid: In uence of Radiation on Turbulent Flow Characteristics in Pipe

1.   Introduction

Infectious diseases are known to have caused huge devastation and loss of human life since ancient times, and they have been posing a great threat, especially to developing countries. Over the last two decades, human beings have witnessed numbers of major outbreaks of infectious diseases such as SARS (2003), H7N9 (2013) in China, and the Ebola virus (2014) in West Africa ^[1,2]. These outbreaks have huge negative impacts on people's health and social stability. Hence, how to prevent the spread of diseases effectively becomes an important and hot issue. Meanwhile, more and more researchers have been focusing on studying the transmission mechanism of epidemic diseases in recent years; see ^[3,4,5,6,7].

It has been widely agreed that the mathematical modeling of infectious diseases is an effective tool and plays a crucial role in investigating the transmission mechanism and dynamics behaviors of various communicable diseases ^[8]. One of the pioneer works in this field was done by Kermack and McKendrick ^[9,10,11], where the authors established two classic compartmental epidemic models called susceptible-infected-recovered (SIR) and susceptible-infected-susceptible (SIS) models. From then on, many mathematical models about the prevalence of diseases which descend from the two fundamental epidemic models have been widely used in investigating the spreading mechanics of epidemic diseases ^[3,5,6,12]. In SIR models, one usually supposes that recovered individuals could not be infected again because infected individuals become permanently immune once recovered. However, for some diseases (influenza, malaria), the recovered individuals may lose immunity after a while and they will be susceptible again. By taking this factor into account, SIRS models are proposed and investigated ^[3,5]. Moreover, in some bacterial agent diseases such as plague and venereal diseases, the recovered individuals cannot keep immunity for a long time. Therefore, it is more reasonable and appropriate to incorporate the case that a part of infected individuals may go back directly to the susceptible class after some treatments into epidemiology modeling ^[5,6,12]. In ^[6], the authors established an SIRS model with nonlinear incidence rate as well as transfer from infectious to susceptible and investigated the global dynamics of the model. In these compartmental epidemic models, there is always an underlying assumption that the population is sufficiently large and all individuals are mixed uniformly. It means that every individual has the same possibility to contact others, whereas it cannot reflect the realistic feature of the epidemic transmission mechanics completely since different individuals may have different numbers of acquaintances, and the contact behaviors of individuals exhibit heterogeneity ^[13,14]. Thus, it is essential to take the effect of contact heterogeneity into consideration in investigating the transmission mechanics of epidemic diseases.

It is well known that complex networks provide a powerful framework for describing and quantifying the topological structures of various social, economic and biological systems ^[15]. In particular, the heterogeneity of contact patterns can be well characterized by degree fluctuation of heterogeneous networks ^[16]. In view of this, the structures of complex network are embedded into the traditional epidemic models, and the epidemic dynamics in complex networks have attracted increasing attention and been studied extensively in recent years ^{[17,18,19,20,21,22,23,24,25,26,27]}. In 2001, Pastor-Satorras and Vespignani ^[20] proposed and studied an SIS epidemic model in highly heterogeneous networks (i.e., scale-free networks) and showed that a highly heterogeneous contact pattern can result in the absence of any epidemic threshold for the first time, i, e., the threshold approaches zero in the limit of a large number of edges and nodes, and even quite a small infectious rate can lead to a major epidemic outbreaks. This is a new epidemic spreading phenomenon which is completely different from previous works. And this result was proved rigorously by Wang and Dai in ^[21]. The dynamics of SIR model in heterogeneous networks was also investigated in ^[23], and the authors found that the epidemic threshold will increase with network size on finite networks. In ^[27], Huo et al. proposed a fractional SIR model with birth and death rates on heterogeneous complex networks and obtained that the threshold value $ \mathcal{R}_0 $ determines the dynamics of the model. In order to investigate the heterogeneities of disease transmission about SIRS models, Li et al. ^[25] proposed a new SIRS model with nonlinear infectivity as well as birth and death rates on complex networks and obtained that the disease-free equilibrium is globally asymptotically stable when the basic reproduction number $ \mathcal{R}_0 < 1 $; when $ \mathcal{R}_0 > 1 $, then there exists a unique endemic equilibrium which is globally asymptotically stable. In ^[24] and ^[18], the authors proposed and investigated an SIRS epidemic model with infective individuals entering into the removed or susceptible on complex network respectively. But both of them only focused on the threshold of the epidemic models and the dynamics of equilibria were not discussed.

To the best of our knowledge, the factor of population turnover is not considered in most of aforementioned models, and there are few studies ^{[25,27,28,29,30]} about incorporating demographics into network disease models. Inspired by the works of ^[18,24,25] and ^[28], in this paper, we shall establish an improved SIRS model on complex heterogeneous networks by taking both demographics and transfer from infectious to susceptible into consideration. Our main goal is to discuss the global epidemic dynamics of the model and provide some strategies to prevent the epidemic outbreaks. The remainder of this article is organized as follows. A network-based SIRS model with demographics and transfer from infectious to susceptible is proposed in Section 2. The basic reproduction number of the model and the stability of equilibria are investigated in Section 3 and Section 4. In Section 5, the effects of three major immunization strategies are investigated and compared. In Section 6, some numerical simulations are given to support the theoretical analysis. Finally, conclusions are drawn in Section 7.

2.   Epidemic model on networks

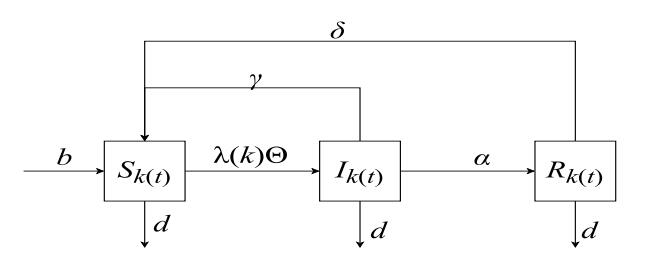
In this paper, we define the whole population as a finite size network. Every node of the network represents an individual and the edges are the interactions among individuals. The degree $ k $ of a node denotes the number of edges connected to the node. Let $ S_{k}(t) $, $ I_{k}(t) $ and $ R_{k}(t) $ be the number of the susceptible, infected and recovered nodes with degree $ k $ at time $ t $, respectively, for $ k = 1, 2, ..., n $, where $ n $ is the maximal degree of the nodes among the network. The transmission sketch is shown in Figure 1.

Based on the mean-field theory, the dynamics of the network-based model can be described by the following differential equations

where the parameter $ b $ denotes the number of newly born susceptible nodes with degree $ k $ per unit time; $ \lambda(k) $ (degree-dependent) is the infected rate of a susceptible individual; $ d $ represents the death rate; $ \gamma $ is the transfer rate from the infected class to the susceptible class; $ \delta $ denotes the immunity loss rate; $ \alpha $ represents the recovery rate from infected individuals. The parameters $ b, \; d, \; \lambda(k), \; \alpha, \; \gamma\; \mbox{and} \; \delta $ are all nonnegative by their epidemiological meaning. $ \Theta(t) $ represents the probability that a randomly chosen edge of a node degree $ k $ points to an infected node at time $ t $ and it satisfies the following equation.

where $ P(i\mid k) $ represents the probability that a node with degree $ k $ is connected to a node with degree $ i $. In this paper, we investigate epidemic transmission on uncorrelated networks, then the probability is considered independent of the connectivity of the node from which the link is emanating^[20]. Hence $ P(i\mid k) $ = $ iP(i)/\langle k\rangle $, where $ P(k) $ represents the probability of a randomly chosen node with degree $ k $ and $ \sum_{k = 1}^{n}P(k) = 1 $. $ \langle k\rangle = \sum_{k = 1}^{n}kP(k) $ is the average degree of the network. $ \varphi(i) $ represents the infectivity of a node with degree $ i $, that is, the mean number of edges from which a node with degree $ i $ can transmit diseases ^[19]. $ N_k(t) = S_k(t)+I_k(t)+R_k(t) $ denotes the number of nodes with degree $ k $ at time $ t $.

Adding the three equations of model (2.1), we have $ \frac{{\rm d}N_k(t)}{{\rm d}t} = b-dN_k(t) $. Then $ N_{k}(t) = N_k(0)e^{-dt}+\frac{b}{d}(1-e^{-dt}) $. For the purpose of having a population of constant size, throughout this paper we always assume that

$ {\bf(H_1)}\quad S_k(0)+I_k(0)+R_k(0) = N_k(0) = \frac{b}{d}. $

Hence, we have $ S_k(t)+I_k(t)+R_k(t) = N_k(t) = \frac{b}{d} $ for all $ t\geq 0 $. Thus

For the practical consideration, the initial conditions of system (2.1) take the form

In this paper, beside the hypothesis $ \bf(H_1) $, we also need some hypotheses shown as below:

$ {\bf(H_2)} $ the infection rate is bounded, i.e., there exists two constants $ \mu, \; \nu > 0 $, such that $ 0 < \mu\leq \lambda(k)\leq\nu $;

$ {\bf(H_3)} $ the network should be static, that is, the degree of each node is time invariant.

Now, we reveal some properties of solutions of system (2.1).

Lemma 2.1. Suppose $ (S_1(t), I_1(t), R_1(t), \cdots, S_n(t), I_n(t), R_n(t)) $ is a solution of system (2.1) with the initial conditions (2.2). Then we have the following conclusion

Proof. Firstly, we prove $ \Theta(t) > 0 $ for all $ t > 0 $. By the second equation of system (2.1), we have

Obviously, we have

Since $ \Theta(0) > 0 $, one can obtain that $ \Theta(t) > 0 $ for all $ t > 0 $.

Note that $ S_k(0) > 0 $. Based on the fact of the first equation of system (2.1) and the continuity of $ S_k(t) $, we could find a sufficiently small $ t_0 > 0 $ such that $ S_k(t) > 0 $ for $ t\in(0, t_0) $. We now prove that $ S_k(t) > 0 $ for all $ t > 0 $. Assume $ S_k(t) > 0 $ is not always valid, then there exists $ i\in\{1, 2, ...n\} $ and the first time $ t_1\geq t_0 > 0 $ such that $ S_i(t_1) = 0 $ and $ S_i (t) > 0 $ for $ t\in (0, t_1) $. From the second equation of system (2.1), we have $ \frac{{\rm d}I_i(t)}{{\rm d}t} > -(\gamma+d+\alpha)I_i(t) $ for $ t\in (0, t_1) $. Thus, $ I_i(t) > I_i(0)e^{-(\gamma+d+\alpha)t}\geq0 $ for $ t\in (0, t_1) $.

Combining $ I_i(t)\geq0 $ for $ t\in (0, t_1) $ with the third equation of system (2.1), we have $ \frac{{\rm d}R_i(t)}{{\rm d}t} > -(d+\delta)R_i(t) $ for $ t\in (0, t_1) $. Hence, one can obtain that $ R_i(t) > R_i(0)e^{-(d+\delta)t} $ for $ t\in (0, t_1) $. By the continuity of $ I_i(t) $ and $ R_i(t) $, we know $ I_i(t_1)\geq0 $ and $ R_i(t)\geq0 $. Then the first equation of system (2.1) shows

So, one can find that $ S_i(t) < S_i(t_1) $ for $ t\in(0, t_1) $. Due to $ S_i(t_1) = 0 $, it contradicts to $ S_k(t) > 0 $ obviously. Therefore, $ S_k(t) > 0 $ for all $ t > 0 $ and all $ k = 1, 2, ..., n $. By similar discussions, we also have $ I_k(t)\geq0 $ and $ R_k(t)\geq0 $ for all $ t > 0 $. Therefore, this completes the proof.

Hence, we only need to focus on the dynamics of solutions of system (2.1) in the following feasible bounded region

Remark 2.1. It's remarkable that system (2.1) includes some special cases, if $ b = d = \alpha = \delta = 0 $, system (2.1) turns into an SIS model ^[20]; if $ b = d = \gamma = 0 $, model (2.1) is an SIR model ^[23]; if $ \gamma = 0 $ and $ b = d $, system (2.1) is an SIRS model ^[25].

Remark 2.2. In recent years, many different types of $ \lambda(k) $ and $ \varphi(k) $ have been studied. The most common types for $ \lambda(k) $ is $ \lambda(k) = \lambda k $ (see, ^[30,21]). For $ \varphi(k) $, one can see $ \varphi(k) = k $ is choosen in ^[30,18]. Furthermore, in ^[23], the authors adopt a general form of $ \varphi(k) = \frac{ak^\alpha}{1+vk^\alpha} $, where $ 0\leq\alpha\leq 1, \; a > 0 $ and $ v\geq 0 $. The types $ \varphi(k) = C $ ($ C $ is a constant) ^[22] and $ \varphi(k) = k^m $ $ (0 < m\leq1) $ ^[17] are discussed as well.

3.   Basic reproduction number and equilibria

In epidemiological investigations, the basic reproduction number $ \mathcal{R}_0 $ is widely used to measure the epidemic potential.The term basic reproduction number represents the mean number of secondary cases produced by a typical infectious individual during its entire infectious period in a completely susceptible population ^[31,32]. By the methods in ^[31], the transmission matrix $ F $ for the rate of appearance of new infections and the transition matrix $ V $ for the transfer rate of individuals among compartments around the disease-free equilibrium $ E_0 $ are denoted as follows, respectively

and

Hence, the basic reproduction number $ \mathcal{R}_0 = \rho(FV^{-1}) $ is the spectral radius of the next generation matrix $ FV^{-1} $. By direct calculations, we have

where $ \langle\lambda(k)\varphi(k)\rangle = \sum_{k = 1}^n{\lambda(k)\varphi(k)P(k)} $.

Next, we will investigate the existence of equilibria of system (2.1).

Theorem 3.1. Consider system (2.1), then we have following results:

(i) There always exists a disease-free equilibrium $ E_0 = (\frac{b}{d}, 0, 0, \cdots, \frac{b}{d}, 0, 0) $.

(ii) There is a unique endemic equilibrium $ E^* = (S_1^*, I_1^*, R_1^*, \cdots, S_n^*, I_n^*, R_n^*) $ when $ \mathcal{R}_0 > 1 $, where

with $ \Theta^{*} = \frac{1}{\langle k \rangle}\frac{d}{b}\sum_{k = 1}^n{\varphi(k)P(k)I_{k}^*}, \; k = 1, 2, \cdots, \; n $.

Proof. Clearly, $ E_0 $ is always a disease-free equilibrium of system (2.1).

Now, let us consider the existence of $ E^* $. Note that the equilibrium $ E^* $ satisfies the following equalities

From the second and the third equations of (3.1), we have

Substituting (3.2) and (3.3) into the first equation of (3.1), one can obtain

Substituting (3.4) into the expression of $ \Theta^* $, we obtain a self-consistency equation about $ \Theta^* $.

Obviously, $ \Theta^* = 0 $ is a solution of (3.5). Note that

If $ \mathcal{R}_0 > 1 $, then we have $ \frac{{\rm d}f(\Theta^*)}{{\rm d}\Theta^*}|_{\Theta^* = 0} > 1 $. Consequently, the equation (3.5) has a unique nontrivial solution $ \Theta^*(\Theta^* \in (0, 1)) $. It means that there exists one and only one endemic equilibrium when $ \mathcal{R}_0 > 1 $. This finishes the proof.

Remark 3.1. From Theorem 3.1, we know that the existence of the endemic equilibrium depends on $ \mathcal{R}_0 $. Obviously, $ \mathcal{R}_0 $ is in proportion to the heterogeneous parameter $ \frac{\langle\lambda(k)\varphi(k)\rangle}{\langle k\rangle} $ which is related to the topology of the networks closely. We also find that $ \mathcal{R}_0 $ has nothing to do with the immunity loss rate $ \delta $. It seems that the transfer rate $ \gamma $ and the recovery rate $ \alpha $ have the same effects on $ \mathcal{R}_0 $, i.e., increasing the transfer rate $ \gamma $ and the recovery rate $ \alpha $ will decrease $ \mathcal{R}_0 $.

4.   Global dynamics of the model

In this section, we will consider the global stability of equilibria $ E_0 $ and $ E^* $. To begin with we will discuss the local asymptotical stability of the disease-free equilibrium $ E_0 $.

Theorem 4.1. The disease-free equilibrium $ E_0 $ of system (2.1) is locally asymptotically stable when $ \mathcal{R}_0 < 1 $ and is unstable when $ \mathcal{R}_0 > 1 $.

Proof. As shown in Section 2, for the purpose of having a population of constant size, we assume that the initial values always satisfy the hypothesis $ \bf{(H_1)} $. Then we can obtain $ S_k(t)+I_k(t)+R_k(t) = N_k(t) = \frac{b}{d} $. Hence, system (2.1) can be reduced in the following form:

The Jacobian matrix of the disease-free equilibrium $ E_0 $ of system (4.1) is given by

where

By induction, the characteristic equation can be shown as follows

It's obvious that $ J $ has $ n-1 $ negative eigenvalues that equal to $ -(\gamma+d+\alpha) $ and $ n $ negative eigenvalues that equal to $ -(d+\delta) $. The $ 2n $-$ th $ eigenvalue completely depends on

When $ \mathcal{R}_0 < 1 $, then $ x < 0 $; when $ \mathcal{R}_0 > 1 $, then $ x > 0 $. Consequently, $ E_0 $ is locally asymptotically stable if $ \mathcal{R}_0 < 1 $ and is unstable if $ \mathcal{R}_0 > 1 $. The proof is complete.

Next, we proceed to study the global attractivity of $ E_0 $. For this purpose, we need the following results.

Lemma 4.1. ^[33] If $ a > 0, \; b > 0 $, and $ \frac{{\rm d}x(t)}{{\rm d}t}\leq b-ax $, when $ t\geq 0 $ and $ x(0)\geq 0 $, then $ \limsup\limits_{t\rightarrow\infty}x(t)\leq\frac{b}{a} $.

We are now in a position to establish the following results about the global asymptotical stability of the disease-free equilibrium $ E_0 $ by employing above lemma.

Theorem 4.2. The disease-free equilibrium $ E_0 $ of system (2.1) is globally asymptotically stable when $ \mathcal{R}_0 < 1 $.

Proof. Equation (2.3) implies that

where $ r = (\gamma+d+\alpha)(\mathcal{R}_0-1) $, it follows from $ \mathcal{R}_0\leq 1 $ that $ r\leq 0 $.

$ (i) $ if $ r = 0 $, then we have $ \frac{{\rm d}\Theta(t)}{{\rm d}t}\leq-\mu\Theta^2(t) $. Using following comparison equation

Obviously, we can see that $ \Theta(t)\leq x(t) = \frac{\Theta(0)}{1+\mu\Theta(0)t} $, and hence $ \lim\limits_{t\rightarrow \infty}\Theta(t) = 0 $.

$ (ii) $ if $ r < 0 $, consider the comparison equation

By using the comparison principle, one can obtain $ \Theta(t)\leq y(t) = \frac{rce^{rt}}{1+c\mu e^{rt}} $, where $ c = \frac{\Theta(0)}{r-\mu\Theta(0)} $. Therefore, $ \lim\limits_{t\rightarrow \infty}\Theta(t) = 0 $.

From $ (i) $ and $ (ii) $, we have

Since $ \varphi(k) > 0 $ and $ P(k) > 0 $ for all $ k $, then we have $ \lim\limits_{t\rightarrow \infty}I_k(t) = 0 $.

Next, we will prove $ \lim\limits_{t\rightarrow \infty}R_k(t) = 0 $. Owing to $ \lim\limits_{t\rightarrow \infty}I_k(t) = 0 $, then for any given sufficiently small constant $ \varepsilon > 0 $, there exists $ t_1 > 0 $ such that $ 0\leq I_k(t)\leq \varepsilon $ for $ t > t_1 $. According to the third equation of system (2.1), we have

By Lemma 2, we obtain that $ \limsup\limits_{t\rightarrow +\infty}R_k(t)\leq\frac{\alpha}{(d+\delta)}\varepsilon $. Setting $ \varepsilon\rightarrow 0 $, then $ \limsup\limits_{t\rightarrow +\infty}R_k(t)\leq 0 $, and hence $ \lim\limits_{t\rightarrow \infty}R_k(t) = 0 $.

Finally, due to $ S_k(t) = \frac{b}{d}-I_k(t)-R_k(t) $ we have $ \lim\limits_{t\rightarrow\infty}S_k(t) = \frac{b}{d} $. This implies that the disease-free equilibrium $ E_0 $ of system (2.1) is globally attractive when $ \mathcal{R}_0\leq 1 $. Note that $ E_0 $ is locally asymptotically stable if $ \mathcal{R}_0 < 1 $ by Theorem 4.1. Therefore, we obtain that $ E_0 $ is globally asymptotically stable if $ \mathcal{R}_0 < 1 $. This completes the proof.

In the following, we will prove the persistence of the disease by employing Theorem 4.6 in ^[34].

Theorem 4.3. The disease is permanent when $ \mathcal{R}_0 > 1 $, i.e., there exists a $ \zeta > 0 $, such that

Proof. Define

It is obvious that $ \Gamma $ is positively invariant with respect to system (2.1). Note that $ \Theta(0) > 0 $, one can deduce that $ I_k(0) > 0 $ for some $ k $ and $ \sum_{k = 1}^n P(k) I_k(0) > 0 $ for all $ k $. Owing to

then we have

Thus, $ X_0 $ is positively invariant as well. Furthermore, there exists a compact set $ \bf{B} $ in which all solutions of (2.1) initiated in $ \Gamma $ will enter and remain forever after. The compactness condition ($ C_{4.2} $) for the set $ \bf{B} $ in ^[34] is verified easily. Let

where $ \tilde{x}_0 = (S_{1}(0), I_{1}(0), R_1(0), \cdots, S_{n}(0), I_{n}(0), R_{n}(0)), \; \omega(\tilde{x}_0) $ is the omega limit set of the solutions of system (2.1) starting at $ \tilde{x}_0 \in \Gamma $. Restricting system (2.1) on $ M_{\partial} $, we obtain that

It is clear that system (4.4) has a unique equilibrium $ E_0 $ in $ \Gamma $, and $ E_0 $ is also the unique equilibrium of system (2.1) in $ M_{\partial} $. Then, we can easily prove that $ E_0 $ is globally asymptotically stable. Therefore $ \Omega = \{{E_0\}} $. $ E_0 $ is a covering of $ \Omega $, which is isolated and acyclic (there exists no nontrivial solution in $ M_{\partial} $ which links $ E_0 $ to itself). Finally, to complete the proof, we only need to show that $ E_0 $ is a weak repeller for $ X_0 $, i.e.

where $ \Psi(t; \tilde{x}_0) $ is an arbitrarily solution starting in $ \tilde{x}_0\in X_0 $. In order to prove (4.5), we need to verify $ W^s(E_0) \cap X_0 = \varnothing $ by the method in ^[35], where $ W^s(E_0) $ is the stable manifold of $ E_0 $. Assume it is not true, then there exists a solution $ \tilde{x}_t\in X_0 $, such that

Hence, for any $ \xi > 0 $, there exists a $ T > 0 $ such that for all $ t > T $

Since $ \mathcal{R}_0 = \frac{\langle\lambda(k)\varphi(k)\rangle}{(\gamma+d+\alpha)\langle k\rangle} > 1 $, namely $ \frac{\langle\lambda(k)\varphi(k)\rangle}{\langle k\rangle}-(\gamma+d+\alpha) > 0 $, then we can choose a sufficiently small $ \xi > 0 $, such that $ \frac{d}{b}\frac{\langle\lambda(k)\varphi(k)\rangle}{\langle k\rangle}(\frac{b}{d}-\xi)-(\gamma+ d+\alpha) > 0 $.

Let $ L(t) = \Theta(t) $, obviously, $ L(t) $ is bounded and the derivative of $ L $ along the solution is

Due to

then we have $ \Theta(t) > \Theta(0)e^{\sigma t} $. Hence $ L(t) = \Theta(t)\rightarrow +\infty $ as $ t\rightarrow +\infty $, which is inconsistent with the boundedness of $ L(t) $. This proof is complete.

Finally, we will further show that the endemic equilibrium $ E^* $ is globally asymptotically stable by constructing a suitable Lyapunov function.

Theorem 4.4. If $ \mathcal{R}_0 > 1 $ and $ \delta > \gamma $, then the endemic equilibrium $ E^* $ of system (2.1) is globally asymptotically stable.

Proof. system (2.1) can be written as

where $ \Lambda = (1+\frac{\gamma}{d}) $, and the components of endemic equilibrium $ E^* $ satisfy the following equations

For the second equation of (4.8), multiplying by $ \varphi(k)P(k) $ and summing both sides with respect to $ k $, we have

Submitting $ I_{k}^*(t) = \frac{b}{d}-S_k^*-R_k^* $ into the third equation of (4.8), then we obtain

Now we investigate a non-negative solution $ (S_1(t), I_1(t), R_1(t), \cdots, S_n(t), I_n(t), R_n(t)) $ of system (2.1). Motivated by Li et al. ^[25], we consider the following Lyapunov function

where $ \rho_1(k) = \frac{d\varphi(k)P(k)}{b\langle k\rangle S_k^*} > 0 $ and $ \rho_2(k) = \frac{\delta-\gamma}{\alpha}\rho_1(k) > 0 $. Clearly, $ V(t) > 0 $ except at $ E^* $, and taking the derivative of $ V(t) $ along the positive solution of (4.7), it follows that

Therefore, $ \frac{{\rm d}V(t)}{{\rm d}t} = 0 $ if and only if $ S_k = S_k^*, \; I_k = I_k^*, \; R_k = R_k^* $ for $ k = 1, 2, \cdots, n $. It means that the largest compact invariant subset contained in the set $ \{\frac{{\rm d}V(t)}{{\rm d}t} = 0\} $ is the singleton $ \{E^*\} $. From the Lasalle Invariance Principle ^[36], one can obtain that the endemic equilibrium $ E^* $ is globally asymptotically stable if $ \mathcal{R}_0 > 1 $ and $ \delta > \gamma $. This completes the proof.

5.   Immunization strategies

From Section 3 and Section 4, we know the basic reproduction number $ \mathcal{R}_0 $ is a key parameter which determines the global dynamics of the epidemic model, and if the basic reproduction number $ \mathcal{R}_0 $ can be reduced to a value less than one, the epidemic disease will die out. Moreover, immunization is one of effective ways in controlling preventable diseases ^{[37,38,39,40]} by reducing the basic reproduction number. However, it is always impossible to vaccinate all individuals in reality because of the high costs and effort. Therefore, in this section we will discuss the impacts of three immunization strategies (i.e., the random immunization, the targeted immunization and the acquaintance immunization) about system (2.1) on the heterogenous networks.

5.1.   Random immunization

Random immunization is the simplest immunization strategy which vaccinates a fraction of the population without selectivity. Let $ p $ $ (0 < p < 1) $ be the immunization rate, then system (2.1) can be written as

Through similar derivations in Section 3, we obtain the basic reproduction number $ \mathcal{R}_0^{r} $ for system (5.1)

Then, similar results are obtained.

Theorem 5.1. Assume $ \mathcal{R}_0 > 1 $. Define $ p_c = 1-\frac{1}{\mathcal{R}_0} $, then

(i) If $ p > p_c $ i.e. $ \mathcal{R}_0^{r} < 1 $, then the disease free equilibrium of system (5.1) is globally asymptotically stable. That is to say, the disease will die out ultimately.

(ii) If $ 0 < p < p_c $ ($ 1 < \mathcal{R}_0^{r} < \mathcal{R}_0 $), then there always exists a unique endemic equilibrium $ E_{r}^{*} $ of system (5.1) which is globally asymptotically stable when $ \delta > \gamma $. That indicates that the random immunization is effective, but cannot eliminate the disease in the network.

5.2.   Targeted immunization

There is a fact that random immunization strategy ignores the heterogeneous connectivity of the network. In order to take this factor into account, the targeted immunization strategy was proposed ^[37,38]. This immunization strategy is to immunize the most highly connected nodes because they are vulnerable to selective attacks in the network. Assuming that all nodes with $ k\geq k_t $ will be immunized, where $ k_t $ is the upper threshold. Then the immunization rate $ p_k $ can be denoted as

Then, system (2.1) becomes

By similar derivations in Section 3, we obtain the basic reproduction number $ \mathcal{R}_0^{t} $ for system (5.2)

Let $ \bar p = \sum_{k = 1}^{n}p_{k}P(k) $ be the average immunization rate, then

where $ Cov(\cdot, \cdot) $ represents the covariance of two variables. For appropriately small $ k_t $, $ p_k-\bar p $ and $ \lambda(k)\varphi(k)-\langle\lambda(k)\varphi(k)\rangle $ have the same signs, except that $ k $'s where $ p_k = \bar p $ or $ \lambda(k)\varphi(k) = \langle\lambda(k)\varphi(k)\rangle $, then $ Cov(p_{k}, \lambda(k)\varphi(k)) > 0 $. That is to say for some $ k_t $, $ \langle p_k\lambda(k)\varphi(k)\rangle > \langle p_k\rangle \langle\lambda(k)\varphi(k)\rangle $. Hence, we have following conclusions.

Theorem 5.2. Consider system (5.2), then we have following results:

(i) If $ \mathcal{R}_0^{t} < 1 < \mathcal{R}_0 $, then the disease free equilibrium of system (5.2) is globally asymptotically stable, i.e. the disease can be controlled by the targeted immunization strategy.

(ii) If $ 1 < \mathcal{R}_0^{t} < \mathcal{R}_0 $, there will always exists a unique endemic equilibrium $ E_{t}^{*} $ of system (5.2), which is globally asymptotically stable when $ \delta > \gamma $.

(iii) For some $ k_t $, $ \langle p_k\lambda(k)\varphi(k)\rangle > \langle p_k\rangle \langle\lambda(k)\varphi(k)\rangle $, then $ \mathcal{R}_0^{t} < \mathcal{R}_0^{r} $. This shows that the targeted immunization is more effective than random immunization.

5.3.   Acquaintance immunization

Since the targeted immunization requires us to know the global connectivity information of each node in networks, and it is always much difficult to carry out in reality. In order to deal with this dilemma, R. Cohen, S. Havlin and D. Ben-Avraham ^[37] proposed the acquaintance immunization scheme for the immunization of random acquaintances of random nodes. Specifically, choose a fraction $ q $ of $ N $ nodes randomly, the probability that a particular node with degree $ k $ is selected for immunization is $ kP(k)/(N\langle k\rangle) $ ^[37,41]. Hence, substituting $ p_k = pN\cdot kP(k)/(N\langle k\rangle) = kP(k)(p/\langle k\rangle) $ to (5.3), then the basic reproduction number for acquaintance immunization is

This implies that acquaintance immunization scheme is effective as well.

Theorem 5.3. For system (5.2), we have following results:

(i) If $ \mathcal{R}_0^{a} < 1 < \mathcal{R}_0 $, then the disease can be controlled by this immunization scheme, i.e., the disease will be eradicated from the network ultimately.

(ii) If $ 1 < \mathcal{R}_0^{a} < \mathcal{R}_0 $, then the disease is uniformly persistent in the network and there always exists a unique endemic equilibrium $ E_{a}^{*} $.

6.   Numerical simulation

In this section, we present several numerical simulations to demonstrate the correctness and effectiveness of the main results. These simulations are based on scale-free networks. We first start with a graph with 5 vertexes, a node with one edge is added into the graph in each time step, and then a BA scale-free network G with 100 nodes is obtained by using preferential attachment mechanism in ^[42]. There will give several numerical examples with different infectivities $ \varphi(k) $ to illustrate the theoretical analysis.

6.1.   Global stability of disease-free equilibrium $ E_0 $

In Figures 2, 3 and 4, we adopt the infected rate $ \lambda(k) = \beta k $ and give infectivity $ \varphi(k) $ three types such as linear, constant and nonlinear infectivity to verify the stability of the disease-free equilibrium.

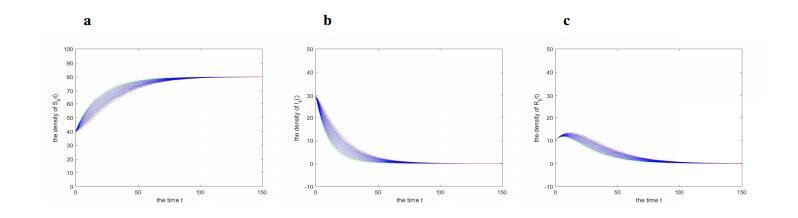
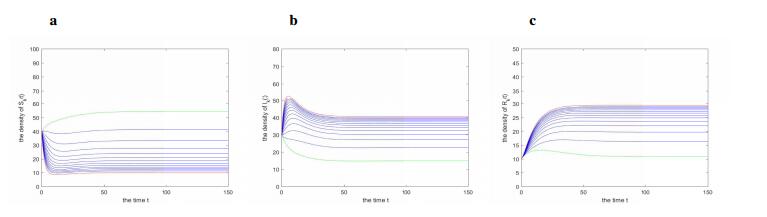
Case ⅰ. Let $ n = 11, \; \varphi(k) = k $, $ b = 2, \; \gamma = 0.04, \; \beta = 0.01, \; d = 0.025, \; \alpha = 0.04, \; \delta = 0.03 $ and the initial values: $ S_k(0) = 40, \; I_k(0) = 30, \; R_k(0) = 10 $. Then we have $ \mathcal{R}_0 = 0.8884 < 1 $. From our results, the disease will die out if $ \mathcal{R}_0 = 0.8884 < 1 $, and the time evolution of the densities of each state for the initial value is drawn in Figure 2. It agrees with Theorem 4.2.

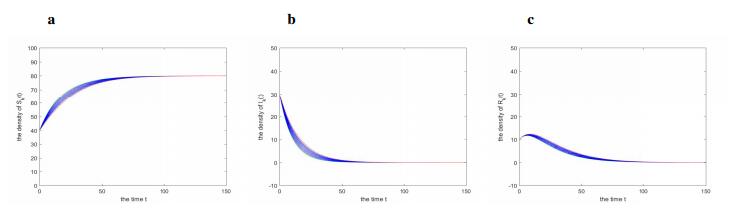
Case ⅱ. Choose $ n = 13, \; \varphi(k) = 4 $ and other parameters are the same as in Case ⅰ. Then one can obtain $ \mathcal{R}_0 = 0.2857 < 1 $. It follows from Theorem 4.2, disease-free equilibrium $ E_0 $ is globally asymptotically stable. The Figure 3 shows the time evolution of the number of each state for the initial value.

Case ⅲ. We choose $ n = 13 $, the nonlinear infectivity $ \varphi(k) = k^{0.5} $ and other parameters are the same as in Case ⅰ as well. Then $ \mathcal{R}_0 = 0.2369 < 1 $, and by Theorem 4.2 the disease-free equilibrium $ E_0 $ is globally asymptotically stable. The time evolution of the densities of each state for the initial value is shown in Figure 3.

6.2.   Global stability of endemic equilibrium $ E^* $

Next, in the same network architecture in Subsection 6.1, we will verify the global asymptotical stability of the endemic equilibrium $ E^* $. Similarly, we choose $ \lambda(k) = \beta k $ and give three types of the infectivity $ \varphi(k) $.

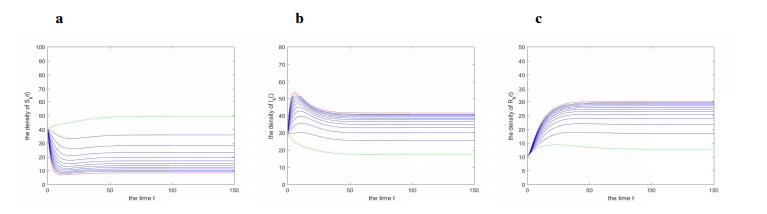
Case ⅳ. We make $ n = 13, \; \varphi(k) = k $, $ b = 2, \; \gamma = 0.02, \; \beta = 0.06, \; d = 0.025, \; \alpha = 0.04, \; \delta = 0.03 $ and the initial value: $ S_k(0) = 40, \; I_k(0) = 30, \; R_k(0) = 10 $. We obtain $ \mathcal{R}_0 = 5.9765 > 1 $, which implies that $ E^* $ is global asymptotical stable from Theorem 4.4. The time evolution of the densities of each state for the initial value is depicted in Figure 5.

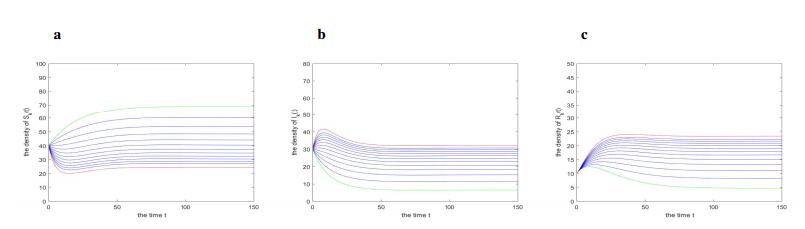
Case ⅴ. Setting $ n = 15, \; \varphi(k) = 4 $ and other parameters are the same as in Case ⅳ. Then one can verify $ \mathcal{R}_0 = 2.1176 > 1 $. Hence it follows from Theorem 4.4 that the endemic equilibrium $ E^* $ is globally asymptotically stable. The Figure 6 shows the time evolution of the densities of each state for the initial values.

Case ⅵ. We choose $ n = 13 $, the nonlinear infectivity $ \varphi(k) = k^{0.5} $ and other parameters are the same as in Case ⅳ as well. Then we obtain $ \mathcal{R}_0 = 1.7420 > 1 $, and the time evolution of the densities of each state for the initial value is presented in Figure 7. It agrees with Theorem 4.4.

As shown in the Figures 5, 6 and 7, it follows from Theorem 4.4 that the endemic equilibrium $ E^* $ is globally asymptotically stable when $ \mathcal{R}_0 > 1 $ and $ \delta > \gamma $. In addition, if we choose $ n = 14, \; \lambda(k) = \beta k $, $ \varphi(k) = k $, $ b = 2, \; \gamma = 0.04, \; \beta = 0.06, \; d = 0.025, \; \alpha = 0.04 $ and $ \delta = 0.03 $, then we can obtain that $ \mathcal{R}_0 = 4.1789 > 1 $ and $ \delta\leq\gamma $ hold. The time evolution of the densities of each state is shown in Figure 8. It seems that the endemic equilibrium $ E^* $ is also globally attractive. However, we could not give a rigorous proof for the global attractivity of $ E^* $ when $ \mathcal{R}_0 > 1 $ and $ \delta\leq\gamma $, which we leave as our future work.

7.   Conclusion

By incorporating demographics and transfer from infectious to susceptible individuals into network disease models, we propose an improved SIRS model on complex networks in this paper. We derive the basic reproduction number $ \mathcal{R}_0 $ by using the next generation matrix method and obtain that the basic reproduction number $ \mathcal{R}_0 $ determines not only the existence of the endemic equilibrium $ E^* $ but also the global stability of equilibria $ E_0 $ and $ E^* $, i.e., the disease-free equilibrium $ E_0 $ is globally asymptotically stable when $ \mathcal{R}_0 < 1 $; when $ \mathcal{R}_0 > 1 $, there exists a unique endemic equilibrium $ E^* $ and the disease is permanent on the network, which indicates that reducing the basic reproduction number $ \mathcal{R}_0 $ below one could eradicate the disease. Meanwhile, by employing the method of Lyapunov function, we prove that if $ \mathcal{R}_0 > 1 $ and $ \delta > \gamma $, the endemic equilibrium $ E^* $ is globally asymptotically stable. Compared with the model in literature ^[27], our model is more general by considering the degree-related infection rate $ \lambda(k) $ and the general form of infectivity $ \varphi(k) $. At the same time, the global dynamics of the disease-free equilibrium and the endemic equilibrium under different forms of infectivity are discussed by some numerical simulations. It also confirms the correctness of the theoretical analysis. In addition, from our numerical simulations, the endemic equilibrium $ E^* $ is globally asymptotically stable when $ \mathcal{R}_0 > 1 $ with $ \delta < \gamma $ which is not proved in the present paper and will be investigated in further exploration.

Some new insights in this paper may help us to understand the spreading of diseases and provide some effective intervening measures to prevent the epidemic outbreaks. As one can see, the basic reproduction number $ \mathcal{R}_0 $ is an important index in disease control, which is closely related to the topology of the networks and some model parameters. One can obtain that increasing the transfer rate $ \gamma $ and the recovery rate $ \alpha $ will decrease $ \mathcal{R}_0 $ to restrict the spreading of the epidemic diseases. Moreover, it is worth noting that $ \mathcal{R}_0 $ is not dependent on the immunity loss rate $ \delta $, which indicates that strengthening the treatment is very important. According to the investigation on three immunization strategies about system (2.1) on the heterogenous networks, we can find that immunizations are also effective ways in controlling diseases transmission by decreasing $ \mathcal{R}_0 $. Furthermore, one can see that the targeted immunization is more effective than random immunization, and the acquaintance immunization is more economical and more easier to be carried out.

Acknowledgments

The authors are grateful to the anonymous referee for the valuable comments. The work is partially supported by NNSF of China (Nos. 11771059, 11401051, 71471020), Hunan Provincial Natural Science Foundation (Nos. 2015JJ3013, 2016JJ1001) and the Scientific Research Fund of Hunan Provincial Education Department of China (No. 18B152).

Conflict of interest

All authors declare no conflicts of interest in this paper.