1. Introduction

A business cycle model, as an important tool for explaining the laws of economic operation, is used to study the fluctuation situation of incomes, costs, investments and other factors in the economic system under the market mechanism. A linear business cycle model can reflect the formation of the business cycle generated by changes of income and investment in economic movements, but such a model cannot accurately describe the nonlinear property of the real economic variable functions and the time lag quality in economic activities. Kaldor (1940) first attempted to analyze the nonlinear effect of dynamic economics and built the Kaldor nonlinear business cycle model, which proved the existence of business cycle, by assuming both the investment and the saving functions are nonlinear ones of the output and capital stock. But this model cannot describe the fact that, in reality, no investment can make consecutive profits at the time of investment. In fact, before Kaldor (1940), Kalechi (1935) had already made some assumptions about business cycle model: the saving portion of the profits is used for investment; the capital increase is due to the past investment decisions; and a pregnant period or a time delay is necessary while the capital equipments are put into production.

Krawiec and Szydlowsk (1999) synthesized the thoughts of Kaldor (1940) and Kalechi (1935) and successfully constructed the Krawiec-Szydlowsk business cycle model by introducing the time lag caused by the delay of past investment decisions. Their research shows that with the increase of time lag, the model system exhibits cyclical behavior or even complicated chaotic behavior. Krawiec (2001) also discovered that past investment decisions can influence the change of the capital stock. Krawiec and Szydlowsk (2008) thus held that in a more reasonable capital accumulation equation, time delay should be introduced into both GDP and capital stock functions. Duboi (2004) employed the differential equation with expectation and delay, combining with the Krawiec-Szydlowsk business cycle model, and further illustrated the importance of expectation to investment decision-making and organizational change. Taking into account the impact caused by both the time delay in investment and the expectation time about the capital stock in investment decision-making, Cheng (2011) built a new model based on the hybrid functional differential equation by introducing the time delay in investment and the expectation time about the capital stock into the Krawiec-Szydlowsk business cycle model; he thus studied the impact of both factors on the business cycle. It is obvious that the typical asymmetry of the actual time series and complex economic phenomena can be described through a nonlinear business cycle model instead of a linear one; besides, by introducing these two variables (parameters) into the nonlinear business cycle model and describing their impact on the formation of business cycle, the investment delay effect can be revealed more accurately.

A lot of researchers applied the bifurcation method in studying the non-linear business cycle model. The bifurcation theory is based on the transformation from the business cycle model to the differential dynamic system. It is used to explore the stability of the system and the existence of periodic orbits; it is also employed to explain the equilibrium solution of the business cycle model, the conditions of economic cycle formation, and even complex Chaos. Comparing to the traditional method, which can only reveal the harmonic oscillation with constant frequencies, the bifurcation method is more effective in describing the dynamic behavior of complicated economic operation. For example, Beretta and Kuang (2001) analyzed the stability of the system relying on the time delay parameter; Wu (2012) cited several bifurcation types of the Kaldor-Kalechi business cycle model with time delay and proved the conditions of their existence; Cesare and Sportelli (2012) utilized the bifurcation theory to describe the complicated economic behavior of fiscal policy delay and income adjustment process.

Taking into account the impact of government expenditure on economic development and the function of the investment decision-making behavior to achieve the desired objectives, this paper studies the dynamic economic behavior of the business cycle model with the following innovative points: (1) Based on the dynamic multiplication-acceleration model theory, combining the investment delay and the expectation time about capital stock, this paper constructs a business cycle model with a fixed time delay and fixed government spending; (2) By employing the Hopf bifurcation theory of the modern dynamical system theory, this paper tries to find out the factors of the business cycle formation; (3) The paper uses numerical simulation to test dynamic behavior with parameter settings of different factors and provides a reasonable perspective for investors to make decisions.

The paper proceeds as follows: Section 2 is about building a business cycle model. Section 3 makes a dynamic analysis of the model. Section 4 presents the simulation and analyses the results. Section 5 concludes.

---

2. Model Construction

---

2.1. The Theory of the Dynamic Multiplication-acceleration Model

In economy investment, GDP, and consumption influence and adjust mutually. If government expenditure is established (that is, the government does not intervene in the economy), relying only on self-regulation of economy, the business cycle thus forms.

The Samuelson-Hicks dynamic multiplication-acceleration model describes the nonlinear business cycle model. Its specific form is as follows:

$\left\{ {\begin{array}{*{20}{c}} {Y'(t) = \alpha (I(Y(t),K(t)) + C(t) + G - Y(t)}\\ {\begin{array}{*{20}{c}} {C(t) = \sigma {Y^d}(t) = \sigma (Y(t) - T(t)),0 < \sigma < 1}\\ \begin{array}{l} T(t) = \varepsilon Y(t),0 < \varepsilon < 1\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{}&{} \end{array}}&{} \end{array}}&{} \end{array}\\ K'(t) = \gamma (\upsilon Y(t) - K(t)),0 < \gamma < 1,0 < \upsilon < 1 \end{array} \end{array}} \end{array}} \right.$

(1)

In this model, Y(t) denotes the GDP, K(t) denotes the capital stock, C(t) denotes the consumption, α > 0 denotes the adjustment coefficient of production market, υ denotes the acceleration parameter, and Constant G denotes the government expenditure. I(Y, K) and S(Y, K) denote respectively the investment function and the saving function; The consumption assumption obeys Keynes behavioral assumptions, that is $C(t) = \sigma {Y^d}(t)$. ${Y^d}(t)$ is disposable income, T(t) is tax income, and Constant ε is tax rate.

Under the framework of nonlinear dynamic multiplication-acceleration model theory, the specific process of business cycle formation is that, the increased investment through the multiplier effect causes a greater growth in GDP, meanwhile the greater GDP growth incents larger investment increase through accelerating effect, thus appears the economic prosperity. However, when GDP reaches a certain level where there is no GDP growth due to the constraints of social needs and resources, then the investment will reduce due to the acceleration principle, and the investment reduction will further decrease GDP because of the multiplier effect. The combined effects of both reductions make the economy fall into recession. Various stages of the business cycle result from the interaction between the multiplier and the acceleration principle. While in this self-regulation, investment plays a critical role in the formation of the business cycle.

---

2.2. The Business Cycle Model with a Fixed-time Delay

In economic activities, investment will not get the consecutive interest at the time of investing, but after a short or long time interval, economic benefits can be achieved, that is to say, there is a time delay existing directly in the investment and the economic benefits. Considering the impact of past investment decisions on the transformation of the capital stock, Kaldor and some others thought that in a more reasonable investment accumulation equation, both the GDP and capital stock should be introduced with the time delay. On the basis of the Kaldor cycle model, considering the investment lag caused by the GDP and the capital stock in the process of capital accumulation, the capital accumulation equation is as follows:

$K'(t) = I(Y(t - \tau ),K(t - \tau )) - \delta K(t)$

(2)

Here, $\delta \in \left({0, 1} \right)$ is the depreciation rate of the capital stock, τ ≥ 0 is the constant time delay. The investment delay and the expectation time about the capital stock during making investment decisions both can influence investment activities. The expected capital stock is directly related to the potential future value of the current capital stock. The investment decision-making is bound to be impacted by the expected capital stock, and thus in the first equation of model (1), it is necessary to treat the investment as a function about the expected capital stock and GDP, that is

$I = I(Y(t),K(t + \tau ))$

(3)

Therefore, now considering the dynamic economic model as

$\left\{ {\begin{array}{*{20}{c}} {Y'(t) = \alpha (I(Y(t),K(t + \tau )) + (\sigma (1 - \varepsilon ) - 1)Y(t) + G)}\\ {K'(t) = I(Y(t - \tau ),K(t - \tau )) - \delta K(t)\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{} \end{array}}&{} \end{array}}&{} \end{array}} \end{array}} \right.$

(4)

Where Y, K, I, G, α, δ, σ and ε bear the same meaning as in model (1). τ > 0 in the first equation represents the expectation time of the capital stock, but in the second equation, it represents the investment lag. $K(t + \tau)$ denotes the expected capital stock.

According to Krawiec (1999), assuming the investment function $I(Y, K) = I(Y) -\beta K$, Where ${I_Y} > 0$, $\beta > 0$, then model (4) can be transformed into the business cycle model with a fixed-time delay:

$\left\{ \begin{array}{l} Y'(t) = \alpha (I(Y(t)) - \beta K(t + \tau ) + (\sigma (1 - \varepsilon ) - 1)Y(t) + G)\\ K'(t) = I(Y(t - \tau )) - \beta K(t - \tau ) - \delta K(t) \end{array} \right.$

(5)

Let $W(t) = K(t + \tau)$, then model (5) turns into the following form:

$\left\{ \begin{array}{l} Y'(t) = \alpha (I(Y(t)) - \beta W(t) + (\sigma (1 - \varepsilon ) - 1)Y(t) + G)\\ W'(t) = I(Y(t)) - \beta W(t - \tau ) - \delta W(t) \end{array} \right.$

(6)

The Kaldor model assumes that the investment function depends on the profit principle rather than the acceleration principle. The model's nature is dependent on the nonlinearity of the investment function. The investment function, by introducing the marginal investment propensity, can explain both the stable and unstable equilibrium, but it reveals no cyclical movement in economy. Therefore, the linear fashion investment function cannot explain the cyclical phenomenon.

This paper introduces a nonlinear investment function, and considers that investment depends not only on income but also on the existing capital stock. Under the condition of an established income, the greater the capital stock is, the smaller the investment requires; conversely, the smaller the capital stock is, the greater the investment requires. Under the condition of established capital stock, the greater the income is, the larger the investment is, both the investment and the income change in the same direction. Using nonlinear, income and capital stock as the variables of the investment function, Kaldor explains that the business cycle is originated from investment. Meanwhile, the capital accumulation equation and the investment equation with the same fixed-time delay can be used to describe that, in the process of investment, the investment delay and the expectation time about the capital stock while making investment decision have impact on the generation of business cycle.

---

3. Theoretical Dynamic Analysis of the Business Cycle Model with a Fixed-time Delay

In this section, the delay in investment is introduced as the bifurcation parameter to study the stability of the equilibrium in the model and the conditions of Hopf branch in generating the business cycle.

Assuming the economy system (6) has an isolated equilibrium ${E^ * } = ({Y^ * }, {W^ * })$, then a relation exists between ${Y^ * }$ and ${W^ * }$:

$\left\{ \begin{array}{l} I({Y^ * }) - \beta {W^ * } + (\sigma (1 - \varepsilon ) - 1){Y^ * } + G = 0\\ I({Y^ * }) - (\beta + \delta ){W^ * } = 0 \end{array} \right.$

(7)

Let $b = I'({Y^ * })$, ${u_1} = Y -{Y^ * }$, ${u_2} = W -{W^ * }$, then linearizing system (6) into

$\left\{ \begin{array}{l} \frac{{d{u_1}(t)}}{{dt}} = \alpha (b + (\sigma (1 - \varepsilon ) - 1)){u_1}(t) - \alpha \beta {u_2} + \alpha G\\ \frac{{d{u_2}(t)}}{{dt}} = b{u_1} - \beta {u_2}(t - \tau ) - \delta {u_2}(t) \end{array} \right.$

(8)

So, the corresponding characteristic equation of system (8) is given by

$\begin{array}{l} \quad \quad \Delta (\lambda ,\tau ) = {\lambda ^2} + A\lambda + B + (\beta \lambda + C){e^{ - \lambda \tau }} = 0\\ A = \delta - \alpha (b + \sigma - \sigma \varepsilon - 1)),B = \alpha \left( {\beta b + \delta + \delta \sigma \varepsilon - \delta b - \delta \sigma } \right),C = \alpha \beta (1 + \sigma \varepsilon - b - \sigma ) \end{array}$

(9)

When τ = 0, there is no delay in investment, thus the characteristic equation is given as:

$\Delta (\lambda ,0) = {\lambda ^2} + (A + \beta )\lambda + (B + C) = 0$

(10)

Knowing that polynomial (10) has a negative root or a root with a negative real part if and only if it meets the following conditions:

$\left( {{\rm{H1}}} \right)\;\;\;\;\left\{ \begin{array}{l} A + \beta = \delta - \alpha (b + \sigma - \sigma \varepsilon - 1) + \beta > 0\\ B + C = \alpha \left( {\beta b + \delta + \delta \sigma \varepsilon - \delta b - \delta \sigma } \right) + \alpha \beta (1 + \sigma \varepsilon - b - \sigma ) > 0 \end{array} \right.$

Thus educe Theorem1 as follows:

Theorem1: When $\tau = 0$, if $\min (\frac{{\delta + \beta }}{\alpha }, \frac{{\beta b}}{{\delta + \beta }}) > b + \sigma -\sigma \varepsilon -1$, then the equilibrium point ${E^ * } = ({Y^ * }, {W^ * })$ is locally asymptotically stable.

Proof. See Appendix A: The proof of Theorem 1

It can be seen that when the marginal propensity is introduced into the non-linear investment function without delay, the stable and unstable equilibrium can be explained, which means the reasons for the stability or fluctuation of economy can be explained. But the economy has no corresponding cyclical movement. Therefore, the investment function with no delay cannot explain the cyclical phenomenon.

When τ > 0, with the changing of τ, only when one null point of the characteristic equation appears in the imaginary axis or goes across the imaginary axis, the stability of the system will change at the equilibrium point and thus generate the Hopf bifurcation. Analyzing the root distribution of equation (9) according to the economic parameters, three major conditions are discussed as follows:

1. When equation (9) has a root with positive real part, the equilibrium point ${E^ * } = ({Y^ * }, {W^ * })$ is unstable.

2. When all real parts of the roots of equation (9) are negative, the equilibrium point ${E^ * } = ({Y^ * }, {W^ * })$ achieves gradual stability.

3. When equation (9) bears a pair of pure imaginary roots, and the real parts of the rest roots are negative, system (6) forms a Hopf bifurcation at the equilibrium point ${E^ * } = ({Y^ * }, {W^ * })$, thus generates the business cycle.

Theorem 2 is educed like this:

Theorem 2: When $\tau \ne 0$, according to business model (5), there are three conclusions as follows:

1. If ${B^2} -{C^2} > 0$ and ${\beta ^2} + 2B -{A^2} > 0$, then for any $\tau > 0$, the equilibrium point ${E^ * } = ({Y^ * }, {W^ * })$ is locally asymptotically stable.

2. If ${B^2} -{C^2} < 0$, then when $\tau \in \left({0, \tau _0^ + } \right)$, the equilibrium point ${E^ * } = ({Y^ * }, {W^ * })$ is locally asymptotically stable. When $\tau > \tau _0^ +$, the equilibrium point ${E^ * } = ({Y^ * }, {W^ * })$ is unstable. When $\tau {\rm{ = }}\tau _n^ + (n = 0, 1, 2 \cdots)$, system (5) forms a Hopf bifurcation at the equilibrium point ${E^ * } = ({Y^ * }, {W^ * })$, thus generates the business cycle.

3. If ${B^2} -{C^2} > 0$, ${\beta ^2} + 2B -{A^2} > 0$, and ${({\beta ^2} + 2B -{A^2})^2} > 4({B^2} -{C^2})$, then there exists a integer k, and when $\tau \in (\tau _n^ -, \tau _{n + 1}^ +), \tau _n^ -= 0, n = -1, 0, 1, \cdots, k -2$, the equilibrium point ${E^ * } = ({Y^ * }, {W^ * })$ is locally asymptotically stable. When $\tau = \tau _n^ -, \tau _{n + 1}^ +, n = 0, 1, \cdots, k -2$, the Hopf bifurcation is formed and thus generates the business cycle.

Proof. See Appendix T2.

As can be seen, after introducing the delay, the investment function which comprises non-linear, income, and capital stock variables exhibits complicated dynamic behavior. This function can not only reflect the stability or instability of the economic performance but also illustrate the causes of investment on the economic cycle.

---

4. Numerical Simulation and Experimental Results

This section further illustrates the impact of the investment delay and the expectation time about the capital stock $\tau$ on the formation of the business cycle. The MATLAB software is used to perform the numerical simulation (Shmpine and Thompson, 2001), so as to verify the conclusion.

---

4.1. The numerical Model

In the numerical simulation, the Kaldor model investment function is $I\left(Y \right) = \frac{{{e^Y}}}{{1 + {e^Y}}}$. Except parameter $\tau$, other parameters are given the following values as:$\alpha = 3$, $\beta = 0.7$, $\sigma = 0.6$, $\varepsilon = 0.2$, $\delta = 0.1$.

In order to study the dynamic behavior of the economic performance, we set situations according to the government spending parameter and change the delay accordingly. The specific situation is like this:

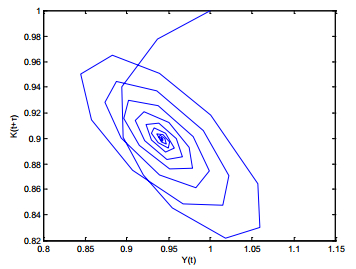
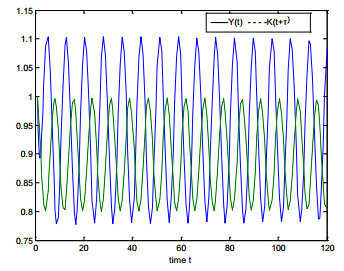
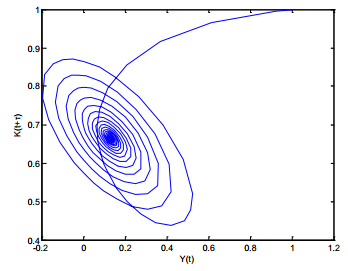
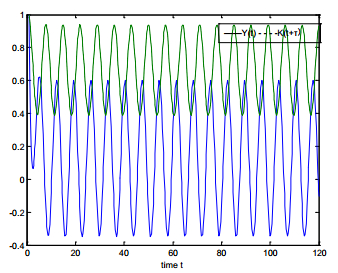
1. Assuming the government spending G = 0.4, according to the selected investment function and the related parameters, the equilibrium point of system (5) is calculated as ${E^*} = \left({0.9422, 0.8994} \right)$, and then the hold value of the business cycle is $\tau _0^ + = 2.5839$. Furthermore, $b = 0.2018$, and ${B^2} -{C^2} = -0.1769 < 0$; according to the second conclusion of theorem2, when $\tau \in (0, 2.5839)$, the equilibrium point ${E^*} = \left({0.9422, 0.8994} \right)$ is locally asymptotically stable; when $\tau > 2.5839$, the equilibrium point is unstable; when $\tau = 2.5839$, system (5) forms a Hopf bifurcation at the equilibrium point ${E^*} = \left({0.9422, 0.8994} \right)$, thus generates the business cycle. Meanwhile, the corresponding business cycle is $\frac{{2\pi }}{\omega } = 7.6336$.

¹ System (5) is locally asymptotically stable.

² A business cycle appears.

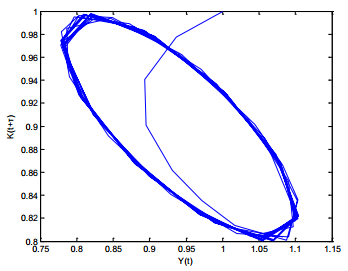
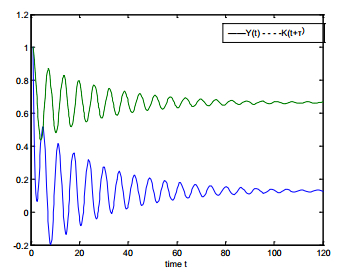
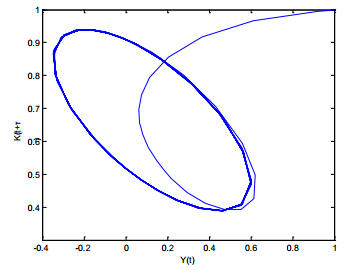
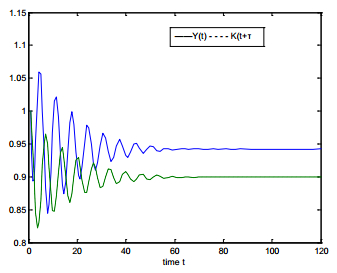
2. Assuming the government spending G=0, according to the selected investment function and the related parameters, the equilibrium point of system (5) is calculated as ${E^*} = \left({0.1279, 0.6649} \right)$, and then the hold value of the business cycle is $\tau _0^ + = 2.412$. Further, we get $b = 0.2490$, ${B^2} -{C^2} = 0.0412 > 0$, ${\beta ^2} + 2B -{A^2} = 0.8648 > 0$, and ${({\beta ^2} + 2B -{A^2})^2} -4({B^2} -{C^2}) = 0.5832 > 0$; then according to the third conclusion of Theorem 2, when $\tau \in (0, 2.412)$, the equilibrium point ${E^*} = \left({0.1279, 0.6649} \right)$ is locally asymptotically stable; When $\tau = 2.412$, a Hopf bifurcation is generated, thus appears a business cycle. Meanwhile, the corresponding business cycle is $\frac{{2\pi }}{\omega } = {\rm{ 6}}{\rm{.9627}}$.

³ System (5) is locally asymptotically stable.

⁴ A business cycle appears.

---

4.2. Discussion

Through the numerical simulation, we can get the findings as followed:

The investment delay is one incentive in generating the business cycle. When the investment delay is comparatively small, the economy performance tends to stay stable; but when the investment delay increases, there will be periodic solutions in the model, and thus exhibits the business cycle phenomenon, the delay point depending on the model's relative parameters. To put it in another way, if the expectation time about the capital stock is comparatively short during making investment decision, and the time consumption of decision execution is also short, then after a certain time of market operation, the GDP and the expectation stock inclines to achieve equilibrium gradually, and the economy will show a trend of stable development; conversely, if the expectation time about the capital stock is comparatively long during making investment decision, and the time consumption of decision execution is also long, then after a certain time of market operation, the GDP and the expectation stock vibrate cyclically, thus generate the business cycle.

The government spending and the investment delay have different impacts on the business cycle respectively. The government spending is introduced into the model to explore its impact on the business cycle, study the process of making expectation target by the policy makers, and avoid large-scale business fluctuation. The government spending has no influence on the formation condition of the business cycle after the linearization of the business cycle model, and it mainly bears an indirect impact on the business cycle through the form of an investment function. However, the government spending has a great influence on the target of the economic equilibrium, and it plays a guiding role in the decision-makers' investment activity.

The investment policy can be used for counter-cyclical regulation. While making the investment policy, assuming the policymaker already knows the investment parameter, together with other parameters like the market adjustment coefficient, and the capital depreciation rate, it is apparent that the economic equilibrium level depends on the government spending. Therefore, if the policymaker set a goal of economic equilibrium, then through adjusting the government spending and investment parameters, the economic equilibrium value can be stabilized, or the whole system can be maintained stable with slight volatility.

---

5. Conclusion

Considering the nonlinear quality of the variable function and the delay in economic activity, this paper constructs a nonlinear business cycle model with fixed-time delay. By using the Hopf bifurcation theory, this paper makes the delay in investment as the bifurcation parameter and discusses the dynamic behavior of the business cycle model.

A nonlinear investment function is educed through a dynamic analysis of the model. The function illustrates that the model has a stable or an unstable equilibrium, which explains the causes of economic stability or volatility, but it shows no cyclical movement. After introducing time delay into the nonlinear investment function, as the investment time delay increases, there will be periodic solutions in the model, and the time delay is the cause of generating business cycle.

By using numerical simulations, this paper first introduces the government spending into the model, then explores its impact on the business cycle, and studies that policymakers can help avoid large volatility in the business cycle by setting expectation targets. But this paper also discovers that government spending and investment delays make different impact on the business cycle. Besides, by adjusting the investment parameters in the investment policies, the whole system can be maintained stable with slight volatility, and the policies can be used for counter-cyclical regulation.

---

Acknowledgment

We are grateful to the fund project -the national social science fund (No. 15BTJ007) providing us with funding support.

---

Conflict of Interest

All authors declare no conflict of interest in this paper.

---

Appendix A

T1: The Proof of Theorem 1

When $\tau = 0$, the characteristic equation is equation (10), and according to condition (H1), the first equation $\frac{{\delta + \beta }}{\alpha } > b + \sigma -\sigma \varepsilon -1$and the second equation $\frac{{\beta b}}{{\delta + \beta }} > b + \sigma -\sigma \varepsilon -1$ are obtained, then $\min (\frac{{\delta + \beta }}{\alpha }, \frac{{\beta b}}{{\delta + \beta }}) > b + \sigma -\sigma \varepsilon -1$, and therefore the real part of the two roots of equation (10) are negative. The conclusion is obvious.

T2: The Proof of Theorem 2

The following discussion is about the impact of the time delay $\tau$ on the stability of the system's equilibrium point. According to Beretta (2002), the pure imaginary root of equation (9) is required. Assuming $\lambda = \omega i(\omega > 0)$ is a pure imaginary root, with no doubt, $\lambda = -\omega i$ is also a root of equation (9) (because the time delay is not smaller than 0, then this root will not be considered). To put it into the characteristic equation (9) and separate the real part and the imaginary part, thus gets

$\left\{ \begin{array}{l} \beta \omega \sin (\omega \tau ) + C\cos (\omega \tau ) = {\omega ^2} - B\\ \beta \omega \cos (\omega \tau ) - C\sin (\omega \tau ) = - A\omega \end{array} \right.$

${\rm{That}}\;{\rm{is}}\left\{ \begin{array}{l} \tan \left( {\omega \tau } \right) = \frac{{\beta \omega ({\omega ^2} - B) + AC\omega }}{{C({\omega ^2} - B) - A\beta {\omega ^2}}}\\ {\left( {\frac{{\beta \omega ({\omega ^2} - B) + AC\omega }}{{{\beta ^2}{\omega ^2} + {C^2}}}} \right)^2} + {\left( {\frac{{C({\omega ^2} - B) - A\beta {\omega ^2}}}{{{\beta ^2}{\omega ^2} + {C^2}}}} \right)^2} = 1 \end{array} \right.$

${\rm{Therefore}},{\tau _n} = \frac{1}{\omega }\arctan \frac{{\beta \omega ({\omega ^2} - B) + AC\omega }}{{C({\omega ^2} - B) - A\beta {\omega ^2}}} + \frac{{2n\pi }}{\omega },n = 0,1,2 \cdots \;{\rm{and}}$

${\omega ^4} + ({A^2} - {\beta ^2} - 2B){\omega ^2} + ({B^2} - {C^2}) = 0$

(11)

That is $\omega _ \pm ^2 = \frac{{({\beta ^2} + 2B -{A^2}) \pm \sqrt {{{({\beta ^2} + 2B -{A^2})}^2} -4({B^2} -{C^2})} }}{2}$

1. If ${B^2} -{C^2} < 0$, then equation (10) has an imaginary root $\lambda = i{\omega _ + }, {\omega _ + } > 0$;

2. If ${B^2} -{C^2} > 0$, ${\beta ^2} + 2B -{A^2} > 0$, and ${({\beta ^2} + 2B -{A^2})^2} > 4({B^2} -{C^2})$, then equation (10) has two imaginary roots ${\lambda _ \pm } = i{\omega _ \pm }, {\omega _ + } > {\omega _ -} > 0$.Meanwhile, if and only if when ${\tau ^ * } = \frac{1}{{{\omega ^ * }}}\phi \left({{\omega ^ * }} \right) + \frac{{2n\pi }}{{{\omega ^ * }}}, n = 0, 1, 2 \cdots$, the solution $\omega$ of equation (11) corresponds the solution $i\omega$ which is one solution of the characteristic equation (10). $\phi \left(\omega \right) = \arctan \frac{{\beta \omega ({\omega ^2} -B) + AC\omega }}{{C({\omega ^2} -B) -A\beta {\omega ^2}}}$.

For the changes of a null point of the characteristic equation at or across the imaginary axis, we can examine the sign of taking derivation of the real part of the characteristic equation (10) with respect to $\tau$ at ${\tau ^ \pm }$.

Taking derivation of the real part of the characteristic equation (10) with respect to $\tau$, thus gets

$\left\{ {2\lambda + A + \left[ {\beta - \tau (\beta \lambda + C)} \right]{e^{ - \lambda \tau }}} \right\}\frac{{d\lambda }}{{d\tau }} = \lambda (\beta \lambda + C){e^{ - \lambda \tau }}$

Here is apparent that all the pure imaginary roots are simple roots (unless A = B = C= β= 0), and

${\left( {\frac{{d\lambda }}{{d\tau }}} \right)^{ - 1}} = \frac{{(2\lambda + A){e^{\lambda \tau }} + \beta }}{{\lambda \left( {\beta \lambda + C} \right)}} - \frac{\tau }{\lambda },{e^{\lambda \tau }} = \frac{{ - \left( {\beta \lambda + C} \right)}}{{{\lambda ^2} + A\lambda + B}}$

Then, $sign\left\{ {\frac{{d{\mathop{\rm Re}\nolimits} \left(\lambda \right)}}{{d\tau }}\left| {_{\tau = {\tau ^ \pm }}} \right.} \right\} = sign\left\{ {{A^2} -{\beta ^2} -2B + 2{{\left({{\omega ^ \pm }} \right)}^2}} \right\}$,

Obviously, $sign\left\{ {\frac{{d{\mathop{\rm Re}\nolimits} \left(\lambda \right)}}{{d\tau }}\left| {_{\tau = {\tau ^ + }}} \right.} \right\} > 0$, and $sign\left\{ {\frac{{d{\mathop{\rm Re}\nolimits} \left(\lambda \right)}}{{d\tau }}\left| {_{\tau = {\tau ^ -}}} \right.} \right\} < 0$.

(1) If ${B^2} -{C^2} > 0$, ${\beta ^2} + 2B -{A^2} > 0$, all roots of equation (10) have negative real parts, and the conclusion is obvious.

(2) If ${B^2} -{C^2} < 0$, for $\tau = \tau _0^ +$, equation (10) has an imaginary root with a negative real part, for $\tau = \tau _0^ +$, there is a pure imaginary root, and because $sign\left\{ {\frac{{d{\mathop{\rm Re}\nolimits} \left(\lambda \right)}}{{d\tau }}\left| {_{\tau = {\tau ^ + }}} \right.} \right\} > 0$, the real part of the root increases continuously with the increase of $\tau$. When $\tau \in \left({0, \tau _0^ + } \right)$, all real parts of the roots of equation (10) are negative, so the equilibrium point ${E^ * } = ({Y^ * }, {W^ * })$ is locally asymptotically stable; when $\tau > \tau _0^ +$, there is at least one root with a positive real part in equation (10), therefore, the equilibrium point ${E^ * } = ({Y^ * }, {W^ * })$ is unstable.

(3) If ${B^2} -{C^2} < 0$, ${\beta ^2} + 2B -{A^2} > 0$, and $({\beta ^2} + 2B -{A^2}) > 4({B^2} -{C^2})$, equation (10) bears two imaginary roots ${\lambda _ \pm } = i{\omega _ \pm }, {\omega _ + } > {\omega _ -} > 0$; if exists an integer $k$, $\tau _k^ + -\tau _{k -1}^ + = \frac{{2\pi }}{{{\omega _ + }}} < \frac{{2\pi }}{{{\omega _ -}}} = \tau _{k -1}^ --\tau _{k -2}^ -$, the equilibrium point ${E^ * } = ({Y^ * }, {W^ * })$ is locally asymptotically stable; when the parameter makes $\tau _1^ - < \tau _1^ + < \tau _1^ - < , \cdots, < \tau _k^ + < \tau _k^ -$, the stability of the equilibrium point can change at most finite number of times, and is ultimate unstable.

---