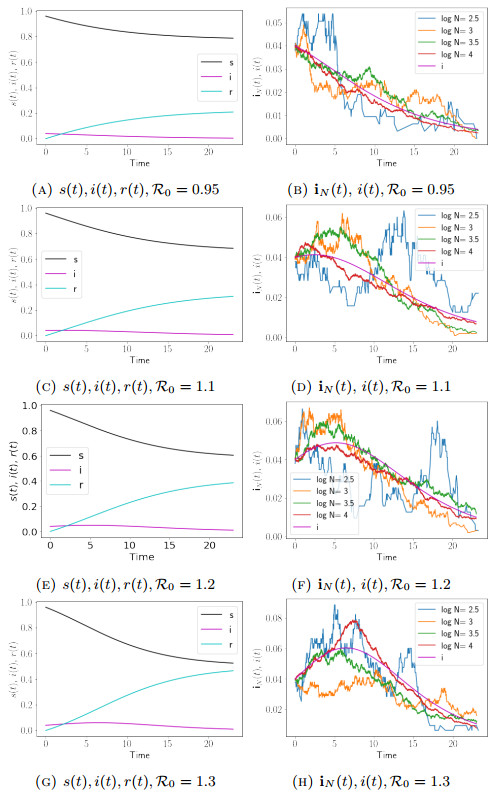
Plots of infected compartment fractions
Deterministic compartmental models for infectious diseases give the mean behaviour of stochastic agent-based models. These models work well for counterfactual studies in which a fully mixed large-scale population is relevant. However, with finite size populations, chance variations may lead to significant departures from the mean. In real-life applications, finite size effects arise from the variance of individual realizations of an epidemic course about its fluid limit. In this article, we consider the classical stochastic Susceptible-Infected-Recovered (SIR) model, and derive a martingale formulation consisting of a deterministic and a stochastic component. The deterministic part coincides with the classical deterministic SIR model and we provide an upper bound for the stochastic part. Through analysis of the stochastic component depending on varying population size, we provide a theoretical explanation of finite size effects. Our theory is supported by quantitative and direct numerical simulations of theoretical infinitesimal variance. Case studies of coronavirus disease 2019 (COVID-19) transmission in smaller populations illustrate that the theory provides an envelope of possible outcomes that includes the field data.
Citation: Xia Li, Chuntian Wang, Hao Li, Andrea L. Bertozzi. A martingale formulation for stochastic compartmental susceptible-infected-recovered (SIR) models to analyze finite size effects in COVID-19 case studies[J]. Networks and Heterogeneous Media, 2022, 17(3): 311-331. doi: 10.3934/nhm.2022009
| [1] | Martin Heida, Benedikt Jahnel, Anh Duc Vu . Regularized homogenization on irregularly perforated domains. Networks and Heterogeneous Media, 2025, 20(1): 165-212. doi: 10.3934/nhm.2025010 |
| [2] | Tong Li . Qualitative analysis of some PDE models of traffic flow. Networks and Heterogeneous Media, 2013, 8(3): 773-781. doi: 10.3934/nhm.2013.8.773 |
| [3] | Xia Li, Andrea L. Bertozzi, P. Jeffrey Brantingham, Yevgeniy Vorobeychik . Optimal policy for control of epidemics with constrained time intervals and region-based interactions. Networks and Heterogeneous Media, 2024, 19(2): 867-886. doi: 10.3934/nhm.2024039 |
| [4] | Luca Lussardi, Stefano Marini, Marco Veneroni . Stochastic homogenization of maximal monotone relations and applications. Networks and Heterogeneous Media, 2018, 13(1): 27-45. doi: 10.3934/nhm.2018002 |
| [5] | Mostafa Bendahmane, Kenneth H. Karlsen . Martingale solutions of stochastic nonlocal cross-diffusion systems. Networks and Heterogeneous Media, 2022, 17(5): 719-752. doi: 10.3934/nhm.2022024 |
| [6] | András Bátkai, Istvan Z. Kiss, Eszter Sikolya, Péter L. Simon . Differential equation approximations of stochastic network processes: An operator semigroup approach. Networks and Heterogeneous Media, 2012, 7(1): 43-58. doi: 10.3934/nhm.2012.7.43 |
| [7] | Nicola Bellomo, Francesca Colasuonno, Damián Knopoff, Juan Soler . From a systems theory of sociology to modeling the onset and evolution of criminality. Networks and Heterogeneous Media, 2015, 10(3): 421-441. doi: 10.3934/nhm.2015.10.421 |
| [8] | Ciro D'Apice, Peter I. Kogut, Rosanna Manzo . On relaxation of state constrained optimal control problem for a PDE-ODE model of supply chains. Networks and Heterogeneous Media, 2014, 9(3): 501-518. doi: 10.3934/nhm.2014.9.501 |
| [9] | A.C. Rocha, L.H.A. Monteiro . On the spread of charitable behavior in a social network: a model based on game theory. Networks and Heterogeneous Media, 2023, 18(2): 842-854. doi: 10.3934/nhm.2023036 |
| [10] | Yves Achdou, Victor Perez . Iterative strategies for solving linearized discrete mean field games systems. Networks and Heterogeneous Media, 2012, 7(2): 197-217. doi: 10.3934/nhm.2012.7.197 |
Deterministic compartmental models for infectious diseases give the mean behaviour of stochastic agent-based models. These models work well for counterfactual studies in which a fully mixed large-scale population is relevant. However, with finite size populations, chance variations may lead to significant departures from the mean. In real-life applications, finite size effects arise from the variance of individual realizations of an epidemic course about its fluid limit. In this article, we consider the classical stochastic Susceptible-Infected-Recovered (SIR) model, and derive a martingale formulation consisting of a deterministic and a stochastic component. The deterministic part coincides with the classical deterministic SIR model and we provide an upper bound for the stochastic part. Through analysis of the stochastic component depending on varying population size, we provide a theoretical explanation of finite size effects. Our theory is supported by quantitative and direct numerical simulations of theoretical infinitesimal variance. Case studies of coronavirus disease 2019 (COVID-19) transmission in smaller populations illustrate that the theory provides an envelope of possible outcomes that includes the field data.
The COVID-19 pandemic provides the first instance in 100 years to study the worldwide dynamics of a novel virus outbreak. Early on in the pandemic we observed many localized outbreaks on cruise ships, skilled nursing facilities, and through other congregating mechanisms such as conferences, parties, and places of worship. Several groups developed models to inform public health, the most notable being the March 16, 2020 report by Imperial College [24] that forecast over 2 million deaths in the US and over 500,000 deaths in the UK if non-pharaceutical interventions (NPIs) were not implemented. Within days, lockdowns were enforced in both countries. Over a year since that time we have observed a variety of patterns, most of which did not follow the trends predicted by the early reports. The most obvious reason for these differences is the reduction of the reproductive number due to NPIs. An additional important factor is the departure from simple mixture models that results from isolating populations because of NPIs or simply because of geography. One way to model such effects is to consider an agent-based model within a finite population size in which the role of stochasticity is more pronounced due to the population size. This is the focus of our work.
Mathematical modeling has an important role in studying infectious diseases on both long and short timescales - for modern viruses such as AIDS, Severe Acute Respiratory Syndrome (SARS), Zika, and the novel coronavirus disease 2019 (COVID-19). For epidemic modeling, the standard approach involves compartmental models in which the population is divided into compartments representing individuals in one of several states, e.g. the susceptible (S), infectious (I), recovered (R) and exposed (E). This mathematical framework can lead to a variety of epidemic models, such as SIR, SIS, SEIR, SIRS (see e.g. [45], [49], [43], [9]). Compartmental modeling has been applied to epidemic study of COVID-19, HIV, etc [63,50,11,7,8]. These models can have an agent-based form with the most granular being the stochastic models. Between the stochastic SIR and the continuum limit are the Hawkes and HawkesN models in which a single self-exciting point process describes virus transmission between people [11]. Recent work has shown a theoretical connection between HawkesN and continuum compartmental models [59]. Because of the granularity of the stochastic compartmental model, its fluid limit is often adopted to reduce computational complexity. By the law of large numbers, stochastic compartment models with Markov processes can be approximated by their deterministic ODE counterpart. The central limit effect arises under the diffusion scaling. And the fluid-scaled model converges to a Gaussian diffusion of stochastic differential equations about the deterministic solution. All these approximation methods require a large population size to control variances. As the population size decreases the fluid-limit approximation acquires larger stochastic variances, and finite size effects may arise. For example, empirical variances of realizations of stochastic models can be at the same magnitude of the inverse of the total population size ([33,34]). Since population scale within a relatively small community (like small counties, cruise ships) is very likely to fall within the regime of considerable stochastic deviations, quantitative study and analysis of finite size effects is relevant to real disease statistics. To this end, we investigate stochastic variability in the stochastic SIR model driven by independent Poisson clocks, which will be referred to as the SIR-IPC Model. We adopt Poisson clocks, rather than time steps discretized with a fixed duration. A more realistic model should treat all events as occurring independently, according to their own stochastic clock, rather than occurring at regular intervals, and arriving according to the same schedule. Time steps are turned into exponentially distributed random variables with the introduction of Poisson clocks. Moreover, independent Poisson clocks allow us to use the theory of continuous-time Markov pure jump processes, e.g. a martingale approach (see e.g. [20,44,46,47,48]). And this leads to a martingale formulation. In prior literature, only the components of the martingale formulation are derived (see e.g. [1], [2], [72]), while study of the complete formulation has been lacking. Specifically, theoretical infinitesimal variances have also been studied in e.g. [14,49], [2], [72], [73]. However, their main purpose is to explore ways to approximate stochastic compartmental models with a large population size, such as fluid limit, diffusion limit, and linear SDE approximations. With the martingale formula applicable to all population scales, we can quantitatively analyze the finite size effects under small populations.
It is possible to merge independent Poisson clocks to obtain systems that are driven by only one or two Poisson clocks. And this idea is worked out in [1], [2], [72]. There the SIR Models are driven by two Poisson clocks, one for transitions from S to I compartment, the other for those from I to R compartment. Here in our model, we assume that individual events each occur at a certain Poisson rate. These events include infectious contacts of each pair of susceptible and infected individuals, and recovery of each infectious individuals. We also assume the absence of vital dynamics with a deterministic population size parameter
Furthermore, we conduct numerical experiments with several sets of parameters that mimic real world cases, including smaller US counties and a cruise ship. As the pandemic progresses, it permeates smaller counties and rural areas [51] [61]. Since the outbreak of COVID-19 on the Diamond Princess Cruise Ship at least 25 other such vessels have confirmed COVID-19 cases and studies of the transmission of the disease on cruise ship have drawn consideration attention (e.g. [6]).
The article is organized as follows. In Section 2, the stochastic SIR Model is introduced. The martingale formulation is derived in Section 3. Based on the martingale formulation, a deterministic and continuum analogue of the stochastic SIR model is derived (Section 3.3). Simulations are run to compare the stochastic SIR model to its continuum limit, illustrating the importance of finite size effects (Section 3.4). In Section 4 the finite size effects are analyzed theoretically based upon the martingale formulation. The theory is supported by simulations and field data in Section 5.
Our setting is similar to the continuous-time-Markov-processes stochastic SIR models in [1], [59] and [72]. We assume a continuous time variable
| (SN(ω,0),IN(ω,0),RN(ω,0))=(S0N,I0N,R0N). | (1) |
A Poisson clock governs the infectious contact of any pair of a susceptible and an infectious individuals. There are in total
Another Poisson clock governs the recovery of the infectious individuals. Each infectious individual is assigned a Poisson clock, denoted as "r-clock", which advances with rate
All the Poisson clocks are exponentially distributed independent random variables and are independent with time increments. As in the classical SIR literature,
| R0=βp1γp2. | (2) |
Remark 1. To facilitate the computation of the SIR-IPC model, we show the following equivalent description of the SIR-IPC model with merged Poisson clocks. All the i-clocks can be merged into one master i-clock to govern the arrivals of infectious contact. Once the master i-clock advances, with probability
| Var(N∑n=1Xn(t))=N∑n=1Var(Xn(t))=N∑n=1λnt=tN∑n=1λn. | (3) |
When
| Var(N∑n=1Xn(t))=tNλ. | (4) |
We denote the fractions of each compartment as
| (sN(ω,t),iN(ω,t),rN(ω,t)):=(SNN(ω,t),INN(ω,t),RNN(ω,t)). | (5) |
with the initial condition of population fractions denoted as
| (sN(ω,0),iN(ω,0),rN(ω,0)):=(s0N,i0N,r0N). | (6) |
This together with (1) implies that
| (s0N,i0N,r0N)=(S0NN,I0NN,R0NN). | (7) |
With similar idea as in e.g. [1], we derive the small-time-interval probabilities for compartment fractions. For
| P(ΔsN(ω,t),ΔiN(ω,t)))=(k,j)|(sN(ω,t),iN(ω,t)=(s,i))={p1βNisΔt+o1(Δt),(k,j)=(−1N,1N),p2γNiΔt+o2(Δt),(k,j)=(0,−1N),1−p1βNisΔt−p2γNiΔt+o3(Δt),(k,j)=(0,0),0,otherwise, | (8) |
where
Remark 2. Although the set up of the Markov pure jump process implies (8), the inverse is not true. For example, the set of small-time-interval equations do not uniquely determine the rates of the Poisson clocks. For the same reason, combining the parameters
The martingale formulation of a Markov pure jump process characterizes the process as the sum of an integral part involving the infinitesimal mean and a martingale part involving the infinitesimal variance.
For every
Definition 3.1. It is possible that for a certain realization of SIR-IPC Model, the Poisson clocks may generate time increments that add up to be finite, say time
In the previous literature (e.g. [73,72,1,2,3,14,34,35]), there are works that consider the infinitesimal mean and variance of stochastic SIR models but typically only in the cases when the total population
Theorem 3.2. Before the possible blow-up time,
| {sN(t)=s0N+∫t0G(1)N(w)dw+M(1)N(t),iN(t)=i0N+∫t0G(2)N(w)dw+M(2)N(t),rN(t)=r0N+∫t0G(3)N(w)dw+M(3)N(t), | (9) |
where
| G(1)N(t)=−p1βiN(t)sN(t), | (10) |
| G(2)N(t)=p1βiN(t)sN(t)−p2γiN(t) | (11) |
| G(3)N(t)=p2γiN(t). | (12) |
The variances of
| Var(M(l)N(t)))=∫t0E[V(l)N(w)]dw,l=1,2,3, | (13) |
where
| V(1)N(t)=1Np1βiN(t)sN(t), | (14) |
| V(2)N(t)=1Np1βiN(t)sN(t)+1Np2γiN(t), | (15) |
| V(3)N(t)=1Np2γiN(t). | (16) |
Proof of Theorem 3.2. To prove Theorem 3.2, we compute the infinitesimal means and variances for the Markov pure jump process
As
| V(1)N(t)=limΔt→01ΔtE[(ΔsN(t−))2|((sN(t−),iN(t−),rN(t−)))] | (17) |
From (17) we obtain (14). In a similar way we obtain (15), and (16). With the infinitesimal means and variances obtained, we apply Theorem (1.6), [20] or Theorem 3.32, [48], to obtain (9), and apply Exercise 3.8.12 of [13] to obtain (13). The proof of Theorem 3.2 is completed.
Here we derive upper bounds for variances of martingales of the martingale formulation (9).
Theorem 3.3. Before the possible blow-up time, we have the following estimates:
| Var(M(1)N(t)))≤1Ns0N, | (18) |
| Var(M(2)N(t)))≤1N[s0N+p2γ(i0N+s0N)t], | (19) |
| Var(M(3)N(t)))≤1Np2γ(i0N+s0N)t. | (20) |
Proof of Theorem 3.3. Taking expectation on both sides of (9)
| E[sN(t)]=s0N+∫t0E[G(1)N(w)]dw. | (21) |
This together with (10), (13) and (14) implies
| Var(M(1)N(t)))=1N∫t0E[p1βiN(w)sN(w)]dw=1N(s0N−E[sN(t)]). | (22) |
As
From (13) and (16) we infer
| Var(M(3)N(t)))=1Np2γ∫t0E[iN(w)]dw≤1Np2γ∫t0(i0N+s0N)dw=1Np2γ(i0N+s0N)t. | (23) |
From (23) we obtain (20).
From (13) - (16) and we obtain
| Var(M(2)N(t)))=Var(M(1)N(t)))+Var(M(3)N(t))). | (24) |
This together with (18) and (20) implies (19).
Theorem 3.3 implies that the variances of the martingales of
With a similar derivation of the hydrodynamic limit of Markov pure jump processes [23,27,40,39,62,64,68,69], we can find a deterministic analogue of the (renormalized) stochastic SIR model when
And we see that for
| {∂s(t)∂t=−p1βi(t)s(t),∂i(t)∂t=p1βi(t)s(t)−p2γi(t),∂r(t)∂t=p2γi(t),s(0)=s0,i(0)=i0,r(0)=r0, | (25) |
where
We compare the stochastic and deterministic analogue of the stochastic SIR model through simulations. For the stochastic case, we use the classical Gillespie algorithm for continuous-time Markov processes (see e.g. [25]). Roughly speaking, we first simulate the sojourn times using exponential distribution generators, and then simulate the sample paths of the embedded discrete-time Markov process as described in Section 2.1. The algorithm ensures that independent Poisson clocks advance randomly without a prescribed diagram. Namely, we do not require that the i-clocks and r-clocks advance sequentially with a pre-determined arrangement. In this way, we are able to produce a number of sample paths corresponding to random realizations of sequences of events. The predictive power of our simulation is strengthened by this effort of proper usage of the algorithm.
We focus on the cases when the reproduction number
1As a specific example we note that the dynamic reproductive number has been estimated weekly in Los Angeles County using a Bayesian SEIR model applied to hospital demand data - during the period July 2020-April 2021 it remained within a 25% window of one [10].
In all the cases, we show output of the SIR-IPC model simulations with

Plots of infected compartment fractions
The finite size effects are exhibited. As the population size decreases, deviations of dynamics of the stochastic SIR Model from its continuum equation increase. The same simulation output is also observed over other random paths.
In Theorem 3.3, a global upper bound of the same order of magnitude of
We analyze the deterministic and stochastic component of the martingale formulation with varying population size
| (s0N,i0N,r0N)≡(s0,i0,r0). | (26) |
We analyze the martingale formulation of the stochastic SIR model with varying population size
| {sN(t+Δt)=sN(t)+G(1)N(t)Δt+M(1)N(t+Δt)−M(1)N(t),iN(t+Δt)=iN(t)+G(2)N(t)Δt+M(2)N(t+Δt)−M(2)N(t),rN(t+Δt)=rN(t)+G(3)N(t)Δt+M(3)N(t+Δt)−M(3)N(t). | (27) |
By (13) and additivity of the variance in time for martingales, we have
| √Var(ΔM(l)N(t))≅√E[V(l)N(t)]Δt,l=1,2,3, | (28) |
where
We perform estimates at the first time step. At time zero, from (14) - (16) we infer
| V(1)N(0)=1Np1βi0s0, | (29) |
| V(2)N(0)=1N(p1βi0s0+p2γi0), | (30) |
| V(3)N(0)=1Np2γi0, | (31) |
which implies that the infinitesimal variances for the attractiveness are each inversely proportional to
| V(l)N(0)∝1N,l=1,2,3. | (32) |
This together with (28) implies that at the first time step we have
| Var(M(l)N(Δt))∝1N,l=1,2,3. | (33) |
From (33) and (27) we infer that at the first time step a smaller value of
| V(l)N(t)>V(l)˜N(t), for 0<N<˜N and t>0,l=1,2,3, | (34) |
which leads to a theory of the finite size effects at an arbitrary later time.
Next we estimate the right-hand-side of formulas (14) - (16), so that we can estimate
We conjecture that formulas (29) - (31) can be written for an arbitrary
| V(1)N(t)∝1Np1βi0s0, | (35) |
| V(2)N(t)∝1N(p1βi0s0+p2γi0), | (36) |
| V(3)N(t)∝1Np2γi0. | (37) |
If our conjecture above is true, then we can fix a time period
| ¯V(1)N∝1Np1βi0s0, | (38) |
| ¯V(2)N∝1N(p1βi0s0+p2γi0), | (39) |
| ¯V(3)N∝1Np2γi0, | (40) |
where
| ¯V(l)N:=1T2−T1∫T2T1V(l)N(t)dt,l=1,2,3. | (41) |
Here we slightly abuse the notation and omit the dependence of the time average over
To check the validity of (34), we perform direct simulations of the infinitesimal standard deviations, namely
| σ(l)N(t)=√V(l)N(t),l=1,2,3. | (42) |
Example output can be found in Figure. 2.

Examples of the infinitesimal standard deviation for
Figs. 2a, 2c, and 2e show results of
The output of the simulations supports the validity of (34). The same simulation results are also observed over other random paths.
We validate our conjecture of (38) - (40) through the following numerical simulation. Fig. 3 shows the log–log plot with error bars for (38) - (40). The lines show the theoretical scaling with slope as
| (x,y)=(logN,log(¯V(l)N)),l=1,2,3, | (43) |

Comparisons of the log–log plot of the theoretical and empirical scaling for
for
Figs. 3a, 3c, and 3e show results in the cases when
The output shows that the error bars are short and fall mostly on the straight lines representing the theory. The same simulation results are also observed over other random paths. These results support the validity of equations (38) - (40) and our theory for the finite size effects based on the martingale formulation.
In the following experiments, we set parameters to mimic real world cases of a small county or a cruise ship. And we will display plots for the fractional of compartment and the infinitesimal standard deviations, and analyze the role of stochastic variances in each case. The infinitesimal variances represent chance variations that leads to deviations from the deterministic SIR model. Through simulations of infinitesimal variances as in (14) - (16), we can produce envelopes that encompass a majority of the random paths. Realistically, our findings suggest that for small populations, the probabilities of rare events, e.g. the early-die-out or early-outbreak are important.
We study the outbreak of COVID-19 in Churchill County, Nevada from July, 2020 to March, 2021 and on the Diamond Princess cruise ship from February to March, 2020. Since early testing on the Diamond Princess was done by sampling from the population due to limited availability of testing, there is an under-reporting issue in the infected counts. The data of Churchill County was collected from [19] and the reported number of confirmed cases of Princess Diamond, and the quarantine process were retrieved from publicly available sources including the Princess Cruise website of the Carnival Cooperation [18] and the official website of Ministry of Health, Labor and Welfare, Japan (Ministry of Health, Labor and Welfare, Japan [54].
We plot the daily confirmed cases with 30 realisations from the SIR-IPC models in fig. 4. For fig. 4a, the total population is set to be Churchill County's population
Compartmental models are a powerful tool to predict and control infectious diseases. In this article, we study theoretically and quantitatively the finite size effects arising in stochastic compartmental models, where individual realizations of the models deviate from their mean-field limit.
We apply compound Poisson processes to classical SIR compartmental models without vital dynamics. The result is a continuous-time Markov pure jump process, and a martingale approach can be applied to this process. The process is expressed as the sum of a deterministic and a stochastic component, which provides us with a tool to study both the statistical and stochastic features of the process. The deterministic part coincides with the classical deterministic SIR model. By providing a bound of the variances of the martingale, we show that the continuum mean-field limit is indeed the deterministic SIR model. Simulations results also align with the conclusion.
However, a small population size leads to stochastic fluctuations that deviate from the deterministic SIR model. Quantitative and theoretical analysis of these finite size effects have not been well-studied. We find a theoretical explanation for the finite size effects by observing that the stochastic component of the martingale formulation scales as the inverse of the square root of the population size. A larger variance both in the outbreak size and its temporal behavior arises as population size decreases. This scaling property is verified at time zero with equilibrium initial data. Direct numerical simulations of the theoretical infinitesimal variance support our theory as output shows that the dependence on population size remains to be true in later times. Here we simulate with fixed initial compartment fractions and vary the total population size. To the best of our knowledge, this is the first time that simulations of theoretical infinitesimal variances for stochastic compartmental models are implemented. In previous works only empirical variations are simulated (see e.g. [59], [33]), and the focus was on the effects of statistical fluctuations on the reproduction number assuming varying initial compartment fractions [4]. We also simulate finite size effects with small populations and analyze with real data. All the simulations support our theory. Our results exhibit the danger of fitting data collected during an outbreak to deterministic counterparts of the stochastic compartmental models, especially for small populations.
Finite size effects are observed in Markov processes for population dynamics in many fields ([15,26,28,29,32,36,41,42,55,65,66,70]). But there have been few quantitative studies to date about finite size effects in epidemics. On one hand, the methodology developed here may be broadly useful for quantitative social and natural sciences. On the other, this work provides a mathematical and theoretical framework that may contribute to epidemic policy for public health agencies.
So far, the analysis is purely theoretical. It remains an open problem to integrate the real-world data to the model and gleam some indicators from the data to control the disease. One example is that in order to control the spread, the government should know when and where to take certain measures to reduce
From Figure 5c, with a smaller population, the envelope of synthetic data can be wide. Additionally, the process with a smaller population also has more paths that die out early in the process(see fig. 2a, 2c, 2e), and 5a. Our work provides a good guide for authorities of smaller populations like cruise ships and small towns to estimate risk over time in order to prepare for the outbreak. It is important to bear in mind that the broader variations in the pandemic caused by the smaller population would lead to a wide outcome when it comes to estimating risk. In the past hundreds of years of human history, there have been several infectious diseases, including SARS, MERS and H1N1. However, only few of them, e.g. COVID-19 and 1918 influenza escalated into a pandemic. It is important to understand when, why and how a disease dies out and our next step is to quantitatively study the die-out event and its relations to finite size population and reproduction number
We thank Professors Thomas Liggett, Jingyu Huang, Qiang Zeng, and Martina Hofmanova for helpful discussions.
| [1] |
L. J. S. Allen, An introduction to stochastic epidemic models, In Mathematical Epidemiology, Lecture Notes in Math., 1945 (2008), 81–130. |
| [2] | (2011) An Introduction to Stochastic Processes with Applications to Biology. Boca Raton, FL: CRC Press. |
| [3] |
L. J. Allen and E. J. Allen, A comparison of three different stochastic population models with regard to persistence time, Theoretical Population Biology, 64 (2003), 439–449, https://www.sciencedirect.com/science/article/pii/S0040580903001047. |
| [4] |
On SIR-models with Markov-modulated events: Length of an outbreak, total size of the epidemic and number of secondary infections. Discrete Contin. Dyn. Syst. Ser. B (2018) 23: 2153-2176. 
|
| [5] |
D. Applebaum, Lévy Processes and Stochastic Calculus, vol. 116 of Cambridge Studies in Advanced Mathematics, 2nd edition, Cambridge Studies in Advanced Mathematics, 116. Cambridge University Press, Cambridge, 2009. |
| [6] |
P. Azimi, Z. Keshavarz, J. G. Cedeno Laurent, B. Stephens and J. G. Allen, Mechanistic transmission modeling of COVID-19 on the diamond princess cruise ship demonstrates the importance of aerosol transmission, Proceedings of the National Academy of Sciences, 118 (2021). |
| [7] |
N. T. J. Bailey, The Mathematical Theory of Infectious Diseases and Its Applications, 2nd edition, Hafner Press [Macmillan Publishing Co., Inc.], New York, 1975. |
| [8] |
The critical community size for measles in the united states. Journal of the Royal Statistical Society: Series A (General) (1960) 123: 37-44. 
|
| [9] |
A review of seir-d agent-based model. Distributed Computing and Artificial Intelligence, 16th International Conference, Special Sessions (2019) 1004: 133-140. 
|
| [10] |
T. Belin, A. Bertozzi, N. Chaudhary, T. Graves, J. Guterman, M. C. Jarashow, R. J. Lewis, J. Marion, F. Schoenberg, M. Shah, J. Tolles, E. Traub, K. Viele and F. Wu, Projections of Hospital-based Healthcare Demand due to COVID-19 in Los Angeles County May 24, 2021, 2021, http://file.lacounty.gov/SDSInter/dhs/1107440_COVID-19ProjectionPublicUpdateLewis05.24.21English.pdf., |
| [11] |
A. L. Bertozzi, E. Franco, G. Mohler, M. B. Short and D. Sledge, The challenges of modeling and forecasting the spread of COVID-19, Proc. Natl. Acad. Sci., 117 (2020), 16732–16738, https://www.pnas.org/content/117/29/16732. |
| [12] |
Martingale estimation functions for discretely observed diffusion processes. Bernoulli (1995) 1: 17-39. 
|
| [13] |
(2002) Stochastic Integration with Jumps. Cambridge: Encyclopedia of Mathematics and its Applications, 89. Cambridge University Press. 
|
| [14] |
Gaussian process approximations for fast inference from infectious disease data. Math. Biosci. (2018) 301: 111-120. 
|
| [15] |
Refined stability thresholds for localized spot patterns for the Brusselator model in R2. European J. Appl. Math. (2019) 30: 791-828. 
|
| [16] |
K. L. Chung and R. J. Williams, Introduction to Stochastic Integration, 2nd edition, Modern Birkhäuser Classics, Birkhäuser/Springer, New York, 2014. |
| [17] |
Nonparametric estimation for stochastic differential equations with random effects. Stochastic Process. Appl. (2013) 123: 2522-2551. 
|
| [18] |
P. Cruises, Princess cruise lines (2020) Diamond Princess updates, 2021, https://www.princess.com/news/notices_and_advisories/notices/diamond-princess-update.html. |
| [19] |
An interactive web-based dashboard to track COVID-19 in real time. The Lancet Infectious Diseases (2020) 20: 533-534. 
|
| [20] | (1996) Stochastic Calculus. Boca Raton, FL: A practical introduction. Probability and Stochastics Series. CRC Press. |
| [21] |
R. Durrett, Essentials of Stochastic Processes, Springer Texts in Statistics, Springer-Verlag, New York, 1999. |
| [22] |
R. Durrett, Probability Models for DNA Sequence Evolution, Probability and its Applications (New York), Springer-Verlag, New York, 2002. |
| [23] |
S. N. Ethier and T. G. Kurtz, Markov Processes: Characterization and Convergence., Wiley Series in Probability and Mathematical Statistics: Probability and Mathematical Statistics, John Wiley & Sons, Inc., New York, 1986. |
| [24] |
N. M. Ferguson, D. Laydon, G. Nedjati-Gilani, N. Imai, K. Ainslie, M. Baguelin, S. Bhatia, A. Boonyasiri, Z. Cucunubá, G. Cuomo-Dannenburg, A. Dighe, I. Dorigatti, H. Fu, K. Gaythorpe, W. Green, A. Hamlet, W. Hinsley, L. C. Okell, S. v. Elsland, H. Thompson, R. Verity, E. Volz, H. Wang, Y. Wang, P. G. Walker, C. Walters, P. Winskill, C. Whittaker, C. A. Donnelly, S. Riley and A. C. Ghani, Impact of non-pharmaceutical interventions (NPIs) to reduce COVID-19 mortality and healthcare demand, Report 9, Imperial College COVID-19 Response Team, Imperial College London, London, United Kingdom, 2020. |
| [25] |
A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. J. Comput. Phys. (1976) 22: 403-434. 
|
| [26] |
The linear stability of symmetric spike patterns for a bulk-membrane coupled Gierer-Meinhardt model. SIAM J. Appl. Dyn. Syst. (2019) 18: 729-768. 
|
| [27] |
M. Z. Guo, G. C. Papanicolaou and S. R. S. Varadhan, Nonlinear diffusion limit for a system with nearest neighbor interactions, Comm. Math. Phys., 118 (1988), 31–59, http://projecteuclid.org/euclid.cmp/1104161907. |
| [28] |
Turbulent energy density in scale space for inhomogeneous turbulence. J. Fluid Mech. (2018) 842: 532-553. 
|
| [29] |
Geometric decomposition of the conformation tensor in viscoelastic turbulence. J. Fluid Mech. (2018) 842: 395-427. 
|
| [30] |
S. W. He, J. G. Wang and J. A. Yan, Semimartingale Theory and Stochastic Calculus, Kexue Chubanshe (Science Press), Beijing; CRC Press, Boca Raton, FL, 1992. |
| [31] |
P. G. Hoel, S. C. Port and C. J. Stone, Introduction to Stochastic Processes, The Houghton Mifflin Series in Statistics, Houghton Mifflin Co., Boston, Mass., 1972. |
| [32] |
Estimating large-scale structures in wall turbulence using linear models. J. Fluid Mech. (2018) 842: 146-162. 
|
| [33] |
Assessing the variability of stochastic epidemics. Mathematical Biosciences (1991) 107: 209-224. 
|
| [34] |
V. Isham, Stochastic models for epidemics with special reference to AIDS, Ann. Appl. Probab., 3 (1993), 1–27, http://links.jstor.org/sici?sici=1050-5164(199302)3:1<1:SMFEWS>2.0.CO;2-4&origin=MSN. |
| [35] |
V. Isham, Stochastic models for epidemics, In Celebrating Statistics, Oxford Statist. Sci. Ser., Oxford Univ. Press, Oxford, 33 (2005), 27–54. |
| [36] |
J. Jiménez, Coherent structures in wall-bounded turbulence, J. Fluid Mech., 842 (2018), P1,100. |
| [37] |
S. Karlin and H. M. Taylor, A Second Course in Stochastic Processes, Academic Press, Inc. [Harcourt Brace Jovanovich, Publishers], New York-London, 1981. |
| [38] |
W. O. Kermack, A. G. McKendrick and G. T. Walker, A contribution to the mathematical theory of epidemics, Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character, 115 (1927), 700–721, https://royalsocietypublishing.org/doi/abs/10.1098/rspa.1927.0118. |
| [39] |
Hydrodynamics and large deviation for simple exclusion processes. Comm. Pure Appl. Math. (1989) 42: 115-137. 
|
| [40] |
C. Kipnis and C. Landim, Scaling Limits of Interacting Particle Systems, Springer-Verlag, Berlin, 1999. |
| [41] |
T. Kolokolnikov, M. Ward, J. Tzou and J. Wei, Stabilizing a homoclinic stripe, Philos. Trans. Roy. Soc. A, 376 (2018), 20180110, 13 pp. |
| [42] |
Pattern formation in a reaction-diffusion system with space-dependent feed rate. SIAM Rev. (2018) 60: 626-645. 
|
| [43] |
Novel moment closure approximations in stochastic epidemics. Bull. Math. Biol. (2005) 67: 855-873. 
|
| [44] |
H. Kunita, Lectures on Stochastic Flows and Applications, Springer-Verlag, Berlin, 1986. |
| [45] |
Comparison of three sis epidemic models: Deterministic, stochastic and uncertain. Journal of Intelligent & Fuzzy Systems (2018) 35: 5785-5796. 
|
| [46] |
T. M. Liggett, Interacting Markov processes, In Biological Growth and Spread (Proc. Conf., Heidelberg, 1979), 38 (1980), 145–156. |
| [47] |
T. M. Liggett, Interacting Particle Systems, Springer-Verlag, New York, 1985. |
| [48] |
T. M. Liggett, Continuous Time Markov Processes, American Mathematical Society, Providence, RI, 2010. |
| [49] |
Approximation methods for analyzing multiscale stochastic vector-borne epidemic models. Math. Biosci. (2019) 309: 42-65. 
|
| [50] |
A. L. Lloyd, Realistic distributions of infectious periods in epidemic models: Changing patterns of persistence and dynamics, Theoretical Population Biology, 60 (2001), 59–71, http://www.sciencedirect.com/science/article/pii/S0040580901915254. |
| [51] |
S. McMiNN, R. Talbot and J. ENG, America's 200,000 COVID-19 deaths: Small cities and towns bear a growing share, https://www.npr.org, https://www.npr.org/sections/health-shots/2020/09/22/914578634/americas-200-000-COVID-19-deaths-small-cities-and-towns-bear-a-growing-share. |
| [52] |
M. Métivier, Semimartingales, A course on stochastic processes. de Gruyter Studies in Mathematics, 2. Walter de Gruyter & Co., Berlin-New York, 1982. |
| [53] |
M. Métivier and J. Pellaumail, Stochastic Integration, Academic Press [Harcourt Brace Jovanovich, Publishers], New York-London-Toronto, Ont., 1980 |
| [54] |
L. Ministry of Health and J. Welfare, Ministry of health, labor and welfare, Japan (2020) about coronavirus disease 2019 (COVID-19), 2020., https://www.mhlw.go.jp/stf/newpage_09276.html. |
| [55] |
Pattern formation and oscillatory dynamics in a two-dimensional coupled bulk-surface reaction-diffusion system. SIAM J. Appl. Dyn. Syst. (2019) 18: 1334-1390. 
|
| [56] |
(2007) Stochastic Partial Differential Equations with Lévy Noise. Cambridge: Cambridge University Press. 
|
| [57] |
B. L. S. Prakasa Rao, Statistical Inference for Diffusion Type Processes, Edward Arnold, London; Oxford University Press, New York, 1999. |
| [58] |
P. E. Protter, Stochastic Integration and Differential Equations, 2nd edition, Springer-Verlag, Berlin, 2005. |
| [59] |
M.-A. Rizoiu, S. Mishra, Q. Kong, M. Carman and L. Xie, SIR-Hawkes: Linking epidemic models and hawkes processes to model diffusions in finite populations, International World Wide Web Conferences Steering Committee, Republic and Canton of Geneva, CHE, (2018), 419–428. |
| [60] |
J. Rocklöv, H. Sjödin and A. Wilder-Smith, COVID-19 outbreak on the diamond princess cruise ship: Estimating the epidemic potential and effectiveness of public health countermeasures, Journal of Travel Medicine, 27 (2020), taaa030. |
| [61] |
E. Schumaker and M. Nichols, An american tragedy: Inside the towns hardest hit by coronavirus, abcNEWS, https://abcnews.go.com/Health/small-towns-face-COVID-19-pandemic-us-passes/story?id=74271392. |
| [62] |
D. W. Stroock and S. R. S. Varadhan, Multidimensional Diffusion Processes, Classics in Mathematics, Springer-Verlag, Berlin, 2006 |
| [63] |
A general markov model of the hiv epidemic in populations involving both sexual contact and iv drug use. Mathematical and Computer Modelling (1994) 19: 83-132. 
|
| [64] |
Onsager relations and Eulerian hydrodynamic limit for systems with several conservation laws. J. Statist. Phys. (2003) 112: 497-521. 
|
| [65] |
Asynchronous instabilities of crime hotspots for a 1-D reaction-diffusion model of urban crime with focused police patrol. SIAM J. Appl. Dyn. Syst. (2018) 17: 2018-2075. 
|
| [66] |
Anomalous scaling of Hopf bifurcation thresholds for the stability of localized spot patterns for reaction-diffusion systems in two dimensions. SIAM J. Appl. Dyn. Syst. (2018) 17: 982-1022. 
|
| [67] |
Approximate martingale estimating functions for stochastic differential equations with small noises. Stochastic Process. Appl. (2008) 118: 1706-1721. 
|
| [68] |
S. R. S. Varadhan, Entropy methods in hydrodynamic scaling, In Proceedings of the International Congress of Mathematicians, 1 (1995), 196–208. |
| [69] |
S. R. S. Varadhan, Lectures on hydrodynamic scaling, In Hydrodynamic Limits and Related Topics (Toronto, ON, 1998), Fields Inst. Commun., Amer. Math. Soc., Providence, RI, 27 (2000), 3–40. |
| [70] |
Spots, traps, and patches: Asymptotic analysis of localized solutions to some linear and nonlinear diffusive systems. Nonlinearity (2018) 31: 189-239. 
|
| [71] |
G.-W. Weber, P. Taylan, Z.-K. Görgülü, H. A. Rahman and A. Bahar, Parameter estimation in stochastic differential equations, In Dynamics, Games and Science. II, 2 (2011), 703–733. |
| [72] |
P. Yan, Distribution theory, stochastic processes and infectious disease modelling, In Mathematical Epidemiology, Lecture Notes in Math., 1945 (2008), 229–293. |
| [73] |
Beyond the initial phase: Compartment models for disease transmission. Quantitative Methods for Investigating Infectious Disease Outbreaks (2019) 70: 135-182. 
|
| 1. | Yachun Tong, Inkyung Ahn, Zhigui Lin, Threshold dynamics of a nonlocal dispersal SIS epidemic model with free boundaries, 2025, 18, 1793-5245, 10.1142/S179352452350095X |
Plots of infected compartment fractions
Examples of the infinitesimal standard deviation for
Comparisons of the log–log plot of the theoretical and empirical scaling for
Comparison of field data (solid black line) for daily confirmed case percentages with 30 realisations of the stochastic SIR model for Churchill County, NV and the Diamond Princess Cruise Ship