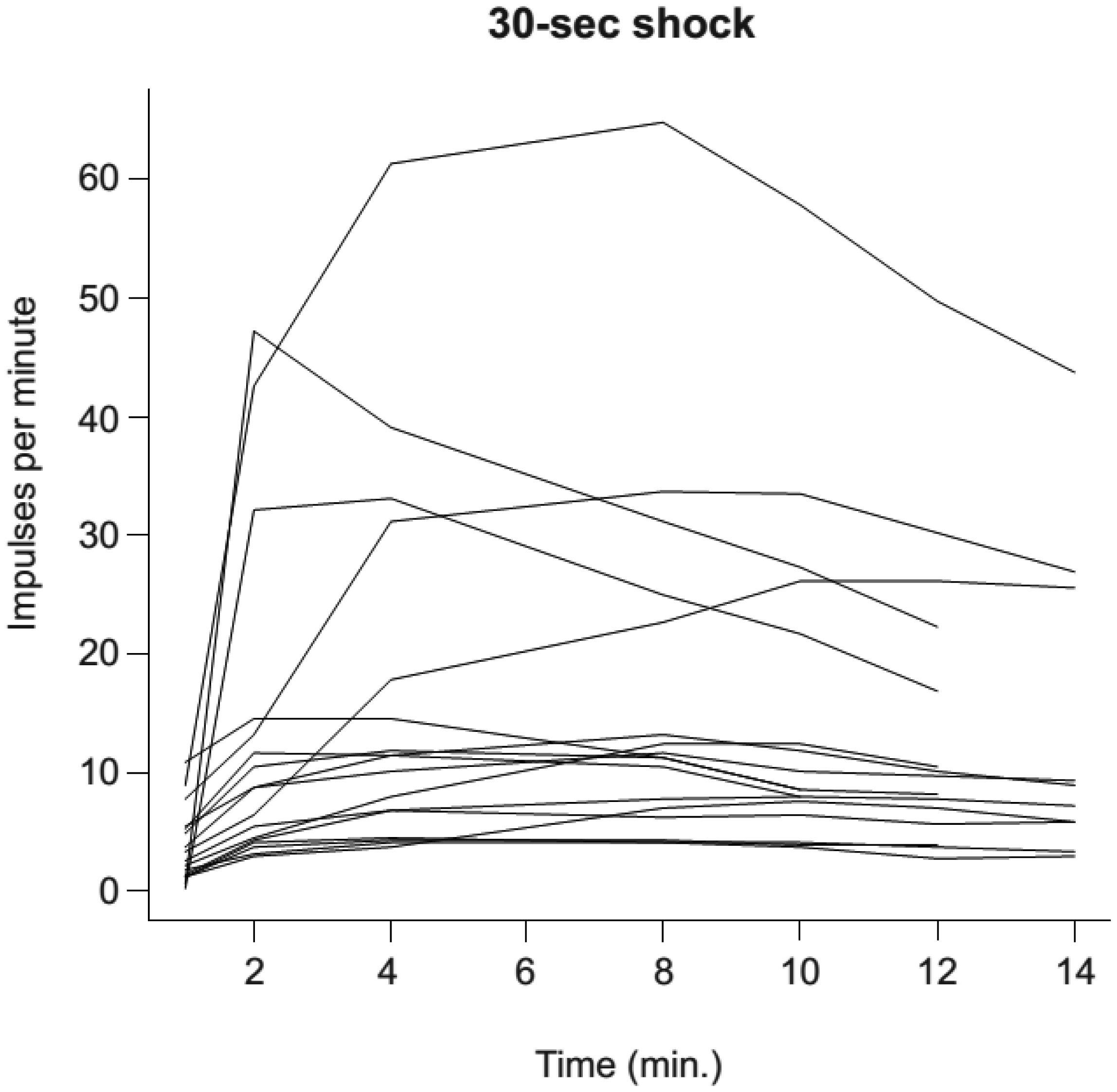
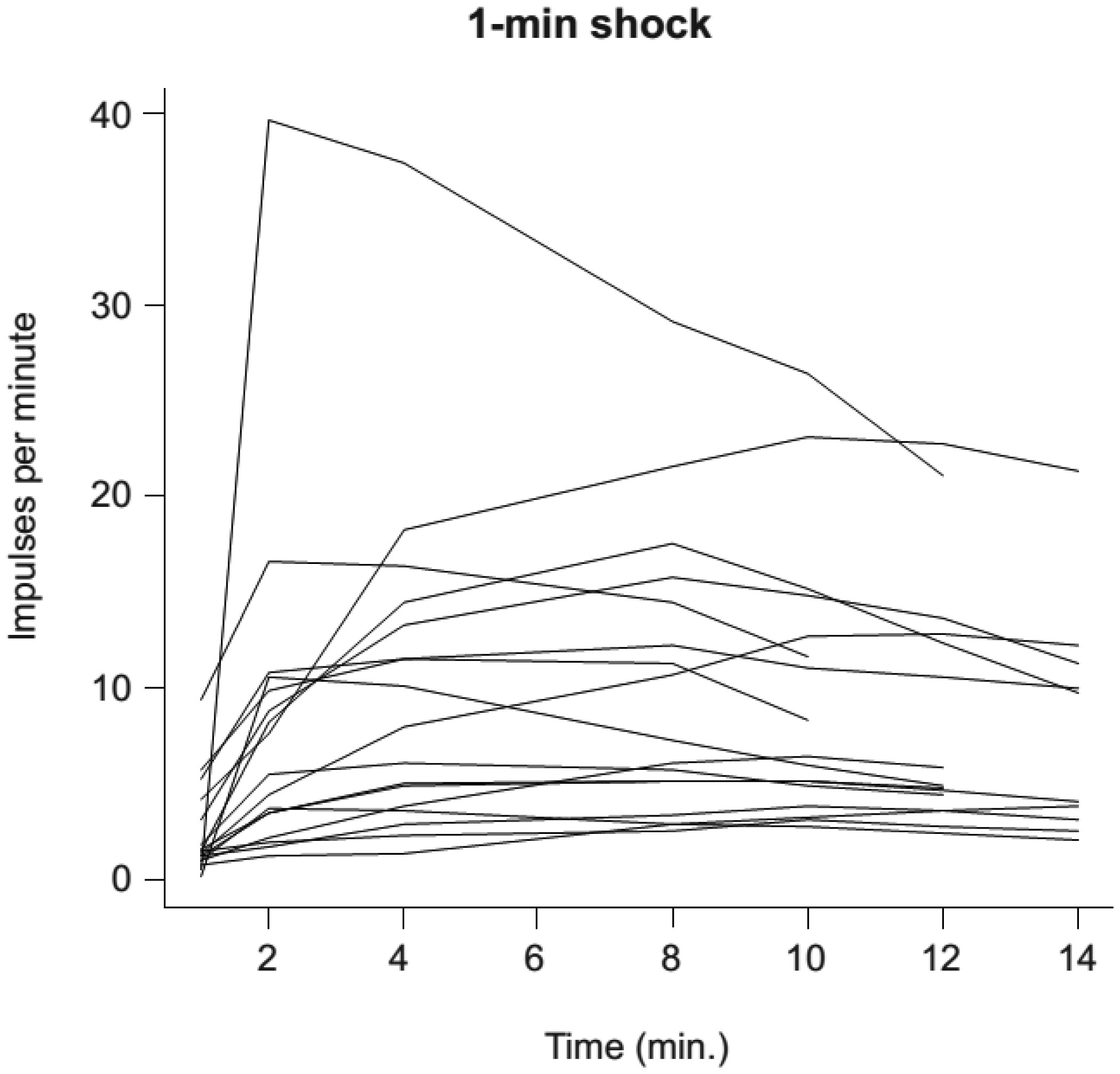
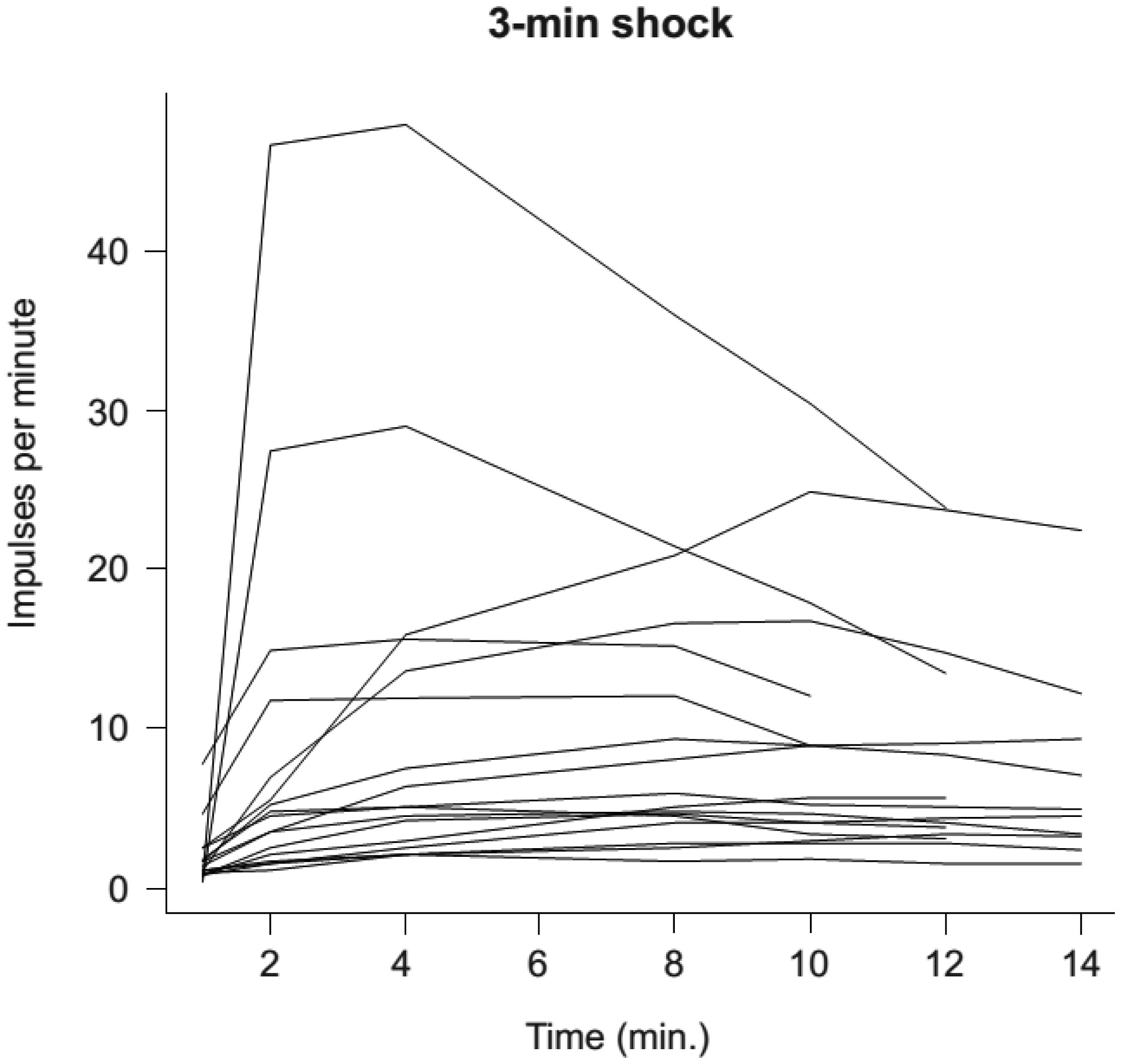
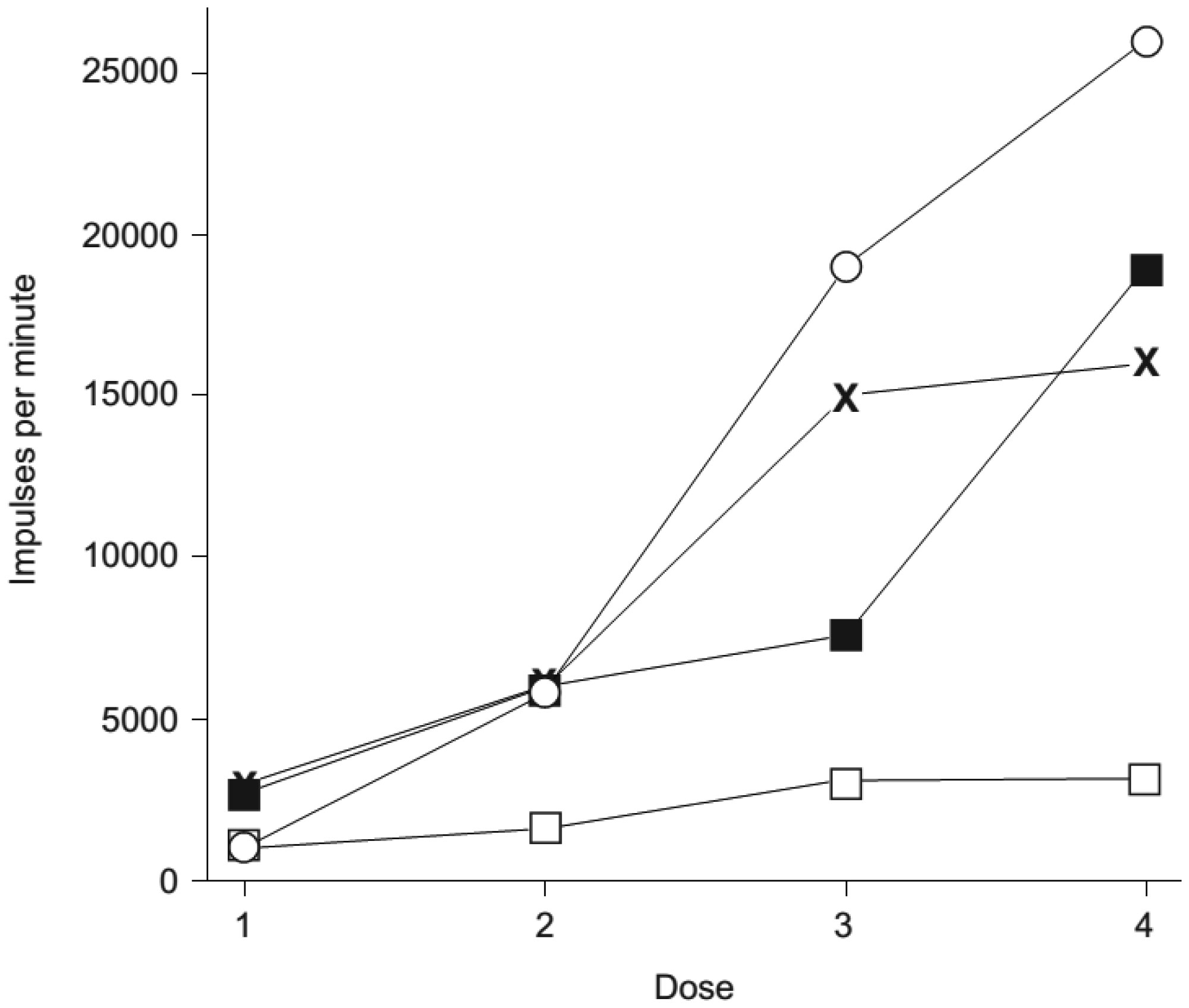
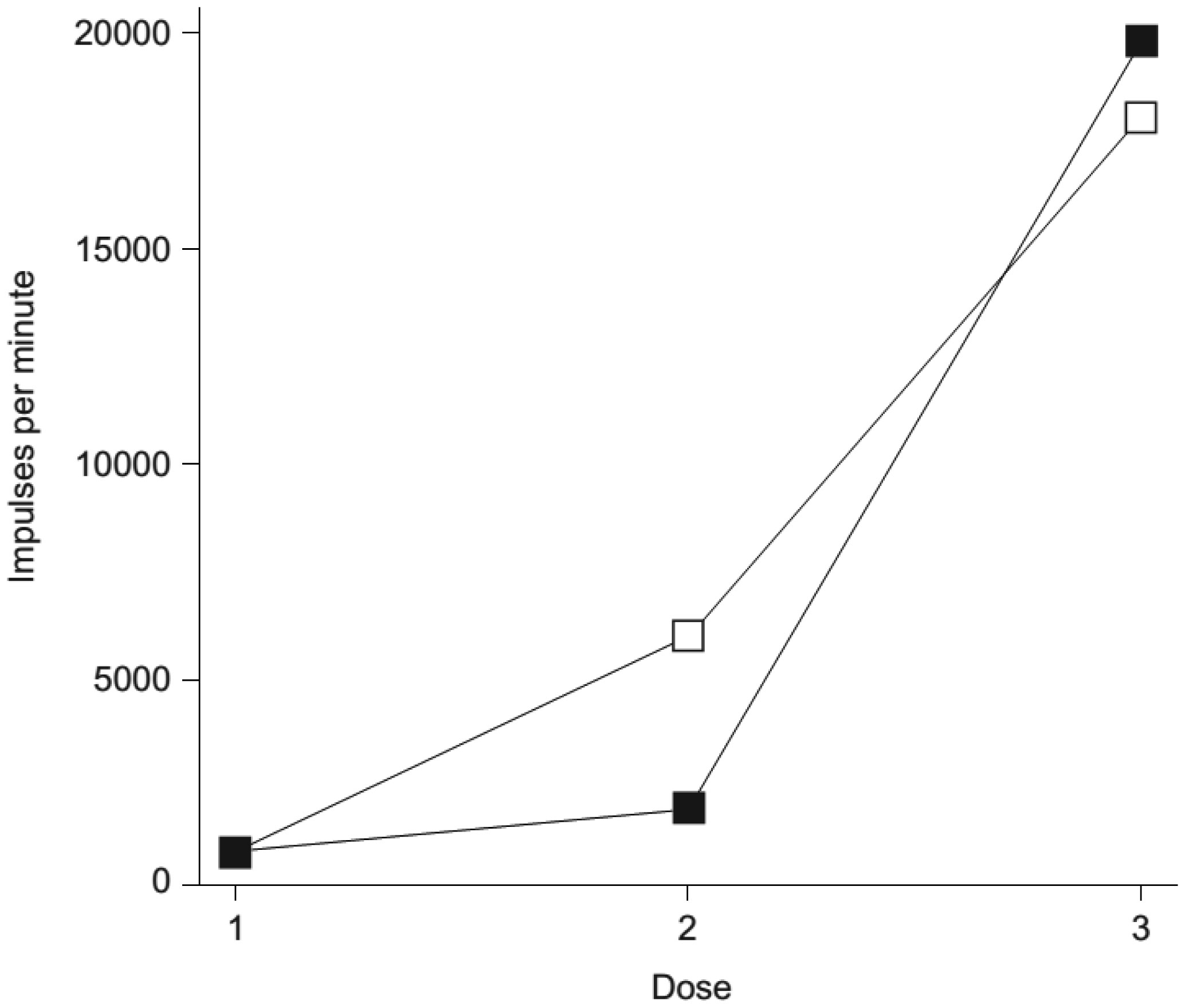
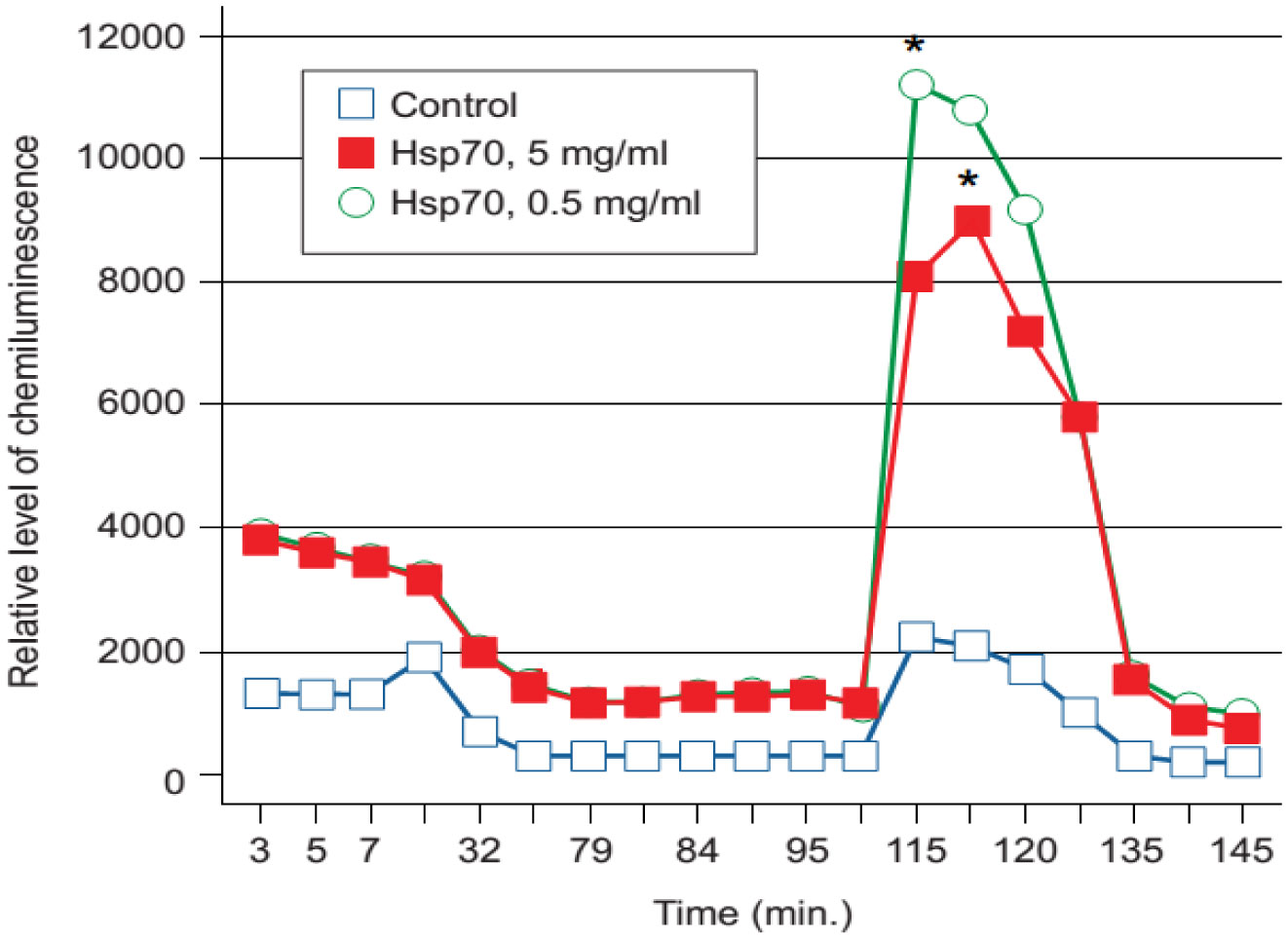
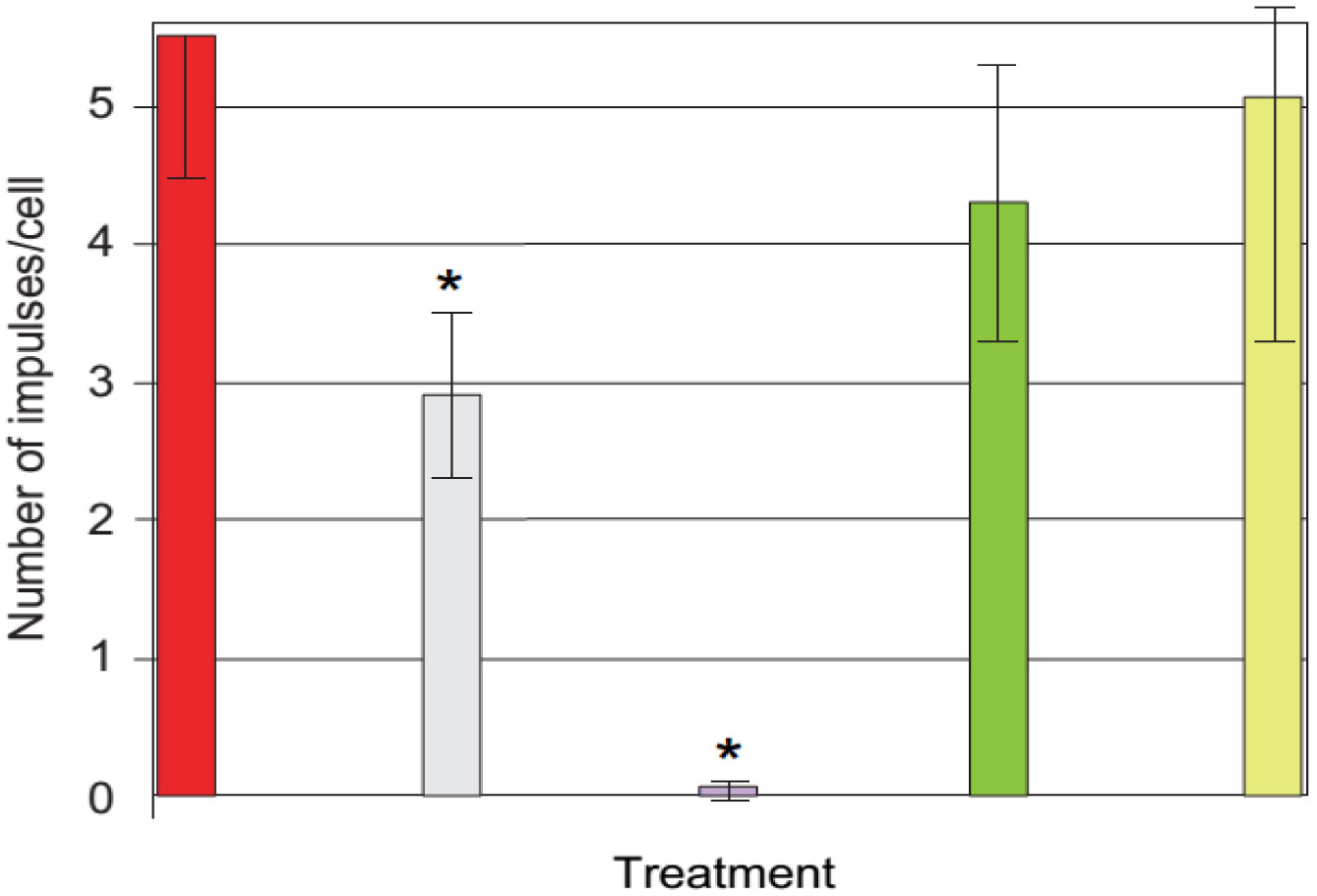
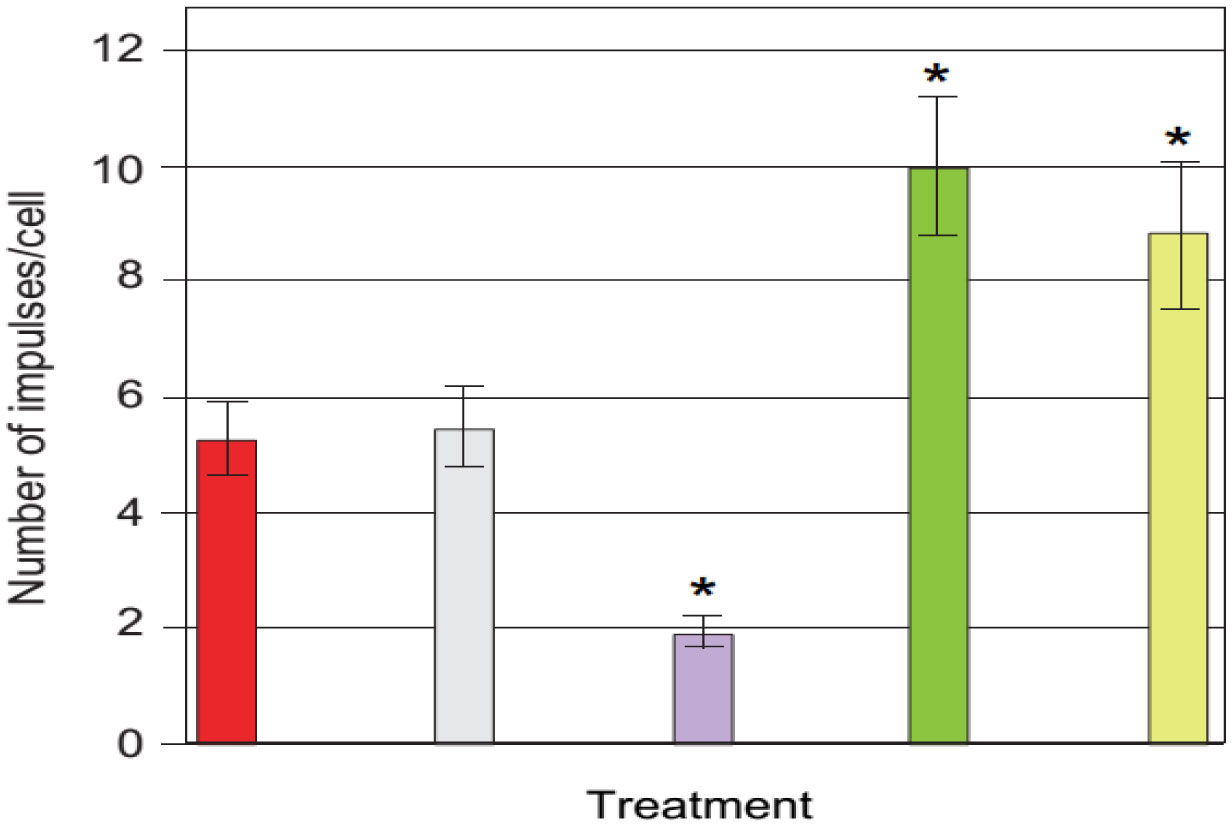
We have developed a simple and reliable method to measure the sensitivity of individuals to oxidative stress. This method utilizes luminol-amplified chemiluminescence to quantify production of reactive oxygen species (ROS) by opsonized zymosan-stimulated neutrophils that have been subjected to short-term stress via heat shock. In this study, the chemiluminescence reaction was used to monitor the dynamics of ROS production in neutrophils derived from 17 patients of different ages and genders before and after these neutrophils were subjected to heat shock. In addition, we determined expression of Toll-like receptors using fluorescent-labeled antibody. The effects of adrenaline, dexamethasone, aspirin, and indomethacin, as well as different doses of exogenous heat shock protein 70 (Hsp70), on the production of ROS by stimulated neutrophils was also investigated. Our data showed that adrenaline and exogenous Hsp70 both suppressed ROS production by stimulated neutrophils. Furthermore, TLR4 expression was upregulated upon heat stress. Thus, adrenaline, HSPs, and TLRs may all play a role in regulating stress responses in phagocytes.
1.
Introduction
Malaria, a vector-borne disease, instigated by Plasmodium protozoan parasites of female Anopheles mosquitoes, has been a serious threat to human health for ages. According to the reports of WHO, the disease caused nearly 241 million cases and claimed 627, 000 lives worldwide in the year 2020 [1]. In 2019, there were 227 million cases and nearly 69, 000 fewer deaths due to malaria than in 2020 [1]. There are more than 200 known species of Plasmodium parasite which infect humans as well as other vertebrates. Out of these species of Plasmodium parasite, P. falciparum, P. vivax, P. malariae, P. ovale and P. knowlesi are known to infect humans. The first two of these pose the greatest threat to human populations, and P. knowlesi causes zoonotic malaria that occurs in South-east Asia [2].
There are almost 3500 known species of mosquitoes, which are grouped into 41 genera. Malaria is transmitted in the human population only by the females of the genus Anopheles. The epicenter of malaria lies in the tropical and subtropical regions of the world, which are the natural breeding sites of Anopheles mosquito populations. The life cycle of Anopheles mosquitoes begins with laying their eggs in stagnant water, which further hatch into larvae and then mature into adult mosquitoes. The male mosquitoes feed upon sources of sugar such as nectar. The females also feed on sources of sugar to meet their energy requirements but require a blood meal to mature their fertilized eggs. During this course the female mosquito may become infected by sucking blood of a malaria-infected individual and becomes a source of transmission of Plasmodium parasites to susceptible individuals. Among 475 species named in the genus Anopheles, only 41 species, such as An. gambiae, An. funestus, etc., have been identified as dominant vectors of human malaria. The remaining either bite humans seldomly or cannot sustain development of malaria parasites. It is also noteworthy that different Anopheles species are responsible for Malaria transmission in different geographic regions[3].
However, the transmission of Plasmodium parasite through the malarious mosquito requires a viable environment, usually provided by natural as well as household discharges into the atmosphere in residential population areas, so that the life span of the mosquito is enough for the parasite to successfully nurture itself and then be ready to invade the human population. [4,5,6]. Water tanks, ponds, the moist gardens, unplanned drainage of sewage water, poor solid waste disposal, etc. [7] provide conducive environments for fertilization and breeding of the female Anopheles mosquitoes in residential areas, thereby leading to increased malarial contacts with humans [8]. Changes in the environment caused due to deforestation, agricultural activities and urbanization are also seen to have a huge impact on malaria transmission [9].
It is also seen that the mosquito-borne diseases are directly affected by population density related factors [10]. One of the major factors contributing to malaria transmission is the migration of human population, which may either be long-term migration or short-term movement of persons between locations with low and high malaria burdens. Therefore, it is very important to study the effect of household and other natural discharges on growth of vector population density leading to the spread of vector-borne infectious diseases.
Mathematical models have long been used to provide a definitive structure for better understanding of the disease-dynamics of malaria. Bailey et al. developed quantitative approaches to study malaria transmission [4]. Thereafter, many other researchers have done modeling and analysis of the dissemination of infectious diseases including malaria [11,12,13,14,15,16]. Singh et al. have conducted mathematical studies of effects of human population related factors on the spread of malaria [17]. Ghosh et al. have proposed an optimal control model of malaria using larvivorous fishes as control measures [18]. Ndamuzi et al. have proposed a deterministic model of malaria transmission in mosquito and human populations in Burundi, an East African country [19]. They have shown that the probabilities of a mosquito being infected and a human being bitten by an infectious mosquito must be reduced by applying optimal control strategies to curb the spread of malaria. Wu et al. have proposed a differential mathematical model to study the effect of time delay on stability of equilibria considering treated and successfully treated classes of human populations [20]. Traoré et al. have shown through a mathematical model that the global behavior of malaria transmission dynamics is dependent strongly on the vector reproduction ratio and basic reproduction ratio [21]. Elaiw et al. have studied a reaction diffusion model of malaria transmission [22]. Noeiaghdam et al. have analyzed several non-linear mathematical models of malaria infection [23,24].
In most of these models, the density dependent contact rates and the effect of non-emigrating population of the habitat along with parameters concerning natural and household discharges have not been considered in the modeling processes, but in a realistic situation, the contact rates between susceptible and infective populations depend upon non-emigrating and total populations of the human habitat [25,26,27]. Thus, the effect of a variable transmission rate as a function of emigrating population of the habitat should to be studied mathematically. Also, the study of effects of natural as well as anthropogenic discharges on dissemination of the disease needs to be focused on. In this paper, the effects of household and other natural discharges on the growth of the vector population in the environment, leading to the spread of infectious diseases, are studied by considering the density dependent contact rates between susceptible and infective populations as a linear function of total population.
The following important assumptions are made in the modeling process:
● In this paper, we have considered those female Anopheles mosquito species which are able to transmit Plasmodium parasites responsible for human infections in a given region.
● The malarial contact rate between the susceptible human population and infected mosquito population is increased with the increase in the density of non-emigrating population of the habitat and decreases as the emigration increases [28,29].
● The density of the vector (female Anopheles mosquito) population is assumed to be governed by a logistic model with the intrinsic growth rate as a linear function of the cumulative density of household and other natural discharges [30].
● The growth rate of the vector population decreases with a rate which is proportional to the vector population due to natural causes as well as use of pesticides and other control measures.
● The growth rate of cumulative density of household and other natural discharges depends on the current population in the habitat. Also, it increases with a constant rate caused by natural factors, but it decreases with a constant rate which is proportional to the cumulative density of household and other natural discharges.
2.
Materials and methods
Let total population density of the human habitat be $ N(t) $, which is divided into two subclasses as susceptible population density $ X(t) $ and infective population density $ Y(t) $ at time $ t $, respectively, so that $ X(t)+Y(t) = N(t) $. The vector (female Anopheles mosquito) population density at time $ t $ is $ N_1(t) $, which is divided into two subclasses $ X_1(t) $ and $ Y_1(t) $, here $ X_1(t) $ represents the susceptible vector population density, and $ Y_1(t) $ denotes the infectious vector population density. $ C(t) $ is cumulative density of household and other natural discharges in the habitat.
The contact rate between susceptible humans and infectious vectors is assumed to be $ \beta(N) = \beta- \beta_0 (N-N_0) $, where $ N_0 $ is density of the non-emigrating human population of the habitat.
In view of the above, we propose the following set of non-linear differential equations which governs the dynamics of the model:
where $ X(0) > 0, \; Y(0)\geq 0, \; N(0) > 0, \; X_1(0)\geq 0, \; Y_1(0)\geq 0, \; N_1(0) > 0, \; C(0) > 0. $ The positive constants of model (2.1) are defined as follows:
$ A $: Immigration of human population.
$ \beta $: Constant coefficient of interaction due to infective population density.
$ \beta_0 $: Emigration dependent coefficient of interaction due to infective population density.
$ \beta_2 $: Coefficient of interaction between infective population density and susceptible vector population.
$ d $: Natural death rate coefficient of human population
$ \alpha $: Disease related death rate coefficient of infective human population.
$ \mu $: Recovery rate coefficient of infectives.
$ \phi_0 $: Constant intrinsic growth rate coefficient of vector population density.
$ \phi $: The depletion rate coefficient of vector population density due to competition.
$ \phi_1 $: The growth rate coefficient of vector population density due to household and other natural discharges.
$ Q_0 $: Natural house hold discharges.
$ \alpha_1 $: Rate coefficient of household discharges due to human activities.
$ \alpha_0 $: The depletion rate of household and other natural discharges.
$ \alpha_m $: Death rate coefficient of vector population due to pesticides or other preventive measures.
$ d_m $: Natural death rate coefficient of vector population density.
For the analysis of mathematical model (2.1), we get an equivalent form by using $ X = N-Y $ and $ X_1 = N_1-Y_1 $ as follows:
with the initial conditions $ Y(0)\geq 0, \; N(0) > 0, \; Y_1(0)\geq 0, \; N_1(0) > 0, \; C(0) > 0. $
3.
Equilibrium analysis
First, to analyze the long term behavior of the model system (2.2)–(2.6), we obtain the region of attraction of solution trajectories. The following lemma provides us the region of attraction, which is required for further analysis of the model system [31].
Lemma 3.1. The region of attraction for the model system (2.2)–(2.6) is given by the set defined as:
where $ C_m = C_0+\frac{A\alpha_1 \alpha}{\alpha_0(\alpha+d)} $, $ {N_1}_m = \frac{\phi_1C_0+\phi_0-d_m-\alpha_m}{\phi}+\frac{A\alpha_1 \alpha \phi_1}{\phi \alpha_0(\alpha+d)} $ and $ {Y_1}_m = \frac{\beta_2 A^2}{d(\alpha_m+d_m)(\alpha+d)} $.
It attracts all the solutions initiating in the interior of the region.
Theorem 3.2. There are three equilibrium points in the region of attraction for the model system (2.2) –(2.6):
(i) $ E_0 (0, \frac{A}{d}, 0, 0, C_0), $ the infected human population-free and vector-free equilibrium point. This equilibrium point exists without any condition and represents the complete eradication of malaria along with the vector population.
(ii) $ E_1(0, \frac{A}{d}, 0, \bar{N_1}, C_0), $ the infective human population free and infectious vector population-free equilibrium point. This disease free equilibrium exists if $ \phi_0-\alpha_m-d_m > 0 $ where $ \bar{N_1} = \frac{\phi_0-\alpha_m-d_m}{\phi} $.
(iii) $ E_2(Y^*, N^*, Y_1^*, N_1^*, C^*), $ non-trivial endemic equilibrium point, provided
Proof. The existence of $ E_0(0, \frac{A}{d}, 0, 0, C_0) $, and $ E_1(0, \frac{A}{d}, 0, \bar{N_1}, C_0) $ are obvious. We prove the existence of $ E_2(Y^*, N^*, Y_1^*, N_1^*, C^*) $ from model system (2.2)–(2.6).
By using $ Y\neq0 $ and $ N_1\neq0, $ we get
By using Eqs (3.3)–(3.5), we get
By using (3.2)–(3.7), we define a polynomial function $ F(Y) $.
By using (3.8), we get the followings:
(i) $ F(0) = \left\{\left(\beta +\beta_0N_0-\beta_0\frac{A}{d}\right)\frac{\beta_2 A(\phi_0-\alpha_m-d_m)}{\phi d}-\left(\mu+\alpha +d\right)(\alpha_m+d_m)\right\} > 0 $, for $ R_0 > 1 $ as defined in (3.1).
(ii) $ F(\frac{A}{\alpha+d}) = -(\mu+\alpha+d)(\alpha_m+d_m+\frac{\beta_2A}{\alpha +d}) < 0 $.
Since the function $ F(Y) $ is a polynomial function of degree three in $ Y $, it is continuous and differentiable. Hence, the equation $ F(Y) = 0 $ has at least one root lying in $ 0 < Y < \frac{A}{\alpha+d} $. To show the uniqueness of the root, we prove $ F(Y) $ is monotonic (non-increasing) in $ 0 < Y < \frac{A}{\alpha+d} $, and for this we prove $ F'(Y) < 0 $. By differentiating (3.8) with respect to $ Y $, we get
Then, by using (3.8) again, we have
On simplification, we get- $ YF'(Y) < 0 $ for $ R_0 > 1. $ Thus, the polynomial equation $ F(Y) = 0 $ has a unique solution $ Y = Y^* $ in $ 0 < Y < \frac{A}{(\alpha+d)}. $ Now, by using the value of $ Y^* $ the value of $ N^* $ can be determined from (3.3), and the values of other variables can be determined uniquely from Eqs (3.4) to (3.6). Hence, $ E_2(Y^*, N^*, Y_1^*, N_1^*, C^*) $ exists if $ R_0 > 1. $
4.
Stability analysis
The results related to stability of the equilibrium points $ E_0(0, \frac{A}{d}, 0, 0, C_0) $, $ E_1(0, \frac{A}{d}, 0, \bar{N_1}, C_0) $ and $ E_2 (Y^*, N^*, Y_1^*, N_1^*, C^*) $ are stated in the following theorems [32].
Theorem 4.1. The equilibrium point $ E_0 (0, \frac{A}{d}, 0, 0, C_0) $ is unstable when $ \phi_0-\alpha_m-d_m > 0 $, and $ E_1(0, \frac{A}{d}, 0, \bar{N}, C_0) $ is unstable whenever $ R_0 > 1 $. The non-trivial equilibrium $ E_2(Y^*, N^*, Y_1^*, N_1^*, C^*) $ is locally asymptotically stable provided the following conditions are satisfied:
and
Proof. From the model system (2.2)–(2.6)
For the model system, we find the Jacobian matrix as follows:
where
The Jacobian matrix at the equilibrium point $ E_0(0, \frac{A}{d}, 0, 0, C_0) $ is
For the above Jacobian matrix one of the eigenvalues is $ \phi_0-\alpha_m-d_m > 0 $, which is the condition for existence of $ E_1 $. Hence, $ E_0(0, \frac{A}{d}, 0, 0, C_0) $ is unstable whenever $ E_1 $ exists.
Now, the Jacobian matrix for the equilibrium point $ E_1(0, \frac{A}{d}, 0, \bar{N_1}, C_0), $ is
It is clear from the above matrix that one of the eigenvalues $ AN_0\bar{N_1}\beta_0\beta_2d+A\bar{N_1}\beta \beta_2 d-A^2\beta_0\beta_2\bar{N_1}-d^2(d_m+\alpha_m)(\alpha+d+\mu) $ is positive, as $ R_0 > 1 $. Hence, the equilibrium point $ E_1(\bar{Y}, \bar{N}, 0, \bar{N_1}, C_0) $ is unstable when $ E_2 $ exists.
Local stability behavior of $ E_2(Y^*, N^*, Y_1^*, N_1^*, C^*) $-
We study the local stability behavior of $ E_2(Y^*, N^*, Y_1^*, N_1^*, C^*) $ by using Lyapunov's direct method. By using the transformations $ Y = Y^*+y, \; \; \; N = N^*+n, \; \; \; Y_1 = Y_1^*+y_1, \; \; \; N_1 = N_1^*+n_1\; \; \; \; C = C^*+c $, we linearize the model system. We consider the positive definite function
Differentiating (4.7) with respect to $ t $, we get
We linearise the model system about $ E_2(Y^*, N^*, Y_1^*, N_1^*, C^*) $ as follows:
Using the equations from (4.9)–(4.13) in (4.8), we have
In (4.14), we choose the constant $ k_1 $ such that $ k_1 = \frac{Y_1^*\beta(N^*)}{\alpha} $, and we get
Rewriting (4.15), we get
The derivative $ \dot{V} < 0 $ if the inequalities given below are satisfied.
By combining inequalities (4.16)–(4.20), we get the conditions stated in Theorem 4.1.
and
Theorem 4.2. The equilibrium point $ E_2 (Y^*, N^*, Y_1^*, N_1^*, C^*) $ is non-linearly stable in $ \Gamma $ provided the following two inequalities are satisfied.
Proof. For non-linear stability, we consider the following positive definite function.
On differentiating (4.23) with respect to $ t $, we get
By using model system (2.2)–(2.6), we get
By using (4.25)–(4.29) in (4.24), we get
We choose constant $ K_1 $ such that $ K_1 = \frac{Y_1^*\beta(N^*)}{\alpha} $ and the reduced form of 4.30 is as follows:
Thus, $ \dot{U} < 0 $ if the following inequalities are satisfied.
By combining conditions (4.32)–(4.35) and using the value of $ K_1 $, we get the conditions stated in Theorem 4.2.
5.
Numerical simulation of the mathematical model
In this section, we illustrate the analytical findings of the model by choosing a set of parameter values. We numerically find the nontrivial endemic equilibrium point $ E_2(Y^*, N^*, Y_1^*, N_1^*, C^*) $ and discuss its stability behavior for the parameter values given in Table 1 by using MAPLE.
For these values of parameters, the local and global stability conditions are satisfied. The non-zero equilibrium point $ E_2 (Y^*, N^*, B^*, C^*) $ corresponding to (2.2)–(2.6) is obtained as follows:
The Jacobian matrix at $ E_2(Y^*, N^*, Y_1^*, N_1^*, C^*) $ for the values of parameters given in Table 1 is
The Eigenvalues corresponding to the Jacobian matrix at the equilibrium point $ E_2(Y^*, N^*, Y_1^*, N_1^*, C^*) $ are- [-0.2130, -0.0026, -0.0741, -0.0346+0.0340i, -0.0346-0.0340i]. Since three eigenvalues are negative, and two eigenvalues have negative real part, the equilibrium point $ E_2(Y^*, N^*, Y_1^*, N_1^*, C^*) $ is asymptotically stable for this set of values.
To illustrate the non-linear behavior of the equilibrium point $ E_2(Y^*, N^*, Y_1^*, N_1^*, C^*) $ and the effect of various parameters on infected human population $ Y $, the models (2.2)–(2.6) is used to plot Figures 1–8.
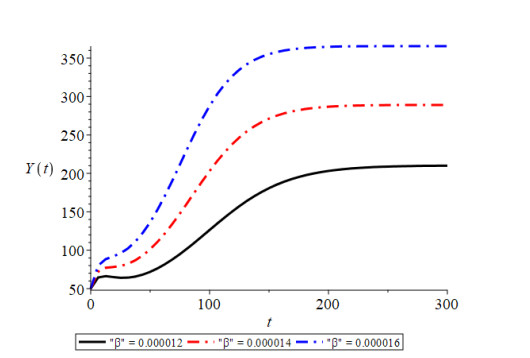
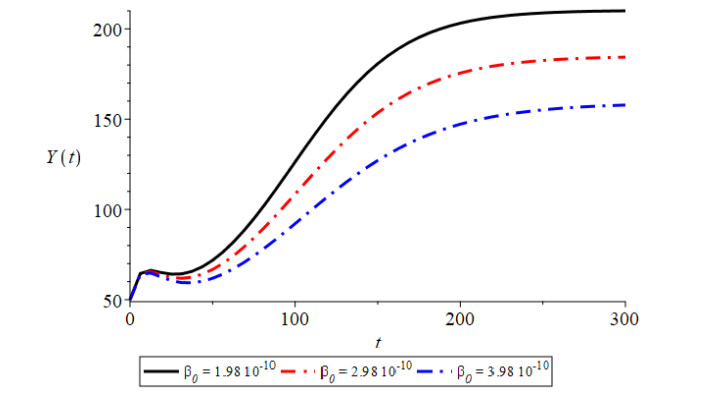
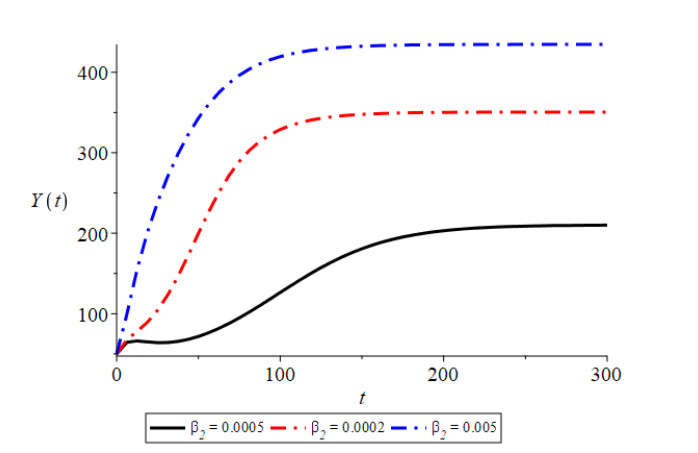
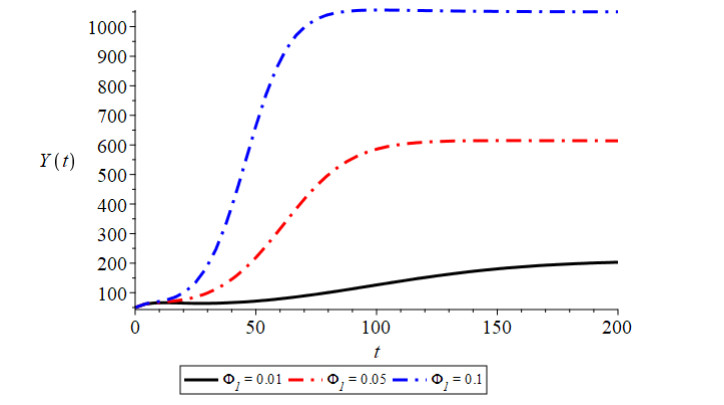
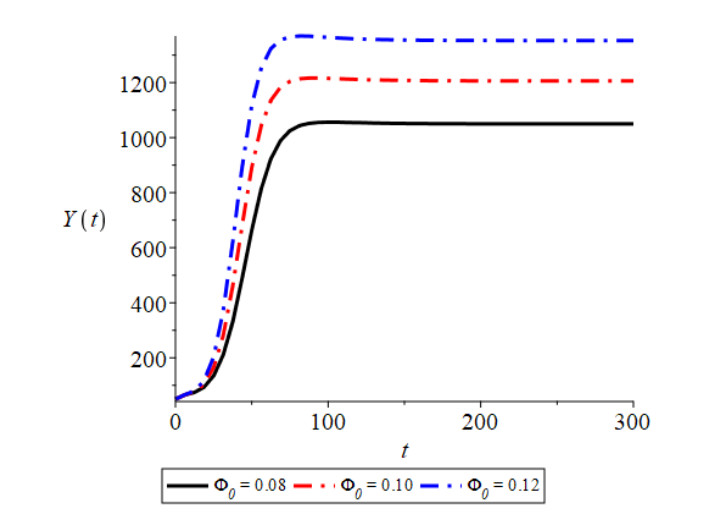
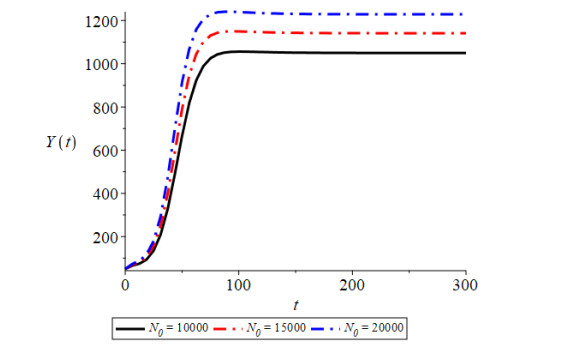
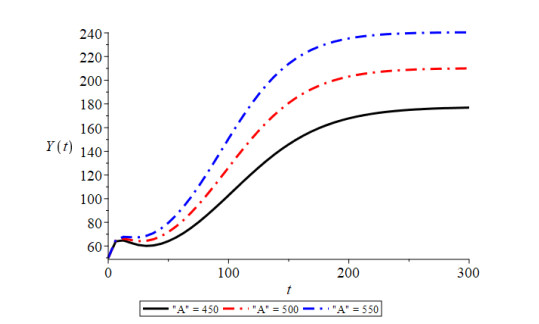
Figure 1 shows that the trajectories initiating from different initial conditions are convergent to the equilibrium point $ E_2(Y^*, N^*, Y_1^*, N_1^*, C^*), $ which indicates the global stability of equilibrium point $ E_2(Y^*, N^*, Y_1^*, $ $ N_1^*, C^*) $. In this figure, we have plotted four curves with different colors, each curve initiating from a different point, i.e., initial condition. All these curves approach the equilibrium point as the time progresses. Here, the curves with red, black, green and blue colors correspond to the initial condions ($ C(0) = 312.51, N_1(0) = 500, N(0) = 10000, Y_1(0) = 100, Y(0) = 700 $), ($ C(0) = 312.51, N_1 (0) = 500, N (0) = 15000, Y_1 (0) = 100, Y(0) = 1000 $), ($ C(0) = 312.51, N_1 (0) = 500, N (0) = 20000, Y_1 (0) = 100, Y(0) = 50 $) and ($ C(0) = 312.51, N_1 (0) = 500, N (0) = 8000, Y_1 (0) = 100, Y(0) = 50 $), respectively, which are all converging at $ E_2 $. From Figure 2 we see that with the increase in the constant rate of contact between susceptible humans and infected vectors, infective human population of the habitat increases. By Figure 3, it can be seen that as emigration dependent contact rate between susceptibles and infectives increases, the infective population density of the habitat decreases. Figure 4 shows that as the constant rate of contact between susceptible and infective vector population increases, the infected humans in the habitat are increased. From Figure 5, it is noted that as growth rate coefficient due to household and other natural discharges increases, the total vector population of the habitat and infected human population density of the habitat also increase. By Figure 6, it is also observed that with the increase in constant intrinsic growth rate coefficient of vector population density, the infectives of the habitat are increased. By Figure 7 it is observed that the non-emigrating population of the habitat also has a positive effect on the infected human population. In Figure 8, the effect of increase in the constant immigration rate on the infected population density is observed.
6.
Sensitivity analysis
In this section, we conduct the basic differential sensitivity analysis of the model system (2.2)–(2.6) for the parameters $ \beta, \beta_2, \phi_0, \phi_1 $ following Bortz and Nelson [33]. This is quite useful for the comparative study of impacts of changes in these parameters on the behavior of the model system. For instance, the sensitivity systems with respect to parameter $ \beta $ is as follows:
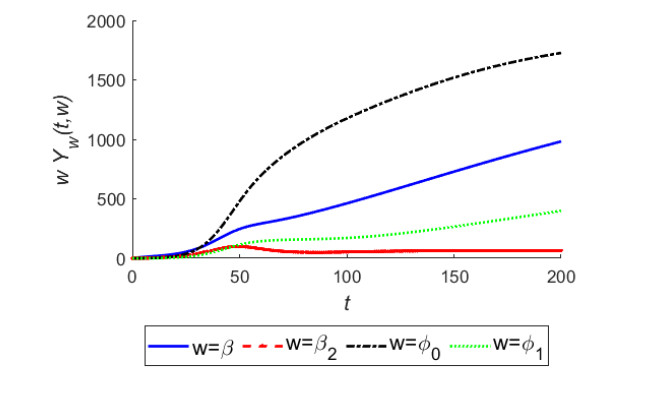
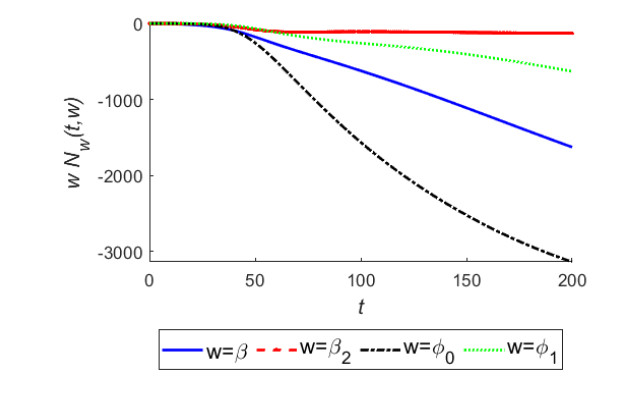
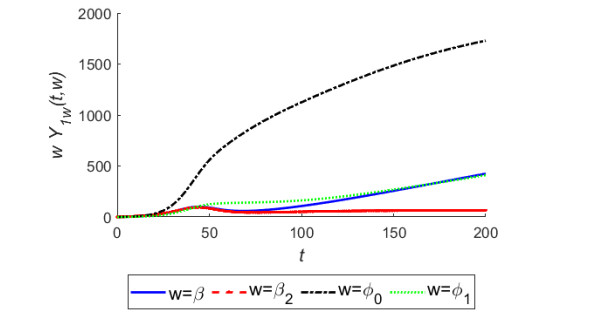
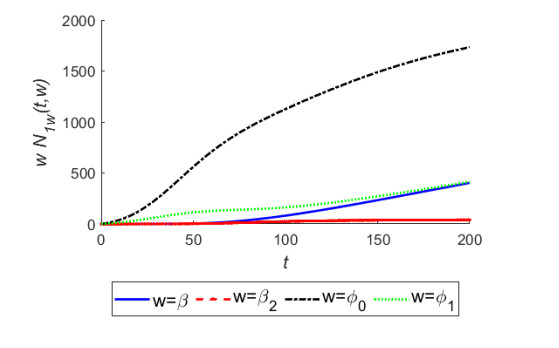
Here, $ Y_w(t, w) $ represents the sensitivity function of Y with respect to the corresponding parameter w. In Figures 9 to 12, we have plotted semi-relative sensitivity solutions to show the impacts of doubling of parameters $ \beta, \beta_2, \phi_0, \phi_1 $ respectively on variables of the model system (2.2)–(2.6) following Bortz and Nelson [33].
From Figures 9 and 10, it is evident that the parameters $ \phi_0, \beta, \phi_1 $ have significant influence over the infected and total human population densities. From Figure 9, we see that on doubling the intrinsic growth rate of the vector population, there will be a sharp increase of 1725 in the infected human population of the habitat in 200 years. We also see from this figure that doubling the constant coefficient of interaction between susceptible humans and infected vectors causes an increase of 981 cases in the infected population. The doubling of growth rate coefficient of vectors due to various discharges causes an increase of 409 infectives in the considered human habitat in 200 years. From Figure 10, we observe the adverse effects of doubling of the same parameters on total human population. For instance, we see that doubling of growth rate of vectors due to discharges causes a decrease of 630 in the total human population of the habitat. Similar trends are observed in Figures 11 and 12 for vector population density.
7.
Conclusions
Natural and household discharges such as water tanks, ponds, unplanned disposal of solid wastes, etc., provide a favorable environments for growth of various vectors and vector dependent infectious diseases. Changes in the demography of the region due to immigration and emigration are also among the root causes behind the spread of vector-borne diseases, including malaria. Due to these reasons, despite considerable advancements in medical research in recent decades, malaria continues to be among the leading killers in the twenty-first century.
In this paper, a non-linear epidemic model has been proposed and analyzed to study the effects of household discharges on the spread of malarious mosquito populations, further causing spread of malaria in human populations. The rates of contact have been assumed to be density dependent. In the model, we have considered five time dependent variables, namely, the susceptible population density $ X(t) $, the infective population density $ Y(t) $, the susceptible vector population density $ X_1(t) $, infective vector population density $ Y_1(t) $ and the cumulative density of household and other natural discharges $ C(t) $. The variable contact rate between susceptibles and infectives is considered to be emigration dependent. The growth of the vector population in the habitat has been considered to follow a logistic model, the intrinsic growth rate of which depends linearly on the infective population density as well as on the cumulative density of household and other natural discharges.
We have obtained three equilibrium states of the model. Two of the equilibrium points are free of infective human and vector populations. One of these two ($ E_0 $) is completely vector free, and the other ($ E_1 $) has a non-zero equilibrium value of susceptible vector population but is infectious vector-free. An important relation among growth rate and depletion rate coefficients of vector population is obtained for the existence of $ E_1 $. From the stability analysis, it is found that $ E_0 $ is unstable whenever $ E_1 $ exists. The third equilibrium $ E_2 $ is a non-trivial endemic equilibrium which exists if $ R_0 > 1 $. The quantity $ R_0 $ depends on various system parameters. If we decrease $ \beta, \beta_0, $ and $ N_0 $ then $ R_0 $ also decreases and if we restrict $ R_0 $ to be less than 1, we get only disease free equilibrium points. From stability analysis, we observe that $ E_1 $ is unstable whenever $ E_2 $ exists. The local and global stability conditions for $ E_2 $ are obtained by using Lyapunov's stability method. These stability conditions show that the disease related death rate, the rate of household discharges, the growth rate of vectors due the various discharges and emigration dependent coefficient of interaction have destabilizing effects on the system at $ E_2 $.
The numerical simulation is done to illustrate the model findings. The simulation of the epidemic model shows that the spread of vector dependent infectious diseases increases as the density of cumulative household and other natural discharges increases. It is shown further that the infective population density decreases as emigrating population of the habitat increases. If the non-emigrating population density of the habitat increases, the interaction between populations of the habitat increases, i.e., infective population density increases. To examine the sensitivity of model solutions with respect to the key parameters, a basic differential sensitivity analysis is also performed. The simulation study of the model has confirmed the obtained analytical results.
Acknowledgments
Sunil Sharma is thankful to the Deanship of Scientific Research at Majmaah University for supporting this work under project no. R-2022-334. The authors are grateful to the handling editor and the anonymous reviewers for their valuable suggestions, which helped in improving the quality of the paper.
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad: