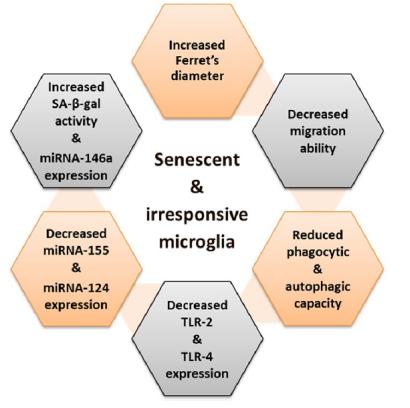
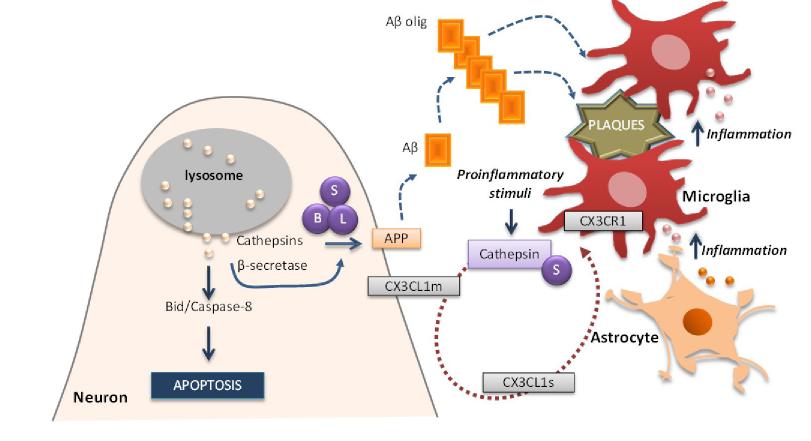
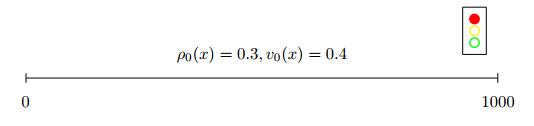Cellular senescence is viewed as an irreversible cell-cycle arrest mechanism involving a complexity of biological progressive processes and the acquisition of diverse cellular phenotypes. Several cell-intrinsic and extrinsic causes (stresses) may lead to diverse cellular signaling cascades that include oxidative stress, mitochondrial dysfunction, DNA damage, excessive accumulation of misfolded proteins, impaired microRNA processing and inflammation. Here we review recent advances in the causes and consequences of brain cell ageing, including the senescence of endothelial cells at the central nervous system barriers, as well as of neurons and glial cells. We address what makes ageing an important risk factor for neurodegenerative disorders, such as Alzheimer's disease, Parkinson's disease, amyotrophic lateral sclerosis and cerebrovascular disease. In particular, we highlight the importance of defects in mitochondrial dynamics, in the cathepsin activity imbalance, in cell-cell communication, in the accumulation of misfolded and unfolded proteins and in the microRNA profiling as having potential impact on cellular ageing processes. Another important aspect is that the absence of specific senescence biomarkers has hampered the characterization of senescent cells in ageing and age-associated diseases. In accordance, the senescence-associated secretory phenotype (SASP) or secretome was shown to vary in distinct cell types and upon different stressors, and SASP heterogeneity is believed to create subsets of senenescent cells. In addition to secreted proteins, we then place extracellular vesicles (exosomes and ectosomes) as important mediators of intercellular communication with pathophysiological roles in disease spreading, and as emerging targets for therapeutic intervention. We also discuss the application of engineered extracellular vesicles as vehicles for drug delivery. Finally, we summarize current knowledge on methods to rejuvenate senescent cells and we review cell replacement therapeutic strategies. A deeper understanding of the molecular mechanisms underlying the senescence of cells may open novel therapeutic approaches for age-related pathologies and for extending healthy human life span.
1.
Introduction
Second order traffic models have been investigated since the early 70's (e.g. [27,33]) and refined with the introduction of the Aw-Rascle-Zhang (ARZ) model [3] and are still subject of current research. Traffic models in general range from individual based microscopic to averaged macroscopic considerations, see [9,15,19,32] and the references therein. The motivation for the consideration of second order traffic models is that on the one hand microscopic models may explode for a large number of cars and, on the other hand, first order models are supposed to be dependent on the traffic density only and hence lack of real-world effects. In particular, macroscopic traffic flow models with delay terms have gained special attention recently, see [30,26]. While second order traffic models without delay terms are well understood on a theoretical and analytical level [3,9,15], models of this type including time delays are less considered so far [26], and if considered, the delay is usually rewritten by a Taylor approximation [30,26]. In contrast, the explicit modeling of reaction times via delays is a well-known approach in microscopic traffic modeling, see e.g. [6], and therefore the intention is that the introduction of an explicit delay can make macroscopic models more reasonable. More precisely, we expect similar effects as in microscopic delayed models such as the developing of stop-and-go waves based on the reaction time.
Starting from car-following type models, our aim is therefore to develop and study second order macroscopic models with an explicit dependence on the delay term. For this purpose, we consider the explicit derivation of delayed second order models from delayed microscopic models in three different ways following [4,22,30]. We will end up with a system of equations for the traffic density $ \rho $ in the sense of mass conservation and a second equation for the velocity $ v $ with an additional delay dependent term on the right-hand side. It turns out that for reasonably small delays all proposed macroscopic delayed models coincide with the classical (or undelayed) ARZ model [3] which reads in Eulerian coordinates for some positive initial state $ \big( \rho_0(x), v_0(x) \big) $:
where $ w = v + P(\rho) $ and $ P(\rho) $ is a known pressure function.
For the numerical simulation of the delayed macroscopic models, we use finite differences methods in a straightforward way and combine the method of lines with solvers for delayed differential equations. We analyze numerically the delayed models and compare the solutions to the classical the ARZ model. A comparison to real data and the corresponding fit of parameters (similar to [14]) is also presented.
This work is organized as follows: In section 2 we rigorously derive three second order macroscopic models based on the delayed microscopic model description according to [4,22,30]. The connection to the classical non-delayed ARZ model is also shown. In section 3, we introduce and discuss numerical methods for the solution of microscopic models with delay and second order delayed traffic models using ideas from [5]. In section 4, we present simulation results for comparisons of the different model level of descriptions and particularly stress on phenomena of the delayed macroscopic models.
2.
From microscopic to macroscopic models
In this section we derive macroscopic traffic models from delayed microscopic models of the car-following or follow-the-leader-type using three different approaches, cf. [4,22,30]. The resulting models are hyperbolic delay partial differential equations, where the time delay is explicitly kept and appears as an additional term in the equation for the velocity. As we will see, this new type of models gives rise to potential new dynamical behavior.
2.1. Microscopic model
The microscopic model under consideration dates back to the 1950s and belongs to the class of car-following models, see e.g. [6]. In particular, we consider a system of ordinary differential equations for the location $ x_i $ and speed $ v_i $ of the vehicle $ i $ at time $ t \in \mathbb{R}^+ $
with $ T>0 $ the uniform constant reaction time and model constants $ C>0 $ and $ \gamma\geq 0, $ cf. [4]. As initial data, we have to prescribe an initial history function on the time interval $ [-T, 0] $ to get a well-posed solution of the problem starting at $ t = 0. $
Apparently, the acceleration at time $ t $ depends on the reciprocal distance between vehicles and the difference in speed to the leading vehicle. Next, we define $ \Delta X $, $ \Delta X \in \mathbb{R}^+ $, as the length of a vehicle and the coefficient $ C = v_{\text{ref}}\Delta X^{\gamma} $, where $ v_{\text{ref}}>0 $ refers to the reference speed. We assume that the delay $ T $ is always positive and can be therefore interpreted as a reaction time, in contrast to an anticipation $ T<0 $. Then, we rewrite (2) to
The microscopic model equations (3) are the staring point for the macroscopic equations. We focus on three approaches, i.e. reverse spatial discretization [4], coarse graining [22], Taylor method [30], to derive the corresponding macroscopic delayed models. All approaches lead to second order traffic models that which mainly differ in the delay term.
2.2. Reverse spatial discretization
The first approach we are interested in is based on a derivation proposed in [4], where the classical ARZ model is derived from (2). Here, we apply the same technique to the delayed equations (3) by identifying the local density $ \rho_i $ with the free headway, i.e.,
We further define $ \tau_i(t): = \rho_i^{-1}(t) $ and $ w_i(t): = v_i(t)+P(\tau_i(t)) $, where $ P(\tau) $ can be understood as a function describing the anticipation of the road conditions in front of the drivers:
Then, the new variables $ \tau_i $ and $ w_i $ allow to equivalently reformulate system (3) as
since $ P'(\tau) = -v_{\text{ref}}\frac{1}{\tau^{\gamma+1}} $ for $ \gamma \geq 0 $. The system (4) can be interpreted as a semi-discretization of the following delay partial differential equation for $ \Delta X\rightarrow0 $:
where $ \tau $ and $ \rho $ are the limiting expressions of $ \tau_i $ and $ \rho_i $. Note that the classical ARZ model (1) in Lagrangian coordinates reads
In fact, a direct computation shows that (5) is equivalent to
applying the definitions of $ w $ and $ \tau $ as well as information on $ P'(\tau) $.
Let us take a closer look at the right-hand side of the momentum equation (7). Compared to the classical model, we now get the temporal change in speed dependent on the density and the spatial derivative of speed from an earlier time. For the interpretation of $ w $, which is a Riemann-constant/invariant in the classical ARZ model, we refer to [14], where $ w $ is used as the empty road speed. However, $ w $ is not necessarily constant in the delayed model and changes due to the difference in the product of density and the spatial derivative of speed. This means the empty road speed, i.e. the speed a driver would have on an empty road, is not only dependent on the driver but also on the traffic behavior around leading to a more cautious actions.
So far, we have considered the Lagrangian macroscopic equations (5) and (7), respectively. In a next step, we transform these equations into Eulerian coordinates by introducing the new variables $ (\hat{x}, \hat{t}) $ with
or, exploiting $ \hat{t} = t $,
In the following, we write $ t $ instead of $ \hat{t} $ since $ \hat{t} = t $. Then, we obtain from (5) the new equations
which are obviously closely related to the undelayed ARZ model.
2.3. Coarse-graining
Another approach to derive a delayed macroscopic equation is the so-called coarse-graining (CG) proposed in [12,22]. Here, we focus on [22] and highlight the most important steps. Although the method is different from reverse spatial discretization (RSD) from subsection 2.2, we note that the resulting equations are quite similar.
We start by defining the density $ \hat{\rho}(x, t) $ and flux field $ \hat{q}(x, t) $ of traffic flow as follows:
where $ x_i(t) $ is the position of the $ i $-th car at time $ t $ and $ \delta $ denotes the $ \delta $-distribution. We now coarse-grain these fields and obtain
by applying the coarse graining envelope function $ \Phi(x, t) $ which has a peak at $ (0, 0) $ and is normalized in the sense $ \int\Phi(x, t)\text{d}x\text{d}t = 1 $. According to [22], we can derive the following system of equations from (12) for the density $ \rho $ and flux $ q $:
with the bracketed average of a quantity $ f_i(x, t) $ defined as
By introducing $ v(x, t) = \langle \dot{x}_i(t')\rangle_{(x, t)} = \frac{q(x, t)}{\rho(x, t)} $ and $ \Theta(x, t) = \langle \dot{x}^2_i(t')\rangle-v^2(x, t) $ we can rewrite the second equation in (13) to
The first equation for the density is obviously the same as in (10) and the derivation so far is independent on microscopic dynamics. However, the second equation for the momentum involves a term $ \langle\ddot{x}_i(t')\rangle_{(x, t)} $ which is dependent on individual drivers' behavior and therefore needs a careful discussion.
Let us first consider the general case of a car-following model of the form
Then coarse graining leads to the approximated momentum equation
where we further approximate
Plugging in and expanding around $ (\rho^{-1}(x, t), 0, v(x, t)) $ yields
where $ B_i = \partial_{z_i}B(z_1, z_2, z_3)|_{(\rho^{-1}, 0, v)} $. We end up with an equation of type
We remark that it is also possible to include terms of higher order leading to higher order approximations as well as higher order derivatives. Since we are interested in delayed models driven by (3), we can identify $ B $ as follows:
The system of equations is then
In conservative form, we may write the system of equations
which is (up to the term $ \partial_{x}v(x, t) $) directly comparable to (10).
For completeness, we also state the Lagrangian representation of (18). If we use the inverse transformation from subsection 2.2 and write the equations dependent on $ \tau $ instead of $ \rho $ we end up with
2.4. Taylor expansion
The last approach we present is based on a Taylor expansion which was originally introduced in [30]. However, in contrast to the original approach, we derive a second order delayed model instead of a first order model only. Furthermore, we keep the explicit delay while the new model is derived from the microscopic level and do not apply a diffusive approximation.
We start by expanding the delayed variables position $ x_i $ and speed $ v_i $ up to first order. This leads directly to
and equivalently
By using the microscopic description (3) we can characterize the following delayed system:
The definition $ \Delta x_i(t): = x_{i+1}(t)-x_i(t) $ then allows to approximate
and
To derive macroscopic equations, we use again $ \rho_i(t): = \frac{\Delta X}{x_{i+1}(t)-x_i(t)} $ and obtain the conservation of mass by introducing $ \tau_i = \rho_i^{-1} $ in the limit $ \Delta X\rightarrow0 $:
where $ \tau $ and $ \rho $ denote the respective limit versions of $ \tau_i $ and $ \rho_i $. The second equation for the velocity is derived as follows:
For simplicity, we omit the terms $ \mathcal O(T^2) $ in the latter representation. Doing the same scaling procedure and using the same definitions as above, we end up with
in Lagrangian coordinates. However, the interpretation of the right-hand side is now different compared to (7) and (19).
By the use of Taylor expansion, correction terms enter the model. This can be interpreted as a correction towards the fact that drivers do not react immediately but after some delay. These correction terms are, as in the previous models, dependent on the product of density, the spatial derivative of speed and the (current and past) state of the traffic. Note that in the case we ignore the terms depending on $ T $, we recover the classical ARZ model.
3.
Properties of delayed macroscopic models
As already seen, the introduction of time delays lead to a right-hand side in the equation for the velocity that includes different states of traffic. This can be interpreted as an anticipation of the change in traffic based on the current and past state. Hence, we are able to model the drivers ability to 'extrapolate' the traffic situation to change his/her driving behavior.
Similar to the microscopic case, the introduction of explicit delays requires the extension of the initial data time span to ensure well-posedness. For all states $ (\rho, v) $ that appear in a delayed form, initial values at $ t = 0 $ are not enough and we need initial histories. These are functions prescribing the states on at least the interval $ [-T, 0] $.
We now aim to discuss some key properties of the delayed macroscopic models. First, we show that for vanishing delays the models coincide with the classical ARZ model. In this context, we also refer to the weak solutions of the ARZ model and investigate the changes caused by the delayed case. Second, we comment on the positivity of solutions. Closely related to this discussion is the question of stability. We inverstigate the system of delayed differential equations (DDEs) resulting from discretizing in space and derive properties to ensure stable solutions.
3.1. Convergence to the classical ARZ model
Lemma 3.1. The macroscopic delayed models (7), (19) and (21) converge to the undelayed ARZ model for $ T\rightarrow0 $.
Proof. The first equation of all proposed models is mass conservation and has no explicit dependence on the delay $ T $. We focus on the second equation in Lagrangian coordinates and need to show that $ \partial_t w(x, t) = 0 $ is satisfied.
Therefore, the velocity equation needs to be expressed in terms of $ w $ for all models (7), (19) and (21). We use that $ w = v+P $ and get the following representation for the models derived by reverse spatial discretization (7) and coarse-graining (19):
and
respectively. The velocity equation for the model derived by Taylor expansion (21) reads
Then, in the limit $ T\rightarrow0 $, we end up with $ \partial_t w(x, t) = 0 $ for all equations.
3.2. Comparison to weak solutions of the ARZ model
In this section, we discuss the solutions to Riemann problems for the ARZ model (1) and explain how the delayed models fit into this framework. The ARZ model is a system of conservation laws and we have three basic types of weak solutions to the Riemann problem, i.e. contact discontinuities, shocks and rarefaction waves, see [3,15] for an overview. We define $ u = (\rho, \rho w)^T $ and rewrite the fluxes for the ARZ model as
For further investigations, we consider the ARZ model in the form
where $ \lambda_i(u) $ and $ r_i(u) $ are the eigenvalues and eigenvectors of $ \nabla f $, dependent of the state vector $ u $. After defining genuine nonlinear and linear degenerate eigenvalues, we can state the weak solutions. For the ARZ model, the eigenvalues and eigenvectors are
with $ \lambda_1 $ being genuine nonlinear and $ \lambda_2 $ being linear degenerate. While lifting this analysis to the delayed models, the first problem occurs since $ \nabla f $ (and its properties) needs to be derived. However, except for $ \gamma = 0 $, a suitable flux function has not been found yet since it would depend on the current and past state, respectively.
Now, let us focus on the weak solutions to Riemann problems with left state $ u_l = (\rho_l, \rho_l w_l)^T $ and right state $ u_r = (\rho_r, \rho_r w_r)^T. $ The contact discontinuity belongs to the linear degenerate eigenvalue and appears when $ \lambda_2(u_l) = \lambda_1(u_r) $. This means $ v_l = v_r $. The solution is then given by the initial date moving with $ v_l = v_r $
For the delayed models, we do not necessarily get the same solution for $ v_l = v_r $. However, if also the history is such that $ v_l = v_r $ for all $ [-T, 0] $, the solution looks quite similar.
For the shock solution, we consider the Rankine Hugoniot condition
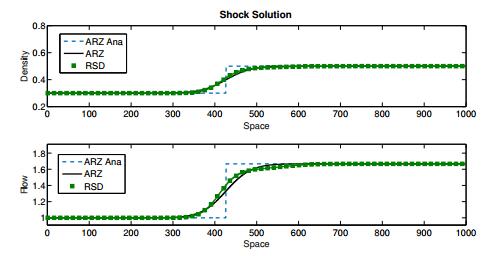
This gives for every state a curve which can be connected to the latter by a shock. The shock solution belongs to the genuine nonlinear eigenvalue. In the ARZ model, a fixed $ u_l $ can be connected by a shock to states $ u $ with $ w_l = w $. Furthermore, the shock is admissible if $ \rho_l<\rho_r $ and looks like
It remains unclear how the delayed models fit into this framework due to the missing definition of a flux function and hence the evaluation of the Rankine Hugoniot condition.
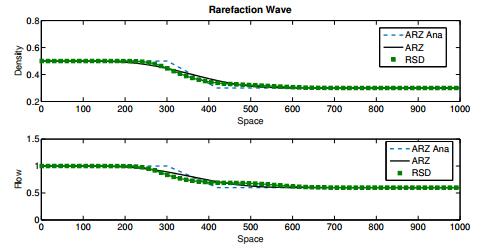
Similar to the shock solution, the rarefaction wave also belongs to the genuine nonlinear eigenvalue $ \lambda_j $. The solution is given by
where $ v $ is such that $ v'(\zeta) = r_j(v(\zeta)) $ and $ \lambda_j(v(\zeta)) = \zeta $. For the ARZ model, it holds $ v(\zeta) = (\zeta, w_l)^T $. In the case of delayed models, no conclusions can be made since eigenvalues and eigenvectors cannot be determined.
To illustrate the behavior of approximate solutions to the delayed model, we refer to our numerical study in section 4, in particular figures 5, 6 and 7.
3.3. Positivity of solutions
The early proposed second order models, i.e. the Payne-Whitham-model, suffered from the problem that in some Riemann problems the density and velocity could become negative. This was first pointed out by Daganzo [10] and the ARZ model has been developed to overcome this drawback. Unfortunately, the delayed models we have derived, converge certainly to the classical ARZ model, but might lose the positivity of $ v $ and $ \rho $ due to the delay terms. This can be seen by considering the momentum equation for each model and assuming sufficiently smooth initial data.
For the first approach (reverse spatial discretization) we have to analyze equation (7). We investigate the case that we have non-negative initial data and need to ensure that the solution remains non-negative. However, the solution would become negative in the case $ v(x, t) = 0 $ and $ \partial_t v(x, t)<0 $, i.e.,
with $ v_{\text{ref}} $ and $ \rho(x, t-T)^{\gamma+1} $ are both positive by assumption. However, for the term $ \partial_x v(x, t-T) $ no statement is possible and hence the velocity can become negative.
For the coarse-graining approach (19) we have a different situation:
Since the term $ \partial_x v(x, t-T) $ does not appear here, but $ \partial_x v(x, t) $ instead, the solution could become negative only if $ \partial_x v(x, t)<0 $. So assuming non-negative data and $ v = 0 $, we have at least for differentiable solutions that $ \partial_x v(x, t) = 0 $ (since $ v = 0 $ is a minimum) and thus $ v $ remains positive.
The last approach, the Taylor model (21), would become negative if $ v = 0 $ and the term
is smaller than $ 0 $. Using the same arguments as before, we can reduce the latter expression to
and can conclude that the speed can become negative.
Remark 1. Negative velocities also appear in the microscopic model (2). This is the case when a driver is quite close to the vehicle in front and the driver in front suddenly reduces the velocity within the given delay time, see e.g. [21] where this effect is seen for a similar microscopic model. The non-physical solutions obtained in this way are avoided by the choice of our numerical experiments.
3.4. Stability of discretized system
From theory we know the concept of linear stability for DDEs, see [25]. To apply this idea to the PDE-type delayed models we have derived, we need to discretize the equations in space. For the model based on reverse spatial discretization (7), we get for $ \gamma = 0 $
exploiting $ \tau(x, t-T)^{-1} = \rho(x, t-T). $ The steady state is obtained by $ v^* $ constant in time and space, i.e. $ v^*(x_i, t) = v^*(x_{i+1}, t) = v^*(x_{i+1}, t-T) = v^*(x_i, t-T) $, and $ \tau^* $ arbitrary. We disturb this steady state $ (\tau^*, v^*)^T $ by adding a small disturbance $ \eta(t) $. For the linear stability analysis, we look at the linearized system around the steady state, which is
Inserting the disturbed steady state, we get
Since $ \eta_2 $ is independent of $ \eta_1 $, we consider $ \eta_2 $ first. Assuming the solution $ \eta_2 $ (omitting $ x_i $) has the form $ \eta_2(t) = \eta_{0, 2}e^{\lambda_2t} $, this gives
This equation is equivalent to
This type of equation can be solved for $ \lambda_2 $ using the Lambert $ W- $function, see [8],
and hence the solution for $ \eta_2(t) $. In a next step, $ \eta_1 $ is given by integrating
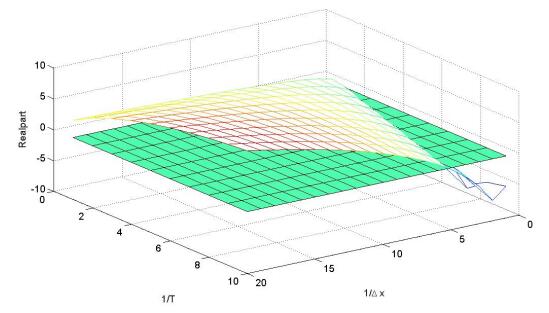
This means, we have stability in a linear sense if $ Re(W(\frac{-Tv_{\text{ref}}}{\tau^*\Delta x}))<0 $. For some values of $ T $ and $ \Delta x $ the real part is shown in figure 1. We observe that the system is stable for small $ T $. This result seems plausible since a large delay is known to destabilize the traffic system in the microscopic case, cf. [21]. Furthermore, small step sizes $ \Delta x $ also lead to unstable systems.
4.
Numerical results
First, we have to introduce suitable discretization schemes for the microscopic and macroscopic delayed models. We make use of already well-established numerical methods for undelayed models and discuss how the delay term can be treated within this framework.
The microscopic model (2) is a system of DDEs. The numerical discretization of the delay term can be done with method of steps, cf. [5]. The concept behind this method is to separate the original initial history problem into several initial value problems stated by ordinary differential equations (ODE) and then apply standard schemes for ODEs.
To do so, we need to split our foreseen time interval into sub-intervals of smaller size such that the delay is still included. If we look at the first interval, we have all delayed values given by the initial history since the interval is smaller than the delay. Therefore, we can plug in the history and get a classical ODE for this first interval that needs to be solved numerically. For the second interval, we can plug in the history and the solution of the first interval for the delayed parts and get again an ODE. Iteratively, we use this strategy to solve the problem on the whole time interval. A good interpolation of the solution is necessary since we might need values in later iterations which do not correspond to the fixed time grid points.
We use the Matlab solver dde23 to simulate (2). This solver uses an explicit Runge-Kutta (2, 3) pair combined with the method of steps.
0https://de.mathworks.com/help/matlab/ref/dde23.html
For the comparison with the microscopic model, we use a method-of-lines like approach for the discretization of the delayed macroscopic model. We discretize the model in space to get a system of DDEs and apply a forward finite differences discretization to (7), (19) and (21) in Lagrangian coordinates as follows:
Discretization of (7):
Discretization of (19):
Discretization of (21):
The resulting system can be solved with the method of steps again using the Matlab solver dde23. All discretization procedures need an initial history function. For simplicity, we choose a constant history function with the value of the states at $ t = 0 $.
We remark that the different numerical schemes are used because they showed to be better suited for the respective equation. Moreover, due to the potential instabilities, we can not decrease $ \Delta x $ arbitrarily, which in fact poses a problem.
4.1. Comparison of delayed models
4.1.1. Microscopic versus macroscopic approaches
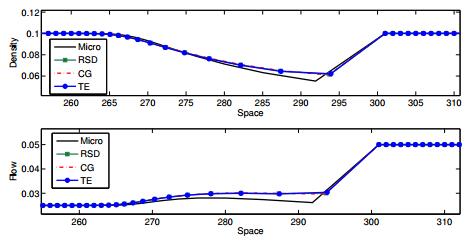
The first numerical experiment we focus on is the numerical comparison between the microscopic model (2) and the different derivations of delayed macroscopic models called reverse spatial discretization (RSD) - eq. (7), coarse-graining (CG) and Taylor expansion (TE). Therefore, we present the following scenario: We consider a street with constant initial density in the macroscopic case which means initially uniformly distributed cars in the microscopic situation, i.e. $ \rho_0 = 0.1 $. For the initial speeds on the first half of the road, the traffic is slow, i.e., $ v_0 = 0.25 $, while on the second half the traffic moves significantly faster, i.e. $ v_0 = 0.5 $. In this way, we create a vacuum situation, where the traffic in the second half moves away from the slower cars in the first section. The spacegrid is equidistant with $ \Delta x = 1 $ and the timestep is chosen by the DDE solver.
We simulate a time interval of 100s and the delay is $ T = 0.5 $. The boundary conditions for the macroscopic models are introduced by ghost cells copying the first and last cell values. The results are shown in Figure 2 and 3 for a snapshot of the solution.
We see that the models resolve the vacuum solution well and are close to each other.
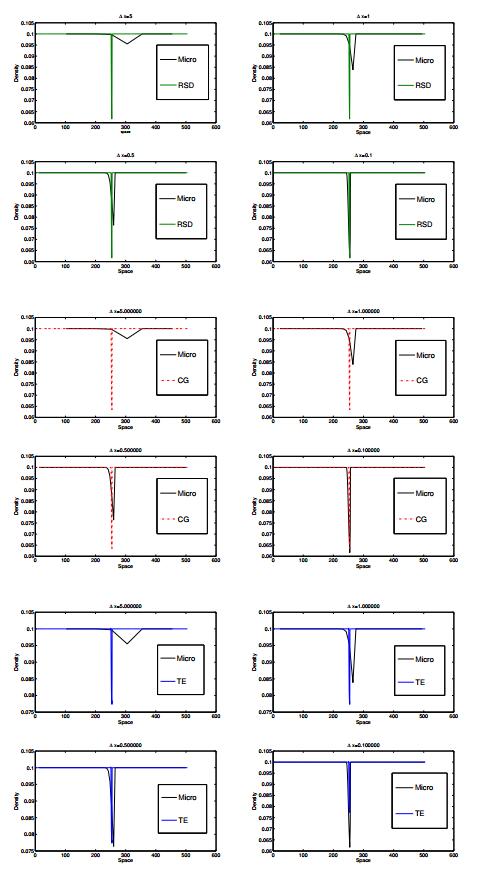
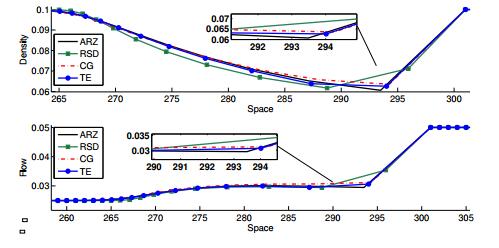
If we now zoom in space and consider different values for $ \Delta x $, we observe the convergence behavior as depicted in Table 1 and Figure 4.
4.1.2. Classical ARZ model versus macroscopic approaches
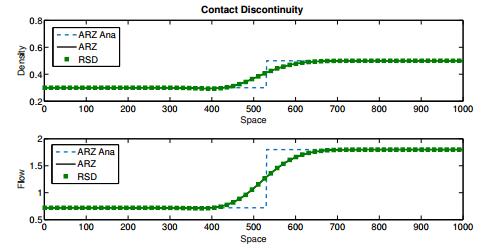
In section 3.2 we have seen that weak solutions to the classical ARZ model are hard to interpret for the delayed models. However, from a numerical point of view, a first idea of weak solutions to the delayed model can be given. Here, we focus on the numerical solutions to the RSD model and make comparisons to the three different types of Riemann solutions, see (24) - (26), on the same grid sizes. The results are given in figures 5, 6 and 7.
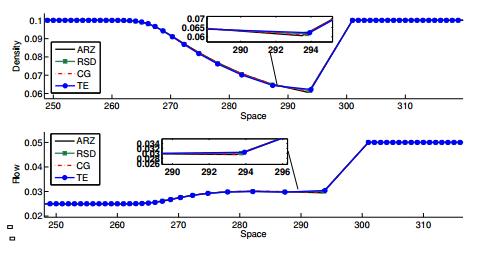
In a second experiment, we compare the delayed macroscopic models to the classical ARZ model for a delay of $ T = 0.5 $ and $ T = 5 $, respectively, see figure 8 and 9.
Due to lemma 3.1, all delayed macroscopic models converge to the classical ARZ model, cf. Figure 8. However, the situation changes for a larger delay, e.g. $ T = 5 $. We see a slightly different behavior of the models at the point, where the density changes from falling to rising, cf. Figure 9. There are additional sections with different slopes in the delayed models. This is obviously an effect driven by the time delay as the direct comparison with Figure 8 shows.
4.1.3. Taylor model (TE) versus convection-diffusion flow model [30]
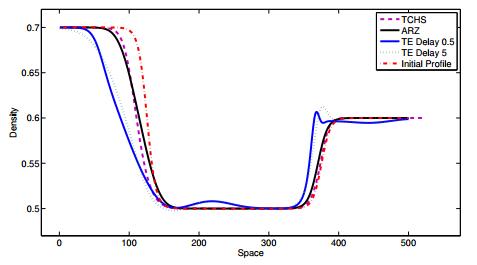
The third experiment compares our TE approach (21) to the first order convection-diffusion flow model (TCHS) derived in [30]. Since the TE approach is inspired by the derivation introduced in [30], we aim to point out how the two approaches differ regarding the explicit tracking of the delay, cf. discussion in subsection 2.4.
The model in [30] is given by
with $ V(\rho) = (1-\rho) $ and reads in Langrangian coordinates
This model is solved by a finite difference based method of lines discretization, where the ODE solver is a forward Euler method.
For our comparison, we consider a street with a smooth initial density profile such that we have a relatively high density in the beginning, i.e. $ \rho_0(x) = 0.7 $, a density drop in the middle, i.e. $ \rho_0(x) = 0.5 $, and let the density rise again to $ \rho_0(x) = 0.6 $ in the end, cf. Figure 10. The time delay is $ T = 0.5 $s and $ T = 5 $s, as for smaller delays the difference is not as pronounced. The total time horizon is $ 30 $s and the discretization is $ \Delta x = 0.5, \Delta t = 0.01 $ in space and time, respectively. The results can be seen in Figure 10 after 30s. The Taylor model (21) introduces some new effects we do not see in the models TCHS and ARZ, in particular at $ x = 350 $ when the density arises from 0.5 to 0.6 and vehicles start to queue. In the TCHS model, all dependencies on the delay of higher order are excluded while the model keeping the delay still leads to oscillatory effects. We also see that the oscillations increase for larger delays.
4.2. Applications of delayed macroscopic models
For the next numerical studies and applications, we introduce an alternative numerical discretization of the macroscopic models based on the Eulerian coordinates representation. This is useful since the scenarios we investigate are on a fixed road segment and so Eulerian coordinates are better suited to tackle the boundary conditions. To set up a suitable numerical scheme, we use known methods for hyperbolic partial differential (PDE) equations coupled to a splitting technique, cf. [23]. This means, considering for example the reverse spatial discretization (RSD), we split the model (10) into the classical ARZ model solved in a first step and an additional delayed part solved in a second step with a forward differences approach. We solve the hyperbolic PDE part with the Lax-Friedrichs method using the index $ j $ as space index. Then, we get for (10)
where $ f_{\rho} $ and $ f_{\rho w} $ are as in (22). We also have to consider the CFL condition while using the Lax-Friedrichs method. The eigenvalues are given in (23) and due to the delay we can except the speed of information in the delayed case to be less or equal than in the undelayed case.
Since the Lax-Friedrichs method is consistent, stable, monotone and $ l_1 $- contractive, it is sufficient to provide a small enough time step. Now, we have to look at the discretization. Let us start considering the method of lines. There, we spatially discretize the equation which can be done in several ways, e.g. [17] or [29]. We end up with a system of DDEs solved by the method of steps again. However, the method of steps uses ODE solvers [16]. Moreover, we have an influence of the history which can not be ignored. Since the history function appears in the ODEs that are solved within the method of steps, numerical difficulties may arise.
In the following, we introduce two examples to emphasize the impact of delayed macroscopic models in the case of real-world applications.
4.2.1. Traffic lights
The first application we have in mind is a frequent traffic light switching. We intend to compare the model (10) to the classical ARZ model (1). The experimental setting is introduced in Figure 11, where at the end of the street, i.e. at $ x = 1000 $, a traffic light is installed.
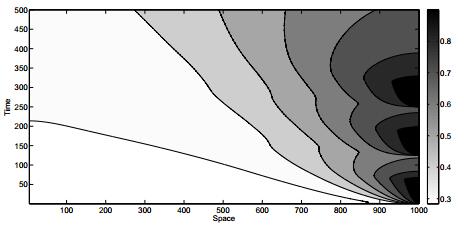
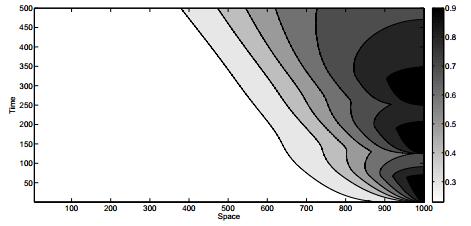
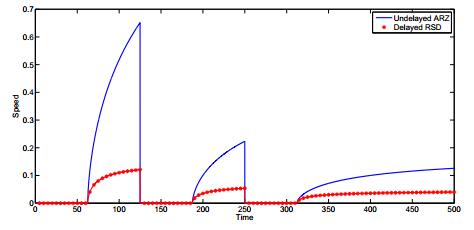
Initially, the density and the velocity are $ \rho_0(x) = 0.3, v_0 = (x) = 0.4 $ for $ x \in [0, 1000] $. The delay is fixed to $ T = 0.5s $. The traffic light starts with a red phase which is simulated by a boundary value of $ \rho(1000, t) = 1 $ and $ v(200, t) = 0 $. Then, the traffic light switches 3 times from red to green and splits the simulated time horizon of $ 500s $ into 6 phases: the first 5 phases are $ 62.5s $ long and the last is $ 187.5s $. The discretization is $ \Delta x = 5 $ and $ \Delta t = 0.05 $. The numerical results in terms of $ \rho $ at $ t = 500 $ are shown for the delayed and undelayed ARZ model in Figures 12 and 13.
We see that the presence of the delay term leads to phenomena which can not be observed in the classical ARZ model as for example the broader density plateaus to resolve the stop-and-go behavior. The difference of the two models can be also recognized for the speed $ v(1000, t) $, see Figure 14. The speed is zero in both models when the traffic light is red. However, when the green phase starts, the speed in the undelayed model increases with a steeper slope leading to a higher speed. Here, the delayed model seems to be more realistic as sudden steep peaks of speed is not what one would expect.
4.2.2. Data fitting
As a second application, we analyze the performance of the models regarding real-measured data. Therefore, we fit the classical (1) and delayed (10) model to real-life data and compare the numerical results.
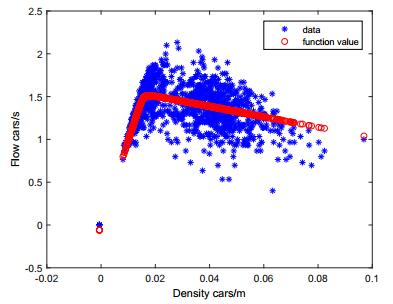
We start to investigate the fundamental diagram, i.e. the relation between traffic density and traffic flow, for real data taken from the Minnesota Department of Transportation. The data shows a reverse lambda shape, see Figure 15. At low densities, there is a clear linear relation between flow and density. At medium densities however, we get a wide spread of flows, making a functional relation hard or even impossible to identify. We remark that in the classical ARZ model (1) the artificial variable $ w $ can be interpreted as a way to get a whole class of functions to cover this spread. The relation between density and flux gets more clear again for high densities.
0http://data.dot.state.mn.us/datatools/
In a next step, we follow the approach in [14] to fit the classical and RSD model to this data. We use data collected by the Regional Transportation Management Center, a division of the Minnesota Department of Transportation (RTMC data), in the same way as described in [14] and approximate the relation between density $ \rho $ and flow $ q $ by a function $ Q(\rho) $ that fits the fundamental diagram data in a least squares sense. The function family we intend to optimize consists of three parameters $ \alpha, \lambda, p $, cf. [14],
and the resulting solution is plotted in Figure 15.
From $ Q(\rho) $, we can derive a data-fitted pressure function $ P(\rho) = U(0)-U(\rho) $, where $ U(\rho) = \frac{Q(\rho)}{\rho} $ and $ U(0) = Q'(0) $ are velocities. This way enables us to use the data in our models as follows: Plugging in the pressure function $ P(\rho) $ into model (7) by exploiting the connection between the modeling parameter $ C $ in the microscopic model (2) and $ P' $ we obtain
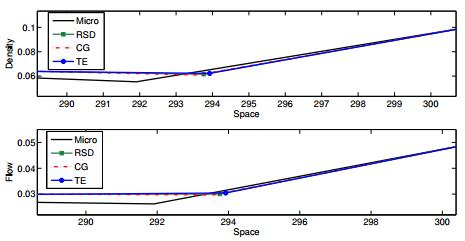
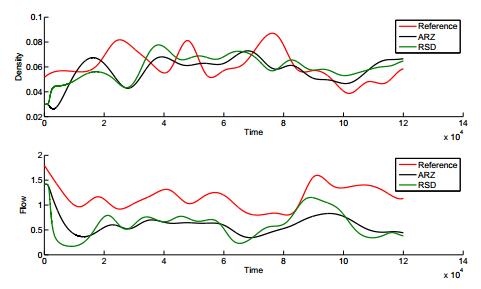
Now, we test the data-fitted model (27) with RTMC data to check the performance. We follow again [14] and take a segment of street with no on- or off-ramps and three measurement stations. The first and the third station deliver the boundary values for our simulation, while the station in the middle is the reference point, i.e. we will compare the simulation results with the measured data of the second station. So we simulate the segment of road, use the real data as boundary values and get a simulated traffic profile. This profile we compare at the point of the second station with the real data. For a time interval of 600 seconds, i.e. 16:00-16:10 on a workday, the results are plotted in Figure 16 for the fitted delayed and undelayed ARZ model. The images represent the whole time sequence at the reference station in the middle of the segment.
It seems that the undelayed ARZ model tends to avoid deviations while the delayed model has stronger peaks. Beyond that, both models seem to fit the flow better than the density, but this might be due to the specific example. For further discussions on the data-fitted classical ARZ model, which might be useful for this kind of experiment, we refer to [14] and [13].
Instead, let us look at the error between the real data and the simulated the models. We therefore make use of the error defined in [14] which is
for every position $ x $ and time $ t $ and normalization constants $ \Delta \rho $ and $ \Delta u $. Due to the measured data at only one reference point, the temporal average is given by
The normalization factors $ \Delta\rho $ and $ \Delta v $ are the ranges of the density and speed from the fundamental diagram. The errors we derive consider only the last 300s of the simulations, although we simulate 600s in total. In the example above, the error $ E $ for the undelayed model is 0.6404 and the error of the delayed model is 0.6034. To validate the impression that the delayed model performs better, we study further examples. The data is again from workdays and the time is 16:00-16:10. We investigated 10 randomly chosen weeks, i.e. 50 days. To compare the errors of the simulations, we look at the following definition
where $ \text{E}_{\text{undel}} $ is the error $ E $ in the undelayed and $ \text{E}_{\text{del}} $ the error $ E $ in the delayed simulation. This means, we rate the difference between the errors on the basis of the mean of both errors. We evaluate this error for every day and observe a mixed performance behavior, i.e. in some cases the undelayed model outperforms the delayed model or vice versa. The extrema are that the undelayed model is in the most extreme case better with $ \epsilon = -1.0203 $ while the delayed model is in the most extreme case better than the undelayed model with $ \epsilon = 1.6160 $. So the undelayed model outperforms the delayed model at best with $ 102.03\% $ while the delayed model outperforms the undelayed one with $ 161.6\% $ at best. The mean over the 50 days is $ \epsilon = 0.1102 $ which might indicate that the delayed model performs better.
Conclusion
Summarizing, we have derived a new type of macroscopic second order traffic models including a delay from a microscopic follow-the-leader model in three different ways. The proposed approaches are adapted from well-established models known for the derivation of undelayed macroscopic traffic flow models, i.e. reverse spatial discretization, coarse graining and Taylor expansion. We have also suggested different methods to numerically tackle the resulting equations. The numerical results show that the delayed macroscopic equations lead to reasonable results, in particular in comparison with the classical ARZ model.
Future work includes further theoretical investigations for the delayed PDEs that have been already established for related problems, see for example [1,2] and [31]. Furthermore, deeper investigations on suitable numerical methods for this kind of delayed equations are necessary. From an application point of view, an extension to traffic networks would be interesting.









 DownLoad:
DownLoad: