Bifurcation of relative periodic solutions in symmetric systems with hysteretic constitutive relations

1.   Introduction

Hysteresis operators are used as models of complex non-linear history-dependent constitutive relations of materials and media. Examples include models of the stress-strain constitutive relation of elastoplastic materials (e.g., Prandtl's elastic-ideally plastic element ^[21]; Prandtl-Ishlinskii hysteresis model and its generalizations ^[13]; rate-independent yield criteria ^[14,20]; Armstrong-Frederick ^[7], Chaboche ^[15], Mroz nonlinear hardening rules ^[17]); related models of dry friction and creep-fatigue damage counting (Maxwell-slip friction model ^[1]; rainflow-counting algorithm of calculating fatigue ^[23]); magnetizing field-magnetization constitutive laws of magnetic materials (Preisach independent domain model ^[22]; Bouc-Wen, Jiles-Atherton, Stoner-Wohlfarth models ^[8,24,26]; Krasnosel'skii-Pokrovskii and Mayergoyz-Friedman models ^[11,16]); pressure-saturation constitutive equations of flows through porous media (Parlange and Mualem hysteresis models ^[18,19]); models of smart materials such as piezoelectric, ferroelectric and magnetostrictive materials, shape-memory alloys and shape-memory polymers with coupled mechanical, magneto-electric and temperature variables ^[6,9].

The defining property of hysteresis operators is rate-independence ^[25], i.e., a hysteresis operator commutes with invertible transformations of time. As such, hysteresis operators are non-smooth.

In engineering applications, constitutive relations between physical quantities are coupled to differential equations of motion, resulting in a smooth dynamical system if the constitutive relation is smooth. For instance, the harmonic oscillator equation is obtained by coupling Newton's second law with the linear constitutive relation between the stress and strain variables (Hooke's law). On the other hand, coupling equations of motion to a constitutive relation in the form of a hysteresis operator leads to a non-smooth dynamical system. The phase space of this system is typically a metric space lacking linear structure. Naturally, effective tools for the analysis of existence problems for non-smooth dynamical systems are provided by topological degree methods.

Several variants of equivariant degree adapt the Brouwer and Schauder topological degrees to symmetric settings. Their application relies on the differentiability of the vector field at its zeros because the classification of solutions according to their symmetric properties is based on the linearization. In particular, given a $\Gamma$-equivariant dynamical system with a finite symmetry group $\Gamma$, the twisted equivariant degree is suitable for detecting branches of periodic orbits characterized by different twisted symmetries.

The required differentiability at particular points can sometimes be warranted for non-smooth vector fields associated with operator-differential systems with hysteresis operators. In ^[2], a restriction of a hysteresis operator to the space of periodic functions was shown to be differentiable on constant functions. This restriction was sufficient for developing an application of the twisted degree to the $\Gamma$-equivariant Hopf bifurcation problem.

In this work, the method of ^[2] is extended to $\Gamma\times S^1$-equivariant systems, i.e., we establish the existence of symmetric branches of the so-called relative periodic solutions (with their associated symmetries) bifurcating from a symmetric relative equilibrium. Moreover, these branches belong to the phase space of the operator-differential system, while in ^[2] the branches are located in the extended phase space. Adapting the method of ^[2] to this $\Gamma\times S^1$-equivariant setting, we revise specifics of the construction of the hysteresis operator in the space of periodic functions and the proof of its differentiability on relative equilibrium solutions.

The paper is organized as follows: Section 2 presents preliminaries, which include the definition and basic properties of the Preisach hysteresis operator and an operator-differential system with this operator; the construction of the restriction of the Preisach operator to the space of periodic continuous functions; and, a reformulation of the periodic problem using this restriction. Further, we discuss the conditions that warrant $S^1$-equivariance and $\Gamma\times S^1$-equivariance of the operator-differential system and define the equivariant Hopf bifurcation point where a branch of relative periodic solutions bifurcates from a branch of relative equilibria. Sections 3 and 4 present the main result (Theorem 3.2) and an example of its application to an $S_5\times S^1$-equivariant model of an electromechanical system with plastic hysteresis (Propositions 4.2 and 4.3), respectively. Appendix A includes a brief overview of the properties of the Preisach operator related to the periodic problem. Specifically, Lemma A.3 and Corollary A.4 ensure that the restriction of the Preisach operator to the space of periodic functions has zero derivative on constant functions. In addition, we recall the definition of the Prandtl–Ishlinskii operator (an operator of Preisach type) and adapt Theorem 3.2 to equations with this operator (Theorem A.6), preparing the proof of the example. Appendix B contains the proofs. It begins with abstract Theorem B.10 (presented here for completeness; see, ^[3,4]), which underpins the following proof of Theorem 3.2 and is based on the application of the twisted equivariant degree. The further steps of the proof focus on the construction of the equivariant vector field with the zero set consisting of relative equilibria and relative periodic solutions. This construction ensures the differentiability at the bifurcation point, thus allowing us to compute the linearization and use Theorem B.10. The appendix concludes with the derivation of Propositions 4.2, 4.3 from Theorem A.6. The isotypic crossing numbers for this illustrative example are obtained numerically.

2.   Preliminaries

2.1.   Preisach operator

The Preisach model of hysteresis was originally defined using a superposition of elementary relay operators ^[22]. Here we use an alternative definition following the geometric construction by Krasnsel'skii, Pokrovskii ^[11] and the representation theorem by Krejčí ^[12]. Denote by $\mathfrak V_0$ the class of all the continuous piecewise continuously differentiable and piecewise monotone functions $v = v(\xi): [0, d]\to \mathbb{R}$ such that

The functions $v(\cdot)\in \mathfrak V_0$ are referred to as states of the Preisach model.

Let $I$ be an infinite time interval $I = [t_0, \infty)$ or a finite time interval $I = [t_0, t_e]$. Denote by $\mathcal{M}(I; \mathbb{R})$ the set of all the continuous piecewise monotone inputs $x = x(t): I\to \mathbb{R}$. Now, we consider the direct product of $\mathcal{M}(I; \mathbb{R})$ with the state space $\mathfrak V_0$ as the domain of the input-state operator of the Preisach model, which is completely defined on this domain by the two simple rules:

● If an input $x(t)$ increases on an interval $[t_1, t_2]$, then the evolution of the normalized state on this interval is determined by

● If $x(t)$ decreases on $[t_1, t_2]$, then for $t\in [ t_1, t_2]$,

Given any initial state $v_0(\cdot)\in \mathfrak V_0$ (the state at $t = t_0$) and any input $x(\cdot)\in \mathcal{M}(I; \mathbb{R})$, these rules are successively applied on the intervals of monotonicity of the input to obtain the state $v(t, \cdot)\in \mathfrak V_0$ at any moment $t\in I$. We use the notation

for this state.

Next, we endow the state space and the space of inputs with a metric. Namely, we set

Thus, the state space $\mathfrak V_0$ becomes a subset of the Banach space $C([0, d];\mathbb{R})$ equipped with the standard sup-norm $\|\cdot\|_\infty$. Similarly, we endow the set $\mathcal{M}(I; \mathbb{R})$ of piecewise monotone inputs with the sup-norm, i.e., $\mathcal{M}(I; \mathbb{R})\subset C(I; \mathbb{R})$ (in case of the infinite interval $I = [t_0, \infty)$, we consider the family of seminorms $\|x\|_{C([t_0, \tau]; \mathbb{R})} = \max\limits_{t\in[t_0, \tau]}|x(t)|$ in $C(I; \mathbb{R})\ni x$). It turns out that for every initial state $v_0\in \mathfrak V_0$ and every input $x\in \mathcal{M}(I; \mathbb{R})$, the function $v: I\to \mathfrak V_0$ defined by (2.4) belongs to $C(I; \mathfrak V_0)$. Hence, (2.4) defines a map $\Upsilon: \mathfrak V_0\times \mathcal{M}(I; \mathbb{R})\to C(I; \mathfrak V_0)$ (with the arguments $v_0\in\mathfrak V_0$, $x\in \mathcal M(I; \mathbb{R})$) called the input-state operator of the Preisach model. Moreover, this map is globally Lipschitz continuous (see, for example, ^[11]): for an arbitrary pair of initial states $v_0^1, v_0^2\in \mathfrak V_0$ and an arbitrary pair of inputs $x_1, x_2\in \mathcal{M}(I; \mathbb{R})$ the states

satisfy for each $\tau\in I$ the estimate

The Lipschitz continuity property (2.6) allows one to extend the input-state operator (2.4) by continuity from its domain $\mathcal{M}(I; \mathbb{R})\times \mathfrak V_0 \ni (x, v_0)$ to the closure of this domain in $C(I; \mathbb{R}) \times C([0, d];\mathbb{R})$. We keep the same notation (2.4) for this continuous extension, and wherever we refer to the input-state operator of the Preisach model, this continuous extension is meant. As the set $\mathcal{M}(I; \mathbb{R})$ of the piecewise monotone continuous inputs is dense in $C(I; \mathbb{R})$, the extended input-state operator (2.4) is defined for every continuous input $x$ and every initial state $v_0$ from the closure $\mathfrak V$ of the set $\mathfrak V_0$ in $C([0, d];\mathbb{R})$. The state space $\mathfrak V\subset C([0, d];\mathbb{R})$ thus consists of all the functions $v: [0, d]\to \mathbb{R}$ that satisfy

The extended input-state operator $\Upsilon$ satisfies the Lipschitz condition (2.6) on its domain $\mathfrak{D} = C(I; \mathbb{R}) \times \mathfrak V\ni (x, v_0)$, hence $\Upsilon$ is a Lipschitz continuous operator from the product space $C(I; \mathbb{R})\times \mathfrak V$ to the space $C(I; \mathfrak V)$ of mappings $v(\cdot): I\to \mathfrak V$, which is endowed with sup-seminorms

Finally, the output of the Preisach model is a scalar-valued function $y = y(t)$ ($t\in I$) of time defined as follows. Consider the domain

and a bounded integrable non-negative function $q:\Pi\to \mathbb{R}_+$ (called the Preisach density function). Define the so-called state-output functional $\Phi: \mathbb{R}\times \mathfrak V \to \mathbb{R}$ by

Then, the output is related to the input and state by

In other words, the input-output operator of the Preisach model assigns the output $y:I\to\mathbb{R}$ to an initial state $v_0\in \mathfrak V$ and an input $x\in C(I; \mathbb{R})$ according to (2.4), (2.9). For this operator, we use the notation

Since the function $v(\cdot, \cdot): \mathbb{R}\times [0, d]\times \mathbb{R}$ defined by (2.4) is continuous, the output (2.9) is also continuous. Hence the input-output operator (2.10) maps the product space $\mathfrak V\times C(I; \mathbb{R}) \ni (v_0, x)$ to the state of outputs $C(I; \mathbb{R})\ni y$. Because, by definition, this operator is a composition of the state-output functional $\Phi$ and the input-state operator $\Upsilon$, the global Lipschitz continuity of the functional (2.8) and relation (2.6) imply the global Lipschitz continuity of the input-output operator on its domain:

Due to (2.11), for any fixed initial state $v_0\in \mathfrak{V}$, the operator (2.10) taking inputs of the Preisach model to its outputs, is Lipschitz continuous in the space $C(I; \mathbb{R})$. However, this operator is not differentiable in the space of continuous functions with the uniform norm, neither in other natural functional spaces.

2.2.   Differential system

Let us consider a system of the form

where $\dot z_k(\cdot)$ is the derivative of $z_k(\cdot)$; the function $y_k(\cdot)$ is the output of the Preisach operator, and the input of this operator is related to the variable $z_k\in \mathbb{R}^{m_k}$ by the relation $x_k(t) = b_k \bullet z_k(t)$, where '$\bullet$' is a scalar product in $\mathbb{R}^{m_k}$. In other words, Eq (2.12) is coupled to equations

where (2.14) and (2.15) are the input-state and the state-output relations of the $k$-th Preisach operator, respectively. The functions $F_k : \mathbb{R}\times \mathbb{R}^N\to\mathbb{R}^{m_k}$, where $N = m_1 +\cdots+m_n$, $\mathbb{R}^N = \mathbb{R}^{m_1}\oplus \cdots \oplus \mathbb{R}^{m_n}$, are assumed to be Lipschitz continuous.

Remark 2.1. In (2.15), we use the same density function $q:\Pi\to\mathbb{R}$ for all the Preisach operators (equivalently, all $n$ Preisach operators have the same state-output functional $\Phi$). This is sufficient for our presentation but similarly one can deal with $n$ Preisach operators having different density functions $q_k$, which define different functionals $\Phi_k$.

Define $v: = (v^1, ..., v^n)\in {\mathfrak V}^n: = \mathfrak V \times \cdots \times \mathfrak V$ ($n$ times), where $v^k$ is interpreted as the state of the $k$-th Preisach operator. A solution to system (2.12)–(2.15) on an interval $I = [t_0, t_1)$ is a mapping $(z, v): I \to \mathbb{R}^N\times {\mathfrak V}^n$, with a continuously differentiable component $z$ and a continuous component $v$. That is, Eq (2.12) holds pointwise, $(z(t), v(t, \cdot))\in \mathbb{R}^N\times {\mathfrak V}^n$ for each $t\in I$, and both sides of these equations are continuous functions of $t$ for any solution. Thus, the product $\mathfrak{U} = \mathbb{R}^N\times {\mathfrak V}^n$ is considered to be the natural phase space for system (2.12)–(2.15). A few standard facts about solutions and the initial-value problem for system (2.12)–(2.15) are recounted in A.4 of Appendix A.

2.3.   Periodic solutions

The simplest solutions of system (2.12)–(2.15) are stationary (equilibrium) solutions, i.e., solutions of the form $(z(t), v(t)) = (z_0, v_0)\in \mathbb{R}^N\times \mathfrak V^n$ for all $t$. The rate-independence property (A.1) of the input-state and input-output operators of the Preisach model (see Appendix A) implies that the state (2.14) and output (2.15) are constant for any constant input $x\equiv x_0$ and any initial state $v_0$.

A solution $(z(t), v(t, \cdot))$ to system (2.12)–(2.15) defined on a time interval $t\ge t_0$ is called periodic with a period $T$ if both components are $T$-periodic, i.e., $z(t+T) = z(t)$, $v(t+T, \cdot) = v(t, \cdot)$ for all $t\ge t_0$. The periodic conditions

which include the state, ensure periodicity of the solution and periodicity of the outputs (2.15) of the Preisach operators. Without loss of generality, we set $t_0 = 0$ and use the spaces of periodic functions

with the sup-norm. We identify $T$-periodic functions with their restriction to the interval $[0, T]$. Periodic solutions can also be extended to the whole time axis in the sense that a restriction of such periodic extension to any left-bounded interval $[t_0, \infty)$ is a periodic solution.

Let us define a one-parameter family of operators $\hat P^T_\lambda : C_{per}([0, T];\mathbb{R}) \to C_{per}([0, T];\mathbb{R})$ where $\lambda\in[0, 1]$, each mapping a periofic input to a periodic output of the Preisach model. To this end, we consider the states

define the operators $\hat P^T_1, \hat P^T_0 : C_{per}([0, T];\mathbb{R})\to C_{per}([0, T];\mathbb{R})$ by

with

and put

Note that from the congruency property of the Preisach operator (cf. (A.5) and (A.6)), it follows that

which implies

for any $\lambda\in [0, 1]$ and $x\in C_{per}([0, T];\mathbb{R})$. In particular, $\hat P^T_\lambda = \hat P^T_0$ for all $\lambda$ if $\text{osc}\, x\ge 2d$, where $\text{osc}\, x = \max x(t)-\min x(t).$ On the other hand, if the opposite inequality $\text{osc}\, x < 2d$ holds and the function $q:\Pi\to\mathbb{R}$ in (2.8) is strictly positive, then any two operators $\hat P^T_{\lambda_1}$ and $\hat P^T_{\lambda_2}$ with $\lambda_1\ne \lambda_2$ differ by a non-zero constant. Now, given an input $x\in C_{per}([0, T];\mathbb{R})$, we partition the state space $\mathfrak V$ of the Preisach operator into subsets $\mathfrak V_{\lambda, x}$ defined as follows. We write $v_0\in \mathfrak V_{\lambda, x}$ if

Lemma 2.2. Suppose (2.15) is the state-output functional (2.8) with a nonnegative Preisach density function $q: \Pi\to \mathbb{R}_+$. Then, for any $x\in C_{per}([0, T];\mathbb{R})$, one has

Further, if

then $\mathfrak V_{\lambda, x} = \mathfrak V$ for each $\lambda$. On the other hand, if

then

and the subset $\mathfrak V_{\lambda, x}$ of $\mathfrak V$ depends continuously on $x\in C_{per}([0, T];\mathbb{R})$ and $\lambda\in [0, 1]$ in the Hausdorff metric.

Proof. Preisach input-state operator has the following monotonicity property:

where the states $v_k(\cdot, \cdot)$ are defined by (2.5), and the inequalities are satisfied pointwise for all $t\in I$, $\xi\in [0, d]$. Indeed, for monotone inputs, (2.24) follows from (2.2), (2.3) of the input-state operator. The extension procedure described in Section 2.1 ensures that (2.24) holds for arbitrary inputs $x_1, x_2\in C(I; \mathbb{R})$ and initial states $v_0^1, v_0^2\in \mathfrak V$. For $q\ge 0$, relations (2.8) and (2.24) imply a similar monotonicity property for the input-output operator:

where all the inequalities again hold pointwise for all $t\in I$, $\xi\in [0, d]$.

Relations (2.7) ensure that every state $v_0\in \mathfrak V$ satisfies \(v_-(\xi)\le v_0(\xi)\le v_+(\xi) \) on $\xi\in[0, d]$. Therefore, monotonicity property (2.25) implies

for any input $x\in C_{per}([0, T];\mathbb{R})$. Due to these inequalities, if (2.22) holds, then (2.21) is satisfied for all $\lambda\in [0, 1]$, $v_0\in \mathfrak V$, i.e., $\mathfrak V_{\lambda, x} = \mathfrak V$ for each $\lambda$. On the other hand, if (2.23) holds, then (2.21) defines $\lambda = \lambda(v_0)\in [0, 1]$ uniquely for each $v_0\in \mathfrak V$. In the latter case, due to continuity of the Preisach operator, the map $(P[0, \cdot]x)(T): \mathfrak V\to \mathbb{R}$ (with a fixed $x\in C_{per}([0, T];\mathbb{R})$) is continuous, and so is the map $\lambda: \mathfrak V \to [0, 1]$ defined by (2.21). Since (2.21) implies $\lambda(v_-) = 0$ and $\lambda(v_+) = 1$, the segment $\{v \in \mathfrak V:\ v = (1-s) v_-+ s v_+, \ s\in[0, 1]\}$ is mapped onto the segment $[0, 1]$ by the map $\lambda(\cdot)$. Finally, the continuity of the Preisach operator implies that $\mathfrak V_{\lambda, x}$ depends continuously on $x$ and $\lambda$ in the Hausdorff metric.□

The following lemma follows from Lemma 2.2 and further properties of the Preisach operator, see relations (A.3)–(A.6) in Appendix A.

Lemma 2.3. Suppose (2.15) is the state-output functional (2.8) with a nonnegative Preisach density function $q: \Pi\to \mathbb{R}_+$. Let $\lambda_k\in[0, 1]$ for each $k = 1, \ldots, n$. A function $z (t) = (z_1(t), ..., z_n(t)) \in C_{per}([0, T];\mathbb{R}^N)$ is a solution to system

if and only if system (2.12)–(2.15) has a class of periodic solutions $(z(\cdot), v(\cdot))$ of period $T$, where the components of $v(\cdot) = (v^1(\cdot), ..., v^n(\cdot))$ are defined by

where $x_k(\cdot) = b_k \bullet z_k(\cdot)$ $(k = 1, ..., n)$ and the parameter $v_0^k$ in (2.27) ranges over the set of states ${\mathfrak V}_{\lambda_k, x_k}$ for each $k = 1, \ldots, n$.

According to Lemma 2.3, a periodic solution is generally embedded into a connected set of such solutions, and the $z$-components of the solutions from this set form an $m$-parametric set with $m\le n$. In particular, $m = n$ if the Preisach density function $q:\Pi\to \mathbb{R}$ is strictly positive and $\text{osc}\, x_k < 2d$ for all $k = 1, \ldots, n$.

2.4.   Equivariant notation

We will need some basic equivariant notation. Let $H$ be a subgroup of a (compact Lie) group $G$. We denote by $(H)$ the conjugacy class of $H$ in $G$. The set of congugacy classes has a natural partial order defined by

If $G$ acts on a space $X$, then $X$ is called a $G$-space, the set $G(x): = \{gx: g\in G\}\subset X$ is called the orbit of $x\in X$, the subgroup $G_{x} : = \{g\in G:gx = x\}$ is called the isotropy group or the symmetry group of $x\in X$, and the conjugacy class $(G_{x})$ is called the orbit type of $x\in X$. If $(G_x) = (H)$, then $G(x)$ is called an $(H)$-orbit. Any maximal element with respect to partial order (2.28) on the set

is called a maximal orbit type. If $(G_x)\ge (H)$ for a subgroup $H\subset G$, then $x\in X$ is said to have symmetries at least $(H)$. The subspace $X^{H} : = \{x\in X: (G_{x})\ge (H)\}$ of $X$ is called the $(H)$-fixed-point subspace.

Given two $G$-spaces $X$ and $Y$, a continuous map $f : X \to Y$ is called $G$-equivariant if $f(gx) = gf(x)$ for each $x \in X$ and $g \in G$.

2.5.   Relative equilibria of an $S^1$-equivariant system

For the rest of this paper, we restrict further consideration to equations with one Preisach operator:

with a continuous function $F: \mathbb{R} \times V \to V$. The results can be extended to systems (2.12)–(2.15) with multiple Preisach operators in a straightforward fashion.

In what follows, system (2.29)–(2.32) is assumed to be (spatially) $S^1$-equivariant. More precisely, let $V = \mathbb R^N$ be an orthogonal $S^1$-representation such that the $S^1$-action on $V$ is given by a homomorphism $\mathscr R:S^1\to O(N)$ and satisfies

where $O(N)$ is the orthogonal group and $J$ is the infinitesimal operator

of the subgroup $\mathscr R(S^1)\subset O(N)$. Let $V = V_0 \oplus V_1 \oplus \dots \oplus V_\ell$ be the $S^1$-isotypic decomposition of $V$, where $V_0 = V^{S^1}$ and $V_k$, $k > 0$, is modeled on the $S^1$-irreducible representation $\mathbb{C}$ with the $S^1$-action given by the complex multiplication, i.e., $e^{i\tau}a: = e^{ik\tau}\cdot a$ ($a\in \mathbb C$). Then, each of the components $V_k$, $k > 0$, has a natural complex structure such that $e^{i\tau} z = e^{ik\tau}\cdot z,$ $J z = i k \cdot z$ for $z\in V_k$, and $V_0$ is the kernel of $J$. Further, the state space $V\times \mathfrak V$ of system (2.29)–(2.32) is an isometric $S^1$-representation with the action given by

i.e., the action of $S^1$ on the state space $\mathfrak V$ of the Preisach operator is trivial.

Let us assume that the function $F(\alpha, \cdot): V\to V$ is $S^1$-equivariant for each $\alpha$, i.e.,

Moreover,

where $J^T$ is the adjoint (transpose) map for $J$ (cf. (2.30)). These assumptions ensure that system (2.29)–(2.32) is $S^1$-equivariant. Therefore, it can have solutions of the form

for which the input, state and output of the Preisach operator are constant in time. In particular, for such a solution, (2.37) implies that input (2.30) equals

Hence, by Lemma 2.2, the state satisfies

for some $\lambda\in[0, 1]$, and the corresponding constant output (2.32) according to (2.21) equals

Substituting Eqs (2.38) and (2.39) into (2.29) and using (2.36) gives the algebraic system

with unknown $\lambda\in [0, 1]$, $\omega\in \mathbb{R}$, $z^o\in V$ and a free parameter $\alpha$. This system is also $S^1$-equivariant, and its solutions come in $S^1$-orbits $(\alpha, \lambda, \omega, e^{ \tau J}z^o)$, $e^{i\tau}\in S^1$.

In particular, if (2.40) holds for a $z^o\in V_0 = V^{ S^1}$ (in which case $Jz^o = 0$), then $(z^o, v_0)$ is an equilibrium of system (2.29)–(2.32) for every state $v_0\in \mathfrak V_{\lambda, x_0}$ with $x_0 = b\bullet z^o$.

On the other hand, solutions $(\alpha, \lambda, \omega, z^o)$ of Eq (2.40) with $z^o\not\in V_0$ come as one-dimensional orbits $(\alpha, \lambda, \omega, S^1 (z^o))$. In this case, $Jz^o\ne 0$.

Definition 2.4. If $(\alpha, \lambda, \omega, z^o)$ is a solution of Eq (2.40) with $z^o\not\in V_0$, then $(\alpha, \lambda, \omega, S^1 (z^o))$ is called a relative equilibrium of system (2.29)–(2.32).

If $(\alpha, \lambda, \omega, S^1 (z^o))$ is a relative equilibrium with $\omega \ne 0$, then $(S^1 (z^o), v_0)$ is the trajectory for the time-periodic solutions

in the phase space $V\times \mathfrak V$ of system (2.29)–(2.32) for each $v_0\in \mathfrak V_{\lambda, x_0}$. These solutions are called rotating waves. If $\omega = 0$, then $(S^1 (z^o), v_0)$ is called a frozen wave because it consists of equilibrium states $(e^{\tau J}z^o, v_0)$, $e^{i\tau} \in S^1$, for each $v_0\in \mathfrak V_{\lambda, x_0}$. Note that the first equation of system (2.40) doesn't include $\lambda$, and the second equation is linear in $\lambda$.

Suppose that $F$ is differentiable with respect to $z$, and the derivative $D_{z} F$ is continuous. As we know, if $(\alpha_o, \lambda_o, \omega_o, S^1 (z^o))$ is a relative equilibrium, then due to $S^1$-equivariance, the eigenvector $J z^o$ of the map $D_{z} F (\alpha_o, z^o)-\omega_o J$ belongs to its kernel. We introduce the following definition.

Definition 2.5. A relative equilibrium $(\alpha_o, \lambda_o, \omega_o, S^1 (z^o))$ of system (2.29)–(2.32) is called regular if zero is a simple eigenvalue of $D_{z} F (\alpha_o, z^o)-\omega_o J$ and $\lambda_o\in (0, 1)$.

Assume that $(\alpha_o, \lambda_o, \omega_o, S^1(z^o))$ is a regular relative equilibrium of system (2.29)–(2.32). Then, by the Implicit Function Theorem, there is an open neighborhood $\mathfrak A$ of $\alpha_o$ and a continuous curve

of solutions to system (2.40) such that $\lambda_{\mathcal O}(\alpha_o) = \lambda_o$, $\omega_{\mathcal O}(\alpha_o) = \omega_o$, $z_{\mathcal O}(\alpha_o) = z^o$ and the kernel of $D_{z} F (\alpha, z_{\mathcal O}(\alpha))-\omega_{\mathcal O}(\alpha) J$ is one-dimensional for each $\alpha\in \mathfrak A$. The corresponding set ${\mathcal O}: = \bigl(\alpha, \lambda_{\mathcal O}(\alpha), \omega_{\mathcal O}(\lambda), S^1(z_{\mathcal O}(\alpha)\bigr)$, $\alpha\in \mathfrak A$, of regular relative equilibria will be referred to as a (continuous) branch of relative equilibria.

2.6.   Relative periodic solutions

Relative periodic solutions of an $S^1$-equivariant system (2.29)–(2.32) are solutions of the form

with an a priori unknown $\omega\in\mathbb{R}$, where $\zeta:\mathbb{R}\to V$ and $v:\mathbb{R}\to \mathfrak V$ are $T$-periodic functions of an a priori unknown period $T$. Condition (2.37) ensures that the input (2.30) of the Preisach operator in system (2.29)–(2.32) is periodic if $z(t) = e^{\omega t J }\zeta(t)$ with a periodic $\zeta(\cdot)$.

The following statement adapts Lemma 2.3 to the $S^1$-equivariant setting; the proof is omitted.

Lemma 2.6. Let conditions (2.36) and (2.37) hold. Then, a periodic function $\zeta(\cdot)\in C_{per}([0, T];\mathbb{R}^N)$ is a solution to the equation

for a given $\lambda\in[0, 1]$ if and only if system (2.29)–(2.32) has a class of relative periodic solutions (2.42) with the initial state $v(t_0)$ ranging over the set ${\mathfrak V}_{\lambda, x}$, where $x(\cdot) = b \bullet z(\cdot) = b\bullet \zeta(\cdot)$.

For further discussion, it is convenient to normalize the period of the function $\zeta(\cdot)$ by introducing the parameter $\beta = 2\pi/T$ and adjusting the time scale. As such, the $T$-periodic problem for Eq (2.43) is equivalent to $2\pi$-periodic problem

with a priori unknown parameters $\beta$ and $\omega$, where $\zeta(\cdot)\in C_{per}([0, 2\pi]; \mathbb{R}^N)$ is a solution of (2.44) if and only if $\zeta(\beta t)\in C_{per}([0, T];\mathbb{R}^N)$ is a solution of (2.43) for $T = 2\pi/\beta$.

Equations (2.40) and (2.44), can be matched using the notation

More precisely, relative equilibria of system (2.29)–(2.32), system (2.43)–(2.45) and system (2.44)-(2.45) are defined by the same Eq (2.40). In Appendix B, we define a bifurcation of a branch of non-trivial solutions from a branch of trivial solutions for an equation in a metric space (see Definitions B.7 and B.8). When adapted to this abstract setting, stationary solutions

of system (2.44)-(2.45), where $\zeta(\cdot) = z^o\not \in V_0$ for all $t\in [0, 2\pi]$ and $(\alpha, \lambda, \omega, z^o)$ is a solution of (2.40), identify with the set $M\subset \mathscr E$ of trivial solutions; non-stationary solutions of (2.44)-(2.45) identify with the set $\mathscr S\subset \mathscr E$ of non-trivial solutions. A trivial solution is called regular if the corresponding relative equilibrium is regular according to Definition 2.5. Each trivial solution $(\alpha_o, \lambda_o, \omega_o, \beta_o, z^o)\in M$ is embedded into the set of trivial solutions $(\alpha_o, \lambda_o, \omega_o, \beta, e^{\tau J}z^o)\in M$ with arbitrary $\beta > 0$ and $\tau\in \mathbb{R}$. Lemma 2.6 relates the stationary and non-stationary solutions of system (2.44)-(2.45) to relative equilibria and relative periodic solutions of system (2.29)–(2.32), respectively. As such, combining Lemma 2.6 with Definition B.7 leads to the following definition of a branch of relative periodic solutions bifurcating from a branch of relative equilibria of system (2.29)–(2.32).

Definition 2.7. Let conditions (2.36) and (2.37) hold. Let $M$ be the set of all stationary solutions of system (2.44)-(2.45) and $\mathscr S\subset \mathscr E$ the set of all non-stationary $2\pi$-periodic solutions of this system. A non-empty set $\mathscr C\subset \mathscr S$ is called a branch of non-stationary periodic solutions if $\mathscr C = \mathscr S\cap \mathscr D$ where $\mathscr D$ is a connected component of $\overline{\mathscr S}$. Moreover, if the set $\overline{\mathscr C}$ contains a stationary solution $(\alpha_o, \lambda_o, \omega_o, \beta_0, z^o)\in M$, then we say that the branch $\mathscr C$ bifurcates from the set of stationary solutions at the bifurcation point $(\alpha_o, \lambda_o, \omega_o, \beta_0, z^o)$. Equivalently, we say that a Hopf bifurcation of relative periodic solutions (2.42) of system (2.29)–(2.32) occurs from its relative equilibrium $(\alpha_o, \lambda_o, \omega_o, S^1(z^o))$ with the limit frequency $\beta_o$ and the limit period $2\pi/\beta_o$.

This definition is extended to a $\Gamma\times S^1$-equivariant setting in the next subsection.

2.7.   $\Gamma\times S^1$-equivariant systems

Now, we additionally assume equivariance with respect to an action of a finite group $\Gamma$. Let $V = \mathbb R^N$ be an orthogonal $\Gamma\times S^1$-representation, where the $S^1$-action on $V$ is given by (2.33), (2.34). We denote $\mathcal G: = \Gamma\times S^1$. Hence, the phase space $V\times \mathfrak V$ of system (2.29)–(2.32) is an isometric $\mathcal G$-representation with the action given by

(cf. (2.35)). Suppose that the function $F(\cdot, \alpha): V\to V$ in (2.29) is $\mathcal G$-equivariant for each $\alpha$:

Further, in addition to (2.37), we assume that

where $\gamma^T$ is the adjoint (transpose) map of map $\gamma$. Conditions (2.37), (2.46), (2.47) ensure the $\mathcal G$-equivariance of system (2.29)–(2.32).

The element $(\gamma, e^{i\tau})\in \Gamma\times S^1 = \mathcal G$ is a symmetry of a relative equilibrium (2.38) if

The element $(\gamma, e^{i\tau}, e^{i \theta}) \in \Gamma \times S^1\times S^1 = \mathcal G\times S^1$ is a spatio-temporal symmetry of a relative periodic solution (2.42) if

If $\zeta(\cdot)$ is non-stationary, a twisted (one-folded) subgroup of $\mathcal G \times S^1$ consisting of all the spatio-temporal symmetries of the solution (2.42), together with all the conjugate subgroups, constitute a twisted orbit type. We are interested in the equivariant Hopf bifurcation of relative periodic solutions, including the classification of their orbit types, from a relative equilibrium, which has a group of symmetries $\mathcal H \le \mathcal G$. Lemma 2.6 combined with Definition B.8 extends Definition 2.7 to this setting.

Definition 2.8. Let conditions (2.36), (2.46) and (2.47) hold. Using the notation of Section 2.4 and Definition 2.7, given subgroups $\mathcal H \le \mathcal G = \Gamma \times S^1$ and $H\le G: = \mathcal H\times S^1\le \mathcal G \times S^1$, a set $\mathscr C\subset \mathscr S^{H}$ is called a branch of non-stationary periodic solutions with symmetries at least $(H)$ if $\mathscr C = \mathscr S^{H} \cap \mathscr D$ where $\mathscr D$ is a connected component of $\overline{\mathscr S}^{H}$. Moreover, we say that an equivariant Hopf bifurcation of relative periodic solutions of system (2.29)–(2.32) with the limit frequency $\beta_o$ (and the limit period ${2\pi}/{\beta_o}$) occurs from a relative equilibrium $(\alpha_o, \lambda_o, \omega_o, S^1(z^o))$ if a branch $\mathscr C\subset \mathscr S^{H}$ of non-stationary periodic solutions with symmetries at least $(H)$ bifurcates from the stationary solution $(\alpha_o, \lambda_o, \omega_o, \beta_o, z^o)\in M^{\mathcal H}$, which is called a Hopf bifurcation point. In this case, $\alpha_o$ can also be called the bifurcation point when this doesn't lead to a confusion.

3.   Main result

Let conditions (2.37), (2.46), and (2.47) hold. Suppose ${\mathcal O} = (\alpha, \lambda_{\mathcal O}(\alpha), \omega_{\mathcal O}(\alpha), S^1(z_{\mathcal O}(\alpha))$, $\alpha\in \mathfrak A$, is a branch of regular relative equilibria of system (2.29)–(2.32), i.e., the Jacobi matrix

depends continuously on $\alpha\in \mathfrak A$ and the matrix $A(\alpha)-\omega_{\mathcal O}(\alpha) J$ has a simple zero eigenvalue with the eigenvector $J z_{\mathcal O}(\alpha)$, see Section 2.5. We further assume that these regular relative equilibria admit a twisted group symmetry $\mathcal H \le \mathcal G$ (due to equivariance, the twisted symmetry group $\mathcal H$ is the same for all the relative equilibria from the branch).

Let us put $G: = \mathcal H \times S^1$ and consider the $G$-isotypic decomposition

where $S^1$-action is given by the complex multiplication. Due to equivariance, each isotypic component $V_{l}$ is invariant for the map $A(\alpha)$ and for $J$. Therefore, the characteristic polynomial

of the matrix $A(\alpha)-\omega_{\mathcal O}(\alpha) J$ admits the factorization

where the factor

is the characteristic polynomial for the restriction of the matrix $A(\alpha)-\omega_{\mathcal O}(\alpha)J$ to the isotypic component $V_{l}$.

Suppose that

and

for a sufficiently small $\delta > 0$ such that $(\alpha_o-\delta, \alpha_o+\delta)\subset \mathfrak A$. Then, each so-called $V_{l}$-isotypic crossing number is well-defined by

where $\mathfrak t_{1, l}^+(\alpha_o, \beta_o)$ (resp. $\mathfrak t_{1, l}^-(\alpha_o, \beta_o)$) equals the number of roots $\mu$ of the polynomial ${\mathcal P}_l(\alpha+\delta, \cdot)$ (resp. ${\mathcal P}_l(\alpha-\delta, \cdot)$), counted with their multiplicities, which satisfy $\text{Re}\, \mu > 0$, $|\mu-i\beta_o| < \delta$ for any sufficiently small $\delta > 0$. Assumption (3.7) ensures that the integers $\mathfrak t_{1, l}^\pm(\alpha_o, \beta_o)$ are independent of a particular choice of a sufficiently small $\delta$.

Remark 3.1. Due to equivariance, the linearization at any point $e^{\tau J}z_{\mathcal O}(\alpha)$ of the relative equilibrium $S^1(z_{\mathcal O}(\alpha))$ results in the same characteristic polynomial $\varphi(\alpha, \cdot)$ and the same isotypic crossing numbers (3.8).

Theorem 3.2. Suppose that $\Gamma\times S^1$-equivariance assumptions (2.37), (2.46) and (2.47) are satisfied for system (2.29)–(2.32), where the state-output functional (2.32) is given by (2.8) with a density function $q\ge 0$. Assume that $(\alpha, \lambda_{\mathcal O}(\alpha), \omega_{\mathcal O}(\alpha), S^1(z_{\mathcal O}(\alpha)))$, $\alpha\in \mathfrak A = (\alpha_o-\delta, \alpha_o+\delta)$, is a branch of regular relative equilibria, which admit a group of symmetries $(\mathcal H)$, where $\mathcal H\le \mathcal G = \Gamma\times S^1$. Let conditions (3.6) and (3.7) hold, and the state-output functional satisfy

Let ${G} = \mathcal H\times S^1$, let $(H)$ be a maximal twisted orbit type in the $G$-representation $V^c$ and $\mathfrak M^H$ be the set of all $G$-isotypic components $V_{l}$ in (3.2), in which $(H)$ is an orbit type. Assume that there exists $V_{l'} \in \mathfrak M^H$ such that:

$\rm (i)$ $(H)$ is a maximal twisted orbit type in $V_{l'}$;

$\rm (ii)$ $\mathfrak t_{1, l'}(\alpha_o, \beta_o) \not = 0$;

$\rm (iii)$ ${\mathfrak t}_{1, l}(\alpha_o, \beta_o) \cdot {\mathfrak t}_{1, l'}(\alpha_o, \beta_o) \geq 0$ for all $V_{l} \in \mathfrak M^H$ $\rm ($cf. (3.8)${\rm)}$.

Then, a branch of relative periodic solutions with symmetries at least $(H)$ bifurcates from the branch of relative equilibria at the Hopf bifurcation point $(\alpha_o, \lambda_{\mathcal O}(\alpha_o), \omega_{\mathcal O}(\alpha_o), \beta_o, z_{\mathcal O}(\alpha_o))$.

The proof is presented in Appendix B.

Remark 3.3. Condition (3.9) ensures that $\partial \lambda_{\mathcal O}/\partial \alpha (\alpha_o) > 0$ due to the second equation in (2.40).

4.   Example

4.1.   $S^1$-equivariant electromechanical oscillator

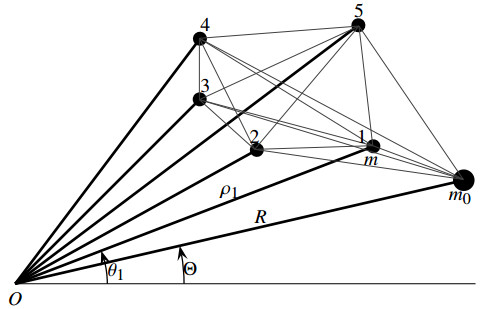
In this section, we consider an example of system (2.29)–(2.32). We use equations of motion of an electromechanical system with plastic hysteresis. This system is obtained by coupling $n$ identical electromechanical rotors (motors) of mass $m$ and a passive rotor of mass $m_0$ via elastic mechanical connections, see Figure 1. The mass of each rotor is concentrated at one point, and all the point masses $m$ and $m_0$ rotate in a horizontal plane around the same pivot.

Let us start with equations of motion for a single rotor of mass $m$ sketched in Figure 2:

Here $u$ is the voltage across the capacitor with the capacitance $C$; $w$ denotes the current through the motor and the inductor with the inductance $L$; the active circuit element composed of the battery and the tunnel diode is assumed to have the cubic current-voltage characteristic $i = - \sigma_1 u + \sigma_2 u^3$ with $\sigma_2 > 0$; $j$ is the constant current from the DC current source. The motor's point mass $m$ has polar coordinates $(\theta, \rho)$, where $\theta$ is the polar angle. The term $-\sigma (\rho-\rho_0)$ is the linear elastic force with Young's modulus $\sigma$; and, $\gamma \dot\rho$ and $\gamma\rho\dot\theta$ are the radial component and the torque component of the friction force, respectively, with the viscous damping coefficient $\gamma$. Further, for simplicity, let us assume that all losses are due to friction, while the losses associated with electrical resistance and conversion of the electrical energy into the mechanical energy are negligible. Hence, $u_m w = \tau \dot \theta$, where $u_m$ is the voltage applied to the motor and $\tau$ is the torque which is proportional to the current, $\tau = \kappa w$, where $\kappa$ is the motor torque constant.

System (4.1) is spatially $S^1$-equivariant with respect to the group $S^1$ of shifts of the angular variable $\theta$. Since the system is also autonomous, i.e., invariant with respect to time shifts, a periodic problem for Eq (4.1) is $S^1\times S^1$-equivariant.

If the mechanical component is disconnected, i.e., $\kappa = 0$, then the electrical circuit is the van der Pol oscillator which sustains self-oscillations for $\sigma_1 > 0$. Therefore, considering $\sigma_1: = \alpha$ as a bifurcation parameter with the other parameters fixed, the supercritical Hopf bifurcation occurs at $\alpha_0 = 0$. On the other hand, the electro-mechanical system (4.1) with $\kappa > 0$ admits a relative equilibrium defined by the equations

which imply

Next, we consider a passive rotor represented by a point mass $m_0$ with the polar coordinates $(\Theta, R)$. We assume the presence of a plasticity effect in the link connecting the point mass $m_0$ to the pivot point. This effect produces hysteresis with the associated energy losses. It can be taken into account by introducing a hysteresis operator into the equations of motion. Specifically, we use the standard Prandtl–Ishlinskii model of the constitutive relation between stress and strain in the elastoplastic material of the link ^{[10,11,13,21]}. The Prandtl–Ishlinskii hysteresis operator is essentially the Preisach operator with a modified state-output functional (A.13), see Subsection A.5 of Appendix A. Under these assumptions, the equations of motion of the passive rotor modeled by a point mass $m_0$ attached to a rotating weightless elastoplastic rod read as

with the Prandtl–Ishlinskii hysteresis operator $P$ given by (2.4), (2.9) and (A.13).

Remark 4.1. The Prandtl–Ishlinskii operator $P[t_0, v_0]R$ in (4.3) can be replaced by $P[t_0, v_0](R-R_0)$ with an arbitrary constant $R_0$ because the Prandtl–Ishlinskii operator by definition satisfies the identity

4.2.   Coupled $S_n \times S_1$-equivariant electromechanical system

The system of $n$ motors and a passive rotor shown in Figure 1 can be modeled by equations of motion (4.3) coupled to $n$ copies of Eq (4.1):

with $k = 1, \ldots, n$, where $R, \Theta$ and $\rho_k, \theta_k$ are the polar coordinates of the point masses $m_0$ and $m_k$, respectively; $\delta$ and $\varepsilon$ are stiffnesses of the elastic links between the masses; the variables $u_k, w_k$ and the other parameters are defined above in Subsection 4.1. One can see that system (4.4) is spatially $\Gamma\times S^1$-equivariant where $S^1$ is the group of simultaneous shifts $\Theta \to \Theta+c$, $\theta_k \to \theta_k+c$, $k\in \mathbb{Z}_n$, of all the angular variables by the same value $c\in [0, 2\pi)$, and the symmetric group $\Gamma = S_n$ permutes the indices $k$.

By inspection, system (4.4) admits a fully synchronized fully symmetric relative equilibrium solution defined by the relations

where $\alpha$ equals the constant output of the Prandtl–Ishlinskii operator $P$. Further, $\alpha$ is a related to the initial state $v_0\in \mathfrak V$, which is a free parameter:

(cf. (A.12) and (A.13)). Theorem 3.2 can be used to analyze symmetries of branches of relative periodic solutions bifurcating from the branch $\mathcal O$ of relative equilibria (4.5), which have symmetry group $\mathcal H = S_n\times \{1\}\le S_n\times S^1$. More precisely, we adapt this theorem to systems with the Prandtl–Ishlinskii state-output functional in Subsection A.6 of Appendix A (see Theorem A.6).

4.3.   Example

As an example, let us consider system (4.4) for $n = 5$. Relative equilibria (4.5) admit the group symmetry $\mathcal H = S_5\times \{1\}\le \mathcal G = S_5\times S^1$. To apply Theorem 3.2 to the branch $\mathcal O$ of these relative equilibria, one needs to evaluate the spectrum of the linearization of system (4.4), and its dependence on the parameter $\alpha$ (cf. (3.4) and (4.6)). We do it numerically for a specific parameter set given in Tables 1 and 2. Based on this computation, Theorem 3.2 (and its adapted version Theorem A.6) predicts the existence of multiple branches of relative periodic solutions (with their associated symmetry groups) bifurcating from the branch of relative equilibria $\mathcal O$. Propositions 4.2 and 4.3 list a few of these branches. Their symmetry groups are subgroups of $G = \mathcal H\times S^1 = S_5 \times \{1\} \times S^1$. In particular, the following symbols are used for selected twisted subgroups of $G$ (where where $S_n$ is the symmetric group, $D_n$ is the dihedral group and $\xi_m: = e^{\frac{2\pi i}{m}}$):

Proposition 4.2. Consider system (4.4) with $n = 5$, $j = 0$ and the other parameters specified in the caption of Table 1. This system has the $(S_5)$-symmetric branch $\mathcal O$ of relative equilibria with $\omega_{\mathcal O} = 0$ (frozen waves, cf. Definition 2.4) given by

and several branches of relative periodic solutions bifurcating from $\mathcal O$ at different points $\alpha$ (cf. Definition 2.8). In particular, these branches of relative periodic solutions include:

● a branch with symmetry at least $(\mathbf{\mathbb S_5})$ bifurcating from $\mathcal O$ at $\alpha\approx -2.29532$ with the limit frequency $\beta_o\approx 1.06$;

● branches with symmetries at least $(\mathbf {\mathbb D_6})$, $(\mathbf {\mathbb S_4})$, $(\mathbf {\mathbb D_6^{\mathbf d}})$, $(\mathbf {\mathbb D_4^{\mathbf d}})$, $(\mathbf {\mathbb Z_4^{\mathbf t_1}})$, $(\mathbf {\mathbb Z_5^{\mathbf t}})$, $(\mathbf {\mathbb Z_6^{\mathbf{t_2}}})$ bifurcating from $\mathcal O$ at $\alpha\approx-0.8973$ with the limit frequency $\beta_o\approx 0.811$.

Symmetries of other branches of relative periodic solutions bifurcating from the branch $\mathcal O$ of relative equilibria (4.7), and from other branches of relative equilibria, can be classified in a similar manner.

Proposition 4.3. Consider system (4.4) with $n = 5$ and the parameters specified in the caption of Table 2. This system has an $(S_5)$-symmetric branch $\mathcal O$ of relative equilibria (4.5) with $\omega_{\mathcal O}(\alpha)\not = 0$ (rotating waves, cf. Definition 2.4) and several branches of relative periodic solutions bifurcating from $\mathcal O$ at different points $\alpha$. In particular, these branches of relative periodic solutions include:

● a branch with symmetry at least $(\mathbf{\mathbb S_5})$ bifurcating from $\mathcal O$ at $\alpha\approx -4.6401$ with the limit frequency $\beta_o\approx 0.94$;

● branches with symmetries at least $(\mathbf {\mathbb D_6})$, $(\mathbf {\mathbb S_4})$, $(\mathbf {\mathbb D_6^{\mathbf d}})$, $(\mathbf {\mathbb D_4^{\mathbf d}})$, $(\mathbf {\mathbb Z_4^{\mathbf t_1}})$, $(\mathbf {\mathbb Z_5^{\mathbf t}})$, $(\mathbf {\mathbb Z_6^{\mathbf{t_2}}})$ bifurcating from $\mathcal O$ at $\alpha\approx-4.5636$ with the limit frequency $\beta_o\approx 1.06$.

In B.5 of Appendix B, we outline how the above bifurcations can be deduced from Theorems 3.2 and A.6. We find the isotypic decomposition of the $S_5 \times S^1$-representation $V^c = V_{0}\oplus V_{1}$ (cf. (3.2)), list maximal orbit types in each $S_5 \times S^1$-isotypic component $V_{j}$, obtain the characteristic polynomial $\varphi_{j}$ associated with each $V_{j}$ (cf. (3.5)) and verify (numerically) that the roots of these polynomials satisfy conditions (ii) and (iii) of the theorem. Tables 1 and 2 illustrate how the roots $\varphi_{j}$ cross the imaginary axis as the bifurcation parameter $\alpha$ is varied. An entry of a given cell indicates the number of unstable roots of the polynomial $\varphi_{j}$, which is associated with the isotypic component $V_{j}$ (shown in the left column), for the corresponding interval of $\alpha$-values (shown in the upper row). One can see the changes of the dimension of the unstable manifold as $\alpha$ increases. An entry of the table is circled to indicate a "jump" in the number of unstable roots at a Hopf bifurcation point. The conclusions of Propositions 4.2 and 4.3 are based on these tables.

5.   Conclusions

We considered an application of the equivariant topological degree to the $\Gamma\times S^1$-equivariant Hopf bifurcation in differential systems with a hysteresis operator. This application allows one to classify branches of relative periodic solutions bifurcating from a relative equilibrium according to their symmetries. We identified a set of conditions that ensure the $\Gamma\times S^1$-equivariance. By adapting a method that had been used earlier to analyze the $\Gamma$-equivariant Hopf bifurcation, we constructed $\Gamma\times S^1$-equivariant vector fields that have zeros at the relative periodic solutions. These vector fields, although non-differentiable on a dense subset of their domain due to hysteresis terms, are still differentiable at the relative equilibria, which is sufficient for an effective computation of the topological degree. The results formulated for systems with the Preisach hysteresis operator were illustrated using equations of motion of an electro-mechanical system with the Prandtl–Ishlinskii operator model of an elastoplastic component.

Use of Generative-AI tools declaration

The author declares he has not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgements

The author thanks A. Zagvozdkin and W. Krawcewicz for insightful discussions of several important aspects of this work.

Conflict of interest

Prof. Dmitrii Rachinskii is a Guest Editor of special issue "Multi-Rate Processes and Hysteresis" for Mathematics in Engineering. Prof. Dmitrii Rachinskii was not involved in the editorial review and the decision to publish this article.

The author declares no conflict of interest.

Appendix

Appendix A.   Properties of Preisach operator

A.1.   General properties of hysteresis operators

The following properties of input-state operator (2.4) and input-output operator (2.10) play an important rule.

Causality. The state (2.4) at a moment $t' \ge t_0$ depends on the values of the input $x = x(t)$ on the segment $t_0\le t\le t'$ only and does not depend on the future values of $x$. More precisely, for two inputs $x_1, x_2\in C([t_0, \infty); \mathbb{R})$ and any initial state $v_0\in \mathfrak V$,

Rate-independence. This property is considered to be the defining property of hysteresis operators ^[25]. It says that changing the time scale of the input results in the same change of the time scale of state function (2.4) and output (2.10). More specifically, for any continuous increasing change of time

any input $x\in C([t_0, \infty); \mathbb{R})$ and initial state $v_0\in \mathfrak V$, define

Then,

Semigroup property. Given an input $x\in C([t_0, \infty); \mathbb{R})$ and $t' > t_0$, define the restriction $x_{t'}\in C([t', \infty); \mathbb{R})$ of the input to the interval $t\ge t'$ by $x_{t'}(t) = x(t)$. The input-state operator satisfies

Causality and rate-independence of input-state operator (2.4) imply the same properties of input-output operator (2.10).

Remark A.1. The above properties are used as a general definition of a hysteresis operator.

Definition A.2. An input-state operator (2.4) and input-output operator (2.10) defined by (2.9) are called hysteresis operators if the operator (2.4) is causal, rate-independent and satisfies the semi-group property.

This definition is adapted from ^[11,25]. Equivalent definitions based on discrete time sequences were used in ^[5].

A.2.   Monocyclic property and congruency of hysteresis loops

The following properties of the input-state-output operators are important for analyzing periodic inputs, states and outputs. If an input $x:[t_0, \infty)\to\mathbb{R}$ is periodic (with a period $T$), i.e.,

then for any initial state $v_0\in \mathfrak V$, the variable state (2.4) and the output (2.10) are periodic after the first period:

Moreover, for any pair of initial states $v_0^1, v_0^2\in \mathfrak V$,

Note that relations (A.3)–(A.6) are generally not true for $t_0\le t\le t_0+T$. The partial differentiation is used in (A.5) because the function $v = v(t, \xi)$ defined by (2.4) is a function of two variables $t$ and $\xi$.

Relations (A.3) and (A.4) are referred to as the monocyclic property of the Preisach operator. Equalities (A.5) and (A.6) are known as the congruency property of hysteresis loops, which is one of the two characteristic properties of the Preisach model according to the identification theorem by Mayergoyz ^[16]. Equalities (A.3)–(A.6) are a consequence of Eqs (2.2) and (2.3).

A.3.   Differentiability on constant solutions

The Preisach operator $P$ is not differentiable on an everywhere dense subset of its domain. The same is true for the operator $\hat P_\lambda^T$ defined by relations (2.16)–(2.19). However, these operators are differentiable on constant inputs, allowing the linearization of system (2.29)–(2.32) on its relative equilibria, which is crucial for the statement and proof of Theorem 3.2.

Lemma A.3. For any $\lambda\in [0, 1]$, the operator $\hat P^T_\lambda$ defined by (2.16)–(2.19) is globally Lipschitz continuous in its domain $C_{per}([0, T];\mathbb{R})$ and satisfies the global estimate

The Lipschitz continuity of the operator $\hat P^T_\lambda$ follows from the monocyclic and congruency properties of the input-output operator of the Preisach model (cf. (A.3)–(A.6)) and the Lipschitz estimate (2.11). Relation (A.7) derives from the definition of the operator $\hat P^T_\lambda$, and the monotonicity property (2.25) of the Preisach operator.

Given an $x_o\in\mathbb{R}$, let the Preisach state-output functional satisfy $\Phi(x_o, v_-) < \Phi(x_o, v_+)$ and let

(cf. (2.16), (3.9)). Condition (A.8) ensures that there exists a continuous functional $\Lambda_\alpha: B_\varepsilon (x_o)\to (0, 1)$ defined on a sufficiently small ball $B_\varepsilon (x_o) = \{x\in C_{per}([0, T];\mathbb{R}): |x(t)-x_o| < \varepsilon, \ t\in [0, T]\}$ such that

and $\Lambda_\alpha$ depends continuously on $\alpha$.

Lemma A.3 implies the following statement.

Corollary A.4. If (A.8) holds, then relations $x\in B_\varepsilon (x_o), \ \lambda = \Lambda_\alpha(x)$ imply

The operator $\hat P^T_\lambda$ maps any constant (stationary) input to a constant output, hence the constant input $x\equiv x_o$ is mapped to the constant output $(\hat P^T_\lambda x_o)\equiv \alpha$ for $\lambda = \Lambda_\alpha(x_o)$. Therefore, Corollary A.4 implies

In other words, the operator $\hat P^T_{\Lambda_\alpha(\cdot)}(\cdot)$ has the zero derivative on the constant inputs $x\equiv x_o$ satisfying (A.8).

A.4.   Initial value problem

Initial conditions for system (2.12)–(2.15) include an initial value for the variable $z$,

and a collection of initial states

of Preisach operators (2.14) at an initial moment $t_0$. The phase space is endowed with the natural metric induced by the metric of $\mathfrak{V}$.

It is important to note that solutions are not extendable backwards in time (an attempt at backward extension leads to non-uniqueness). However, most other standard facts of the theory of ordinary differential equations are valid for system (2.12)–(2.15). In particular, the local existence and forward uniqueness result from the Lipschitz estimate (2.11) for a sufficiently small interval $[t_0, t_0+\delta)$. Hence, any initial moment $t_0$ and any initial point $(z_0, v_0(\cdot))$ of the phase space $\mathfrak{U} = \mathbb{R}^N\times {\mathfrak V}^n$ define a solution $(z(\cdot), v(\cdot, \cdot)): I\to \mathfrak{U}$ starting from this initial point at $t = t_0$ and extending to some interval $I = [t_0, t_1)\ni t$. This can be proved, for example, using the Picard–Lindelöf type of argument, or by applying the contraction mapping principle to the integral equation, which is equivalent to system (2.12)–(2.15). Further, every solution is extendable to a maximum interval $I_{max} = [t_0, t_1)$, either finite or infinite, and if the maximal interval is finite, then $|z(t)|\to \infty$ as $t\to t_1$. Standard linear estimates of the function $F = (F_1, \ldots, F_n):\mathbb{R}^N\to\mathbb{R}^N$ ensure that the maximal interval is infinite. For example, the global estimate $|F(z)|\le a_1|z|+a_2$ ensures that $I_{max} = [t_0, \infty)$. Due to semigroup property (A.2) of the Preisach hysteresis operator, the solutions of system (2.12)–(2.15) induce a continuous semi-flow in the phase space $\mathfrak U$ of this system. Since the Preisach operator is rate-independent (see Appendix A), it commutes with time shifts $t\to t+c$, which implies that system (2.12)–(2.15) is autonomous.

A.5.   Prandtl–Ishlinskii operator

Let us recall that a hysteresis operator is, in general, a composition of an input-state operator and a state-output functional. The Prandtl–Ishlinskii and Preisach hysteresis models have the same input-state operator (2.5). Krejčí's representation theorem proves that the state-output functional of the Prandtl–Ishlinskii hysteresis operator is the sum of a linear functional and the state-output functional (2.8) of the Preisach operator of a particular type ^[12]. Let us consider a class of state-output functionals, which includes the state-output functionals of both the Preisach and Prandtl–Ishlinskii models. To this end, let us rewrite formula (2.8) equivalently as

where

and

Replacing the integral $\int_{-\infty}^{\infty} \tilde q_{ev}(\xi, u)\, du$ by its Cauchy principal value in the above formula, and adding the linear function $\varkappa x_0$, we define the class of functionals

for which the Preisach state-output functional (2.8) is a particular case. On the other hand, as shown in ^[12], the Prandt–Ishlinskii operator is the composition of the operator (2.4) and the functional (A.11) with $\tilde q_{od}, \tilde q_{ev}$ given by (A.10) and

where a bounded integrable function $\hat q: [0, d]\to \mathbb{R}_+$ is known as the loading curve. Substituting (A.12) into (A.11), one can see that the state-output functional of the Prandtl–Ishlinskii operator is simply

Remark A.5. A straightforward modification of the proof shows that the statement of Lemmas 2.2 and 2.3 remains valid if the state-output functional (2.9) is defined by Eq (A.11) or Eq (A.13) with a nonnegative density function $\hat q: [0, d]\to \mathbb{R}_+$ rather than by Eq (2.8), in other words, if the Preisach operator is replaced by the Prandtl–Ishliskii operator.

A.6.   Equivariant Hopf bifurcation of relative periodic solutions for systems with Prandtl–Ishlinskii operator

Theorem 3.2 can be extended to systems (2.29)–(2.32), where the Preisach state-output functional (2.8) in (2.32) is replaced by the more general functional (A.11). To this end, one naturally needs to adapt the definition (3.1) of the matrix $A(\alpha)$ and replace it with the following definition:

where $\varkappa$ is the coefficient of the linear term in (A.11). Then, the conditions of Theorem 3.2 ensure the existence of a branch of relative periodic solutions with symmetries at least $(H)$, bifurcating from the branch of relative equilibria. As particular cases, this statement includes systems with the Preisach state-output functional (2.8) (in the case, $\kappa = 0$) and the Prandtl–Ishlinskii state-output functional (A.13). More specifically, the following statement holds for systems with the Prandtl–Ishlinskii operator.

Theorem A.6. Let Eqs (2.29)–(2.32) satisfy the $\Gamma\times S^1$-equivariance assumptions (2.37), (2.46), and (2.47), where the state-output functional (2.32) is given by Eq (A.13) with a positive density function $\hat q: [0, d]\to\mathbb{R}_+$. Let this system have a branch of regular relative equilibria

which admit a group of symmetries $(\mathcal H)$, where $\mathcal H\le \mathcal G = \Gamma\times S^1$. Set ${G} = \mathcal H\times S^1$, define the matrix $A(\alpha)$ by (A.14) with $\varkappa = \int_0^d \hat q(\xi)\, d\xi$, assume that the characteristic polynomial $\varphi$ of the matrix $A(\alpha)-\omega_{\mathcal O}(\alpha) J$ satisfies conditions (3.6), (3.7), and consider the factorization (3.4) induced by the $G$-isotypic decomposition (3.2) with the associated $G$-isotypic crossing numbers $\mathfrak t_{1, j}(\alpha_o, \beta_o)$. Given a maximal twisted orbit type $(H)$ in the ${G}$-representation (3.2) and the set of all $G$-isotypic components $V_{j}$, in which $(H)$ is an orbit type, assume that conditions $\rm (i)–(iii)$ of Theorem 3.2 hold for $V_{j'} \in \mathfrak M^H$. Then, a branch of relative periodic solutions with symmetries at least $(H)$ bifurcates from the branch of relative equilibria $\mathcal O$ at the bifurcation point $(\alpha_o, \lambda_{\mathcal O}(\alpha_o), \omega_{\mathcal O}(\alpha_o), \beta_o, z_{\mathcal O}(\alpha_o))$.

This theorem is a straightforward modification of Theorem 3.2, hence we omit the proof.

Appendix B.   Equivariant Hopf bifurcation

B.1.   Bifurcation from a trivial solution

In this and the following subsections we present an abstract Theorem B.10, which serves as a basis for the proof of Theorems 3.2 and A.6. Theorems 3.2 is proved in Subsections B.3 and B.4. B.5 outlines the proof of Propositions 4.2 and 4.3.

Let $G: = {\mathcal H}\times S^1$, where $\mathcal H$ is a finite group (one can use any compact Lie group). We assume that a Banach space $\mathbb E$ is an isometric $G$-representation and consider the $G$-representation $\mathbb{R}^2\times \mathbb E$, where $G$ acts trivially on the parameter space $\mathbb{R}^2$.

Let ${\mathscr F}: \mathbb{R}^2 \times \mathbb E \to \mathbb E$ be a completely continuous $G$-equivariant vector field:

Assume that

The points $(\eta, 0)\in \mathbb{R}^2 \times \mathbb E$ will be called trivial solutions of the equation

We denote by

the set of trivial solutions and by

the set of all non-trivial solutions to Eq (B.3).

In what follows, $\overline \Omega$ denotes the closure of a set $\Omega$.

Definition B.7. A non-empty set $\mathscr C\subset \mathcal S$ is called a branch of non-trivial solutions to Eq (B.3) if $\mathscr C = \mathcal S\cap \mathscr D$ where $\mathscr D$ is a connected component of $\overline{\mathcal S}$. Moreover, if $(\eta_o, 0)\in \overline{\mathscr C}$, then we say that the branch $\mathscr C$ bifurcates from the trivial solution $(\eta_o, 0)$ and $(\eta_o, 0)$ is a bifurcation point for Eq (B.3).

In a symmetric setting (cf. Subsection 2.4), given a subgroup $H\le G$ and a set $\Omega\subset \mathbb{R}^2 \times \mathbb E$, the notation $\Omega^H$ is used for the subset $\Omega^H\subset\Omega$ of all $H$-symmetric points:

Definition B.8. Under the assumptions of Definition B.7, for a given subgroup $H\le G$, a set $\mathscr C'\subset \mathcal S^H$ is called a branch with symmetries at least $(H)$ if $\mathscr C' = \mathcal S^H \cap \mathscr D'$ where $\mathscr D'$ is a connected component of $\overline{\mathcal S^H}$. Moreover, if $(\eta_o, 0)\in \overline{\mathscr C'}$, then we say that $\mathscr C'$ bifurcates from the point $(\eta_o, 0)$.

Assume that $\mathscr F$ is differentiable with respect to $u$ on $\mathcal M$, the derivative $\mathscr A(\eta): = D_u\mathscr F(\eta, 0):\mathbb E\to \mathbb E$ depends continuously on $\eta \in \mathbb{R}^2$ and

Definition B.9. A point $(\eta_o, 0)$ is called critical for Eq (B.3) if $\mathcal A(\eta_o):\mathbb E\to \mathbb E$ is not an isomorphism.

Let $\mathscr L\subset \mathcal M$ be the set of all critical points in $\mathcal M$, i.e.,

One can show that if $(\eta_o, 0)$ is a bifurcation point, then it must be critical for (B.3), i.e., $(\eta_o, 0)\in \mathscr L$. Below we consider an isolated critical point $(\eta_o, 0)$. In other words, it is assumed that

for some $\delta > 0$. We assume that the restriction $\mathscr A(\eta_o)|_{\mathbb{E}^{S^1}}$ of $\mathscr A(\eta_o)$ to the subspace $\mathbb{E}^{S^1}$ where the group $S^1$ acts trivially is a bijection:

An isolated critical point $(\eta_o, 0)$ satisfying (B.7) is called regular.

B.2.   Bifurcation invariant

The existence of branches of non-trivial solutions bifurcating from an isolated critical point $(\eta_o, 0)$ of the field $\mathscr F$ can be proved using topological (bifurcation) invariants such as the Brouwer degree, $S^1$-equivariant degree or, in a symmetric setting, their equivariant counterparts—equivariant Brouwer degree and twisted equivariant degree ^[3]. If the bifurcation invariant associated with $(\eta_o, 0)$ is different from zero, then there is a branch $\mathscr C$ of non-trivial solutions to (B.3) bifurcating from the trivial solution $(\eta_o, 0)$. Moreover, in the equivariant setting, the bifurcation invariant contains information about symmetries $(H)$ of branches $\mathscr C^H$ of non-trivial solutions bifurcating from $(\eta_o, 0)$.

The computation of the bifurcation invariant is based on the linearization $\mathscr A$ of the field $\mathscr F$ at the critical point and the so-called crossing numbers of the linearization. To be specific, let us consider a $G$-isotypic decomposition

with

where each $G$-isotypic component $V_{k, l}$ is assumed to be finite. Here $V_{k, l}$ is modeled on a $G$-irreducible representation $\mathscr V_{k, l}$, i.e.,

where $\{\mathscr V_{0, l}\}_{l = 0, 1, \ldots, r}\cup \{\mathscr V_{k, l}\}_{k\ge1, \; l = 0, 1, \ldots, p}$ is a complete list of pairwise non-equivalent irreducible $G$-representations and

Since the field $\mathscr F$ is $G$-equivariant, so is the linear map $\mathscr A(\eta): \mathbb{E}\to \mathbb{E}$ (for every $\eta\in\mathbb{R}^2$), therefore each subspace $V_{k, l}$ is invariant for $\mathscr A(\eta)$, and the finite-dimensional restriction

is well-defined. Notice that subspaces $V_{k, l}$ with $k\ge 1$ have a natural complex structure induced by the $S^1$-action. Moreover, the irreducible $G$-representation $\mathscr V_{k, l}$ is also an irreducible complex $\mathcal H$-representation, and as such, $\mathscr V_{k, l}$ is a complex absolutely irreducible $\mathcal H$-representation. Consequently, the $G$-equivariant linear map $\mathscr A_{k, l}(\eta) : V_{k, l}\to V_{k, l}$ can be identified with a complex matrix $\widetilde{\mathscr A}_{k, l}(\eta)$. Put

By assumption, $(\eta_o, 0)\in \mathscr L$ is a regular isolated critical point, hence there exist $l$ and $k > 0$ such that $\mathscr A_{k, l}(\eta_o)$ is not an isomorphism, i.e.,

We assume that in some coordinate system $\eta = (\alpha, \beta)\in \mathbb{R}^2$, the point $\eta_o = (\alpha_o, \beta_o)$ satisfies $\beta_o > 0$ and the function ${\varphi} _{k, l}(\alpha_o, \cdot)$ is analytic in a neighborhood of the point $\beta_o$. Therefore, relation (B.14) implies that

where $m > 0$ is the multiplicity of the isolated zero $\beta_o$ of the function ${\varphi}_{k, l}(\alpha_o, \cdot)$, i.e., $\phi(\beta_o)\ne 0$. Moreover, we assume that in some neighborhood of the point $\eta_o = (\alpha_o, \beta_o)$,

where the polynomial

of degree $m\ge1$ depends continuously on $\alpha$ and satisfies

and, the continuous function $\phi$ satisfies

Notice that formulas (B.16)–(B.19) are in agreement with (B.15) at $\alpha = \alpha_o$; the complex $i$ is used in (B.16) merely to mathch the standard setting of the Hopf bifurcation problem; polynomial (B.17) is called the characteristic polynomial for the map $\mathscr A|_{V_{k, l}}$.

The isotypic crossing number $\mathfrak t_{k, l}(\alpha_o, \beta_o)$ associated with the $G$-isotypic component $V_{k, l}$ is the number of roots $\mu_j(\alpha)$ of the characteristic polynomial, which cross the imaginary axis through the point $i\beta_o$ from the left to the right half-plane of the complex plane $\mathbb{C}$, minus the number of roots crossing the imaginary axis from right to left through the same point, as the parameter $\alpha$ increases from $\alpha_o-\delta$ to $\alpha_o+\delta$ (for a sufficiently small $\delta$). More precisely, the assumption that $(\eta_o, 0) = (\alpha_o, \beta_o, 0)$ is an isolated critical point of $\mathscr A(\eta) = \mathscr A(\alpha, \beta)$ (cf. (B.6)) and relation (B.18) ensure that all the $m$ roots $\mu_j(\alpha)$ of $\mathscr P(\alpha, \cdot)$ satisfy

for a sufficiently small $\delta > 0$, and the isotypic crossing number associated with $V_{k, l}$ equals

where $\mathfrak t_{k, l}^-(\alpha_o, \beta_o)$ (respectively, $\mathfrak t_{k, l}^+(\alpha_o, \beta_o)$) is the number of roots $\mu_j(\alpha_o-\delta)$ (respectively, $\mu_j(\alpha_o+\delta)$), counted with their multiplicities, which satisfy $\Re{e}\, \mu_j < 0$, i.e.,

with $\# S$ denoting the cardinality of the set $S$. Due to the continuous dependence of the roots on $\alpha$, the integers $\mathfrak t_{k, l}^\pm(\alpha_o, \beta_o)$ are independent of a particular choice of $\delta$ such that (B.20) holds.

Theorem B.10. Let the field $\mathscr F:\mathbb{R}^2\times \mathbb{E}\to \mathbb{E}$ satisfy assumptions (B.1), (B.2) and (B.4). Let $(\eta_o, 0)\in \mathscr L$ be a regular isolated critical point for Eq (B.3). Assume that $(H)$ is a maximal orbit type in $\bigoplus _{l = 0}^{p} V_{k, l}$ for some $k\ge 1$, and

$\rm(i)$ $\mathfrak t_{k, l}(\eta_o)\not = 0$ for at least one $l\in \{0, 1, \dots, p\}$ such that $(H)$ is an orbit type in $V_{k, l}$;

$\rm(ii)$ $\mathfrak t_{k, l}(\eta_o)\cdot \mathfrak t_{k, l'}(\eta_o)\ge 0$ for every $l'\in \{0, 1, \dots, p\}$ such that $(H)$ is an orbit type in $V_{k, l'}$.

Then, there exists a branch $\mathscr C$ of non-trivial solutions with symmetries at least $(H)$, which bifurcates from the critical point $(\eta_o, 0)$ of Eq (B.3).

We refer an interested reader for the proof to ^[3,4].

Remark B.11. Consider an isometric $\mathcal H$-representation $V = \mathbb{R}^N$ with a $\mathcal H$-isotypic decomposition

where the $\mathcal H$-isotypic component $\tilde V_{l}$ is modeled on an irreducible $\mathcal H$-representation $\mathscr V_{0, l}$ (we assume that $\{\mathscr V_{0, l}\}_{l = 0}^{r}$ is a complete list of real irreducible $\mathcal H$-representations with $\mathscr V_{0, 0}$ being the trivial representation). Let $G = \mathcal H\times S^1$. Consider the complexification $V^c$ of the $\mathcal H$-representation $V$ as the $G$-representation with the $S^1$-action given by $k$-folding

where '$\cdot$' stands for the complex multiplication. Let

be a $G$-isotypic decomposition, where the $G$-isotypic component $V_{l}$ is modeled on an irreducible $G$-representation $\mathscr V_{k, l}$^*. Let $\mathbb{E} = C_{per}([0, 2\pi]; V)$, then $\mathbb E$ is an isometric $G$-representation with the action given by

^*In the examples presented in this paper, $V_{l}\cong \tilde V^c_l$, $\mathscr V_{k, l}\cong \mathscr V_{0, l}^c$ and $p = r$, but it is not necessarily so in general.

Using the standard Fourier modes decomposition of the space $\mathbb{E}$, one obtains $G$-isotypic decomposition (B.8) and (B.9) in which $V_{0, l}\cong \tilde V_l$ stands for the subspace of constant $\tilde V_l$-valued functions and subspaces $V_{k, l} \cong V_{l}$ for $k\ge 1$ are defined by

Accordingly, the spatio-temporal symmetry group of a non-constant periodic function $u: \mathbb{R}\to V$ of minimal period $T > 0$ is the twisted subgroup $H\le G = \mathcal H\times S^1$ defined by

B.3.   Proof of Theorem 3.2: setting in functional spaces

Let $\mathcal O = (\alpha, \lambda_{\mathcal O}(\alpha), \omega_{\mathcal O}(\alpha), z_{\mathcal O}(\alpha))$, $\alpha\in \mathfrak A$, be the branch of regular stationary solutions (2.41) of Eq (2.44). Following Lemma 2.6, we look for non-stationary $2\pi$-periodic solutions $(\alpha, \lambda, \omega, \beta, \zeta)$ to this equation, where $\alpha\in \mathfrak A$ is related to $\lambda$ and $\zeta$ by Eq (2.45). In other words, $\lambda$ is given by the implicit function

according to (A.9). Now, we write

and set up a completely continuous vector field $\mathscr F$ (cf. Subsections B.1 and B.2) associated with the $2\pi$-periodic problem for Eq (2.44) in the Sobolev space

where $u\in \mathbb{E}$ is identified with its $2\pi$-periodic extension.

The next step reflects the specifics of the bifurcation of relative periodic solutions from a relative equilibrium. In order to extract a unique (up to time shifts) representative from the $S^1$-orbit $(\alpha, \lambda, \omega, \beta, e^{i\phi}\zeta(\cdot))$, $\phi\in \mathbb{R}$, of solutions, we impose a constraint on $\zeta$. The assumption that stationary solutions (2.41) are regular (see Definition 2.5) implies that the kernel of the linear map (matrix) $D_{z} F (\alpha, z_{\mathcal O}(\alpha))-\omega_{\mathcal O}(\alpha) J$ is the one-dimensional linear span of the vector $J z_{\mathcal O}(\alpha)$ for any $\alpha\in \mathscr{U}$. Denote by $g^\dagger(\alpha)$ the adjoint eigenvector corresponding to the simple zero eigenvalue of the adjoint (transpose) map $D_{z} F (\alpha, z_{\mathcal O}(\alpha))^T-\omega_{\mathcal O}(\alpha) J^T$:

One way to impose the constraint is to require that

To construct the vector field $\mathscr F$, set $\mathcal {E} = L^{2}([0, 2\pi]; V)$ and define the differentiation operator $L: \mathbb{E} \to \mathcal{E}$ by $Lu = \dot u$. Notice that the natural embedding $\mathfrak i: \mathbb{E} \to \mathcal{E}$ is compact and the operator $\mathfrak i+L: \mathbb{E} \to \mathcal{E}$ has a bounded inverse $(\mathfrak i+L)^{-1}: \mathcal{E} \to \mathbb{E}$, i.e., the periodic problem

has a unique solution $u = (\mathfrak i+L)^{-1} f\in \mathbb{E}$ for any $f\in \mathcal E$. Further, define the operator $N_F: \mathfrak A\times \mathbb{E}\to \mathcal E$ by

where $\lambda, \zeta, \omega$ are given by (B.29)–(B.31) and we use the natural embeddings $\mathbb{E}\subset C_{per}([0, 2\pi]; V)\subset \mathcal E$. Now, we can equivalently rewrite the $2\pi$-periodic problem for (2.44) with the additional constraint (B.31) as

and using the inverse $(\mathfrak i+L)^{-1}$ as

Using the completely continuous vector field

Eq (B.32) is equivalent to (B.3).

Let $G = \mathcal H\times S^1$, where $\mathcal H$ is the symmetry group of $z_{\mathcal O}(\alpha)$. Then, each of the spaces $\mathbb{E}$, $\mathcal{E}$ is an isometric $G$-representation with the action given by (B.26), and the $\Gamma\times S^1$-equivariance assumptions (2.37), (2.46), and (2.47) imply the $G$-equivariance of the vector field (B.33) (with $G$ acting trivially on $\mathfrak A\times \mathbb{R}_+\ni \nu$).

Remark B.12. Observe that since $F$ is $\mathcal H$-equivariant (cf. (2.46)), from $z_{\mathcal O}(\alpha)\in V^{\mathcal H}$ it follows that the linear map $D_{z} F (\alpha, z_{\mathcal O}(\alpha))-\omega_{\mathcal O}(\alpha) J: V\to V$ is $\mathcal H$-equivariant as well, which implies that its eigenvector satisfies $J z_{\mathcal O}(\alpha)\in V^{\mathcal H}$ for each $\alpha\in \mathfrak A$.

B.4.   Proof of Theorem 3.2: linearization

Let us consider the linearization of the vector field (B.33) on its zero $u = 0$. Using the $\mathcal H$-equivariant Jacobi matrix $A(\alpha) = D_zF(\alpha, z_{\mathcal O}(\alpha))$ of $F$ (cf. (3.1)), define the Nemytskii operator $N_A: \mathfrak A\times \mathbb{E}\to \mathcal E$ by

From Corollary A.4 and (B.31) of the affine functional $W_\alpha: \mathbb{E}\to \mathbb{R}$, it follows that the Fréchet derivative of the vector field (B.33) (with respect to $u$) at $u = 0$ is the $G$-equivariant compact vector field

By inspection, the subspace $\mathbb{E}^{S^1}\subset \mathbb{E}$ of constant $V$-valued functions is invariant for $\mathscr A(\eta): \mathbb{E}\to\mathbb{E}$, and the spectrum $\sigma\bigl(\mathscr A(\eta)|_{\mathbb{E}^{S^1}}\bigr)$ of the restriction $\mathscr A(\eta)|_{\mathbb{E}^{S^1}}$ to $\mathbb{E}^{S^1}$ is related to the spectrum $\sigma\bigl(\omega_{\mathcal O}(\alpha)J-A(\alpha)\bigr)$ of the map $\omega_{\mathcal O}(\alpha)J-A(\alpha): V\to V$ by

hence $\mathscr A(\eta)|_{\mathbb{E}^{S^1}}$ is an isomorphism, i.e., (B.7) holds. Moreover, zeros of $\mathscr A$ are solutions of the periodic problem

Now, let us consider a $G$-isotypic decomposition (B.25) and the associated $G$-representation (B.8) of $\mathbb{E}$ with the isotypic components (B.27), which are all invariant for $\mathscr A(\eta)$, hence the restriction (B.12) of $\mathscr A(\eta)$ to each $G$-isotypic component $V_{k, l}$ is well-defined. By inspection, the corresponding function (B.13) for the restriction $\mathscr A(\eta)|_{V_{k, l}}$ with $k\ge 1$, $l = 0, 1, \ldots, p$ is given by

where $(\omega_{\mathcal O}(\alpha)J-A(\alpha))|_{V_{l}}$ is the restriction of the $G$-equivariant complexification $\omega_{\mathcal O}(\alpha)J-A(\alpha): V^c\to V^c$ of the map $\omega_{\mathcal O}(\alpha)J-A(\alpha): V\to V$ to the $G$-isotypic component $V_{l}$ of $G$-decomposition (B.25) of the $G$-representation $V^c$. Since each subspace $V_{l}$ is invariant for the $G$-equivariant map $A(\alpha)-\omega_{\mathcal O}(\alpha)J$, the characteristic polynomial (3.3) of this map admits factorization (3.4) and (3.5). Comparing (3.5) and (B.35), one can see that

Hence, conditions (3.6) and (3.7) ensure that $(\alpha_o, \beta_o, 0)$ is a regular isolated critical point for (B.34). Moreover, for $k = 1$, the isotypic crossing number $\mathfrak t_{1, l}(\alpha_o, \beta_o)$ is well-defined for each $l = 0, 1, \ldots, p$ by Eqs (B.21)–(B.23). Due to (B.35), $\mathfrak t_{1, l}(\alpha_o, \beta_o)$ equals the number of roots $\mu_j^l(\alpha)$ of the characteristic polynomial $\mathcal P_l(\alpha, \cdot)$, which cross the imaginary axis through the point $i\beta_o$ from the left to the right half-plane of the complex plane $\mathbb{C}$, minus the number of roots crossing the imaginary axis from right to left through the same point, as the parameter $\alpha$ increases from $\alpha_o-\delta$ to $\alpha_o+\delta$ (for any sufficiently small $\delta$), i.e.,

Hence Theorem 3.2 follows from Theorem B.10.

B.5.   Outline of the proof of Propositions 4.2 and 4.3

Theorem 3.2 can be used to analyze symmetries of branches of relative periodic solutions bifurcating from the branch $\mathcal O$ of relative equilibria (4.5), which have symmetry group $\mathcal H = S_5\times \{1\}$. In order to compute the linearization (A.14) on the relative equilibrium, it is convenient to use the Cartesian coordinates $\mathbf z = (z_0, z_1, \ldots, z_n)^T$ with $z_0 = (X, Y, \dot X, \dot Y)$, $z_k = (u_k, w_k, x_k, y_k, \dot x_k, \dot y_k)$, $k = 1, \ldots, n = 5$, where

Denote

Then, the phase space of system (4.4) is $V\times \mathfrak V$. In the Cartesian coordinates, matrix (A.14) has the form

where the matrces $C_0:\mathcal V\to \mathcal V_0$, $C:\mathcal V_0\to \mathcal V$ and $D: \mathcal V\to \mathcal V$ are given by

According to Eq (A.11), when calculating the matrix $B_0$, one should replace the hysteresis term $P[t_0, v_0]R$ in the second equation of system (4.4) with the term $\varkappa R$, where $\varkappa$ is defined by (A.12).

We proceed with the $\mathcal H$-isotypic decomposition of the space $V^c$ for $\mathcal H = S_5\times \{1\}$. Let $\mathscr V_0^c = \mathbb C^4$ and $\mathscr V^c = \mathbb C^6$ be the complexifications of the subspaces $\mathscr V_0$ and $\mathscr V$, respectively, defined by (B.36). Then, $V^c = \mathscr V_0^c\times (\mathscr V^c)^5 = \mathbb C^{34}$. First, we consider the subgroup $\mathbb Z_5\simeq\mathbb Z_5\times\{1\}$ of $\mathcal H$ and describe the $\mathbb Z_5$-isotypic decomposition of $V^c$. Namely, $V^c = V_0\oplus V_1\oplus V_2$, where $V_0 = \{(z_0, z, z, z, z, z)^T:\, z_0\in\mathbb C^4, \, z\in\mathbb C^6\}$, and $V_j = V_j^+\oplus V^-_j$ with

where $\xi$ acts on vectors $z_0 = (z^1_0, z^2_0, z^3_0, z^4_0)^T \in \mathscr V^c_0$, $z = (z^1, z^2, z^3, z^4, z^5, z^6)^T \in \mathscr V^c$ by

One can see that the matrix $A(\alpha): V^c\to V^c$ given by (B.37) preserves the $\mathbb Z_5$-isotypic components. Indeed, by inspection,

where the identity $1+\xi+\xi^2+\xi^3+\xi^4 = 0$ is used to obtain the second equation. Using this $\mathbb Z_5$-isotypic decomposition, one obtains the $S_5$-isotypic decomposition $V^c = V_0\oplus V_1$, where

Furthermore, the restriction of the linearization to each of the two isotypic components $V_0$ and $V_1$ is defined by relations (B.38) and (B.39). Hence, for the $\mathcal H$-representation $V^c$, there are the following list of maximal twisted types in the isotypic components:

(i) for $V_{0}$: $({S_5})$;

(ii) for $V_{1}$: $({D_6})$, $({S_4})$, $({D^{\mathbf d}_6})$, $({D_4^{\mathbf d}})$, $({\mathbb Z_4^{\mathbf {t_1}}})$, $({\mathbb Z_5^{\mathbf{t_1}}})$, $({\mathbb Z_6^{\mathbf{t_2}}})$.

Put $G: = S_5 \times \{1\}\times S^1 = \mathcal H\times S^1$. The natural $S^1$-action induced by the complex multiplication converts the complex $\mathcal H$-isotypic decomposition $V^c = V_0\oplus V_1$ into the (real) $G$-isotypic decomposition $V^c = V_{0}\oplus V_{1}$ with the maximal twisted orbit types listed in Proposition 4.2. Moreover, if $(H)$ is a maximal twisted orbit type in a $G$-isotypic component $V_{j}$, then $(H)$ is a maximal twisted orbit type in $V^c$ itself.

Decomposition (3.4) has the form $\varphi(\alpha, \cdot) = \varphi_{0}(\alpha, \cdot) \varphi_{1}(\alpha, \cdot)$, where $\varphi_{0}(\alpha, \cdot)$ is the characteristic polynomial (of degree 10) of the matrix

(cf. (B.37)), where $0$ denotes zero matrices,

and, $\varphi_{1}(\alpha, \cdot) = \tilde\varphi^4(\alpha, \cdot)$, where $\tilde\varphi(\alpha, \cdot)$ is the characteristic polynomial (of degree 6) of the matrix $B-D-\omega_{\mathcal O}(\alpha) J_6$. Tables 1 and 2 provide an evidence that conditions (ii) and (iii) of Theorem 3.2 are satisfied for the roots of $\varphi_{j}$ at each bifurcation point listed in Propositions 4.2 and 4.3, hence this proposition follows from Theorem A.6.