Reconstruction of shear force in Atomic Force Microscopy from measured displacement of the cone-shaped cantilever tip

1.   Introduction

In this paper, we study the following inverse boundary value problem of reconstructing the unknown transverse shear force $g(t)$ in

from the measured displacement

Here and below, $\Omega_T: = (0, \ell)\times(0, T)$, with the final time instant $T > 0$, $\rho_A(x): = \rho(x)A_s(x)$, where $\rho(x) > 0$ and $A_s(x) > 0$ are the mass density and the cross-sectional area of the nonhomogeneous cantilever, $r(x): = E(x)I(x) > 0$ is the flexural rigidity (or bending stiffness) of the cantilever while $E(x) > 0$ is the elasticity modulus and $I(x) > 0$ is the moment of inertia. The coefficient $\kappa(x): = c_d(x)I(x)$ represents energy dissipated by friction internal to the beam, while $c_d > 0$ is the strain-rate damping coefficient ^[3]. The external and internal damping mechanisms are given by the terms $\mu(x)u_t$ and $(\kappa(x)u_{xxt})_{xx}$, respectively. The coefficients $\mu(x)\ge 0$ and $\kappa(x) > 0$ are called the viscous (internal) damping and the strain-rate or Kelvin-Voigt damping coefficients, respectively.

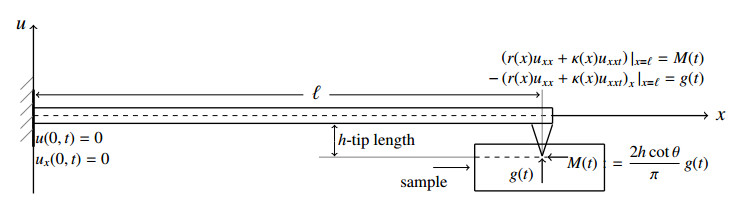
Problem (1.1) is a mathematical model of the tip-sample interaction of an Atomic Force Microscopy (AFM) cone-shaped cantilever, within the scope of damped Euler-Bernoulli equation. The processing of the sample using an AFM cone-shaped cantilever is schematically depicted in Figure 1. This cantilever, with length $\ell > 0$ is clamped at the left end $x = 0$. The tip-sample interaction is modeled by a vertical reaction force, which is the transverse shear force with the negative sign, that is $-g(t)$, at the right end $x = \ell$, and the moment $M(t): = -2h\cot \theta\, g(t)/\pi$, generated by this force, where $h, \, \theta > 0$ are the tip length and half-conic angle, respectively. As a consequence, reconstructing the shear force $g(t)$ in the inverse problem (1.1)-(1.2) actually means determining the moment $M(t)$ as well, given the above relationship between shear force and moment.

It is well known that micro-cantilever plays a key role in nanomachining process using an AFM which was originally developed to provide surface topography information ^[4]. Nowadays, AFM can provide high resolution images in different settings including ambient, aqueous and vacuum environments (see ^[4,17,18,21] and references therein). In standard AFMs, the micro-cantilever is mounted horizontally and the devices are operated in a contact or intermittent-contact mode. The cantilever tip-sample interaction creates a transverse shear force on the tip of the cantilever ^[13]. Estimation of the unknown shear force signal allows better interpretation and understanding of scan results. Since this force can only be measured indirectly, via a laser based sensor system, starting from 2000 ^[1], various models and inversion algorithms were developed for reconstruction of the transverse shear force in atomic and dynamic force microscopy, using the measured displacement of the cantilever tip as an available data ^[2,5,22]. The basis of all of these models is the Euler-Bernoulli beam theory, and the majority of these models are unsuitable for non-homogeneous cantilevers since they require the constant coefficients Euler-Bernoulli equation $EI\left (Y_{xx} +\alpha\, Y_{t}\right)_{xx}+\rho A\, y_{tt}+\mu\, y_{t} = 0$ to ensure that the analytical methods used are suitable. Later, these models, along with the mathematical framework and algorithms for numerical solutions to corresponding reconstruction problems, were developed in ^[8,10,11,15], for the variable coefficient Euler-Bernoulli equation $\rho_A(x) u_{tt}+\mu(x)u_{t}+ (r(x)u_{xx}+\kappa(x)u_{xxt})_{xx} = 0$.

In all of the tip-sample interaction models developed in the above cited studies, the tip geometry of the cantilever end was not taken into account; that is, it was assumed that the cantilever is a straight beam. However, the mechanical properties of silicon-based probes are governed mainly by the geometrical specifications of cantilevers. Furthermore, the mechanical features of the cantilever, such as the spring constant and resonance frequency, as well as the tip geometry, can all be changed depending on the application and sample characteristics to get the best sensing ^[21]. Traditionally, mechanical properties of silicon-based probes are mostly governed by geometrical specifications of cantilevers. In fact, the elastic modulus has a small tuning range, and tip shapes are often restricted to cones or pyramids with set aspect ratios because there are only a few options for etching materials ^[17,18]. On the other hand, geometric parameters of the cone-shaped tip impact the dynamics of AFM cantilevers. Namely, theoretical and experimental results presented in ^[19] show that these parameters have a significant influence on the behavior of the cantilever. The results obtained in ^[19] demonstrate also that the first four frequencies decrease as the slope factor increase.

The reasons listed above reveal the necessity of taking geometric parameters into account in the mathematical model for studying the dynamics of the AFM cone-shaped cantilever. In this case, the cantilever tip-sample interaction creates not only a transverse shear force but also a bending moment on the tip of the cantilever. The mathematical model introduced mentioned in (1.1) results from this. In this context, we note that a simple mathematical model for the shear force reconstruction problem for the AFM cone-shaped cantilever tip-sample interaction, which takes into consideration the geometry of the tip, has first been proposed in ^[5]. Namely, this model considers the cutting system as the inverse problem of reconstructing the cutting force $F_y(t)$ in

from the available measured displacement

Here, $F_x = \left (2 h \cot \theta \, F_y \right)/\pi$ for a cone-shaped cantilever with the half-conic angle $\theta$, and $h > 0$ is the cantilever tip length. In accordance with the accepted terminology of the theory of inverse problems, (1.3)-(1.4) is an inverse problem defined by two Neumann inputs. It is important to emphasize that in the AFM cone-shaped cantilever tip-sample interaction model (1.3) is based on the simplified and constant coefficient Euler-Bernoulli beam equation, without the viscous external ($\mu(x) u_t$) and the internal or Kelvin-Voigt ($\left (\kappa (x) u_{xxt}\right)_{xx}$) damping terms. Thus, in these models, not all physical properties of the cantilever are taken into account. However, the influence of these above mentioned properties on the dynamic behavior of the AFM cantilever is enormous, and needs to be studied carefully ^[3,19].

Thus, model (1.1) is a comprehensive mathematical model of AFM cone-shaped cantilever tip-sample interaction that involves variable physical quantities, damping parameters, and, most importantly, geometric parameters of the cantilever tip. Furthermore, in the studies cited above, there is an inverse problem defined with a single Neumann input, while (1.1)-(1.2) is an inverse problem with two Neumann inputs. Similar to ^[10,15], in this study also the weak solution theory for the direct problem (1.1), and the least square approach combined with the adjoint method for the inverse problem (1.1)-(1.2) is used. However, different from ^[10,15], in this study both a priori estimates and the gradient formula involves geometric parameters. All of this enables the simulation of the dynamic behavior of the tip-sample interaction of an AFM cone-shaped cantilever and, as we shall see below, the development of numerical algorithms that allow us to investigate of the effects of geometric parameters on this behavior.

In this paper we propose a new mathematical model of the tip-sample interaction of an AFM cone-shaped cantilever. In the following meanings, this model is a generalization of known mathematical models:

(a) The model involves all physical and geometric parameters, namely the area $A$ and the moment of inertia $I$ of the beam's cross section, the length $\ell$, the material's Young modulus $E$ and mass density $\rho$. It includes also the both damping terms $\mu$ and $c_d$, respectively the viscous and strain-rate damping coefficients, as explained when (1.1) was presented.

(b) The model is based on the variable coefficient Euler-Bernoulli equation.

(c) The time interval $[0, T]$ required to generate measured output can be arbitrarity small. Because of this, obtaining measurement data $\{\nu(t) : t\in [0, T]\}$, that is, the displacement at the free tip of the beam during the interval of time $[0, T]$, introduced in (1.2) is made easier, and the function $g(t)$ can be found even with data collected over a relatively short period of time.

(d) The model allows us to derive a gradient formula that contains the geometric parameters of the cone-shaped cantilever tip explicitly.

(e) The measured output, which is generated synthetically by an algorithm, contains random noise.

(f) The inputs in the model may not be smooth enough as the basic conditions (1.2) below show.

Within the proposed model, we formulate the inverse problem of reconstructing the unknown shear force from measured displacement of the cone-shaped cantilever tip. We provide a detailed mathematical and numerical analysis of the problem. Based on this analysis, we derive an explicit gradient formula for the least square functional. This allows us to construct an effective and fast reconstruction algorithm, as the presented results of computational experiments show.

The paper is organized as follows. In Section 2 the reconstruction problem (1.1)-(1.2) is formulated as the inverse problem, introducing first the Neumann-to-Dirichlet operator and then the least square functional. Necessary estimates for the weak solution of problem (1.1) are derived in Section 3. Section 4 describes compactness and Lipschitz continuity of the Neumann-to-Dirichlet operator which leads to existence of a quasi-solution of the inverse problem. Fréchet differentiability of the least square functional is proved in Section 5. Based on this result, the gradient formula is derived. Numerical algorithm and its implementations to the direct and inverse problems are presented in Section 6, with the results of computational experiments. Some concluding remarks are given in the final Section 7.

2.   The reconstruction problem (1.1)-(1.2)

Consider the inverse boundary value problem of reconstructing the unknown transverse shear force $g(t)$ and the moment $M(t)$ in (1.1) from knowledge of the measured displacement $\nu(t)$ introduced in (1.2).

We assume that the following basic conditions are satisfied:

Introduce the set of admissible shear forces

where $C_g > 0$ is a constant independent on $g(t)$. Denote by $u(x, t; g)$ the solution of the forward problem (1.1) for a given $g \in \mathcal{G}$, while $u(\ell, t; g)$ in defined as an output. Introduce the Neumann-to-Dirichlet operator:

defined on the set of admissible shear forces. In view of this operator, we can reformulate the inverse problem as the linear operator equation:

Since the measured output $\nu(t)$ obtained as a result of measurement, it contains random noise. Hence the exact equality between the output $u(\ell, t; g)$ and the measured outputs $\nu(t)$ can never be achieved. As a consequence, there can never be an exact solution to the inverse problem (1.1)-(1.2).

We introduce the least square functional

and look for the quasi-solution of the inverse problem (1.1)-(1.2): Find $g \in \mathcal{G}$ such that

3.   Necessary estimates for the weak solution of problem (1.1)

In the case when $M(t) = 0$, the existence and uniqueness of the weak solution $u\in L^2(0, T; \mathcal{V}^2(0, \ell))$, with $u_t\in L^2(0, T; L^2(0, \ell))$ and $u_{tt}\in L^2(0, T; H^{-2}(0, \ell))$ of the initial boundary value problem (1.1) is proved in ^[15], where

For the direct problem (1.1) the same results can be proved in the same way. We derive here some a priori estimates for the weak solution which are necessary in the analysis of the inverse problem (1.1)-(1.2).

Note that in none of the previous studies, including articles ^[10,15], a priori estimates were made on constants containing geometric parameters. However, such estimates are needed to see the role of these parameters in the behavior of the solution and in the continuity of the least square functional.

Theorem 1. Assume that the inputs in (1.1) satisfy the basic conditions (2.1). Then the following estimates holds:

where

and $r_0, \rho_0, \kappa_0 > 0$ are the constants introduced in (2.1)

Proof. Multiply both sides of Eq (1.1) by $2 u_t(x, t)$, integrate it over $\Omega_t: = (0, \ell)\times (0, t)$, $t\in (0, T]$, and employ the identities

Applying the integration by parts formula multiple times, using the initial and boundary conditions in (1.1) we obtain the following energy identity:

for all $t \in (0, T]$. Now, applying the integration by parts to the right hand side integrals, taking into account the condition $M(0) = 0$ and then the $\varepsilon$-inequality $2 \vert a\, b\vert \le \varepsilon\, a^2+b^2/\varepsilon$, we get:

Use also the auxiliary inequalities ([12, Chapter 11, formula (11.1.30)]):

for all $t \in [0, T]$. Taking these inequalities with the identity

into account in the energy identity above, we get the following inequality:

where $\widehat{\ell}, \, C_{\theta} > 0$ are the constants introduced in (3.2). Choosing here the arbitrary parameter $\varepsilon > 0$ from the condition $r_0-\widehat{\ell}\, \varepsilon > 0$ as $\varepsilon = r_0/(2\widehat{\ell})$ we finally obtain the main integral inequality:

where $C_0 > 0$ is the constant introduced in (3.2).

The first consequence of (3.4) is the inequality

With the Grönwall-Bellmann inequality ([12, Appendix B, Lemma B.0.1]) this implies:

Both of the first two estimates in (3.1) are easily derived from this inequality.

The second consequence of (3.4) is the inequality

With (3.5) this leads to the third estimate in (3.1).

The fourth estimate in (3.1) is proved in the same way. □

Remark 1. The results of Theorem 1 are valid, with slightly different from the constants introduced in (3.2), also for the case where the consistency condition $g(0) = 0$ in (2.1) is not met.

Corollary 1. Assume that conditions of Theorem 1 hold. Then for the $H^1$-norm of the output $u(\ell, t; g)$ the following trace estimate holds:

Proof. Proof follows from the trace inequalities

which are the consequence of the first inequality in (3.3) and estimates in (3.1). □

4.   Analysis of the inverse problem

The compactness property is one of the main properties of the input-output operators corresponding to problems, since the ill-posedness of an inverse problem is the result of this property. For the simplified version, with one Neumann input ($M(t) = 0$) and with $\kappa(t) = 0$, the compactness of the Neumann-to-Dirichlet operator (2.3) is proven in ^[10] for the regular weak solution. For the model (1.1) we are considering, the regularity condition is not necessary, as we shall see below. That is, this property is also preserved in the case of the weak solution, which shows the role of the Kelvin–Voigt damping coefficient $\kappa(x) > 0$.

Lemma 1. Under the basic conditions (2.1), the Neumann-to-Dirichlet operator $\Psi :\mathcal{G} \subset H^1(0, T)\mapsto L^2(0, T)$ introduced in (2.3) is a linear compact operator.

Proof. Let $\{g_m\} \subset \mathcal{G}$, $m = 1, 2, \, ...\,$, be a sequence of inputs, bounded in the norm of $H^1(0, T)$, according to the definition (2.2) of set of admissible shear forces. Denote by $\{u^{(m)}(x, t)\}$, where $u^{(m)}(x, t): = u(x, t; g_m)$, the corresponding sequence of weak solutions of the direct problem (1.1). By the estimate (3.6), the sequence of outputs $\{u^{(m)}(x, t)\}$ is bounded in $H^1(0, T)$. Then by the Rellich-Kondrachov compactness theorem (see for instance ^[6]), $\psi$ is compact operator. □

Lemma 2. Assume that the basic conditions (2.1) hold. Then the Neumann-to-Dirichlet operator is Lipschitz continuous, that is

with here $L_0 = \sqrt{\ell^3/3}\, C_1 > 0$ is the Lipschitz constant and $C_1 > 0$ is the constant introduced in (3.2).

Proof. Let $u_k(x, t): = u(x, t; g_k)$, $k = 1, 2$, be two weak solutions of the direct problem (1.1) corresponding to the inputs $g_1, \, g_2 \in \mathcal{G}$. Then the function $\delta u(x, t) = u_1(x, t)-u_2(x, t)$ solves the problem

subject to the inputs $\delta M(t) = C^2_{\theta} \, \delta g(t)$ and $\delta g(t) = g_1(t)- g_2(t)$. By the definition (2.3) of the input-output operator we have:

In view of the first inequality in (3.3) and the second estimate in (3.1) applied to the weak solution $\delta u(x, t)$ of problem (4.2) we deduce that

This leads to (4.1). □

The Lipschitz continuity of the Neumann-to-Dirichlet operator leads to the Lipschitz continuity of the least square functional introduced in (2.5), and this, in turn, leads to the existence of the quasi-solution of the inverse problem (1.1)-(1.2), by Theorem 6.5.2 ^[12].

Theorem 2. Assume that the inputs in (1.1) satisfy the basic conditions (2.1). Suppose that the measured output $\nu(t)$ belongs to $L^2(0, T)$. Then there exists a quasi-solution of the inverse problem (1.1)-(1.2) in the set of admissible shear forces $\mathcal{G}$.

5.   Fréchet differentiability of the least square functional and gradient formula

For $g, g+\delta g \in \mathcal{G}$ we find the increment $\delta J(g): = J(g+\delta g)-J(g)$ of the least square functional introduced in (2.5) is

where $\delta u(x, t)$ is the solution of the sensitivity problem (4.2).

Multiplying both sides of Eq (4.2) by arbitrary function $\phi(x, t)$, integrating it over $(0, T)$ and applying the integration by parts formula multiple times, we obtain:

We require now $\phi(x, t)$ solves the well-posed backward problem

The control function $p(t)$ here is the arbitrary Neumann input and is specified below.

In view of the initial, final and boundary conditions in (1.1) and (4.2) we deduce from (5.3) the following integral relationship:

where $C_{\theta} > 0$ is the constant introduced in (3.2).

Taking into account the increment formula (5.1) we choose the control function $p(t)$ as follows:

The backward problem with this input, i.e., the problem

is called the adjoint problem corresponding to the inverse problem (1.1)-(1.2).

Substituting (5.5) into (5.4) we obtain the input-output relationship:

which contains the output $u(\ell, t; g)$ and the measured output $\nu(t)$. Comparing (5.1) and (5.7) we deduce that

Theorem 3. Assume that the inputs in (1.1) satisfy the basic conditions (2.1). Suppose, in addition, the measured output $\nu(t)$ belongs to $H^1(0, T)$. Then the least square functional introduced in (2.5) is Fréchet differentiable. Furthermore, for the Fréchet gradient of this functional the following gradient formula holds:

Proof. Applying the first inequality in (3.3) with the second estimate in (3.1) to the weak solution $\delta u(x, t)$ of problem (4.2) we conclude that the second right hand side integral in (5.8) of the order $\mathcal{O}(\Vert g' \Vert_{L^2(0, T)})$. This means that the least square functional is Fréchet differentiable. □

The constant $C_{\theta} = \left (2h\cot \theta\right)/\pi$ in formula (5.9) shows that the tip length $h > 0$ and half-conic angle $\theta > 0$, which are the fundamental geometric properties of the cone-shaped cantilever, are now involved in the gradient formula, in contrast to all previous gradient formulas. Furthermore, this formula (5.9) expressed in terms of the weak solution $\phi(x, t)$ of the adjoint problem (5.6) forms the basis of the algorithm for numerical solving the inverse problem (1.1)-(1.2).

6.   Numerical algorithms and computational experiments

In this section, a detailed description of an efficient numerical method is presented to solve the inverse problem (1.1)-(1.2). This process has several steps and each of them should be considered carefully due to the sensitivity of the identification process. First, measured data $\nu(x): = u(\ell, t)$ is generated by solving the direct problem. It is critical to keep the error as low as possible in this step. This requires a successful algorithm for the solution of the direct problem (1.1). Due to the effectiveness of the method of lines approach used in our several published previous studies ^[8,9,10,11] on an optimized mesh, an improved version of this method is employed here.

6.1.   The Method of Lines (MOL) approach for the numerical solution of direct problem

Basically, the MOL is based on the principle of independent discretization of space and time variables. More specifically, a semi-analytical structure is obtained by expressing the variational formulation in finite dimensional space denoted by $V_h$. The method here is a finite element approximation with cubic Hermite basis functions which ensures continuity of both deflection and slope throughout the beam. These shape functions is defined on uniformly discretizing spatial domain $0 = x_0 < x_1 < \cdots < x_{M} = \ell$ (where $h = \ell/M$). Formally, the solution $U_h(t): = u_h(\cdot, t)\approx u(\cdot, t)$ satisfies the following semi-discrete version of the variational formulation of (1.1).

For all $t\in(0, T]$, find $U_h(t)\in V_h \subset \mathcal{V}^2(0, \ell)$ such that $\forall v_h\in V_h$

Here the symmetric bilinear functional $a_\psi:H^2(0, \ell)\times H^2(0, \ell)\rightarrow \mathbb{R}$ is defined, for $\psi\in L^2(0, \ell)$, by

The next discretization step is performed for temporal derivatives. At this level the second order system of ODE in (6.1) can be approximately solved by using any temporal finite difference method. It is crucial that the approach to be used here have to be practical, fast and stable. These requirements can be met through the following second order backward finite difference approximations of $U_h''$ and $U_h'$ with uniform temporal discretization $0 = t_0 < t_1 < \cdots < t_{N} = T$ (where $\tau = T/N$).

The full-discrete algebraic systems of equations are obtained by substituting these difference expressions with $U''_h(t)$ and $U'_h(t)$ in (6.1). Solutions of the resulted equations are provided desired approximations $U_h^j\approx u(x, t_j)$ for $j = 0:N$. Note that for $j = 1, 2$, the necessary a priori approximations can be obtained by combining the ghost point technique within the central difference scheme.

Finally, several numerical tests in ^[14] are compared to determine the effective values of the pair $(M, N)$ and optimized with the ratio $h/\tau\simeq 142$.

6.2.   Reconstruction with Conjugate Gradient Algorithm (CGA)

The explicit gradient formula in (5.9) is very important in determining the minimizer of the least square functional (2.3) for any unconstrained optimization techniques. Here we use CGA, one of the most suitable and stable one. It is known that this method is based on the conjugate directions and these directions are determined by the solution of the adjoint problem (5.6). This requires the MOL technique at each iteration step. Although CGA is a self-stabilized method, the quality of the reconstruction process also depends on the success of solving both adjoint and direct problem. The details of the CGA is as follows.

● From $g^{(i)}(t)$, calculate the decent direction

● Define the next iteration $g^{(i+1)}(t) = g^{(i)}(t)+\alpha_*^{(i)} p^{(i)}(t)$. Here $\alpha_i^*$ solution of the minimization problem

and has the following explicit form,

● If the following stopping condition based on Mozorov's discrepancy principle holds,

for known parameter $\varepsilon > 0$, stop the iteration; otherwise, repeat the process by taking $g^{(i)}(t): = g^{(i+1)}(t)$.

For the first iteration, an arbitrary choice of $g^{(0)}(t)$ can be made, but if there is no prior knowledge it is better to choose $g^{(0)}(t) = 0$ and $p^{(i)}(t): = -\nabla J(g^{(0)})(t)$. As a note, the first iteration has no significant effect to the success of the algorithm.

Here a standard method is used for the derivation of synthetic noise with a given noise level $\gamma > 0$. In deed, the formula $\nu^{\gamma}(t_j): = \nu(t_j)+ \gamma \, \Vert \nu\Vert_{L^2(0, T)}\, R_j$ for $j = 1, \cdots, N$ generates measured noisy data. The vector $R$ has $M$ random numbers array normally distributed with mean $0$ and standard deviation $\sigma = 1$.

In CGA steps, both Fréchet derivative $\nabla J(g)$ and $L^2(0, T)$ norms are computed by Simpson's numerical integration while in MOL algorithm, a three-point Gauss quadrature rule is employed for all computation on each element.

6.3.   Computational experiments

In the reconstruction process, we work on two different test problems. One of them is based on engineering applications (realistic parameters), while the other one is preferred to test the applicability of the method.

It is a general approach to use error analysis when comparing the quality of the methods. In the literature, two quantities are frequently used. These are Convergence and Accuracy Errors as follows.

and

As can be seen from their definitions, the Accuracy Error determines the success of the reconstruction. On the other hand, especially in the case of noisy data, the stop criterion is very crucial to prevent divergence of the approximation and it is completely related to Convergence Error. Therefore, these quantities should be evaluated together to analyze the process.

For the first test problem, the parameters are selected in accordance with real engineering applications and are based on those proposed in ^[7,16,20]. We take a beam of length of $200\, \mbox{nm}$ and observe it for a time interval of $10^{-3}\, \mbox{s}$. After a simple change of variables, to re-scale the problem so that the length of the beam and the time observation length interval become $\ell = 1$ and $T = 1$ respectively, the numerical values adopted for this study become as follows:

and domain parameters are $\ell = 1$ and $T = 1$, both non-dimensional. As for the tip length, it usually ranges from $5 \ \mbox{nm}$ to $50 \ \mbox{nm}$ ^[13]. After the re-scaling for doing our numerical simulations, we take as a reasonable value $h = 0.2$ (non-dimensional).

We tested the performance of the algorithm for the unknown shear force $g(t) = t\ \sin(7\pi t/2)$ with $\theta_\pi = \left (\cot(\pi/36)\right)/(5\pi)$. The graph on the left in Figure 2 shows noisy free as well as random noisy output data with the noise levels $\gamma = 3\%$ and $6 \%$. Then unknown target $g(t)$ is identified by using each of these data. Results can be seen on the right in Figure 2.

Figure 3 reveals the general characteristics of an iteration. Especially the rapid deterioration in the Accuracy Error indicates that the sensitivity of the stopping which is directly determined by the Convergence Error. In case this balance is not determined appropriately, the success of the construction process can be adversely affected.

The second computational experiment aims to test the accuracy of CGA regardless of the realizability of the parameters. For this goal, reconstruction of the following discontinues target source $g(t)$ is studied under high noise levels.

and

Here $H(x)$ is the Heaviside step function. Moreover, all problem parameters are imposed as non-constant case as follows with unit domain parameters $\ell = 1$ and $T = 1$.

Synthetic noise free and noisy data are plotted in Figure 4 (left) with noise levels $\gamma = 5\%$ and $10 \%$. Then CGA is applied for identification of the temporal function $g(t)$ and results are illustrated in Figure 4 (right). Here, due to the effect of high noise levels and discontinuity on $g(t)$, non-physical distortions are naturally observed in the reconstruction.

Convergence and Accuracy Errors are plotted in Figure 5 on the left and on the right, respectively. Similar behavior of these error quantities examined in the first problem is also observed in this second experiment.

The results of the two experiments presented here show that CGA is effective and successful for the solution of the inverse problem under consideration, provided that certain sensitivities are taken into account. Nevertheless, the algorithm may need to be improved for further applications. Especially in realistic cases, it is required to choose a small final time such as $T = 10^{-3}$ for stable calculations using the Finite Element Method. Since the method suggested here is just a preliminary numerical study of the inverse problem related to Atomic Force Microscopy, we only aimed to present the general principles.

7.   Conclusions

In this study, a novel mathematical model of tip-sample processing with AFM cone-shaped cantilever is proposed. Compared to the models known in the literature, this model is a fairly advanced model, and takes into account not only both viscous and internal damping parameters, but also the geometric parameters of the cone-shaped tip. A detailed mathematical analysis of the model has been carried out. A new gradient formula for the Fréchet derivative of the least square functional that specifically takes the geometric parameters into account is derived. This allows us to construct the fast Conjugate Gradient Algorithm for the numerical reconstruction of the shear force. Numerical experiments carried out with real physical and geometric parameters show the high accuracy of the algorithm.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The research of the first and second authors have been supported by FAPESP, through the Visiting Researcher Program, proc. 2021/08936-1, in Escola Politécnica, University of São Paulo, Brazil, during the period November 02 - December 18, 2022. We thank the referees for their careful reading of the manuscript and their insightful comments, which helped to improve the revised manuscript significantly.

Conflict of interest

All authors declare no conflicts of interest in this paper.